1 Introduction
Understanding pollutant transfer in the subsurface systems is of great interest and essential to the protection of groundwater resources, which account for more than 90% of the domestic water supply in North Algeria (Kadri et al., 2011), from contamination by particle-bound contaminants. Particle transport takes place in different types of soil environments: saturated and unsaturated zones, underground aquifers, fissured rocks (Corapcioglu and Jiang, 1993; Masséi et al., 2003; Pang et al., 1998). Solid particles can be detached from the soil matrix under the influence of physicochemical parameters (salinity, organic agents, pH) or mechanical ones (hydrodynamic forces) (Kanti Sen and Khilar, 2006), and can travel far in the subsurface system. Owing to their very important specific surface, fine particles are excellent agents for pollutant adsorption, which are transported over large distances (Kretzschmar et al., 1999; McCarthy and Zachara, 1989; McDowell-Boyer et al., 1986; Ryan and Elimelech, 1996). Many studies are devoted to dissolved elements and colloids transport, while suspended particles are less considered (Ahfir et al., 2007; Benamar et al., 2007; Masséi et al., 2002; Wang et al., 2000).
Several processes (straining, wedging, deposit), other than physicochemical filtration long-time investigated, can affect the transport behaviour of fine particles in saturated porous media. Particle straining represents the main immobilization process that occurs in the groundwater system when a pore space is too small to allow the passage of particles (Bradford and Bettahar, 2006). During the flow of suspended particles through a porous medium, particle transport and retention derived from several forces and mechanisms depending on particle size, pore distribution, and flow rate (Ahfir et al., 2007; Benamar et al., 2005; Silliman, 1995). The particle retention may reduce the permeability of the porous medium, as observed during the artificial recharge of aquifers or the exploitation of oil wells (Moghadasi et al., 2004). Recent researches indicate that the rate of particle straining within saturated porous media is sensitive to the ratio of particle diameter (dp) to sand grain diameter (dg), the shape of surface roughness of the solid matrix, particle size non-uniformity, pore-scale hydrodynamics, and pore water chemistry (Bradford et al., 2007; Keller and Ausset, 2007; Porubcan and Xu, 2011; Xu and Saiers, 2009; Xu et al., 2006). Most studies on particle straining have mainly relied on experiments conducted with uniform sand packs. Natural soil and alluvium, however, are usually characterized with physical heterogeneity, which originates from the mixing of sand grains of various sizes.
The Sebaou River in northern Algeria supplies an alluvial groundwater submitted to a hydrological and environmental stress. Excessive pumping causes a dramatic lowering of the groundwater level, and the extraction of aggregates significantly reduces the thickness of the filtering layer. Both processes make the groundwater vulnerable towards the surface pollution. This study is devoted to the influence of the grain size variability of the alluvial layers on the transport and the deposition kinetics during particle transfer.
2 Materials and methods
2.1 Column transport experiments
Transport experiments were performed in a horizontal column under constant flow conditions using the step-input injection method. In this investigation, a Plexiglas column with an inner diameter of 6.4 cm and a length of 33 cm is used. The column was equipped with four equally spaced (9 cm) piezometers, allowing one to measure pressure variations during the suspended particles’ injection in the porous medium. The column was packed in 5 cm increments by pouring the sand into the column, mixed with deionised water (saturated conditions) to avoid trapping air bubbles. Using a Master-Flex peristaltic pump (Cole-Parmer Instruments), the column is fed by two reservoirs (Fig. 1); the first one contains deionised water (pH of 6.8 ± 0.1) and the other one contains suspended particles subjected to a permanent agitation with the help of a motorised stirrer. When the steady-state flow conditions are reached with deionised water, the valve is switched to the second reservoir and the flow of suspended particles is directed toward the column. So, a perfect step-input injection was assumed to be achieved, even if Taylor dispersion occurs at the boundary of the system (Mainhagu et al., 2012). However, the distance between the reservoir and the cell was kept as short as possible in order to minimize the Taylor dispersion effect.
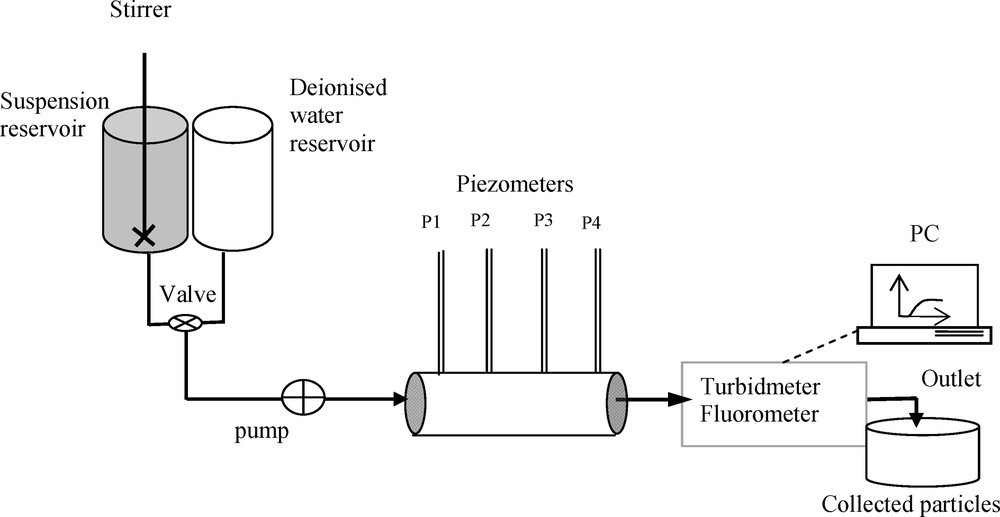
Experimental set-up.
The detection system consists of a Kobold Instrument turbidimeter (calibrated with respect to the suspended particles concentrations) and a Turner Designs 10-AU fluorometer (calibrated with respect to the fluorescein concentrations).
The used material as porous medium is alluvial sand (collected from Sebaou River, Algeria), whose grains present a smooth angular and elongated shape. Two size distributions were selected from this material (Fig. 2): fine medium, and coarse medium. A third medium (noted mixture) was obtained by mixing the fine and the coarse media (50% mass from each). The shape of the grain size distributions of the used media are linked to the uniformity coefficient Cu, whose values are reported in Table 1. Coarse and fine media provide a narrowly graded curve, while the mixture presents a broadly graded size distribution.
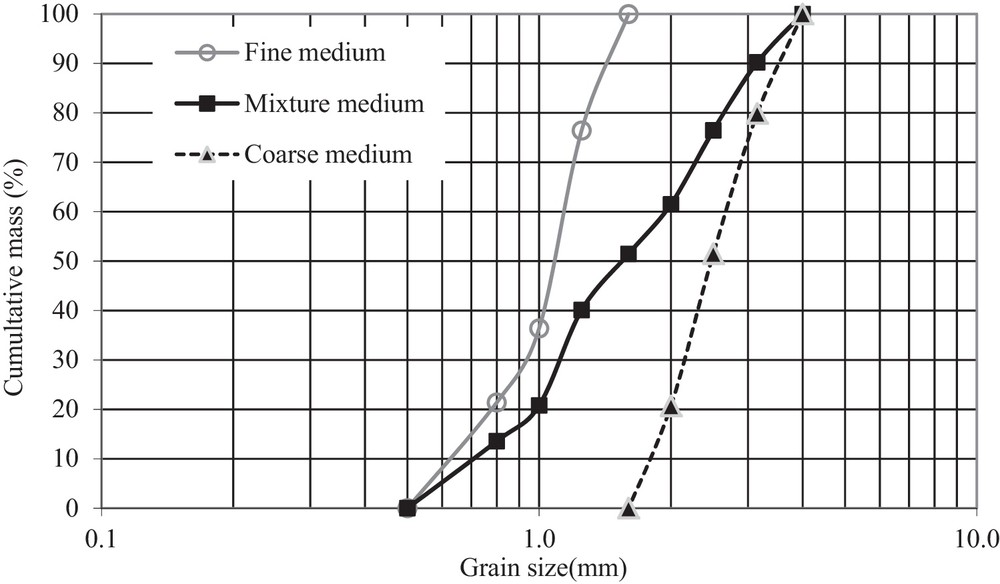
Particle size distribution of the three porous media.
Physical parameters of the used porous media.
| Medium | dg50 (mm) | Porosity (%) | C u | Permeability (m/s) |
| Fine medium (0.5–1.6 mm) | 1.1 | 35.6 | 1.9 | 3.6 × 10-3 |
| Coarse medium (1.6–4.0 mm) | 2.5 | 38.7 | 1.6 | 2.4 × 10-3 |
| Mixture medium (0.5–4.0 mm) | 1.6 | 31.0 | 2.9 | 3.3 × 10-3 |
Permeability tests were carried out to characterize the porous media (clean bed). The column was fed from the deionised water reservoir under constant head. The measurements of the different pressures along the column allowed us to determine the permeability of the porous medium using Darcy's law. The porosity of various media was measured using the bulk density method. Table 1 summarizes the main characteristics of the used porous media.
A mercury porosimeter (Micromeritics) was used to measure the pore size distribution of the three media. The results show that the mixture presents the widest pore size distribution (Fig. 3) with two modal pore size values (200 μm and 450 μm), while coarse and fine media provide narrow distributions with modal pore size close to 550 μm and 280 μm, respectively. The average pore diameters are 336.6 μm, 237.3 μm and 182.2 μm respectively for coarse, fine and mixture media. These results show that the mixture of the coarse and fine sands leads to build narrow pores, owing to the small grains that take place between the coarse ones. Studies conducted with several porous media show that the porosity and pore size decrease for a wide grain size distribution (Bradford and Bettahar, 2006; Porubcan and Xu, 2011). X–ray synchrotron microtomography study of the assemblage of silt grains with a clay phase showed that the voids resulting can be considered as fully connected (Rozenbaum et al., 2012).
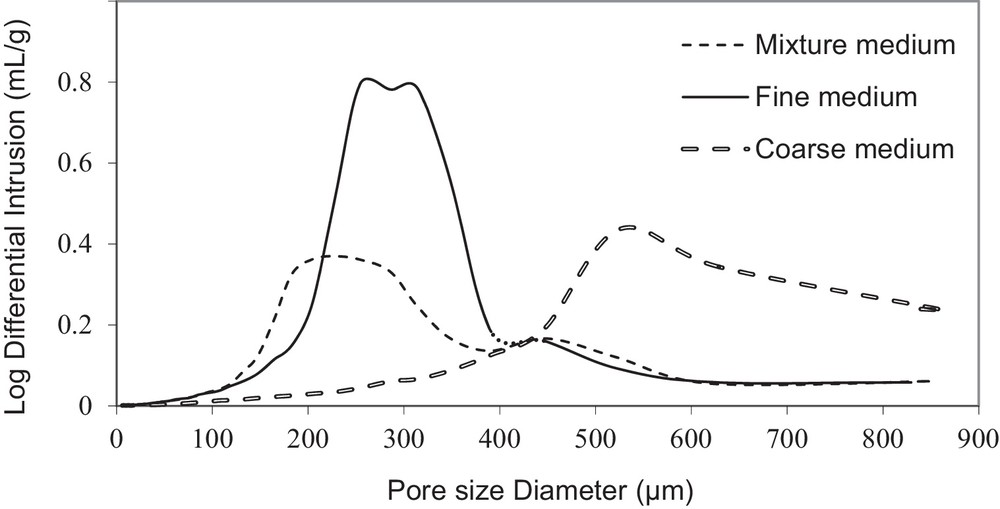
Pore size distribution (mercury porosimeter) of the tested media.
The injected fine particles are of quartz silt selected from Sebaou River alluviums. According to the grain size analysis (Malvern Multisizer 2000), the particle size ranges from 0.3 to 40 μm, with an average diameter dp50 = 7 μm. The suspended particles and dissolved tracer (fluorescein) injection experiments were conducted with a constant injected concentration C0 = 0.5 g/L and 100 μg/L, respectively. Eight tracer tests were performed either with dissolved tracer or suspended particles for each medium at flow rates ranging from 55 to 750 mL/min, corresponding to Darcy's velocities U ranging between 0.029 and 0.39 cm/s. The Reynolds number is defined by Re = Udg50ρ/ν, where dg50 is the mean size grain of the medium, ρ is the fluid density, and ν is the dynamic viscosity. The values of Re obtained over the tested porous media range between 0.32 and 9.75, which confirms that the experiments were conducted under laminar flow conditions (de Marsily, 1986). Thus, Darcy's law remains applicable in this investigation. The molecular Péclet number is defined as Ped = Updg50/D0, where Up is the pore velocity and D0 is the molecular diffusion coefficient. For D0 = 10−9 m2/s (diffusion of fluorescein in water), Ped values range between 800 and 9600. Also, these experiments conform to regime IV (300 < Ped < 105) defined by Pfannkuch (1963) for the dissolved tracer, indicating that mechanical dispersion is the main dominant process and that molecular diffusion can be neglected.
To determine the size of particles transported out of the porous medium, the samples were collected for grain size analysis using a laser device (Malvern Multisizer, 2000).
2.2 Theoretical considerations and analysis of experimental data
With the assumption that the deposition of the suspended particles does not substantially modify the properties of the porous medium for low concentrations and a short duration of test (measures being analyzed over 3.5 pore volumes), and under steady-state and saturated flow conditions, the transport of suspended particles can be described by the convection–dispersion equation with a first order deposition kinetics (Kretzschmar et al., 1997; Wang et al., 2000):
| (1) |
The initial and boundary conditions for a semi-infinite medium are given in Eq. (2):
| (2) |
The analytical solution of equation (1) according to equation (2) is as follows (Van Genuchten, 1981):
| (3) |
| (4) |
| (5) |
Eq. (3) can be written as follows:
| (6) |
When Kdep = 0 (φ = 1), Eq. (6) becomes the classic one for a dissolved tracer case (Ogata and Banks, 1961). Sauty (1977) showed graphically that the second term of equation (6) can be neglected when the dynamic Péclet number (Pedyn) is larger than 20. Over all the tests performed, the calculated values of Pedyn range between 19 and 58, and the calculations show that the amount representing the second term of the analytical solution remains less than 5% of simplified solution. Then, it can be assumed that the second term of equation (6) can be neglected, and so equation (6) reduces to:
| (7) |
When time tends toward ∞, the concentration reaches the plateau Cp given by equation (8):
| (8) |
Dividing equation (7) by equation (8), we obtain:
| (9) |
Drawing on the linear graphical method (Wang et al., 1987), the above simplification leading to the previous equation allows the transformation of equation (9) as follows:
| (10) |
By matching the measured breakthrough curves (BTCs) with the provided analytical solution, pore velocity Up, longitudinal dispersion coefficient DL and kinetic deposition coefficient Kdep were determined. The filtration coefficient λ was so deduced by the following equation (Kretzschmar et al., 1997):
| (11) |
3 Results and discussion
3.1 General considerations and transport parameters
The transformation of the analytical solution [Eq. (10)] by the linear regression method (LRM) provides a practical way to identify the model parameters. The best fit of our experimental curves with the analytical solution is obtained for both dissolved tracer and suspended particles with different tested flow velocities (Fig. 4). The dissolved tracer is completely recovered (C/C0 = 1) whatever the flow velocity. However, the suspended particles recovery varies with the flow velocity and its values are less than 85% (i.e. C/C0 < 0.85), indicating that a portion of the particles is retained in the porous medium. The higher the flow velocity is, the higher the maximum concentration and the shorter the residence time are. The recovery rate is obtained by integrating the experimental breakthrough curve over the test duration, and the results show that it increases with the flow velocity, as reported in the literature (Benamar et al., 2005; Grolimund et al., 1998; Kretzschmar et al., 1997). However, the recovery rate obtained for the particles is low (ranging from 32% for the lowest flow velocity to 86% for the highest one), which indicates a systematic capture of the coarsest fractions: particles larger than 25 μm are not recovered (see further, Section 3.2.2).
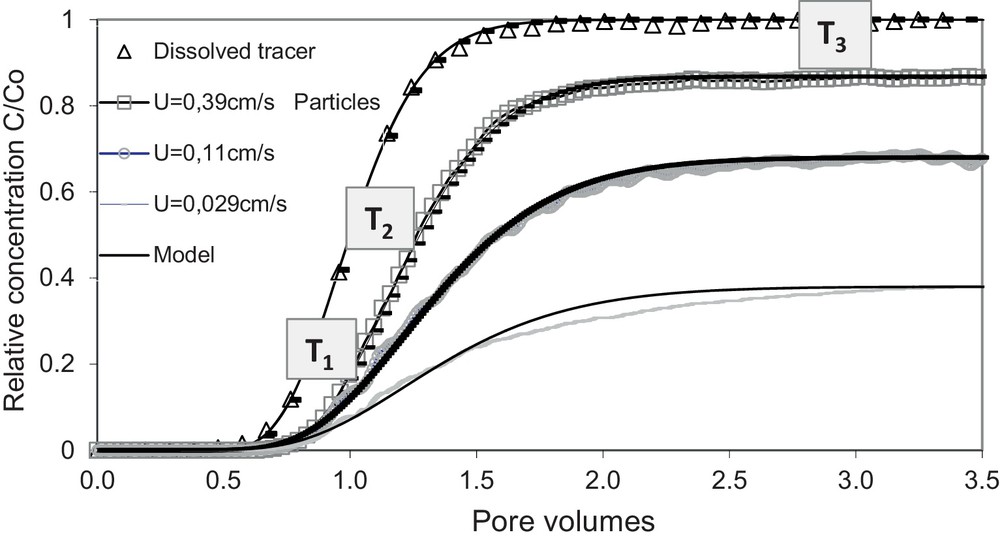
Adjustment of experimental BTCs by the analytical solution through LRM, T1, T2, T3 being the sampling times corresponding respectively to 1, 1.3, and 3 Vp of injected suspension.
The recovery mass is obtained through the integration of the breakthrough curve over time experiment. Fig. 5 presents the variation of the recovery rate R of the silt particles with the pore velocity (Up) for the considered porous media. The general trend is a non-linear (logarithmic) increase of R with pore velocity. The recovery rate observed for the particles at the lowest velocity was close to 30%, while the highest velocity provides a recovery rate greater than 80%, indicating that more particles are moved by the flow from the soil to the outlet. When comparing the recovery rate within the three porous media, the results show that the recovery decreases when the average pore size decreases. The mixture medium provides the lowest recovery rate (highest retention rate) owing to the wide distribution of pore size, forming multiple retention sites (sites of constriction, crevice, and cavern). Also, weak pore connectivity involves actively the capture of suspended particles (Elimelech and O’Melia, 1990; Lahav and Tropp, 1980; Wang et al., 2000).
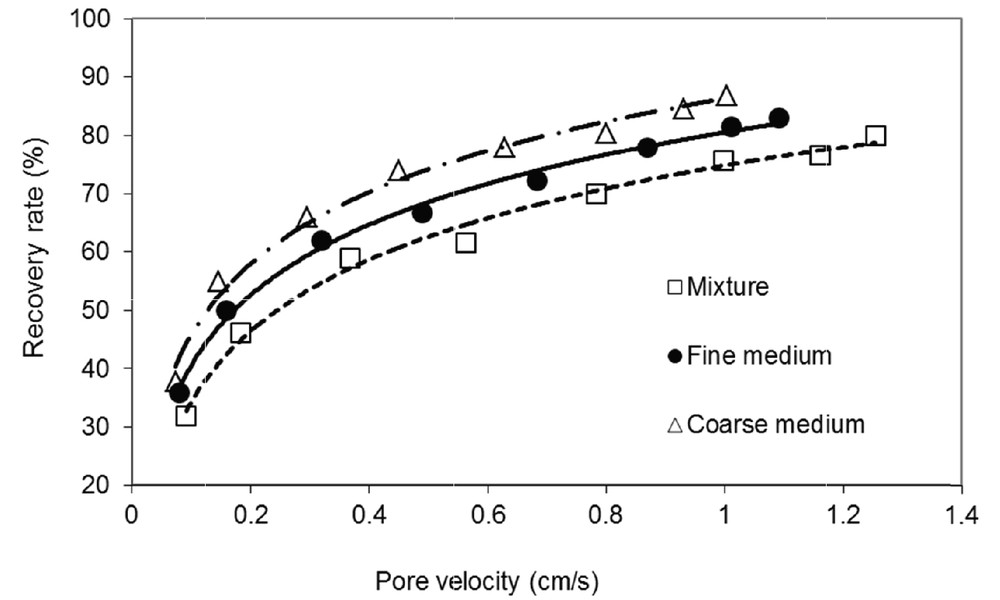
Effect of the flow velocity on the retention of suspended particles for the different porous media.
When the values of the diffusion Péclet number are larger than 300, the molecular diffusion may be neglected (Pfannkuch, 1963), and the hydrodynamic dispersion can be expressed by Eq. (12):
| (12) |
Hu and Brusseau., 1994 suggested that the value of coefficient m ranges between 1.0 and 1.3. According to Ahfir et al. (2009), the values of m range rather between 0.75 and 0.90.
The coefficient of longitudinal dispersion DL was determined for both used tracers (dissolved tracer and suspended particles). Fig. 6 displays the variation of the dispersion coefficient of suspended particles with the pore velocity within the three tested media. The results show that the longitudinal dispersion coefficient increases with increasing pore water velocity. The same evolution was observed for the different tested media. The relationship between the dispersion coefficient and the pore velocity was rather described by a linear law, and the longitudinal dispersivity value, αL, was close to 0.8 cm. According to equation (12), the coefficient m for these tests takes a value close to unit. Thus, for the two types of tracers (dissolved and particles), the variation of the dispersion coefficients with pore velocity is shown in Fig. 7 and the longitudinal dispersivity αL of each tracer was derived. When comparing the dispersion of the two tracers within the tested porous media, the dispersion coefficient of the suspended particles is greater than that of the dissolved tracer, and the difference increases with increasing flow velocity. The results further demonstrate that the dispersivity of the dissolved tracer (αL = 0.66) is smaller than that of the suspended particles (αL = 0.80 cm) over the media investigated (Fig. 7). This behaviour can be explained by the large size distribution of the suspended particles (0.3 to 40 μm), which involves a large dispersion of the flow velocities of the particles. The difference behaviour, which is more marked for large flow velocities (Ahfir et al., 2009) owing to the inertial effects, can also be linked to the size exclusion effect, which is more marked at high flow velocities (Benamar et al., 2007; Kretzschmar et al., 1997). The use of an experimental device (Hele–Shaw cell) to investigate the dispersion process inside a fracture (Mainhagu et al., 2012) showed that the longitudinal macro-dispersion obtained suggests an asymptotical behaviour of the plume spread. The longitudinal dispersivity derived from moments method was found to be increasing linearly with the Péclet number computed at the mass centre of the plume.
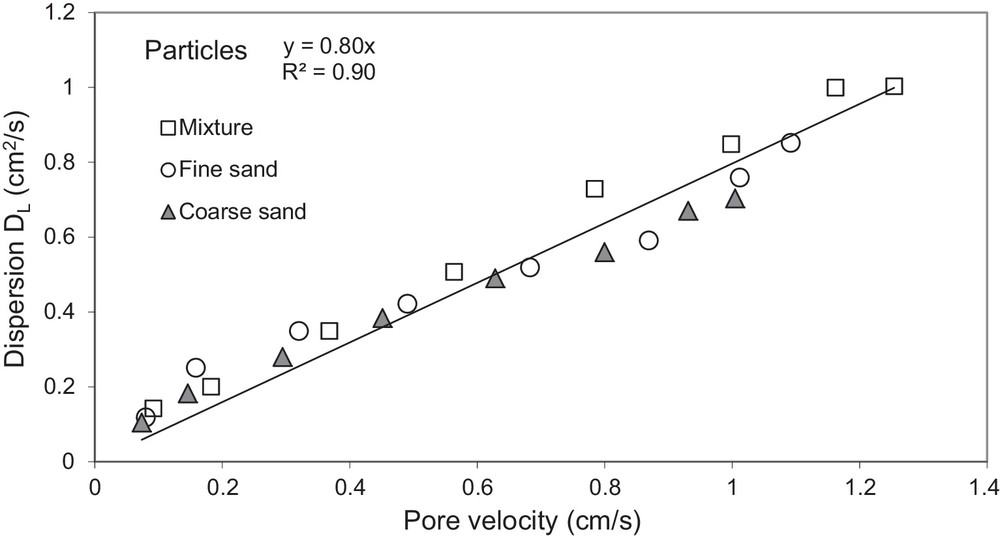
Evolution of the dispersion coefficient of suspended particles with pore flow velocity for the tested media.
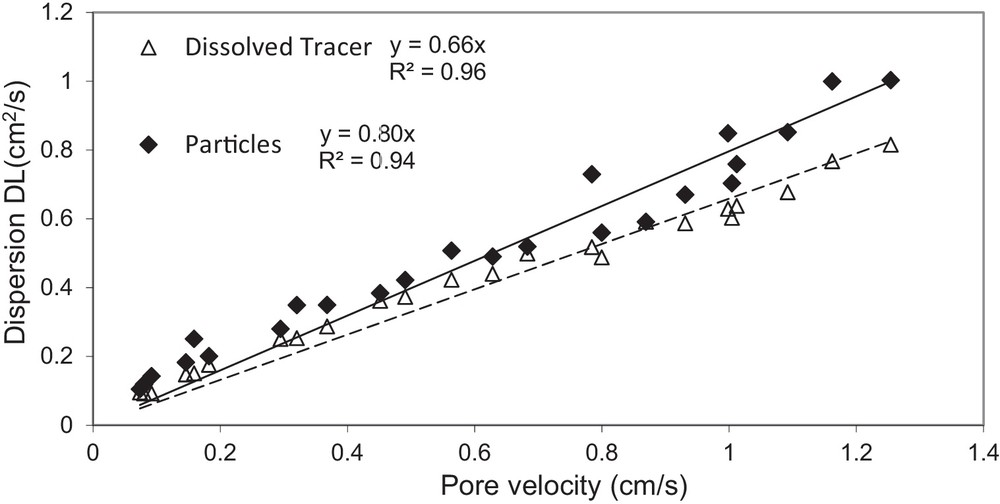
Comparison between the dispersion of the dissolved tracer and the suspended particles in the tested porous media.
This section discusses the comparison between the transport behaviour of the suspended particles and the dissolved tracer. The results reported in literature (Ahfir et al., 2007; Benamar et al., 2005; Grolimund et al., 1998; Kretzschmar et al., 1997; Masséi et al., 2002) reveal that the breakthrough of the suspended solid particles occurred earlier than the dissolved tracer, and suggest that the fast transport of the suspended particles compared to the dissolved tracer is attributed to the size exclusion effect where the suspended particles are transported in preferential pathways. Corapcioglu and Jiang (1993), Grindrod et al. (1994) have shown that the transfer time of the colloidal particles is lower than that of the solute molecules, which can be accessed by their small size and their high diffusion coefficient to an important share of the porosity space. However, results reported by Masséi et al. (2002) show that the longer transfer time of suspended particles could occur beyond a threshold flow velocity value.
The residence time is defined as the time when a half of the maximum concentration is reached in the breakthrough curve. In this study, the residence time of the suspended particles in the three tested media is longer than that of the dissolved conservative tracer. The retardation factor, noted Vr, is defined as the ratio between the flow velocities of particles and the dissolved tracer (i.e. the ratio between the dissolved tracer's residence time and the suspended particles’ residence time). Fig. 8 displays the variation of the retardation factor Vr as a function of the pore flow velocity Up. Whatever the flow velocity and the porous medium tested, Vr is always lower than 1. Thus, the residence time of the particles in the medium is longer than that of the dissolved tracer. However, the recovery delay of the suspended particles decreases when flow velocity increases and the retardation factor approaches the unit value in the mixture medium for the highest velocity tested (Fig. 8). The lower the flow velocity is, the more significant is this retardation of particles in comparison with the dissolved tracer. Such a result is in accordance with those obtained by Masséi et al. (2002) with similar flow velocities. According to Fig. 8, the retardation of the recovered particles is generally greater in the coarse medium than in the fine one, the lowest retardation being observed in the mixture medium. This behaviour is related to the availability of trapping in narrow constrictions and settling of heavy particles. Due to the large porosity of the coarse medium and the low pore velocity, the particles are trapped or evolve by collisions with grains, leading to a recovery delay. An enhanced collision effect would affect particles, whereas a dissolved tracer would be rather unconcerned by such mechanical effects. Further results about recovered particles size evidenced that larger particles are provided by the coarse medium, suggesting that the delay of restored particles increases with their size. This is likely due to the gravitational and inertial effect. When the inertia of a particle is high, it may no longer follow exactly the streamlines and will therefore be able to impact the medium's grains. The greater the inertia of a particle is, the greater is the probability of collisions between suspended particles and grains. The effect of gravity increases with particle size and can lead to a more complex trajectory than that of the dissolved tracer.
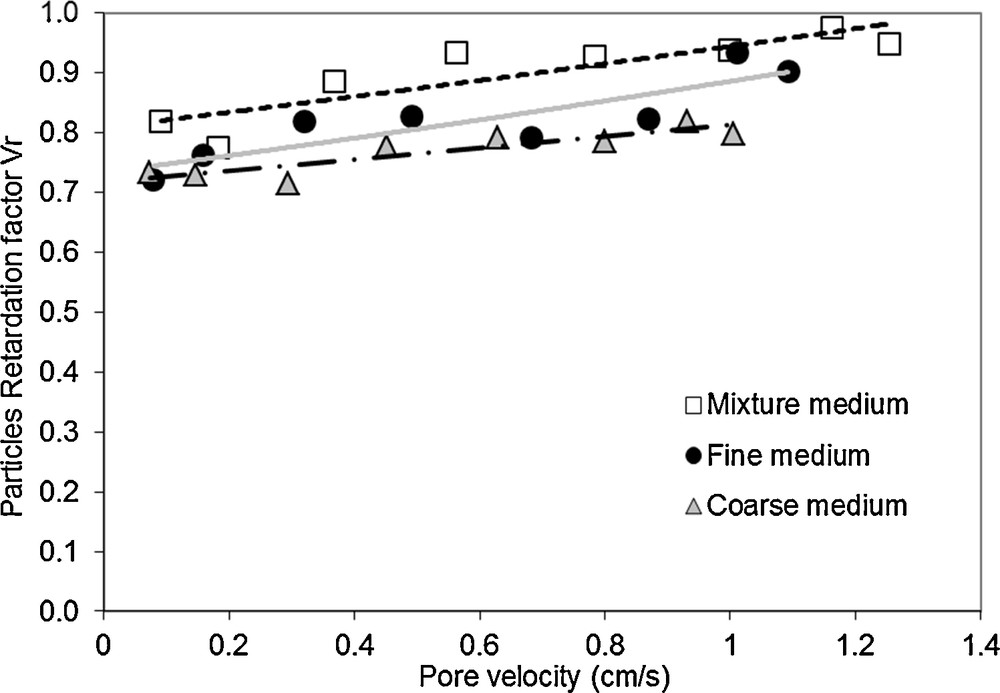
Variation of the retardation factor Vr with flow velocity for the three porous media.
The deposition kinetics coefficient Kdep is determined from breakthrough curves adjustment. The best fit values of Kdep range from 9 to 36 h−1. The lower values are associated with the coarse medium and the lowest velocity, while the greater values are observed for the highest velocity within the mixture medium. The deposition kinetics coefficient is linked to the filtration coefficient through Eq. (10). The proportionality between the deposition kinetics coefficient and the pore velocity leads to a unique coefficient λ that can be used to evaluate the filtration behaviour. The filtration coefficient λ, for the three tested media, decreases with increasing flow velocity (Fig. 9), according to an exponential trend. The comparison of the filtration coefficient values from different media shows that the mixture medium provides the highest values, while the coarse medium presents the lowest ones. These results are consistent with those widely reported in literature (Grolimund et al., 1998; Masséi et al., 2002; Porubcan and Xu, 2011; Xu and Saiers, 2009). By using the microscopic approach (Djehiche et al., 2009), the collector–particle model showed that the collector efficiency decreases as the flow's velocity increases.
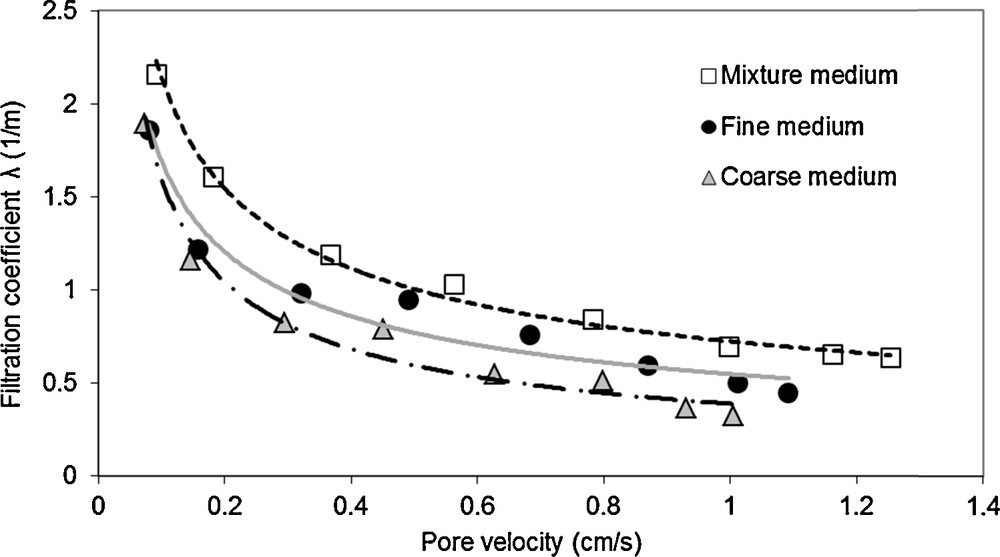
Variation of the filtration coefficient λ according to pore velocity and effect of the porous medium.
When the mass-averaged grain and particle sizes (respectively dg50 and dp50 for which 50% of the mass is finer) were used to represent the size of such materials, there appeared to be an increase in coefficient Kdep with ratio dp50/dg50 for the uniform media (coarse and fine), while the mixture medium presents a greater value of Kdep even if the value of the ratio dp50/dg50 locates between the values of both uniform media. This trend is similar to that obtained for the dispersivity and reveals that the representation of a medium by the averaged size parameters may lead to some discrepancy when heterogeneous materials are investigated. If considering the results obtained by Porubcan and Xu (2011) for colloids retention in fine sands, the lowest Kdep value obtained in this study is many times higher than that obtained by previous authors for colloids. In accordance with their results, when using the mass-averaged grain to represent the size of the porous media, the variation of Kdep with the ratio dp50/dg50 shows that the values of Kdep obtained using the mixture medium were higher than those estimated from our experiments with the two other media.
3.2 Size analysis of the recovered particles
3.2.1 Particle size distribution during breakthrough
In this section, the analysis of the particle size distribution of the suspended particles recovered at the column outlet is presented. Effluent samples were collected at three periodic times during the recovery process of suspended particles in order to carry out a particle size analysis (Malvern Multisizer 2000). Sampling times T1, T2, and T3 correspond to a number of injected pore volume equal to 1, 1.3, and 3 Vp, respectively (Fig. 4). The mass-averaged size dp50 being used to represent the mean size of the recovered particles, Fig. 10 presents the evolution of the average diameter of the recovered particles from the experiments carried out with different flow velocities in the fine medium. The average size of the suspended particles initially injected is close to 7 μm. For clarity, only the size analysis performed for some flow velocities are presented. The particle size distributions show that among the recovered particles, the coarser ones (10–25 μm) are transferred more rapidly than the fine ones. The same result was obtained by Masséi et al. (2002) using a pulse injection of the suspended particles. The finest particles arrive later compared to the larger ones, and the particle average size decreases with decreasing the flow's velocity (Fig. 10). The maximum concentration during recovery (time T3) involves a great part of the fine particles. Large particles are excluded from the section of the pores that are smaller than the diameter of the particles. The average diameter dp50 decreases over time during the breakthrough, rapidly from time T1 to time T2, and then slightly to time T3. This result can be related to the filtration of the coarse particles occurring after one pore volume (T2 to T3) of inlet. The finest particles, recovered later, can access a large part of the pore structure and are delayed with respect to the coarsest particles. Most of them spread more widely in the medium and are delayed because of a more complex trajectory than that of coarser particles that take preferential paths consisting of large pores, owing to size exclusion phenomena (Masséi et al., 2002).
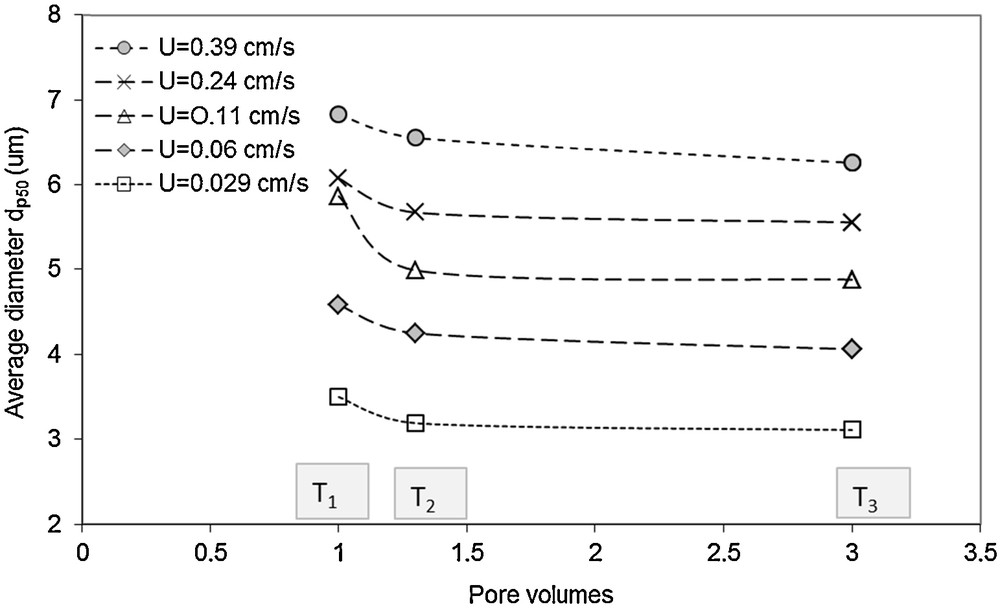
Evolution of average diameter (dp50) of recovered particles with time (inlet pore volumes) in the fine medium, T1, T2, T3 being the sampling times corresponding respectively to 1, 1.3, and 3 pore volumes of injected suspension.
3.2.2 Effect of flow velocity and pore structure on particles recovery (size selection)
The increase of flow rate leads to greater pore flow velocity, which in turn, enhance pore flow contribution to the particle transfer. From the size distribution analysis of the recovered particles with different flow velocities, the particle average diameter (Fig. 10) decreases with decreasing the pore velocity over the recovery time in the mixture medium. So, over all tested flow velocities, a size selection is operated and the particle size distribution approaches ultimately the inlet one for the highest tested velocity. This behaviour is also observed for the two other media (fine and coarse ones). These results show that the coarser particles are better recovered with high flow velocities, while small particles are mostly recovered at low flow velocities (Ahfir et al., 2009). High velocities enhance the drag forces and minimize settling and trapping. The analysis of particle size distribution reveals that the coarse fraction (> 25 μm) of the injected particles is not recovered over the testing program. Owing to their size, the relevant particles remain systematically trapped within the porosity. So, we can assume that the filter opening of the medium is mostly close to 25 μm.
The experiments carried out at different flow rates allow the development of an approach concerning the relation between the particle size distribution of the recovered particles and the characteristics of the medium's porosity. The variation of recovery of such polydispersive suspension would provide a useful tool for understanding the media pore structure. It was known from the literature (Bradford et al., 2007; Porubcan and Xu, 2011; Xu and Saiers, 2009; Xu et al., 2006) that the rate of particle straining within saturated porous media is sensitive to the ratio of the particle diameter dp to the sand grain diameter dg, and usual filtration criteria involve this ratio. Several models were also developed to predict the mechanical blockage (straining) of the particles flowing through a porous medium. Bradford and Bettahar (2006) showed that the straining rate coefficient was related to the ratio of the particle diameter and the median sand grain size through a power function. Xu et al. (2006) suggested that the mechanical blockage may be important when the ratio of the mass-averaged diameter dg50 of the porous medium and the particle diameter dp, dg50/dp is lower than 120.5 when using particles of the same size, while Bradford et al. (2004) proposed the value 200 for this ratio. Size non-uniformity can also have a significant impact on straining kinetics: the straining of smaller particles was enhanced by the presence of larger particles due to the blockage of pore opening by the larger particles, while the straining of the larger particles was reduced by the smaller particles primarily due to the faster depletion of straining capacities (Xu et al., 2006).
It is usual in soil filter design to address the filter criteria through the opening filter size and the maximum particle size. In order to assess the suitability of such criterion of mechanical straining, the ratios dg50/dp50 and dg50/dp90 of the three tested media were derived. The ratios values obtained are respectively (357, 157 and 228.5) and (125, 55 and 80) for coarse, fine and mixture media. If considering the ratio 200 as an upper limit for particle blocking, the mechanical straining increases from fine medium to mixture medium, and finally to coarse medium. Fig. 11 displays the variation of the mass-averaged size of the recovered particles with the flow velocity for the three media. The average size of the recovered particles increases with increasing the flow velocity and the relationship is represented by a logarithmic trend for the three media. The average diameter of recovered particles increases from mixture to fine medium and then to coarse medium. The smaller the pores size (from coarse medium to mixture medium), the finer are the recovered particles.

Evolution of the average size of the recovered particles at time T3 with flow velocity, for the three porous media.
It is pointed out from Fig. 11 that the significant variation of the average size of recovered particles with the porous medium arises only when pore velocity exceeds a value close to 0.2 cm/s. This result indicates that no size selection (with respect to the three media) occurs for low flow velocities and only fine particles are recovered owing to settling of large particles. Then, the pore structure affects the particle size recovery beyond a threshold value of flow velocity, where coarse and fine media allow a greater transfer (size exclusion by preferential paths) of large particles than for mixture medium. For the higher pore velocity tested (close to 1.02 cm/s), the average diameter of the recovered particles in the coarse medium is close to that of the injected particles, i.e. 7 μm, indicating that the particle size selection does not operate. The corresponding ratio dg50/dp90 in this case is equal to 125, a limit value above that no blocking occur in the porous medium for high flow rates. This result is in accordance with that suggested by Xu et al. (2006), who reported that below a threshold value of 125, the straining rate coefficient increases linearly with the ratio of colloid diameter and the average diameter of sand grains.
4 Conclusions
This study was undertaken to understand particle transfer in the natural alluvial soils of Sebaou River (Algeria). An experimental and analytical study aiming at investigating the influence of geometrical and hydrodynamic effects on the transport and deposition processes of suspended particles in the porous medium is presented. The results yielded valuable insight on the processes of particle transport and deposition in these soils. The porous medium obtained by mixing (by equal mass) two materials (coarse and fine media) of quite uniform grain size distribution provides a relative broadly graded sand with narrow pores. Filtration experiments using suspended particles (silt) provide steady effluent particle concentrations. These results enabled the estimation of the filtration coefficient, which may be used to characterize the particle retention capacity of the media. The results showed that the retention kinetics decreases with increasing flow velocity and decreasing the size of the pores of the medium. The wider the pore size distribution is, leading to narrow pores, and the more important filtration is. The dispersion of suspended particles is higher than that of the dissolved tracer due to inertial and gravity effects. It increases with flow velocity and reaches the highest values in the mixture medium owing to the formation of a wide range of pore sizes. The analysis of breakthrough curves showed that the dissolved tracer is recovered before the suspended particles. We addressed the retardation of the suspended particles with respect to the dissolved tracer. This retardation factor increases with increasing flow velocity and decreases from the coarse medium to the mixture medium. The quite high velocities tested lead to particle retardation owing to collisions arising between particles and medium's grains. Furthermore, the analysis of size distribution of recovered particles showed that the larger particles travel faster than the fine ones, which can access by their small size and their high dispersion coefficient into an important portion of the porosity (matrix porosity), thus inducing a recovery delay compared to coarse particles (size exclusion effect). The recovered particle size increases with flow velocity because of the importance of hydrodynamic forces exerted on the suspended particles; however particles larger than 25 μm were not recovered over all performed tests. Experimental results showed that two materials mixed as heterogeneous (broadly graded) porous medium could significantly enhance the straining of suspended particles. The analysis of the recovered particle size indicate that a limit value of the ratio dg50/dp90 equal to 125 can be achieved for particle straining, using the mass-average size to represent the size of porous media's grains and particles. Our results indicate that straining influences particle retention over a range of dp/dg values, as suggested by published experimental studies on colloid transport; mechanisms involved in particle transport being significantly different from those associated with colloid transport.
Acknowledgements
This work was supported by the governmental French–Algerian education program PROFAS and the Région Haute-Normandie, France (CPER).


