1. Introduction
The interaction of folding, thrust faulting, and mechanical behaviour in contractional settings, particularly fold-and-thrust belts, has been recognized in deformed sequence so that assessment of these relationships is fundamental for understanding deformation processes, kinematic and mechanical completion of the structures, and structural style [Brandes and Tanner 2014, Derikvand et al. (2018, Motamedi and Gharabeigli 201]. There are several assumptions to consider when analysing thrust belts, where one of the most important assumptions is that internal layer deformation occurs via simple shear parallel to bedding [e.g., Rowan et al. 2019]. As a result, a wide range of studies have been conducted to investigate the determinants based on these assumptions [Ridley and Casey 1989, Marshak et al. 1992, Corredor et al. 2005]. Many fold-and-thrust belts, for example, are the result of orthogonal or oblique convergence–subduction and/or collision. There are studies being conducted to investigate the influencing factors in the evaluation of thrust belts, such as those formed by convergence and the influence of convergence rate on structural style, which is a critical factor in the formation of fold-and-thrust belts [e.g., Bonini 2003, McClay et al. 2004, Farzipour-Saein and Koyi 2014, Schori et al. 2015, Ghanadian et al. 2017, Chen et al. 2018, Cui et al. 2020, Pla et al. 2019, Gu et al. 2021].
Structural terminologies of fold-and-thrust structures in contractional settings have been investigated using kinematic models of fault-related folds including detachment (or décollement), fault-bend, fault-propagation, and trishear folds [e.g., Brandes and Tanner 2014, Cosgrove 2015, Butler et al. 2018]. Moreover, fold-and-thrust belts often possess rich hydrocarbon reserves, leading to do wide attention to their structures and evolution [e.g., Kendall et al. 2019, Hammerstein et al. 2020]. Therefore, the evaluation of fault-related folds influences the development and exploration of a hydrocarbon-bearing basin by affecting the trap, seal capacity, reservoir quality, migration and also drilling costs and hazards. According to many studies on fault-related folds, folds geometry generally is controlled by fault geometry and fault slip/fault-propagation ratio in fault-propagation folds, and fault displacement and décollement layer thickness in detachment folds [e.g., Jamison 1987, Mitra 1990, Allmendinger 1998, Suppe et al. 2004, Brandes and Tanner 2014].
Among these models, décollement folds are considered as a prevalent structural style in fold-and-thrust belts and in most cases thin-skinned (décollement-dominated) tectonics. Décollement fold structures have formed from the shortening of a competent rock layers upper a décollement layer played as a lower competent layer such as over-pressured shales, salts and evaporates. These folds are not related to ramps and the propagating thrust segments is sub-horizontal. Their geometries range from concentric, chevron, to box-shape fold in geometry [Dean et al. 2013, Meng and Hodgetts 2019b]. Detachment folds can have a variety of structural styles, like: symmetric, asymmetric, disharmonic, lift-off, multi-detachment to faulted [e.g., Mitra and Namson 1989, Poblet and McClay 1996, Mitra 2003, Wallace and Homza 2004, Suppe 2011, Morley et al. 2017, Li and Mitra 2020]. Mitra [2003] demonstrates buckling of the above décollement levels where mobile material is placed beneath synclines and flows into anticline hinges. As contraction and distributed simple shear increases, décollement folds, in addition to amplification, can be asymmetric or overturned due to limb rotation and hinge migration. Faulting in their final phase of deformation is also common to form fault-bend and or fault-propagation folds [e.g., Mitra 2003, Morley et al. 2017, Nabavi et al. 2019].
Décollement folds are abundant in fold-and-thrust belts, for example, the Appalachian fold-and-thrust belt [e.g., Lammie et al. 2020], the Jura Mountains [e.g., Schori et al. 2015], the Zagros fold and thrust [e.g., Sherkati et al. 2005, 2006, Vergés et al. 2011], the Mexican Ridges fold belt [e.g., Yarbuh et al. 2018], and the deep-water Niger Delta [e.g., Briggs et al. 2006, Morley et al. 2011]. Studies on décollement folds have been successfully conducted using different kinds of approaches such as field data [e.g., Suppe 2011, Morley et al. 2017], subsurface seismic reflection data [e.g., Derikvand et al. (2018, Morley et al. 2017, Li and Mitra 2020], analogue [e.g., Farzipour-Saein 2017, Ghanadian et al. 2017, Li and Mitra 2017] and various numerical techniques such as FEM or DEM. For example, studies conducted by the discrete element technique [e.g., Schöpfer et al. 2006, 2017, Hardy and Finch 2005, Meng and Hodgetts 2019b].
Proper interpretation of the structural evolution and structural style are essential to build the accurate understanding of the surface and subsurface geometry of structures. In this way, numerical modelling using the discrete element method (DEM), provides means for simulating and tracking the spatial and temporal evolution of stress distribution, characteristic and sequential evolution of structures, strain localization and the prediction of onset of associated geological structures at different scales, for example, the studies of the development of normal and thrust faults [Saltzer and Pollard 1992, Donzé et al. (1994, Abe et al. 2011, Schöpfer et al. 2006, 2016, 2017, Hardy 2011, 2013, Smart et al. 2011, Deng et al. 2017, Finch and Gawthorpe 2017], relay structures [Imber et al. 2004], décollement and fault-related folds [Finch et al. 2003, Cardozo et al. 2005, Hardy and Finch 2005, 2006, 2007, Benesh et al. 2007, Hughes et al. 2014], accretionary wedges and FAT belts [Burbidge and Braun 2002, Naylor et al. 2005, Yamada et al. 2006, Hardy et al. 2009, Dean et al. 2013, Morgan 2015, Morgan and Bangs 2017, Meng and Hodgetts 2019a,b]. In this regard, we utilize results from a series of numerical DE-models using PFC3D® software package that can be followed during deformation process, for example, décollement slip, onset and amplification of décollement folds, and the initiation and propagation of discrete thrust faults.
This study seeks to address the importance and influence of (1) the thickness of décollement layer, and (2) the number of strong and weak layers within the sedimentary cover sequence under an applied horizontal pressure, on the structural and mechanical formation of décollement folds in a contractional setting. It should be noted that the presented models are simplistic. Geological processes such as diagenesis, erosion, fluid flow, temperature, etc., are not considered. The primary reason for this approach is that we seek to isolate the effects of a few selected parameters in order to keep the analysis traceable [Nabavi et al. 2020]. The outcome of this study is compared to a natural example from the central Iran structural zone as well as the Zagros fold-and-thrust belt and large-scale fold-and-thrust belt in South China.
2. The discrete element modelling method (DEM)
2.1. Basic principles
In this study, a series of DE-mechanical models and a particle-based numerical method is applied for simulation of deformation of rock layers during shortening situation. This approach uses a finite difference approach to solve Newton’s equations of motion. The rock mass is considered as an assemblage of soft circular, spheres, or disc, which interacts with each other in pairs as if connected by breakable elastic bonds (springs) and undergo motion relative to one other. These particles interact through elastic, gravitational, frictional, and viscous forces. At each discrete time step, the particles are displaced to their new positions within the model by integrating their equations of motion using Newtonian laws and a velocity-Verlet-based numerical scheme.1 The particle bonding is controlled by normal and shear bond stiffness, bond strength, and bond radius. In this regard, the normal and shear contact forces (Mohr–Coulomb criterion) are calculated between two overlapping or contacting particles using a rheological contact law. Bonds are broken when the inter-particle forces exceed the bond strength. In this regard, slip that is resisted by a frictional strength can occur between particles that are not bonded. Thus, discontinuities and heterogeneities form and evolve in response to changing stress condition and material properties [e.g., Cundall and Strack 1979, Hardy et al. 2009, Hughes et al. 2014, Morgan 2015, Smart et al. 2011, Hardy 2019, Meng and Hodgetts 2019b]. Many previous investigations have used the DE-models and have successfully produced realistic styles of geological and tectonic features such as normal faulting in layered sequences [e.g., Botter et al. 2014, Hardy 2019], fault-bend folding [e.g., Benesh et al. 2007, Hughes et al. 2014], fault-propagation folding [e.g., Hardy and Finch 2006, Hughes and Shaw 2015], and fold-and-thrust belts [e.g., Hardy et al. 2009, Morgan 2015, Meng and Hodgetts 2019b]. Hence, DEM, is an appropriate approach to study the initiation, propagation, interaction and linkage, and the evolution of folding, fracturing, and faulting in a realistic manner involving large deformation and large relative displacements.
2.2. Model setup
The mechanical modelling method we utilize is DEM that was developed using the Itasca Particle Flow Code (PFC3D®, version 6,13, Itasca Consulting Group) 3D software package. PFC® was initially developed for describing the mechanical behaviour of material (Soil or rocks), allows flexibility in simulations and is widely used among geologists as it permits modelling of large deformations.
The initial design and boundary conditions for discrete element models. The models were made up of 21,403 elements with radii ranging from 25 to 41 m for the décollement and cover layers, the red lower décollement, and a series of weak and strong layers in a hexagonal box (10 km length, 1 km width, 0.5 km thickness). The boundary condition is considered free in surface. The left sidewall is moving towards right side. The fs = shear stress, fn = normal stress, and b is particle bond.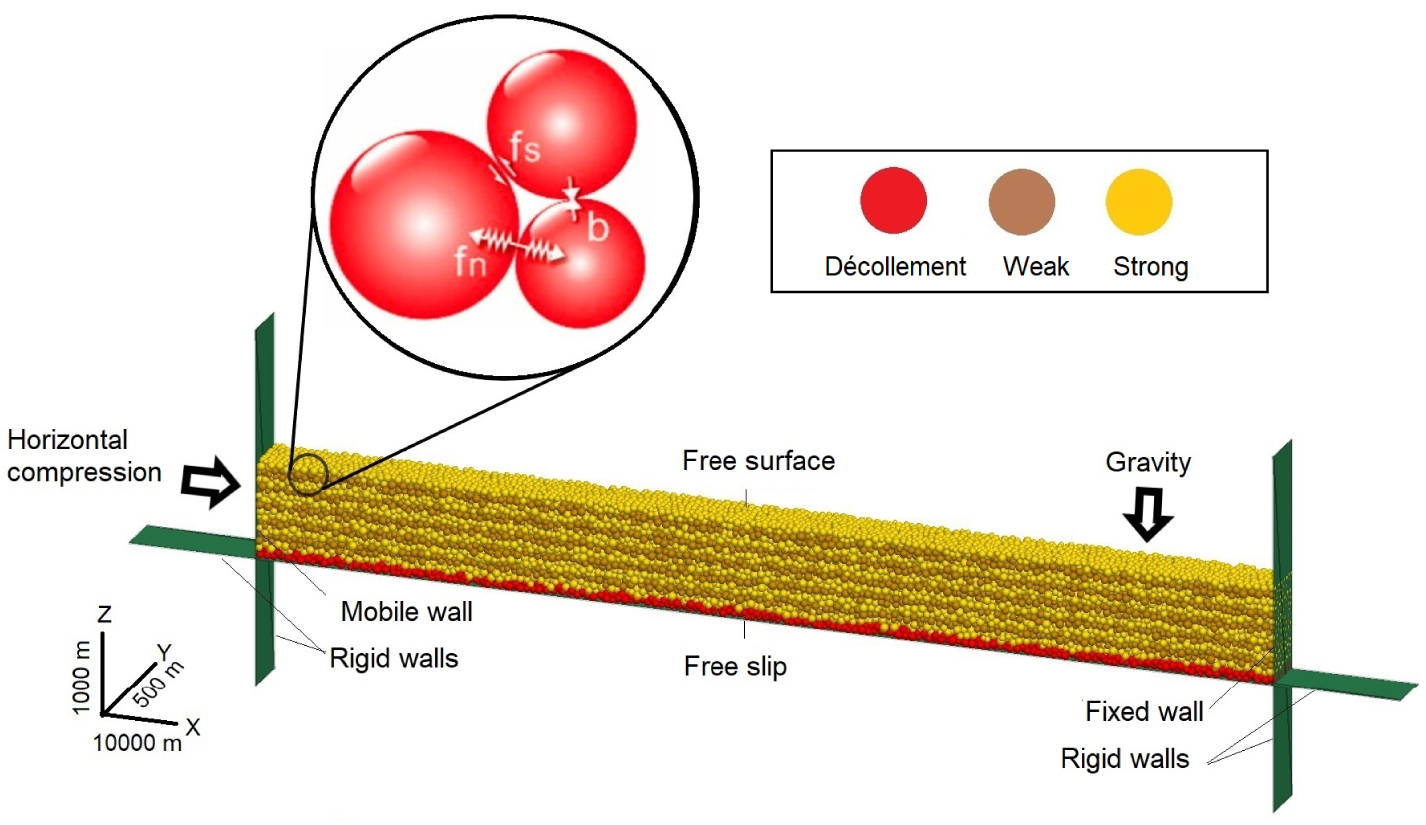
Summary of material properties and parameters used in DE-models
| Parameters | Décollement layer | Overburden | |
|---|---|---|---|
| Weak layers | Strong layers | ||
| Particle radius | 25–41 m | ||
| Contact Young’s modulus | 0.1 × 109 | 0.5 × 109 | 1 × 109 |
| Contact friction | 0 | 0.5 | |
| Tensile bond strength | 0 | 2.5 × 106 | 5 × 106 |
| Average density | 3000 kg/m3 | ||
We created a regular hexagonal model (Figure 1) consisting of 21,403 spherical particles in the part of upper crust model with dimensions of 10 km length × 1 km width × 0.5 km thickness (x,y,z). The particle radii range from 25 to 41 m both for the décollement and cover layers that follow a Gaussian distribution for particle size. The mechanically layered cover sequence consists of alternating relatively “strong” layer and relatively “weak” layers. The average rock density (𝜌) for all particles is about 3000 kg/m3. Particle stiffness values of 1 × 109, 0.5 × 109, and 0.1 × 109 N/m, for strong, weak, and décollement layer, respectively, were assigned for normal (kn) and shear (ks) stiffness (Table 1). The coefficient of sliding friction between particles (𝜇) was assigned as 0.5, whereas the décollement layer is frictionless to ensure its low strength [e.g., Morgan 2015, Meng and Hodgetts 2019b].
Presented various initial configurations of the models
| Model No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Td | 0.1 | 0.1 | 0.1 | 0.2 | 0.2 | 0.2 | 0.3 | 0.3 | 0.3 |
| N | 5 | 4 | 3 | 5 | 4 | 3 | 5 | 4 | 3 |
Each model has unique initial setting as (Td, N) that Td is the thickness of basal décollement layer as a fraction of total thickness (0.1, 0.2, 0.3 km of total thickness or 100 m, 200 m, 300 m) and N is the number of weak layers.
We examined nine models (Table 2) with varying décollement layer thickness as a fraction of total initial thickness (0.1, 0.2, 0.3 km of total thickness or 100 m, 200 m, 300 m) and the number of strong and weak layers within the sedimentary cover (5 weak layers in models 1, 4, 7; 4 weak layers in models 2, 5, 7; and 3 weak layers in models 3, 6, 9). Coloured layers within the cover sequence above the décollement layer indicate contrast in material properties.
Our experimental setup consists of a horizontal surface and two vertical boundaries. All surfaces are defined in the model by rigid, frictional boundary walls (i.e., free-slip boundary conditions). Numerically, free surface boundary conditions are applied on the top model, thus permitting self-consistent evolution of topography [Nabavi et al. 2020]. Acceleration due to gravity (9.81 m/s2) is imposed throughout the deformation as a body force. In all models, the horizontal, vertical, compressional load was imposed horizontally [i.e., displacement-based boundary conditions; Nabavi et al. 2018, 2020]. All results are shown here after 10%, 20%, and 30% shortening, which is equal to 1000 m, 2000 m, after 10%, 20%, and 30% shortening, which is equal to 1000 m, 2000 m, and 3000 m displacement on the décollement and overburden layers. The shear strength 5 × 106 N/m and 2.5 × 106 N/m for strong and weak layers, respectively.
3. Results
We present the main features observed in a series of DE-models after 30% (3000 m displacement) horizontal shortening to investigate décollement folding above a flat décollement layer. There are large number of possible model setups that we could present, however, we discussed the effects of décollement layer thickness and the number of strong and weak layers within the sedimentary cover on the mechanical evolution and structural style of box-shaped décollement folds in a contractional environment through nine different models which is based on progressive deformation events. In all models, the sedimentary cover sequence overly a décollement horizon at the base of models.
3.3. Models with a thin décollement
Evolution of DEM to show the folding in the models 1, 2, and 3 with thin décollement after 30% (3000 m displacement) orthogonal shortening in three steps of shortening 10%, 20%, and 30%. The models are the same in terms of the thickness of the décollement (Td = 0.1) and different in the sedimentary sequences (N). The value of N is equal to 5, 4, and 3 weak layers, respectively, for models 1, 2, and 3. The final geometries are denoted by a 30% shortening. The uplift is about 1.5 km for model 1, 1.65 km for model 2, and 1.5 km for model 3.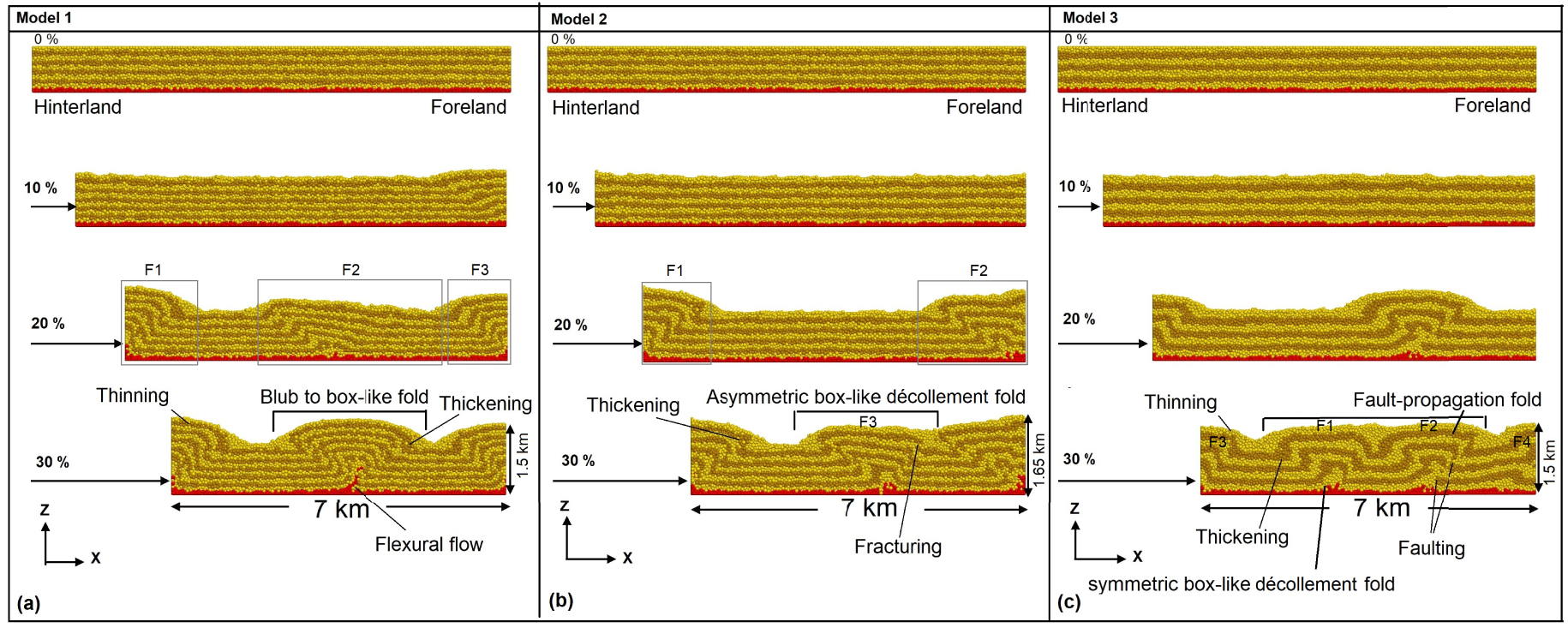
The structures observed in a set of numerical models exhibit a wide range of structural style that varies as a result and the function of model design, boundary conditions, and the material being deformed. Model 1 (Figure 2a) presents how a thin décollement layer affects deformation, the structural style and evolution of décollement folding, and its spatial and temporal geometric evolution is shown in three models and displacement steps at intervals of 100 m of shortening. In this model, the sedimentary cover layers consisted of a series of strong bonded layers (six layers thick) intercalated with weak bonded layers (five layers thick). The décollement layer in this model is 0.1 km thick. After the primary phase of homogeneous shortening 10%, the deformation shows pure-shear thickening (contraction or buckling) with the low-amplitude asymmetric décollement fold at the onset of deformation. Increasing deformation (20%) causes three major asymmetric anticlines at different locations of the model above the décollement layer including F1 in the hinterland (left sidewall), F2 at the model centre, and F3 in the foreland (right sidewall) (Model 1 in Figure 2). Anticlines have higher amplitude for those bounded by the lateral boundaries of the model. With increasing horizontal shortening and displacement, both fold limbs rotate about 10° and lengthen through time. After 30% shortening, the middle anticline gradually becomes symmetric and amplifying due to strain accumulation in the décollement layer (i.e., flexural slip) and localized strain zones. Finally, developing to the nearly symmetric sinusoidal, bulb-like to box-shaped décollement fold with a curved hinge. The curved hinge is bounded by a set of conjugate high-strain shear zones, that are closed to the strong layers, whereas its wavelength did not show significant changes through time. Figure 2(a) shows the final geometry that demonstrates most of the strain after 30% shortening and that propagates the fold structure upwards. At the end of shortening, the basal layers were folded isoclinally in the core of the structure, with limbs dipping sub-vertically in the lower layers. Upper layers did not dip as steeply and were extended and thinned in crestal areas as a result of buckling of the uppermost hanging-wall strata, whereas they were folded and thickened in adjacent synclinal areas. The crest of folds widened outwards and upwards from the core of them, which generally the resulting structure was upright and symmetrical box-shaped décollement fold. Furthermore, Figure 2(a) indicates flexural flow developed in the core of the box-shaped décollement folds, so that it is filled with weak material that evacuated beneath synclines and flowed into the anticline core. Some minor faults and shear bands develop in limbs of the box-shaped décollement fold to accommodate contraction as penetrative strain [e.g., Burberry 2015, Nabavi et al. 2019] that does not propagate across the entire multilayer but rather links the weak layers with the layered rock sequence.
Model 2 (Figure 2b) has the same décollement thickness of 0.1 km, but the number of weak layers inside the sedimentary cover is reduced to four, and the model is dominated by strong layers. In 10% of shortening, there are deformation in the surface that shaped the topography. Increasing deformation (20%) causes two major asymmetric anticlines at two parts of the model above the décollement layer including F1 in the hinterland (left sidewall) and F2 in the foreland (right sidewall). Anticlines have constant wavelength and amplitude for those bounded by the lateral boundaries of the model. As the deformation progresses (30% horizontal shortening), F3, an upright and asymmetric box-shaped décollement fold and low-amplitude anticline developing and amplifying at the middle part of the model due to continuous contraction, strain accumulation in the décollement layer (i.e., flexural slip) and localized strain zones. This low-amplitude anticline finally may bound by a set of conjugate faults or high-strain shear zones, which are more restricted to the strong layers to accommodate contraction as penetrative strain, and developed an asymmetric faulted décollement fold. Like Model 1, fold limbs both rotated and lengthened though time due to distributed strain throughout the fold limbs. As the limbs steepen, slip becomes more localized on flexural slip surfaces, then finally strain localizes at the synclinal axial zones where more material is progressively incorporated into the structure. At the end of the shortening, the basal layers were folded isoclinally in the core of the structure and limb dips were 80–90° in the lower layers. Upper layers did not dip as steeply and were extended and thinned in crestal areas as a result of buckling of the uppermost hanging-wall strata, whereas they were folded and thickened in adjacent synclinal areas. In contrast to model 1, the folds formed in model 2 have much higher amplitudes. Similar to Model 1, Model 2 (Figure 2b) shows the core of décollement folds filled with weak material that evacuated beneath synclines and flowed into the anticline core.
Model 3 (Figure 2c) has the same décollement thickness of 0.1 as Models 1 and 2, but there are three weak layers and the model is dominated by strong layers. The whole sedimentary cover sequence, as previously indicated, is deposited over a basal weak décollement level. Figure 2c depicts the evolution of this model. Model 3 developed two main folds (F1 and F2 in the middle part of the model) and two minor folds at two parts of the model above the décollement layer including F3 in the hinterland (left sidewall) and F4 in the foreland (right sidewall) to accommodate shortening. However, in addition to the symmetric box-shape décollement fold and differently from Models 1 and 2, fault-propagation fold takes over décollement fold as one of the main fold type in this model after 20–30% horizontal shortening (Figure 2c). The faults accommodated shortening by thrusting (both fore thrust and back thrust). The thrusts and accumulated fault displacement gradually and dip angles approximately keeping unchanged. However, after this step, the development of the structure changed, fault-propagation folding ceased, and instead the structure tightened and developed a classically upright and symmetric box-shaped décollement fold with continued displacement.
3.2. Models with an intermediate-thick décollement
Models 4, 5, and 6 show how an intermediate-thick décollement with a 0.2 km thickness affects deformation and structural styles. In these models, the sedimentary cover sequence consisted of a series of strong bonded layers (six, five, and four strong layers thick, respectively, for Model 4, Model 5, and Model 6) intercalated with weak bonded layers (six, five and three weak layers thick, respectively, for Model 4, Model 5 and Model 6). In Model 4 (Figure 3a), first, deformation is essentially pure-shear thickening (contraction or buckling) with the low-amplitude asymmetric décollement fold at the onset of deformation. Increasing deformation through time causes two major nearly symmetric anticlines F1 and F2 as sinusoidal, bulb-like to box-shaped geometries at different locations of the model above the décollement layer including.
Evolution of DEM to show the folding in the models 4, 5, and 6 with an intermediate-thick décollement after 30% (3000 m displacement) orthogonal shortening in three steps of shortening 10%, 20%, and 30%. The models are the same in terms of the thickness of the décollement (Td = 0.2) and different in the sedimentary sequences (N). The value of N is equal to 5, 4, and 3 weak layers, respectively, for models 1, 2, and 3. The final geometries are denoted by a 30% shortening. The uplift is about 1.59 km for model 1, 1.75 km for model 2, and 1.64 km for model 3.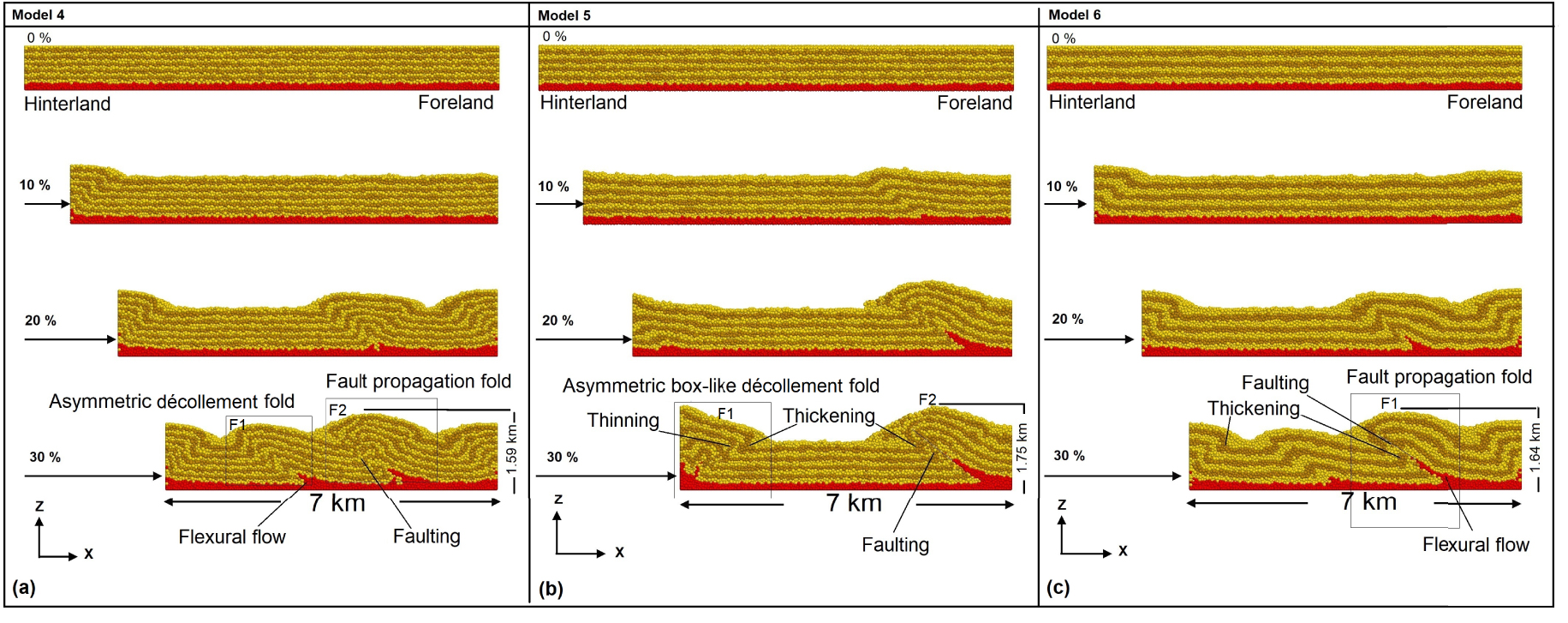
In Model 5 (Figure 3b), the deformation that is pure-shear thickening (contraction or buckling) started from 10% of shortening by changes in the surface with the low-amplitude asymmetric fold. Increasing deformation through time (deformation 20 to 30%) accommodated by a combination of the asymmetric box-shaped décollement fold F1 and the foreland fault-propagation fold F2, so that flexural flow with a distinct fault segment developed in the lower part and core of the fault-propagation fold and it is filled with weak material that evacuated beneath synclines and flowed into the anticline core (Figure 3b in 30%). High-strain shear zones or bands are more restricted to the strong layers of the left-hand limb of the structure. Upper layers dip as moderately to steeply (25° to 45°) as faulted décollement folds and fault-related folds develop and were extended and thinned in crestal areas with possible extensional faulting and collapse structures as a result of buckling of the uppermost hanging-wall strata, whereas they were folded and thickened in adjacent synclinal areas.
The final model in this series (Model 6 or c in Figure 3) responses to 10% shortening by deformation from left side, also at the model centre (20% in Model 6 in Figure 3c), and in the foreland (right sidewall). Anticlines are more cylindrical and have higher amplitude for those bounded by the lateral boundaries of the model. With increasing horizontal shortening and displacement, both fold limbs rotate and lengthen through time. As the deformation progresses and after 30% shortening, the middle anticline F1, gradually became asymmetric and amplifying due to strain accumulation in the décollement layer as both flexural slip and flexural flow, respectively in strong and weak layer. In addition, localized strain zones are developed in different domains of Model 6, where its wavelength increases through time but in a rather irregularly spaced with a steep to overturned left-hand limb and a shallower and longer right-hand limb (i.e., highly asymmetric décollement folds), and the contractional fault-propagation fold so that flexural flow with a distinct fault segment developed in the lower part and core of this fold and it is filled with weak material that evacuated beneath synclines and flowed into the anticline core. Some minor faults and shear bands develop in limbs of décollement folds to accommodate contraction as penetrative strain that does not propagate across the entire multilayer but rather links the weak layers with the layered rock sequence.
3.3. Models with a thick décollement
Evolution of DEM to show the folding in the models 7, 8, and 9 with a thick décollement after 30% (3000 m displacement) orthogonal shortening in three steps of shortening 10%, 20%, and 30%. The models are the same in terms of the thickness of the décollement (Td = 0.3) and different in the sedimentary sequences (N). The value of N is equal to 5, 4, and 3 weak layers, respectively, for models 1, 2, and 3. The final geometries are denoted by a 30% shortening. The uplift is about 1.54 km for model 1, 1.62 km for model 2, and 1.62 km for model 3.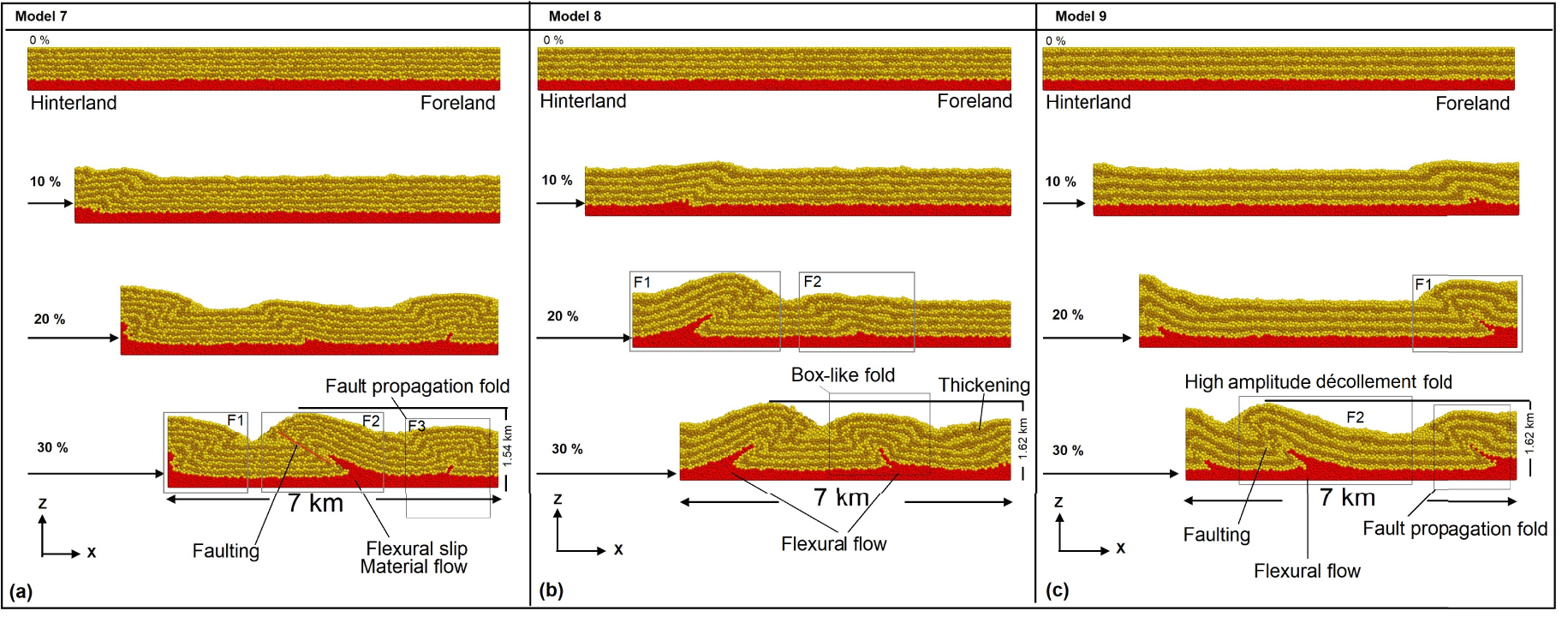
Model 7 (Figure 4a) depicts how a thick décollement layer influences deformation, the structural style, and evolution of décollement folding. The sedimentary cover sequence in these models was made up of a succession of strongly bonded layers (six strong layers deep) separated by weak layers (five weak layers thick). In this model, the décollement layer is 0.3 km thick. Overall, following the first stage of homogeneous shortening, the deformation is essentially pure-shear thickening (contraction or buckling) with the foreland-verging low-amplitude asymmetric décollement fold at the onset of 10% deformation. Increasing deformation through time (deformation 20%) causes three major nearly symmetric anticlines as sinusoidal, bulb-like to box-shaped geometries at the different location of the model above the décollement layer including F1 in the hinterland (left sidewall), F2 at the model centre, and F3 in the foreland (right sidewall). With increasing horizontal shortening and displacement, both fold limbs rotate and lengthen through time. As the deformation progresses and after 30% shortening, the middle anticline gradually became highly asymmetric and amplifying due to strain accumulation in the décollement layer as both flexural slip and flexural flow, respectively in strong and weak layers, with localized strain zones and a distinct fault segment developed in the lower part and core of this fold, which finally develops to the fault-propagation fold, whereas two box-like décollement folds in hinterland and foreland domains do not show any significant changes in their geometries through time. In the latter case, thrusts would preferentially develop to accommodate applied horizontal shortening rather than buckling. High-strain shear zones or bands are more restricted to the strong layers of the left-hand limb of the structure. Upper layers dip as moderately to steeply as fault-related folds develop and were extended and thinned in crestal areas with possible extensional faulting and collapse structures as a result of buckling of the uppermost hanging-wall strata, whereas they were folded and thickened in adjacent synclinal areas.
Model 8 (Figure 4b) illustrates how a thick décollement layer determines the structural style and evolution of a sedimentary overlay succession composed of a sequence of strong bonded layers (five strong layers thick) intercalated with weak bonded layers (four weak layers thick). In this model, the décollement layer is 0.3 km thick. The deformation is mainly pure-shear thickening (contraction or buckling) with the foreland-verging low-amplitude asymmetric décollement fold at the initiation of deformation, after an early phase of homogeneous shortening of the model. With the passing of time, the degree of deformation increases (deformation 20%) causes the foreland-verging fault-propagation fold with localized strain zones and a distinct fault segment developed in the lower part and core of this fold in the hinterland (left sidewall) and the low-amplitude asymmetric décollement fold at the middle domain of the model. In this case, thrusts would preferentially develop to accommodate applied horizontal shortening rather than buckling. As the deformation progresses and after 30% shortening, the F1 fault-propagation fold further develops and its asymmetry increases, and also F2 the middle anticline gradually became more symmetric and amplifying due to strain accumulation in the décollement layer as a box-like décollement fold with the low-amplitude asymmetric décollement fold in the foreland (right sidewall). Upper layers dip as moderately to steeply as fault-related folds develop and were extended and thinned in crestal areas with possible extensional faulting and collapse structures as a result of buckling of the uppermost hanging-wall strata, whereas they were folded and thickened in adjacent synclinal areas (Figure 4b).
Model 9 (Figure 4c) exhibits that a thick décollement layer impacts the structural style and evolution of a sedimentary cover sequence composed of four strong bonded layers intercalated with weak bonded layers (three weak layers thick). In this model, the décollement layer is 0.3 km thick. Overall, the deformation is mainly pure-shear thickening (contraction or buckling) with the hinterland-verging low-amplitude asymmetric décollement fold (F1) at the initiation of deformation following an initial step of homogeneous shortening of the model. With the passage of time, the deformity becomes more evident (deformation 20%) and develops two hinterland-verging fault-propagation folds with localized strain zones and distinct fault segments developed in lower parts and core of folds in the hinterland (left sidewall) and foreland (right sidewall). In this case, thrusts would preferentially develop to accommodate applied horizontal shortening rather than buckling. As the deformation progresses and after 30% shortening, the fault-propagation folds further develop and their asymmetries increase, however, a new well-developed fault-propagation fold F2, is also formed at the middle part of the model. Increasing shortening causes both flexural slip and flexural flow, respectively, in high-strain zones and in the lower parts of fault-related folds so that they are filled with weak material that evacuated beneath synclines and flowed into the anticline core. Upper layers dip as moderately to steeply (15° to 25°) as fault-related folds develop and were extended and thinned in crestal areas with possible extensional faulting and collapse structures as a result of buckling of the uppermost hanging-wall strata, whereas they were folded and thickened in adjacent synclinal areas (Figure 4c).
4. Discussion
4.1. Comparison to natural examples
Using a series of DE-models, we have model circumstances and structures in the contractional environment during progressive deformation. We make no attempt to simulate the exact structure of any natural example; however, in order to validate the final results, we compared one of the modelling results with a well-exposed décollement fold example developed in the Central Iran structural zone, near Isfahan city (Lat.: 33° 09′ 30′′ N, Long.: 51° 46′ 30′′ E) (Figure 5). In this area, the upper layers consisted of limestone and lower part included shale and silty shale so that there are interesting structures in this area such as asymmetric box-shape décollement fold (Figure 5d). The shape and characteristic of box-shape model that is depicted in the modelling results (e.g. Model 4 in Figure 3) are compatible with the mentioned box fold in the nature that consisted of weak and strong layers as overburden and the silty shale as the décollement layer (Figure 6). The nature of weak layer in lower part and the décollement thickness is similar to the structure in the field.
(a) Simplified topographic map of central Iran. The rectangle indicates the natural example located at central Iran structural zone, near Isfahan city (Lat.: 33° 09′ 30′′ N, Long.: 51° 46′ 30′′ E). (b) Geological map that is part of 1:100,000 TARQ quadrangle map from geological survey of Iran showing the location of the natural example. The lithology of the structure consists of limestone for upper layers and shale for lower part. The rectangle shows the exact position of the studied structure. (c) Perspective of the structure in nature near the road between Natanz city and Esfahan city in Iran.
(a) The geometry and characteristic of box-shape structure are compatible with (b) the box fold in model 4 (depicted in Figure 3) in final stage of shortening that consisted of weak and strong layers as overburden and the silty shale as the décollement layer.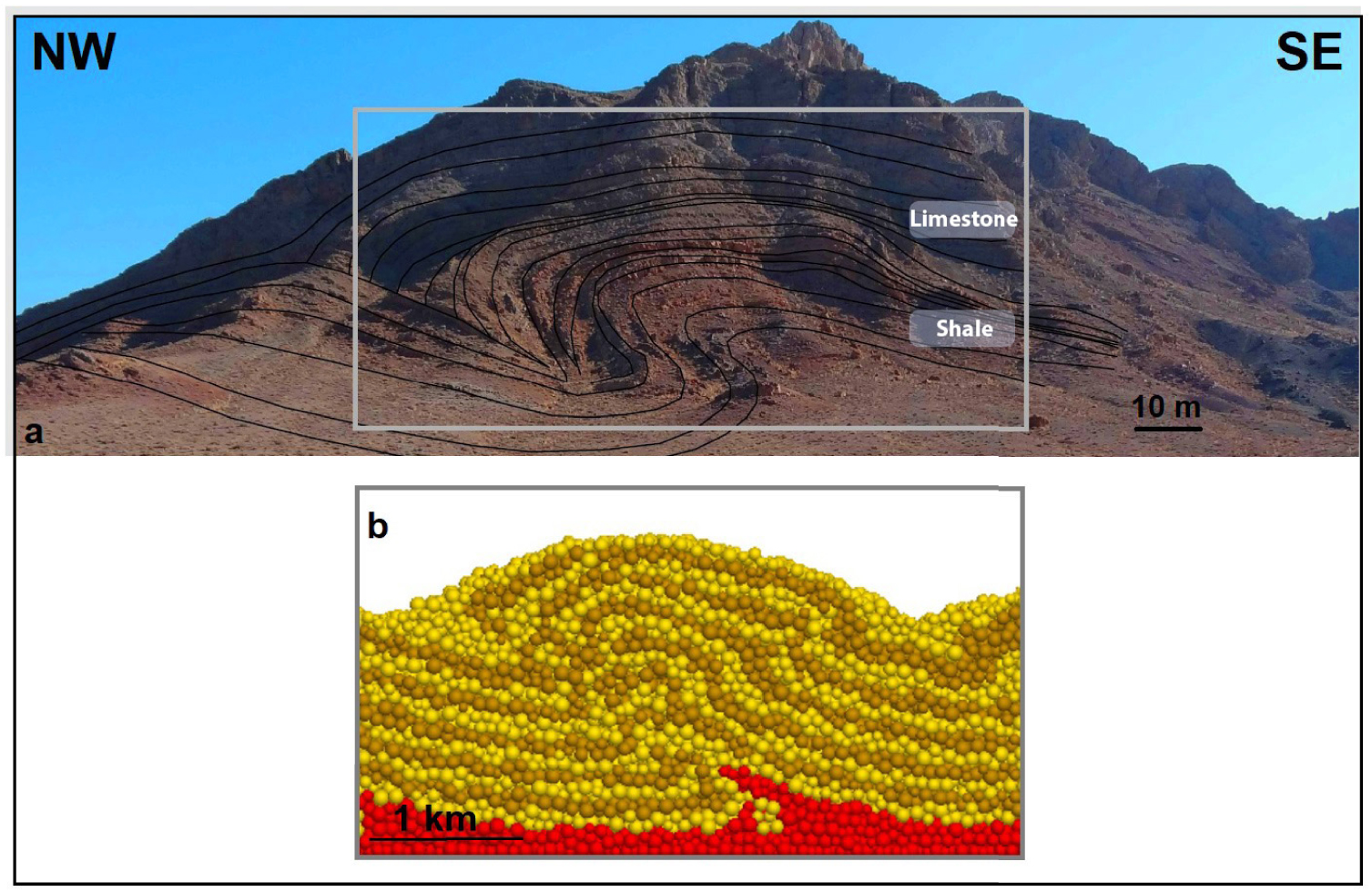
In addition to the natural example mentioned above, we can also compare them to other regional and tectonic-scale examples in order to verify the applicability of numerical models, for example, the Zagros fold-and-thrust belt (Iran). The Zagros fold-and-thrust belt is a structural zone which is associated with the significant influence of mechanical stratigraphy through sedimentary sequences and multi-décollement layers [e.g., Sherkati et al. 2005, 2006, Alavi 2007, Vergés et al. 2011]. Furthermore, the Zagros fold-and-thrust belt is often recognized as one of the regions in the world showing the best examples of large-scale décollement folds as shown by their regular and well-rounded geometries [Sherkati et al. 2005, Meng and Hodgetts 2019b]. The result of this study showed that the thickness changes of décollement horizon is one of the controlling factors of variations in the geometry, also as seen in the other example named the Zeloi anticline in the Zagros belt (SW Iran) that is a symmetric and asymmetric faulted décollement fold.
Another good example is the analysis conducted by Gu et al. [2021] about large-scale fold-and-thrust belt in South China. The stratigraphic succession is composed of competent layers separated by three main incompetent layers which act as décollements. The basal décollement, the Cambrian evaporites, played a dominant role in the deformation; the intermediate and upper décollement accommodated the displacement during deformation. Structural styles are dominated by faulted décollement folds with the breakthroughs of the fore- and/or backlimbs.
Comparison of the present study with previous researches show that the décollement thickness is one of the main controlling factors of the structural evolution and style of the tectonic setting.
4.2. Variation in geometry and kinematics of models as a function of décollement thickness and mechanical stratigraphy
Our modelling results indicated that the geometry and kinematics of structures developed above a décollement level significantly changes in dependence on the décollement thickness and number of weak layers, which are considered as our main variables in the present study. Décollement folds can also develop ahead of the upper tip of a bedding-parallel thrust [Poblet and McClay 1996] in more competent rocks and are often filled by less competent rocks [Homza and Wallace 1995]. Distinct décollement folds can only form if there is enough ductile material present in the décollement layer to penetrate the core of the growing anticline [Stewart 1996]. If there is not enough material to fill the core of the fold, fold growth will finish and shortening may be completed by faulting [Stewart 1996] as we can see in the models with less décollement thickness such as Model 1 that faulting developed by increasing shortening. Mitra [2002, 2003] presented a kinematic model for décollement folds that explains why a large number of geometrically different décollement folds can occur as seen in Figures 2, 3, and 4. Based on the modelling results it concluded that the fold develops in a competent rock layer that is underlain by a less competent unit. The fold mainly deforms by flexural slip with some additional faulting and fracturing. The wavelength of the fold is controlled by the thickness of the involved rock layers. Successive deformation leads to increasing amplitude and wavelength of the fold. This is motivated by the rotation of limb segments and hinge migration [Mitra 2003]. Looking into models such as Model 4 in Figure 3 revealed that in the models defined with more number of layers, the deformation formed by more complicated structures that is comparable with the findings presented by Mitra [2003] and it is possible to compare the décollement folding styles showed in (Figure 3) with the structural variations that is presented by Mitra [2003]. The similarity of the numerical models and kinematic models are significantly presented that the prepared numerical models are similar to the algorithms in nature (Figure 6).
As described in model results, contractional fault-related folds that formed as a result of horizontal shortening exhibit varied geometries especially wavelength and amplitude. Generally, it is demonstrated that the thicker basal décollement layer result in the higher the maximum flexural flow height. Similarly, surface uplift and fold amplification are mainly progressively affected by the basal décollement thickness so that uplift and fold amplitude increase from model with a thin décollement to models with intermediate to thick décollement. In this regard, the fold amplification (i.e., vertical growth of folds) with fold cores filled with basal materials through flexural flow led to a more significant uplift. Moreover, the number of ideal décollement folds and thrust-related folds and also their geometry developed in models influenced by the material strength and the décollement layer thickness, so that models with thick décollement layer result in more thrust-related folds and less ideal décollement folds at a specific shortening value. Box-like folds tend to show tight cores and broad, flat crests. Therefore, model results show that décollement thickness is able of effecting the fold geometries. With the growth of the fold, the fold limbs lengthen and become steeper, because of hinge migration and limb rotation [Mitra 2003]. As the fold tightens and the anticlinal area increases, the synclinal area decreases. Therefore, in the late stage of the deformation, the units almost return to their regional positions in the synclines [Li and Mitra 2020]. This mechanism is clearly visible in the models such as Models 6 and 8. It should be noted that this study considered just two main variables that are important in the formation of décollement folds, and the presented models are by no means perfect. Although considering more parameters led to hardness in distinguishing the determinants, for more understanding of the evolution of these kinds of folds, it is suggested that future models should incorporate other sets of controlling factors that are not considered in this paper.
5. Conclusions
In this research, we created a series of discrete element models (DEM) to assess the importance of geometric and mechanical factors in the evolution of décollement folds in sedimentary layers. The results reached from a series of modelling process showed us that shortening was mainly accommodated by décollement folds (sinusoidal, bulb- and box-like folds), fault-propagation folds, with thinning and thickening in the models. By changing the considered variables such as décollement thickness and number of weak and strong sedimentary upper layers, a range of models produced. The first groups or models with a thin décollement (Figure 2) accommodated by more distributed strain and décollement folds as box, lift-off and disharmonic folds, whereas more localized strain and contractional fault-related folds, such as faulted décollement and fault-propagation folds, are developed in intermediate to thick décollement models. Surface uplift and fold amplification are mainly progressively affected by the basal décollement thickness so that uplift and fold amplitude increase from model with a thin décollement to models with intermediate to thick décollement. Moreover, model results show that as the number of weak layers’ decreases, shortening was mainly accommodated by brittle deformation and faulting. Therefore, it could be concluded that with intermediate and thick décollement, the structural styles that developed are more complex. Finally, comprising the modelling results with the structures in the field such as central part of Iran or Zagros fold-and-thrust belt demonstrated that thickness changes of the décollement level and the overburden layers are both contributing factors in the structural styles of décollement folding during horizontal shortening.
Conflicts of interest
Authors have no conflict of interest to declare.
Acknowledgement
We greatly thank Professor Martin Schöpfer (University of Wien) for his careful help and comments regarding numerical modelling process.
1The velocity-Verlet integration is a numerical method used to integrate Newton’s equations of motion as this integrator strike a good balance between computational cost, stability, and accuracy.




 CC-BY 4.0
CC-BY 4.0