1. Introduction
In 1842 two articles were published in the Comptes-Rendus de l’Académie des Sciences which marked the beginning of guided optics and optical fibers. In the first article, J. D. Colladon describes the experience of the luminous fountain that he had just discovered the previous year [Colladon 1842]. Upon receipt of this article, F. Arago, then perpetual secretary of the Academy of Sciences invites Babinet to describe his experience of guiding light in a glass rod [Babinet 1842]. Although Babinet attached little importance to his discovery, he nevertheless mentioned two potential applications concerning lighting for microscopes as well as for medicine. These two ideas will be applied at the end of the 19th century and the beginning of the 20th century and will lead to the advent of optical fiber in the 1960s following the work of C. K. Kao, Nobel Prize for Physics in 2009 [Kao and Hockham 1966].
If the telecommunications industry has been a major player in the development of optical fiber technology, the characteristics of these waveguides quickly proved to be very attractive for other applications such as lasers and sensors [Koester and Snitzer 1964; Culshaw and Kersey 2008]. Indeed, they are small in size (125 μm in diameter), insensitive to electro-magnetic interference, passive and resistant to harsh environment. In addition, sensors based on conventional optical fibers (telecom fiber) benefit from all the technology already developed for telecommunications networks (light sources, detectors, optical components, etc.). Optical fiber-based sensors therefore offer many advantages over mechanical or electrical sensors. In particular, the monitoring of the physical parameters (such as temperature, strain, chemical concentrations, etc.) can be carried out in a distributed manner all along the fiber. Measurement range (maximum length of the sensing fiber) can vary from a few centimeters to several tens of kilometers, while the spatial resolution can vary from less than one millimeter [Luo et al. 2019] to a few meters [Palmieri and Schenato 2013]. Another distinctive feature of optical fiber sensors is the capability of having many sensing points along a single fiber or cable. This can be obtained either by exploiting scattering phenomena in the so-called distributed sensing, with more than 1,000,000 sensing points per fiber [Denisov et al. 2016], or by using Fiber-Bragg gratings (FBGs) multiplexing, up to thousands of sensing point per fiber, in some specific implementation [Guo et al. 2015] and [Götten et al. 2020]. However, one major drawback is the cost of the interrogators, which is quite high compared to those employed by most classical sensor technologies, such as thermocouples or strain gauges. Nonetheless, the cost per sensing point becomes favorable for fibre optic sensors (FOS) when large numbers of sensing points are required.
In this review we focus our interest on fiber sensors for strain detection, of interest not only for geosciences but also for medical sciences. In Section 2, we describe the three main scattering mechanisms involved in the detection, i.e. Raman, Brillouin and Rayleigh scattering. Section 3 is devoted to fiber fabrication (FBGs and nanoparticle-containing fibers). Long-range applications in geophyscial and geotechnical areas are described in Section 4. Last section deals with short-range applications for the medical domain.
2. Scattering mechanism
Scattering phenomena occurring in optical fibers are the ground principle of operation of the present generation of distributed optical fiber sensors [Bao and Chen 2012; Schenato 2017], as they provide a continuous reflectivity in each span of the fiber that can be localized with optical time- or frequency-domain reflectometry methods.
(a) Sketch of elastic scattering occurring in an optical fiber. (b) Wavelength (𝜆) dependency of scattering processes in optical fibers when the input light is a laser having wavelength 𝜆0.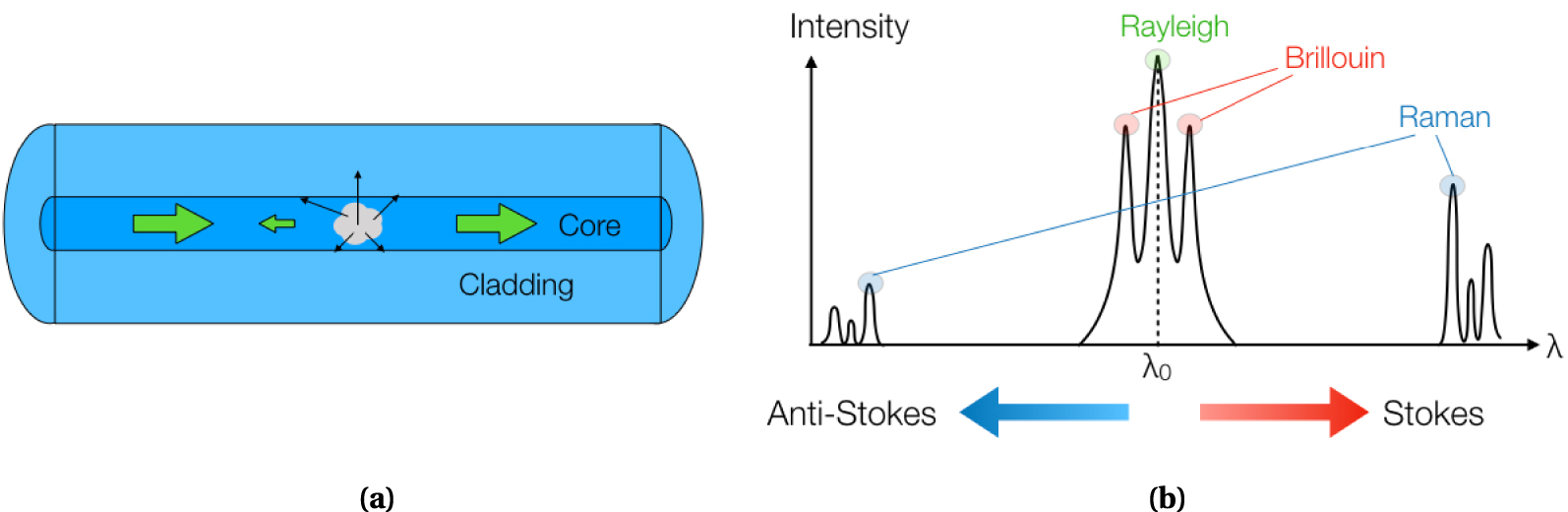
Figure 1(a) shows a sketch of the scattering events that occur in an optical fiber, which are caused by the interaction between the incoming light and the optical medium. When light is propagating into an optical fiber, it interacts with the constitutive atoms and molecules that are part of the fiber. The light electric field that travels in each section of the fiber generates time-dependent electric dipoles, which cause secondary light waves that scatter around the fiber. The scattering signal has a power several orders of magnitude inferior to the input light, and therefore it does not affect the light propagation in a significant matter. The light scattered by the fiber instead is emitted in a broad range of directions; a part of this emission is coupled backwards into the fiber, and constitutes the so-called backscattering that we can observe in each section of the optical fiber. Distributed optical sensors interrogate the backscattering signal that is continuously emitted by the fiber under test, and detect the intensity changes and the frequency shift occurring in each section of the fiber. In this regard, distributed sensors differ from other optical fiber sensors because they do not use devices that are inscribed (such as gratings) or externally fabricated (such as interferometers) into the fiber to act as a sensing device, but rather the fiber itself behaves as a continuous sensor, resolving the physical measurand along the fiber length [Bao and Chen 2012].
Distributed sensors can interrogate Rayleigh, Raman, or Brillouin scattering phenomena, which have a wavelength dependency illustrated in Figure 1(b). Rayleigh scattering is used in several distributed sensors, most notably by optical backscatter reflectometry (OBR) [Froggatt and Moore 1998] for short-distance sensing, and phase optical time-domain reflectometry (𝜙-OTDR) for long-range sensing [Eickhoff and Ulrich 1981]. The key characteristic of Rayleigh scattering is that the reflected waves have the same wavelength as that of the input wave, and therefore it is an elastic scattering. Optically, it can be modelled as a space/time-dependent variation of the refractive index of the fiber core; since the refractive index of silica depends on the temperature and on the strain exerted on the fiber, the interrogation of Rayleigh scattering is directly linked to distributed measurements of strain or temperature [Bao and Chen 2012; Froggatt and Moore 1998].
Inelastic scattering instead involves a change of frequency of the light waves scattered by the fiber with respect to the input wave. The wavelength of the light backreflected by inelastic scattering events has both components that are red-shifted (Stokes) and blue-shifted (anti-Stokes) with respect to the input light [Bao and Chen 2012]. Raman scattering involves the widest wavelength shift between the input and Stokes/anti-Stokes components, about 90 nm for sensors operating at 1550 nm. Although not used directly in strain sensing, Raman scattering is at the base of long-range distributed temperature sensors, as the ratio between the anti-Stokes and Stokes light intensity depends on the temperature [Farahani and Gogolla 1999]; for this reason, Raman scattering is one building block of distributed temperature and strain sensors (DTSS) which are used in pipeline monitoring [Inaudi and Glisic 2010].
Scattering trace of enhanced backscattering fibers, reporting the return loss analyzed on OBR instrument for each fiber section. (a) Analysis of a high-gain fiber and determination of the scattering parameters; (b) Attenuation uniformity of a low-loss fiber, reporting the one-way fiber attenuation in each section.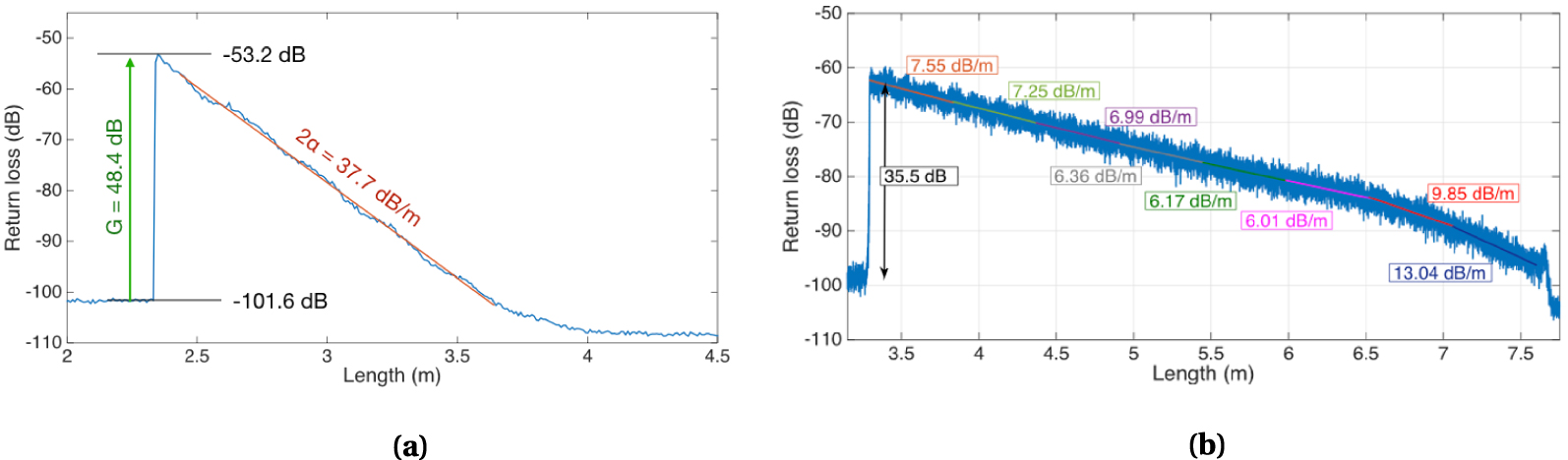
Brillouin scattering involves the acoustic oscillations of glass, and for this reason it allows the detection of dynamic strain or acoustic signals along the fiber [Coscetta et al. 2020]. The acoustic fields acting on the fiber induce periodical variations of the fiber refractive index due to the elasto-optic effect, which results in a backreflected wave having a slight wavelength shift (about 90 pm at 1550 nm) that is proportional to the acoustic wave velocity. A wide range of distributed strain and acoustic distributed sensors has been developed, either analyzing the light reflected by the fiber, or using two optical sources at each side of the sensing fiber [Brillouin optical time-domain analyzer (BOTDA) Li et al. 2008a].
Rayleigh scattering (and in minor part inelastic scattering) is a loss factor of optical fibers, and for this reason research efforts have been addressed to design single-mode fibers (SMFs) that minimize light scattering, down to the current attenuation of 0.14 dB/km [Hasegawa et al. 2018]. The advent of distributed sensors, however, has recently reversed the trend [Tosi et al. 2020b]: as scattering is the signal detected by distributed sensors, researchers have tried to engineer fibers that have a higher scattering, at the expense of higher propagation losses. Enhanced backscattering fibers (EBFs) accomplish two goals: they return a higher signal-to-noise ratio in strain sensing, which has improved the accuracy in shape sensing technologies for medical imaging [Parent et al. 2018]; and they enable scattering-level multiplexing (SLMux) [Tosi et al. 2020b] which converts a single-channel interrogator into a multi-fiber sensing network, which is essential for shape sensing or rigid medical devices in three dimensions [Beisenova et al. 2019].
A successful implementation of an EBF makes use of MgO-based nanoparticles elongated in the fiber core, to increase the local reflectivity by a significant amount. Figure 2(a) shows the scattering trace of such EBF, which achieves a scattering increment of about five orders of magnitude [Tosi et al. 2020a]. The scattering gain is defined as the increment of scattering provided by the EBF with respect to a SMF, and is measured at the EBF–SMF interconnection; the fiber reported in Figure 2(a) has a gain G = 48.4 dB, and is one of the highest values recorded so far as it approaches the reflectivity levels of weak gratings. Conversely, EBF fibers have a high two-way attenuation (2𝛼), which is estimated as the slope of the scattering trace (37.7 dB/m). Different designs of the MgO-based fibers have shown attenuation ranging from 300 dB/m down to the recently reported 14.3 dB/m [Tosi et al. 2021]. Since nanoparticles have a rather random distribution in the fiber, in terms of local density and relative position with respect to the core, the attenuation is not constant but rather fluctuates: Figure 2(b) shows the attenuation of a low-loss MgO-based nanoparticle-doped fiber, which ranges from 6.0 dB/m to 13.0 dB/m two-way, and is one of the lowest values reported so far for high-scattering fibers.
The main alternatives to the MgO-doped fibers are based on increasing the local reflectivity in the fiber through the inscription of nano-gratings [Yan et al. 2017], distributed Bragg reflectors [Monet et al. 2019], nanopores [Reupert et al. 2019; Donko et al. 2018; Blanc et al. 2020] or other nanoparticles composition [Veber et al. 2019; Bulot et al. 2021]; most relevantly a 25-cm inscription of a broadband weak reflector using a fs laser, achieving up to 45 dB scattering gain, was reported by Yan et al. [2017].
3. Optical fiber fabrication
Optical fibers are generally obtained by drawing at high temperature a rod called a preform. The advent of preform preparation processes by chemical vapor deposition in the 1970s significantly reduced optical attenuation, from 1000 down to 0.2 dB/km in 10 years. Vapor phase deposition consists of reacting gases (SiCl4 and O2 for example) to form soot (SiO2) which is deposited on a substrate. The main preform manufacturing processes are Outside Vapor Deposition (OVD), Vapor Axial Deposition (VAD) and Modified Chemical Vapor Deposition (MCVD). These processes have been developed in order to prepare a “perfect” glass: (i) the most homogeneous glass to reduce light scattering (i.e. to improve the transparency) and (ii) to limit the presence of defects or impurities that can induce absorption bands. The fibers presented in this review rely instead on the presence of these defects. Defects such as Oxygen Deficient Center (ODC) make glass photosensitive [Skuja 1998] and allow to photo-inscribe Bragg gratings, and the presence of nanoparticles increases light scattering.
3.1. Fiber-Bragg gratings
Initially developed for telecommunication industry, FBGs are now commonly used in sensing applications [Kashyap 2009], also in harsh and extreme environments [Mihailov 2012; Kumari et al. 2019]. Basically, FBG is an optical filter that reflects targeted wavelengths. To reach this goal, the structure of a FBG corresponds to a longitudinal periodic modulation of the refractive index of the fiber core. The interaction between the light and the FBG can be analyzed through the Bragg condition expressed as 𝜆B = 2 ⋅ neff ⋅𝛬G where neff is the effective refractive index seen by the light, and 𝛬G is the period of the index variation. All the Bragg wavelengths (𝜆B) satisfying this condition are reflected. As both the refractive index and the grating period vary with temperature or mechanical perturbations, FBG can be used as sensor by measuring the Bragg wavelength shift [Kersey et al. 1997]. The most common manner to obtain a FBG is by using the photo-sensitivity of the fiber core. Doping elements such as germanium (commonly used in telecommunication fibers to raise refractive index) induce refractive index increase when they are exposed to visible or UV light. To obtain the spatial modulation in the longitudinal direction, a diffraction grating such as a phase mask is used to create interference pattern. FBGs can be discriminated, based on their formation mechanism. The most common FBG is the type I. Small refractive index change can be obtained by irradiating with UV light (typically 244 nm) to excite the ODC. Densification of glass allows to increase refractive index change. Such FBG can operate to temperature up to 400–500 °C. In addition, type I FBGs can be written through different coatings also by using IR femtosecond laser [Habel et al. 2017]. For type II, a high peak power UV femtosecond laser is used. Refractive index change is caused by multiphoton ionization which modifies the amorphous glass network. High reflectivity and high operating temperature (800–1000 °C) characterize these FBGs. As they necessitate a single shot laser exposure, type II gratings can be photowritten while the fiber is drawn [Askins et al. 1994].
The photosensitivity of fibers can be enhanced by exposing the fiber to high pressure of hydrogen (“hydrogen loading”). Nonetheless, according to the literature, this process may hamper the temperature stability of the FBGs, which can be recovered upon proper thermal treatment of the fibers, such as thermal annealing [Li et al. 2008b], which is a well-known method to obtain regenerated FBGs [Polz et al. 2021]. Hydrogen loading, in this sense, is important, but not essential, to obtain an index modulation with sufficient magnitude for extreme temperature operation [Canning et al. 2008, 2010]; nonetheless, it has been shown that regeneration can be obtained even without hydrogen loading, although for FBGs limited to lower temperature operation [Linder et al. 2009].
Another class of Bragg gratings is the so-called long-period gratings (LPGs) [Wang 2010]. They differ from standard FBG because their refractive index varies with a period of hundreds of micrometers. Due to the longer grating period, the fundamental core guided mode couples to discrete, forward-propagating cladding modes, which quickly attenuate during the propagation. Therefore, the transmission spectra present a series of loss bands corresponding to a distinct cladding mode coupling. The corresponding transmitted peak-loss wavelength is given by , where neff and are the effective index of the mode travelling in the core, and the LP0m cladding mode to which the core mode is coupled, respectively. Moreover, other single point sensors, exploiting interferometric effects such as Fabry–Perot and Michelson cavity can be directly fabricated on an optical fiber [Miliou 2021]. Despite the interest due to the intrinsic high resolution and accuracy, these sensors are difficult to multiplex and, therefore, they are outside the scope of this review.
3.2. Fibers containing particles
The MCVD technique is the process used to prepare preforms drawn into particle-containing fibers reported in this review [Blanc et al. 2011]. Since its development in the 1970s, this method is commonly used in industry to prepare specialty optical fibers such as fiber lasers or sensors [Li 2012]. As a first step, vitreous layers are deposited inside a silica tube. The composition of those layers are determined by the use of different reactive gases carried in the tube by oxygen. Gaseous species are limited to SiCl4, GeCl4, POCl3, fluorine and boron carriers. Additive elements (such as Mg) are incorporated during the solution doping step. In this method, a porous layer, deposited by MCVD on the inner surface of the silica tube, is soaked with a solution of salts of metal chlorides (e.g. MgCl2) dissolved in alcohol or water. After removing the solution, the porous layer is dried, densified and vitrified at high temperature (up to 1800 °C). Finally, the tube is closed during the so-called collapse step (at temperature higher than 2000 °C) to form a rod called preform. To draw this preform into fiber, temperature must be higher than the softening temperature (≈1650 °C for silica glass), typically 2000 °C.
SEM images of the longitudinal cross-section of (a) a preform and (b) a fiber containing nanoparticles. The drawing axis is horizontal. (c) SEM image in cross section of a fiber containing nanoparticles.
Typical SEM images of the preform and the fiber containing MgO-based silicate nanoparticles are presented in Figure 3. Particles, whose average diameter depends on the concentration in the doping solution, are whiter than the glass matrix because magnesium is mostly partitioned in the silicate particles. However, their composition follows a complex path. Indeed, it has been reported that the composition of the particles depends on their sizes: a higher concentration of Mg is measured in the largest particles [Blanc et al. 2019]. For particles much larger than 10 nm, the drawing stage is an important step to be considered as they can elongate and even break-up due to Rayleigh–Plateau instability [Vermillac et al. 2017, 2019]. Then, characteristics of the porous layer, concentration of the doping solution and drawing conditions must be carefully determined to optimize particle features (size, density, morphology, etc), i.e. to tune light scattering properties.
4. Long-range applications in geophysical and geotechnical applications
In the last 20 years, distributed optical fiber sensors have been proposed to address monitoring problems in many different fields. One particular field of application where the exploitation of distributed optical fiber sensing has greatly flourished is geophysical and geotechnical monitoring. Indeed, the capability of measuring different physical parameters over very long distances with a high spatial density of measuring points, the remote powering and control, and the sensor ruggedness make this technology befitting to tackle the specific challenges of these fields of application. Since these monitoring fields often require covering large areas, distributed FOS (DFOS) has started to be used. Some DFOS solutions have even reached the market and have become well-explored and widely-accepted tools.
In this section, we will introduce some selected examples of DFOS for geophysical and geotechnical long-range monitoring. With the term long-range, we specifically intend those applications where the sensing optical fiber length ranges from a few tens of meters up to some kilometers. Although many specific applications of DFOS exist, we have opted to address and summarize only some selected works related to static strain and temperature monitoring of geohazards, and seismic monitoring. The interested reader is referred to the ample reviews of literature for details [Schenato 2017; Fenta et al. 2021; Shi et al. 2021].
The most commonly used distributed sensing technology for strain and displacement monitoring is the Brillouin-scattering-based sensing. In contrast, Raman-scattering-based sensing, which is insensitive to strain, is the most used for temperature monitoring. Additionally, Rayleigh-scattering-based sensors are also used for static strain monitoring in geotechnics, but they are mostly employed for seismic monitoring.
4.1. Distributed strain sensing
Regarding static strain monitoring, DFOS are widely used for monitoring geomorphic processes e.g., for landslides, subsidence and ground motion, levee, and dike. Landslides are often triggered by heavy rainfall that saturates the soil, thereby destabilizing it and determining its failure under shear stress. Early ground movement detection is crucial to give enough time to the authorities for the evacuation of the population. With the aim of monitoring the strain exerted by the soil movement, the optical fibers need to be coupled to the soil, so to be dragged by the ground movement: when the soil undergoes collapse or sliding, the fiber gets stretched accordingly. The sensing optical fiber cables are often embedded in shallow trenches or simply anchored to the ground through stakes. Depending on the installation, both shallow landslides and slow slope movements can be detected through the elongation induced in the sensing fiber.
Strain field vs. time along a 16 m-deep borehole drilled into a landslide in Japan as well as the soil stratigraphy and precipitation information [reprinted with permission from Kogure and Okuda 2018].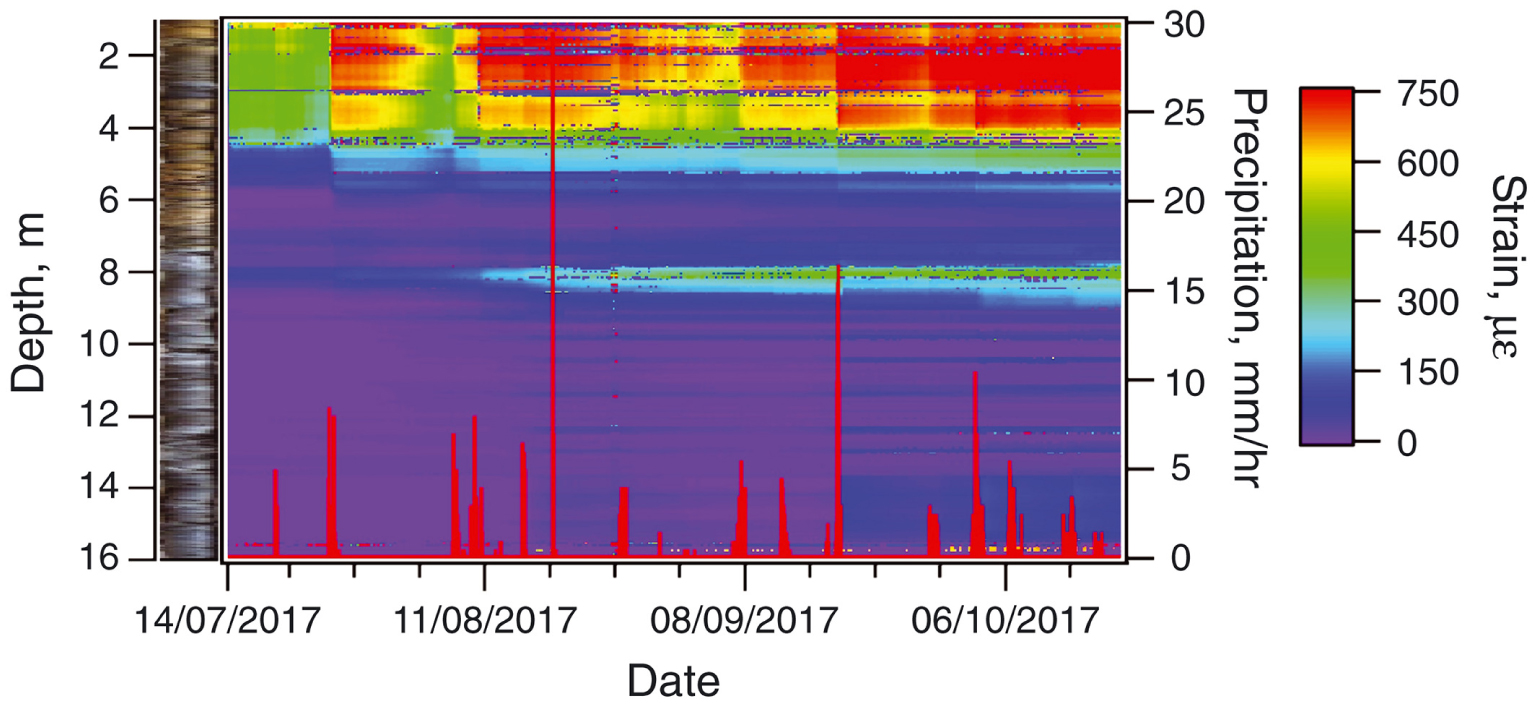
One of the first examples of landslide monitoring employing Brillouin-based DFOS is provided in Yoshida et al. [2002]. The landslide area, consisting of approx. 70 ha (1500 × 500 m) was instrumented with approximately 1200 m of fiber. The fiber was arranged in a square grid layout running 90 m in the landslide moving direction and 80 m in the transverse one. Part of the cable was buried under the ground at 50 cm depth, and part was anchored via fixing metal plates. The spatial resolution of the Brillouin interrogator was limited to 1 m, enough to provide a detailed map of the strain field in the monitored area. A similar approach, with a Brillouin-based sensor and with the cable transversely intercepting the landslide movement, has been proposed in Iten et al. [2009]. In this work, only 80 m of cable was laid in the ground beneath a hiking path, inside a small trench, and coupled to the soil by micro-anchors. In the same paper, mention is made of the implementation of a geotechnical DFOS monitoring system applied to a 60 km LNG pipeline section in Peru, affected by geohazards.
Another approach, enabled by the long range capability of the DFOSs, consists in installing the fiber in loop configuration through an array of soil nails, inclinometers tubes, and frame beams, such as in Shi et al. [2008]. A similar deployment was also proposed by Hoepffner et al. [2008], at the Aggenalm landslide (Bavarian Alps) where a Brillouin interrogator (along with a Raman interrogator for temperature compensation) was used to probe a 90 m long sensing cable, partly embedded in the soil and partly inside an inclinometer borehole in a loop configuration. More recently, in Kogure and Okuda [2018], a DFOS-based on Rayleigh backscattering, was installed in a borehole to a depth of 16 m to detect the vertical strain profile of a landslide with 10 cm spatial resolution. Despite the limited length of the fiber deployed in the borehole, the overall cable length was more than 450 m with the remote interrogator hosted at more than 200 m from the borehole in a safe structure. In this study, the strain variation along the borehole depth was correlated with the soil stratigraphy, while its temporal evolution showed a clear correlation with the precipitation data that triggered the landslide (Figure 4).
Similarly, Zhang et al. [2018] embedded a fiber optic cable into a borehole and mapped the compaction or rebound zone along the vertical profile up to 150 m depth by means of Brillouin-based technique. The simultaneous deployment of DFOS-equipped boreholes and cables laid across the boundary of a landslide has also been used to produce and validate more accurate models on the shear deformation at different locations of a landslide as in Sang et al. [2019].
The limited invasiveness of the fiber optic cable allows also the integration of DFOS in soil anchors, which are geotechnical sub-horizontal reinforcements for remediation of unstable slopes. A soil anchor is a hollow steel bar, installed by a self-drilling technique in the soil or rock, and it is often integrated with tendons cemented in the inner hole. In Cola et al. [2019], the authors installed an optical fiber cable within the hole of some soil anchors, side-by-side to the tendons and cemented with them. The anchors were 40-m long and the fiber cables were interrogated by a Rayleigh-based OFDR with 1 cm spatial resolution with the aim of determining the distributed strain profile along the nails. The system ultimately measures both the axial force distribution in the anchor and the soil–anchor interface friction. More specifically, the integration of DFOS makes possible to infer information about the health condition of the anchor, but also promotes the anchor itself as a sensor, allowing to probe the evolution of the stress field in the surrounding soils and therefore providing information about the landslide, such as the position of the sliding interface. Similarly, information about the structural health and about the soil friction can be inferred by embedding DFOS in foundation piles under static load testing [Pelecanos et al. 2018; Bersan et al. 2018].
Although those installations could resemble an inclinometer, DFOSs measure strain or its variation, whereas inclinometers measure slope inclination changes and actual deformation. Despite that, several authors have tried to implement DFOS inclinometers equipping borehole tubes or casings, up to some tens of meters depth, with three or more optical fibers and exploiting the Euler–Bernoulli beam theory and relying on the application of a quadratic integral method or classical conjugate beam method [Lenke et al. 2011; Minardo et al. 2014; Sun et al. 2016; Huang et al. 2018; Minutolo et al. 2020; Zhang et al. 2020]. An example of one of this inclinometer, installed in a landslide at the Three Gorges Reservoir Area is shown in Figure 5.
(a) Example of fibers arrangement in a DFOS inclinometer. (b) Displacement measured by a standard inclinometer and a DFOS-based inclinometer during the evolution of a landslide [reprinted with permission from Sun et al. 2016].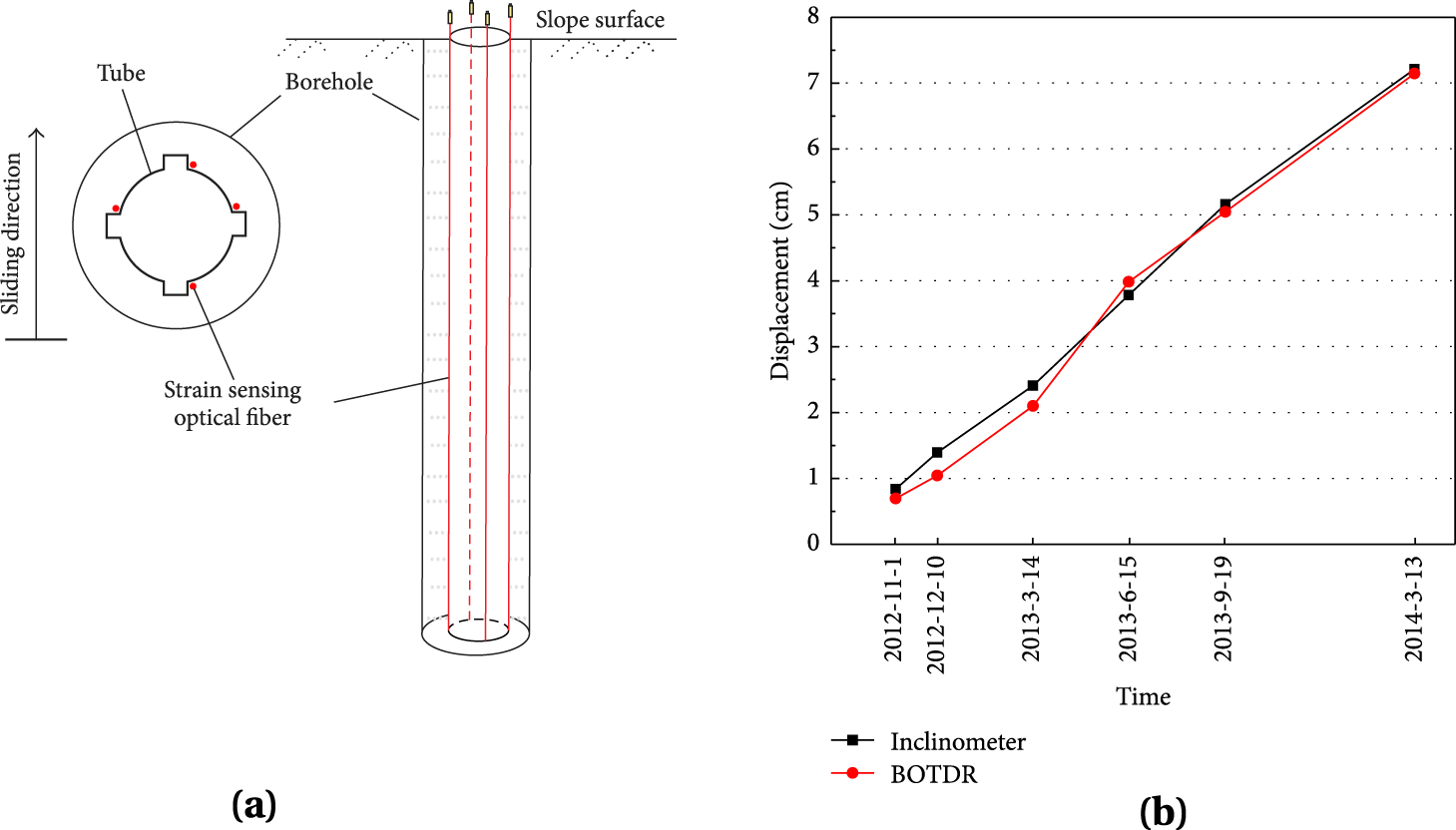
Over the years, the improvement in the spatial resolution of the interrogators, allowed to perform experiments in physical models, where centimeters-scale spatial resolution is required due to the limited size of the setup. For example, in Schenato et al. [2017], the researchers instrumented a large-scale physical model (6 × 2 × 3.5 m) with 30 m of engineered corrugated fiber cable deployed in a meandering path oriented along the landslide direction. The fiber was deployed below the surface at a pre-determined sliding interface and the corrugation on the fiber sheath guaranteed sufficient coupling to the soil. By means of artificial rainfall, the slope was driven to collapse while monitoring the strain along the fiber. The authors were therefore able to provide a detail map of the strain spatial distribution and evolution over time, with indication about the coupling efficiency and even early signs of slope failure. Figure 6 shows the physical model on the left and the map of the strain field at different stages of the landslide and soil–cable coupling: from left to right are shown the initial coupling, the full coupling, the partial coupling and the post-collapse phase. Similar experiments were carried out by other groups, but in smaller physical models, exploiting both Brillouin- [Damiano et al. 2017; Song et al. 2017; Darban et al. 2019] and Rayleigh-based techniques [Papini et al. 2020].
(a) Physical model of a landslide instrumented with optical fiber for strain sensing. (b) Evolution of the strain field, with reference to the coupling between the collapsing soil and the fiber cable [reprinted and modified with permission from Schenato et al. 2017].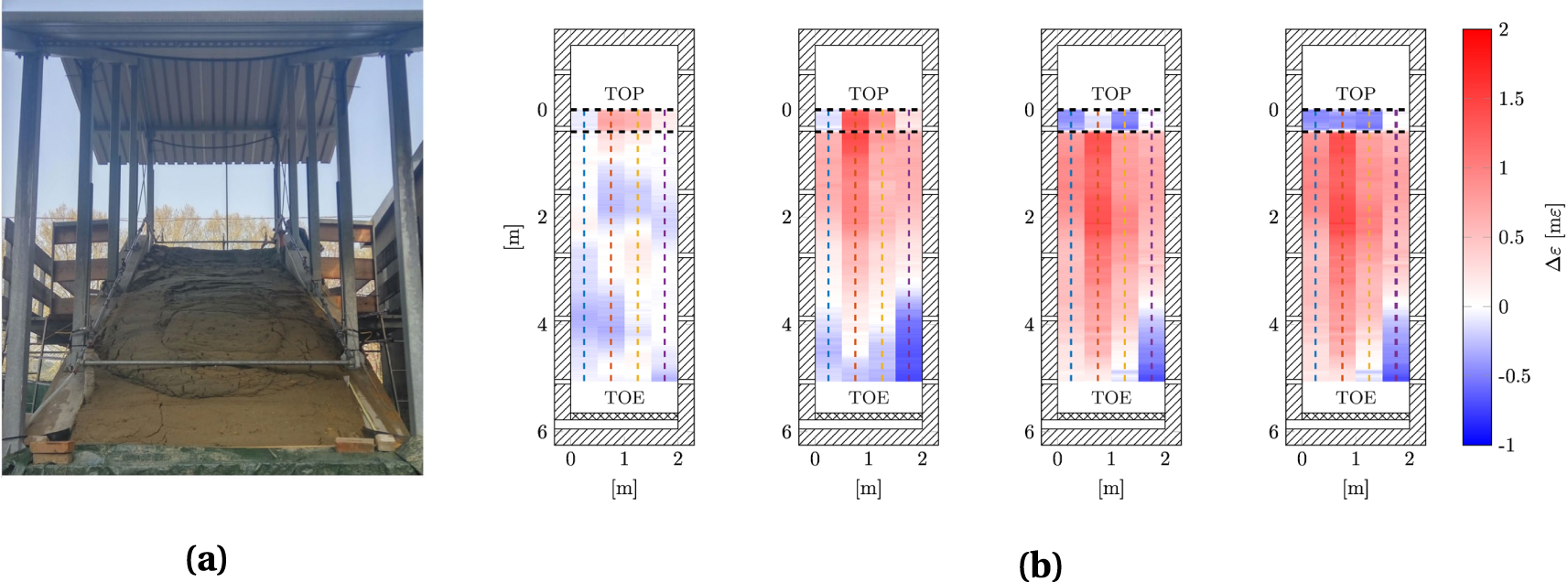
Distributed strain sensing has been applied also to river embankments since the very early 2000s [Naruse et al. 2000; Zhang et al. 2010; Lei et al. 2012; Zhou et al. 2013]. The aim of these works was the early detection of collapse, via Brillouin-based technique for strain monitoring. Typically, the fiber cables were buried at few tens of centimeter depth in the embankment scarps in meandering path whose strands follow the direction of the embankment. Only few of them implemented temperature compensation with portion of fibers left in strain-free conditions or by employing an additional Raman-based system. To improve the spatial coverage of sensors over the embankment scarp, Nöther et al. [2008] and Artières et al. [2010] proposed the use of engineered geotextiles equipped with optical fibers.
4.2. Distributed temperature and pressure sensing
Embankment monitoring is also one of the most early application of DFOS for the distributed measurement of temperature within the soil, via Raman-based technique. The goal of this kind of monitoring is the detection of anomalous temperature behavior within the soil, often correlated to dangerous filtration path and seepages, which may lead to the erosion and the final collapse of the structure. In order to effectively identify critical events, it is mandatory to have an a-priori long term measurement campaign to determine the normal thermal behavior of the structure, which fluctuates with season. Furthermore, the sensing system has to probe the structure with an adequate spatial resolution, as early filtration paths are likely very small. Current standard commercial Raman interrogators provide a spatial resolution of 0.25–1 m over a range of some kilometers. Nonetheless, despite this long range capability, in most of the reported installations the fiber length is limited to some hundreds of meters [Shanafield et al. 2018]. The accuracy needed to detect anomalous temperature change has to be quite large, in the order of 0.1 °C, as very often the filtration water flow rapidly reaches thermal equilibrium with the surrounding soil. This usually requires long measurement time, in the order of some minutes, still matching with the needs of this field of application [Bersan et al. 2019].
Temperature measured in the embankment during the heating of the hybrid cable according to the “active” thermometric method (curves with different colours correspond to different time stamps). The section of the cable where the temperature drops corresponds to the seepage position, where the soil has a larger thermal conductivity [reprinted with permission from Pyayt et al. 2014].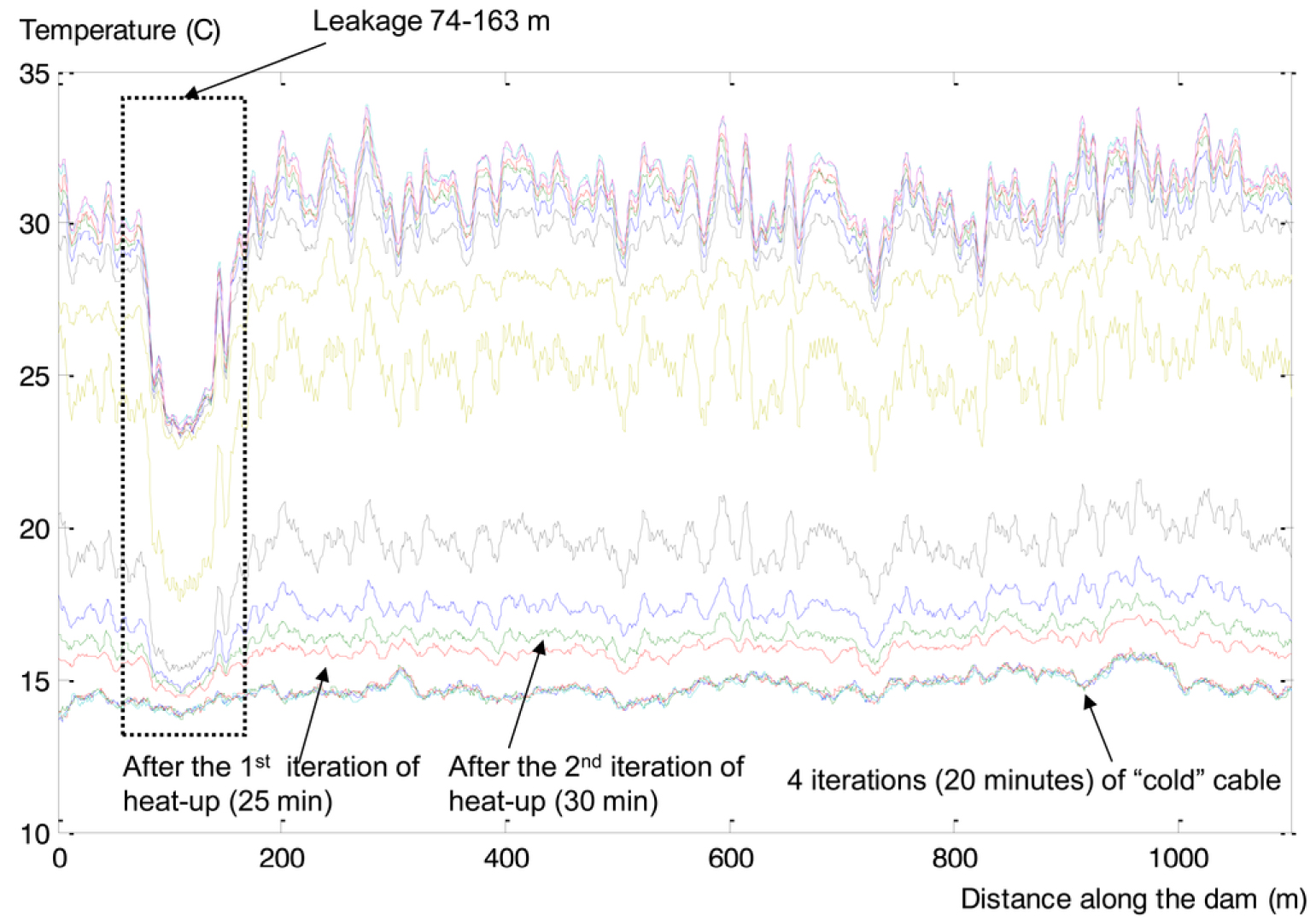
Based on these premises, the early installations of temperature DFOSs in embankments [Albalat and Garnero 1995; Fry 1997; Aufleger et al. 1997; Johansson and Sjödahl 2004], struggled to effectively identify such anomalies. Nowadays, much of the research on the use of DFOS in embankment monitoring are based on the so-called “heat-up” or “active” thermometric method [Perzlmaier et al. 2004; Sayde et al. 2010; Cola et al. 2021]. This method consists of measuring the temperature along an heated optical fiber; usually the heating is achieved by injecting current into electrical wires bundled with the fibers in the same cable. Instead of the actual temperature, the time-constant of the heating and cooling phases are used to characterize the degree of saturation of the soil and also to track active filtration flows that dissipate the heat more rapidly [Pyayt et al. 2014], as shown in Figure 7.
About the use of other DFOS technologies for temperature measurement, few works can be found in the literature, either Brillouin- or Rayleigh-based ones: these solutions require the fibers not to be affected by the strain and are mostly limited to small-scale physical models [Zhu et al. 2007; Wang et al. 2016; Bersan et al. 2017; Cheng et al. 2021].
Alternatively, the distributed measurement of pressure has been envisaged as an effective way to monitor an embankment’s health. Pore-water and total pressures lead to the development of hydraulic forces that affect the dam’s shear strength, determining a dangerous localized strain. These processes occur well before the collapse but may lead to a rapid failure as they determine the backward erosion piping mechanism. These anomalous pressure regimes, if detected, could be used as precursory signals of failure because they take place well before the strain arises, which initially occur without any surface evidence. Unfortunately, high spatial and pressure resolution are required for that aim. Despite many types of FBG-based pressure sensors having been reported in the literature [Zhou et al. 2006; Wei et al. 2018; Schenato et al. 2019; Ho et al. 2021], to date, there have been only a few examples of distributed pressure sensors capable of achieving such performances, and they have been implemented only in bare fibers [Teng et al. 2016; Kim et al. 2016; Schenato et al. 2020a] by means of Brillouin-based techniques. Recently, a proof-of-concept of a very high-sensitive, high-spatial-resolution distributed pressure sensing cable based on an engineered cable cross-section and suitable for hydrological applications has been proposed [Schenato et al. 2020b]. The cable was designed to transfer effectively the external pressure into strain affecting the embedded fiber, then measured by means of a Rayleigh-based technique.
4.3. Distributed acoustic sensing
An additional technology that has entered powerfully in geophysics is the distributed acoustic sensing (DAS) technology. DAS is based on the coherent-detection of the Rayleigh backscattering generated by a narrow band source. Upon the illumination of a coherent source, the heterogeneity and density fluctuations of the silica generate coherent backscattering signals that vectorially sum, resulting in a specific interference pattern, which encodes the spatial distribution of the heterogeneity and the corresponding relative optical phases. Strain and temperature variations affect and perturb that interference pattern, and therefore, they can be measured through its variation. Several optical schemes to retrieve such a pattern at a very high speed have been implemented, all substantially based on the so-called 𝜙OTDR [Juškaitis et al. 1994; He and Liu 2021]. This technique promotes the optical fiber to act as an array of in-phase geophones, measuring the surrounding acoustic or vibration field with a resolution of some meters over a range of several kilometers [Zhan 2020]. Differently from a geophone, which records ground motion (velocity), a DAS typically measures strain-rate, and the data from the DAS requires a proper spatial integration to be converted into geophone-equivalent data [Lior et al. 2021].
(a) Raw DAS data (Ten seconds of raw distributed acoustic sensing (DAS) data along the last 5 km of the array): coherent signals from ocean and seismic waves propagating both landward and seaward across the array can be identified. (b) Mean power spectral density (PSD) of raw DAS strain data of 1 h of data in the same position of the left plot [reprinted with permission from Williams et al. 2019].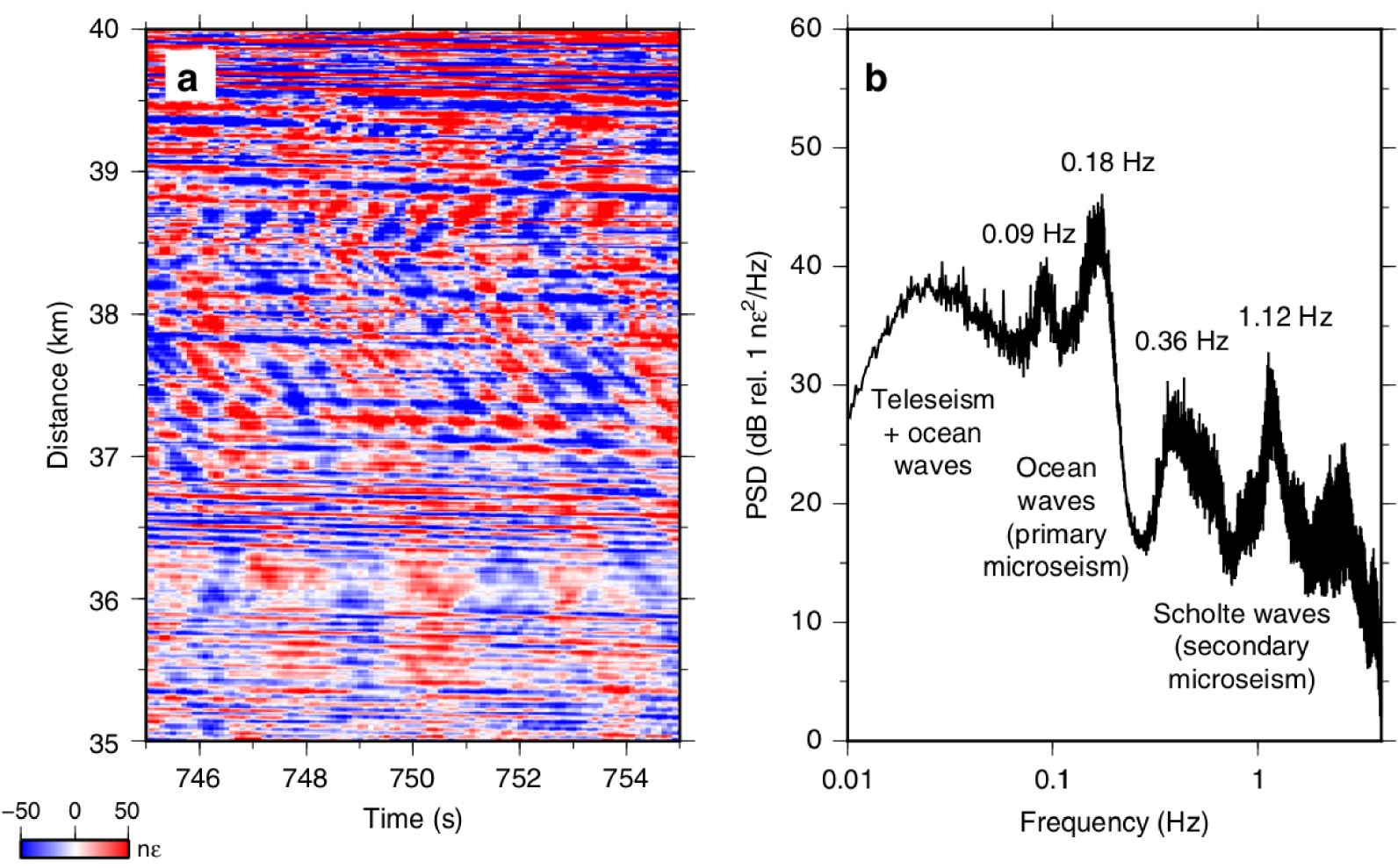
Initial applications of DAS in geophysics have regarded the vertical seismic profiling in the oil and gas industry [Mestayer et al. 2011; Daley et al. 2013; Mateeva et al. 2013; Parker et al. 2014]. Nowadays, several works have been published about the use of DAS as long-range distributed earthquake seismometers [Lindsey et al. 2017; Jousset et al. 2018; Williams et al. 2019; Sladen et al. 2019; Lellouch et al. 2021]. In these works, dark fibers, i.e., unused laid optical fibers with no traffic running on it, in existing standard telecom cables have been probed with a DAS. These works showed that even micro-earthquakes hundreds of kilometers away can be successfully detected [Sladen et al. 2019]. In Williams et al. [2019], the system was shown to be able to record the seismic waves of different types (see Figure 8). Moreover, a deep earthquake with moment magnitude 8.2 striking the Fiji area was detected with a 40 km-long ocean-bottom fiber optic cable offshore Belgium.
DAS has also been proposed for vibration-based landslide monitoring as a replacement for geophones. The sensitivity of DAS is typically worse than that of geophones per single sensing point. Still, this approach’s advantage consists of the very large number of coherent sensing points that can be probed. The feasibility of this method has been tested so far in a small-scale physical model of a landslide [Michlmayr et al. 2017], and more recently in a physical model of debris flows [Schenato et al. 2020c]. In this last work, despite the smaller size of the model (approx. 2 m-long), 800 m of fiber coiled in 20 mandrels have been deployed, and probed.
Other geophysical applications where seismic monitoring is of paramount importance are related to ocean bottom surveys and volcano-triggered earthquakes. Despite occurring in completely diverse environments, they share similar issues related to the extreme harshness of the operative conditions and the required spatial extensiveness of monitoring. Initially addressed by massive arrays of quasi-distributed FBGs [Kringlebotn 2010; Sorge et al. 2005], they have been only recently addressed by DAS technology, with outstanding results [Williams et al. 2019; Nishimura et al. 2021; Jousset et al. 2022].
Worthy of mention, in ocean environment, is the wildlife monitoring of baleen whales in the Arctic using DAS that employs the globally available infrastructure of sub-sea telecommunication fiber optic cables [Bouffaut et al. 2022].
5. Short-range applications in medical sciences
5.1. Distributed fiber optics strain sensors
While distributed fiber optics strain sensing has found its own place in modern science and technology showing great potential in long-range applications, particularly in the field of geotechnical applications. the applications for the short-distance have started emerging over the last few years. The key factor that creates interest regarding distributed fiber sensing for short-range applications is the possibility to compact a large number of sensing points in a short space, thereby obtaining sub-centimeter detection. The main short distance class of applications that can fully exploit the potential of distributed fiber sensing is the field of bio-medical applications [Tosi et al. 2018].
Concerning bio-medical applications, there are some niche sectors that can strongly benefit from the use of distributed fiber optics strain sensing, mainly where high level of precise measurements, as well as minimal invasive sensing, is required [Amanzadeh et al. 2018]. Some of these sectors include colonoscopy, epidural administration, intra-arterial therapies, cardiac procedures, end ophthalmic robotic surgery, i.e. applications where it can be beneficial to use a needle catheter equipped with optical fiber sensors for strain measurement or shape reconstruction [Mandal et al. 2016; Gonenc et al. 2017; Khan et al. 2019]. In this regard, it is also necessary to stress that the use of optical fiber technology is not only beneficial for the purpose of precise strain sensing, but also introduces advantages given by the nature and the material of the sensing medium. In fact, glass optical fiber presents peculiar properties such as compact size, robustness, chemical inertness, bio-compatibility, and immunity to external electromagnetism, that makes fiber sensors perfect for bio-medical applications [Lee 2003].
It is worth noting that the research for new and innovative bio-medical devices based on fiber optics sensing technology has been mainly focused on the use of FBGs or arrays of FBGs, since they represent a mature technology, reliable, and easily available on the market. In the field of medical devices that require strain measurement to enable their functionalities, the use of FBGs is a good solution until the precision of the measurement and the spatial concentration of the sensing points become a mandatory requirement for the sensing system. The FGB, in fact, is a single point sensor and the information on the strain measurement is limited to its spatial location. The use of arrays of FBGs can improve the situation by promoting the system to a multi-point sensing device, however the technology of FBGs inscription limits the distance between the elements of the array to roughly 1 cm. For some applications it does not represent a problem, in a way that the limited number of sensing points or the distance center-to-center between the sensing points can be overcome by a careful analysis of the output data, as it can be in the case of a catheter for colon endoscopy whose bending can be reconstructed with a certain amount of precision by using a set of FBG arrays [Waltermann et al. 2014]. On the other hand, other applications can be significantly improved by the use of sub-centimeter distributed fiber sensing. An interesting case is represented by the identification of the achievement of epidural space during the procedure of epidural anesthesia.
Color map of the strain occurring on a sensorized needle during the insertion into a phantom over time. The change of strain indicates the passage through the various layers of the phantom, which reproduces the anatomy of the spine.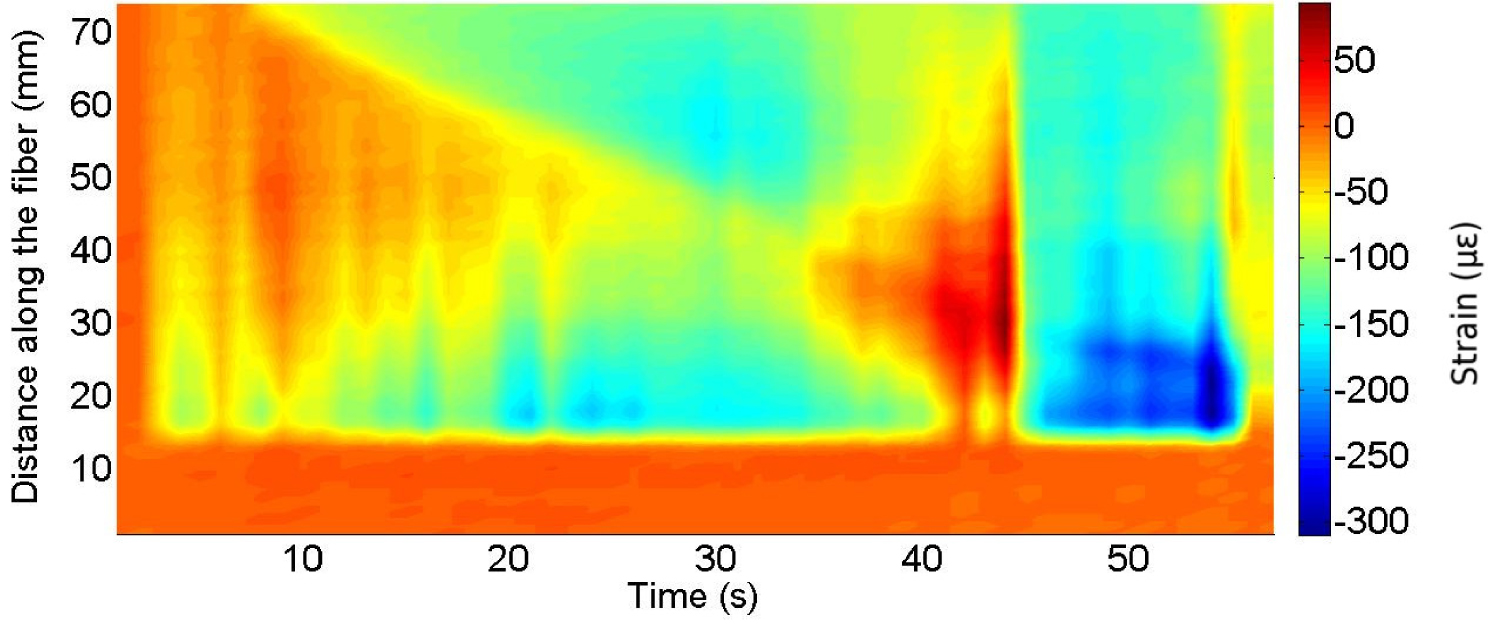
Epidural anesthesia is a largely used pain-relief method, whose main use is delivering anesthetic to pregnant women during labour [Eltzschig et al. 2003]. The procedure consists in reaching the epidural space, a small space of 2–6 cm located in spinal cord between ligamentum flavum and dura mater. The success of this method of anesthesia depends on the correct identification of the epidural space, which can be a difficult target to reach. Even if some manual methodologies have been developed in medical practice for improving the procedure of epidural anesthesia [Hoffmann et al. 1999], the success of the operation results in a certain percentage of failure, which can be quantified to be around 10% [Hermanides et al. 2012]. To improve the success of achieving epidural space and to assist the clinicians during the procedure, different quantitative technological methodologies and tools have been proposed, some of them making use of fiber optics sensing technology. An FBG was inserted inside the epidural needle nearby the tip in order to detect the pressure variation that occurred during the penetration of the needle into the spine tissue by Carotenuto et al. [2017]. A similar approach has been studied by equipping a needle for lumbar punctures in order to detect the force occurring on the device [Ambastha et al. 2016]. Both these solutions rely on the use of a single point of sensing since the physical property to detect is limited to the pressure/force occurring on the tip of the device. Even if the scientific result is valid, a larger amount of sensing data can be retrieved by equipping the epidural needle with an optical fiber sensor and by using a distributed approach. Based on this idea, Beisenova et al. [2018] have glued an SMF-28 fiber longitudinally along an epidural needle and measured the distributed strain occurring during needle penetration into a custom-made phantom. The distributed stain measurement has been obtained by using a Luna OBR interrogator. The typical strain map is shown in Figure 9. In the figure it is possible to distinguish the change of strain associated with the passage in different layers of the phantom, representing the anatomy of the spine. The fact that the entire strain measurement along the needle is detected permits, in principle, to have a wider collection of information. Therefore a more precise behavior of the needle can be reconstructed including: rotation, misalignment, and displacement. Moreover, this approach introduces a more comprehensive perspective for distributed stain measurement, which involves the reconstruction of the 3D shape sensing of the medical device, for tracing the direction of the needle during the insertion.
5.2. 3D shape sensing for medical application
The impact of shape sensing, for both industrial and medical applications, has significantly triggered the interest of the scientific community in the last decade [Waltermann et al. 2015]. There is no doubt that shape sensors based on fiber optics technology, mainly in the context of precision bio-medical applications, present advantages with respect to shape sensors based on electronic technology [Amanzadeh et al. 2018]. The small size of sensors based on fiber optics technology is intrinsically associated with the possibility of having both multi-point or distributed sensing configuration; the first uses the FBGs technology, the second exploits the natural back-scattering, occurring in the fiber, and the OFDR detection strategy.
The problem of shape sensing, achieved by using fiber technology, can be translated to the problem of detecting the fiber bending curvature and direction. In order to measure the bending, there are two different approaches proposed in literature: the first is measuring the change of optical intensity in a multi-core fiber, the second is to detect the strain induced by the fiber bending. The last detecting strategy has become predominant, mainly because of the maturity of the FBG technology, that offers a consistent and reliable sensing platform. Nevertheless, it is well known that a FBG offers a single point measurement, so that to target a complete shape sensing we need to equip the device with multiple fibers with inscribed arrays of FBGs [Roesthuis et al. 2014]. Another possibility relies on the use of multi-core fiber provided with inscribed FBGs [Flockhart et al. 2003]. The geometrical arrangement of the fibers, used to equip the device, is strictly dependent on the geometry of the object whose shape is to be detected. In case of object with beam shape, which is a common geometry for medical devices like catheters and needles, a full 3D shape measurement can be achieved by using three fibers (or a fiber with three cores) arrange in a triangular shape [Waltermann et al. 2014]. By twisting the fibers it is also possible to detect the twist of the beam [Askins et al. 2008], while by adding a fourth fiber it is possible to compensate for the temperature [Beisenova et al. 2019]. Fibers presenting multiple cores, with a number larger than four, can be used to implement advanced shape reconstruction algorithms in order to improve the precision [Floris et al. 2019].
Epidural needle sensorized with a parallel of four fibers, exploiting SLMux (a); schematic of the fibers attached on the needle and forming an angle of 90° (b); enhanced bending reconstructed by measuring the strain of each fiber along z-direction at different times (c); corresponding needle bending reconstructed in 3D space at different times (d).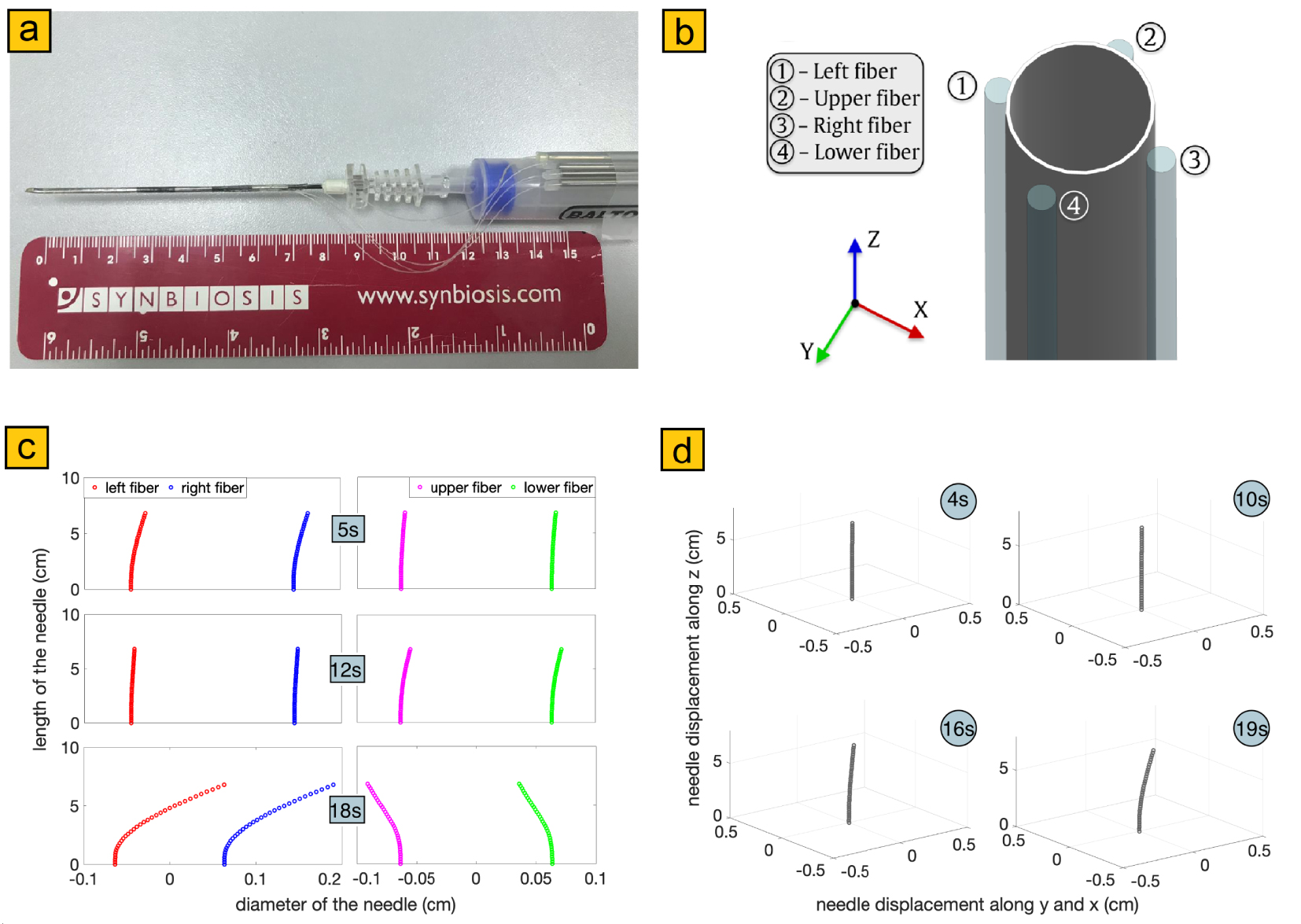
As mentioned before, the use of multi-point fiber sensors can be a limitation in the case of precise and critical bio-medical applications. In this case, a larger number of sensing points, located on the longitudinal direction of the device is required. Distributed strain sensing is the solution for boosting the accuracy of shape sensors [Bao and Chen 2012]. However to achieve shape sensing of a medical tool, like a needle or a catheter, it is necessary to supply the tool with a number of optical fibers, three or four according to the standard configurations proposed in literature. This, in principle, represents a problem since detection systems like OBR can be fed with only one fiber sensor as input. A parallel of optical fiber, used to feed the OBR, will result in an incoherent overlap of the back-scattering coming from each fiber, making it impossible to detect the strain and its spatial location. Beisenova et al. solved this, apparently tough, issue by using a nanoparticle-doped high scattering fiber with an operating protocol called SLMux [Beisenova et al. 2019]. The high back-scattering is generated by the presence of MgO-based nanoparticles located in the fiber core [Blanc et al. 2011]. Exploiting the high scattering, a parallel of fiber can be created, so that the high scattering fiber overlaps only with low scattering SMF pigtails. Because the scattering level of MgO-based nanoparticle fiber is 30–40 dB higher that the normal fiber scattering, the SMF-28 scattering can be treated as noise.
Beisenova et al. exploited the new SLMux capability for demonstrating 3D shape sensing of an epidural needle [Beisenova et al. 2019]. As shown in Figure 10(a), four cuts of nanoparticle-doped fibers have been glued longitudinally on an epidural needle, connected to the OBR by the SLMux configuration. The fibers were organized in a 90° configuration, so that each couple of opposite fibers measures the strain along one of the coordinate axis, as depicted in Figure 10(b). Counting two fibers for each axis permits improving the precision of the strain measurement. Moreover, since the geometrical problem of 3D shape sensing requires three fibers to be fully determined, the presence of four fibers can be used to discriminate the offset given by the presence of temperature, which affects uniformly all the four fibers. The strain on the fiber sensors has been detected with a resolution of 2 mm by the OBR. The strain information has been converted into bending data by a simple algorithm. Several insertions into a custom-made phantom have been performed to validate the 3D shape sensing model. An example of 3D reconstruction is shown in Figure 10(c, d). As it is possible to notice, the system is able to detect minimal bending angle, permitting an ultra-precise shape reconstruction, impossible for FBG-based systems. This new distributed strain sensing paradigm can potentially open new frontiers in critical bio-medical applications like ophthalmic surgery.
6. Conclusion
Thanks to its characteristics (small size, immune to electromagnetic interference, passive, resistant to harsh environment, etc.), optical fibers have become in recent decades a technology of choice for making sensors. In addition, its ability to be sensitive over lengths ranging from cm to more than 100 km makes it possible to produce distributed sensors for fields as diverse as geology or medicine.
In the context of geology, detection mainly exploits Brillouin scattering to detect strain and Raman scattering for temperature measurements. To monitor geomorphic processes such as landslides, DFOS are embedded in shallow trenches or simply anchored to the ground. A detailed map of the strain field in the monitored area can be obtained thanks to the ability of the fibers to be arranged in a square grid. The vertical strain profile can be detected by installing the DFOS in a borehole. Such DFOS are also of interest to monitor the health condition of river embankments and soil anchors. Coupled to a Raman-based technique, distributed measurement of temperature can be performed to detect early filtration path. Based on the coherent-detection of the Rayleigh backscattering, the distributed acoustic sensing is an additional technology to measure the acoustic or vibration field. Long-range distributed earthquake seismometers and landslide monitors are based on this technology.
For the applications relying on short-range DFOS, strain and temperature detection is mainly based on FBG technology and Rayleigh backscattered light. Due to the minimally invasive size and its biocompatibility, short-range DFOS are of interest in bio-medical applications. For instance, fibers glued around a needle allow monitoring of strain to reconstruct its shape during the insertion. Such DFOS can be based on multi-core fiber or FBGs photo-inscribed in fiber core. Recently, the use of nanoparticle-doped high scattering fibers promoted a new protocol (SLMux) to measure simultaneously information from several fibers with a large number of sensing points.
DFOSs have found a place in modern science and technology showing great potential in long-range applications, particularly in the field of geophysics. The applications for short distance are in niche sectors and are emerging in the last few years. The new distributed strain sensing paradgim (SLMux) can potentially open new frontiers in critical bio-medical applications.
Conflicts of interest
The authors declare no competing financial interest.
Dedication
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
Acknowledgements
The authors thank Martiane Cabie (CP2M, Marseille, France) for the SEM images. This work was partly funded by ANR Project NanoSlim (ANR-17-CE08-0002), and by Nazarbayev University, under grants EPICGuide (code: 240919FD3908) and SMARTER (code: 091019CRP2117).




 CC-BY 4.0
CC-BY 4.0