Abridged version
Karstic systems are characterised by high spatial and temporal heterogeneities. In previous works [3–6], continuous and multiresolution wavelet analyses were used in order to qualitatively extract this unsteadiness. Then, a continuous Morlet cross-wavelet transform was proposed and applied in order to highlight time variations in the rainfall–discharge relationship.
Here, we present a more quantitative cross-analysis of the rainfall–discharge relationship introducing a cross-wavelet multiresolution analysis. Multiresolution analyses effectively allow a time-scale representation of these two main hydrological signals. Therefore, a classical cross-correlation is applied to the different scales of each signal, in order to extract the degree of causality of the relation. A low cross-correlation coefficient indicates a low causality, whereas a large cross-correlation coefficient indicates a high causality.
These techniques are applied to three karstic systems located in the Pyrenees (France): Aliou, Baget and Fontestorbes. Rainfall and discharge data are available both on a large period of 30 years at daily sampling rate and yearly at a 30-minute sampling rate for the Aliou basin.
This application leads to two main results.
– At a daily sampling rate, the degree of causality increases with the scale of observation from one day to one year, with a maximum corresponding to the annual recharge. Moreover, the cross-correlation increases differently between the different basins: the increase appears as being rapid facing the scale of observation for very karstified basins such as Aliou, whereas this increase appears as linear facing the scale of observation for less karstified basins such as Fontestorbes. This method, in a same manner than classical cross-correlation, can therefore lead to a rapid but more precise classification of the aquifers as a function of their degree of karstification.
– At a half-hourly sampling rate, it appears that no significant correlation can be found for scales inferior to 16 h, which indicates that the Aliou system does not integrate in its hydrological response high frequency processes included in rainfall. Then, the degree of correlation increases more rapidly, which indicates that the system integrates these processes in its global response (discharge).
To conclude, cross-correlation multiresolution analysis provides an easy and synthetic method for describing quantitatively the causality of the rainfall–discharge relationship for a karstic basin. It allows evidencing the degree of karstification of the basin and also possible small-scale cut in the rainfall–discharge relationship.
1 Introduction et motivations
Les systèmes karstiques sont des bassins versants caractérisés par de fortes hétérogénéités spatiales, à la fois physiques et dynamiques. Celles-ci impliquent notamment un comportement à la fois non linéaire et non stationnaire.
Diverses analyses ont déjà été réalisées afin de rendre compte de la relation pluie–débits, parmi lesquelles des analyses corrélatoire et spectrale [5,10], mais aussi des analyses en ondelette continue et en multirésolution [3,4,6,7]. Ces résultats sont ici complétés par l'utilisation conjointe de l'analyse multirésolution et de l'analyse corrélatoire croisée (fonction d'intercorrélation). L'utilisation de ces deux méthodes permet de compléter l'interprétation de la relation pluie–débits en l'examinant échelle de temps par échelle de temps. La combinaison de ces deux analyses sera par la suite appelée « analyse multirésolution croisée ».
2 Présentation de l'analyse multirésolution
L'analyse multirésolution permet de mettre en évidence les divers phénomènes présents dans le signal, depuis les petites échelles de temps jusqu'aux phénomènes à plus long terme.
2.1 Analyse en ondelette multirésolution
La transformée en ondelette est une méthode d'analyse dont les applications en hydrologie et géophysique sont de plus en plus variées [2]. L'analyse en ondelette croisée n'a été utilisée qu'en mécanique des fluides par Li et Nozaki [8], Onaroto et al. [11] et Salvetti et al. [12]. Ces techniques permettent une représentation temps–échelle des relations entre deux processus.
Les coefficients de l'analyse en ondelette multirésolution d'un signal discret X(i) sont alors donnés par le produit de convolution entre le signal et les éléments d'une base orthonormale à deux paramètres, notés [1], dans laquelle j est l'ordre de la décomposition : (1)
| (2) |
Le signal discret X(i) peut être approché par ses approximations successives, constituant une analyse multirésolution [9]. L'approximation du signal discret X(i) à l'échelle de temps m, notée Am, et le « détail » du signal discret X(i) à l'échelle m, noté Dm, sont alors donnés par : (3)
Dans l'équation (3), ϕm est appelée « fonction d'échelle S » et ψm est nommée « fonction ondelette W ». Ces fonctions sont obtenues par résolution d'une équation récurrente [1,13]. Des exemples de fonctions S et W de type Daubechies sont donnés en Fig. 1a. Afin d'illustrer la décomposition multirésolution, un exemple d'analyse est présenté sur la Fig. 1b, dans le cas de pluies et débits journaliers. Ces deux signaux sont décomposés en composantes diverses, correspondant à diverses échelles temporelles, depuis 1 jour (échelle m=0 soit 20 jours) jusqu'à 512 jours (échelle m=9 soit 29 jours).
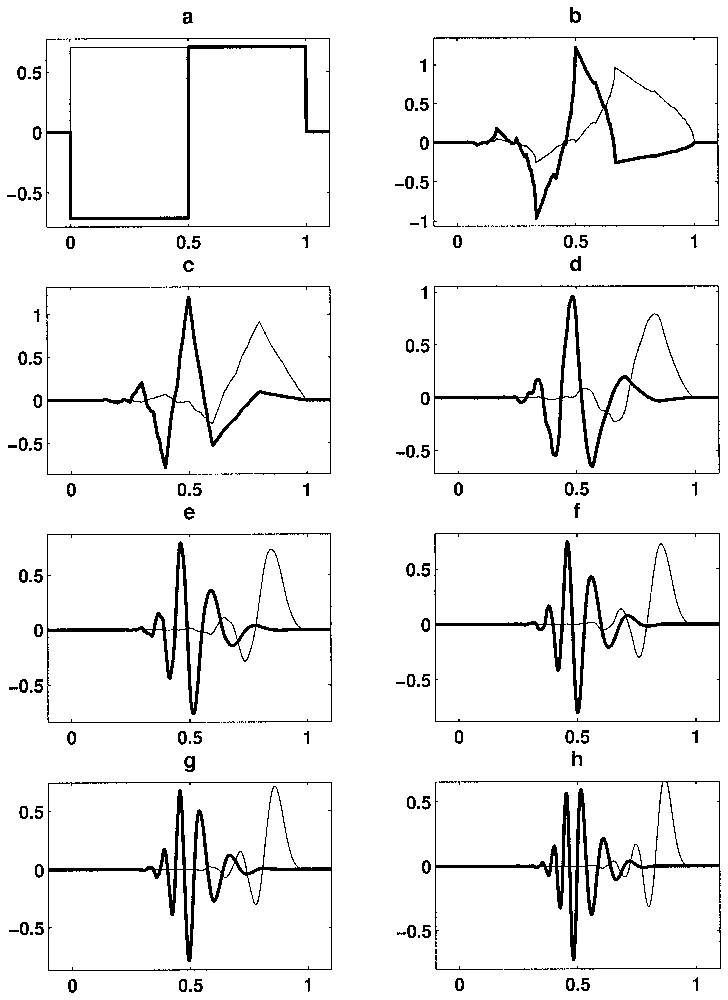
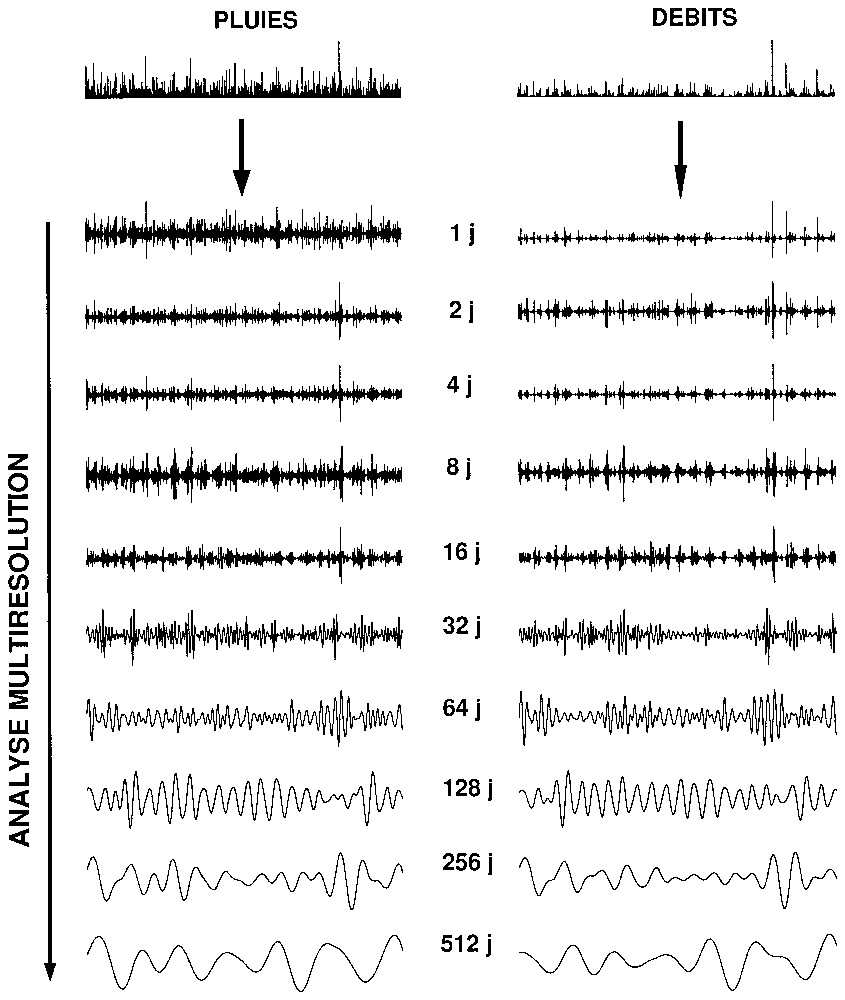
À gauche : exemples d'ondelettes (S en trait fin et W en trait gras) de type Daubechies d'ordre croissant. Notons que plus cet ordre est élevé, plus l'ondelette obtenue est régulière (a : ordre 2, b : ordre 4, c : ordre 6, d : ordre 8, e : ordre 12, f : ordre 14, g : ordre 16, h : ordre 20). À droite : analyse en ondelettes multirésolution (Daubechies 20) de pluies et débits mesurés à la source d'Aliou. Du haut vers le bas sont représentés les différents termes de la décomposition multirésolution (détails), depuis les processus à très court terme jusqu'aux phénomènes à plus long terme. Les différents termes correspondent, du haut vers le bas, à m =0,…,9 soit des échelles de temps allant de 20 jusqu'à 29 jours.
On the left: examples of Daubechies wavelets (S and W) of increasing orders. Note that the higher the order, the higher the wavelet regularity (a: order 2, b: order 4, c: order 6, d: order 8, e: order 12, f: order 14, g: order 16, h: order 20). On the right: wavelet multiresolution analysis of rainfall rate and runoffs measured at the outlet of Aliou karstic spring using Daubechies 20 wavelet. From top to bottom, we represent the different terms (details) of the multiresolution decomposition from short-term processes to long-term processes. The different terms of the decomposition correspond from top to bottom to m=0,…,9, which corresponds to time scales varying from 20 to 29 days.
3 Résultats et interprétation
L'objectif de cette note est de proposer des éléments de réponse à la question suivante : « Comment quantifier le degré de causalité de la relation pluie–débits en fonction de l'échelle de décomposition ? »
Une « analyse multirésolution croisée » est appliquée aux pluies et aux débits journaliers et semi-horaires, mesurés sur trois bassins karstiques pyrénéens : Aliou, Baget et Fontestorbes. Cette analyse correspond à une analyse corrélatoire croisée [10] entre les différentes composantes de l'analyse multirésolution des pluies et des débits, au même ordre d'approximation m. Les caractéristiques de ces trois bassins sont présentées dans Mangin [10]. Les ondelettes analysantes ϕ et ψ sont des ondelettes de type Daubechies, avec des ordres compris entre 2 et 20 [1].
Le maximum de la fonction d'intercorrélation échelle par échelle est donc représenté en fonction de l'échelle de la décomposition. Ce maximum constitue un indice de causalité : plus ce maximum est élevé, plus la causalité de la relation sera vérifiée dans le cadre de la modélisation de la relation pluie–débits, à l'échelle correspondante.
L'analyse multirésolution croisée des pluies et des débits journaliers met en évidence une différence de comportement très nette entre les divers aquifères. Nous avons représenté sur la Fig. 2 le maximum de la fonction d'intercorrélation entre détail de pluies et détail de débits, en fonction de l'échelle pour les trois aquifères et pour différentes ondelettes de Daubechies. Des systèmes fortement karstifiés, donc à système karstique développé, tels que Aliou ou le Baget [10], sont caractérisés par une montée rapide du maximum d'intercorrélation en fonction de l'échelle de décomposition, avec une asymptote atteinte pour des échelles de l'ordre de trois mois, tandis que Fontestorbes, moins développé, est caractérisé par une croissance linéaire sans asymptote. Les valeurs d'intercorrélation maximale à court terme sont aussi croissantes en fonction du degré de développement du système. L'asymptote, de l'ordre de 1, indique que les débits à long terme (échelles supérieures à 1 an) sont gouvernés par les phénomènes à long terme contenus dans les pluies. Ainsi, plus un système est développé, plus il intègre les phénomènes à court terme présents dans la pluie. De plus, à petite échelle, le résultat s'avère comme peu dépendant de l'ondelette choisie.
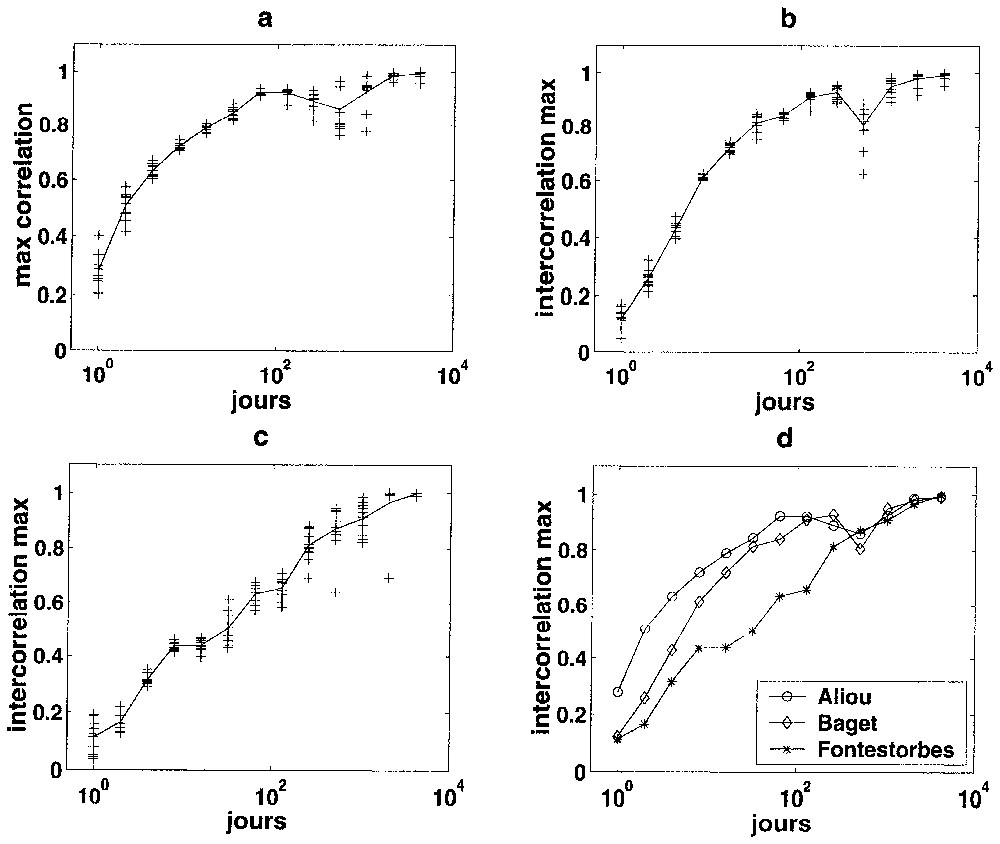
Maximum de la fonction d'intercorrélation entre détails de pluies et détails de débits journaliers, en fonction de l'échelle, pour diverses ondelettes de Daubechies, d'ordres variant entre 2 et 20. Les résultats obtenus avec les diverses ondelettes sont représentés par + (a : Aliou, b : Baget, c : Fontestorbes et d : comparaison entre les trois aquifères). La période d'étude s'étend du 23/09/1974 au 25/02/1997.
Maximum of the intercorrelation function between daily rainfall rates details and daily runoffs details as a function of the scale for different Daubechies wavelets of orders varying between 2 and 20. The results obtained by various wavelets are represented by + (a: Aliou, b: Baget, c: Fontestorbes and d: comparison between the three aquifers). The period extends from 23/09/1974 to 25/02/1997.
Une analyse de trois chroniques disjointes temporellement (Fig. 3) de pluies et débits semi-horaires mesurés sur le bassin d'Aliou indique la présence de plusieurs intervalles. Pour des échelles inférieures à 16 h, le maximum d'intercorrélation est quasiment constant : le système n'intègre donc pas les processus inférieurs à cette échelle, présents dans l'information d'entrée pluies. Puis, pour des échelles comprises entre 16 et 128 h (soit une semaine approximativement), le maximum d'intercorrélation croı̂t plus rapidement : le système intègre donc ces processus dans la réponse. Enfin, on retrouve une asymptote de l'ordre de 1, qui indique que les phénomènes à long terme des débits (processus annuel) sont gouvernés par les phénomènes à long terme, présents dans les précipitations.
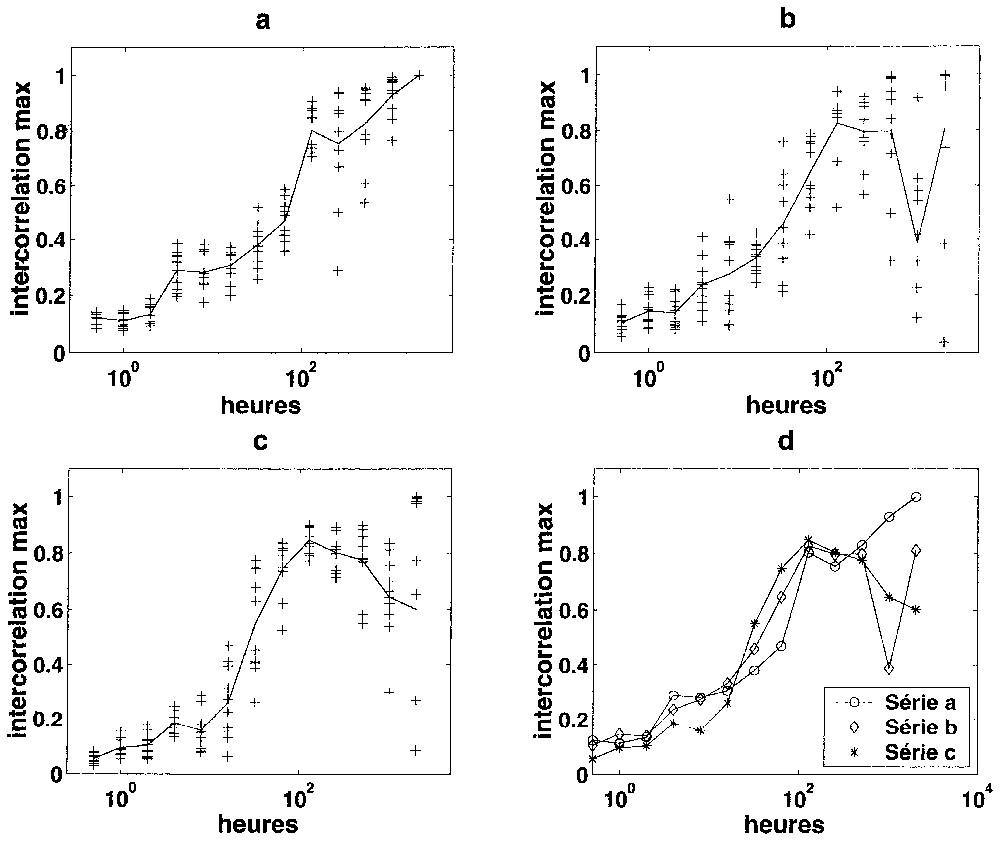
Maximum de la fonction d'intercorrélation entre détails de pluies et détails de débits au pas semi-horaire en fonction de l'échelle, calculé pour diverses ondelettes de Daubechies, d'ordres variant entre 2 et 20. Les résultats obtenus avec les diverses ondelettes sont représentés par +. Les a, b et c correspondent à trois séries de 8192 données successives, sur des intervalles de temps disjoints ; d permet de comparer les résultats obtenus pour les trois séries. [La série a s'étend du 16/02/1994 au 06/08/1994, la série b s'étend du 07/08/1994 au 23/01/1995 et la série c s'étend du 23/08/1995 au 08/02/1996.]
Maximum of the intercorrelation function between half-hourly rainfall rates details and half-hourly runoffs details, as a function of the observation scale calculated with different Daubechies wavelets of orders varying between 2 and 20. The results obtained by various wavelets are represented by +. a, b and c correspond to three non-overlapping series of 8192 successive data; d allows to compare the results for the three series. [Series a extends from 16/02/1994 to 06/08/1994, series b extends from 07/08/1994 to 23/01/1995 and series c extends from 23/08/1995 to 08/02/1996.]
Toutefois, à ce pas d'échantillonnage, le problème du choix de l'ondelette analysante apparaı̂t comme plus problématique, la dispersion entre ondelettes différentes étant relativement importante aux plus grandes échelles. C'est pourquoi, nous préconisons d'opérer une moyenne sur plusieurs ondelettes (Fig. 3d).
4 Conclusions
Une analyse multirésolution croisée (analyse en ondelette multirésolution, suivie d'une analyse corrélatoire croisée) est appliquée à des pluies et débits de sources karstiques. Cette analyse multirésolution croisée permet de quantifier le degré de causalité de la relation pluie–débits à diverses échelles temporelles et de mettre en évidence des échelles caractéristiques dans le cas des données semi-horaires. Ces résultats pourront ensuite être utilisés dans le cadre de modèles de simulation de ces aquifères.
Remerciements
Nous remercions le parc naturel régional des Grands Causses pour son aide matérielle et logistique.



