Abridged English version
Introduction
The evaluation of the ground response to seismic motion needs some geological, accelerometric and macroseismic data. Respective limits and complementarity of instrumental and macroseismic methods have been reviewed by several authors (e.g., [2,8,11]). Because of a great spatial as well as temporal coverage, macroseismic data have been widely used to study attenuation properties of several regions [1], to detect site effects [3,10], and to determine magnitude and depth of historical earthquakes [2,9,11]. Ambraseys [1] set up an intensity attenuation law for Northwest Europe, based on Sponheuer's model. This kind of model depends on the focal depth, but it only takes into account a subset of the whole information contained in the value of the epicentral intensity
This study is carried out from SISFRANCE macroseismic database (BRGM, EDF, IRSN). We selected 420 events that occurred between 1711 and 2001 (Fig. 1a), and for which 26 551 intensity observations are available (Fig. 1b). Their epicentral intensities range between IV and IX. The number of data is listed in Table 1 for each class of integer epicentral intensity.
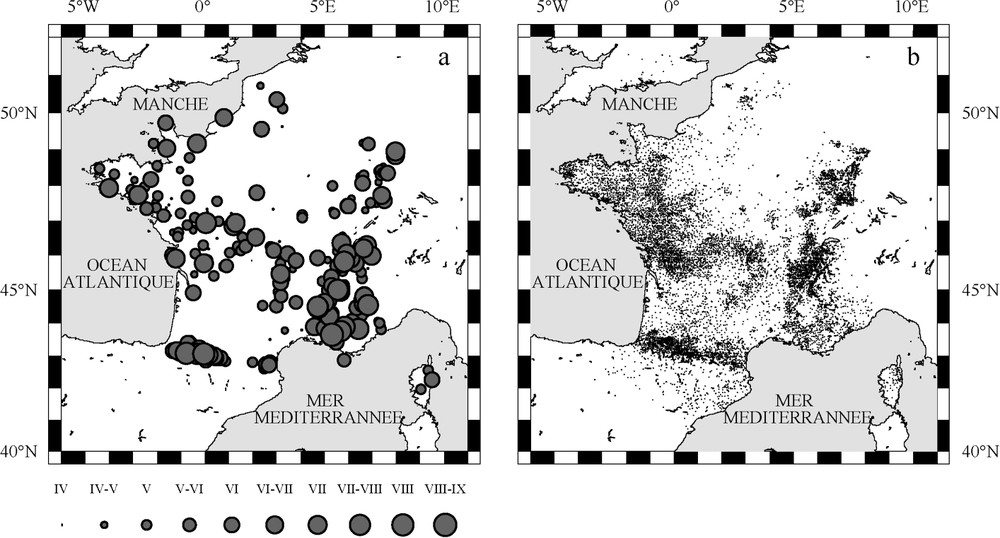
(a) Carte de localisation des 420 séismes sélectionnés dans la base de données macrosismiques SisFrance. (b) Carte de localisation des 26 551 observations d'intensité analysées.
(a) Location map of the 420 earthquakes selected in SISFRANCE macroseismic database. (b) Location map of the 26 551 intensity observations analysed in this work.
Valeurs des paramètres
Values of the parameters
|
|
|
|
|
|||||||||||
| A | B | A | B | A | B | |||||||||
| A | B | A | B | A | B | A | B | |||||||
| IV | 88 | 137 | 1915 | 3244 | 76 | 82 | 6,5 | 2,6 | 64,9 | 60,1 | 379 | 663 | 354 | 350 |
| V | 199 | 226 | 8956 | 11056 | 186 | 215 | −2,4 | 3,1 | 28,7 | 32,8 | 1080 | 925 | 243 | 250 |
| VI | 75 | 91 | 6558 | 8592 | 242 | 249 | 3,0 | 1,7 | 29,5 | 26,3 | 1135 | 1250 | 248 | 252 |
| VII | 44 | 55 | 6203 | 8136 | 324 | 336 | −1,2 | −1,0 | 22,8 | 29,3 | 1637 | 1697 | 230 | 231 |
| VIII | 13 | 14 | 2609 | 2919 | 249 | 267 | −1,3 | −0,8 | 29,5 | 30,3 | 1842 | 1842 | 259 | 261 |
| IX | 1 | 1 | 310 | 310 | 77 | 77 | −0,3 | 58,6 | 40,9 | 40,2 | 1923 | 1923 | 285 | 281 |
Reference model
The decay laws usually encountered in the literature only take into account the effect of the source depth. For instance, Sponheuer's model [12] looks for a decay of the form:
| (1) |
Influence of the source depth
Sponheuer's model was used by Ambraseys [1] to analyse 152 earthquakes of northwestern Europe. The result of the analysis was:
| (2) |
By removing the explicit dependence of ΔI with respect to focal depth, Ambraseys [1] obtained a law depending only on the epicentral distance D:
| (3) |
For large distances, D can be considered as equivalent to R and (2) and (3) can be compared. Fig. 2a shows that Eq. (3) would correspond to a depth of approximately 10 km, which is a reasonable value for Northwest European earthquakes, usually confined in the upper crust.
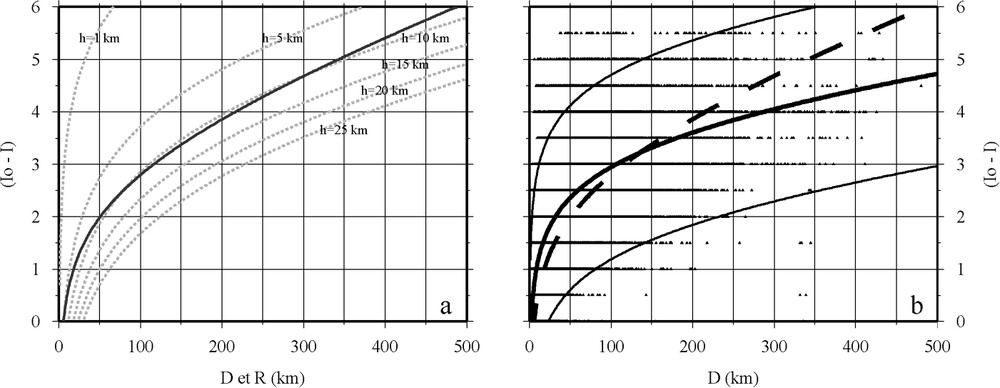
(a) Lois d'Ambraseys [1] et influence de la profondeur de la source. En gris : ΔI=f(R,h) (Éq. (2)). En noir : ΔI=f(D) (Éq. (3)). Si on assimile R à D, l'Éq. (3) correspond à l'Éq. (2) pour une profondeur moyenne d'une dizaine de kilomètres, ce qui paraît raisonnable pour les séismes d'Europe du Nord-Ouest. (b) Atténuation de l'intensité (ΔI) en fonction de la distance. Les 26 551 observations étudiées sont représentées par les points noirs. La ligne en pointillé correspond à la loi de décroissance établie par Ambraseys [1] pour l'Europe du Nord-Ouest (Éq. (3)). Le modèle obtenu suivant une loi similaire à partir des observations analysées (ce travail, Éq. (4)) est représenté par le trait continu épais, et ses limites à 1 σ par les traits continus fins. Le modèle d'Ambraseys [1] est situé dans ces limites, mais tend néanmoins à surestimer l'atténuation pour les grandes distances. Masquer
(a) Lois d'Ambraseys [1] et influence de la profondeur de la source. En gris : ΔI=f(R,h) (Éq. (2)). En noir : ΔI=f(D) (Éq. (3)). Si on assimile R à ... Lire la suite
(a) Ambraseys' laws [1] and source depth influence. Grey lines: ΔI=f(R,h) (Eq. (2)). Black line: ΔI=f(D) (Eq. (3)). If one considers that D and R are equivalent, Eq. (3) corresponds to Eq. (2) for an approximate mean depth of 10 km, which is a reasonable value for Northwest European earthquakes. (b) Intensity attenuation (ΔI) as a function of epicentral distance. The black circles show the location of the 26 551 observations we analysed. The dashed line corresponds to the intensity fall-off law set up by Ambraseys [1] for Northwest Europe (Eq. (3)). The model we obtained from the SISFRANCE data following a similar law (Eq. (4)) is shown by the thick solid line, and its confidence limits by the thin ones. Ambraseys' model [1] is located inside the confidence domain. However, it tends to overestimate the attenuation for large distances. Masquer
(a) Ambraseys' laws [1] and source depth influence. Grey lines: ΔI=f(R,h) (Eq. (2)). Black line: ΔI=f(D) (Eq. (3)). If one considers that D and R are equivalent, Eq. ... Lire la suite
The least-square inversion [13] of SISFRANCE database, with a similar law, gives:
| (4) |
The standard deviation of the data to (4) is 0.88, whereas it reaches a value of 1.06 to Eq. (3), i.e. it is improved by 17%. In the case of Metropolitan France, Ambraseys' law [1] tends to overestimate the intensity decay for the largest distances (Fig. 2b).
Influence of the epicentral intensity
Since both magnitude and focal depth are unknown for most historical earthquakes, we propose to modify Sponheuer's model by including a dependence of the coefficients
| (5) |
In order to check the impact of the possibly large uncertainty associated with the value of
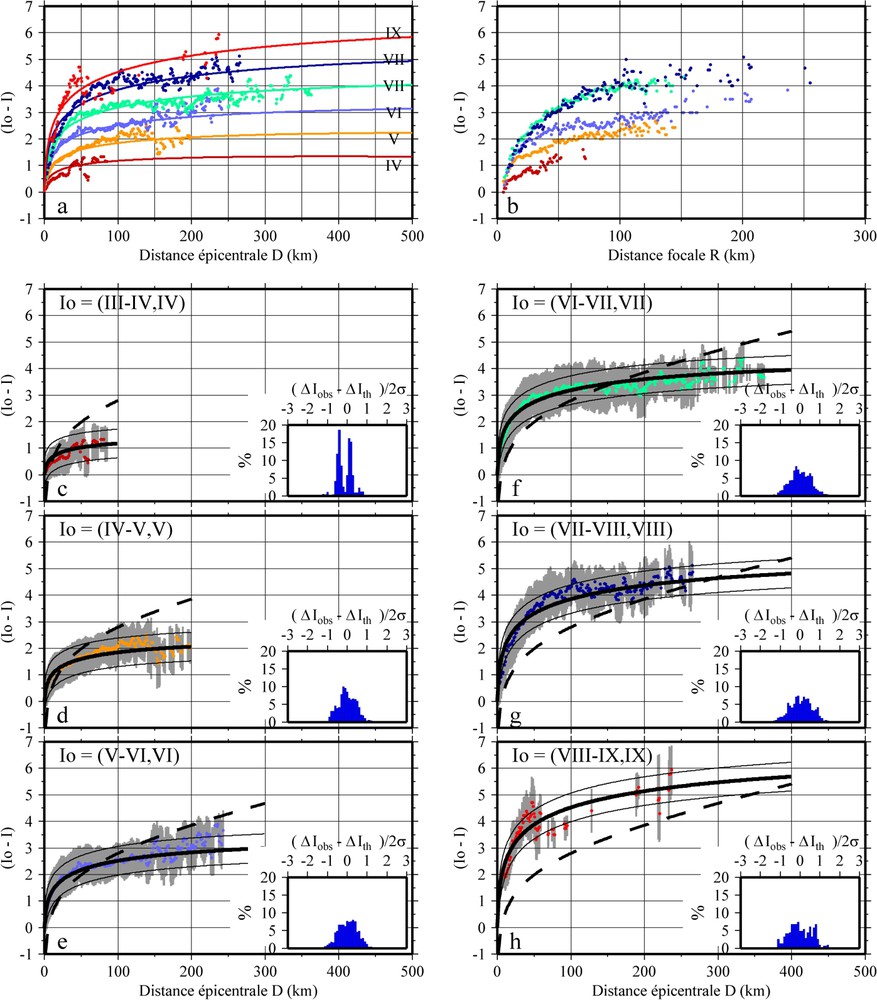
(a) Loi d'atténuation de l'intensité en fonction de la distance épicentrale D [Éq. (5)] pour toutes les classes de
(a) Loi d'atténuation de l'intensité en fonction de la distance épicentrale D [Éq. (5)] pour toutes les classes de
(a) Attenuation laws of intensity as a function of the epicentral distance D (Eq. (5)) for all
(a) Attenuation laws of intensity as a function of the epicentral distance D (Eq. (5)) for all
According to Eqs. (3) and (4), ΔI exhibits a logarithmic pattern in the near-field (
| (6) |
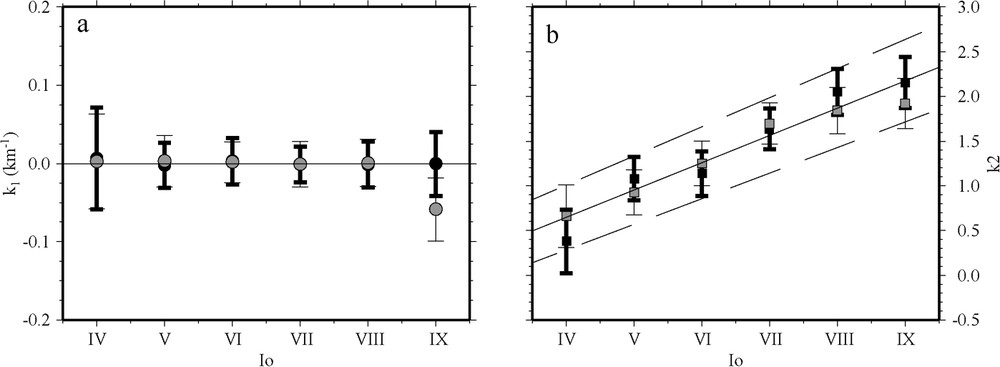
(a) Paramètre
(a) Paramètre
(a)
(a)
According to the respective standard deviation associated with the parameters of relation (6), the latter predicts that the difference between the ΔI values obtained for
| (7) |
This inversion gives the following results:
| (8a) |
| (8b) |
| (8c) |
These values are coherent with Eq. (6). The standard deviation of
Spatial variations of the attenuation
The laws (7) and (8) are used as a reference model to highlight some possible significant variations of the ground response. Once the standard deviation
| (9) |
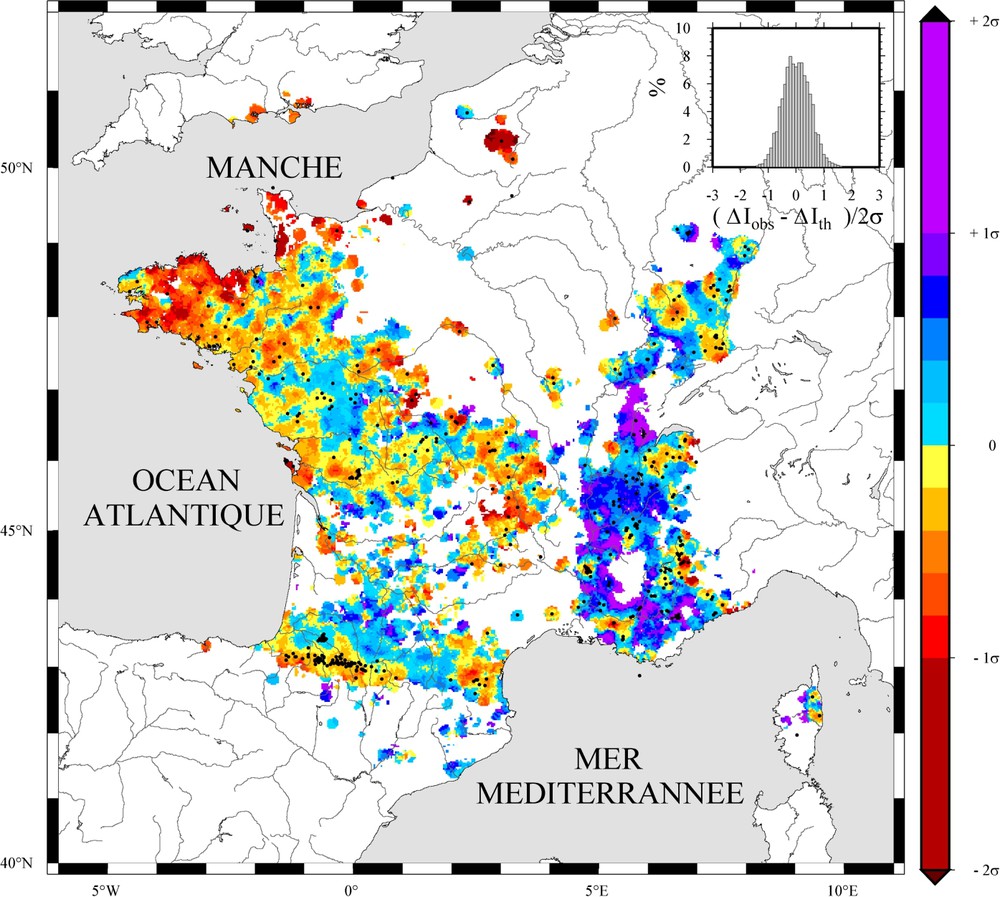
Distribution spatiale des résidus
Distribution spatiale des résidus
Spatial distribution of the residuals
Spatial distribution of the residuals
Discussion and conclusions
The analysis of the SISFRANCE macroseismic database enabled us to determine a reference law for intensity decay in Metropolitan France. The basic hypothesis of the classical attenuation law is that the intensity decay is independent of the magnitude. As previously pointed out by Hough et al. [7], this assumption is not necessarily valid. Instrumental studies [4,5,15] show that the attenuation of the amplitude of the peak ground acceleration (PGA) as a function of distance depends on the magnitude: the larger the magnitude (correlatively the PGA at the source), the faster the attenuation, especially at short distances (<100 km). Our study shows that the macroseismic intensity decay behaves in a similar way: the higher the epicentral intensity, the faster the decay, particularly in the near-field. This observation is in a good agreement with the nonlinear behaviour of acceleration attenuation close to the epicentre.
The originality of our approach consists in taking implicitly into account both the unknown magnitude and focal depth of the events, by means of the epicentral intensity. The comparison of our model with Ambraseys' one [1] suggests that the latter cannot be applied just as it is to France. Taking the epicentral intensity into account makes it possible to significantly reduce the difference between observed and theoretical intensities. An attenuation model that would not be a function of this parameter could only be applied for values of
At the scale of Metropolitan France, the residuals are homogeneously distributed, with no important ‘amplification’ phenomenon, i.e. [
1 Introduction
L'évaluation de la réponse du sol aux mouvements sismiques nécessite de disposer de données géologiques, accélérométriques et macrosismiques. Les limites respectives et la complémentarité des méthodes instrumentales et macrosismiques ont été synthétisées par plusieurs auteurs (par exemple, [2,8,11]). Les données instrumentales fournissent des mesures fréquentielles précises et objectives de la réponse du sol, mais elles ne sont pas nécessairement représentatives à une échelle régionale. Par ailleurs, les réseaux accélérométriques en France métropolitaine sont irrégulièrement distribués et généralement récents. Les données macrosismiques résultent d'une mise en commun d'observations et de témoignages moins précis, mais qui offrent l'avantage d'une couverture spatiale et temporelle sans équivalent instrumental. C'est pourquoi les observations d'intensité macrosismique ont été largement exploitées pour déduire les propriétés d'atténuation de diverses régions [1], pour mettre en évidence des effets de site potentiels [3,10] et pour déterminer la magnitude et la profondeur des séismes historiques [2,9,11]. Ambraseys [1] a établi une loi d'atténuation de l'intensité en fonction de la distance épicentrale pour l'Europe du Nord-Ouest à partir de séismes historiques et instrumentaux ressentis entre 1816 et 1984. Cette loi empirique (modèle de Sponheuer) dépend de la profondeur focale, mais ne prend pas en compte la totalité de l'information contenue dans la valeur de l'intensité épicentrale
L'étude est menée à partir de la base de données SisFrance (BRGM, EDF, IRSN), auparavant nommée Sirene. Environ 6000 événements y sont répertoriés, depuis le Ve siècle jusqu'à nos jours. Parmi ceux-ci, 1253 événements ont une intensité épicentrale échelonnée entre III et IX sur l'échelle MSK 1964. Les critères de Bossu et al. [3] sont utilisés pour la sélection des épicentres : seuls sont retenus les séismes pour lesquels la base de données SisFrance indique une incertitude sur la localisation épicentrale inférieure à 10 km. Seules les intensités dont l'indice de qualité est A ou B (critère SisFrance) sont utilisées, et les intensités inférieures à II sont écartées. Dans les calculs qui suivent, nous attribuons des poids respectifs de 1,0 et de 0,5 aux données dont l'indice de qualité est A et B. Ces critères permettent de sélectionner 420 séismes advenus entre 1711 et 2001, auxquels sont associées 26 551 observations d'intensité (Fig. 1). Les valeurs d'intensité épicentrale des séismes sélectionnés varient entre IV et IX. Le nombre de données analysées pour chaque classe d'intensité est indiqué dans le Tableau 1.
2 Établissement du modèle de référence
Dans un milieu isotrope et pour une source ponctuelle dont les éventuels effets de directivité ne sont pas pris en compte, la décroissance de l'intensité macrosismique (ΔI) avec la distance peut être décrite par le modèle de Sponheuer [12] :
| (1) |
2.1 Influence de la profondeur de source
À partir d'observations d'intensité pour 152 séismes d'Europe du Nord-Ouest, Ambraseys [1] obtient :
| (2) |
Quelle que soit la distance focale, l'expression (2) conduit à une variation de ΔI de 2, suivant que la source est située à 5 ou à 25 km de profondeur. En ne prenant pas en compte la dépendance explicite de ΔI par rapport à la profondeur focale, Ambraseys [1] obtient une loi qui dépend uniquement de la distance épicentrale D, exprimée en kilomètres :
| (3) |
Lorsque la distance épicentrale est très supérieure à la profondeur de la source, D devient équivalent à R, et l'on peut alors comparer les courbes d'Éqs. (2) et (3). Les paramètres de l'Éq. (3) sont compatibles avec une profondeur moyenne d'une dizaine de kilomètres (Fig. 2a). Cela paraît acceptable pour les séismes intraplaques d'Europe du Nord-Ouest et de France en particulier, généralement confinés dans la croûte supérieure.
Une inversion de type moindres carrés [13] des observations que nous avons sélectionnées dans la base de données SisFrance donne :
| (4) |
L'écart-type des données SisFrance par rapport à l'Éq. (3) est de 1,06, tandis qu'il est de 0,88 par rapport à l'Éq. (4), ce qui correspond à une amélioration de 17%. Il apparaît donc que la loi établie par Ambraseys [1] pour l'ensemble de l'Europe de l'Ouest n'est pas directement applicable à la France métropolitaine. Elle tend à surestimer la décroissance de l'intensité pour de grandes distances (Fig. 2b).
2.2 Influence de l'intensité épicentrale
Les effets de la valeur de
Conformément aux Éqs. (3) et (4), l'intensité macrosismique décroît de manière logarithmique en champ proche (
Comme la magnitude et la profondeur focale sont inconnues pour la plupart des séismes historiques, nous proposons d'utiliser le modèle (4) en y incluant une dépendance des coefficients
| (5) |
La relation (5) vérifie
| (6) |
Si l'on prend en compte les incertitudes sur les paramètres de la relation (6), celle-ci prédit une différence entre les valeurs de ΔI obtenues pour
| (7) |
Les résultats de l'inversion sont les suivants :
| (8a) |
| (8b) |
| (8c) |
Les coefficients obtenus sont compatibles avec ceux de l'Éq. (6). L'écart-type des données moyennées par rapport au modèle (7) est égal à 0,27. L'écart-type des données brutes est égal à 0,78 pour le même modèle, tandis qu'il est respectivement égal à 1,06 et à 0,88 par rapport aux Éqs. (3) et (4) : les améliorations sont donc de 26 et de 11%. Pour une distance de 100 km, la valeur de ΔI peut varier entre 1 (
3 Variations spatiales de l'atténuation
À partir de l'analyse de 450 séismes de la même base de données, Bossu et al. [3] avaient conclu que seuls les terrains d'âge inférieur à 2 Ma étaient à même de produire des effets de site. L'étude individuelle de 35 événements sélectionnés dans cette base de données avait conduit ces auteurs à proposer une relation entre l'âge des roches et la probabilité qu'elles produisent des effets de site, ce qui les avait enfin amenés à proposer une carte prédictive de ces effets. L'approche présentée ici est différente, puisque toutes les données de tous les séismes sélectionnés ont été inversées simultanément.
Les lois (7) et (8) sont utilisées comme référence pour la détection d'éventuelles variations spatiales de la réponse du sol aux mouvements sismiques. Les écarts-types
| (9) |
| (10) |
Pour une distance épicentrale donnée, un résidu négatif correspond donc à une intensité observée supérieure à l'intensité théorique. La distribution gaussienne des résidus, centrée sur zéro, illustre l'homogénéité de l'ensemble des données et la validité des relations (7) et (8) comme lois empiriques de référence (Fig. 5). La Fig. 5 présente la distribution spatiale des résidus, moyennés sur une fenêtre circulaire de 10 km de rayon, déplacée sur une grille de maille carrée de 1 km. Seuls les nœuds disposant d'au moins cinq observations sont retenus, afin d'éviter des artefacts dus à un nombre insuffisant de données. À l'échelle de la France métropolitaine, les valeurs des résidus sont réparties de manière assez homogène, comme le suggère la distribution gaussienne visible dans l'histogramme.
Une zone d'intensités supérieures à la référence [c'est-à-dire
4 Discussion et conclusion
L'analyse de la base de données d'intensités macrosismiques SisFrance nous a permis de déterminer une loi de référence pour la décroissance de l'intensité en fonction de la distance, pour la France métropolitaine. Les lois classiquement utilisées sont fondées sur l'hypothèse que cette décroissance est indépendante de la magnitude. Or, comme l'ont par exemple souligné Hough et al. [7], cette hypothèse n'est pas nécessairement valide. Les modèles d'atténuation de l'amplitude du pic d'accélération du sol en prédisent une décroissance d'autant plus rapide que la magnitude est élevée (par exemple, [14]). Les résultats obtenus par Dahle et al. [4], dans une gamme de fréquences inférieures à 10 Hz et pour des séismes survenus en domaine continental intraplaque, indiquent, en outre, que cette dépendance à l'amplitude du pic d'accélération à l'épicentre semble exister, quelle que soit la fréquence considérée. Ces résultats, complétés par ceux de l'EPRI [5], sont repris par Van Gelder et Varpasuo [15] et confirmés pour une gamme de fréquences allant jusqu'à 33 Hz. Selon ces modèles, la dépendance de l'atténuation par rapport à la magnitude est particulièrement nette pour des distances inférieures à 100 km. Parallèlement, notre étude montre que la décroissance moyenne de l'intensité macrosismique avec la distance est d'autant plus rapide que l'intensité épicentrale
L'originalité de notre approche réside dans la prise en compte implicite de paramètres dont les valeurs sont généralement inconnues et qui contrôlent la valeur de
À l'échelle de la France métropolitaine, les résidus d'intensité par rapport au modèle (7) se répartissent de façon homogène, sans que des régions entières ne présentent de phénomènes d' « amplification » importants, i.e. [
Remerciements
P.A. remercie le conseil régional des Pays de la Loire pour le financement de sa thèse de 3e cycle, dans laquelle s'intègre ce travail. Nous tenons d'autre part à saluer l'amabilité de H. Modaressi (BRGM), qui nous a autorisés à utiliser la base de données SisFrance. Les remarques constructives de deux experts anonymes ont permis de clarifier la première version de ce manuscrit.


