Modélisation du courant sagittal induit par les vagues au-dessus des systèmes barre/baïne de la côte aquitaine (France)

Bruno Castelle; Philippe Bonneton

doi:10.1016/j.crte.2006.06.003

Océanographie / Oceanography

Modélisation du courant sagittal induit par les vagues au-dessus des systèmes barre/baïne de la côte aquitaine (France)

Présenté par : Xavier Le Pichon

Bruno Castelle ¹ ; Philippe Bonneton ¹

¹ UMR CNRS 5805 EPOC, université Bordeaux-1, avenue des Facultés, 33405 Talence cedex, France

Comptes Rendus. Géoscience, Volume 338 (2006) no. 10, pp. 711-717.

Résumés

Français
Anglais

Le courant sagittal induit par les vagues au-dessus des systèmes barre/baïne est modélisé à l'aide du modèle de courants moyens intégrés sur la verticale MORPHODYN, forcé par le modèle spectral de vagues SWAN. Sur un système barre/baïne représentatif de ceux observés sur la côte aquitaine, les simulations permettent de décrire les mécanismes physiques à l'origine de la formation de ce courant, ainsi que ses principales caractéristiques. Le courant de baïne est entièrement contrôlé par la bathymétrie, la houle au large et la hauteur de la marée. Ce courant est favorisé par la présence de houles frontales et longues. La modulation tidale du courant de baïne est intense, pour les vagues de faible amplitude, le maximum du courant de baïne est observé à mi-marée. Plus les conditions au large sont énergétiques, plus le maximum d'intensité se déplace vers la marée haute. L'introduction de la notion de forçage résiduel permet de mettre en évidence cette modulation tidale et de décrire les mécanismes de formation du courant de baïne.

The spectral wave driver SWAN is coupled with the time- and depth-averaged (2DH) coastal area model MORPHODYN. This coupled model is used to simulate the rip current induced by breaking waves over ridge and runnel systems on the French Aquitanian Coast. Simulations lead to a description of the rip current characteristics and the physical mechanisms leading to its formation. The rip current is controlled by the local bathymetry, the tide level and offshore wave conditions. The presence of this rip current is favoured by shore-normal incidence and long-period swells. During low-energy conditions, the maximum rip current velocity occurs at mid-tide. For higher energy conditions, the maximum rip velocity sweeps to high tide. The residual forcing notion enables to explain and to highlight this tidal modulation and the rip current formation mechanisms.

Métadonnées

Reçu le : 2005-08-10
Accepté le : 2006-06-12
Publié le : 2006-08-01

DOI : 10.1016/j.crte.2006.06.003

Mot clés : Modélisation, Vagues, Courants moyens, Courant sagittal, Forçage résiduel, Modulation tidale, France
Keywords: Modelling, Waves, Mean currents, Rip current, Residual forcing, Tidal modulation, France

Affiliations des auteurs :

Bruno Castelle ¹ ; Philippe Bonneton ¹

¹ UMR CNRS 5805 EPOC, université Bordeaux-1, avenue des Facultés, 33405 Talence cedex, France

@article{CRGEOS_2006__338_10_711_0,
     author = {Bruno Castelle and Philippe Bonneton},
     title = {Mod\'elisation du courant sagittal induit par les vagues au-dessus des syst\`emes barre/ba{\"\i}ne de la c\^ote aquitaine {(France)}},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {711--717},
     publisher = {Elsevier},
     volume = {338},
     number = {10},
     year = {2006},
     doi = {10.1016/j.crte.2006.06.003},
     language = {fr},
}

TY  - JOUR
AU  - Bruno Castelle
AU  - Philippe Bonneton
TI  - Modélisation du courant sagittal induit par les vagues au-dessus des systèmes barre/baïne de la côte aquitaine (France)
JO  - Comptes Rendus. Géoscience
PY  - 2006
SP  - 711
EP  - 717
VL  - 338
IS  - 10
PB  - Elsevier
DO  - 10.1016/j.crte.2006.06.003
LA  - fr
ID  - CRGEOS_2006__338_10_711_0
ER  -

%0 Journal Article
%A Bruno Castelle
%A Philippe Bonneton
%T Modélisation du courant sagittal induit par les vagues au-dessus des systèmes barre/baïne de la côte aquitaine (France)
%J Comptes Rendus. Géoscience
%D 2006
%P 711-717
%V 338
%N 10
%I Elsevier
%R 10.1016/j.crte.2006.06.003
%G fr
%F CRGEOS_2006__338_10_711_0

Bruno Castelle; Philippe Bonneton. Modélisation du courant sagittal induit par les vagues au-dessus des systèmes barre/baïne de la côte aquitaine (France). Comptes Rendus. Géoscience, Volume 338 (2006) no. 10, pp. 711-717. doi : 10.1016/j.crte.2006.06.003. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2006.06.003/

Version originale du texte intégral

Abridged English version

Rip currents are intense and narrow seaward-oriented currents being part of nearshore circulation patterns that play a key role in nearshore morphodynamics. Strong rip currents are induced by breaking waves over the ridge and runnel system on the French Aquitanian Coast (Fig. 1). The time- and depth-averaged flow model MORPHODYN is used to simulate wave-induced currents over a ridge and runnel system. This flow model is forced by SWAN wave rider. Computations show the presence of a strongly tidal-modulated rip current located at the runnel outlet associated with circulation eddies and feeder currents (Fig. 2). The forcing of the feeder currents is the pressure gradients, i.e. is the third term of Eq. (1). A strong setup is generated over the bar and in the trough, and is weaker in channel (Fig. 3). This longshore pressure gradient drives the feeder currents toward the channel and contributes to the formation of a rip current. Pressure gradients are not the only driving force. The major driving mechanism for circulation eddies and rip currents is the combination of radiation stress spatial gradients and pressure gradients. Therefore, the residual forcing ${\vec{F}}_{r}$ [9] is defined to help in describing the net forcing available to drive currents. Simulations show that, for shore-normal incidence swells, radiation stress gradients ${\vec{F}}_{v}$ are mostly balanced by pressure gradient ${\vec{F}}_{p}$ (Fig. 4.1 and 4.2). At the runnel outlet, the two forcings do not balance and a significant amount of residual forcing is available to drive a circulation eddy associated with a rip current (Fig. 4.3 and 4.4). The maximum of residual forcing is located where the beach topography is strongly tridimensional. The sensitivity of this rip current to offshore wave conditions and tide level are investigated. Simulations show that the rip current is favoured by the presence of shore-normal low-frequency waves. For oblique incidence waves, the entire longshore component of the radiation stress gradient is available to drive longshore current that oscillates over the ridge and runnel system (Fig. 5). For short-period swells, refraction due to the three-dimensional behaviour of the topography is weaker, which leads to less intense residual forcing and a weaker rip current. The magnitude of the rip current depends on both residual forcing intensity and the cross-section area of the runnel outlet, thus on tide level. Tidal modulation of the rip current is intense, with maximum flow velocity occurring around mid-tide for moderate energy conditions ( $0.5 m < H_{s} < 1.5 m$ ), and around high tide for energetic conditions ( $H_{s} > 2 m$ ) (Fig. 6). Simulations highlight that the Aquitanian coast rip currents are controlled by the local topography, offshore wave conditions and tide level.

Fig. 1
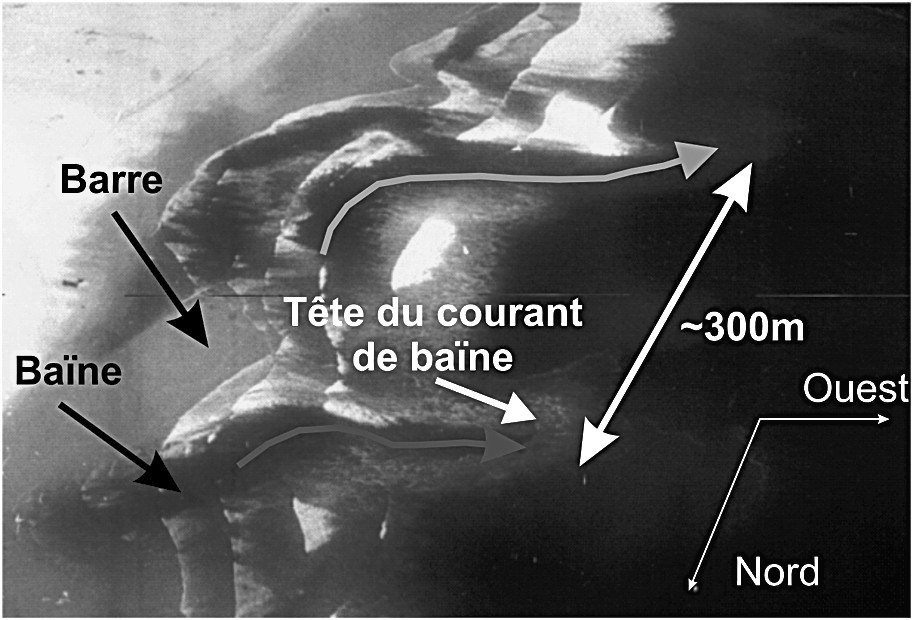
Photo aérienne d'un système barre/baïne sur la côte aquitaine. Le courant sagittal situé à la sortie de la baïne est visible grâce aux deux panaches sédimentaires situés au niveau de la tête des courants. D'après [8].
Aerial photograph of a ridge and runnel system, Aquitanian Coast. Location of rip currents located at the runnel outlets with two sediment plumes are highlighted. After [8].

Fig. 2
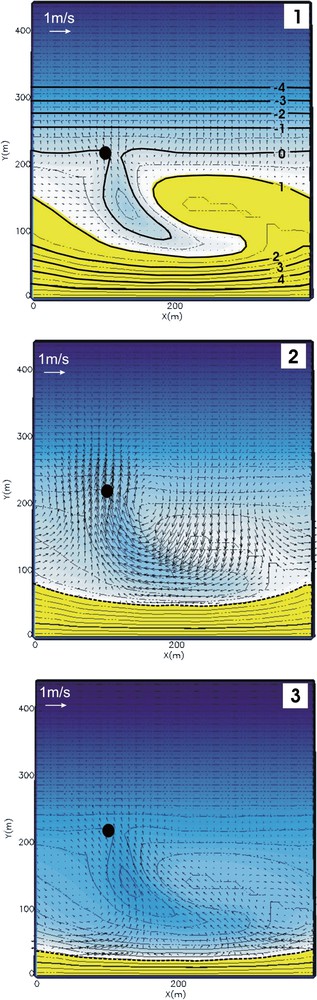
Courants moyens simulés au-dessus du système barre/baïne idéalisé pour différentes hauteurs de marée $h_{m}$ et localisation de la bouée virtuelle à la sortie de la baïne. Conditions de houle au large : $H_{s 0} = 1 m$ , $T_{m 0} = 12 s$ , $θ_{m 0} = 0 °$ . Hauteur de marée (1) : $h_{m} = 1 m$ ; (2) : $h_{m} = 2, 03 m$ ; (3) : $h_{m} = 3, 71 m$ .
Computed mean currents over the ridge and runnel system for different tide levels $h_{m}$ and location of the virtual buoy at the runnel outlet. Offshore wave conditions: $H_{s 0} = 1 m$ , $T_{m 0} = 12 s$ , $θ_{m 0} = 0 °$ . Tide level (1): $h_{m} = 1 m$ ; (2): $h_{m} = 2.03 m$ ; (3): $h_{m} = 3.71 m$ .

Fig. 3
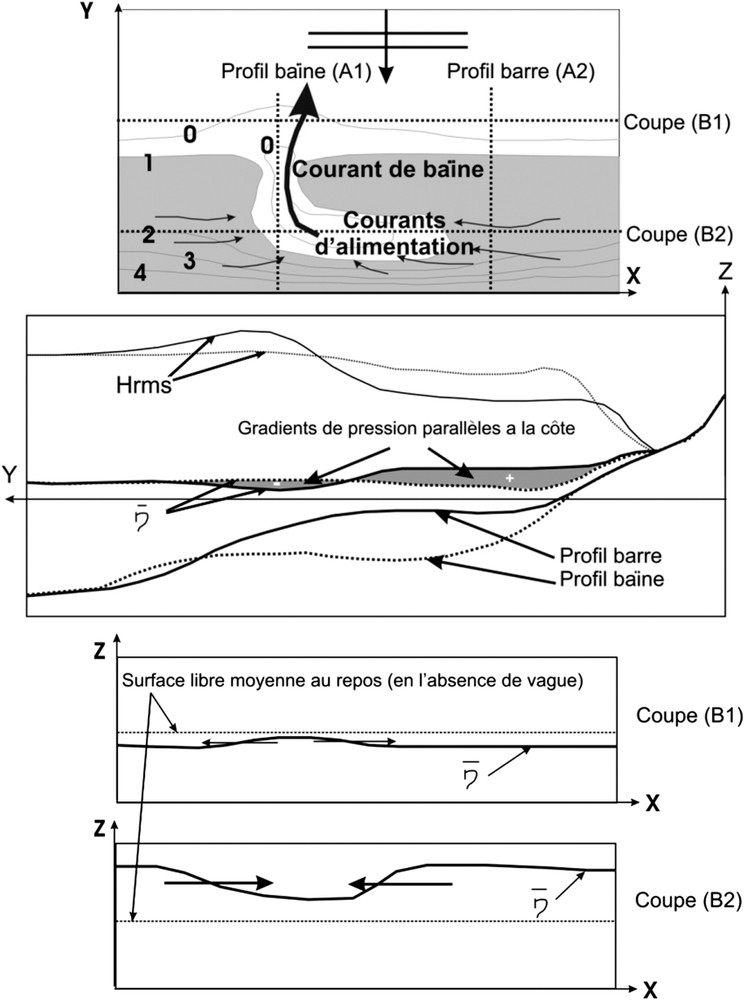
Schématisation de la génération d'un gradient longshore de pression au-dessus d'un système barre/baïne. Visualisation des profils cross-shore et longshore de la surface libre moyenne $\bar{η}$ .
Schematization of longshore pressure gradient generation over a ridge and runnel system. Visualisation of cross-shore and longshore transects of mean surface elevation $\bar{η}$ .

Fig. 4
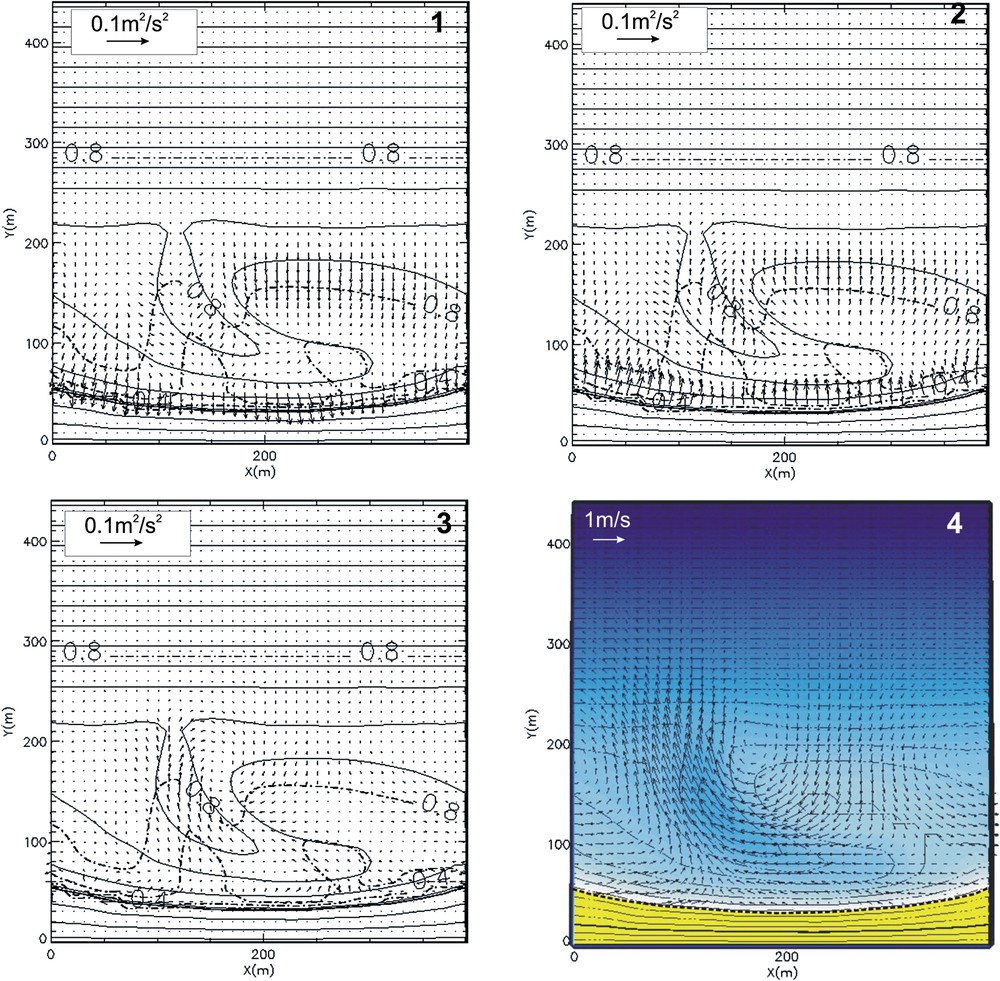
Simulation environ à mi-marée ( $h_{m} = 2, 96 m$ ), houle au large : $H_{s 0} = 1 m$ , $T_{m 0} = 12 s$ , $θ_{m 0} = 0 °$ . (1) Champ des gradients d'excès de quantité de mouvement ${\vec{F}}_{v}$ , iso-hauteurs significatives de vagues ; (2) champ des gradients de pression ${\vec{F}}_{p}$ , iso-hauteurs significatives de vagues ; (3) champ de forçage résiduel $\vec{F}$ ; (4) champ des courants moyens induits ${\vec{U}}_{c}$ .
Simulation around mid-tide ( $h_{m} = 2, 96 m$ ), offshore waves: $H_{s 0} = 1 m$ , $T_{m 0} = 12 s$ , $θ_{m 0} = 0 °$ . (1) Wave forcing ${\vec{F}}_{v}$ , iso-significant wave height; (2) pressure gradient ${\vec{F}}_{p}$ , iso-significant wave height; (3) residual forcing $\vec{F}$ , iso-significant wave height; (4) mean current vectors ${\vec{U}}_{c}$ .

Fig. 5
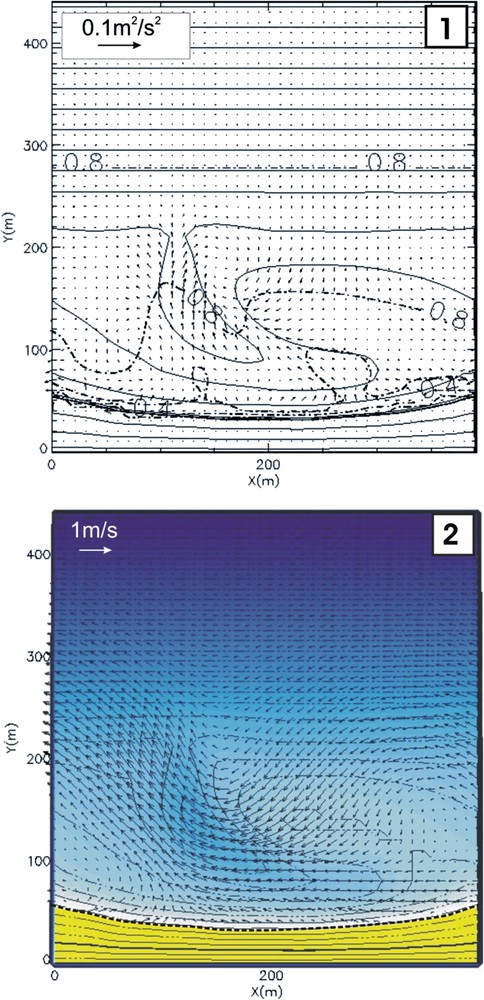
Simulation environ à mi-marée ( $h_{m} = 2, 96 m$ ), houle au large : $H_{s 0} = 1 m$ , $T_{m 0} = 12 s$ , $θ_{m 0} = 10 °$ . (1) Champ de forçage résiduel $\vec{F}$ et iso-hauteurs significatives de vagues ; (2) champ des courants moyens induits ${\vec{U}}_{c}$ .
Simulation around mid-tide ( $h_{m} = 2.96 m$ ), offshore waves: $H_{s 0} = 1 m$ , $T_{m 0} = 12 s$ , $θ_{m 0} = 10 °$ . (1) Residual forcing vectors $\vec{F}$ , and iso-significant wave height; (2) mean current vectors ${\vec{U}}_{c}$ .

Fig. 6
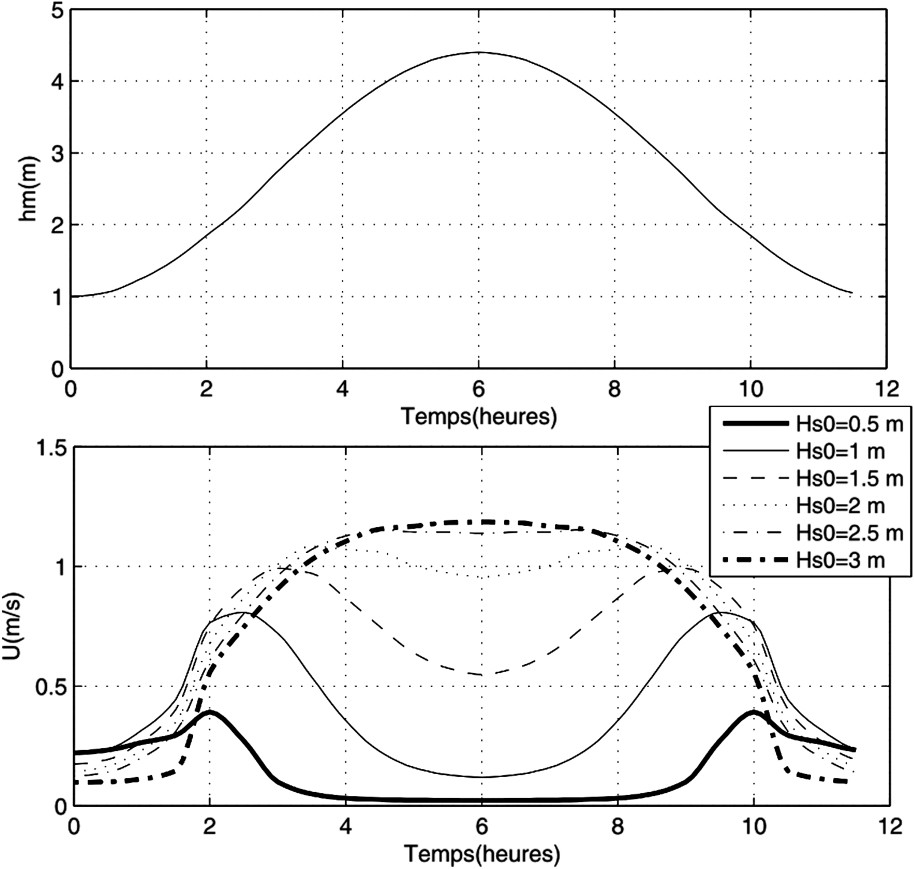
Niveau de marée $h_{m}$ et intensité du courant de baïne U en fonction du temps, au niveau de la bouée virtuelle située à la sortie de la baïne (Fig. 2), pour différentes hauteurs significatives au large $H_{s 0}$ , et pour $T_{m 0} = 12 s$ et θ=0°.
Tide level $h_{m}$ and rip current velocity U as a function of time at the virtual buoy (Fig. 2) for different significant wave heights $H_{s 0}$ , with $T_{m 0} = 12 s$ and $θ_{0} = 0 °$ .

1 Introduction

Le courant sagittal est un courant violent, intense et étroit dirigé vers le large, qui est observé sur de nombreuses plages. Il transporte de grandes quantités de sédiments [5,13]. Il fait également partie d'un ensemble complexe de cellules de circulation des courants moyens, et joue un rôle essentiel dans la morphodynamique côtière et les processus d'érosion [19]. Ce rôle a été également récemment mis en évidence dans les mécanismes de formation et de développement des barres sédimentaires périodiques le long de la côte [9,17]. Des mesures de terrain [5,15] et en laboratoire [11] ont permis de mieux connaître quantitativement la structure horizontale des courants sagittaux et de mettre en évidence sa forte sensibilité au niveau de marée [6,12].

Plusieurs mécanismes ont été évoqués pour expliquer la formation des courants sagittaux. On peut citer, par exemple, la variabilité du forçage des vagues parallèlement à la côte [4] ou encore les interactions vague–courant [10]. En fait, l'hydrodynamique et, en particulier l'occurrence des courants sagittaux, est principalement contrôlée par la bathymétrie locale. La présence de bancs de sable tridimensionnels va induire une focalisation de l'énergie des vagues dans certaines zones et la formation de courants sagittaux.

Sur la côte aquitaine, en France, un courant sagittal, observé quasiment tout le long de l'année, est connu, notamment, parce qu'il est responsable de nombreuses noyades chaque été : le courant de baïne. La Fig. 1 montre la photo aérienne d'une plage de la côte aquitaine, où l'on observe deux baïnes dans la zone intertidale, avec deux forts courants situés à la sortie de chacune d'entre elle. Ces deux courants dirigés vers le large sont reconnaissables sur la photo, car ils transportent des sédiments en suspension et perturbent la surface libre. Récemment, Castelle et al. [8] ont modélisé l'hydrodynamique au-dessus d'une plage aquitaine pendant la campagne PNEC 2001. Les résultats obtenus ont aussi permis, pour la première fois, d'effectuer une étude préliminaire sur le courant de baïne et de calibrer les modules hydrodynamiques du modèle numérique.

L'objectif de ce papier est de décrire en détail les mécanismes physiques à l'origine du courant de baïne, ainsi que ses principales caractéristiques. La sensibilité de ce courant au forçage au large et à la hauteur du plan d'eau est étudiée, et son intensité quantifiée.

2 Modèle

Le modèle d'hydrodynamique sédimentaire côtière MORPHODYN est basé sur l'intégration spatio-temporelle des équations locales de conservation de la masse et de conservation de la quantité de mouvement [2,18]. Ces équations sont résolues numériquement en utilisant un schéma implicite, afin d'obtenir les débits liquides moyens intégrés sur la verticale ${\bar{Q}}_{i}$ et la hauteur d'eau moyenne $\bar{h}$ ( $i = 1, 2$ ) :

\frac{\partial {\bar{Q}}_{i}}{\partial t} + \frac{\partial}{\partial x_{j}} (\frac{{\bar{Q}}_{i} {\bar{Q}}_{j}}{\bar{h}}) = - g \bar{h} \frac{\partial \bar{η}}{\partial x_{i}} - \frac{1}{ρ} \frac{\partial S_{i j}}{\partial x_{j}} - \frac{1}{ρ} \frac{\partial R_{i j}}{\partial x_{j}} + \frac{1}{ρ} \frac{\partial T_{i j}}{\partial x_{j}} - \frac{τ_{i}^{b}}{ρ}

(1)

\frac{\partial \bar{η}}{\partial t} + \frac{\partial {\bar{Q}}_{j}}{\partial x_{j}} = 0

(2)

Dans l'équation de la conservation de la quantité de mouvement (1) et de la conservation de la masse (2),

\bar{η}

est la cote de la surface libre moyenne, g est l'accélération gravitationnelle, ρ la masse volumique de l'eau,

S_{i j}

les tensions de radiation [16],

R_{i j}

l'excès de quantité de mouvement associé au rouleau de déferlement,

τ_{i}^{b}

le frottement moyen au fond et

T_{i j}

le terme de mélange des masses d'eau. Les courants moyens

U_{c i}

obtenus à partir de la décomposition de [16] permettent de prendre en compte la contribution du courant de retour :

U_{c i} = \frac{{\bar{Q}}_{i} - {\hat{Q}}_{i}}{\bar{h}}

(3)

où

{\hat{Q}}_{i}

est l'apport de masse d'eau par les vagues, dû au mouvement organisé et au rouleau de déferlement.

Le modèle spectral de vagues SWAN [3] est utilisé pour calculer le champ de vagues et les termes de forçage $S_{i j}$ et $R_{i j}$ résultants.

Une description détaillée du modèle hydrodynamique et des différentes paramétrisations utilisées est donnée dans la référence [7]. La calibration du modèle avec les données de la campagne de mesure PNEC 2001 sur la plage aquitaine du Truc vert est présentée dans la référence [8].

Pour les simulations qui suivent, nous considérons une bathymétrie idéalisée d'un système barre/baïne d'une périodicité spatiale de 400 m, correspondant à la longueur d'onde moyenne de ces systèmes sur la côte aquitaine [14], et avec une baïne orientée dans la direction de la dérive littorale. Au large du système barre/baïne, une pente douce et homogène de la plage est considérée. Le maillage est régulier, avec $Δ x = Δ y = 10 m$ et on considère des conditions aux limites latérales périodiques.

3 Résultats

3.1 Mécanisme physique

Considérons une houle au large de hauteur significative, de période moyenne et d'incidence définie par rapport à la normale à la côte respectivement $H_{s 0} = 1 m$ , $T_{m 0} = 12 s$ , $θ_{m 0} = 0 °$ . On choisit une houle frontale, car elle favorise la formation des courants sagittaux [7]. La Fig. 2 montre les courants moyens calculés à différents moments de la marée sur la bathymétrie idéalisée, avec $h_{m}$ la hauteur de la marée définie au-dessus du 0 hydrographique. La modulation tidale des courants simulés est intense, avec des vitesses maximales aux environs de la mi-marée (de l'ordre de 0,7 m/s, Fig. 2.2). Ce courant sagittal est associé à une grande cellule de circulation des courants moyens et à des courants d'alimentation en haut de plage, qui convergent vers la sortie de baïne.

Considérons un système barre/baïne, une hauteur de marée suffisante pour que la barre soit immergée et des vagues suffisamment énergétiques pour déferler sur la barre. La Fig. 3 montre schématiquement l'évolution de la hauteur des vagues et du set-up le long d'un profil cross-shore coupant la barre et d'un autre coupant la baïne. Le forçage ( $\frac{\partial}{\partial y} ({\bar{S}}_{y y} + {\bar{R}}_{y y})$ ) contribue à la génération du set-up/set-down. Sur le « profil barre » (Fig. 3), les vagues déferlent sur la barre et induisent un fort set-up derrière celle-ci, tandis que sur le « profil baïne » le déferlement s'effectue plus près du haut de plage et avec une intensité plus faible. Cette variation parallèlement à la côte de la hauteur moyenne du plan d'eau (gradient de pression longshore), de l'ordre de quelques centimètres, est suffisante pour forcer en haut de plage des courants d'alimentation du courant sagittal ( « rip feeders »).

Les gradients de pression longshore ne sont pas l'unique mécanisme à l'origine de la formation du courant de baïne : la combinaison de l'ensemble des gradients de pression et des gradients d'excès de quantité de mouvement joue également un rôle essentiel.

3.2 Notion de forçage résiduel

Dans le cas des plages présentant des structures tridimensionnelles, une partie des gradients cross-shore d'excès de quantité de mouvement vont pouvoir induire un mouvement des masses d'eau et contribuer à la formation de cellules de circulation des courants moyens. La notion de forçage résiduel ${\vec{F}}_{r}$ [12] permet de prendre en compte la combinaison des gradients d'excès de quantité de mouvement et de pression, ce qui permet d'indiquer le forçage net disponible pour forcer le mouvement des masses d'eau :

F_{r i} = - ρ g \bar{h} \frac{\partial \bar{η}}{\partial x_{i}} - \frac{\partial}{\partial x_{j}} ({\bar{S}}_{i j} + {\bar{R}}_{i j}) = F_{p i} + F_{v i}

(4)

où

{\vec{F}}_{p}

correspond aux gradients de pression hydrostatique et

{\vec{F}}_{v}

aux gradients d'excès de quantité de mouvement associés aux vagues.

La Fig. 4 montre la simulation des courants moyens et des différents termes de forçage ${\vec{F}}_{v}$ , ${\vec{F}}_{p}$ et de leur somme ${\vec{F}}_{r}$ pour des vagues au large, telles que $H_{s 0} = 1 m$ , $T_{m 0} = 12 s$ , $θ_{m 0} = 0 °$ . Au niveau de la sortie de la baïne, le déferlement est moins intense que sur la barre, d'où une « poussée » des masses d'eau plus faible (Fig. 4.1). Une grande partie de cette « poussée » va être transmise aux masses d'eau sous la forme de variation du niveau d'eau moyen, induisant des gradients de pression ${\vec{F}}_{p}$ (Fig. 4.2) qui contrebalancent ainsi une grande partie de ${\vec{F}}_{v}$ . Une faible partie de ${\vec{F}}_{v}$ n'est pas contrebalancée et est visible à travers le forçage résiduel. Une grande partie de la contribution de ce forçage résiduel est localisée à la sortie de la baïne, où les gradients longshore de bathymétrie sont les plus importants (Fig. 4.3). Ce forçage est alors entièrement disponible pour générer un courant de baïne intense (Fig. 4.4).

3.3 Sensibilité au forçage au large et à la hauteur du plan d'eau

La Fig. 5 montre le forçage résiduel ${\vec{F}}_{r}$ et les courants induits ${\vec{U}}_{c}$ pour une houle au large de hauteur significative $H_{s 0} = 1 m$ , de période $T_{m 0} = 12 s$ et d'angle d'incidence par rapport à la côte $θ_{m 0} = 10 °$ . On remarque que le forçage résiduel obtenu (Fig. 5.2) est similaire à celui induit par la même houle de $H_{s 0} = 1 m$ , $T_{m 0} = 12 s$ et $θ_{m 0} = 0 °$ (Fig. 4.3). En revanche, le champ des courants moyens induits est sensiblement différent. En effet, une très faible contribution longshore du forçage des vagues ${\vec{F}}_{v}$ peut générer un courant de dérive intense, tandis qu'une grande partie de sa contribution cross-shore est contrebalancée par ${\vec{F}}_{p}$ . Le champ de courant obtenu (Fig. 5.2) montre une oscillation du courant de dérive induit au-dessus du système barre/baïne, le courant de baïne devenant moins chenalisé et dirigé dans le sens du courant de dérive. Pour des houles plus obliques, typiquement pour des angles d'incidence $- 20 ° < θ_{m 0} < 20 °$ , le courant de baïne peut complètement disparaître et un courant de dérive quasiment homogène dans la direction longshore est alors observé [7].

D'autres simulations [7] permettent également de décrire l'influence de la période moyenne $T_{m 0}$ . Les résultats montrent que, pour des vagues telles que $H_{s 0} = 1 m$ et $T_{m 0} = 6 s$ , on aura un maximum de courant de baïne de 0,5 m/s, au lieu de 0,7 m/s pour $T_{m 0} = 12 s$ . En effet, les houles courtes sont moins réfractées et il y a donc moins de focalisation d'énergie des vagues sur la barre, ce qui se traduit par un forçage résiduel beaucoup plus faible au niveau de la sortie de la baïne, pour une même hauteur de marée $h_{m}$ .

La variation de la hauteur de marée influence de façon déterminante la structure des courants moyens au-dessus du système barre/baïne pour une houle au large donnée. L'intensité du courant de baïne dépend de l'intensité du forçage résiduel et de la surface de la section cross-shore de la sortie de baïne. En effet, pour un même forçage résiduel, le rétrécissement de la sortie de baïne, qui dépend essentiellement du niveau de la marée, entraîne une augmentation du courant (par conservation du débit). La Fig. 6 montre l'évolution du courant de baïne simulé au niveau de la bouée virtuelle (Fig. 2) pendant un cycle de marée, pour différentes valeurs de $H_{s 0}$ , en gardant $T_{m 0} = 12 s$ et $θ_{0} = 0 °$ . Plus les conditions de houle sont énergétiques, plus le maximum de courant de baïne se déplace vers la marée haute. Ces résultats confirment les mesures et les simulations préliminaires de [8]. Cette modulation tidale diffère de celles observées sur d'autres environnements [1,5,6] où le maximum est généralement observé à marée basse. Cette différence est directement liée à la morphologie du système. Enfin, on remarque que, suivant la hauteur de marée, les houles peu énergétiques peuvent induire un courant de baïne intense.

4 Conclusion

Le courant de baïne est entièrement contrôlé par la bathymétrie du système, les caractéristiques de houle au large et la hauteur du plan d'eau. L'occurrence d'un courant de baïne intense et étroit est favorisée par la présence d'une houle longue et frontale. Plus les vagues sont énergétiques, plus elles pourront induire un courant de baïne violent. Ce courant sera alors maximum, lorsque le meilleur compromis entre des gradients de pressions longshore intenses et une section longshore de sortie de baïne étroite sera obtenu. Le forçage résiduel ${\vec{F}}_{r}$ correspond au forçage net disponible dans son intégralité pour induire les courants moyens et permet de mettre en évidence la structure du courant de baïne. Ce courant sagittal diffère, dans son comportement, des autres sites étudiés dans la littérature.

Remerciements

Ce travail a été réalisé dans le cadre du Programme national d'environnement côtier, action de recherche thématique 7 (PNEC ART 7), CNRS/INSU. Bruno Castelle était financé par la DGA pour ses travaux de thèse.

Bibliographie

[1] T. Aagaard; B. Greenwood; J. Nielsen Mean currents and sediment transport in a rip channel, Mar. Geol., Volume 140 (1997), pp. 25-45

[2] P. Bonneton Analyse physique et modélisation des processus hydrodynamiques en zone de surf, Oceanis, Volume 29 (2003), pp. 157-179

[3] N. Booij; R. Ris; L. Holthuijsen A third-generation wave model for coastal regions, part i: Model description and validation, J. Geophys. Res., Volume 104 (1999) no. C4, pp. 7649-7666

[4] A. Bowen Rip currents: laboratory and field observations, J. Geophys. Res., Volume 74 (1969), pp. 5479-5490

[5] R. Brander Field observations on the morphodynamic evolution of low-energy rip current system, Mar. Geol., Volume 157 (1999), pp. 199-217

[6] R. Brander Morphodynamics of a large-scale rip current system at Muriwai beach, New Zealand, Mar. Geol., Volume 165 (2000), pp. 27-39

[7] B. Castelle, Modélisation de l'hydrodynamique sédimentaire au-dessus des barres sableuses soumises à l'action de la houle : appliction à la côte aquitaine, thèse, université Bordeaux-1, 2004 (340 p.)

[8] B. Castelle; P. Bonneton; N. Sénéchal; H. Dupuis; R. Butel; D. Michel Dynamics of wave-induced currents over a multiple-barred sandy beach on the Aquitanian coast, Cont. Shelf Res., Volume 26 (2006), pp. 113-131

[9] J. Damgaard; N. Dodd; L. Hall; T. Chesher Morphodynamic modeling of rip channel growth, Coast. Eng., Volume 45 (2002), pp. 199-221

[10] R. Dalrymple; C. Loranzo Wave–current interaction models for rip currents, J. Geophys. Res., Volume 83 (1978), pp. 6063-6071

[11] K. Haas; I. Svendsen Laboratory measurements of the vertical structure of rip current, J. Geophys. Res., Volume 107 (2002) no. C5 | DOI

[12] K. Haas, I. Svendsen, R. Brander, P. Nielsen, Modeling of a rip current system on Moreton Island, Australia, in: Proceeding of the International Conference on Coastal Engineering, ASCE, 2002

[13] D. Inman; R. Tait; C. Nordstrom Mixing in the surf zone, J. Geophys. Res., Volume 76 (1971) no. C15, pp. 3493-3514

[14] V. Lafon; H. Dupuis; R. Butel; B. Castelle; D. Michel; H. Howa; D. De Melo Apoluceno Morphodynamics of nearshore rhythmic sandbars in a mixed-energy environment (SW France): 2. Physical forcing analysis, Estuar. Coast. Shelf Sci., Volume 65 (2005) no. 3, pp. 449-462

[15] J. MacMahan; E. Thornton; T. Stanton; A. Reniers; R. Dean Ripex: Rip-current pulsation measurements, Coast. Eng. (2003), pp. 736-746

[16] O. Philipps The Dynamics of the Upper Ocean, Cambridge University Press, 1977

[17] A. Reniers; J. Roelvink; E. Thornton Morphodynamic modeling of an embayed beach under wave group forcing, J. Geophys. Res., Volume 109 (2004), p. C01030 | DOI

[18] F. Saint-Cast, Modélisation de la morphodynamique des corps sableux en milieu littoral, thèse, université Bordeaux-1, 2002

[19] A. Short Beach systems of the central Netherlands coast: processes, morphology and structural impacts in a storm driven multi-bar system, Mar. Geol., Volume 107 (1992), pp. 103-137

Commentaires - Politique