1 Introduction
The mechanisms by which biological self-organisation occurs from an initially homogenous starting point remain poorly understood. Although over the last 20 years studies in molecular biology have started to reveal some of the genes involved, our understanding of the physical-chemical laws underlying these processes remain uncertain. In equilibrium systems, macroscopic self-organisation rarely occurs, and during the first half of this century scientists found difficulty in reconciling biological self-ordering with the third law of thermodynamics. For example, when two miscible liquids are added one to another, molecular diffusion causes progressive mixing, leading to the gradual appearance of a homogenous solution from the initially inhomogeneous starting point. On the contrary, in living organisms, order and form develop spontaneously from a starting point such as an egg or seed, which is approximately homogenous and largely devoid of form and order. In addition, biological development is characterised by the fact that beyond a certain critical stage, cells of identical genetic content take different developmental pathways, so as to become differentiated from one another
There are two possible physical-chemical approaches that might account for biological self-organisation; one is based on static interactions and statistical physics; the other is based upon non-linear chemical dynamics and co-operative phenomena. This article is wholly concerned with the latter approach. One area in physics, where macroscopic ordering from an initially uniform state occurs by way of non-linear dynamics, is hydrodynamics. At the beginning of this century, D’Arcy Thompson 〚1〛 noticed the resemblance between some biological forms and those produced by liquids in motion. Familiar examples of hydrodynamic forms are the anticyclonic variations in atmospheric pressure represented on meteorological maps, and the spiral shaped vortex that arises when a washing basin is emptied. Other well-known cases of hydrodynamic self-organisation arise in the Bénard instability, and Taylor instability experiments 〚2, 3〛.
In these systems, the equations describing the hydrodynamics of the liquid are non-linear; their solution gives rise to variations in the parameters describing the motion of the liquid that vary periodically with position. Rashevsky in 1942 〚4, 5〛 and then Turing in 1952 〚6〛 advanced the idea that similar mathematical relationships, and hence a similar type of behaviour, might occur chemically. They proposed that in certain types of reaction scheme, the combination of reaction and diffusion could result in periodic variations in the concentration of some of the reactants. This result, contrary to what might be intuitively expected, is a consequence of the chemical system being far-from-equilibrium. During the 1960s and 1970s, Prigogine and co-workers 〚7–9〛 substantially developed the approach initially outlined by Rashevsky and Turing. Rashevsky, Turing, and Prigogine all postulated that such mechanisms might provide an underlying basis for biological morphogenesis and self-organisation.
As in the case of the structures that appear in the Taylor and Bénard experiments, and which are due to specific out-of-equilibrium conditions, the formation of macroscopic chemical patterns requires specific out-of-equilibrium conditions. Chemical energy needs to be put into the system to both form and sustain the pattern. For the case of the Bénard and Taylor experiments, the macroscopic pattern that arises results from physical processes, whereas in the approach developed by Rashevsky, Turing, and Prigogine, the patterns are comprised of differences in chemical concentration that come about through chemical processes. At a molecular level, they arise from a suitable combination of reaction and diffusion, and, starting from an initially homogeneous solution, a stationary chemical pattern progressively develops. They are known as reaction–diffusion or Turing patterns, but because they depend upon chemical energy dissipation, they are also called chemically dissipative structures. Both this type of chemical pattern and hydrodynamic patterns are specific cases of macroscopic self-ordering by way of non-linear dynamics.
In addition to self-organisation, non-linear out-of-equilibrium systems also differ from equilibrium systems by showing bifurcation properties, for example of the bistable type 〚3, 9〛. Non-linear systems can exist in multiple stationary states. At the bifurcation point, a field too weak to effect an equilibrium state can favour the dynamic pathway leading to one of the multiple states over the others, and hence determine the morphology of the self-organised state that forms. Just after the bifurcation, the morphology that will subsequently develop is determined, even though at that time no organisation is as yet visible. Prigogine and co-workers explicitly calculated that in some reaction–diffusion systems, the earth’s gravitational field could cause a bifurcation 〚10, 11〛.
These concepts, although a subject of interest and debate, have never been adopted by the majority of chemists and biologists. One reason is conceptual; many workers are unfamiliar with the principles of non-linear dynamics. There is a reluctance to accept the premise that organisation can result from chemical processes rather than arise from static interactions. However, another more practical reason is that until relatively recently there were no examples of chemical and biochemical systems known to behave this way. For example, in chemistry, it was not until 1990 〚12, 13〛 that a variation of a chemical reaction, the Belousov–Zhabotinsky reaction 〚14–16〛, initially discovered in 1950, was at last accepted by the majority of workers in the field as the first example of a Turing structure. This change seems to have as much to do with the beginning of a general acceptance of such an approach, concomitant with the development of chaos theory, than with the appearance of a substantially new body of experimental evidence. The same situation has prevailed in biology. Many authors have compared the morphologies that occur in biological organisms with the mathematical predictions of reaction–diffusion theories. There is a substantial body of literature in this area 〚17–19〛. Workers 〚20, 21〛 have demonstrated that the patterns of cytosolic calcium waves that occur in vivo arise from reaction–diffusion processes. However, until recently there were no in vitro examples involving a simple biochemical system in a test tube, behaving in the general manner predicted by Rashevsky, Turing, Prigogine, and others.
We have found that the formation in vitro of microtubules 〚22〛, a major component of the cellular skeleton 〚23〛, shows the behaviour predicted by these theories. These microtubule preparations spontaneously self-organise by way of reaction–diffusion processes, and the morphology of the state that forms depends upon the presence of gravity at a critical moment at an early stage in the self-organising process 〚24–32〛.
Microtubules are one of the major components of the cellular skeleton and play an important role in many fundamental cellular processes. During the interphase part of the cell cycle, microtubules irradiate across the cell interior. When cell division occurs, the microtubules disassemble and then reassemble in aligned arrays. These arrays constitute the mitotic spindle along which the chromosomes move. Microtubules control cellular organisation through processes that are not yet understood and are involved in many cellular functions, including the maintenance of shape, motility, signal transmission, and intracellular transport. They play a determining role in the organisational changes that occur during the early stages of embryogenesis.
It is possible to show that the in vitro microtubule self-organising process contains both reactive and diffusive contributions. Self-organisation arises from collective processes in which assembled microtubules partially disassemble and then reassemble 〚27〛. What we did not know was the molecular basis, both of self-organisation and its dependence on external fields such as gravity. On the contrary, one of the advantages of the non-linear approach is that a molecular understanding is not necessary to obtain a qualitative understanding of the phenomenological behaviour. In other words, the macroscopic behaviour can be made sense of in terms of non-linear chemical dynamics, even though nothing at all may be known about what the individual molecules are doing. On the other hand, if everything about the individual molecules were known, and nothing at all known about non-linear chemical dynamics and collective properties, then it would be extremely difficult to predict the overall behaviour.
Having said this, there are strong reasons for wanting to understand the molecular basis for our observations. One reason is that the majority of chemists and biologists reason in terms of individual molecular processes rather than non-linear chemical dynamics. A molecular description of our observations would not only permit a fruitful scientific intercourse with most chemists and biologists, it would also constitute a step towards describing some global biological properties based upon non-linear chemical dynamics, in terms of molecular processes.
These considerations lead us to carry out numerical simulations of the self-organising process based upon a population of microtubules that communicate with one another, and develop a collective behaviour, by way of reaction and diffusion. The development of this model was based upon a schematic molecular hypothesis that first arose from experimental observations. Its successful development could not have been carried out without numerous comparisons with experiment. The simulations have provided considerable insight as to the molecular and microscopic basis of self-organisation, and now in their turn suggest further experiments. In this short article, we shall attempt to highlight the way that the dialogue between experiment and numerical simulation has advanced our understanding.
2 Experimental results
Microtubules 〚22〛 are tubular-shaped supramolecular assemblies, with inner and outer diameters of 16 and 24 nm respectively, and several microns in length. They arise from the self-assembly of a protein, tubulin, by way of reactions involving the hydrolysis of a nucleotide, guanosine triphosphate (GTP), to guanosine diphosphate (GDP). Microtubules can be formed in vitro by warming a solution containing purified tubulin and GTP from about 7 to 36 °C. A series of chemical reactions occur, tubulin assembles into microtubules, and GTP is hydrolysed to GDP. This reaction continues by processes involving microtubule disassembly and reassembly, where tubulin is added to one extremity of a microtubule and is lost from the other 〚33〛 (Fig. 1). There is hence a continual consumption or dissipation of chemical energy through the system.

Schematic illustration of a microtubule undergoing tread milling. Tubulin is added to one end of the microtubule (+) and is lost from the other (–).
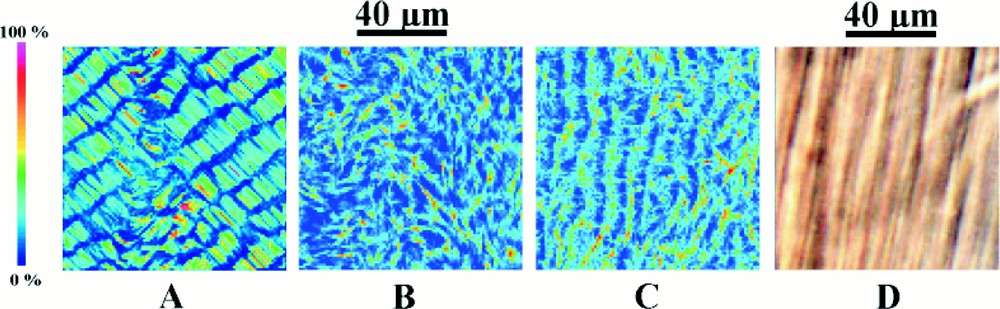
Under appropriate buffer conditions, reaction–diffusion processes give rise to spontaneous macroscopic ordering 〚24–32〛. Following assembly in spectrophotometer cells, a series of periodic horizontal stripes of about 1 mm separation progressively develops over about 5 h (Fig. 2) 〚24〛. Once formed, the striped pattern remains stationary for between 48 to72 h, after which the system runs out of reactants. In each striped band the microtubules are highly oriented at either 45° or 135°, but adjacent stripes differ in having opposite orientations. The periodic variations in microtubule orientation are readily observed as birefringent stripes that, depending on their orientation, have either a yellow or blue interference colour. This orientational pattern coincides with an identical pattern of microtubule concentration, in which the microtubule concentration drops by about 25%, and then rises again, every time the microtubule orientation flips from acute to obtuse 〚30〛 Another series of stripes of about 100 μm separation occurs within the 0.5 mm stripes. These in their turn, contain another set of stripes of about 20 μm separation (Fig. 3A). At distances below this, there is another level of organisation of about 5 μm periodicity and with care it is possible to observe aligned microtubule arrays of about 1 μm separation (Fig. 3B).
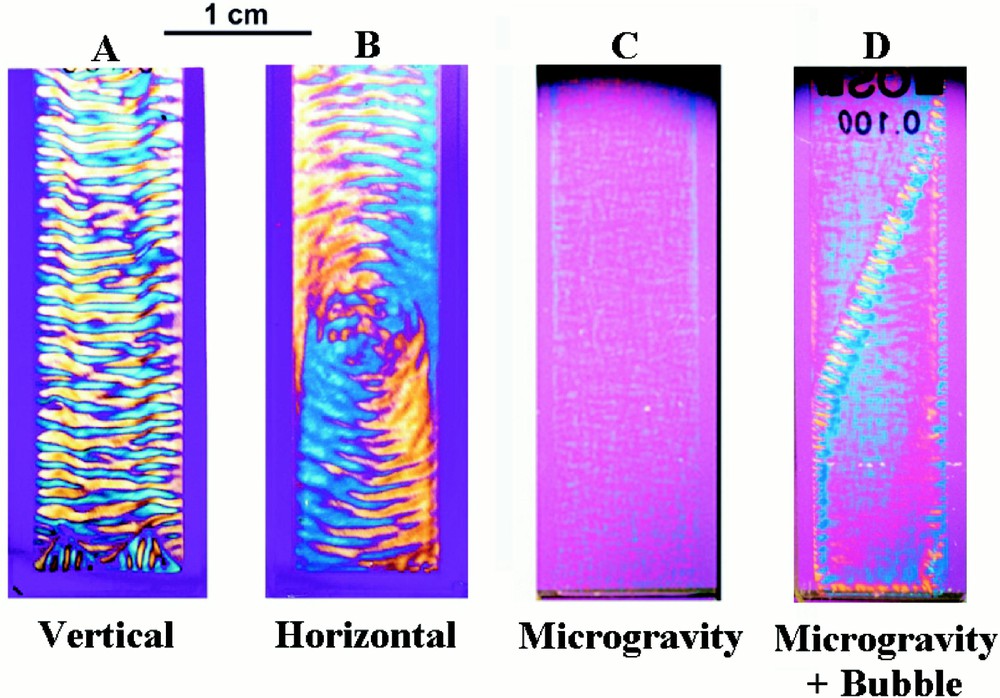
Microtubule structures formed in spectrophotometer cells 4 cm × 1 cm × 0.1 cm. In the presence of gravity, the solution spontaneously self-organises. Stripes form when the sample container is upright (A), but circles arise when the microtubules are assembled with the container flat (B). The structures, which take about 6 h to form, are stationary and independent of the orientation of the cell with respect to gravity. The morphology that forms depends on the orientation of the container at a critical moment at an early stage in the self-organising process and before any pattern has developed. No self-organisation occurs when microtubules are assembled in the absence of gravity for the first 13 min (C). For samples such as (C), the passage of an air bubble through the solution during payload re-entry caused partial self-organisation perpendicular to the bubble trajectory (D). Samples were photographed through linear cross polars with a wavelength retardation plate. The blue interference colour arises from microtubules oriented at about 45°, and the yellow interference colour from those at 135°. Periodic changes in microtubule concentration coincide with the orientational changes.

Self-organisation also occurs over smaller distance scales. (A) is a photograph taken from a sample placed between crossed circular polars. In addition to the periodicity of about 400 μm (a), it also shows periodicities of about 100 μm (b), 20 μm (c) and 5 μm (d). (B) is a photograph at higher magnification using DIC optics and reveals a periodicity of approximately 1.5 μm (e). This level of organisation should be compared with those of the numerical simulations shown in Fig. 7.
Striped morphologies occur when the microtubules are prepared in upright sample containers (Fig. 2A), but a different pattern arises when they are prepared in the same containers lying flat (Fig. 2B). Once formed, the structures are stationary and independent of their orientation with respect to gravity. This behaviour is attributed to the determining role of the direction of the gravitational field during structure formation. So as to test this hypothesis, microtubules were assembled in flat horizontal containers fixed to the turntable of a record player, with the long axis of the sample container along the direction of the centrifugal field (0.14 g) 〚26〛. A striped morphology once again forms, and the direction of the stripes is perpendicular to that of the applied centrifugal field.
To establish at what moment the sample morphology depends upon the orientation with respect to gravity, the following experiment was carried out 〚27〛. Twenty samples of purified tubulin together with GTP, and at 4 °C, were placed in identical optical cells. Microtubule formation was simultaneously instigated with all the cells upright. Consecutive cells were turned from vertical to horizontal at 1 min intervals, and the samples examined 12 h later after the structures had formed. Twenty minutes after instigating microtubule formation, when the last sample was turned from vertical to horizontal, there are no obvious signs of striped structure. Since the structures forms while all the cells are flat, one might expect that they would all form the horizontal pattern. This is the case for samples inverted during the first few minutes. However, samples that were upright for 6 min or more showed striped morphologies similar to preparations that remained vertical all the time. The final morphology of the sample depends upon whether the sample container was horizontal or vertical, at a critical time 6 min after instigating assembly, at an early stage in the self-organising process. The process can be described as a bifurcation between pathways, leading to two different morphological states, and in which the direction of the sample with respect to gravity determines which morphology subsequently forms.
Preparations formed in a rocket of the European Space Agency, under conditions of very low gravity (10–4 g) for the first 13 min of the self-organising process, showed no self-organisation 〚31〛. The experiment was carried out in the following way. Twenty-six flight samples were contained in an experimental module divided into two compartments, a ‘microgravity’ compartment and a ‘1 g on-board’ centrifuge compartment. Sample preparations were installed in the payload before lift-off and maintained at 7 °C. Once microgravity conditions were obtained, the sample temperature was raised to 36 °C, thus instigating microtubule formation, and the 1 g centrifuge switched on. Just prior to re-entry, 13 min after low gravity was achieved, the centrifuge was stopped. Hence, the only difference between the two sets of samples, is that one set was subject to weightlessness during the first 13 min. The payload was recovered, and the experimental module reinstalled in the laboratory at the launch site within 2 h from lift-off. The samples were then left for another 4 h before the module was opened and the samples examined. Some samples were filmed during these 6 h.
The samples formed in the ‘centrifuge’ part of the module formed stripes when the centrifugal field was parallel to the long axis of the cell, and the circular morphology when it was perpendicular. This result shows that the self-organising process is unaffected by payload re-entry and recovery. In contrast, the samples formed in the ‘microgravity’ part of the module show practically no self-organisation (Fig. 2C). The ‘microgravity’ preparations possess only very weak birefringence, demonstrating that the microtubules in these preparations do not have any preferred orientation. Observations down to a distance of 10 μm taken under a polarising microscope showed similarly weak birefringence. Hence, individual microtubules are relatively disordered with respect to one another. This contrasts with the ‘1 g’ preparations that show strong optical birefringence and in which many microtubules are highly oriented along the same direction. Hence in this case, gravity actually triggers the self-organising process. The gravity direction breaks the symmetry of the initially homogenous state and leads to the emergence of form and pattern.
Experimental problems frequently occur in space experiments due to air bubbles. In our case, although care was taken to prevent it, small air bubbles formed in the neck of some of the sample containers. During re-entry, when the sample is subject to high centrifugal fields, the air bubble is pushed through the sample. In one sample this process was filmed. A strongly birefringent line formed along the trajectory of the air bubble. This shows that the bubble oriented the microtubules along its trajectory. Subsequently, striped regions limited in extent, developed perpendicular to this trajectory (Fig. 2D). Hence, orienting the microtubules at an early stage in the process can also trigger self-organisation. We were expecting that self-organisation would not occur in the absence of gravity, and we found the effect of the air bubbles both intriguing and instructive.
3 Hypothetical molecular basis for self-organisation
The reaction scheme for microtubule formation is approximately the following (Fig. 4). Tubulin is incorporated into microtubules from the tubulin–GTP complex, either by addition to the growing end of a microtubule or by nucleation of a new microtubule that subsequently grows. This is associated with hydrolysis and the tubulin is incorporated into the microtubule as tubulin–GDP. Likewise tubulin is lost from the shrinking end of a microtubule as the tubulin–GDP complex. As a microtubule grows from one end, while shrinking from the other, it appears to move. The shrinking end of the microtubule leaves behind it a trail having a high local concentration of tubulin–GDP. Likewise, as it grows and incorporates tubulin–GTP from the front, it will also create a zone locally depleted in tubulin–GTP.
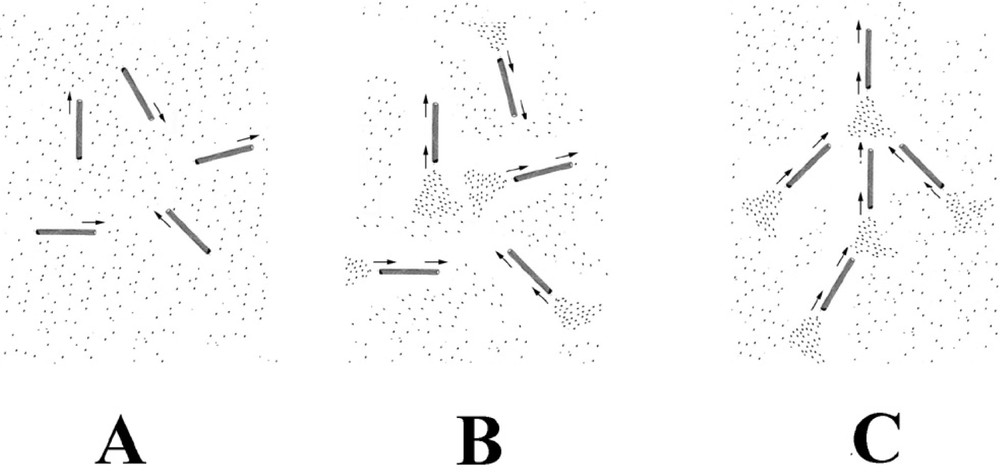
A possible mechanism for the formation of the self-organised structure. Microtubules are chemically anisotropic, growing and shrinking along the direction of their long axis. This leads to the formation of chemical trails, comprised of regions of high and low local tubulin concentration from their shrinking and growing ends respectively. These concentration trails (density fluctuations) are oriented along the direction of the microtubule. Neighbouring microtubules will preferentially grow into regions where the local concentration of tubulin is highest. In (A), microtubules have just formed from the tubulin solution. They are still in a growing phase and have an isotropic arrangement. In (B), microtubule disassembly has started to occur at the bifurcation time. This produces trails of high tubulin concentration from the shrinking ends of the microtubules. In (C), microtubules are growing and forming preferentially into these tubulin trails. The isotropic arrangement shown in (B) is unstable. Once a few microtubules start to take up a preferred orientation, and then neighbouring microtubules will also grow into the same orientation. Once started, the process mutually reinforces itself with time and leads to self-organisation. Any small effect that leads to a slight directional bias will trigger self-organisation. Gravity acts by way of its directional interaction with the macroscopic density fluctuations present in the solution.
The tubulin–GTP complex promotes the formation of microtubules whereas the tubulin–GDP complex inhibits their formation. Once liberated, the inactive tubulin (tubulin–GDP) is progressively regenerated into the active form (tubulin–GTP) with a certain time constant, after which it is once again available to be incorporated into microtubules. During this time, the tubulin is free to diffuse. If the rate of tubulin diffusion was zero, then the tubulin would be found along exactly the same trail as the disassembled tail of the microtubule from which it came. Hence, the microtubules that either grow or reform with this tubulin will do so along exactly the same trail as before. Under these conditions, since the microtubule solution that initially forms from the tubulin solution is macroscopically homogenous, the solution will remain as before, and self-organisation will not occur. Likewise, if tubulin diffusion is very fast, then by the time the tubulin–GDP becomes tubulin–GTP, the solution is once again homogenous in tubulin–GTP. Microtubules will reform or grow in a random manner and once again there will be no self-organisation. If, however, the tubulin diffusion has an intermediate value, then self-organisation can occur. Tubulin will progressively diffuse out from the trails left by shrinking microtubules. Since rates of chemical reaction increase with increasing concentration, growing microtubules will progressively grow along the direction and in the regions where these trails exist. Likewise microtubule nucleation will be greater in a zone of high tubulin–GTP concentration. These microtubules in their turn will leave behind new trails of high tubulin–GDP concentration and so on. The growing end of microtubules will likewise create regions depleted in tubulin–GTP, and these will behave in a complementary manner. Once regions of increased microtubule concentration and of preferred orientation start to form, then the feedback mechanism outlined above will lead to a progressive reinforcement of this process. In such a way, the microtubules ‘talk to each other’ and the coupling of reaction with diffusion then progressively leads to a collective behaviour resulting in self-organisation.
When the microtubule solution first forms from the tubulin preparation, it is isotropic. However, this isotropic arrangement is unstable. Once a few microtubules have taken up a preferred orientation, then neighbouring microtubules will start to grow into the same direction. Orientational order then spreads to its neighbours and so on. Hence any small external effect that will preferentially orient just a few microtubules will trigger progressive self-organisation. As outlined above, the passage of an air bubble through the solution orients the microtubules along its path and triggers self-organisation in its wake.
Using the same argument, we would expect that magnetic fields will also trigger self-organisation. Gravity acts by way of its directional interaction with the macroscopic density fluctuations present in the solution. This will result in ‘diffusion’, which is faster in the up–down direction, thus causing a slight directional bias for the formation of microtubules that triggers self-organisation. According to Kondepudi and Prigogine 〚10, 11〛, the presence of a 1 g field in a suitable reaction–diffusion system can destabilise the equilibrium state at the bifurcation point and thus favour the formation of a macroscopic pattern.
Obviously we wanted to confirm the plausibility of this hypothesis. One approach is experimental verification. However it is difficult to devise experiments that would unambiguously demonstrate the presence and role of the chemical trails outlined above. Another approach is to numerically simulate the behaviour of a population of growing and shrinking microtubules using experimentally determined values of reaction rates and diffusion constants, and to compare this behaviour with experimental observations.
4 Numerical simulations and comparison with experiments
Robert et al. 〚34〛 have proposed a simple model for microtubule self-organisation based upon microtubule growth and tubulin diffusion, and involving approximately ten microtubules. However, in this model the reactive term is extremely simplified and unrealistic. In this model, the microtubules do not nucleate from the tubulin solution but were pre-positioned with a given orientation from a region simulating the centriole. We have developed a reaction–diffusion model based upon realistic reaction kinetics, and extended the simulations to a large population of microtubules.
Numerical simulations were carried out based upon the following premises. Microtubules can grow and shrink from their ends. Tubulin molecules are added as the complex tubulin–GTP at a rate dependent on the local concentration and the reaction rate. Tubulin–GDP is lost from the opposing end. The liberated tubulin–GDP diffuses into the surrounding medium with a given diffusion constant. Due to the large excess of GTP, it is converted to tubulin–GTP at a given rate. This tubulin GTP is available to be incorporated into the growing end of neighbouring microtubules, or of nucleating to form new microtubules.
The following equations represent the reaction scheme; despite their simplified appearance all three are of non-linear form.
Microtubule assembly: n (GTP·tubulin) + microtubulem → microtubulem+n
Microtubule disassembly: microtubulem+n → microtubulem + n (GDP·tubulin) + n Pi
Tubulin regeneration: (GDP·tubulin) + GTP → (GTP·tubulin) + GDP
The microtubule length is not fixed; microtubules are free to grow and shrink according to the reaction scheme outlined above. The simulations incorporated experimentally determined rates of reaction and diffusion taken from the literature 〚35–41〛, and they reproduced the kinetics of microtubule assembly as observed in the self-organising process. To limit calculations to a manageable size, we restricted dimensions to two, even though the experimental samples obviously have three. However, reducing the dimensions to two does not seem to cause any major changes in the calculated self-organising process.
Initially, simulations were carried out on a population containing a small number of microtubules and then extended to larger populations. Obviously, one of the things that we wanted to know was whether the chemical trails hypothesised above might be predicted by such numerical simulations. To test this hypothesis, simulations were carried out with five microtubules contained on a two-dimensional surface, 100 μm × 60 μm. Two microtubules of 10 μm length (a, b) were placed close together, parallel to one another, and with their shrinking ends pointing in the same direction. Behind these microtubules were placed the remaining microtubules (c, d, e). These microtubules were also parallel to one another, and to the first two microtubules, but were significantly further apart from each one another than were microtubules a and b (Fig. 5). The concentration of tubulin–GTP and tubulin–GDP is initially uniform. The simulation was then started. Fig. 5 shows the position of the microtubules and the concentration profiles of tubulin–GTP and tubulin–GDP, at different times. All the microtubules progressively change position, due to tubulin–GTP being added at the growing end, and tubulin–GDP being liberated at the shrinking end, at a rate of about 5 μm per minute. During this process, the microtubules form regions both at the growing end and down the sides, which are depleted in tubulin–GTP. Because of this, the two forward microtubules (a, b) that are close together grow apart. This is because it is more favourable for them to grow into regions rich in tubulin–GTP than into the regions depleted in tubulin–GTP caused by the growth of the nearby neighbour. The shrinking ends of the microtubules liberate tubulin–GDP that is progressively converted to tubulin–GTP. Hence, just behind each microtubule is a small region of high tubulin–GDP concentration. This is followed by a long diffuse trail of tubulin–GTP. The growing ends of the three backward microtubules (c, d, e) grow into the tubulin–GTP trails formed by the forward microtubules (a, b). Fig. 6 illustrates the manner by which, in the simulations, an individual microtubule directs itself towards regions of high tubulin–GTP concentration.
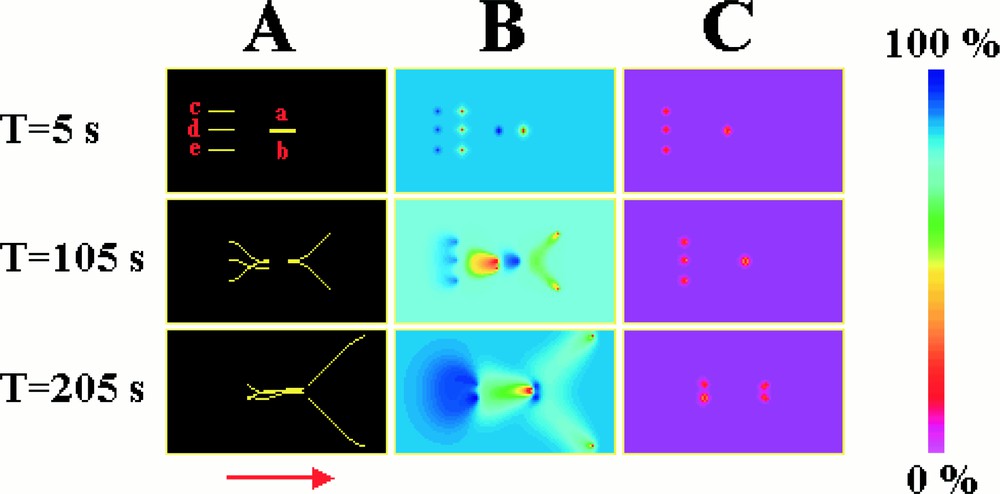
Numerical simulation illustrating the formation of chemical trails. (A) shows the microtubules and (B) and (C) the concentration profiles of tubulin–GTP and tubulin–GDP respectively. Initially, five microtubules were positioned as shown and the simulation started. The growing ends of the microtubules form regions that are depleted in tubulin–GTP, whereas the shrinking ends form trails rich in tubulin–GTP. Microtubules (a) and (b) move apart, away from the region of low tubulin–GTP concentration produced by their neighbour. Conversely, microtubules (c), (d), and (e) grow into the path of the chemical trails of tubulin–GTP produced by the shrinking ends of microtubules (a) and (b).
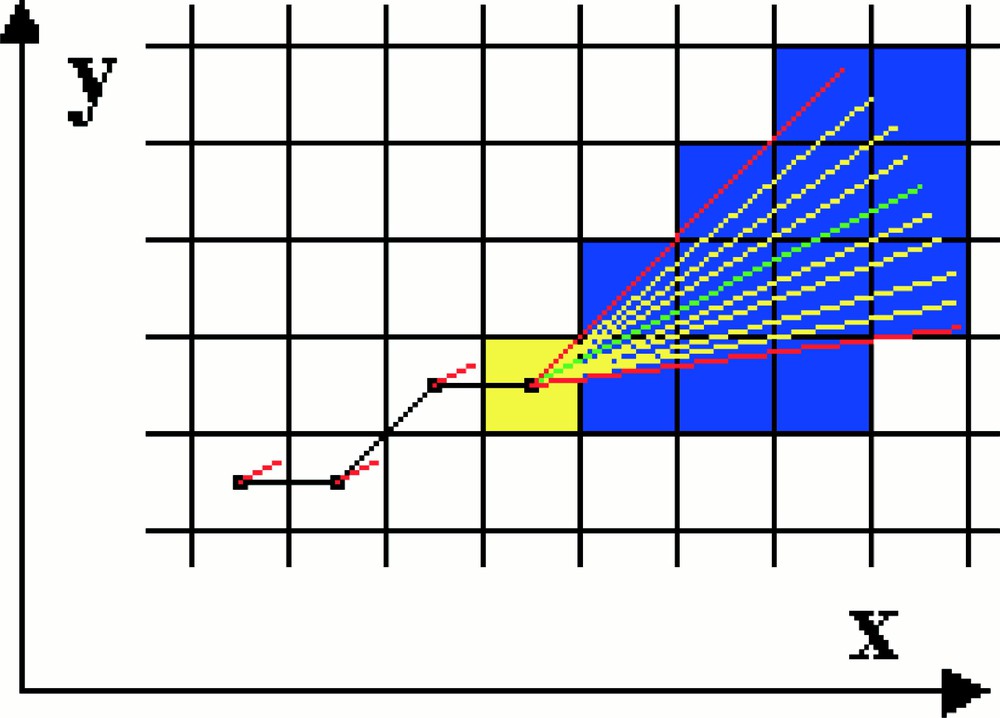
Simulation on a two-dimensional grid of the growth and displacement of an individual microtubule. The microtubule is shown in black. The yellow square represents the region around growing tip of the microtubule. In the algorithm, radial lines are projected from the microtubule tip and the tubulin–GTP concentration profile along them computed. The microtubule is then calculated to grow along the direction of the radial having the highest tubulin–GTP gradient.
We then extended the simulations, to a population of about 30 000 microtubules contained on a surface of 100 μm × 100 μm. In experiments, microtubules initially form from an homogenous solution of tubulin and GTP. So as to imitate these conditions, we started the simulation with a uniform distribution of tubulin–GTP of given concentration, no tubulin GDP, and no microtubules. Nucleation of tubulin–GTP into microtubule germs was taken as being exponentially dependent on tubulin–GTP and tubulin–GDP concentrations, as proposed by Mandelkow et al. 〚41〛. The small microtubule fragments generated this way are initially homogenous and have no preferred orientation. These numerous small fragments are free, by the mechanism already described, either to grow into microtubules, or shrink and disappear. The microtubules that develop, attain an average length of about 10 μm, which is comparable to the experimentally-determined value in the self-organised preparation. Likewise, in agreement with experiment, the microtubules that first form have no preferred orientation and their distribution is uniform. Subsequently, a self-organised structure comprised of regular bands of about 5 μm separation progressively develops (Fig. 7A). This structure is comparable with the type of experimental structure that develops over a similar distance scale. In the simulation, regular variations in microtubule concentration arise because of the progressive build-up of regions that are depleted in tubulin–GTP. Self-organisation takes about 240 000 iterations and corresponds to about 2 h in real time. In experiments self-organisation takes about 5 h.
Reaction–diffusion simulations for a population of microtubules. (A) is a simulation on a reaction space, 100 μm × 100 μm, containing 3×104 microtubules. The diagonal stripes are triggered by a small asymmetry in the part of the algorithm describing diffusion. (B) is a simulation in which this asymmetry is eliminated. The reaction space is 100 μm × 100 μm and contains the same number of microtubules. Although concentration inhomogeneities are present, there is no macroscopic self-organisation. In (C), the simulation is identical to (B), except that diffusion is now twice as fast along the y-axis as along the x-axis. In this case, self-organised stripes develop in which the microtubules are perpendicular to the direction of the stripes. (D) Experimentally observed self-organised structure over the same distance scale.
One of the features of these simulations is that the stripes always formed along the diagonal of the square reaction space. This led us to suspect that an asymmetry favouring this orientation was somehow unwittingly built into the simulation. This turned out to be the case, a very slight asymmetry occurred in the way that diffusion was digitalised as a square wave front, and this small effect sufficed to favour the formation of self-organised stripes along the diagonal. This type of asymmetry is well known in numerical simulations involving diffusion. When we eliminated it, the simulations show concentration inhomogeneities of about 5 μm, but which are uncorrelated and disorganised (Fig. 7B). When an asymmetry was once again introduced into the simulation by using slightly different rates of diffusion in the x and y directions, then, as shown in Fig. 7C, macroscopic self-organisation once again occurred.
5 Conclusions
These numerical simulations demonstrate that a relatively simple scheme, based on experimental rates of reaction and diffusion, predict the overall experimental behaviour. They hence permit a link between the microscopic and macroscopic, and between the molecular and phenomenological. The simulations confirm the hypothesis that self-organisation arises by the formation of anisotropic chemical trails produced as microtubules grow and shrink from opposing ends. Ordering arises not from static interactions but is due to the formation by reactive processes of concentration gradients in chemicals that activate and inhibit the formation of neighbouring microtubules. In this way, microtubules communicate with one another and behave as a macroscopic collective ensemble.
One of the fundamental assumptions of this reaction–diffusion model is that microtubules can change their direction of growth as a function of tubulin concentration gradients. A probable consequence is that, in some parts of the preparation, some of the microtubules will be partially curved. This is indeed the case, electron microscope images of the self-organised preparation show a significant number of partially curved microtubules. The maximum radius of curvature where these microtubules bend is approximately 0.3 μm, significantly higher than the maximum value of 3 μm permitted in the numerical algorithm.
If microtubules were unable to change their direction of growth, remaining completely straight, then self-organisation by the mechanism proposed should not occur. In agreement with this, simulations incorporating this constraint did not result in any self-organisation. This fact, taken with the experimental observation of a significant number of curved microtubules, is supplementary evidence that the reaction–diffusion scheme outlined in this article is a realistic description of the self-organising process.
The simulations also predict another major experimental observation; how self-organisation is dependent upon weak external fields. Any small effect that creates a slight preference for some microtubules to grow along one direction will trigger macroscopic self-organisation. The simulations hence provide a molecular basis for explaining how gravity, magnetic fields, and shearing can act on the system. Magnetic fields and shearing, would act by slightly favouring some microtubule orientations, whereas gravity would act by introducing an asymmetry into molecular diffusion and transport.
In this system there are at least two significant differences from the type of reaction–diffusion scheme originally proposed by Turing. In the Turing system the molecules communicate with one another across the sample by way of diffusion (fast diffusion of the inhibitor and slow diffusion of the activator). In the microtubule system, the molecules communicate by way of the reactivity of the microtubules. The fact that the microtubules are growing from one end at the rate of the order of a micron per minute whilst shrinking by approximately the same, results in a displacement of the microtubule at the same speed. At the same time, they leave behind a trail having a high concentration in inactive tubulin and create in front of them a furrow depleted in active tubulin. These chemical trails determine the pathways taken by surrounding microtubules. It is a reaction–diffusion system, since as already explained, without tubulin diffusion at the appropriate rate, self-organisation would not occur. In terms of a pure Turing system, active tubulin (tubulin–GTP) plays the role of the activator, whereas inactive tubulin (tubulin–GDP) is the inhibitor. However, in this case they both have the same diffusion constant. Self-organisation occurs because displacement of the microtubules by reaction is faster than diffusion of tubulin.
The second major difference with a normal Turing system is the reactive anisotropy of the microtubule system. In a normal reaction–diffusion scheme, the reaction has no inherent anisotropy. This is not the case with microtubules that can obviously only react at their ends. A microtubule can move in only one direction and this will equally lead to anisotropic reactive trails in active and inactive tubulin along the same direction. The system has an in in-built propensity for symmetry breaking under the effect of a weak field or some other external influence.
In this article, for reasons of presentation, we have somewhat arbitrarily separated numerical simulations from both experimental observations and the hypothetical molecular mechanism. In reality, the situation was somewhat different in that initially the proposed molecular basis of self-organisation was qualitative and rather uncertain in its details. As the simulations developed, the model progressively sharpened, leading to new insights. The combination of experiment and numerical simulation has resulted in a considerable deepening of our understanding of the phenomena involved.
Acknowledgements
We thank the European Space Agency for providing the MAXUS flight together with all the flight hardware. We thank the French CNES for financial support.
Version abrégée
Dans les organismes vivants, l’ordre et les formes apparaissent spontanément à partir d’un œuf d’apparence initialement homogène et dépourvu d’ordre. Les mécanismes biologiques par lesquels se fait cette auto-organisation sont encore mal compris. Il existe deux approches physico-chimiques possibles pouvant aboutir à de l’auto-organisation en biologie : la première est fondée sur la physique statistique et les interactions statiques, la deuxième sur les dynamiques chimiques non linéaires et les phénomènes coopératifs. Rashevsky, en 1942, puis Turing, en 1952, ont proposé que, contre toute attente, des réactions chimiques couplées à des processus de transport puissent induire des variations périodiques de concentration des réactifs. Ceci est une conséquence des systèmes chimiques maintenus éloignés de l’équilibre par une consommation permanente d’énergie. Ces systèmes sont instables et peuvent bifurquer vers plusieurs états possibles. Prigogine a prédit que l’action d’un champ externe faible à un moment précis de la réaction pouvait permettre la bifurcation du système vers un état auto-organisé. Ces mécanismes pourraient bien constituer le fondement de la morphogenèse et de l’auto-organisation dans les êtres vivants.
Nous savons que la formation in vitro de microtubules, éléments essentiels du squelette cellulaire, suit ce type de comportement. En effet, les préparations de microtubules s’auto-organisent spontanément par des processus de réaction–diffusion et les morphologies qui se forment dépendent de la présence de la gravité à un moment critique, précoce dans le processus réactif. On peut montrer que le processus d’auto-organisation microtubulaire contient effectivement une composante diffusive et une partie réactive, constituée notamment de l’assemblage et du désassemblage des microtubules.
La théorie nous a permis de comprendre le processus d’auto-organisation et sa dépendance vis-à-vis des champs externes dans sa globalité, mais il nous manquait l’approche d’un point de vue moléculaire, c’est-à-dire en termes de microtubules individuels. Ceci satisferait l’approche moléculaire des chimistes et des biologistes, et surtout permettrait d’établir un lien entre les processus biologiques macroscopiques et la foule d’événements microscopiques non linéaires qui les constituent.
Ces considérations nous ont amenés à réaliser un modèle mathématique du processus d’auto-organisation microtubulaire. Le modèle simule l’évolution d’une population de microtubules ayant chacun une cinétique réaliste propre (assemblage et désassemblage à chaque extrémité) et pouvant communiquer entre eux par l’intermédiaire de la tubuline, libre de diffuser. Les microtubules, après une phase initiale d’assemblage, sont entretenus par ajout de tubuline à l’extrémité croissante, tandis qu’ils se désassemblent à l’autre extrémité, en relâchant derrière eux une traînée concentrée de tubuline. Cette trace concentrée est « sentie » par les microtubules voisins ; ceux-ci peuvent alors croître dans la trace. Le mécanisme décrit permet de synchroniser localement les microtubules entre eux. Si quelques microtubules ont à un moment une orientation privilégiée, alors les microtubules voisins vont croître dans la même direction. Dès lors, n’importe quel petit effet qui provoque un biais directionnel chez les microtubules provoque l’auto-organisation globale de la solution. La gravité agit dans ce sens, par son interaction directionnelle sur les fluctuations de densité présentes dans la solution à un moment critique du processus.
Nous montrons lors des simulations que le comportement collectif de microtubules individuels permet d’expliquer l’auto-organisation de la solution et le rôle des champs externes dans ce processus.
Ce travail illustre bien le dialogue permanent et la complémentarité entre les expériences et les simulations, qui a été nécessaire pour la compréhension des mécanismes de l’auto-organisation en biologie.


