Cytomechanics of cell deformations and migration: from models to experiments

Angélique Stéphanou; Philippe Tracqui

doi:10.1016/S1631-0691(02)01447-6

Cytomechanics of cell deformations and migration: from models to experiments
[Cytomécanique des déformations et de la migration cellulaire : de la modélisation à l'expérimentation.]

Présenté par : Michel Thellier

Angélique Stéphanou ¹ ; Philippe Tracqui ¹

¹ Laboratoire TIMC–IMAG, UMR CNRS 5525, faculté de médecine de Grenoble, 38706 La Tronche cedex, France

Comptes Rendus. Biologies, Volume 325 (2002) no. 4, pp. 295-308.

Résumés

Anglais
Français

A cytomechanical model bas been proposed to analyse cell–cell interactions and cell migration through chemotaxis. We consider as the leading assumption that the cell cortical tension is locally modified by the protrusive activity of neighbour cells and binding of chemoattractant molecules to membrane receptors respectively. The model derives from the one initially proposed by Alt and Tranquillo (1995), which successfully describes experimentally observed cyclic autonomous cell shape changes. It is based on force balance equations coupling intracellular hydrostatic pressure and cell cortex contraction. Considering the protrusive dynamics of L929 fibroblats observed by videomicroscopy, we simulated the influence of neighbouring protrusions on a cell spontaneous pulsating behaviour. We further investigated the role of an extracellular gradient as another kind of external stimulus. The model illustrates how binding of chemoattractant molecules can induce a cell morphological instability that, above an intracellular stress threshold, will break the cell–substratum attachment. As a result, realistic cell chemotaxis can be simulated.

En nous appuyant sur un modèle cytomécanique, nous proposons dans cet article une analyse des interactions cellule–cellule et de la migration cellulaire par chimiotaxie. Nous considérons comme hypothèse principale qu'une modification de la tension corticale cellulaire est induite, dans un cas, par l'activité protrusive des cellules voisines et, dans l'autre, par la fixation de molécules de chimioattractant sur les récepteurs membranaires. Ce modèle, initialement proposé par Alt et Tranquillo (1995), permet de décrire de façon satisfaisante les changements cycliques et spontanés des morphologies cellulaires observées expérimentalement. Il est basé sur l'écriture des équations d'équilibre mécanique couplant la pression hydrostatique intracellulaire à la contraction du cortex de la cellule. À partir d'une étude expérimentale de la dynamique protrusive de fibroblastes L929 observée en vidéomicroscopie, nous avons simulé l'influence de protrusions membranaires voisines sur le comportement pulsant spontané d'une cellule. Nous avons étudié ensuite l'effet d'un autre stimulus extracellulaire, tel qu'un gradient de chimioattractant. Le modèle montre comment la fixation des molécules de chimioattractant induit une instabilité morphologique suivie, au-delà d'un certain niveau de contraintes intracellulaires, par la rupture des adhésions cellule–substrat, l'ensemble conduisant à une simulation réaliste de la migration cellulaire par chimiotaxie.

Métadonnées

Reçu le : 2001-07-18
Accepté le : 2001-09-03
Publié le : 2002-04-01

PMID

DOI : 10.1016/S1631-0691(02)01447-6

Keywords: cell chemotaxis, F-actin oscillations, dynamical instabilities, nonlinear model
Mot clés : chimiotaxie cellulaire, oscillations de F-actine, instabilités dynamiques, modèle non linéaire

Affiliations des auteurs :

Angélique Stéphanou ¹ ; Philippe Tracqui ¹

¹ Laboratoire TIMC–IMAG, UMR CNRS 5525, faculté de médecine de Grenoble, 38706 La Tronche cedex, France

@article{CRBIOL_2002__325_4_295_0,
     author = {Ang\'elique St\'ephanou and Philippe Tracqui},
     title = {Cytomechanics of cell deformations and migration: from models to experiments},
     journal = {Comptes Rendus. Biologies},
     pages = {295--308},
     publisher = {Elsevier},
     volume = {325},
     number = {4},
     year = {2002},
     doi = {10.1016/S1631-0691(02)01447-6},
     language = {en},
}

TY  - JOUR
AU  - Angélique Stéphanou
AU  - Philippe Tracqui
TI  - Cytomechanics of cell deformations and migration: from models to experiments
JO  - Comptes Rendus. Biologies
PY  - 2002
SP  - 295
EP  - 308
VL  - 325
IS  - 4
PB  - Elsevier
DO  - 10.1016/S1631-0691(02)01447-6
LA  - en
ID  - CRBIOL_2002__325_4_295_0
ER  -

%0 Journal Article
%A Angélique Stéphanou
%A Philippe Tracqui
%T Cytomechanics of cell deformations and migration: from models to experiments
%J Comptes Rendus. Biologies
%D 2002
%P 295-308
%V 325
%N 4
%I Elsevier
%R 10.1016/S1631-0691(02)01447-6
%G en
%F CRBIOL_2002__325_4_295_0

Angélique Stéphanou; Philippe Tracqui. Cytomechanics of cell deformations and migration: from models to experiments. Comptes Rendus. Biologies, Volume 325 (2002) no. 4, pp. 295-308. doi : 10.1016/S1631-0691(02)01447-6. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/S1631-0691(02)01447-6/

Version originale du texte intégral

1 Introduction

Cells change their shape and crawl in response to external stimuli by extruding and remodelling cell membrane protrusions, typically in the form of filopodia (finger-like protrusions) or lamellipodia (sheet-like protrusions). These cell shape changes are mainly due to the reorganisation of the filamentous actin (F-actin), a complex and highly dynamic composite contained in the outer rim of eukaryotic cells. Indeed, these filaments are formed from monomeric G-actin and exhibit a fast growing end (barbed end) and a slow growing end (pointed end), according to the ratio of the association rate to the dissociation rate of globular G-actin monomers. Actin polymers have a very high gelation efficiency and form viscoelastic gels at volume fraction below 0.1, thus controlling the viscoelasticity of the cytoplasm. Changes in F-actin levels and F-actin organisation are then intimately associated with the cell biological function and its specific morphologies.

However, the mechanisms driving the formation of cellular protrusions are still controversial. Cell protrusions can be generated by the formation of F-actin bundles which push forward the cytoplasmic membrane in specific places. An alternative view considers that the initiating process is the local polymerisation of an actin gel in a free volume located between the plasma membrane and the cell actin cortex 〚1〛.

While it is usually considered that cell membrane fluctuates without any privileged spatial direction in space nor particular time coherence, it is thus of particular interest to study cell protrusive activity as a self-organised dynamical process. Indeed, different results support the self-organised character of these cell shape changes. Ehrengruber et al. 〚2〛 show that neutrophils undergo periodic cytoskeletal rearrangements that lead to cycles of shape changes, ultimately resulting in cell translocation. In neutrophils, sinusoidal oscillations of F-actin, with periods of 8–10 s, were reported 〚3〛. Other studies also reported other types of self-organised behaviour, like the existence of rotating waves around the cell body 〚4, 5〛. This suggests isovolumetric extension and retraction, i.e. cyclic alteration of cell body size related to veil-like lamellipods changes.

Different models have been proposed to explain the periodic oscillatory movement of the cell membrane and the role of actin polymerisation/depolymerisation cycles in the recurring lamellipod protrusion and retraction dynamic. They usually consider the mechanical interactions of the actin cytoskeleton with: (i) the cytoplasm, through viscoelastic stresses generated by the actomyosin complex; (ii) the cell membrane, through tension forces due to the local membrane curvature. Oster and Perelson 〚6〛 proposed a model of lamellipodial motion based on the physical chemistry of actomyosin gels. The model consists of a sheet of cytogel attached to the substratum by elastic tethers. Permeation at the leading membrane raises the internal calcium concentration, activating the solation factors and the actomyosin contractile machinery. Peskin et al. 〚7〛 formulated a theory to account for the force generated by the polymerisation process itself when the filaments are rigid. They proposed that the addition of sub-units to the end of growing filaments rectified the Brownian motion of any diffusing object in the front of the filament, and showed that this ratcheting of diffusive motion could generate sufficient force to account for a number of motile phenomena. Molginer and Oster 〚8〛 generalise this model when the thermal fluctuations of either the actin fibres or membrane are significant. This extension provides a mechanical explanation for the protrusion of lamellipodia. It is indeed known that temperature can induced sol–gel transition in cross-linked actin networks.

Other models have been proposed, in which biochemical processes are described through a reaction-diffusion model which takes into account the interactions of two states of F-actin, free and linked to nucleation proteins. Oscillatory actin waves are generated within a fixed area modelling the cell periphery 〚9〛. Conversely, in most of the mechanical models, the periodic oscillating behaviour of the cell membrane protrusion is generated by the coupling between intracellular pressure (hydrostatic...) and F-actin network contractility, as in the cytomechanical model of Alt and Tranquillo 〚5〛.

In this paper, we consider this latter model as a theoretical basis for further theoretical investigations of cell–cell interactions. In particular, we propose different extensions of the original model which take into account cell–cell interactions and the influence of extracellular factors through modulation of the membrane protrusivity and cell membrane elasticity. We further analyse how the coupling of the self-oscillating state of the cell with an extracellular gradient could initiate cell migration. As an experimental counterpart of this cell simulated behaviour, we consider fibroblasts morphological changes as they can be observed on videomiscroscopy sequences. Starting from a previous characterisation of the spontaneous pulsating behaviour of isolated fibroblast 〚10〛, we discussed to which extent modifications of the experimentally observed fibroblast shapes can be interpreted as perturbations or bifurcations of the spontaneous self-oscillating cell protrusive behaviour. In a second part of the paper, we further analyse the response of this cytomechanical model to an extracellular gradient of chemoattractant and show that subsequent cell migration can be initiated by only considering local modifications of the cell cortex–membrane properties.

2 Experimental observations of autonomous cell pulsating behaviour

Characterisation of cell membrane deformation dynamics emerges from the contour maps which gives a spatio-temporal picture of the cell morphology. These maps correspond to the reconstruction of the cell boundary (or contour) in polar coordinates where the membrane radial exension L_exp measured from the cell estimated barycentre is plotted against the angular position θ at each time, for distance values greater than ${\bar{L}}_{\exp},$ where ${\bar{L}}_{\exp}$ is the mean length of the membrane extension. This allows to exhibit the protrusive zones of the cell (Fig. 1c).

Fig. 1
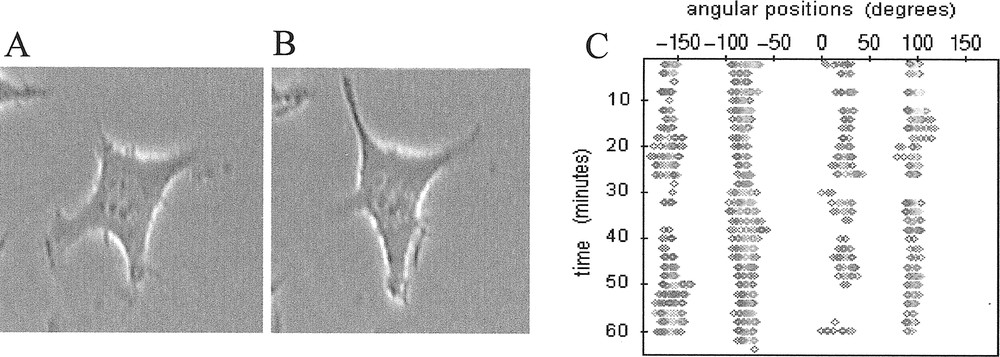
**A, B.** Isolated L929 fibroblast (magnification ×400) taken at two different times with approximately 15 minutes between the two images. This sampling time corresponds to the half-period of pulsation of this cell between its two quasi-perpendicular protrusive directions. C. Associated contour map $L_{\exp} (θ, t),$ where the membrane radial extension L_exp is plotted (gray spots) if $L_{\exp} > {\bar{L}}_{\exp}$ ( ${\bar{L}}_{\exp}$ being the mean length of the membrane extension).

Observations of sub-confluent L929 fibroblasts cultured in vitro on two-dimensional rigid substratum showed that isolated cells spontaneously developed cyclic and pulsating movements of extension/retraction as exemplified in Fig. 1a and 1b, where co-ordinated periodic changes of cell morphology develop between two quasi-perpendicular directions of protrusion. The four protrusive directions involved are clearly exhibited by the associated contour map in Fig. 1c which also reveals their persistence with time.

When cells are no longer spatially isolated, this spontaneous cyclic behaviour interacts with the pulsating protrusive activity of neighbouring cells. We then observe modifications or disappearance of the directions of protrusions, as if cells try to avoid interactions with the neighbouring cells through some kind of physical contact–inhibition mechanism 〚11〛.

In order to characterise interacting cells protrusive behaviour, we define a so called influence domain for each cell within a given group of cells (Fig. 2). This domain is schematically represented by a circle centred on the cell nucleus barycentre, with a radius defined by the maximum recorded amplitude of the cell protrusions in the video-microscopy sequence during the considered observation duration. The intersection of two (or more) influence domains thus represents potential interaction zones, which can be superimposed to the time-varying contour maps determined for each cell.

Fig. 2
A. Group of cells in interaction with their influence domains. **B-D.** Associated contour maps. The interactions zones are represented by grey zones (light grey for interaction zones involving 2 cells and dark grey for interaction zones involving 3 cells).

This characterisation provides a global picture of the contact inhibition phenomenon, which has been reported for various types of cells. We observed that cell protrusions preferentially appear outside the darkest interaction zones (Fig. 2), supporting the idea that contact inhibition is triggered in most cases by physical contacts between cells, which then retract and try to develop their protrusions in other empty spaces. However, since cell protrusive activity is a spatio-temporal coordinated process, it remains to precise how simultaneous competing lamellipodia can integrate such external constraints and trigger morphological cell bifurcation between a free running shape to a constrained one.

3 A cytomechanical model for cell deformations

3.1 The model

We used as a modelling basis the cytomechanical model proposed by Alt and Tranquillo 〚5〛 to describe the spontaneous dynamics of cell deformations, with specific application to the analysis of keratinocytes spatio-temporal deformations. Indeed, the model involves a minimum number of variables, while incorporating salient features of biomechanical cell deformations.

The model considers that cell protrusions dynamics are due to the biophysical properties (visco-elasticity, contractility,...) of the cortical polymer layer or network of actin and myosin filaments which underlies the cell membrane and surrounds the cell body and nucleus. Moreover, this more or less dense network is able (i) to disassemble at locations where it becomes condensed, (ii) to reassemble in cell protrusions, like lamellipodia. Cell protrusions then mainly results from a mechanical non-equilibrium state of the pressure and forces acting on the cell periphery. Subsequent F-actin polymerisation/depolymerisation in a moving protrusion is a consequence of the so-induced intracellular space variation. The networks in the cortex and lamellipodia are assumed to have the same biophysical properties, except the boundary condition imposed by the additional cortex–membrane surface tension. The first part of the model depicts the dynamics of the actin in the cell cortex which is mainly responsible for cell shape reorganisation through its ability (i) to polymerise into F-actin and depolymerise into G-actin, (ii) to interact with myosin to generate the contractile activity in the cell, (iii) to move through the cytoplasm via convection. The local amount of F-actin also determines the intensity of the resistive stress applied on the membrane as the result of actin cytoskeleton-membrane proteins crosslinks. This resistive stress, together with the cortex–membrane curvature-induced stress, balances the intracellular hydrostatic pressure which acts as the ‘driving force’ in the model.

In order to transform the two-dimensional original problem into a simpler one-dimensional version, we moreover assume as in Alt and Tranquillo 〚5〛 that the F-actin density as well as its convective tangential velocity is constant in the radial direction. The first assumption is justified when the width of the cell cortex $L (θ, t),$ remains small in front of the radius of the cell body R₀. The second implies that the cortical network can slip with respect to the membrane, which is also partly justified if considering that membrane proteins involved in the network-membrane connections are mobile within the membrane.

The three variables considered in the cytomechanical model are thus: (i) the F-actin concentration in the cortex $a (θ, t),$ (ii) the F-actin tangential velocity $v (θ, t)$ (taken at the periphery of the cell body delimited by a unit circle of radius R₀=1), (iii) the width of the cell cortex annulus $L (θ, t)$ – or the membrane position taken from the surface of the cell. The spatio-temporal evolution of these three variables is given by the following set of partial differential equations.

The first one stands for the conservation of F-actin in the cortex. Actin polymerisation and depolymerisation are considered to occur with the same rate η. Moreover, the state of polymerisation or depolymerisation depends on the local value of F-actin concentration relatively to the stationary concentration a_*.

\frac{\partial}{\partial t} (L a) + \frac{\partial}{\partial θ} (L a v) = η L (a_{*} - a)

The second equation describes the balance of forces applied on the cortex–membrane in the radial direction. The model takes into account a viscous friction that represents the cell adhesion on the substratum, modulated by the coefficient Φ₁, the intracellular hydrostatic pressure $ϐ_{1},$ the resistive elastic stress due to the cortical network membrane attachment with the elasticity coefficient γ₁ and a curvature-dependent stress due to the surface tension of the cortex–membrane complex, characterised by the coefficient τ₁.

Φ_{1} a \frac{\partial L}{\partial t} = ϐ_{1} - γ_{1} L a + \frac{\partial}{\partial θ} (τ_{1} a \frac{\partial L}{\partial θ})

The third equation concerns the balance of forces in the tangential direction. It includes the frictional force on the network moving in the cytosol, with magnitude controlled by the drag coefficient Φ₀ (related to the attachment of the network with the membrane and the other types of filaments), a viscous stress with viscosity coefficient μ₀ and the membrane curvature induced stress with coefficient τ₀.

Φ_{0} a v = \frac{\partial}{\partial θ} [μ_{0} a \frac{\partial v}{\partial θ} + σ_{0} (a) - \frac{\partial}{\partial θ} (τ_{0} a \frac{\partial L}{\partial θ})]

The contractile activity of the actomyosin network is modelled by the nonlinear function $σ_{0} (a) .$ Two mechanical states can be distinguished according to the value of the network F-actin concentration $a (θ, t)$ with respect to a saturation concentration a_sat. If $a (θ, t)$ is below the saturation concentration value, the contractile stress increases according to a parabolic law. Above the saturation threshold, the stress decreases exponentially as a consequence of the network swelling. The nonlinear function proposed by Alt and Tranquillo (1995) 〚5〛 is the following:

σ_{0} (a) = ψ_{0} a^{2} e^{- a / a_{sat}}

where the coefficient ψ₀ controls the magnitude of the contractile stress.

The partial differential equations system is nondimensionalised by setting the following dimensionless variables:

\begin{matrix} \tilde{t} = t η & \tilde{a} = \frac{a}{a_{0}} & \tilde{L} = \frac{L}{R_{0}} \end{matrix}

The normalised parameters are then:

\begin{matrix} \tilde{ϐ} = \frac{ϐ_{1}}{Φ_{1} a_{0} R_{0} η} & \tilde{γ} = \frac{γ_{1}}{Φ_{1} η} & \tilde{μ} = \frac{μ_{0}}{Φ_{0}} \end{matrix}

\begin{matrix} \tilde{ψ} = \frac{ψ_{0} a_{0}}{Φ_{0} R_{0} η} & {\tilde{a}}_{sat} = \frac{a_{sat}}{a_{0}} & \tilde{τ} = \frac{τ_{0}}{Φ_{0} η^{2}} & \tilde{d} = \frac{τ_{1} Φ_{0}}{τ_{0} Φ_{1}} \end{matrix}

Dropping the tilde for notational simplicity, we obtain the following system of dimensionless differential equations:

\frac{\partial}{\partial t} (L a) = - \frac{\partial}{\partial θ} (L a v) + L (1 - a)

a \frac{\partial L}{\partial t} = ϐ - γ L a + d \frac{\partial}{\partial θ} (τ a \frac{\partial L}{\partial θ})

a v = \frac{\partial}{\partial θ} [μ a \frac{\partial v}{\partial θ} + σ (a) - \frac{\partial}{\partial θ} (τ a \frac{\partial L}{\partial θ})]

The linear stability analysis of this system of equations around the homogeneous steady state $L_{s} = ϐ / γ,$ a_s=1 and v_s=0 is performed in a standard way by analysing perturbations of the form $\exp (λ t + i m θ) .$ The evolution with time of perturbations with spatial mode m is given by the roots of the associated dispersion equation, i.e. the pair of eigenvalues

λ (m) = \frac{1}{2} [- 1 + \frac{m^{2} ρ}{1 + μ m^{2}} - m^{2} d τ \pm \sqrt{{(2 γ - 1 + \frac{m^{2} ρ}{1 + μ m^{2}} + m^{2} d τ)}^{2} - 4 γ (γ + m^{2} d τ) - 4 \frac{m^{4} ϐ τ}{1 + μ m^{2}}}]

with

ρ = \frac{d σ}{d a} |_{a = a_{s}} .

Looking for oscillatory solutions of the model leads to the analysis of Hopf bifurcations and complex conjugated eigenvalues. The real part of the eigenvalues is independent of the coefficient $ϐ$ and γ. The key parameters for unstable modes determination are thus the viscosity coefficient μ, the surface-tension coefficient τ and the drag coefficient d. As it can be intuitively understood, high values of μ and τ tends to strengthen the cell cortex–membrane complex and thus tends to reduce the number of unstable modes. At the opposite, high value of σ, which represents the variation amplitude of the actomyosin network contractility, can favour the destabilisation of a larger number of spatial modes.

3.2 How to take into account cell–cell interactions and cell migration with the cytomechanical model

The model has been successfully used to describe the spontaneous dynamics of various cell lines, including leucocytes 〚12〛 and keratinocytes 〚13〛. Our aim is now to investigate if such a model is a valuable representation for analysing the various aspects of cell interactions through a continuous and integrated description of the cell dynamics. We will especially focus on cell–cell interactions as well as cell migration induced by a gradient of extracellular factor. Indeed, in both situations cell detects and integrates external stimuli, and exhibits a variety of responses, such as contact inhibition and/or the appearence of new dynamical states like migration. Complex pathways of signal transduction are involved in the elaboration of the cell response and these processes are clearly not explicitely described in our present cytomechanical model. However, we can at least simulate the corresponding effects of this signalisation, as reported experimentally, and then examine their consequences on the cell simulated dynamics. Then, adequation of the model simulations and observed cell dynamics response will provide an additional step for the model validation. For example, the observed polarisation of a cell submitted to a gradient of extracellular factor suggests that the membrane morphological instability leading to the polarisation of the membrane is the result of the decrease of the membrane tension 〚14〛. In our model, this effect can be modelled by considering a dependence of the tension coefficient with regard to the local concentration of extracellular factor on the membrane. One further can assume that the inclusion of molecules in the membrane leads to a decrease of the tension, as suggested by various studies on membrane properties 〚15, 16〛.

4 Modelling cell–cell interactions as perturbations of the spontaneous oscillatory protrusions dynamics

4.1 The model

Following the experimental results briefly reported in the second paragraph, we consider the cytomechanical model presented in the previous section as a basis for theoretically analysing physical cell–cell contact inhibitions as possible perturbations of the cell spontaneous periodic protrusive behaviours. The basic assumption is that such a mechanical external signal can be transduced, through different signalling pathways, into structural modifications of the cell cortex, thus resulting in a globally re-adapted co-ordination of cell protrusions. At the cell level, such response would lead to modifications of cell morphologies and/or changes of the characteristic parameters of the cell protrusive behaviour (periodicity, protrusion amplitude...).

We investigated here two different mechanical responses. The first one assumes a local decrease of the protrusive force (coefficient $ϐ$ ) in the cell–cell interaction area. The second one considers that stress receptor activation can lead to a local re-organisation of the cortical network–membrane attachment, leading to a decrease of the curvature-induced surface tension. We thus consider the following step functions to describe the angular variation of the respective model parameters in any given interaction window $[θ_{1}, θ_{2}] :$

ϐ (θ) = {\begin{matrix} ϐ & if & θ < θ_{1} and θ > θ_{2} \\ ϐ_{int} & if & θ_{1} \leq θ \leq θ_{2} \end{matrix} τ (θ) = {\begin{matrix} τ & if & θ < θ_{1} and θ > θ_{2} \\ τ_{int} & if & θ_{1} \leq θ \leq θ_{2} \end{matrix}

The model thus becomes:

\frac{\partial}{\partial t} (L a) = - \frac{\partial}{\partial θ} (L a v) + L (1 - a)

a \frac{\partial L}{\partial t} = ϐ (θ) - γ L a + d \frac{\partial}{\partial θ} (τ (θ) a \frac{\partial L}{\partial θ})

a v = \frac{\partial}{\partial θ} [μ a \frac{\partial v}{\partial θ} + σ (a) - \frac{\partial}{\partial θ} (τ (θ) a \frac{\partial L}{\partial θ})]

with the expression of the derivative function of

τ (θ)

given by:

\frac{\partial τ (θ)}{\partial θ} = (τ - τ_{int}) [δ (θ - θ_{2}) - δ (θ - θ_{1})]

where

δ (θ)

is the Dirac delta function.

4.2 Simulation of mechanically perturbed cell oscillatory morphologies

As initial cell morphology and dynamical state, we consider the spontaneous pulsating movements of extension/retraction of the cell membrane between two perpendicular directions observed for isolated L929 fibroblasts 〚10〛. This behaviour has been simulated with the following set of model parameters: $ϐ = γ = 0.5,$ μ=2, τ=1.5, δ=0.001 a_sat=2 and ψ=5.5. The corresponding spatio-temporal map $L (θ, t)$ of the simulated membrane deformations is plotted in Fig. 3a. This asymptotic periodic steady-state is taken as the initial condition for the simulation of cell–cell mechanical interactions. Above described modifications of the model parameters are then applied to simulate the cell response to the external mechanical stimulus and the progressively emerging dynamical state is recorded. Except in Fig. 3a, where there is no interaction, the interaction window $[θ_{1}, θ_{2}]$ (75 degrees for each simulation) is indicated at the bottom of the map.

Fig. 3
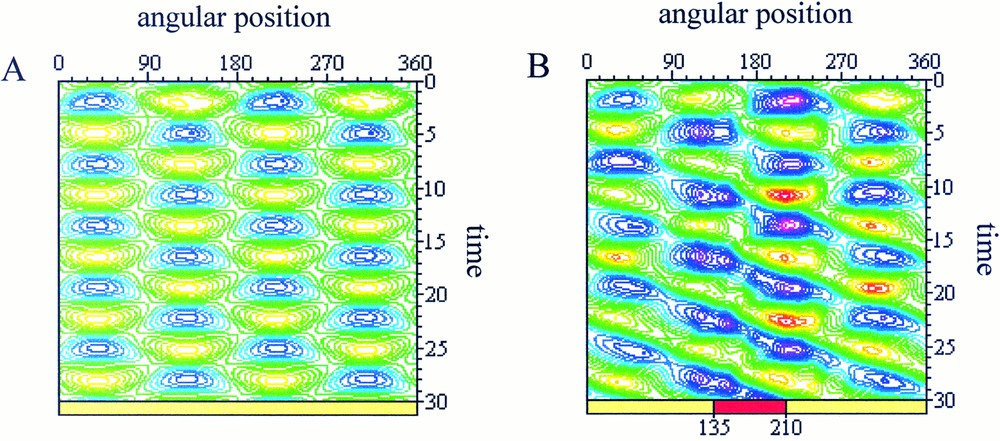
Spatio-temporal maps $L (θ, t)$ of the simulated cell deformations. Blue/purple areas represent contraction zone and yellow/green areas stand for protrusive zones. A. Spontaneous pulsating state between two perpendicular directions. B. Perturbation of the parameters where $ϐ_{int} = 0.4$ and τ_int=0.75 for 135≤θ≤210 (red zone at the bottom of the map). The perturbation appears initially in the interacting zone (t=0 to t=12) and then propagates to influence the overall protrusive dynamic of the cell (t=12 to t=30).

In the simulation presented in Fig. 3b, we observed the modification of the protrusive dynamics starting from the interaction zone (t=0 to t=12), then influencing the overall dynamic of protrusion (t=12 to t=30). In this case, both the hydrostatic pressure and the surface tension have been decreased, with:

ϐ (θ) = {\begin{matrix} 0.5 & if & θ < 135 and θ > 210 \\ 0.4 & if & 135 \leq θ \leq 210 \end{matrix} τ (θ) = {\begin{matrix} 1.5 & if & θ < 135 and θ > 210 \\ 0.75 & if & 135 \leq θ \leq 210 \end{matrix}

In the second case (Fig. 4), only the alteration of the protrusive pressure $ϐ$ has been considered.

Fig. 4
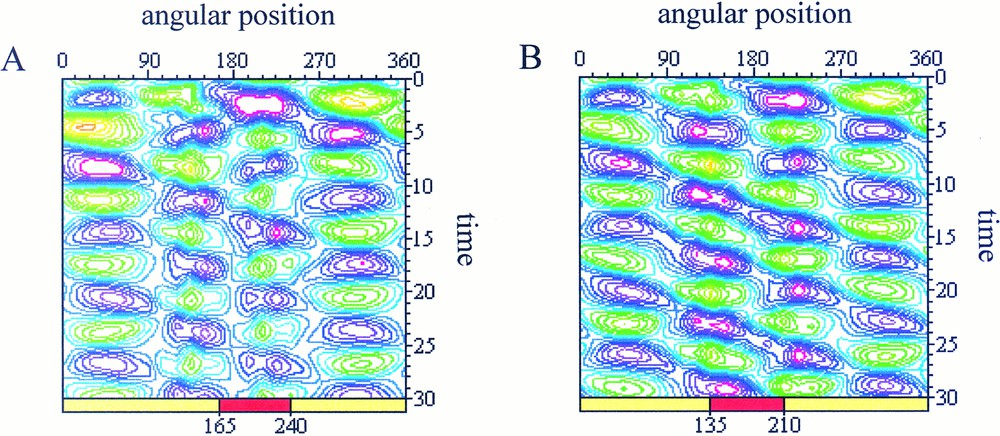
Spatio-temporal maps of simulated cell deformations $L (θ, t) .$ Purple areas represent contraction zone and green areas stand for protrusive zones. The same perturbation $ϐ_{int} = 0.4$ is applied in both cases but the zone of interaction (represented by a red rectangle) is different with: (A) interaction in the range 165≤θ≤240: after a transition period from t=0 to t=15, the cell recovers a pulsating state characterised by iso-amplitude curves which isolate each of the protrusive spots; (B) interaction in the range 135<θ<210: appearance of a rotating wave of deformation characterised by iso-amplitude curves distributed along diagonals which connect together the protrusive spots (in green).

We are now studying the effect on the protrusion dynamics of the interaction zone orientation respectively to the cell position. The simulated behaviour reported in Fig. 4a corresponds to:

ϐ (θ) = {\begin{matrix} 0.5 & if & θ < 165 et θ > 240 \\ 0.4 & if & 165 \leq θ \leq 240 \end{matrix}

The simulation in Fig. 4b is realised in a similar way, except that the interaction zone has been shifted counter clockwise with a 30° angle, i.e.:

ϐ (θ) = {\begin{matrix} 0.5 & if & θ < 135 et θ > 210 \\ 0.4 & if & 135 \leq θ \leq 210 \end{matrix}

In the first case (Fig. 4a), the cell protrusion dynamics is modified mainly in the interaction zone but the cell keeps a pulsating state. However, when the spatial location of the external stimulus has been shifted (Fig. 4b), we observe a global change of the cell dynamical state with the appearance of a rotating wave of deformation around the cell body.

5 From cell deformations to cell chemotaxis

5.1 A model of cellular migration induced by an extracellular factor

Cell chemotaxis can be decomposed into three basic dynamical steps, namely chemo-attractant receptor binding, intracellular signal transduction and induction of biased translocation. Facing the explosion of molecular information, mainly provided through the development of specialised probes, theoretical models can help to identify basic understanding of coupled cell dynamical features including spontaneous oscillatory cell shape changes, random migration and directional response to extracellular gradients. In this section, we analysed the possible induction of cell migration as a phenotypic response to the extracellular stimulus provided by a chemoattractant factor. We assume that this diffusible factor is released from a ponctual source located in the neighbourhood of the cell.

We do not explicitly consider the series of complex biochemical and biophysical responses elicited after chemoattractant binding to specific surface receptors (internalisation, activated G-protein transduction cascade, cytoskeletal association...) On the basis of the here considered cytomechanical model, our aim is rather to correlate temporally and spatially lamellipodia formation with cortical F-actin network dynamical and physical properties, associated with modified cell cortex–membrane surface tension changes. We thus assume that the emerging effect of the signalling pathways triggered by chemoattractant molecule binding to the cell membrane is a modification of the cortex–membrane surface tension, which can be related to structural modification of the large protein complexes and cluster of chemotactic receptors associated with the cell membrane 〚17〛. More precisely, we consider that the associated parameter τ depends linearly on the local concentration C of the extracellular factor at the membrane:

τ (C) = τ - Λ C

Λ is a coefficient which characterises the sensitivity to the extracellular factor and thus provides a control parameter for different down-regulation scheme of receptors sensitivity (decrease in the number of receptors with increasing chemoattractant concentration, integration of signal through the coupling of different transducers 〚17〛). On the other hand, surface tension still remains proportional to the cortical network F-actin concentration.

The corresponding cytomechanical model is thus defined by the following new system of equations:

\frac{\partial (L a)}{\partial t} = - \frac{\partial (L a v)}{\partial θ} + L (1 - a)

a \frac{\partial L}{\partial t} = ϐ - γ L a + d \frac{\partial}{\partial θ} (a τ (C) \frac{\partial L}{\partial θ})

a v = \frac{\partial}{\partial θ} [μ a \frac{\partial v}{\partial θ} + σ (a) - \frac{\partial}{\partial θ} (a τ (C) \frac{\partial L}{\partial θ})]

When the extracellular factor concentration C increases, the membrane stress decreases: this induces both a morphological instability and a cell polarisation toward the extracellular gradient (see next section).

However, it is clear that a temporary cell adhesion to the substratum is a necessary condition for the cell to exert the force required for forward cell body translocation. Cell adhesion is not described explicitly in the model but taken into account implicitly through the definition of a stress threshold above which the breakdown of cell–substrate links will occur. Cell–substratum adhesion/de-adhesion dynamics is thus computed as follows: cell polarisation leads to an asymmetry of the cell morphology relatively to the perpendicular axis of the translocation direction. At the same time, we assume that at the leading lamellipodia, the cell establishes new focal adhesions with the substratum. This morphological asymmetry is associated with the displacement of the cell geometric barycentre from its initial position. When this displacement exceeds a given threshold, interpreted as the admissible limit for the resulting stress applied on the cell cytoskeleton, the rear part of the cell is allowed to move forward up to the point where its centre of mass coincides with the cell geometric barycentre: then, reorganisation of the cell morphology occurs before the next translocation step. Therefore, as long as an extracellular gradient can be detected by the cell, the cell moves toward the source according to this three-phase mechanism, i.e. cell polarisation, displacement of the centre of mass, cell remodelling and reorganisation of intracellular stresses. Such modelling of cell crawling motion, which is characteristic of mesenchymal cells migration, summarises the five-step process described by Sheetz et al. 〚18〛.

5.2 Simulation of cell chemotaxis

We assume that the cell is initially non-stimulated, i.e. circular and non polar with a uniform cortical distribution of F-actin, together with a uniform distribution of receptors on the plasma membrane. Even if the chemoattractant is a diffusible factor, we assume for simplicity that the time scale of the diffusion process is large enough compared to the cell migration velocity, such that a quasi steady-state distribution $C (r)$ of the chemoattractant in the radial direction r can be considered. We take:

C (r) = \frac{Q}{2 \sqrt{π D t_{0}}} \exp (- \frac{r^{2}}{4 D t_{0}})

which is the solution at time t₀ of the 1D-diffusion equation

\frac{\partial C}{\partial t} = D \frac{\partial^{2} C}{\partial r^{2}}

in an infinite medium and for the initial condition

C (r, 0) = Q δ (r) .

Parameter D is the chemoattractant diffusion coefficient, while Q represents the released amount of chemoattractant.

Simulations have been realised with the following set of normalized model parameters: Q=45, D=4.0 and t₀=1 for the chemoattractant, $ϐ = γ = 0.5,$ μ=4, τ=1.5, δ=0.001, a_max=10, a_sat=2 and ψ=5.5 for the cell cytomechanical parameters. The initial cell state and morphology correspond to the spatially homogeneous steady state given by $L = ϐ / γ,$ a=1 and v=0. The cell is initially located at a normalised distance d₀=4.5 from the punctual source of chemoattractant and the threshold for the displacement of the geometric barycentre is set to 0.1.

Three simulations have been performed, according to possible experimental situations. Fig. 5 shows the cell migration towards the chemoattractant source. The progressive destabilisation of the cell membrane, with concomitant appearance of leading protrusions and cell polarisation, are observed, in pace with a slow translocation in the direction of the source. When the cell reaches the source, it tends to collapse as the membrane still responds to the chemoattractant stimulus.

Fig. 5
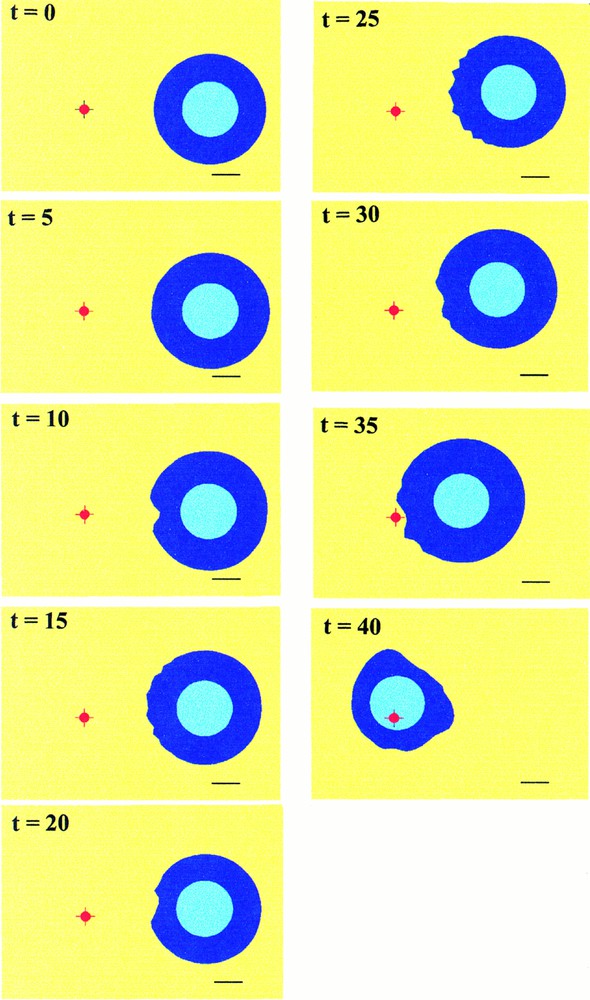
Simulated migration of the cell in the direction of a fixed source represented by the small red spot. The black bar at the bottom of the pictures corresponds to approximately $10 μ m .$ The cell body is represented by the circular light blue zone. Cycles of deformations appears in pace with the morphologic destabilisation of the front of the cell (t=10 to t=15). Then the cell migrates progressively and restabilises before undergoing a new cycle (t=20 to t=25) until it reaches the source (t=40).

To avoid this effect, which is related to our steady-state approximation of the chemoattractant gradient, two new simulations have been performed. The first one (Fig. 6) simulates the displacement of the source. When the cell is about to reach the source, the source is moved instantaneously back to the initial position of the cell. The cell then reorganises its shape and polarises in the opposite direction, toward the new source location. The second case (Fig. 7) corresponds to an extinction of the source. Then, as expected, the cell stops moving and recovers its original homogeneous shape.

Fig. 6
Simulated cell migration as in Fig. 5, except that the source of extracellular factor (red spot) is moved instantaneously back to the initial position of the cell when the cell is about to reach the source (t=35). The cell then polarises instantaneously towards this new source location.

Fig. 7
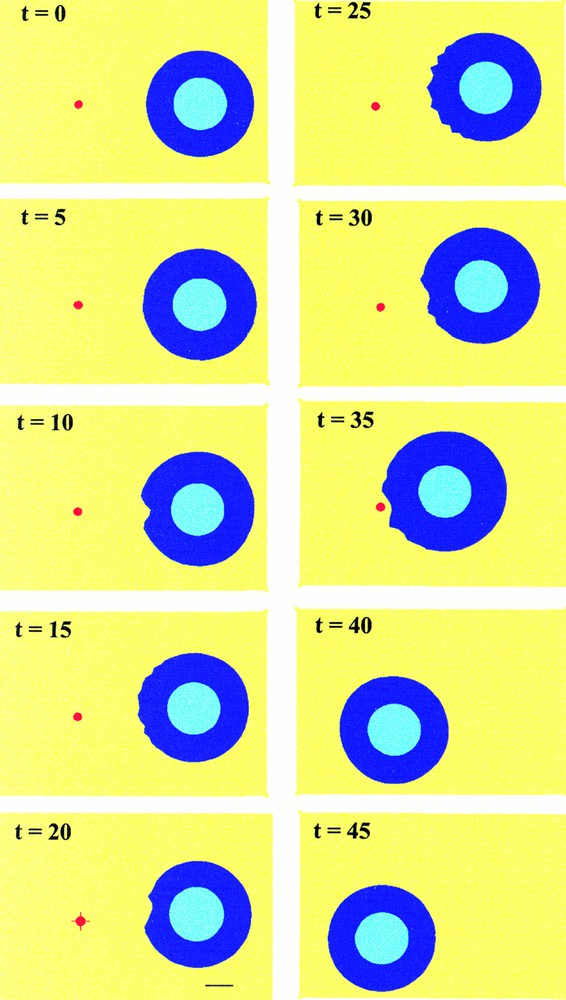
Simulated cell migration as in previous figures, except that finally the source of extracellular factor (red spot) is removed when the cell is about to reach it (t=35). One observes consecutively a slight displacement of the cell before it stops moving.

In order to simulate possible experimental control of cell migration through variations of the extracellular gradients, we simulated cell chemotaxis for different stiffness of the $C (r)$ spatial distribution. Modulation of the chemoattractant gradient is obtained by changing the parameters D or t₀ in the analytical expression of $C (r) .$ In the first simulation (Fig. 5), the migration velocity, evaluated for a cell with diameter of $15 μ m,$ is $0.65 μ m$ per normalised-time unit when t₀=1. For increasing values of the parameter t₀, i.e for a smaller gradient of chemoattractant (Fig. 8), a nonlinear variation of the migration velocity is observed, initially increasing from 0.37 to $0.77 μ m$ per normalised-time unit, then decreasing to $0.48 μ m$ per time unit.

Fig. 8
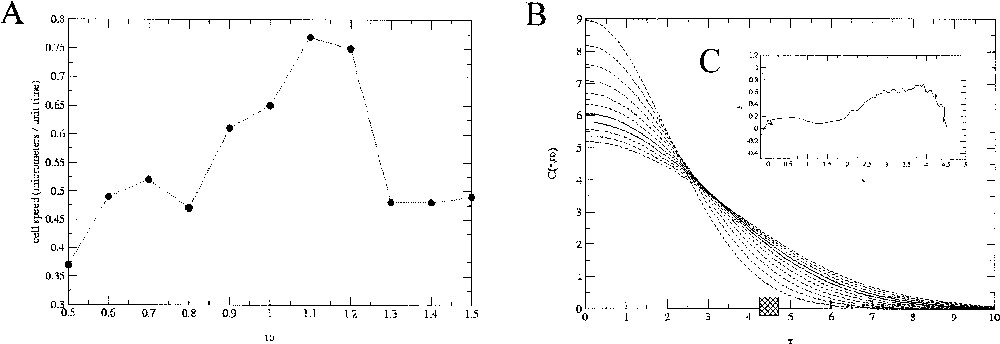
A. Evolution of the simulated cell migration speed as a function of the parameter t₀ controlling the slope of the chemoattractant gradient. B. Associated profiles for each values of t₀. The square box represents the initial position of the cell relatively to the gradient. An example of the path described by the cell barycentre (here for t₀=0.5) is plotted in the C-inserted graph.

Another way of controlling the cell migration velocity is to change the admissible threshold of cell deformation, in relation with the stress threshold above which the link between the membrane receptors, like integrins, and the substratum are broken. The results are presented in Fig. 9, where the cell migration velocity has been computed for thresholds ranging from 0.06 to 0.12. As expected, stronger cell–substratum attachment is correlated with slower cell translocations. Globally, the cell velocity decreases in a nonlinear way from 0.67 to $0.56 μ m$ per normalised-time unit with increasing values of the threshold.

Fig. 9
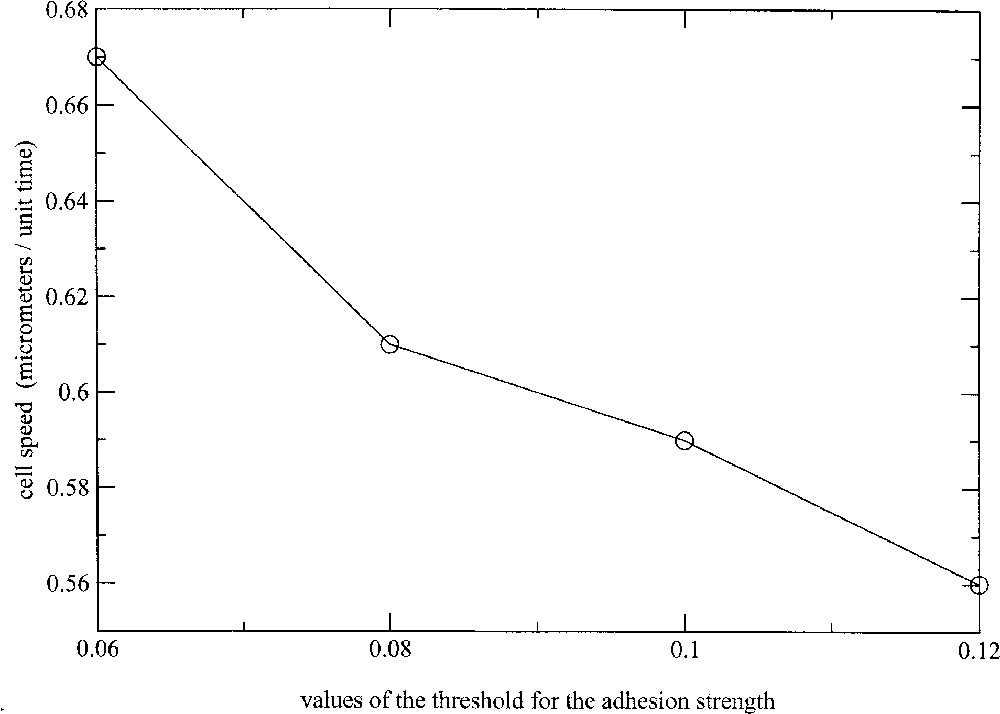
Evolution of the migration speed with increasing values of the cell–substratum attachment threshold.

6 Discussion

A large body of experiments has shown that cells change their shape in response to various environmental signals, let them be chemical or mechanical. Moreover, experimental data obtained with different cell-types have shown that cell shape changes can occur spontaneously, i.e. in absence of external stimuli. Thus, consideration of spontaneous cell shape changes appears as a pre-requisite for further investigations of directional cell migration induced by the dynamics of membrane protrusions. In this paper, we consider a ‘cortical layer’ model of the cell, i.e. an idealised circular cell with a contractive outer annulus mainly composed of F-actin. Dynamic changes of the cell radius result from a mechanical non-equilibrium state between an intracellular hydrostatic pressure, a curvature dependant surface tension stress, which is proportional to the network density of F-actin, and F-actin network contractility and swelling. This model, initially proposed by Alt and Tranquillo (1995) 〚5〛, is able to generate various patterns of spontaneous cycles of membrane extension and retraction, corresponding to oscillatory non-steady states that exist beyond some bifurcation values of the model parameters.

We successfully used this modelling approach to reproduce the self-sustained oscillatory protrusive activity experimentally observed with isolated L929 fibroblast cells 〚10〛. We here extend this model and further analyse cell–cell mechanical interactions and chemotactically induced cell migration by considering spatially inhomogeneous variation of the surface tension of the cortical actin/cell membrane complex. Our working hypothesis is that cell membrane protrusion is associated with a decrease in cell surface tension. This is in agreement with recent experimental data of Raucher and Sheetz (2000) 〚19〛 and with scanning acoustic microscopy measurements 〚20〛 which reveal that lamellipodia extensions take place in cellular region of relatively low stiffness. It has also been reported experimentally for phospholipids bilayers 〚16〛 that membrane molecules inclusion decreases the membrane stiffness.

Our model thus provides a continuous description of the successive stages of the cell morphological changes, from spontaneous oscillatory deformations up to polarisation and then migration. It furthermore provides realistic simulations of cell migration, which keeps some random aspects of the cell trajectory and in which the direction of locomotion is determined by the result of competing lamellipodia occurring simultaneously around the cell and cell progressive polarisation. We especially focus on chemotaxis, which is simulated by considering that the binding of chemoattractant molecules to membrane receptors triggers a transduction pathway which finally results in a decrease of the cortical surface tension. On the other hand, cell adhesion is necessary to insure further development of the cellular traction forces pulling the cell body; this is one of the five-step scenario described by Sheetz et al. (1999) 〚18〛 for cell migration: membrane extension, attachment to the substratum, cell contraction, release of the attachment at the trailing edge and recycling of the receptors. We do not explicitly consider all these steps but rather proposed a simplified view of this mechanism as an all or none process. If the polarisation of the cell exceeds some threshold corresponding to some value of intracellular stress, then local breakdown of cell–substrate will occur. Even if simple, this approach can still take into account data on cell adhesion forces as well as observations of integrins tracks left behind a moving cell as a testimony of the focal adhesions breakdown.

Another extension of this theoretical approach is the model ability to define optimum conditions for cell migration. Controlling cell migration is indeed crucial in many events such as wound healing, where fibroblasts or myofibroblasts migration is critical, or as tumour invasion, where a decrease of the migration speed would help to reduce cancer cell infiltration in normal tissue.

This article illustrates the influence of first the slope of the chemoattractant gradient, second the strength of the cell–substratum attachment. Another way to control cell migration is a direct modification of the cell characteristic parameters, including the cytomechanical parameters. One can thus define a ‘model-driven acquisition’ approach, where biological hypotheses will be translated into modifications of the cytomechanical model parameters values. Associated model simulations will identify the corresponding cell responses (membrane extension rate, number and frequency of membrane extensions, cell velocity...) and thus the range of experimental conditions within which such theoretical cell responses could be potentially observed. For example, the cell response and adaptation to an extracellular factors can be investigated in connection with the results of Raucher and Sheetz 〚19〛, who reported a greater than expected increase of lamellipodial extension rate in PDGF-activated cells. This was interpreted as the result of a localised decrease of the apparent membrane tension, compared to the more global effects of detergent addition, like desoxycholate, which still decrease in a similar way the membrane tension but initiate cell membrane extensions at many new sites. The cytomechanical model here presented can take into account such global shape changes, while distinguishing between different parameters which determine the apparent membrane tension, including the bilayer tension and the membrane-cytoskeleton adhesion modulated by the F-actin concentrations.

Beyond its ability to describe the local but globally coordinated nature of lamelipodial activity, the considered cytomechanical model could thus provide a common basis for understanding morphological changes observed with other cell lines or with cells submitted to different experimental conditions in the framework of nonlinear dynamical systems. For example, it has been reported that slight periodic variations of the pH can induce periodic modification of the cell shape 〚21〛. More generally, a given cellular dynamical state corresponds to a given set of cytomechanical parameters (membrane elasticity, cytoplasm viscosity...) that could differentiate the various cell lines 〚11〛. The different self-organised behaviours experimentally observed on isolated fibroblasts, as well as on other cells 〚4, 12, 13〛 favour this hypothesis. But further data are needed to assess that, in addition to the molecular characterisation based on the use of specific fluorescent probes, quantification of spontaneous membrane deformation could be used as a specific cell line signature.

Acknowledgements

A.S. is supported by a fellowship from the ‘Région Rhône-Alpes’. This work is granted by the program ‘Métrologie du vivant’ from the ‘Région Rhône-Alpes’. We thank Dr Xavier Ronot and Anne Doisy for providing videomicroscopy sequences of cultured fibroblasts and for helpful discussions.

Version abrégée

Les changements de forme cellulaire sont dus à la réorganisation de l'actine filamenteuse (actine-F), un composé complexe et très dynamique, contenu à la périphérie du corps cellulaire dans les cellules eukaryotes. Cependant, les mécanismes à l'origine de la formation des protrusions cellulaires sont toujours controversés. Les observations expérimentales des déformations cellulaires spontanées sur des substrats bi-dimensionnels montrent que les cellules manifestent un comportement auto-organisé, avec l'apparition de schémas de déformation récurrents. Un modèle cytomécanique, basé sur les propriétés viscoélastiques du réseau d'actine-F et sur les propriétés mécaniques de la membrane cellulaire, a permis de simuler la plupart des comportements dynamiques spontanés observés expérimentalement.

Nous nous sommes alors appuyés sur ce modèle pour étudier les interactions cellule–cellule et la migration cellulaire par chimiotaxie. L'observation expérimentale de fibroblastes L929 isolés montre que ces cellules ont spontanément un mouvement cyclique pulsant d'extension/rétraction de la membrane, selon deux directions perpendiculaires. Cette dynamique spontanée est altérée dans le cas des cellules en interaction : les cellules perdent leur configuration symétrique et semblent adopter de nouvelles morphologies limitant les contacts cellule–cellule. À partir de ces observations, nous proposons de prendre en compte ces interactions par une modification locale des paramètres du modèle cytomécanique : la pression hydrostatique protrusive et la tension de surface induite par la courbure membranaire. La localisation de la zone d'interaction par rapport à la géométrie symétrique initiale de la cellule a également été analysée. On observe que la dynamique de déformation est altérée dans les zones d'interactions, tandis qu'une transition dynamique entre une déformation membranaire oscillante stationnaire et une onde de déformation en rotation a été générée.

Le modèle a ensuite été étendu à l'étude de la migration cellulaire induite par un gradient de facteur extracellulaire. Les particules du facteur extracellulaire interagissent avec la membrane et le cortex cellulaire, en modifiant leurs propriétés mécaniques. Ces interactions induisent une instabilité morphologique, qui conduit à la migration de la cellule. Celle-ci remonte alors le gradient extracellulaire selon un processus impliquant deux étapes principales : (i) la polarisation de la cellule dans la direction du gradient, puis (ii) le déplacement de son centre de masse lorsque qu'une polarisation suffisante est atteinte. Ce seuil représente la force nécessaire à la cellule pour contrebalancer sa force d'adhésion au substrat. Trois simulations, associées à des situations expérimentales concrètes, sont proposées : migration de la cellule vers une source fixe, migration de la cellule avec déplacement de la source et migration de la cellule avec extinction de la source. Dans les trois cas, le comportement de la cellule simulée est en accord avec l'expérience. Deux paramètres de contrôle de la vitesse de migration sont ensuite analysés. Une augmentation du coefficient de diffusion du facteur extracellulaire conduit à un ralentissement de la migration. Une augmentation du seuil caractérisant la force d'adhésion de la cellule à son substrat conduit également à un tel ralentissement.

Bibliographie

[〚1〛] J. Condeelis Life at the leading edge: the formation of cell protrusions, Ann. Rev. Cell Biol., Volume 9 (1993), pp. 411-444

[〚2〛] M.U. Ehrengruber; T.D. Coates; D.A. Deranleau Shape oscillations: a fundamental response of human neutrophils stimulated by chemotactic peptides, FEBS Lett., Volume 259 (1995), pp. 229-232

[〚3〛] M.P. Wymann; P. Kernen; T. Bengtsson; T. Andersson; M. Baggiolini; D.A. Deranleau Corresponding oscillations in neutrophil shape and filamentous actin content, J. Biol. Chem., Volume 265 (1990), pp. 619-622

[〚4〛] T. Killich; P.J. Plath; E.C. Hass; X. Wei; H. Bultmann; L. Rensing; M.G. Vicker Cell movement and shape are non-random and determined by intracellular, oscillatory rotating waves in dictyostelium amoebae, Biosystems, Volume 33 (1994), pp. 75-87

[〚5〛] W. Alt; R.T. Tranquillo Basic morphogenetic system modeling shape changes of migrating cells: how to explain fluctuating lamellipodial dynamics, J. Biol. Syst., Volume 3 (1995), pp. 905-916

[〚6〛] G.F. Oster; A.S. Perelson Cell spreading and motility: a model lamellipod, J. Math Biol., Volume 21 (1985), pp. 383-388

[〚7〛] C.S. Peskin; G.M. Odell; G.F. Oster Cellular motions and thermal fluctuations: the Brownian ratchet, Biophys. J., Volume 65 (1993), pp. 316-324

[〚8〛] A. Mogilner; G. Oster The physics of lamellipodial protrusion, Eur. Biophys. J., Volume 25 (1996), pp. 47-53

[〚9〛] H. Le Guyader; C. Hyver Periodic activity of the cortical cytoskeleton of the lymphoblast: modelling by a reaction–diffusion system, C. R. Acad. Sci. Paris, Ser. III, Volume 320 (1997), pp. 59-65

[〚10〛] F. Germain; A. Doisy; X. Ronot; P. Tracqui Characterisation of cell deformation and migration using a parametric estimation of image motion, IEEE Trans. Biomed. Eng., Volume 46 (1999), pp. 584-600

[〚11〛] J. Zoller; K. Brandle; J. Bereiter-Hahn Cellular motility in vitro as revealed by the scanning acoustic microscopy depends on cell–cell contacts, Cell Tissue Res., Volume 290 (1997), pp. 43-50

[〚12〛] W. Alt Mathematical models and analysing methods for the lamellipodial activity of leukocytes, NATO ASI (Adv. Sci. Inst.), Ser. H, Cell. Biol., Volume 42 (1990), pp. 407-422

[〚13〛] W. Alt; O. Brosteanu; B. Hinz; W.H. Kaiser Patterns of spontaneous motility in videomicrographs of human epidermal keratinocytes, Biochem. Cell. Biol., Volume 73 (1995), pp. 441-459

[〚14〛] K.M. Soares; C. Cortez Maghelly Linear instability analysis and mechanical interfacial tension, J. Theor. Biol., Volume 196 (1999), pp. 169-179

[〚15〛] K.S. Kim; J. Neu; G. Oster Curvature mediated interactions between membrane proteins, Biophys. J., Volume 75 (1998), pp. 2274-2291

[〚16〛] C. Nielsen; M. Goulian; O.S. Andersen Energetics of inclusion-induced bilayer deformations, Biophys. J., Volume 74 (1998), pp. 1966-1983

[〚17〛] T.S. Shimizu; N. Le Novère; M.D. Levin; A.J. Beavil; B.J. Sutton; D. Bray Molecular model of a lattice of signalling pro teins involved in bacterial chemotaxis, Nature Cell Biol., Volume 2 (2000), pp. 792-796

[〚18〛] M.P. Sheetz; D. Felsenfeld; C.G. Galbraith; D. Choquet Cell migration as a five-step cycle, Biochem. Soc. Symp., Volume 65 (1999), pp. 233-243

[〚19〛] D. Raucher; M.P. Sheetz Cell spreading and lamellipodial extension rate is regulated by membrane tension, J. Cell Biol., Volume 148 (2000), pp. 127-136

[〚20〛] J. Bereiter-Hahn; H. Luers Subcellular tension fields and mechanical resistance of the lamella front related to the direction of locomotion, Cell. Biochem. Biophys., Volume 29 (1998), pp. 243-262

[〚21〛] C.M. Lo; C.R. Keese; I. Giaver pH changes in pulsed CO₂ incubators cause periodic changes in cell, Exp. Cell Res., Volume 213 (1994), pp. 391-397

Commentaires - Politique