1 Introduction
The upper airway cross sectional area during sleep is highly dependent on the level of neural activation of the dilator muscles. Loss of muscle tone leads to narrowing of the upper airway (UA) during inspiration as the negative inspiratory pressure increases. One of the mechanical consequences of this phenomenon is flow limitation. It is well known that upper pharyngeal collapsibility is much higher in apnoeic subjects than in normal subjects. We previously characterised 〚1〛 the pharyngeal resistance during sleep in a spectrum of sleep-disordered breathing. The relationship between airflow and pressure was analysed for upper airway resistance syndrome (UARS), obstructive sleep apnoea (OSAS), hypopnoea (OSHS) syndrome and simple snoring (SS). It was demonstrated that the variation in the mean resistance value at the peak pressure (Rmax) is a sensitive method to detect episodes of high resistance (HR) during sleep. The model of UA presented in this paper has been partially designed using the results of the analysis of the breath-by-breath variations in Rmax.
Upper airway collapse mechanisms are complex. Theoretical models based on different hypotheses and methods have been tested. Mathematical models of collapsible tubes have been developed 〚2, 3〛. Shome et al. 〚4〛 developed a three-dimensional model of airflow in the pharynx constructed from a finite element mesh. The pharynx walls were assumed to be passive and rigid. These authors investigated the effect of various treatments therapies on local airflow characteristics. Fodil et al. 〚5〛 studied fundamental aspects of the interaction between multiple discrete elastic wall elements. These models did not take into account the neuromechanical-coupling factor. Huang et al. 〚6〛 recently developed a model including the neuromuscular reflex stiffening the pharyngeal wall proportionally to a delayed intraluminal fluid pressure. They studied the snoring mechanisms. They designed a lumped-parameter model where the vibrating part of the oropharynx is represented by a piston and the stiffness induced by neuromuscular activation by a pressure-controlled elastic element.
All of these studies underlined that a major contributing factor of the pharyngeal collapse mechanism is the UA compliance. Compliance is defined by the ratio between variation of the cross-sectional area of the studied element and variation of the transmural pressure. This relationship has been studied under static conditions in patients with OSA. Given that the velopharynx is the most common site of a highly compliant pharyngeal compartment, Isono et al. 〚7〛 endoscopically evaluated its compliance in OSAS patients under hypotonic conditions. These authors found an exponential pressure–area relationship.
Our objective was to breath-by-breath analyse the dynamical pharynx-wall behaviour in OSA during sleep and wakefulness using airflow and pressure signals. We describe in this paper a first step towards this objective. It aims at establishing the cross-sectional area of the UA. The model approach enables us: (i) to identify the critical parameters to be assessed; (ii) to evaluate the cross-sectional area and the compliance of the UA in a less invasive way than by endoscopy; (iii) to obtain a better description and comprehension of mechanical and neuromuscular coupling mechanisms; (iv) to eventually propose an alternative way to Rmax analysis for identifying and detecting obstructive events.
2 Naso and pharyngeal Rmax measurement
Twelve patients (nine men) with sleep-disordered breathing were studied in the sleep laboratory 〚1〛. Two individuals were considered as exhibiting SS, three as having UARS, four as having OSHS, and three as having OSAS. Airflow was measured via a pneumotachometer (Kontron Instrument, Quentin , France) installed on a full-face mask. A solid-state multitransducer catheter was used to simultaneously measure static pressure at three different levels in the pharynx (Gaeltec, Isle of Skye, Scotland, UK). Three pressure transducers were integrated in the Gaeltec and positioned in the nasopharynx, velopharynx and oropharynx (Fig. 1).
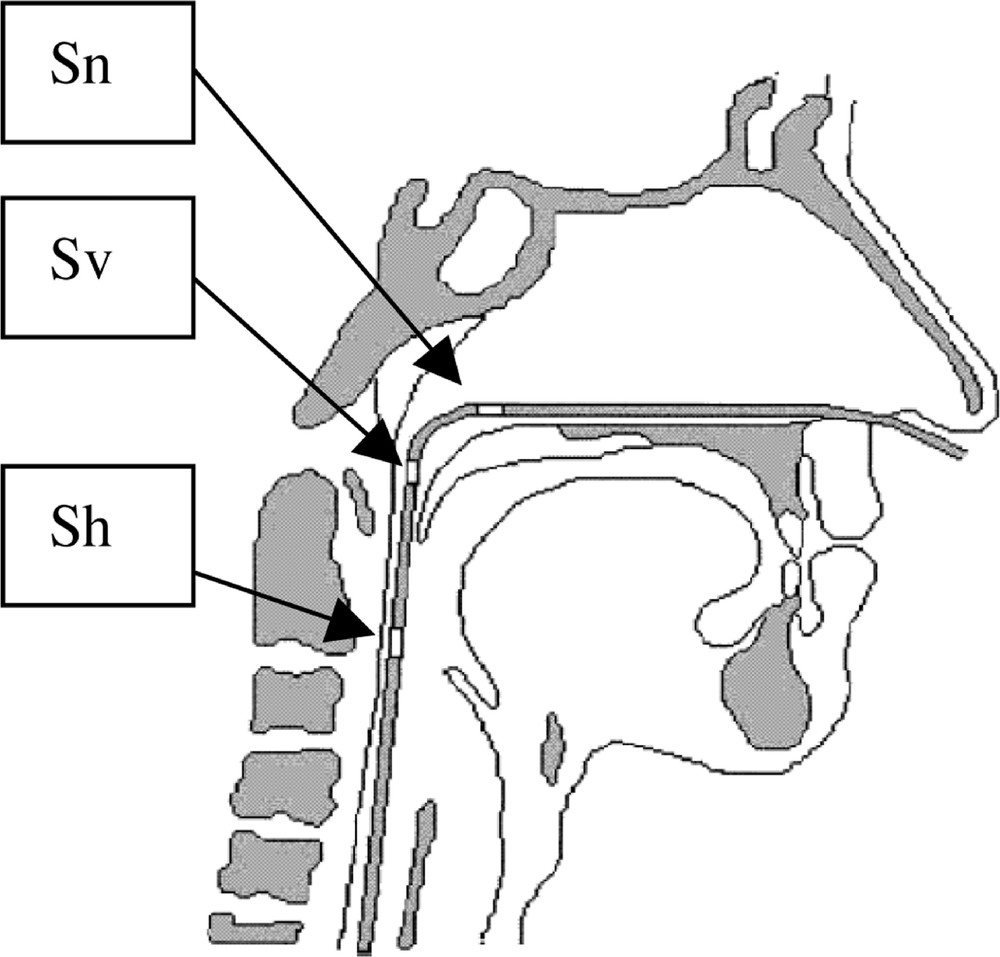
Pressure measurements. Sn: Nasopharynx sensor, Sv: velopharynx sensor; Sh: hypopharynx sensor.
Experimental results
Fig. 2 shows nasal and pharyngeal Rmax variations during a high-resistance (HR) episode in stage II sleep in a UARS patient. The resistance (ΔP/Q) was evaluated by processing the peak flow (Q) and pressure (ΔP) values 〚1〛. This shows that in case of UARS syndrome, both nasal and pharyngeal Rmax exhibit coherent variations. Fig. 3 illustrates the correlation between nasal and pharyngeal Rmax changes. This correlation may reflect: (i) the loss of overall muscle tone; (ii) the aerodynamic coupling between the two UA segments. Fig. 4 and Fig. 5 illustrate the changes in nasal and pharyngeal resistance from wakefulness to deep sleep in the different sleep-disordered syndromes. As it was impossible to systematically place the soft palate pressure sensor at the right location, we were unable to obtain velopharyngeal resistance measurements. Thus, the pharyngeal resistance value shown in Fig. 5 is the sum of both velopharynx and hypopharynx resistances.
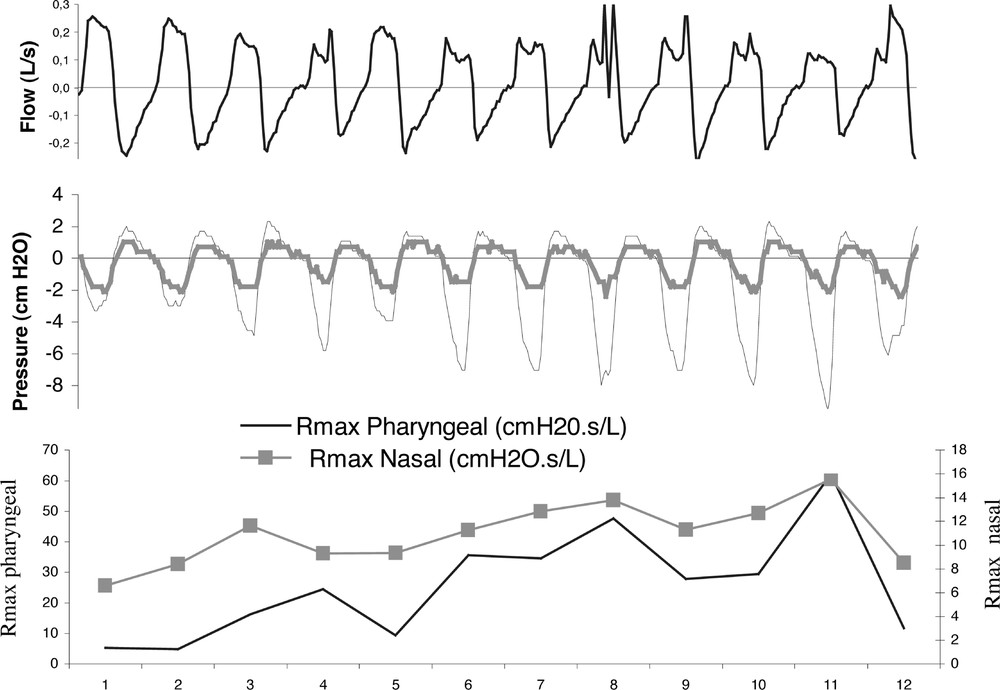
Rmax changes during an HR event.
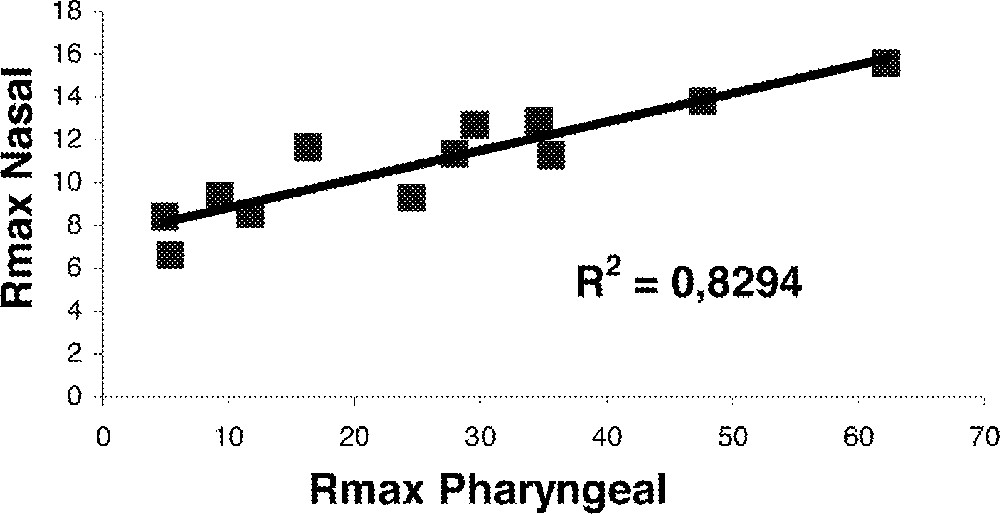
Nasal and pharyngeal Rmax collection.

Nasal resistance collection.
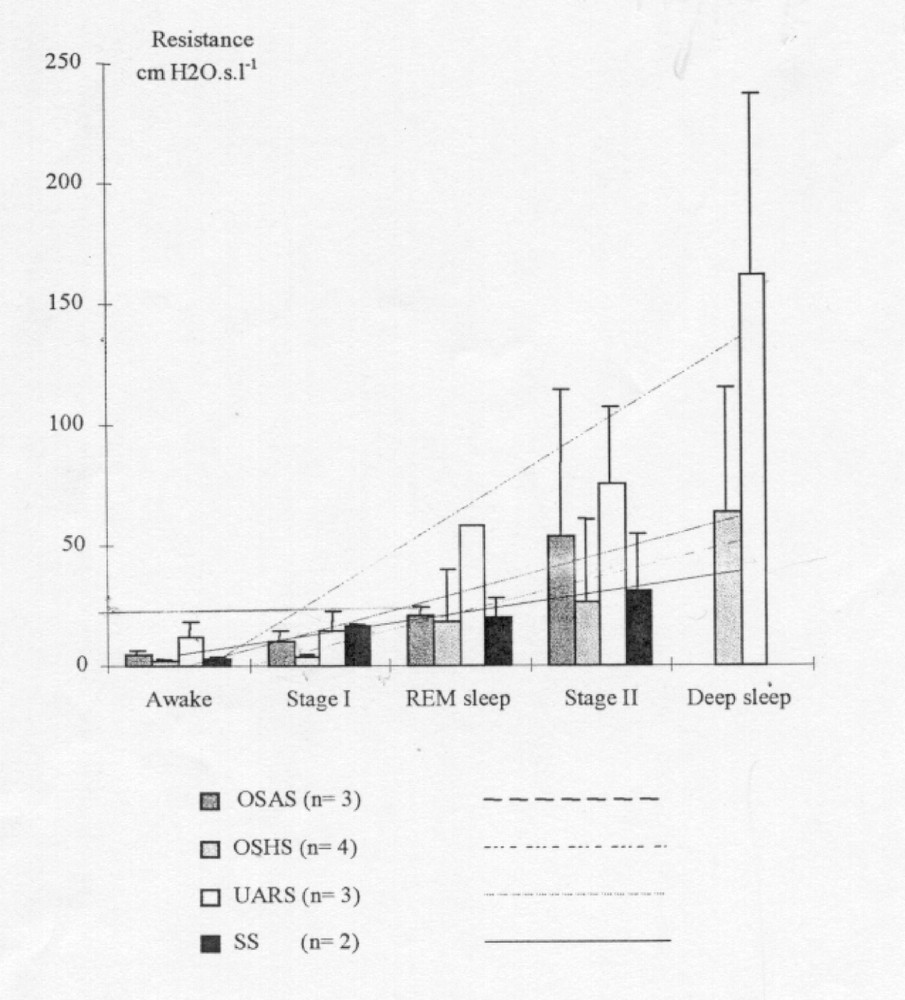
Pharyngeal resistance evolution.
This experimental part gave two major features for our UA model. As it was impossible to obtain a reliable measurement of the velopharynx pressure, we had to use only two segments in the UA model: a nasal and a pharyngeal segment. Since it was shown that both the nasal and the pharyngeal resistance increase during sleep in UARS patients, both segments of our model were collapsible.
3 Modelling
Our aim is to calculate the relative variations of cross-sectional area of nostrils and oro-pharynx from pressure and flow signals acquired on patients.
As shown in Fig. 6, we simply modelled the UA by two collapsible segments (nostrils and oro-pharynx) separated by the fossa.
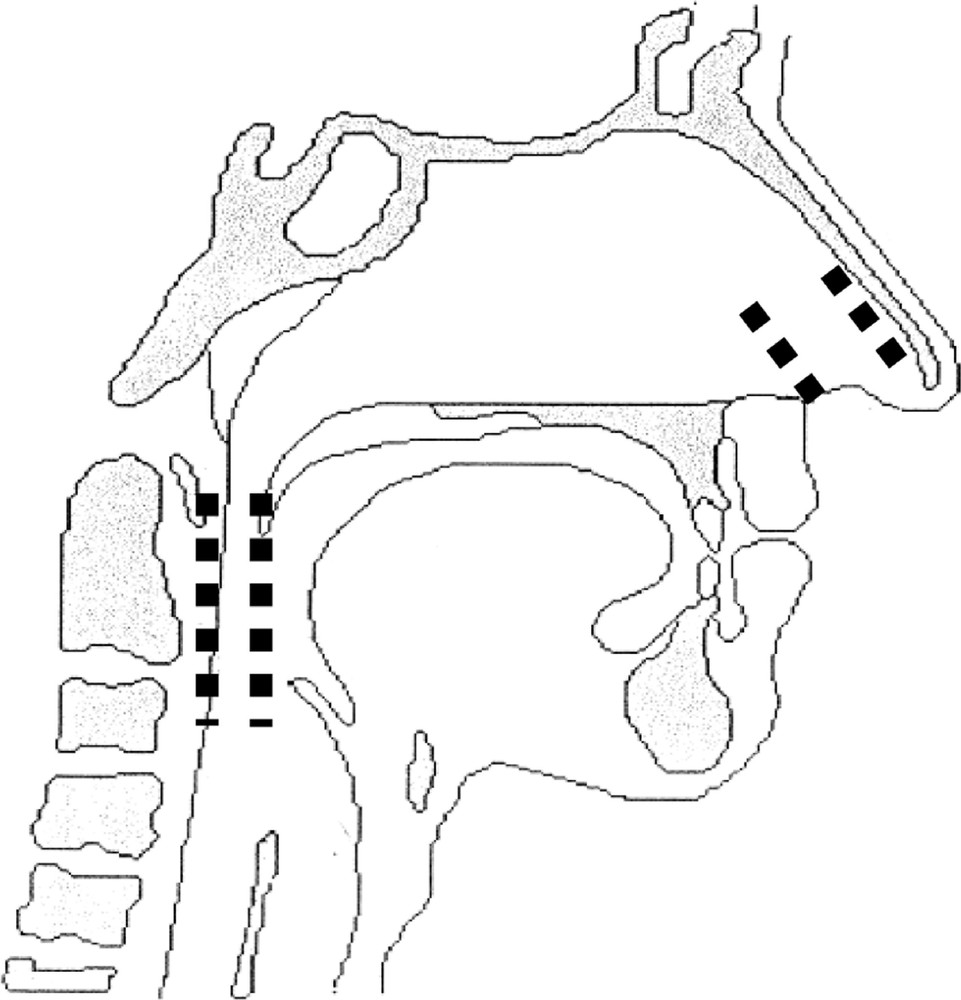
UA model: collapsible elements are represented by dashed lines.
Since the major part of the pressure drop is due to singular effects, the square of the cross-sectional area is roughly proportional to the Q2/ΔP ratio. We also neglected the kinetic energy at the place of pressure measurements considering the fact that the corresponding sections are much greater than those of the collapsible segments. For the same reason, we neglected the pressure drop in the fossa.
Using the former simplifying hypothesis, we wrote for each collapsible segment:
4 Results and discussion
We now present the results obtained on the UA cross-sectional area model calculation (S). As the breath-by-breath changes in Rmax are very sensitive to the high-resistance episodes during sleep, we have chosen to compare the breath-by-breath changes in Rmax with Smax. The Smax parameter corresponds to the section calculated at the maximum inspiratory peak pressure as for the Rmax parameter. We present the results obtained in a UARS syndrome and an OSAS syndrome.
4.1 Smax calculation during an HR episode for the UARS syndrome
Fig. 7 shows the Rmax and Smax changes in both nasal and pharyngeal segments. The corresponding airflow and pressure signals are illustrated in Fig. 2. It can be evidenced that: (i) when there is a crescendo in resistances values, the Smax parameters exhibit a decreasing value; (ii) as Rmax returns to baseline at the end of the event, the Smax values return to values close to the initial ones; (iii) the fifth cycle, which does not exhibit any flow limitation, shows a decrease in resistance values and an increase in sections.

Rmax and Smax changes during the occurrence of an HR event.
This demonstrates that the cycle-by-cycle Smax value changes are highly coherent with the Rmax measurements and perfectly reflect the progressive occurrence of a HR episode.
We can observe in Fig. 8 that the nasal and pharyngeal Smax values exhibit a greater correlation than the Rmax ones. This indicates that Smax and Rmax have a different sensitivity in relation to the HR event. As previously stated, the mechanism underlying flow limitation events is a partial collapse of UA, which corresponds to section narrowing. The Rmax parameter is defined by the ΔP/Q ratio. As written previously, the major part of the pressure drop is due to singular effects thus the square of the cross-sectional area is roughly proportional to the Q2/ΔP ratio. Using the Smax calculation rather than the Rmax one allows us to better reflect the mechanical phenomenon: the most appropriate parameter would be αmax = ΔP/Q2.

Smax nasal and pharyngeal correlation.
4.2 Smax calculation during an apnoea episode for the OSAS syndrome
We now examine the model results during the extreme case of a quasi-apnoea event as shown in the fifth cycle of Fig. 9. It can be observed that: (i) here again, the apnoea episode is detected by both Smax and Rmax; (ii) the αmax parameter exhibits a higher sensitivity to the event as Rmax; (iii) the area of the collapsible element decreases to 16%.
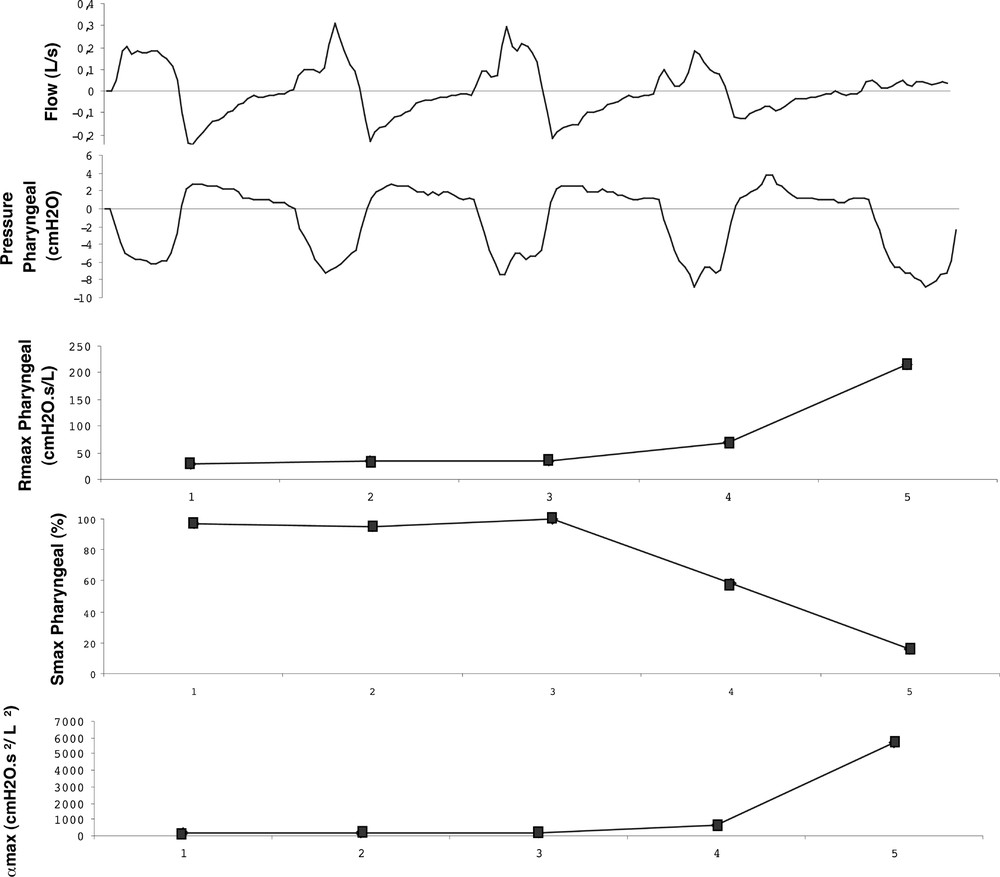
Smax and αmax changes during the occurrence of an apnoea episode.
5 Conclusion and perspectives
The reverse modelling method described in the present paper and applied to a simplified geometric and aerodynamic model of the UA has led us to a first evaluation of two collapsible segments, one for the nostril and one for the pharynx.
The simplicity of the model will enable us to follow the area versus tidal volume relationship in real time. For instance, Fig. 10 shows the changes in the calculated section during two breathing cycles for the same UARS patient, one during wakefulness and the other during a flow limitation event. During the flow limitation event, the section area is clearly lower than during wakefulness, while the relative change in area between inspiration and expiration is much higher. This behaviour may be related to phasic and tonic neuromuscular activity change. In the future, this relation will be analysed more accurately, taking into account EMG genioglossal measurements and so we will be able to extract the compliance from the global wall behaviour.

Evolution of the calculated pharyngeal section area. Top: awake. Bottom: asleep (stage III) during a flow-limitation event.
We will soon be able to further validate our model using section measurements provided via endoscopic measurement.
In the present study, we have demonstrated that, although the resistance of the pharyngeal segment varies coherently with flow limitation events, this is not the most appropriate parameter. It is thus preferable to use ΔP/Q2, which varies as the inverse of the square of the area (i.e. S–2) and is thus more physically significant and related to the narrowing of the UA.
Version abrégée
Dans des travaux antérieurs 〚1〛, nous avons caractérisé l’évolution de la résistance pharyngée pendant le sommeil sur un certain nombre de patients atteints de différents syndromes de hautes résistances. Les modèles existants 〚2–6〛 se révèlent, soit trop compliqués pour fournir des résultats en temps réel, soit incapables de rendre compte des déformations des segments collabables des voies aériennes supérieures (VAS).
Dans cet article, notre objectif est d’analyser cycle par cycle l’évolution relative des sections collabables grâce à un modèle simplifié des voies aériennes supérieures à deux éléments de section variable, séparés par les fosses nasales (narines et hypo-pharynx, Fig. 6) à partir de mesures pressions–débit effectuées sur le patient. Lors des mesures expérimentales en laboratoire du sommeil, nous disposons de deux capteurs de pression, l’un situé en Sn l’autre en Sh (Fig. 1). Le capteur Sv ne donne pas de mesures satisfaisantes (bruits).
La majeure partie des pertes de charges étant de type singulier, le carré de la section sera considéré comme proportionnel au rapport Q2/ΔP. Dans nos hypothèses simplificatrices, nous avons également négligé l’énergie cinétique aux lieux de mesure des pressions, où les sections sont nettement supérieures à celles des sites de collapsus. Pour la même raison, nous avons négligé la perte de charge dans les fosses nasales.
Avec ces hypothèses simplificatrices, nous pouvons écrire, pour chaque segment collabable :
Lorsque l’on compare le comportement des sections calculées par le modèle aux résistances mesurées, on observe une grande cohérence dans les variations (Fig. 7).
De plus, on observe une meilleure corrélation entre les sections nasales et hypo-pharyngées (Fig. 8) qu’entre les résistances (Fig. 3). Nous proposons donc un nouveau paramètre de détection des évènements (α = ΔP/Q2), qui varie comme l’inverse du carré de la section.
Enfin, nous présentons les résultats d’un calcul sur un cycle complet à l’éveil et au cours du stade III de sommeil pendant l’apparition d’une limitation de débit (Fig. 10). Ici encore, on observe une grande cohérence du modèle avec l’événement, c’est-à-dire que les sections sont plus grandes à l’éveil que pendant le sommeil ; l’écart relatif des sections inspiratoires et expiratoires est plus important pendant le sommeil qu’à l’éveil. Ceci traduit la diminution du tonus musculaire durant le sommeil.



