1 Introduction
Wound healing is a familiar, everyday process. But the underlying biology is extremely complex and remains only partially understood, despite extensive research. The majority of this research activity is of course experimental, but over the last decade or so, a significant contribution has been made by theoretical work, using mathematical models. In this review, we will describe the key elements of this theoretical research, as a background to a discussion of what we see as the main challenges and opportunities for future mathematical modelling of wound healing. We focus entirely on mammalian skin, which is the tissue in which wound repair has been most extensively studied; however some mathematical modelling work has been done for other tissues (see e.g. 〚1, 2〛).
An immediate response to skin injury is of course bleeding and the formation of a blood clot. Initially the vasculature constricts to decrease the blood flow but later it dilates and becomes more permeable allowing the blood plasma and various cell types to more easily enter the wound site. During this ‘inflammatory phase’ of healing, many white blood cells aggregate in the wound, and these form an important source of regulatory chemicals in the later phases of repair. The upper part of the blood clot dries out to form the scab, and the epidermal layer of the skin heals by direct cell migration underneath the scab. The lower part of the blood clot provides a scaffold along which fibroblasts and other cells migrate into the wound, from surrounding and underlying tissue, and thus changes from an acellular region to a region rich in cells and capillaries known as granulation tissue. Within the wound, fibroblasts can become actively contractile, and pull the wound edges together: it is this that causes the tension lines familiar around a wound. The fibroblasts also break down the blood clot and replace it with collagen-based scar tissue. These healing processes in the dermal layer of the skin depend on a dense network of capillaries, which form in response to injury, and are responsible for the red appearance of a healing wound.
The repair process described above can be conveniently divided into epidermal healing, changes in dermal matrix, capillary ingrowth, and wound contraction. Although these four components are clearly interrelated, we will discuss them separately.
2 Epidermal healing
Repair of the epidermis is usually fast and effective, both as part of the healing of a deep wound, and when only the epidermis is damaged, for instance in a blister. Nevertheless, epidermal healing is an important clinical issue, and an active research topic. In part, this is because the healing response of the epidermis provide important information about basic epidermal biology, with implications in other pathologies and in development. But also, a detailed understanding of epidermal repair is essential for cultured epidermal autografts, where a cell sheet is grown in culture and transplanted onto a patient with severe burn wounds 〚3〛. This is the “gold standard” for the treatment of chronic burns, but its application is currently limited due to the time and cost of growing the autograft.
Epidermal wound healing is a combination of two key processes: cell migration into the wound, and upregulated cell division near the wound edge (for a review, see 〚4–6〛). Both of these processes are regulated by a wide range of growth factors, and it is this chemical control that has been the focus of both experimental research and mathematical modelling. In simple terms, mathematical models predict how cell numbers will change as a result of the spatiotemporal variations in proliferation and motility. The model equations are formulated using experimental data, usually from in vitro studies, on cell behaviour (for example, data on how cell proliferation rate varies with the concentration of a chemical regulator). The equations are then used to predict the dynamics of the cell population within a healing wound.
The first model of this kind was developed by Sherratt and Murray 〚7〛, and assumes that cell division is regulated by a diffusive chemical produced by the epidermal cells themselves. Fig. 1 shows the simulated healing of a circular epidermal wound, as predicted by their model. In this figure, the colour reflects the concentration of the chemical regulator: this is highest at the wound edge, and drives wound closure. Models of this type enable rapid prediction of how the speed of healing can be changed by adding exogenous growth factors, and this was the focus of work by Dale et al. 〚8〛 and Sheardown and Cheng 〚9〛, who extended the model of Sherratt and Murray 〚7〛 to the specific case of corneal epithelial wounds. Wound shape is also an important area of prediction for mathematical models. Sherratt and Murray 〚10〛 showed that chemical promoters and inhibitors of cell migration could be distinguished by the way in which they cause a wound to change shape during repair. Savakis and Maggelakis 〚11〛 also focus on wound shape in a model for epidermal repair that is based on shrinking clusters, a technique adapted from the study of diffusion limited aggregation.
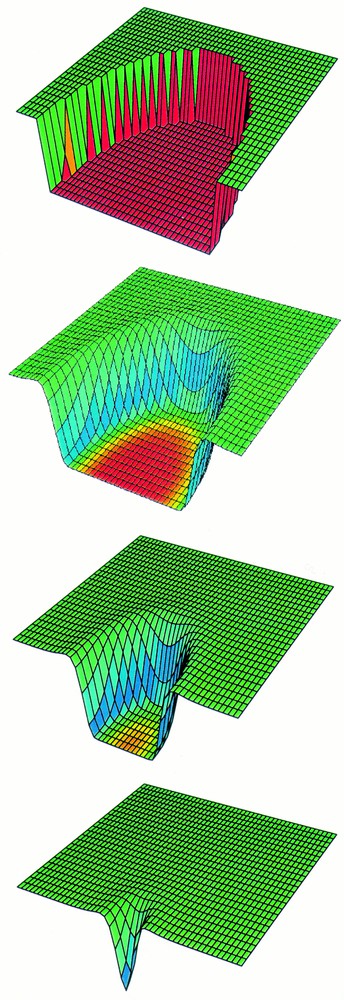
A computer simulation of the healing of a shallow wound. Cell density is plotted for half of a circular wound, at four times during healing. The colours represent the growth factor concentration (red = low, blue = high). The growth factor level is moderate in the tissue around the wound, and higher at the wound edge, where the cells produce the growth factor as a response to being at the edge. Within the wound, the growth factor level is low because there are no cells in this region, and it is the cells that produce the growth factor. Model details are given in 〚7〛.
For many years, the key growth factors regulating epidermal repair were thought to be members of the epidermal growth factor family. But in the mid-1990s, the work of Werner et al. 〚12〛 showed that keratinocyte growth factor (KGF) plays a key role in epidermal healing, and is expressed at very high levels within 24 h of injury. This raises a number of exciting challenges for mathematical modelling, because of the unusual nature of KGF. Although its effects are on epidermal keratinocytes, KGF is produced only within the dermal layer of the skin 〚13〛. This implies a type of tissue interaction that has been studied mathematically in the context of development 〚14, 15〛, but whose implications for wound repair remain unclear. Wearing and Sherratt 〚16〛 have developed a simple model for KGF activity in wounds, which suggests that the high KGF levels found experimentally actually decrease the speed of healing, but provide the benefit of an increased signalling range, causing an increased cell division rate many cell diameters from the wound edge (as is observed experimentally).
The natural focus for future mathematical modelling of epidermal wound healing is the complex interplay of growth factors that regulate the process. KGF is now known to play a key role, but in concert with other signalling molecules such as epidermal growth factor. Which of these dominates? Almost certainly, the answer varies with distance from the wound edge, since epidermal-derived growth factors must propagate through the dense epidermis, while KGF is produced in and can diffuse through the much less dense dermis. Experimental determination of the spatial profiles would be vary laborious, but mathematical modelling provides a natural way of making rapid predictions, suitable for testing in a more focussed experimental study.
3 Repair of the dermal extracellular matrix
Perhaps the single most exciting development in wound healing over the last decade is the discovery that the degree of scarring can be altered by chemical intervention. Work in Mark Ferguson’s laboratory at the University of Manchester, UK, showed that changing the concentration of transforming growth factor β (TGFβ) in a healing wound can reduce scarring 〚17〛. Subsequent work has identified isoform-dependent effects of TGFβ 〚18〛, and an anti-scarring therapy based on this work is currently in clinical trial in the UK. Mathematical modelling has contributed to various stages of this work, and is an important tool for refining anti-scarring therapies.
The starting point for scar tissue formation is the blood clot, a dense random network of fibres made from the protein fibrin. As fibroblasts cells migrate into the wound from surrounding tissue, they break down this fibrin, replacing it with a provisional extracellular matrix (ECM), which in turn is converted to the new dermal tissue whose key constituent is the protein collagen. The fibroblasts will continue to reorganise the ne collagen–based ECM for many months after wounding. Typically the new dermal tissue is different from the original dermal tissue and is called a scar. Two key features of this scar tissue ECM have attracted the attention of mathematical modelling: the details of collagen composition, and the orientation of the fibres.
Of the many different types of collagen, types I and III are most abundant in the dermis, and the proportion of type III collagen is higher in scar tissue than in normal dermis 〚19〛. Because type III collagen decorates the surface of type I fibrils 〚20〛, this results in thinner collagen fibres. The balance between types I and III collagen is regulated by the different isoforms of TGFβ, and this was studied in the mathematical model of Dale et al. 〚21〛. Their model is able to reproduce observed ratios, and predicts that the different collagen composition of normal dermis and scar tissue depends on the way in which different TGFβ isoforms modulate one another. In a follow-up study, investigating spatial dynamics of collagen, Dale et al. 〚22〛 predicted that the observed collagen ratios could only arise if the majority of fibroblast cells enter the wound from underlying tissue, rather than from the sides; this was subsequently confirmed in experiments 〚23〛.
Although collagen composition is an important difference between scar tissue and normal dermis, the differences in fibre orientation are more significant. In normal dermis, the collagen fibres are arranged in a random, ‘basket-weave’ form, whereas in a scar, there is a predominant direction of alignment 〚20, 24〛. It is this difference in fibre alignment that causes a scar to look different from the surrounding skin, and it also gives the scar poorer mechanical properties. The presence of predominant fibre orientations means that scar tissue is anisotropic. A number of inorganic materials, such as graphite, are anisotropic, and there are established methods for studying such materials mathematically. But scar tissue is much more complicated because the anisotropy varies dynamically in space and time, as fibroblasts move into the wound and fibrin is replaced by collagen.
Early attempts to model the ‘dynamic anisotropy’ of scar tissue restricted attention to specific cases such as planar wound fronts, which are simpler mathematically, but biologically rather artificial 〚25〛. Models focussing on changing anisotropy in tissue remodelling have been developed only recently, by Dallon and co-workers 〚26–29〛. Their model differs from those described thus far because the cells are represented individually, rather than as a continuous cell density. From a computational viewpoint, this is feasible because the number of fibroblasts involved in repairing a dermal wound is relatively small (thousands). Dallon et al. 〚26–29〛 formulate rules for changes in cell speed and direction in ECM networks of varying orientation, based on in vitro experimental data. Their model then predicts the movement of these cells as they enter the fibrin-based blood clot, break it down, and replace it with a new, collagen-based matrix. A typical model simulation is illustrated in Fig. 2, which shows the clear anisotropy in the collagen fibres laid down in the scar. The basic reason for this is that the majority of fibroblasts enter the wound from underlying tissue 〚23〛, so that the first collagen fibres laid down are aligned perpendicular to the skin surface. This pattern is then reinforced as successive fibroblasts enter the wound. ‘Mathematical experiments’ using the model predict that this aligned pattern of fibres is most effectively disrupted by increasing the frequency with which fibroblasts change direction within the wound. Since this prediction was made, it has been confirmed experimentally that appropriate isoforms of TGFβ do indeed alter filopodia production in a type of epithelial cells 〚30〛. It has yet to be determined if this affects their tendency to change direction.

A computer simulation of scar tissue formation, 12 days post-wounding showing a cross-section of the wound region with the epidermis at the top. Collagen fibres are indicated by coloured lines, with the orientation of the line reflecting local collagen orientation, and the colour representing collagen density (red = high, blue = low). There is a clear anisotropy in the collagen fibres. The model involves discrete representation of individual fibroblast cells, and the locations of a quarter of the cells are indicated by black dots. Model details are given in Dallon et al. 〚26–29〛.
All of the current modelling work on wound anisotropy is in two space dimensions. A major challenge for the future is the development of models that apply in 3-D. This is particularly important because a large amount of experimental data is available on the alignment patterns of ECM (e.g., 〚31〛), but it is three-dimensional. A separate but equally important research direction is the development of continuum models, based on cell densities rather than on discrete cells. This type of model has the advantage that it can be studied via mathematical analysis as well as computationally. Some preliminary modelling has been done 〚27, 28〛, using modelling techniques developed initially for intracellular alignment of actin filaments 〚32〛. Extensions of this work would enable its results to be compared in detail with the discrete cell models, providing a very powerful theoretical framework. A third and more specific question for future work concerns scar growth in young animals. Experiments show that scars do grow, but not as fast as the animal itself 〚33〛. This fascinating observation has not yet been explained, and provides an exciting challenge for theoreticians.
4 Wound contraction
The familiar tautness of skin around a wound is evidence of wound contraction, the process by which contractile fibroblasts within a wound pull its edges together. This occurs to a much greater extent in animal skin than in humans, because of the absence of the panniculus carnosus, a muscle that connects human dermis to underlying tissue; for example, as much as 90% of wound closure in rats can be due to contraction 〚34〛.
The contractile fibroblasts within wounds are thought by some investigators to have a separate phenotype termed ‘myofibroblasts’ 〚35〛, while others regard the traction force as part of normal fibroblast behaviour. But the basic phenomenon is universally agreed: cells within the wound exert a traction force on their environment 〚36〛. The understanding of this process has been greatly enhanced by experiments using collagen gels, in which fibroblasts are seeded in a freestanding collagen network. From experiments of this type, there is a large volume of data on the way in which different chemicals regulate the contraction process. Moreover, specific mathematical models of the gel contraction assay have been valuable in interpreting experimental results 〚37〛.
Contraction was the first aspect of wound repair to be studied mathematically, by Murray et al. 〚38〛. They showed that a general model for tissue biomechanics can be adapted for the wound situation, and extensions of this work by Tranquillo and Murray 〚39, 40〛 showed very good comparison between predictions and data on the change in wound area with time during healing. This model treats the wound environment as a linear, viscoelastic material, in which the cells exert a traction body force. A subsequent model by Olsen et al. 〚41〛, based on the same general framework, suggested a possible explanation for wound pathologies such as keloid scarring.
In reality, biological tissues have significantly non-linear mechanical properties 〚42〛, and inclusion of these is a very challenging modelling problem. The fullest attempt at this to date is due to Cook 〚43〛, whose model includes the important history-dependence of biological tissues, reflecting the fact that tissue under strain will adjust relatively quickly to its new configuration. Cook 〚43〛 is able to predict the movement of the skin around a wound as it heals, a result that is directly amenable to experimental tests.
Without question, the biggest challenge facing mathematical modelling of wound contraction is inclusion of the effects of the dynamic anisotropy discussed in § 4. Combination of the approaches used to model collagen deposition and reorientation with those used for contraction is probably the most important single goal in the theoretical study of wound repair. From a clinical viewpoint, such a hybrid model would offer valuable insights, not only into the normal wound healing process, but also into a variety of related pathologies such as dermatofibroma and Dupuytren’s contracture 〚44〛.
5 Wound angiogenesis
The macrophages that enter the wound as part of the initial inflammatory phase of healing produce a range of growth factors. Some of these regulate fibroblast influx, such as TGFβ discussed above, but others attract endothelial cells into the wound space, leading to the establishment of a capillary network, which can constitute as much as half of the wound. This process of capillary ingrowth, known as angiogenesis, is essential to healing, since the high levels of metabolic activity in a healing wound cannot occur without a specific blood supply. In fact, from a clinical viewpoint, one of the most pressing concerns in wound healing is the failure of some wounds to heal, because of an inadequate vascular response. This is particularly common in leg ulcers of elderly patients, and is the main cause of hospital bed occupancy in many dermatology wards.
The biology of angiogenesis has been very well studied, mainly in the context of cancer rather than wound repair. Solid tumours require their own vascular network to grow more than a few mm across, and there has been a huge push over the last decade to develop drugs that target this part of tumour progression 〚45, 46〛. Much of the underlying biology discovered in the course of this work applies equally to wound angiogenesis. In response to chemical gradients, the endothelial cells which line blood vessels near the wound begin to migrate, forming small, finger-like capillaries. Proliferation of the cells within these sprouts causes the capillaries to extend into the wound and eventually merge (anastomosis), leading to a capillary network (for review, see 〚47–49〛).
Tumour angiogenesis has been a rich area for mathematical modelling 〚50, 51〛. In particular, an important contribution to the study of angiogenesis has been made by theoretical predictions on the way in which gradients of chemical growth factors and of ECM components combine to produce the observed branched capillary networks 〚52〛. However, in the context of wound healing, there has been relatively little modelling work. Chaplain and Byrne 〚53〛 reviewed the aspects of tumour angiogenesis modelling that can be applied to wound repair, and Olsen et al. 〚54〛 focussed on the particular interaction between endothelial cells and extracellular matrix. However, the most important theoretical work on wound angiogenesis to date is that of Pettet et al. 〚55, 56〛. Their model studies the movement of fibroblasts and endothelial cells in parallel into the wound space, regulated by macrophage-derived chemicals. Crucially, their model reflects the dependence of macrophage activity on local oxygen concentration, which is the basic self-regulatory mechanism in wound angiogenesis, and is a major difference between the process in wounds and in tumours. Fig. 3 illustrates that the model of Pettet et al. 〚55, 56〛 is able to reproduce the failure of wounds to heal when the proliferation rate of endothelial cells is too low. Moreover, they predict that healing can be restored by increasing this production rate. Recently a version of this model was tested against experimental data by Byrne et al. 〚57〛.
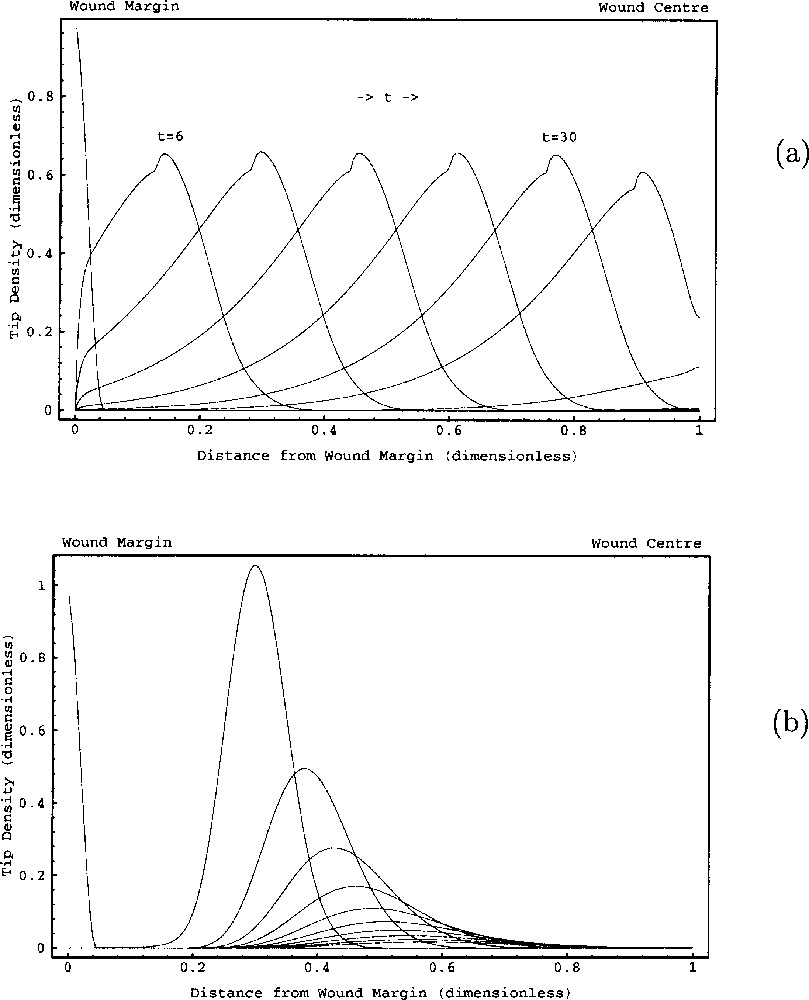
A computer simulation of the growth of blood vessels into a healing wound. The solution plotted is for capillary tips, and (a) represents the case of normal wound healing with the wound rapidly becoming vascularised. In (b), the parameters relating to tip dynamics have been changed, with other parameters the same. This causes wound healing to fail in a manner reminiscent of non-healing wound pathologies. Model details are given in Pettet et al. 〚55, 56〛 This figure is reproduced with the permission of Graeme Pettet.
The work of Pettet et al. 〚55, 56〛 is the first step in an important direction for the modelling of wound healing, namely the bringing together of ideas from tumour angiogenesis and features specific to wound repair. The growth of capillaries into a wound occurs in parallel with the influx of fibroblasts and the formation of a new extracellular matrix. Pettet et al. 〚55, 56〛 include these factors in a simple way, and extensions to include features such as fibre anisotropy and the recent detailed data on fibroblast influx are natural next steps. Work of this kind would bring together models of wound angiogenesis and those of tissue remodelling. It would also enable more detailed predictions to be made concerning non-healing wounds. The key clinical importance of this wound pathology makes this a vital area for future mathematical modelling.
6 Conclusions
Theoretical models of cell biology are most effective in situations where there is a large volume of in vitro data, but a relatively poor understanding of what this data implies for the full system under study. Wound healing is a classic example of this. Specific interactions between particular growth factors or ECM components and particular cells have been studied at great length in the laboratory. The basic scientific challenge is how these numerous pieces fit together to complete the wound-healing puzzle. Theoretical models are an important tool in the response to this challenge. Unfortunately, some wounds do not heal in a timely manner or do not result in a return to functional tissue. These wounds are called chronic wounds and their treatment requires significant resources. Mathematical modelling can help in understanding what causes the different pathologies and in determining the most effective treatments.
Models have already made important contributions to the understanding of components of the healing process, and have made a number of specific biological predictions, some of which have subsequently been confirmed experimentally. But an even more exciting phase of modelling looms large. The details now being built into theoretical models raise the possibility of combining models for different components of wound healing (angiogenesis and matrix remodelling, for example). To date, these components have been treated as separate not only in models, but also in most experimental research. Therefore, the ability of theoretical research to predict how they interact promises to contribute some unexpected and important new insights into the wound healing process.
Acknowledgements
JAS was supported by an EPSRC Advanced Research Fellowship, and by Research Development Grant 107 from the Scottish Higher Education Funding Council. We thank Graeme Pettet for providing electronic versions of Fig. 3.



