1 Introduction
Frogs maintain the saline concentration of their internal medium, even when immersed in a diluted external medium, such as a fresh water pond, due to the activity of a Mg-dependent Na–K–ATPase that creates a steady transepithelial potential difference in the range of a few tens to more than a hundred mV (positive inside). This active ion-pumping system has been studied in great detail, especially by Ussing’s group 〚1,2〛, using the ventral skin of frogs mounted between two aqueous chambers filled with appropriate saline solutions. However, although, for the sake of experimental commodity, most experiments have been carried out by Ussing and followers using samples of the whole skin, it is only the epithelium layer of the skin that controls the ion exchanges and the maintaining of the electric potential difference of the skin 〚3〛. Maintaining the electrical potential of frog skin under these conditions requires sodium in the external medium. Lithium is the only ion that can be used instead 〚4〛. However, when all or part of the external sodium is replaced by lithium, the electric potential frequently oscillates 〚5–7〛, which it never does in the absence of lithium (Fig. 1). Our group has been particularly involved in the understanding of the generation of such oscillations, from both experimental and theoretical points of view 〚7–11〛. As it will be explained in section 3, a set of two ordinary differential equations were obtained to describe the dynamics of a fragment of the skin. It generates periodic oscillations. In section 4, the case of oscillations for which the amplitude fluctuates (Fig. 1b) is investigated. Section 5 gives a conclusion.
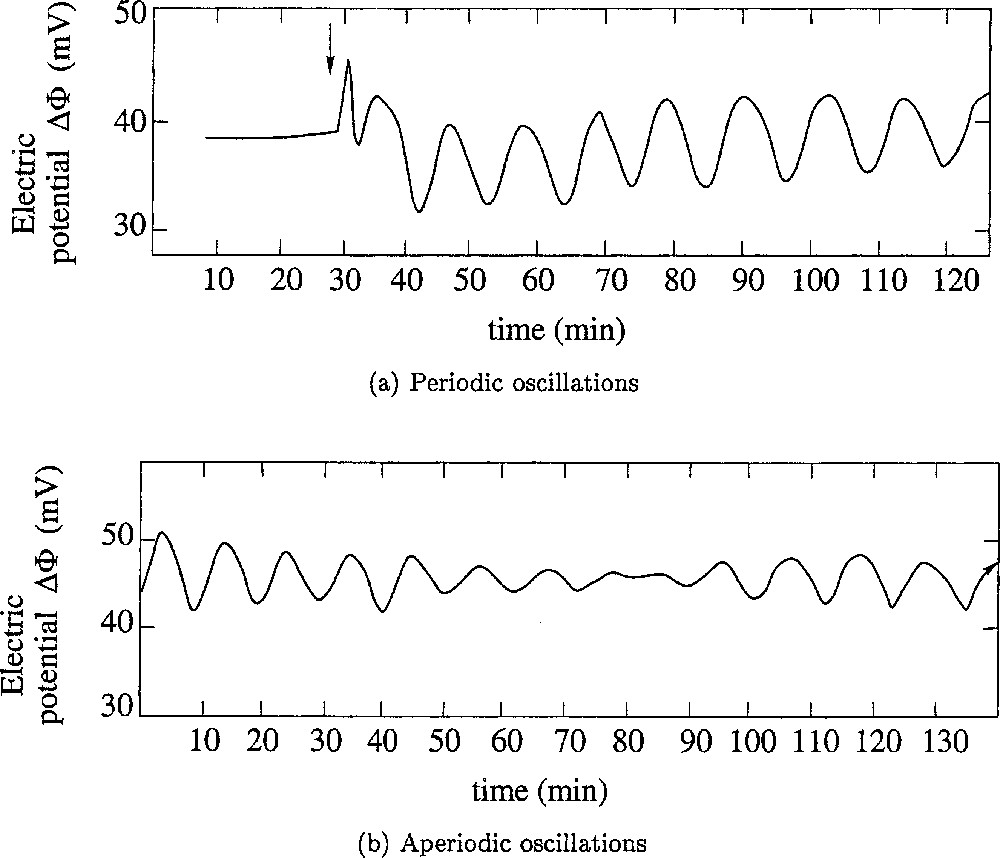
Oscillations of the transepithelial electric potential Δφ (in mV and relative to external medium). (a) Initiation of the oscillation and its stability with time. At the time indicated by the arrow, the external Ringer solution was changed for a 115 mM LiCl solution: oscillations started almost immediately, and were sustained during several hours. (b) A complex type of behaviour was sometimes observed. The oscillations seems to vanish spontaneously and start again. The shape of the oscillation curve suggests the occurrence of an interference between several individual oscillatory processes. Adapted from 〚9〛.
2 Local nature of the oscillator
The first question to be addressed was to determine whether the oscillation has a local character (that is, if it exists at the level of each individual cell or of a small group of cells of the epithelium) or if it is a property of the entire fragment of skin under study. It was technically impossible to carry out an experimental study of the oscillation at the level of a single cell or of a very small group of cells; but when studying three skin fragments, taken from the same frog skin, whose areas where 0.28, 0.8 and 2 cm2, in five successive experiments, the periods of oscillation (min) were found to be (mean ± confidence interval) 6.1 ± 1.4, 6.0 ± 0.9 and 6.3 ± 1.0, respectively, which means that the period of oscillation does not depend significantly on the area of skin under study 〚9〛. In another series of experiments, using subcompartmentalised chambers, it has been possible to study simultaneously different parts of a single skin subjected to identical ionic conditions 〚9〛. It turned out that the different parts of the skin exhibited oscillations of their electric potential difference, but these oscillations were out of phase with each other; moreover, the amplitude of these oscillations and the time during which each of them was sustained varied from one zone of the skin to another. These findings, plus the fact that the processes involved in the maintaining of the skin potential (ion pumping and passive transmembrane ion diffusion) exist at the cellular level, suggest that the skin behaves as a ‘mosaic’ of local oscillators (each oscillating in its own way or perhaps not oscillating at all). This, however, raises the problem of understanding how all the local oscillators are synchronised with one another in order to produce a visible electric oscillation of the whole skin fragment under consideration.
Interpreting the oscillation of the electric potential of the frog skin thus has to be addressed in two steps: (i) functioning of the local oscillator and (ii) synchronisation of local oscillators.
3 Characterisation of the local oscillator
3.1 Summarising the experimental observations
Our group 〚7,9〛 has shown experimentally that (i) when no transepithelial potential is imposed, sustained oscillations with a period of about 10 min are maintained for several hours, (ii) an oscillation of the Na+ influx accompanies the electric oscillation (the two oscillations have approximately the same period but are not in phase), (iii) under conditions of imposed potential the transepithelial electric current has damped oscillations, (iv) the shape of the oscillations in potential is quite variable (from almost sinusoidal to very complex), (v) theophyllin (which induces an accumulation of cyclic AMP within the cells) promotes a significant decrease in the mean electric potential of the skin, but does not affect the characteristics of the oscillation very much, (vi) the osmotic pressure has little effect on the oscillation and (vii) important factors influencing the oscillations include temperature, the permeability of the external membrane to lithium and the potassium concentration in the internal medium.
3.2 Modelling the epithelium
A body of evidence obtained by others and cited in Lassalles et al. 〚10〛 demonstrates that the epithelium separating the external, E, and internal, I, solutions may be modelled as follows (Fig. 2). It is made of a few cell layers with two main cellular compartments, C1 and C2. The membrane, (a) is relatively permeable to Na+ and Li+ at the external face of the epithelium, whilst it is almost impermeable to K+. The membrane, (b), between compartments C1 and C2 is permeable to K+, but not to Na+, and contains the Na–K–ATPase, pumping sodium and (less efficiently) lithium from C1 to C2 and pumping potassium from C2 to C1. When this active pump is fully efficient (Na+ pumping in the absence of any inhibitor), the first cellular layer is enough to pump out practically all of the Na+, but, when it is not fully efficient (Li+ pumping or Na+ pumping in the presence of an inhibitor), the remaining ions diffuse to the other cell layers, which will therefore contribute to their active extrusion; as a consequence, it is likely that the overall transepithelial flux densities obtained for Li+ and Na+ are not too different from each other. The face, (c), between epithelium and internal medium is not an actual membrane, but may be considered rather as a non-selective diffusive barrier.
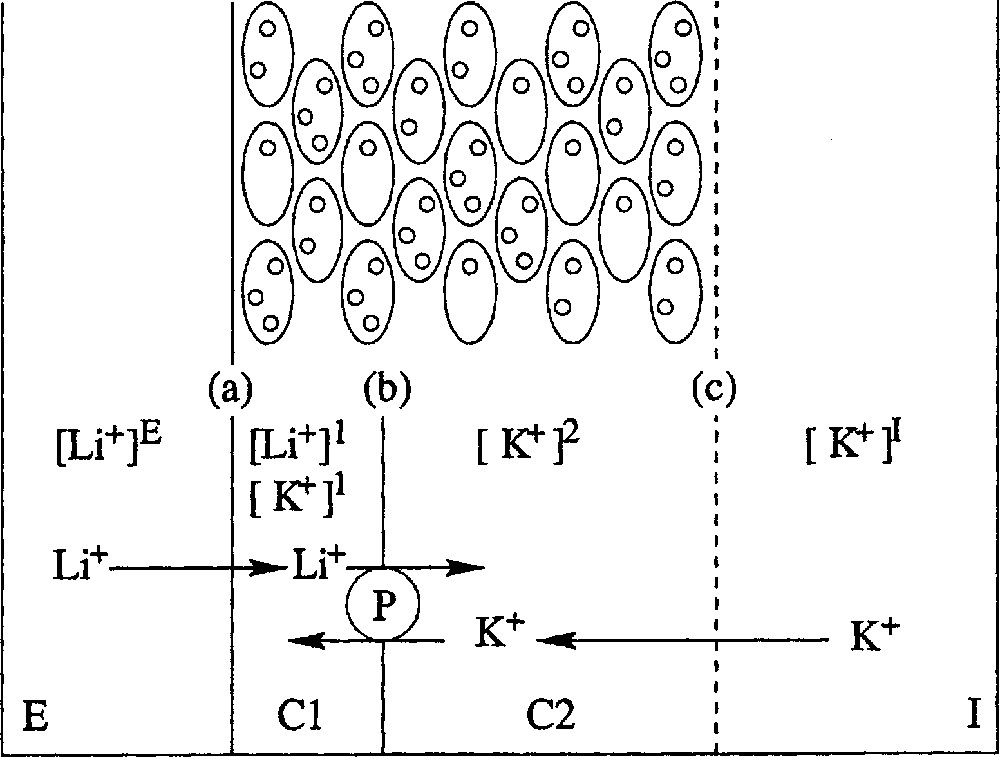
Modelling frog skin epithelium. Top: schematic representation of the cellular structure of frog skin epithelium, mounted between two aqueous, saline solutions, E and I. Bottom: the epithelium model for ionic exchanges. The frog epithelium is modelled as corresponding to two compartments C1 and C2 with three barriers, (a) between E and C1, (b) between C1 and C2 and (c) between C2 and I. Symbol 〚x〛j stands for concentration of cation x in compartment j. The Na–K–ATPase, P, pumps actively Li+ from C1 to C2 and K+ from C2 to C1.
3.3 The local-oscillator model
Combining the experimental observations relative to the electric oscillations of the frog skin (section 3.1) with the epithelium model (section 3.2), it appears 〚8,10〛 that the set of variables involved in the system under study may be reduced to the following set of main variables: the concentration of Li+ in compartment C1, 〚Li+〛1, and that of K+ in compartment C2, 〚K+〛2, the characteristic times, τ1 and τ2, defined as corresponding to variations of the Li+ concentration in C1 and variations of the K+ concentration in C2, the volumes ν1 and ν2 of compartments C1 and C2 per unit surface of epithelium, some permeability coefficients, PbK, PcK and PaLi, of the interfaces (a, b or c) for the ions K+ and Li+, and two parameters, ρ and μ, representing the relative importance of the active to the passive fluxes of Li+ and K+, respectively.
After a normalisation of the variables 〚8〛, a set of two ordinary differential equations is obtained:
| 1 |

Sustained periodic oscillations generated by the local model for the epithelium of a frog skin under effect of lithium (α = 0.2, ρ = 8.0, μ = 10.0, β = 5.0, xm = 0.14 and Kc = 0.1).
It proved impossible 〚10〛 to adjust the numerical simulations (Fig. 3) to the observed characteristics (Fig. 1a) of the oscillatory process, unless the model had the following well-defined properties. ν1 andν2, the volumes of compartments C1 and C2 per unit surface of epithelium, obey the relation ν1/ν2⪡1, i.e. compartment C2 has to be much larger than compartment C1. Two conflicting hypotheses (cited in Lassalles et al. 〚10〛) have been proposed in the literature with regard to the exact nature of compartments C1 and C2. According to the first hypothesis, C1 corresponds to most of the cytoplasmic volume and C2 is restricted to a few endoplasmic cisternae (i.e. C2 is much smaller than C1). According to the second hypothesis, compartment C1 corresponds to a few cytoplasmic vacuoles transporting Na+ (and Li+) and compartment C2 is part or all of the intercellular spaces and possibly some endoplasmic cisternae (i.e. C2 is much larger than C1). Our finding that an oscillatory behaviour can be met only when C2/C1⩾1 thus supports the second hypothesis, while it rules out the first one, which also means that most of the cell cytoplasm would remain inactive in Na+ (or Li+) transport. The ratio of the characteristic times, τ1 and τ2 (corresponding to Li+ modifications in C1 and K+ modifications in C2) obeys the relation 0<τ1/τ2<1 with The parameters, ρ and μ, representing the relative importance of the active to the passive fluxes of Li+ and K+, respectively, must be such that ρ⪢1 and μ⪢1, with (i.e. ρ and μ are of the same order of magnitude) in order to have oscillations. For similar reasons, the permeability coefficients of interfaces a, b and c for ions K+ and Li+ must be such that Pbk/PcK⪡1 and PaLi/PcK⪡1. These conditions have been identified from the model.
4 Synchronisation of the local oscillations
4.1 Summarising the experimental study
In a number of experiments 〚8,9〛, a frog skin was divided into two parts, each mounted between two chambers containing the same internal medium (Ringer solution) and the same external medium (LiCl solution), in order to induce oscillations of the electric potential difference. Electrical bridges were prepared by filling plastic catheters with a gelose gel enriched with mineral salts, their electric resistance, Rc, depending on the saline concentration of the gel. When a single bridge was used (either between the two internal or between the two external solutions), synchronisation never occurred; the two skin fragments continued oscillating independently from each other. When two bridges were used, for connecting the internal solutions with each other on the one hand and the external solutions with each other on the other hand, and when these bridges were with a relatively low electric resistance synchronisation occurred almost immediately. When the electric resistance of the bridges was increased up to several kΩ, the two epithelium fragments again oscillated independently from each other. Moreover, when an electric current was imposed to an oscillating epithelium, using an external electrical source, this tended to damp the oscillation. These data render it very unlikely that synchronisation may be due to a diffusion–reaction process, but they are very consistent with the occurrence of electrical coupling.
4.2 Theoretical interpretation and numerical simulations
Electric potentials pass mainly through internal and external electrolytes. They induce fluctuations of the concentration within the cells 〚8〛. The epithelium is thus considered like a huge cell with a potential ϕ that tends to drive the current in the cell j, with a lithium concentration xj, a potential ϕj and a current Ij. This current induces an additional diffusion flux of lithium through the membrane. In the first equation of the local model (1), a diffusion term within the cell, 1 – xj, is thus added. The term where is the averaged concentration over all the cells, designates the electrical coupling between the epithelium fragments.
The model for n cells thus reads as
| 3 |

Dependence of the main frequency of the local oscillator on the αj-value. The other control parameters are equal to those used in Fig. 3. Thus, varying the values of the parameters αj is sufficient to reproduce the distribution of periods observed in cells within a skin.
The critical value δc of the coupling parameter δ for which synchronisation occurs is estimated to be equal to 0.4 from the experimental data. The critical value observed from numerical simulations is around 0.1145 when four cells are taken into account (Fig. 5). Obviously, the simplifications which have been applied forbid quantitative simulations, but it has been observed that this value increases with the number of cells used for the simulations. For instance, for n = 25, the critical value is approximatively equal to 0.2315. Consequently, increasing the number n of oscillators improves the accuracy of the model. Nevertheless, we observed that the nature of the behaviour is not dependent on that number. Indeed, the synchronisation always occurs according to the same scenario. Only the power spectrum becomes more complicated, but the global behaviour remains a quasi-periodic one, with a dimensionality that mainly depends on the number of significantly different frequences associated with the oscillators. Such a feature results directly from the special form of the coupling between cells. In particular, the fact that the coupling is global and does not result from interactions with nearest neighbours strongly constraints the dynamics. Investigating the nature of synchronisation for a spatially explicit coupling using techniques as reviewed by Pikovsky et al. 〚12〛 is postponed for future works. We will thus describe the nature of the synchronisation only using four cells.
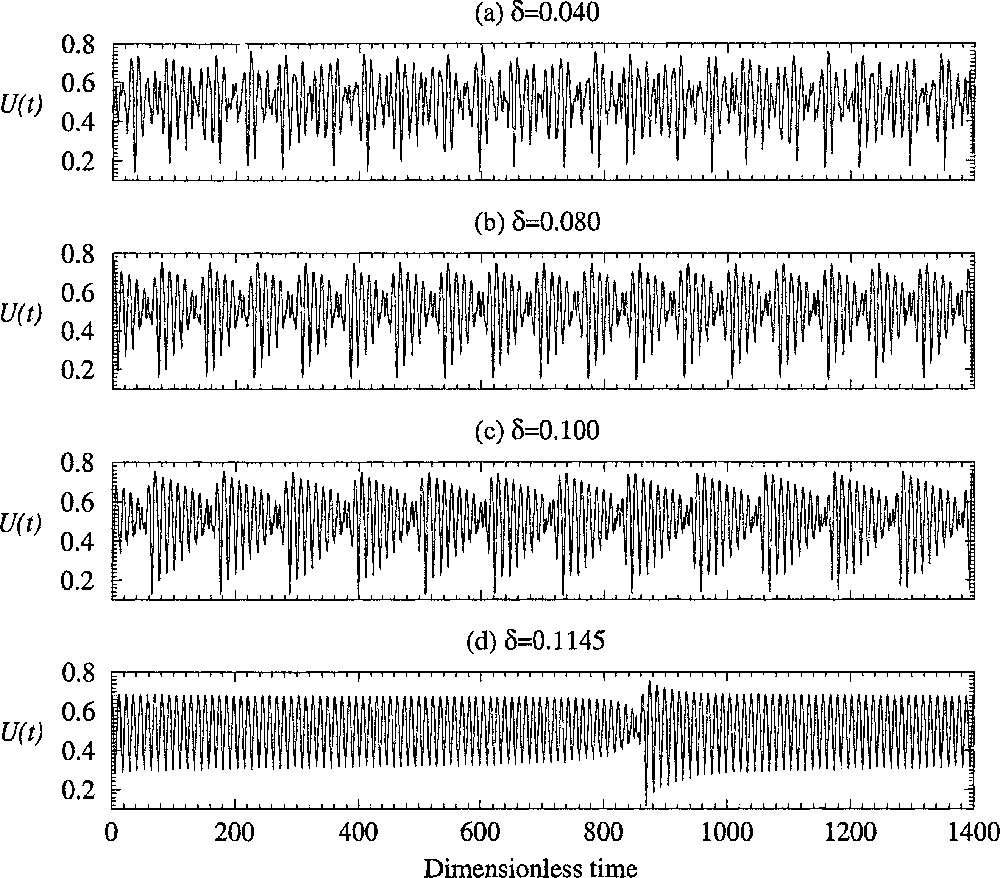
Progressive synchronisation of the different regions of the epithelium versus the coupling constant δ. Four cells are used with parameter α1=0.24, α2=0.14, α3=0.26 and α4=0.10, respectively. The other control parameters are equal to those used in Fig. 3.
In fact, for a given n, such a synchronisation progressively appears when the coupling δ is increased. The evolution of the asymptotic behaviour observed for different values of the coupling constant δ is shown in Fig. 5. When the coupling parameter δ is small, the evolution of the averaged concentration of lithium U seems to be non-periodic (Fig. 5a). Note that in our experiments it is the potential of the whole skin which is measured. Consequently, the variable related to the physical quantity measured is the normalised concentration of Li+ averaged over the four cells. Variables xi and yi (i = 1, ..., 4) cannot be simultaneously measured. When the coupling δ is increased, the asymptotic behaviour becomes more singular (Fig. 5b and c), and when δ is very close to the critical values δc, the behaviour becomes almost periodic during long time intervals (Fig. 5d). Between these so-called laminar phases, bursts, during which the amplitude of oscillation fluctuates significantly, are observed (Fig. 5d). When δ is greater than δc, no burst is observed anymore and the asymptotic behaviour is periodic, as suggested by the experimental data shown in Fig. 1a. Note that what is relevant is the number of cells with different main frequency fj. Indeed, if many cells have the same frequency, the critical value δc decreases.
In order to characterise the transition from the aperiodic behaviours to the periodic ones, it may be convenient to compute power spectra from the normalised concentrations U of Li+ averaged over the four cells (Fig. 6). In the power spectra computed for δ = 0.040, three main frequencies are identified (Fig. 6a). Their values are reported in Table 1. It may seen surprising that only three frequencies are identified, since four cells are involved in our simulations. In fact, two αj values are very close, namely α1=0.24 and α3=0.26. Moreover, the dependence of the frequency on the αj-values around 0.25 is very weak (Fig. 4). Consequently, two local oscillators have almost the same eigenfrequency. In the spectrum shown in Fig. 6a, any frequency fk corresponds to a linear combination between these three frequencies, according to:
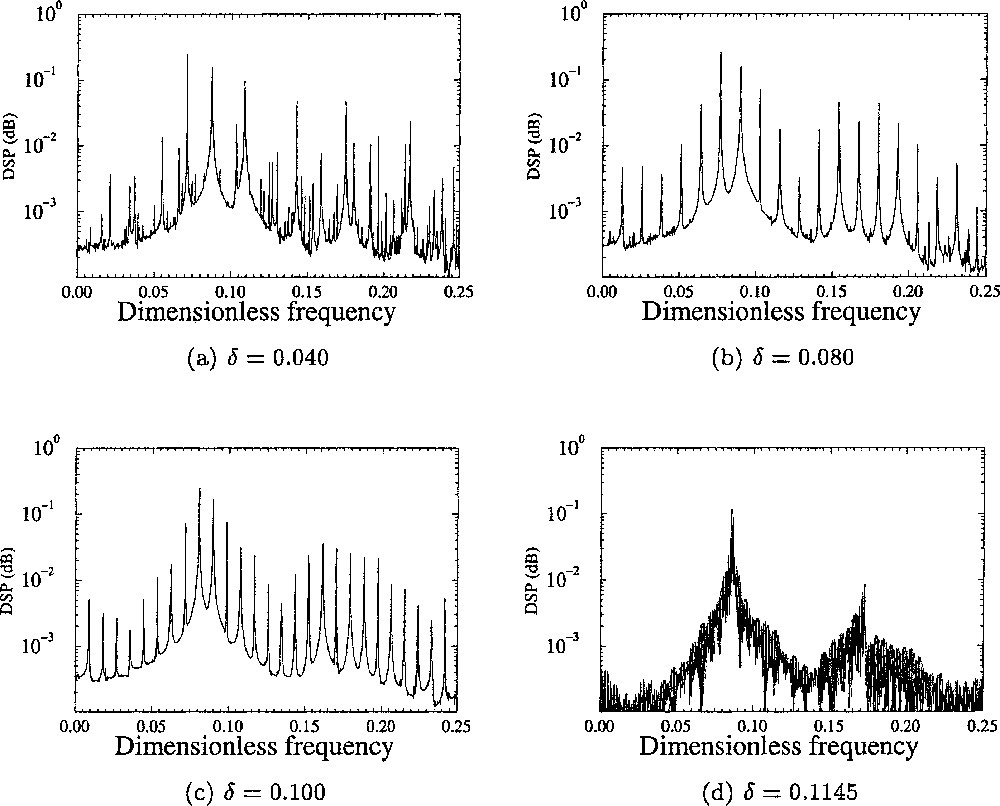
Power spectra computed from the normalised concentrations x̄ of Li+ averaged over the four cells for different values of the coupling constant δ.
Values of the three main frequencies identified in the power spectrum for different values of δ when four cells are involved as in Fig. 5.
| δ | f 1 | f 2 | f 3 |
| 0.040 | 0.072 | 0.088 | 0.109 |
| 0.080 | 0.077 | 0.090 | 0.103 |
| 0.100 | 0.081 | 0.090 | 0.099 |
| 0.1145 | – | 0.086 | – |
| 4 |
When the coupling δ is increased, the three frequencies converge around the averaged frequency (Table 1). As a consequence, the power spectrum becomes more regular. When δ is very close to the critical value δc, a single frequency is recovered (Fig. 6d), as usually observed for periodic oscillations. It is thus important to characterise how the torus T3 evolves when δ is increased. The first step is to investigate the dynamics in the phase space.
Since we are mainly concerned with characterising the behaviour of the whole skin, that is, the global behaviour of the n cells, only the averaged concentration U may be used to investigate the underlying dynamics. One of the most interesting results from the nonlinear dynamical system theory is that it is possible to reconstruct a phase portrait, which is equivalent to the original one, using delay coordinates derived from a single time series 〚14〛. Delay coordinates correspond to a set of independent coordinates derived from , as:
| 5 |
A projection of the phase portrait reconstructed from U and spanned by where the time delay τ is estimated by a visual inspection, is displayed in Fig. 7. Such a visual inspection is guided by the fact that the phase portrait is confined along the first bisecting line when the time delay τ is too small, while it is confined along the second bisecting line and too unfolded when τ is too large 〚20〛. Note that such a phase portrait does not correspond to a chaotic behaviour for which a broad band spectrum is required. The main departure between a chaotic behaviour and a quasi-periodic behaviour is the lack of sensitivity to initial conditions in the latter case.

Phase portrait of the quasi-periodic regime generated by the global model with four cells with a constant δ equal to 0.100. The other control parameters are equal to those used in Fig. 5.
The second step in a global analysis is to compute a first-return map to a Poincaré section. Roughly, a Poincaré section is the set of the intersections between the trajectory in the phase space with a plane which is never tangent to the trajectory. In the case of the phase portrait displayed in Fig. 7, the Poincaré section is defined by the set
| 6 |
The first-return map is then computed by plotting, for instance, the Yn+1-coordinate of the (n + 1)th intersection versus the Yn-coordinate of the nth intersection. For δ = 0.1130, i.e. for a value quite close to the critical value δc, the first-return map looks like a closed curve (Fig. 8). In fact, the first-return map is not a closed curve in Fig. 8, but it would be if a much longer time series were used (a full day of computations was already required for Fig. 8). Such a long integration duration is required because the trajectory spends a lot of time in the regions where the first-return map is tangent to the bisecting line. This is why the departure from periodic oscillations is very weak and why the embedding dimension has been found to be equal to 2 (as discussed above). Note that such a closed curve for a first-return map is a signature of a torus that cannot be embedded within a 2D phase space.
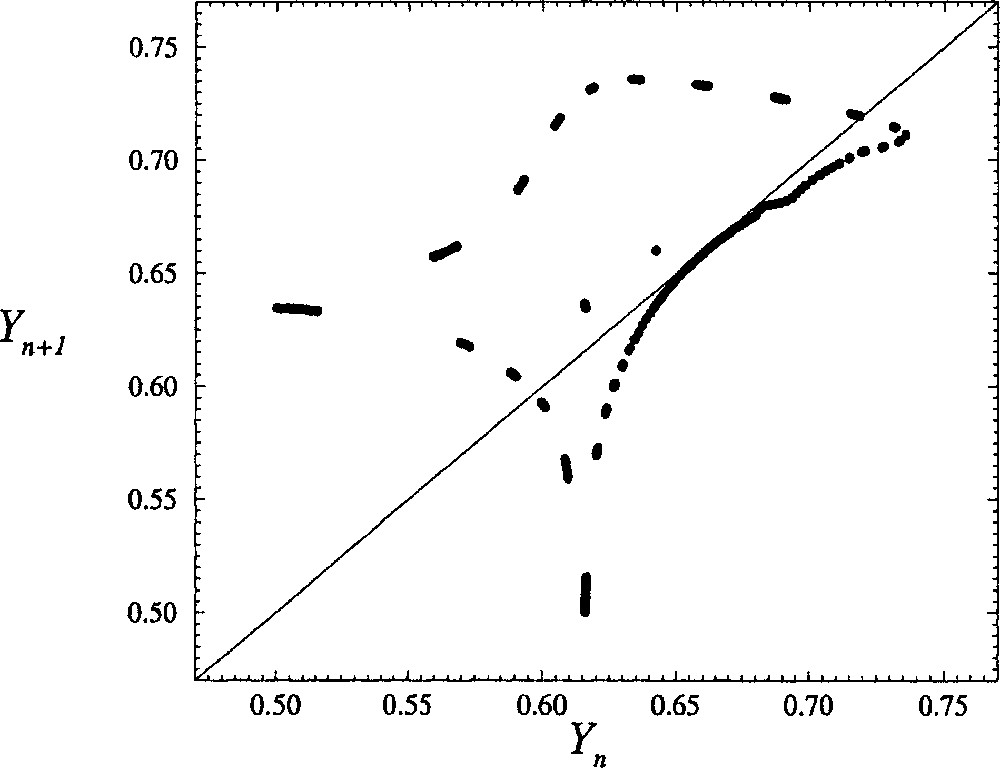
First-return map to a Poincaré section of the reconstructed phase portrait shown in Fig. 7 for a coupling constant δ equal to 0.113. The other control parameters are those used for Fig. 5.
In fact, the bifurcation occurs when the first-return map reaches the bisecting line. After that, the trajectory spends an infinite time at the point where the map touches the bisecting line. In that case, and a periodic orbit is observed. The tangent bifurcation which thus occurs destroys the torus, which is replaced with a stable periodic orbit. The tangent bifurcation is necessarily accompanied with intermittencies between laminar phases during which the behaviour is nearly periodic and bursts associated with significant amplitude fluctuations (Fig. 9). The most often observed intermittencies were introduced by Pomeau and Manneville 〚21〛. The very interesting feature of these new simulations is that during the bursts, the amplitude evolves significantly as it was observed in experiments (Fig. 1b). Indeed, many experimental observations were done in the early 80’s, in which the amplitude of oscillations was constant for a significant time interval and, abruptely, amplitude fluctuations were observed during a relatively short time interval. Such observations were not published by that time since no explanation was available.
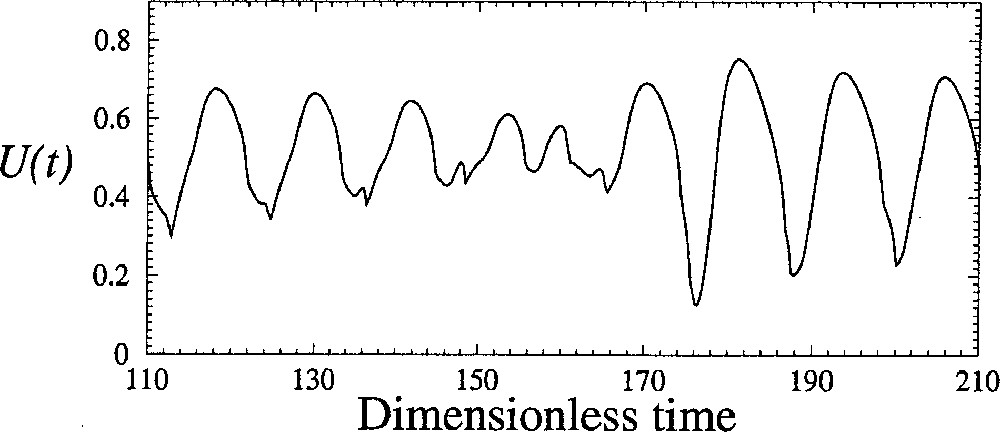
Amplitude fluctuations during bursts between two laminar phases. Numerical simulations with the four-cell models for δ = 0.1145.
5 Conclusion
The model built from an assumption quite simple about the action of the lithium explains, at least qualitatively, different experimental observations. In particular, it allows reproducing the existence of a critical value for the coupling constant beyond which all the cells of the whole skin are synchronised. It describes a situation where the pumping of a charged substance, associated with a non-linear mechanism, allows synchronising a collection of local oscillators without any hormonal action. By using a global analysis in a phase space reconstructed with the delay coordinates, the progressive synchronisation as a function of the coupling constant δ has been identified. It arises through a tangent bifurcation and leads to quasi-periodic behaviours, with amplitude fluctuations which are very characteristic of intermittencies.
Hence, increasing the complexity of the behaviour of the living frog-skin system by inducing electric oscillations via lithium addition to the external solution provided information on this system that could not have been provided by a conventional, reductionist approach. This may be the basis for the introduction of ‘complexification’, as opposed to reductionism, as a method for studying those properties of a complex system that are destroyed when adopting the conventional, reductive, biochemical approaches.


