1 Introduction
The central importance of feedback circuits in biological systems has been very clear since the first elucidation of molecular mechanisms they rely on 〚1〛. But feedback is sometimes perceived as a means for auto-correction of a system, to ensure its stability in the neighbourhood of a specific set of values of parameters, these values being the ones at which the system operates in a satisfactory manner. The kind of feedback associated to such a stabilising effect is negative feedback; positive feedback, exemplified by the singing of audio amplifiers, is sometimes likened to a problematic side-effect in certain situations.
It is our purpose in this paper to prove this view to be incomplete. First, we will show that negative feedback can be destabilising for certain systems, and positive feedback stabilising, where stability applies to steady states of the systems. We will then discuss the role of positive feedback in information processing, and the role of negative feedback in alleviating the dependency of the global behaviour of a system on the specific values of certain kinetic parameters, i.e. in making the system robust.
2 Preliminaries
This section provides the rigorous mathematical framework for the following discussion. It can be skipped by readers not interested in the mathematical detail. Our discussion applies to autonomous differential systems, whose mathematical formulation is as follows: we consider an open domain , a function , a real interval L, and a function such that
Vector x describes the state of the system, and vector gives the direction in which the system will evolve when it starts at point x of its state space. Points where F vanishes, and where the system maintains an equilibrium, are stationary states. We suppose that no stationary state of F is degenerate (which implies that stationary states are isolated). Let be the Jacobian matrix of F at x∈D. can be considered to define an oriented, weighted interaction graph on the set , in which an arc points from i to j if and only if (i.e. if variable j depends on variable i), the associated weight being (reciprocally, by reversing this process, a unique matrix M is associated to a weighted interaction-graph, by setting the value of Mi,j to the weight of the arc pointing from j to i if it exists, and 0 if it does not exist). There is a circuit involving nodes if and only if , where ik+1=i1. A same node is not allowed to appear more than once in the graph circuits considered in the following (i.e. in the previous example, ∀p, s.t. p≠q, ip≠iq ); circuits comprising a single arc (from a vertex to itself) are allowed, and correspond to diagonal, autocatalysis term in the Jacobian, and a variable exerting a direct influence (positive or negative) on itself. The sign of a circuit (positive or negative) is defined as the sign of the product of the weights of the associated arcs; i.e. a circuit is negative if it has an odd number of negative interactions, and positive otherwise. Finally, the weight of a circuit is defined as the product of the weights of its arcs.
A variable is part of a feedback circuit if its corresponding vertex in the interaction graph is part of at least one circuit; if there is such a positive (respectively negative) circuit, the variable is under positive (respectively negative) feedback control. It is possible for a variable to be part of a negative and a positive feedback circuit at the same time.
It should be noted that we consider general feedback circuits whose length can be greater than 1, and that the sign of the circuit is not necessarily the same as the sign of the interaction that links a later part of a pathway to the earlier part (for example, if one considers a biochemical synthesis pathway, the end-product P can inhibit an early enzyme E of the pathway, as in models considered in 〚2〛, but this inhibition can still be part of a positive feedback circuit, if E itself inhibits another enzyme that leads to the creation of P).
Note also that, except in the trivial linear case (which does not give rise to interesting behaviours such as non-degenerate multistationarity), the Jacobian matrix is not constant within the domain D; it is thus possible, and likely, that the weights and the signs of the circuits are not constant, and even that the structure of the interaction graph itself is not constant. Note also that if there are two distinct mechanisms by which a variable depends upon another (these mechanisms possibly being antagonistic), it is the sum of the corresponding derivatives which will appear in the relevant Jacobian term. For example, if a protein whose concentration corresponds to xi exerts a positive but saturable effect on its own synthesis (positive autocatalysis, or auto-activation), and undergoes exponential decay (negative autocatalysis, or auto-inhibition), such that
We will call stationary states stable if and only if they are locally asymptotically stable, i.e. if and only if all eigenvalues of the Jacobian matrix have strictly negative real parts. Due to the strong dependency of the characteristic polynomial of a matrix on its circuit structure, stability exclusively depends on interactions which are part of a feedback circuit; it is only the weight of a circuit which is important (not the weights of its particular elements), because they only appear in the development of the determinant giving the characteristic polynomial. In the following, we will consider stability of dynamical systems around steady states.
While studying the effect of feedback circuits on a particular system, one is confronted with the problem that changes in system parameters lead to changes in weights of feedback circuits at given points of the state space, but stationary states are also displaced as a result of the change of parameter values, and the weight of feedback circuits at the stationary states is thus not always readily controllable. It can thus be that increasing the strength of the interactions in the equations governing a system does not lead to increased feedback circuit weights at the stationary states of the system.
3 Feedback and stability
3.1 Negative feedback can be destabilising
It is quite obvious that the subjection of every variable of a system to negative feedback is mandatory for the stable maintenance of a stationary state. Were a system under no feedback-control, it would ‘drift away’ according to varying inputs or random fluctuations of its state variables. Were a system under exclusive positive feedback-control, it would of course be unstable. However, negative feedback can lead to expanding oscillations, a source of instability. Indeed, a linear system of three or more variables under control of a single negative feedback circuit, as pictured in Fig. 1 (as detailed in section 2, to this graph corresponds a unique matrix, which defines the dynamics of the linear system, with zero as an initial condition), cannot be stable around the origin, whatever the weight of the feedback circuit (the proof is direct, based on the study of the characteristic polynomial). The critical length of a feedback circuit is 2: negative feedback involving one or two state variables provides stability per se to an isolated linear system, while it does not when longer circuits are involved. Intuitively, the corrections to the variations of a variable come ‘too late’, and give rise to an ever-expanding series of ‘over-corrections’, a phenomenon commonly known as hunting. Of course, real-world systems oscillations do no keep expanding, because these systems are not linear and there is a saturation in synthesis rates (such non-linearities are actually necessary for the occurrence of asymptotically-stable limit cycles). Such long negative-feedback circuits seem to be the basis for cicardian clocks 〚3〛 and mitotic oscillations 〚4〛, and it has been shown that they could generate oscillations in MAP-kinase cascades 〚5〛; a model system for a biological clock 〚6〛, which has been implemented in the prokaroyte E. coli, oscillates only when the weight of the negative feedback circuit is strong enough (Fig. 1b in 〚6〛). The necessity of the presence of a negative feedback circuit (of length strictly greater than 1) in the generation of oscillations resulting in a stable limit-cycle has in fact already been shown in 〚7〛 and 〚8〛 (boolean systems whose feedback circuits are all negative have no steady states, but stable cyclic trajectories 〚9〛).
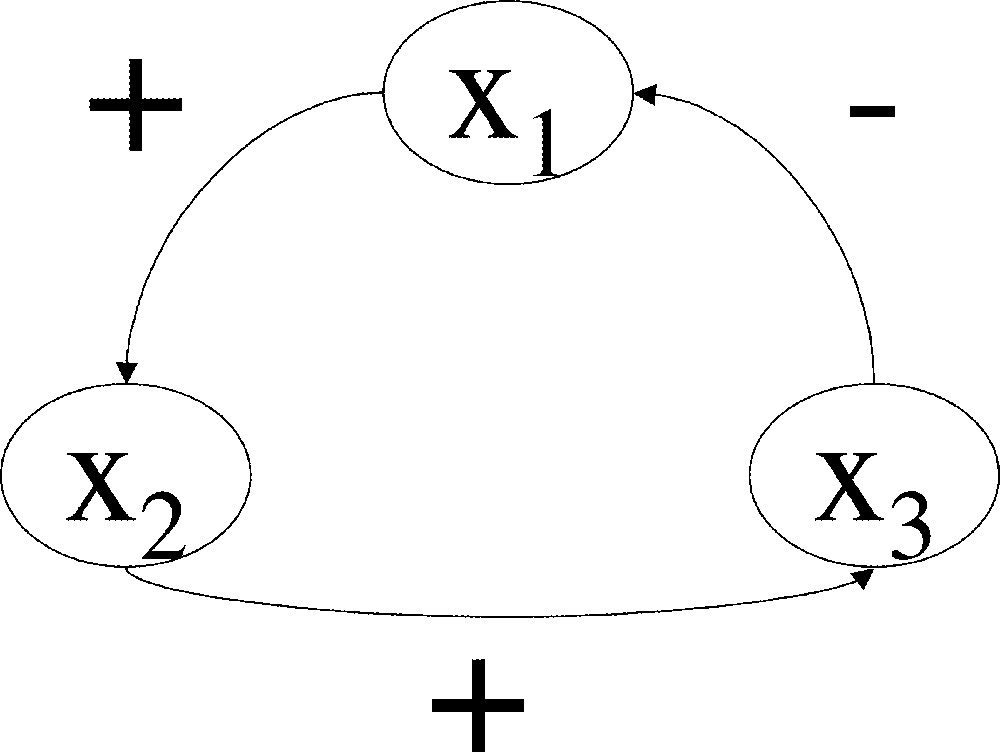
Interaction graph associated to a three-dimensional matrix possessing a single, negative feedback circuit; if such a matrix is the Jacobian matrix of a differential system at a stationary state, the stationary state is unstable.
3.2 Positive feedback can be stabilising
On the other hand, positive feedback can be necessary for a system to preserve its stability. Again we will illustrate this point by two examples, a linear one, for which we do not have generating biological kinetic equations at hand, and one with a more straightforward biological interpretation.
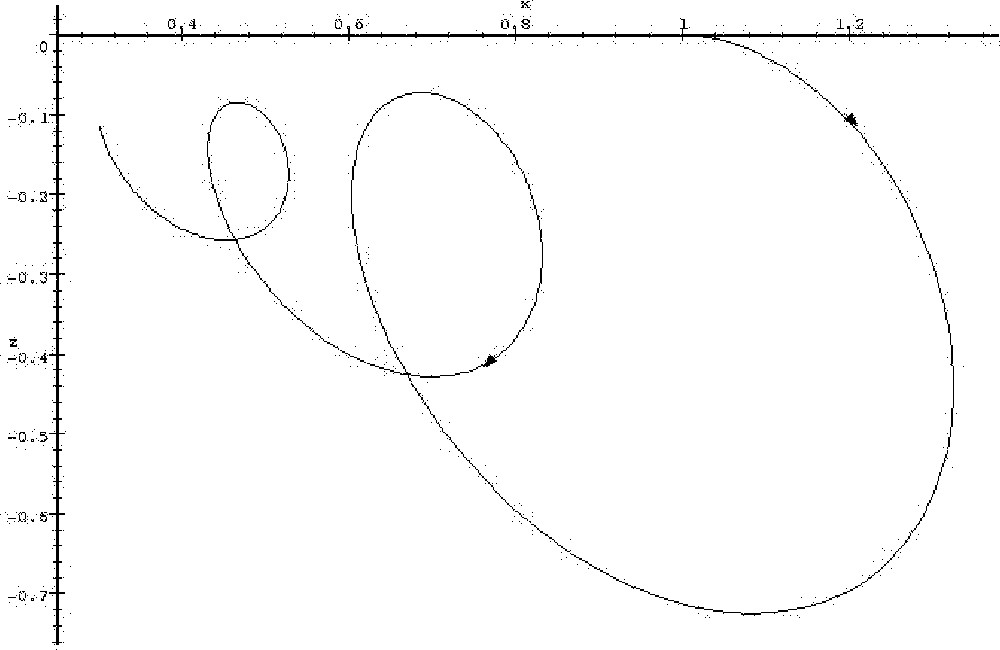
Let us first consider the linear system with three variables x, y, z, whose interaction graph is constant, and is the one shown in Fig. 2 (again, to this graph corresponds a unique linear system with 0 as initial condition). Such a system could arise from the linearisation of biological kinetic equations around a stationary state. The steady state (0,0,0) of this system is stable with the proposed coefficients; however, if the positive feedback on variable z is diminished by a quantity equal at least to 1 (or replaced by negative feedback), other coefficients remaining unmodified, the system becomes unstable. The salient feature of this system is that there is one variable, x, which is under control of a negative feedback circuit of length greater than 2, while other variables are under control of negative feedback circuits of length equal to or less than 2. Intuitively, if the positive feedback on variable z is diminished, the propagation of the ‘error reading’ on x will be too damped for the correction to be effective. Fig. 3 and 4 show parametric timeplots of variables x and z after a perturbation on x, for two different values of z autocatalysis. When the autocatalysis is high enough (Fig. 3), the system goes back to its steady state (0,0,0) in an oscillatory fashion. But when the autocatalysis coefficient is lowered by 1 unit, z does not stay sufficiently negative to bring x back to 0, and the system diverges (Fig. 4): when z has become sufficiently negative, x starts decreasing (first vertical tangent on the plot, starting from the origin), but z then starts going back to 0 (horizontal tangent), and x finally sets on an ever-increasing course (starting from the second vertical tangent). In contrast, sufficient auto-catalysis of z allows a more persistantly negative value of z: even though a decrease in x also causes z to go back toward zero after some time, this time interval is sufficiently great for x to have decreased by a sufficient amount by the time it increases again (and thus causes z to go back toward negative values), for the process to converge.
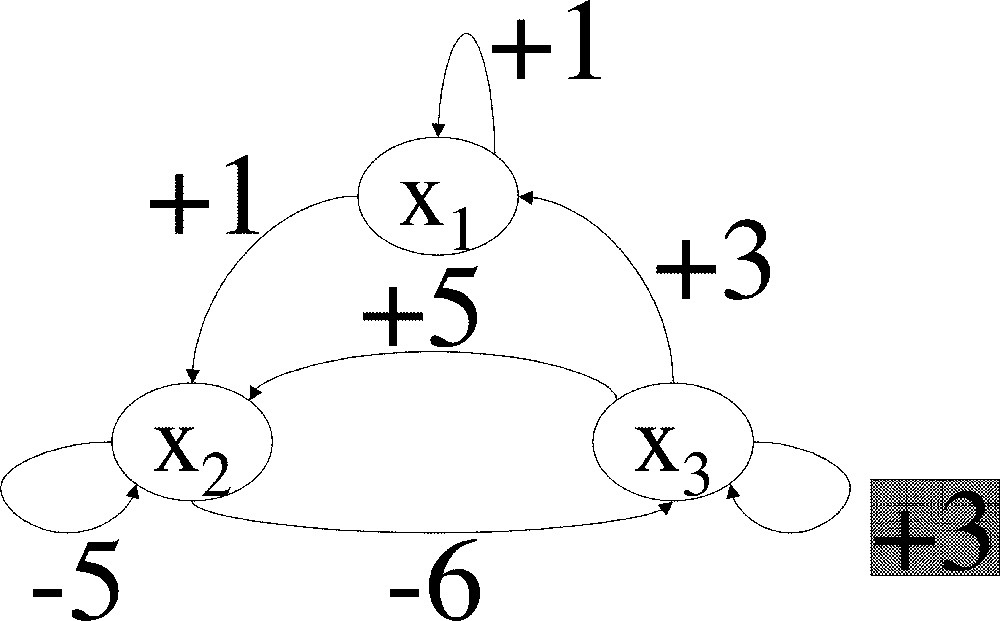
Example of a graph of a Jacobian matrix in which, other things being equal, a positive autocatalysis coefficient (highlighted in the figure) cannot be diminished by a quantity equal at least to 1, without the associated system becoming unstable.
Trajectory of the linear system whose matrix is given by the interaction graph in Figure 2, with initial conditions x=1, y=0, z=0. Arrows mark the direction of evolution of the system. The system converges to 0.

Trajectory of the linear system whose matrix is given by the interaction graph in Fig. 2; the highlighted coefficient being diminished by one, with initial conditions x=1, y=0, z=0. The arrow marks the direction of evolution of the system. The system diverges.
Another example is the following 3-dimensional system. Species and their concentrations are denoted in the same way, by x, y, z. A nefarious biochemical species x is supposed to promote its own synthesis by an enzyme normally serving other purposes, following Michaelis kinetics. The presence of x induces the transcription of an mRNA species y, following the same kinetics. Finally, protein z, translated from mRNA y, can competitively inhibit the auto-promoted creation of x, as well as the expression of its own mRNA y.
An important feature of protein z is that it activates its own translation from mRNA y, with a maximal speed . All three entities are supposed to undergo exponential decay, and translation as well as transcription are supposed to be leaky. The corresponding equations are the following, for a generic choice of parameters (leakage in mRNA and protein synthesis is chosen to be small compared to induced synthesis, and x undergoes decay that is slow compared to its synthesis):
Were there no leakage in y transcription, the only steady state for which x=0 would be x=y=z=0, and would be unstable.
This system possesses a steady state for x=0 and y=0.1, and z given by a quadratic equation which always has a positive root. A bifurcation study using the xppaut program 〚10〛 shows that the steady state with x=0 and z>0 is stable if and only if a>97.4, i.e. if and only if the positive autocatalysis of z is sufficiently strong. If not, small quantities of x are amplified before z can exert its repressing effect. Fig. 5 shows the response of the system to a small perturbation in x, for a = 100, starting from the steady state with x=0 and z>0: z increases sharply, and the system then returns to 0. Fig. 6 shows the response of the system for a=50, also starting from the steady state with x=0 and z>0: the rise in z is not as sharp, and the system does not go back to 0. There is an important difference between the two responses around the region of the plots where t = 0: while for a=100 the evolution of z is markedly quicker than the evolution of x (the parametric curve has a vertical tangent for t = 0), when a=50 the opposite is true (the parametric curve has a flat tangent for t = 0). Intuitively, in the case of a stable steady state, z rises quickly enough to repress x ‘before it is too late’. Note that, in general, increasing parameters involved in positive feedback circuits does not necessarily lead to more positive weights of feedback circuits at stationary states, but to more positive weights at precise points of the state space (because the location of the stationary states is generally altered when the parameters of the system are changed).
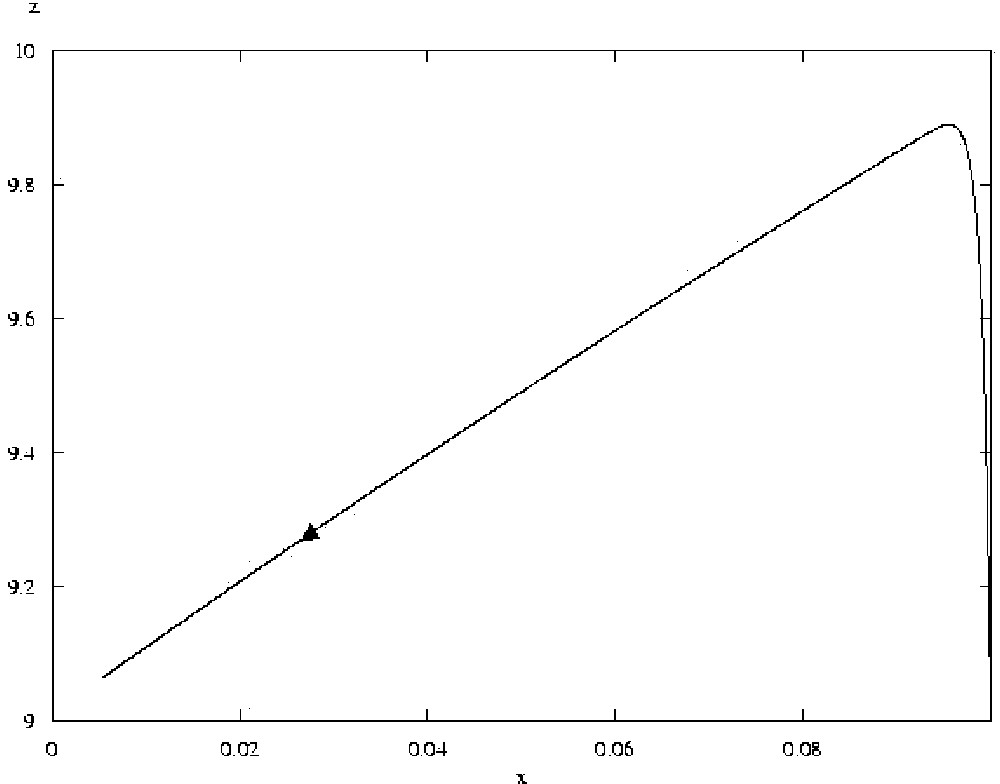
Trajectory of system 2, for a=100, with initial conditions x=0.1, y=0.1, z=9.1 (the value of x being thus slightly increased from the steady state). The arrow marks the direction of evolution of the system. After a sharp increase in z, the system converges back to its steady state where x=0.
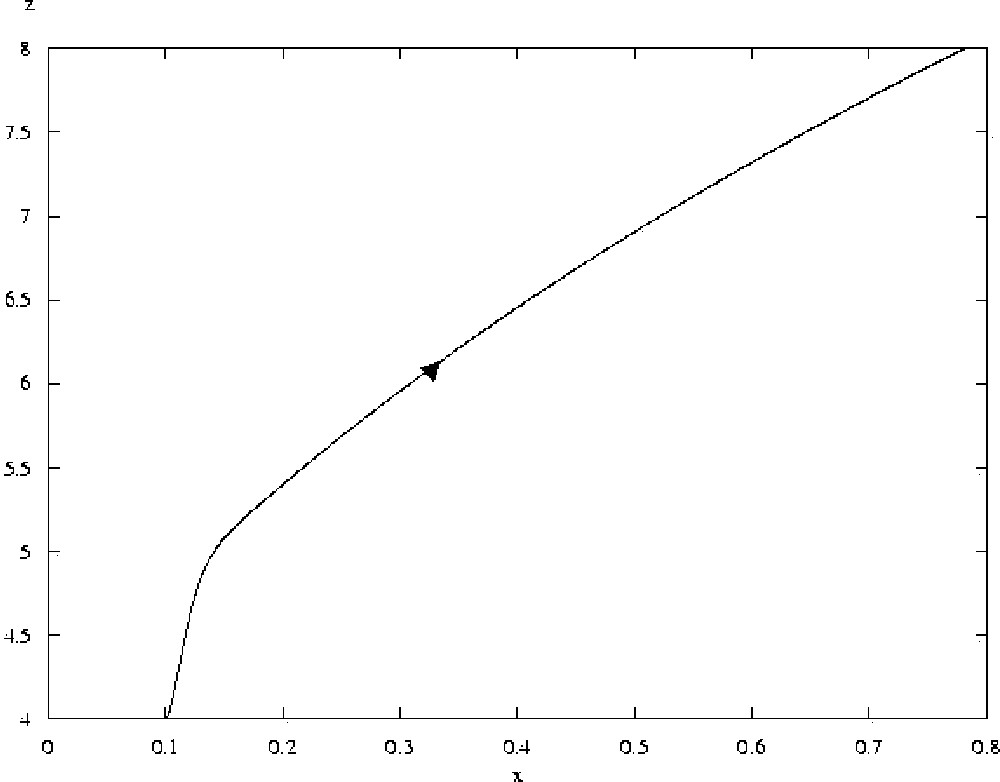
Trajectory of system 2, for a=50, with initial conditions x=0.1, y=0.1, z=4 (the value of x being thus slightly increased from the steady state). The arrow marks the direction of evolution of the system. The system does not return to the steady state where x=0.
It could make sense biologically to have an inducible expression of z if z was costly to produce, or if it interfered not only with the production of x but also with physiologically desirable reactions. Delays between triggering of a signal and mRNA transcription, and then mRNA translation, are very noticeable in cells, especially eukaryotic cells; it could therefore be that positive feedback has a role in stabilising systems that involve long-range negative feedback loops, that length being bounded from below by structural, biological constraints.
Systems in which a variable is under positive auto-catalysis, and under control of a long negative feedback circuit, could also be relevant to the modelling of the immunological system. A virus replicates auto-catalytically, and the acquired immunological response requires many successive steps eventually leading to the prevention of its replication. The presence of memory cells allows subsequent infections to occur with different initial conditions (in the above system, leakage allows z to be non-zero at rest, and makes it possible for the steady state with x=0 to be stable), but there are positive feedback circuits at play in immunological responses, for example between interleukin 12 and interferon γ 〚11〛.
3.3 Stability analysis
These examples show that, while it is generally true that, by adding enough negative feedback, one can stabilise any given system (see below), and that, by adding enough positive feedback, one can destabilise any given system, the behaviour between extremes is more complicated (and it should be because the stability of a variable can depend on a coefficient very far away in the interaction graph). This fact becomes even more obvious when one calculates the Routh–Hurwitz equations for a given system. These equations provide necessary and sufficient inequalities on the coefficients of the Jacobian matrix of a system for this system to be stable. These inequalities, which with current mathematical knowledge can only marginally be generically simplified, are quite complex even if the underlying system is highly structured in a simple fashion. The Routh–Hurwitz inequalities for the system described in Fig. 2 are shown in Table 1.
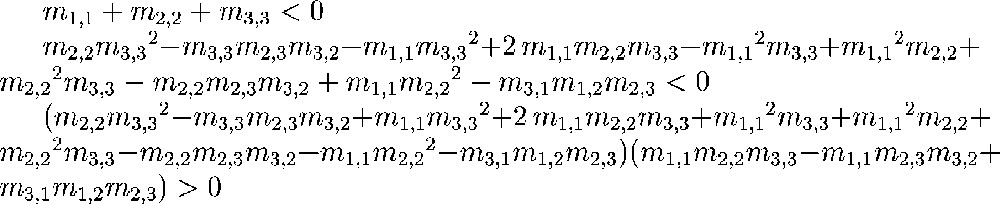
Necessary and sufficient stability conditions on the coefficients of a matrix m, whose non-zero coefficients are the same as those given by the graph in Fig. 2.
Relationships between Jacobian matrix structures and biological or chemical system behaviours have already been investigated extensively (see for example 〚12〛 or 〚13〛, or more recently 〚14〛 and 〚15〛). The problem of the stability of qualitative matrices (matrices grouped according to the signs of their coefficients) has also received extensive attention in the past, before computers made their way into everyday scientific life; important results are summarised in 〚16〛, and we review quickly how those results apply to feedback circuits and stability. Results relevant to our discussion are that if a system comprises a positive autocatalysis loop, a positive circuit of length 2, or any circuit, positive or negative, of length 3 or more, then the system can be made unstable by altering weights of interactions while strictly conserving their signs (this is a direct application of lemma 5.1 in 〚16〛). To make system stability a property robust against changes in values of its interaction weights, an interesting goal from the evolutionary standpoint because it frees the system from certain particular kinetic values, it thus seems necessary to limit to a strict minimum the number of negative feedback circuits of length greater than 2. Positive feedback, if present, can always destabilise the system if its amplitude is sufficiently augmented; however, as will be detailed below, the existence of positive feedback is a necessary condition for certain useful behaviours of regulation systems, and thus often cannot be avoided. Furthermore, it is remarkable that if one modifies a stable system by introducing positive autocatalysis on variables previously not autocatalysed, the resulting system can always be brought back to stability by altering interaction weights without changing their sign (theorem 5.5 in 〚16〛).
The most practical way to deal with the Routh–Hurwitz inequalities seems to be by means of computerised, symbolic computing. We have developed an automated system based on the symbolic computing program MAPLE (and especially on the ‘Hurwitz’ package of MAPLE), to test whether a system of given dimension, whose coefficients are kept symbolic, can be stable for a given set of values of its coefficients (details to be reported elsewhere). This system is useful for proving relationships between system structure and system stability for a given system dimension, and conjecturing that the relationships are also valid for higher dimensions. A conjecture we have come to is the following: if one wants to stabilise a given negative circuit of length strictly greater than two, and if one is allowed negative circuits of length of 2 or 1, then local, negative feedback has to be added to all of the variables but one. This tends to show that stabilisation is best dealt with locally. From an evolutionary standpoint, it should be less costly to provide each system variable with local, negative feedback, rather than to ensure that long feedback circuits are maintained in such a way as to stabilise variables with no local feedback. Local, negative feedback could be provided by specific and non-specific proteolysis (which would thus not only serve the purposes of automatically removing partially degraded proteins or transducing certain signals).
To conclude this discussion of the respective relationships of positive and negative feedback to stability, we point out that autocatalysis has a special role in that it must be negative on average for the system to be stable (the trace of a matrix is the sum of the real parts of its eigenvalues), and that the theorem of the ‘dominant diagonal’ (a well-known theorem from linear algebra, also mentioned in 〚16〛), has the intuitive interpretation that if for each variable the autocatalysis loop has a negative (respectively positive) weight sufficiently higher in absolute value than the sum of other interactions affecting the variable, then the system is stable (respectively unstable).
4 Roles of positive feedback circuits
4.1 Digital processing
The digital processing of signals, which involves making all-or-nothing decisions based on the strength of a signal relative to a threshold, has undeniably been the greatest advance in electronics, and has allowed automated information processing. Many different electronic components, passive (like a diode) or active (like an operational amplifier), can contribute to the shaping of a signal into all-or-nothing forms.
In biology, the processing of information at a cellular level also requires some digital capacity, because the categorisation of inputs and the structuration of an output behaviour require that decisions be made which may not be a compromise between different possibilities. For example, a cell should differentiate into a specific cell type, and should not possess characteristics of different types in varying proportions. Positive feedback has for example been shown to be implicated in the reading out of morphogen gradients, with transcription factors responding differently to concentrations of morphogen, and being part of mutually-repressive positive feedback circuits 〚17〛. Positive feedback circuits are crucial components of models of gradient interpretation, such as those presented in 〚18–20〛 (interestingly, in one of the cases proposed in 〚20〛, positive feedback is necessary for stability, for reasons different from those discussed above). The role of feedback circuits in development has also been investigated in 〚21〛, based on a formalism developed in 〚22〛.
Possible elements to approach all-or-none responses are enzymes exhibiting allosteric kinetics, whose response curves are sigmoidal and not hyperbolic as in classical Michaelis–Menten kinetics, or modifying enzymes functioning in conditions of zero-order ultrasensitivity (〚23〛, see 〚24〛 for an application to thresholds in development). However, sigmoid functions can only come close to Heaviside step functions, and cannot ever be the source of a perfect, all-or-nothing response, as emphasised in 〚18〛; the approximation of this kind of response can be enhanced, at the cost of complexification of the allosteric mechanism, but cannot be made perfect. An active mechanism based on positive feedback can however solve this problem 〚18〛, based on an underlying structural apparatus that needs not be sophisticated. The paradigm is that of a molecule controlled both by positive feedback and negative feedback, and for which negative (respectively positive) feedback predominates at low and high (respectively middle-valued) concentrations. Such a system is quite easy to design in such a way that there are only two stable stationary states, one with a high concentration of the molecule, and one with a low concentration. In such a system there is a third stationary state, which is unstable (and thus never observed in real-world conditions), and which plays the role of a threshold: starting at a concentration below that threshold, the concentration is brought back to its low stationary state, and starting above that threshold, the concentration is brought back to its high stationary state. Examples of biological situations where positive feedback circuits allow for threshold effects, as proposed in 〚18〛, are the activation of blood-coagulation enzymes 〚25〛, or the MAP kinase cascades (see below). The electronic equivalents of bi-stable systems would be ‘Schmitt triggers’.
Positive feedback thus makes it possible, with a very simple mechanism, to constrain a system variable to a fixed set of possible values, and to have a behaviour close to ideal. In the case of discrete systems, the structure of feedback circuits, and especially their sign, has been shown to be an important determinant of the behaviour of the system 〚26〛; it has been shown that the presence of a positive feedback circuit is necessary for a discrete system to have at least two stationary states 〚9, 27〛. In the continuous case, positive feedback is a necessary feature of a wide class of autonomous differential systems having two or more stationary states, if all stationary states are isolated. This was a conjecture made by Thomas 〚28〛, and proven independently in the case of constant signs of the feedback circuits in 〚7〛 and 〚29〛. We recently provided a more general demonstration 〚30〛. The demonstration we proposed shows that for such a multistationary system, there is at least one unstable stationary state that possesses a real, strictly positive eigenvalue in the Jacobian matrix; positive feedback being necessary for the existence of a real, positive eigenvalue, there is a positive feedback in those systems, at least around this unstable stationary state.
Positive feedback is of course no miracle solution, and there are also energetical tradeoffs involved. For the evolution of the system to be quick around unstable stationary states (and thus less sensitive to stochastic fluctuations), the positive and negative forces exerted on the concentration of the relevant molecule must be strong, which is energetically costly.
It would be quite wasteful for a switch molecule to be under strong, simultaneous synthesis and degradation, as would be the case in the paradigmatic example described above. A way in which this can be avoided is by ‘filtering out small stimuli’, as formulated in 〚31〛, so that competition between positive and negative feedback circuits is kept at a minimum. This filtering process can be provided by sigmoidal response curves; MAP kinase cascades, often involved in switch-like responses, exhibit such a type of response 〚31〛, and also have a positive feedback circuit 〚31, 32〛. The situation is thus the following: given a system that already exhibits some switch-like responses, even if quite imperfect, positive feedback circuits make it possible to give to the system an almost perfect switch-like behaviour; the better the original system, the lower the energetical cost to improve it.
An essential difference between positive and negative feedbacks is the existence of a real, positive eigenvalue allowed by positive feedback. Negative feedback can give rise to complex eigenvalues with positive real part; the complex component creates expanding oscillations in the dynamics around the stationary state. Such oscillations are most undesirable in a system trying to make a clear-cut decision.
Positive feedback is useful not only in making decisions, but also in memory, as emphasised in 〚18〛, and shown on a larger scale in 〚33〛. First, positive feedback is a necessary condition for multistationarity, as shown in 〚30〛; the greater the number of attractors of a system, the greater its storage capacity. Second, physical storage of information is a difficult task because of the natural tendency toward degradation; memory must be continuously self-renewed, a natural role of positive feedback. Computer memories make use of positive feedback, and so does the brain, if one goes with the hypothesis that memories are stored as strengths of connections between neurones, activated connections being reinforced (neurones also make use of positive feedback when their membrane depolarises 〚34〛). A form of biological memory relying on positive feedback circuits, identified early on, is that of the lactose permease 〚35〛. Different isoforms of the prion protein could also be a striking example of memory, as discussed in 〚36〛, which would have important implications both from the theoretical and therapeutical points of view. Positive feedback circuits could also provide memory at the level of ecosystems 〚37〛.
Finally, taking further the comparison between biological and computerised information processing, let us note that computers and brains both have highly oscillatory functioning, which, in the case of the computer, makes it possible to treat problems in a stepwise manner and break a complex computation into many elementary ones. It seems likely that intra-cellular regulation systems are not that sophisticated; a fundamental role for oscillations has not been proven so far in intra-cellular computations (but it has been shown that signals can be encoded by different frequencies of Ca2+ oscillations 〚38, 39〛). This however does not mean that temporal aspects are not important in cellular systems: cells can have qualitatively different responses to the same stimulus applied for differents lengths of time (p42 and p44 MAP-kinase pathways seem capable of such responses, as reported in 〚40〛), and often prove capable of desensitisation overtime (which requires the use of integral feedback 〚41〛, which we will not discuss here). The progression through the cell cycle shows that temporal aspects are also important when it comes to arranging a set of tasks for physical, not informational, purposes. Also, cellular oscillations in the production of a messenger molecule makes it possible to create sharp peaks of that molecule, when a large cell population is temporarily synchronised.
These remarks bring us to the role of positive feedback circuits in the generation of oscillations.
4.2 Oscillations
Positive feedback is at the heart of many electronic oscillators, and this is also true of biochemical systems 〚4〛, the paradigm being a product which activates its own synthesis in a cooperative fashion 〚4〛: the product slowly builds up while the synthesising enzyme is active at a low level, activates the enzyme when it reaches a sufficient concentration, which results in substrate depletion and thus in a reduced synthesis rate. Glycolytic oscillations, as well as many cases of Ca2+ oscillations, often involve positive feedback 〚4〛 (interestingly, positive feedback can, in some situations, disfavour glycolytic oscillations 〚42〛, as can enhanced negative feedback due to proteic confinement and non-Michaelian kinetics 〚43〛).
Certain types of oscillators use ‘negative resistance’ components, often provided by positive feedback circuits 〚44〛. Similarly, it has been known for a long time that a positive feedback circuit enhances outer hair cell movements, opposing viscous forces, and is necessary for high frequency selectivity 〚45〛 (see 〚46〛 for a recent review); it has in fact been shown that the hair bundles of these cells have negative stiffness in a certain range of displacements 〚47〛, making realistic a model based on the principle of negative-resistance oscillators. In this case, positive feedback circuits could thus have the role of freeing the system from viscous forces (as in a regenerative amplifier), as first proposed in 〚48〛, bringing it closer to an ‘ideal’ behaviour. This parallels the role of negative feedback circuits discussed in the next section.
5 Negative feedback circuits and robustness
Harold Black, a famous Bell Telephones Laboratories engineer, was met with disbelief when he proposed in the 1930’s that negative feedback could play a significant role in amplifiers, other than avoiding singing. The idea behind his negative-feedback amplifier, described in a patent 〚49〛, was to reduce distortion by feeding back into the amplifier input the error between the input and a scaled-down portion of the output (this error is known as distortion, and results from uneven amplification of different frequency signals).
Such a use of negative feedback is dynamic: one is not concerned with clamping down system variables to certain values, but to provide adjustments between different, dynamic variables. Many biological systems use negative feedback for this purpose. For example, it is crucial for organisms to maintain a fixed stoichiometry between proteic ribosomal subunits: ribosomes are present in great quantities under favourable growth conditions (40% of total dried cellular mass for E. coli under the most favourable laboratory conditions, 〚50〛), and it would be most wasteful to have components present in too high or too low quantities. It is thus imperative that different subunits be produced in similar quantities (note that this quantity is not fixed for a given prokaryotic cell, but rather a function of the growth rate). Nature has engineered sophisticated coupling mechanisms to ensure the concomitant production of two proteins in similar quantities 〚51〛. Such coupling mechanisms are also present within ribosomal operons in E. coli 〚50〛; however, it appears that the number of proteins is too great for their production to be coupled within a single operon, requiring another mechanism, based on negative feedback.
The mechanism, as reviewed in 〚50〛, is basically the following: each operon (whose proteins are synthesised in highly similar quantities) is under negative control of one of the proteins it codes for. If a group of protein is not in excess, it is incorporated into neo-synthesised ribosomes; if however it is in excess, proteins will not be sequestered in ribosomes, and then one of the proteins will be available to inhibit translation of the corresponding mRNA. Sequestering of proteins in ribosomes is where the substraction happens. As with the negative-feedback amplifier, the result of the substraction is fed back into the controlling input of the signal/protein generation system.
The beauty of this system is that it would be difficult (if not impossible) without negative feedback to devise ribosomal proteins in such a way as their production rates are exactly the same, especially since these proteins have different lengths and amino-acid contents. The system is freed from the particular kinetics of protein synthesis, and the stoichiometry cannot be ruined by evolutionary changes of these kinetics. More generally, such negative feedback can make it possible to have a varying number of copies of a same gene without its function being affected, a major evolutionary advantage, keeping a same gene functional for homozygotes and heterozygotes, and allowing duplication, a major source of new genes.
Black’s negative feedback amplifier was criticised on the grounds that the feedback diminished the gain of the amplifier; while the fact is quite true, the criticism missed the point that it was better to have an amplifier that would be slightly less powerful but that would output a better signal. The same applies to ribosomal synthesis: synthesis rates of different proteins align on the lowest one. But, while it is necessary to strive toward higher ribosomal synthesis rates, it is of no use to synthesise some proteins in excess.
Finally, it is interesting to note that electronic engineers and cyberneticians have made an extensive and successful use of negative feedback to render their systems independent of their operating conditions (especially temperature, for electronic systems) and of the imperfections and variabilities inherent to their components. Negative feedback in biological systems might very well lay the same role of guiding a generic system of variable properties toward the correct behaviour, by having it constantly correct itself, and thus of making the system robust against changes in its operating conditions or its internal parameters. From the practical viewpoint of understanding the inner workings of a regulation system, this has the consequence that some parameters may not be important and need not be investigated thoroughly. Considering the great complexity of most biological regulation systems, it is important to be able to concentrate on main parameters, i.e. those to which systems are very sensitive.
6 Conclusion
We have considered so far autonomous differential systems, without delays. Delays are however known to be involved in biological systems, because for example mRNA synthesis and transport (in eukaryotic cells) are certainly not instantaneous. Delays can be a major source of instability in negative feedback circuits (the intuitive situation being that of a correction to an offending variable that is applied too late, and has increased too much by the time it becomes effective, thus causing a swing in the opposite direction of the offending variable), and have been shown to effectively cause oscillations in biological systems 〚52, 53〛. Systems with delays are however most difficult to deal with analytically, because they are differential systems of infinite dimensions, to which one cannot associate finite-dimensional Jacobian matrices. Asynchronous automata have been proposed to describe regulatory networks 〚54〛. It should prove interesting to make use of hybrid automata (whose theory is described in 〚55〛), derived from computer program verification techniques, the disadvantage being that differential equations have to be discretised into piecewise linear systems. Such automata are useful when some system variables are amenable to boolean treatment (which is often the case for regulating genes which have on/off states, see 〚56〛 for a discussion and the description of a boolean formalism for genetic circuits), and can easily take delays into account in simulations; programs are available to prove properties about them, for example that they can (respectively cannot) reach situations which are desirable (respectively not desirable).



