Contribution à la théorie logistique de la croissance : structure temporelle et potentiel de croissance

Roger Buis

doi:10.1016/j.crvi.2003.08.003

Biomodélisation

Contribution à la théorie logistique de la croissance : structure temporelle et potentiel de croissance

Présenté par : Michel Thellier

Roger Buis ¹

¹ Laboratoire de biotechnologie et amélioration des plantes, Institut national polytechnique de Toulouse, Ensa, 31326 Auzeville, France

Comptes Rendus. Biologies, Volume 326 (2003) no. 8, pp. 729-738.

Résumés

Français
Anglais

L'analyse d'une population structurée à trois états cellulaires (juvénile, mature, sénescent) est conduite dans le cadre de la théorie des systèmes de transformation de Delattre. La croissance en nombre, avec dissymétrie des divisions cellulaires, est rapportée à un processus d'autocatalyse sous la contrainte de disponibilité d'une source. Deux modèles sont présentés dont la dynamique aboutit à une croissance de type exponentiel ou de type sigmoı̈de. Dans le cas sigmoı̈de, la fonction logistique (fonction de Richards–Nelder avec adjonction d'une asymptote inférieure Y ≠0) s'ajuste convenablement aux données simulées de l'effectif cellulaire total Y. Nous définissons un potentiel de croissance comme la capacité instantanée d'autocatalyse que l'on exprime en fonction des « ressources mitotiques » actuelles (source + cellules matures n'entrant pas en sénescence). Les variations de l'accélération d²Y/dt² concordent exactement avec le gradient du potentiel de croissance. Cette analyse se généralise à d'autres structurations de population. D'où notre proposition d'interpréter l'équation logistique comme un modèle formel de croissance d'une population structurée soumise à autocatalyse + compétition.

The analysis of a structured population according to three (juvenile, mature and senescent) cellular states is carried out within the framework of Delattre's transformation systems theory. Growth in number, with the dissymmetry of cell divisions, is determined by an autocatalysis process under the constraint of the availability of a source. Two models are presented: their dynamics results in a growth of the exponential type or of the sigmoidal type, respectively. In the sigmoidal case, the logistic equation (Richards–Nelder's function with adjunction of a lower asymptote Y ≠0) fits satisfactorily the simulated data of the total cell number Y. The growth potential is defined as the instantaneous capacity of autocatalysis, which is expressed in relation to the present ‘mitotic resources’ (source + non-senescing mature cells). The acceleration variations d²Y/dt² are in close agreement with the growth potential gradient. The analysis is then generalized to other population structuring. As a result, the logistic equation can be interpreted in terms of a formal model of growth of a structured population submitted to autocatalysis and competition.

Métadonnées

Reçu le : 2003-04-08
Accepté le : 2003-08-21
Publié le : 2003-08-01

PMID

DOI : 10.1016/j.crvi.2003.08.003

Mot clés : cinétique de croissance, modèle logistique, structure temporelle de croissance, autocatalyse, population cellulaire
Keywords: growth kinetics, logistic model, growth temporal structure, autocatalysis, cell population

Affiliations des auteurs :

Roger Buis ¹

¹ Laboratoire de biotechnologie et amélioration des plantes, Institut national polytechnique de Toulouse, Ensa, 31326 Auzeville, France

@article{CRBIOL_2003__326_8_729_0,
     author = {Roger Buis},
     title = {Contribution \`a la th\'eorie logistique de la croissance : structure temporelle et potentiel de croissance},
     journal = {Comptes Rendus. Biologies},
     pages = {729--738},
     publisher = {Elsevier},
     volume = {326},
     number = {8},
     year = {2003},
     doi = {10.1016/j.crvi.2003.08.003},
     language = {fr},
}

TY  - JOUR
AU  - Roger Buis
TI  - Contribution à la théorie logistique de la croissance : structure temporelle et potentiel de croissance
JO  - Comptes Rendus. Biologies
PY  - 2003
SP  - 729
EP  - 738
VL  - 326
IS  - 8
PB  - Elsevier
DO  - 10.1016/j.crvi.2003.08.003
LA  - fr
ID  - CRBIOL_2003__326_8_729_0
ER  -

%0 Journal Article
%A Roger Buis
%T Contribution à la théorie logistique de la croissance : structure temporelle et potentiel de croissance
%J Comptes Rendus. Biologies
%D 2003
%P 729-738
%V 326
%N 8
%I Elsevier
%R 10.1016/j.crvi.2003.08.003
%G fr
%F CRBIOL_2003__326_8_729_0

Roger Buis. Contribution à la théorie logistique de la croissance : structure temporelle et potentiel de croissance. Comptes Rendus. Biologies, Volume 326 (2003) no. 8, pp. 729-738. doi : 10.1016/j.crvi.2003.08.003. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2003.08.003/

Version originale du texte intégral

Abridged English version

1. The growth of a cell population structured according to three cellular states is first considered. Its properties are expressed within the framework of Delattre's transformation systems theory, which allows an accurate formalization of the autocatalysis process:

– occurrence of five classes of functional equivalence: one source y₁, one transient variable at the stationary state x, three cell classes: juvenile y₂, mature y₃ (the only cells that are able to divide) and senescent y₄ cells;
– native dissymmetry of the two daughter cells at the time of any mitosis: y₃→y₂+y₃;
– transformations governing transitions between classes:
$\begin{matrix} y_{1} + y_{3} & \overset{k_{1}}{\to} & x \\ x & \overset{k_{2}}{\to} & y_{2} + 2 y_{3} \\ y_{2} & \overset{k_{3}}{\to} & y_{3} \\ y_{3} & \overset{k_{4}}{\to} & y_{4} \end{matrix}$

The growth of each cell category and that of the total population Y = y₂+y₃+y₄, as well as the chronological development of its structure (proportions of these three cell classes), are then analysed in the following two cases.

Model I is characterized by a non-limiting source (autocatalysis only). Population growth is of the exponential type with a rapid change towards a stable structure (constancy of the relative numbers of the three cell states).

Model II is developed for a source in limited amount (autocatalysis + competition). In this case, Y growth is of the sigmoidal type. This model is used for putting forward an interpretation of the ‘logistic law’ applied to Y(t) kinetics.

2. Interpretation of the logistic function. Richards–Nelder's generalized logistics, with the adjunction of a lower asymptote Y≠0, fits very satisfactorily the data simulated by model II. A biological interpretation of the logistics is then put forward. For that purpose, the concept of growth potential (which is distinct from the classical absolute growth rate dY/dt) is introduced. The growth potential is defined, with reference to the basic process, as the instantaneous capacity of autocatalysis of the population. At any instant, the occurrence and the amount of mitoses are determined by the ‘present mitotic resources’, i.e. concomitantly source + available (non senescing) mature cells, that is k₁(1−k₄)y₁(t)y₃(t).

The time dependence of the gradient of this potential parallels the growth acceleration variations d²Y/dt² of the total population.

The definition of the temporal structure of a logistic growth is recalled, with the discretization of the cursus Y(t) into a series of four phases depending on whether the acceleration is positive or negative, increasing or decreasing. The occurrence of these four phases and their delimitation correspond exactly to the temporal variations of the growth potential. Therefore, the logistic law can be interpreted in terms of a formal model based on the time dependence of the instantaneous mitotic resources of a population that is structured according to a criterion of state.

3. An extension to five (three juveniles, one mature, one senescent) cellular states with other transition rules corroborates the preceding results. The generalization of this type of model to other (dimensional or ponderal) growth types is finally considered. With this change in the physical nature of the variables, the choice of the structuring criterion of the population implies the principle of a spatial discretization of a continuous medium into ‘growth elements’.

1 Introduction

La grande généralité des courbes sigmoı̈des représentatives de la croissance de systèmes biologiques de type densité-dépendant dans le cas monotone rend délicat le problème de leur interprétation. Cette sorte d'ubiquité, au regard de la diversité de la nature physique des systèmes concernés, rend en effet difficile la recherche d'une base théorique précise pouvant justifier le modèle apte à générer de telles courbes. De fait, à l'exception de certains modèles de grandissement cellulaire fondés sur les propriétés mécaniques de la paroi et du cytoplasme ([1,2] par exemple), peu de travaux se sont attachés à cette question ([3], pour un cas particulier de la fonction de Gompertz, par exemple). La plupart visent plus la généralité formelle du modèle et sa flexibilité (avec souvent une augmentation du nombre de paramètres) que son explication en termes biologiques [4–6]. Dans ce but, nous avons proposé [7], dans le cadre des systèmes de transformation de Delattre [8,9], un modèle autocatalytique permettant de rendre compte de courbes sigmoı̈des de dissymétrie variée dans le cas d'une seule variable y(t). Précisons toutefois que ce modèle se rapporte au formalisme général de Bertalanffy [5], plutôt qu'à la forme classique de la logistique qui sera discutée ici.

Rappelons que, selon la théorie logistique de la croissance, les variations temporelles de la variable étudiée y(t) suivent la fonction dite logistique (selon la terminologie de Verhulst [10]) considérée ici selon l'expression de Richards–Nelder [11]. Plaçons-nous ici dans un cas plus général où nous supposons l'existence d'une asymptote inférieure y=K₀≠0. Dans ces conditions, la théorie logistique repose sur l'hypothèse suivante :

\frac{d y}{d t} = \frac{a}{n} (y - K_{0}) [1 - {(\frac{y - K_{0}}{K_{1}})}^{n}]; a, K_{0}, K_{1} > 0; n > - 1 (\neq 0)

(1)

donnant la fonction de croissance :

y (t) = K_{0} + \frac{K_{1}}{{1 + \frac{K_{1}^{n} - {(y_{0} - K_{0})}^{n}}{{(y_{0} - K_{0})}^{n}} \exp (- at)}^{1 / n}}

(2)

où y₀=y(t=0) et y∈[y(0),K₀+K₁]. L'idée de base, selon (1), est de postuler que la vitesse absolue instantanée de croissance est le bilan entre une composante exponentielle (proportionnelle à la variable y) et une « force retardatrice » ou de « freinage » (proportionnelle à la puissance n+1 de y). En réalité, on s'intéresse habituellement au cas particulier où K₀=0, caractérisé par une vitesse spécifique R=(1/y)(dy/dt) qui décroı̂t continûment selon la puissance n de y. Mais ceci est loin de correspondre à la réalité de nombreuses variables biologiques [7].

La présente note élargit le problème aux cas de populations structurées afin de tenir compte de la dépendance de l'activité de croissance vis-à-vis de l'âge ou de l'état des éléments constitutifs de la population. D'une part, cela permet de lever le caractère parfois peu réaliste des modèles usuels de croissance comme la logistique classique, bien que le recours à un modèle multilogistique puisse être parfois une alternative intéressante en décomposant le processus en deux ou plusieurs composantes logistiques [12]. D'autre part, cette approche devrait permettre de mettre en rapport cinétique et structure, qui sont deux caractères fondamentaux de toute dynamique biologique.

2 Système à trois états cellulaires

Prenons pour exemple une population cellulaire dont nous considérons la croissance en nombre d'éléments, et qui est caractérisée par les propriétés suivantes.

– Tout cellule passe par une suite de trois états successifs, dits juvénile, mature et sénescent. Seul l'état mature est apte à la division cellulaire. L'état sénescent constitue un état terminal.
– Toute mitose est dissymétrique : elle génère deux cellules-filles d'état initial différent. Par état initial, nous entendons le « degré de juvénilité », ou temps nécessaire pour acquérir la maturité de division.
– La croissance de la population (en nombre de cellules) est subordonnée à l'existence d'une source nécessaire au déclenchement des mitoses. Sans préjuger de sa nature, ce terme de source est phénoménologiquement l'équivalent des notions écologique de capacité biotique d'un milieu (carrying capacity) ou génétique de capacité mitotique d'une lignée cellulaire (nombre maximum de divisions).

Exprimons les propriétés biologiques élémentaires énoncées ci-dessus à l'aide de la théorie de Delattre dont le formalisme s'applique notamment au processus d'autocatalyse en mettant en jeu une variable transitoire à l'état stationnaire.

2.1 Existence de cinq classes d'équivalence fonctionnelle

E1 : source y₁ déterminant la possibilité des cellules matures à se diviser (son épuisement implique l'arrêt de toute mitose).
E2 : variable x de transition pré-mitotique que l'on suppose à l'état stationnaire.
E3 : cellules juvéniles y₂.
E4 : cellules matures y₃ (seules aptes à se diviser).
E5 : cellules sénescentes y₄.

Ce critère « état cellulaire » structure la population cellulaire en trois classes d'état correspondantes (juvénile, mature, sénescent). À tout instant, elle est ainsi caractérisée par sa distribution dans ces classes E3, E4 et E5, dont les fréquences relatives explicitent la structure de la population.

2.2 Transformations (Fig. 1)

– Toute cellule est soumise aux transitions temporelles de classes : E3 → E4 → E5 (changements d'état) définies par les coefficients de vitesse k_i.
– La division des cellules matures s'opère via la variable transitoire x, dont la formation requiert conjointement les variables y₁ (source) et y₃ (autocatalyse).
– Pour toute mitose, la règle de production cellulaire est : y₃→y₂+y₃. La cellule-fille y₂ doit subir une maturation y₂→y₃ avant de pouvoir se diviser. La cellule-fille y₃ n'est apte à se diviser que si la source est présente, mais compte tenu d'une probabilité de sénescence (coefficient k₄). Soit :
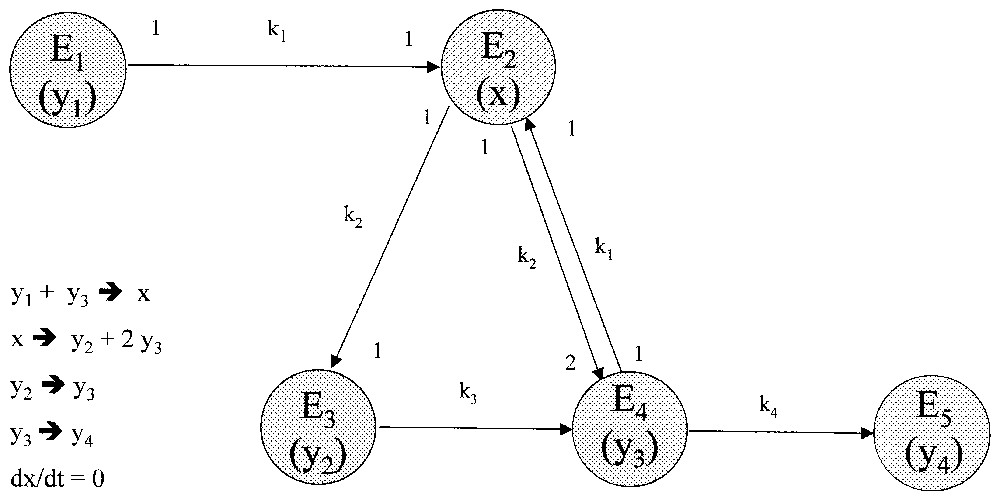
$\begin{matrix} y_{1} + y_{3} & \overset{k_{1}}{\to} & x \\ x & \overset{k_{2}}{\to} & y_{2} + 2 y_{3} \\ y_{2} & \overset{k_{3}}{\to} & y_{3} \\ y_{3} & \overset{k_{4}}{\to} & y_{4} \end{matrix}$

Fig. 1
Système à trois états cellulaires : y₂ (juvénile), y₃ (mature), y₄ (sénescent). y₁ : source ; x : variable transitoire stationnaire.

Ces transformations sont représentées par un graphe orienté (Fig. 1) et s'expriment par les équations suivantes après élimination de la variable x (sachant que dx/dt=0) :

\begin{matrix} \frac{d y_{1}}{d t} = - k_{1} y_{1} y_{3} \\ \frac{d y_{2}}{d t} = k_{1} y_{1} y_{3} - k_{3} y_{2} \\ \frac{d y_{3}}{d t} = k_{1} y_{1} y_{3} + k_{3} y_{2} - k_{4} y_{3} \\ \frac{d y_{4}}{d t} = k_{4} y_{3} \end{matrix}

(3)

y_{i} (i = 1, \dots, 4)

représentant les quantités ou effectifs de la classe correspondante, avec 0<k_i<1.

Deux cas sont à considérer selon que la source y₁ est ou non en quantité limitée.

2.2.1 Modèle I : autocatalyse avec source non limitante

Supposant y₁=S=Cte, (3) se réduit au système linéaire :

\begin{matrix} \frac{d y_{2}}{d t} = k_{1} {Sy}_{3} - k_{3} y_{2} \\ \frac{d y_{3}}{d t} = k_{1} {Sy}_{3} + k_{3} y_{2} - k_{4} y_{3} \\ \frac{d y_{4}}{d t} = k_{4} y_{3} \end{matrix}

(4)

dont la dynamique qualitative est donnée par le comportement du sous-système {y₂,y₃}. On remarque aisément que pour S>k_i (cas habituel où k_i<1) les valeurs propres de celui-ci sont réelles et de signe opposé (état stationnaire de type col ou selle). En règle générale, les variables effectifs n'évoluent donc pas vers un état stationnaire stable. La croissance de la population est de type exponentiel. En revanche, les fréquences relatives tendent plus ou moins rapidement vers des valeurs constantes : la population évolue vers une structure stable (Fig. 2).

Fig. 2
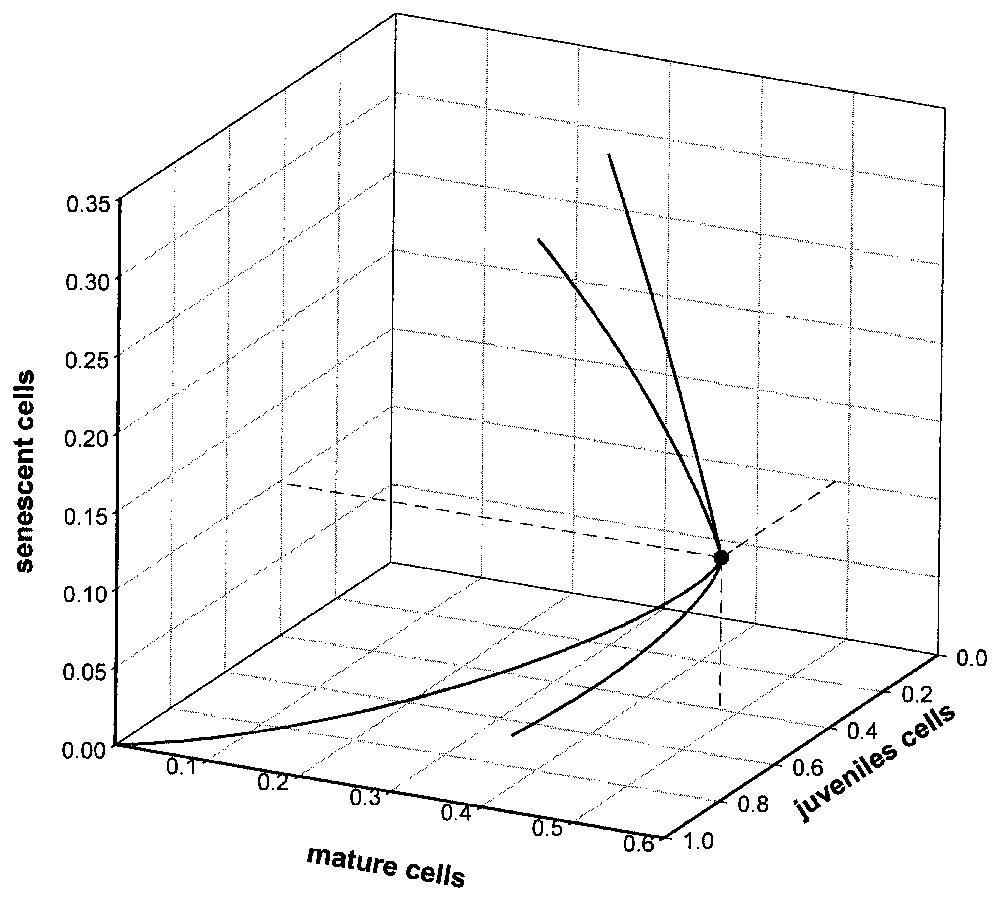
Système à trois états cellulaires (modèle I) : évolution de la structure (proportions des classes cellulaires). S=5 ; k_i=0,1. Les différentes courbes correspondent à diverses conditions initiales. Quelles que soient celles-ci, la population tend vers une structure stable {0,41 ;0,49 ;0,10}.

Au système (4) correspond, par discrétisation du temps, un modèle matriciel dont la matrice de transition (différente des matrices de Leslie stricto sensu) est :

M = [\begin{matrix} 1 - k_{3} & k_{1} S & 0 \\ k_{3} & 1 - k_{1} S - k_{4} & 0 \\ 0 & k_{4} & 1 \end{matrix}]

Cette matrice est irréductible et primitive (λ₁ valeur propre réelle dominante). La fonction de croissance des effectifs

y = [y_{2} y_{3} y_{4}]

est de type exponentiel :

y (t) = M^{t} y (0) = \sum_{i = 2}^{4} c_{i} λ_{i}^{t} v_{i} ≅ c_{1} λ_{1}^{t} v_{1}

où v_i sont les vecteurs propres associés aux valeurs propres λ_i,c_i dépendant des conditions initiales.

Soit $y_{r} = [y_{i} / y_{tot}] (i = 2, \dots, 4)$ le vecteur des fréquences relatives des classes de cellules. La structure de cette population évolue vers un état stationnaire (dy_r(t)/dt=0) qui est globalement stable puisque M est primitive [13]. De plus, cet état stable ${y_{2}^{*}, y_{3}^{*}, y_{4}^{*}}$ est unique et indépendant des conditions initiales (population ergodique).

Exemple : avec S=5 et les k_i=0.1 (Fig. 2), λ₁=1.49 et l'on a une croissance exponentielle (λ₁>1). La structure stable (proportions) est : {0.41,0.49,0.10}.

2.2.2 Modèle II : autocatalyse + compétition (source limitée)

La résolution numérique de (3) montre une croissance de type sigmoı̈de pour y₄ ainsi que pour l'effectif cellulaire total Y=y₂+y₃+y₄, alors que y₂ et y₃ passent par un maximum avant épuisement de la source y₁ (Fig. 3). La structure est différente du modèle précédent (Fig. 4), puisque, par défaut de renouvellement (source limitée), la population évolue vers un état homogène stable, toutes les cellules parvenant en E5.

Fig. 3
Système à trois états cellulaires (modèle II) : cinétique des différentes classes et de la population totale. k_i=0,1 ; y(0)={10,1,0,0}.

Fig. 4
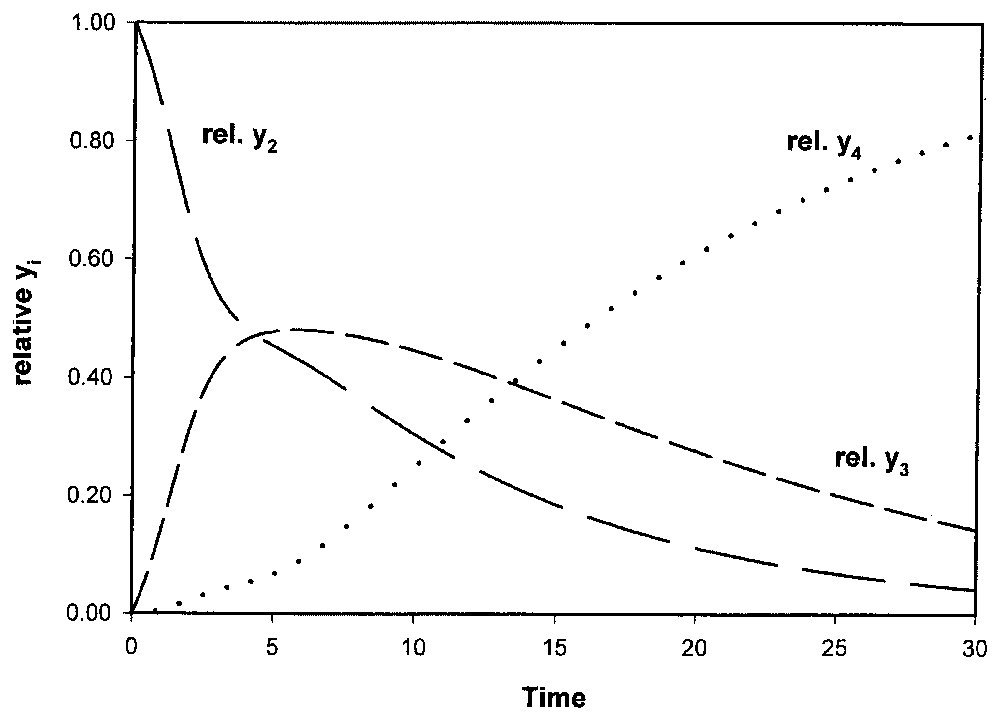
Système à trois états cellulaires (modèle II) : structure de la population (y_i relatifs). Conditions de la Fig. 3.

Le modèle matriciel correspondant est évidemment très différent du précédent car la matrice M (où intervient la source qui est ici une variable) n'est pas constante mais densité-dépendante. On peut l'écrire sous la forme réductible suivante en explicitant la variable y₃ sujette à l'autocatalyse :

M = [\begin{matrix} 1 - k_{1} y_{3} & 0 & 0 & 0 \\ k_{1} y_{3} & 1 - k_{3} & 0 & 0 \\ k_{1} y_{3} & k_{3} & 1 - k_{4} & 0 \\ 0 & 0 & k_{4} & 1 \end{matrix}]

L'analyse de stabilité par approximation linéaire [14, (p. 238)] montre l'existence d'un état stationnaire stable des fréquences qui est en réalité un état homogène {0,0,1}.

Détaillons la dynamique du modèle II. Une fonction logistique généralisée du type (2) s'ajuste correctement aux données de Y telles que simulées par le modèle (3) (Fig. 5), en posant y=Y. Ce modèle génère des courbes de croissance de dissymétrie variée par rapport au point d'inflexion. Dans le cas particulier des logistiques avec K₀=0 (qui est le plus souvent exploité), le paramètre n mesure cette dissymétrie (selon que n<1 ou n>1). Mais, dans le cas général traité ici, où K₀≠0, la symétrie exacte a lieu pour n racine de (1+n)^1/n=2K₁/(K₁−K₀). La dissymétrie des courbes Y(t), notée par le rapport Y_inflexion/(Y_max/2), dépend des valeurs relatives des coefficients de vitesse k_i. 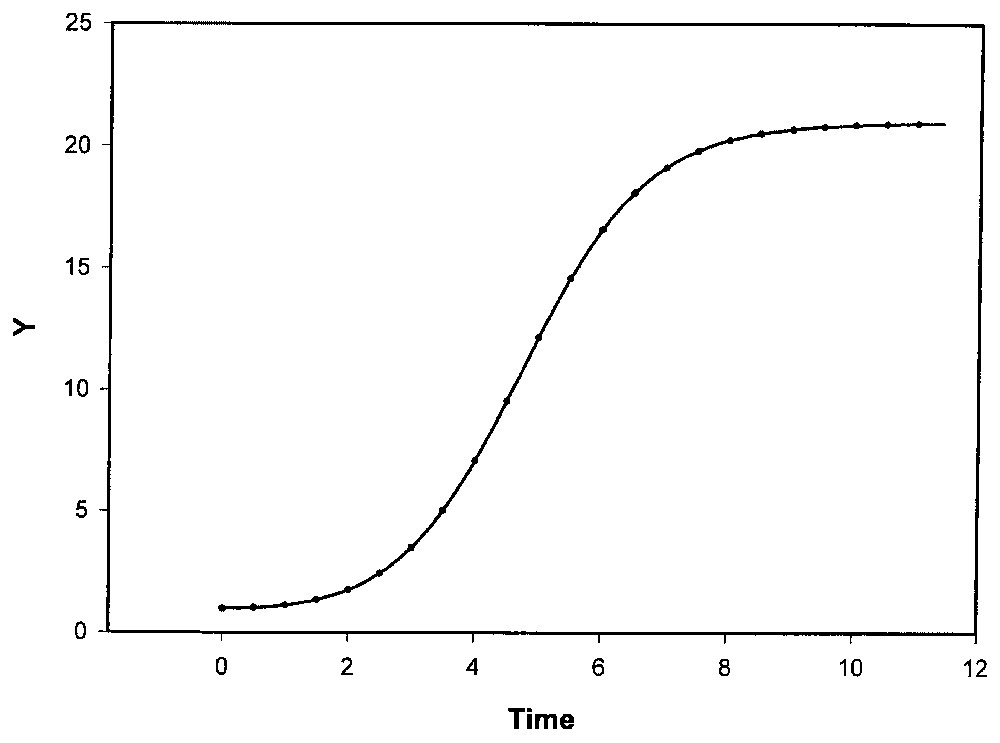Ce rapport vaut approximativement 1 si $k_{1} ≅ k_{4}$ . Il est supérieur (resp. inférieur) à 1 (dissymétrie droite, resp. gauche) si le coefficient dominant est k₁ (resp. k₄). Considérons plutôt la structure temporelle qui nous apporte plus d'informations que ce simple coefficient de symétrie.

Fig. 5
Système à trois états cellulaires (modèle II) : données simulées par le modèle II (•) (conditions de la Fig. 3) et ajustement d'une logistique généralisée. K₀=0,8393; K₁=20,1557 ; a=0,9998 ; n=0,8591. R²ajust. = 0,999997.

2.3 Structure temporelle de la croissance globale Y(t)

Rappelons que la cinétique logistique comporte comme points singuliers de l'activité de croissance les deux extremums de la dérivée seconde (accélération Γ) d²y/dt² et son annulation d²y/dt²=0 [5,15]). Ces valeurs délimitent quatre phases de croissance dénommées {G₁,G₂,G₃,G₄} définies par les valeurs du couple (V,Γ), c'est-à-dire, selon que l'accélération est positive ou négative, croissante ou décroissante. Les durées et quantités de croissance (accroissements) pour chacune de ces phases, en valeurs relatives, caractérisent la structure temporelle de croissance. Ce schéma est donc indépendant de l'ordre de grandeur de la variable en croissance, permettant ainsi de caractériser le phénomène de croissance d'un point de vue strictement cinétique et non dimensionnel. Il montre en particulier l'existence d'une éventuelle phase prédominante, soit en durée, soit en quantité de croissance. Nous l'avons utilisé pour discriminer par exemple différents types cellulaires d'un même organisme [12]. Soulignons que la structure temporelle de Y (discrétisation du cursus de Y(t) en quatre phases) et la structure instantanée de la population {y_i=1,…,k classes cellulaires} sont deux notions distinctes.

La structure temporelle de Y(t) dépend des coefficients k_i. Elle analyse le cursus de croissance plus finement que ne le permet la prise en compte usuelle de la position du point d'inflexion comme indice de dissymétrie. Le Tableau 1 en donne quelques exemples. On voit que la flexibilité du modèle relève de l'ensemble des coefficients k_i, c'est-à-dire de l'ensemble des transitions de classes, alors que l'usage habituel de la fonction (2) se réfère au seul paramètre n. La structure temporelle caractéristique de la logistique simple de Verhulst (K₀=0 et n=1), c'est-à-dire l'égalité G₁ et G₄ d'une part, et G₂ et G₃ d'autre part [5], s'observe très sensiblement dans le cas d'une égalité de k₁ et k₄. Lorsqu'il y a nette dissymétrie, la prédominance de la phase G₁ (resp. G₄) en durée relative est déterminée par un rapport k₁/k₄>1 (resp. <1), en même temps que k₃ contribue fortement à ce que la phase G₃ soit prédominante en quantité de croissance réalisée. De la simple description de la cinétique logistique en une suite de phases G_i, on passe ainsi à son explication par des transitions de classes.

Coefficients k_i	Durée des phases (%)	Quantité de croissance par phase (%)
	G ₁	G ₂	G ₃	G ₄	G ₁	G ₂	G ₃	G ₄
0,5,0,1,0,5,0,1	41	12	18	29	23	26	36	15
0,05,0,1,0,3,0,2	19	12	12	57	16	30	30	24
0,1,0,1,0,1,0,1	36	14	14	36	19	30	30	21

3 Interprétation du modèle logistique de croissance

La bonne adéquation d'une fonction logistique (2) à la croissance globale d'une population structurée (Fig. 5) permet de rechercher la signification biologique de cette fonction classique. L'interprétation proposée ne se situe pas au niveau de la variable globale Y. À ce niveau, en effet, cela se bornerait à reprendre l'hypothèse de base, purement formelle, rappelée plus haut.

Recherchons plutôt le rapport existant entre les points singuliers notés ci-dessus pour la cinétique globale Y(t), et l'évolution de la population à partir des variations chronologiques (i) du nombre de cellules en division, (ii) de la capacité mitotique de la population. Utilisons pour cela les notions suivantes.

Capacité totale de croissance. La taille maximale de la population en fin de croissance dépend exactement des conditions initiales puisque Y_max=2y₁(0)+y₂(0)+y₃(0)+y₄(0) (les k_i influant sur la vitesse et la durée de croissance). À tout instant, l'écart entre cette grandeur et Y(t) exprime la capacité actuelle de croissance. Ceci reprend la notion classique de carrying capacity rappelée précédemment. Elle n'a ici que peu d'intérêt, car elle ne peut expliquer les variations de la vitesse du processus.

Activité instantanée de croissance. Le recours classique à la vitesse spécifique R n'a pas de sens ici, puisqu'elle ne tient pas compte de sa dépendance vis-à-vis de l'état cellulaire. Définissons l'activité de croissance par la possibilité d'occurrence de nouvelles mitoses, formalisée par la transformation : $y_{1} + y_{3} \overset{k_{1}}{\to} y_{2} + 2 y_{3}$ .

Notons que cette « capacité d'autocatalyse » ne dépend pas seulement de la source disponible, ce qui dénue d'intérêt la grandeur dy₁ (qui ne pourrait servir que de mesure du degré d'avancement de la croissance). Elle dépend aussi, conjointement, de la quantité de cellules matures disponibles (celles n'entrant pas en sénescence) y₃^∘. Soit f(y₁(t),y₃^∘(t)). Adoptons pour f, en tenant compte des coefficients k_i, la grandeur suivante, appelée potentiel de division :

pot . div . (t) = k_{1} (1 - k_{4}) y_{1} (t) y_{3} (t)

qui exprime correctement les ressources mitotiques du système en croissance. Ce sont ces ressources qui déterminent la quantité instantanée de divisions cellulaires. Son gradient exprime ainsi les variations de l'activité de croissance de la population (Fig. 6), tout en remarquant qu'il n'y a pas identité entre la vitesse de croissance au sens classique et le potentiel ci-dessus. On en voit l'intérêt pour l'interprétation de la fonction logistique, notamment de la structure temporelle associée, puisque les points singuliers de celle-ci sont chronologiquement identiques aux points singuliers du gradient du potentiel de division. Soulignons que cette interprétation ne se situe pas au niveau d'une relation simple entre cinétique globale et structure de population, par exemple en se rapportant aux fréquences relatives de telle ou telle classe d'états cellulaires. Il nous paraı̂t plus significatif de pouvoir relier la structure temporelle du processus global au mécanisme fondamental déterminant l'intensité de croissance, plutôt qu'à la distribution de fréquences d'états cellulaires qui n'est qu'une conséquence du processus et non son mécanisme.

Fig. 6
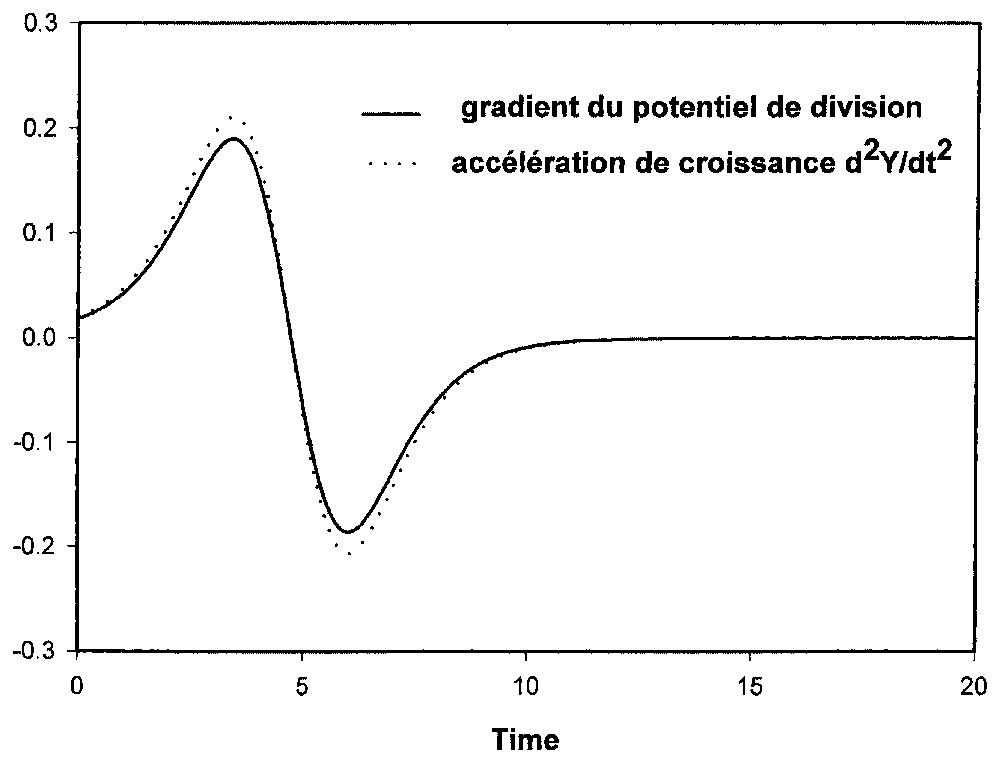
Système à trois états cellulaires (modèle II) : gradient du potentiel de division et accélération de croissance (conditions de la Fig. 3).

4 Généralisation

Ce système « minimal » à trois classes d'état peut être aisément étendu par ajout de processus de mortalité et/ou augmentation du nombre d'états cellulaires ainsi que par changement de l'état initial des deux cellules-filles. Ces modifications n'altèrent nullement le principe de l'analyse et de l'interprétation proposée.

Exemple : soit un système avec source en quantité limitée (y₁) et cinq états cellulaires (trois juvéniles y₂,y₃,y₄, un mature y₅ et un sénescent y₆). Toute mitose de cellule mature non engagée vers la sénescence donne deux cellules juvéniles différentes : y₅→y₂+y₄. Le graphe correspondant résume les différentes transformations (Fig. 7). Comme précédemment, avec une source limitée, la croissance de la population totale Y=y₂+y₃+y₄+y₅ est de type sigmoı̈de. Avec le modèle matriciel correspondant, l'analyse de stabilité de la matrice de transition (densité-dépendante et réductible) conduit aux mêmes conclusions que précédemment.

Fig. 7
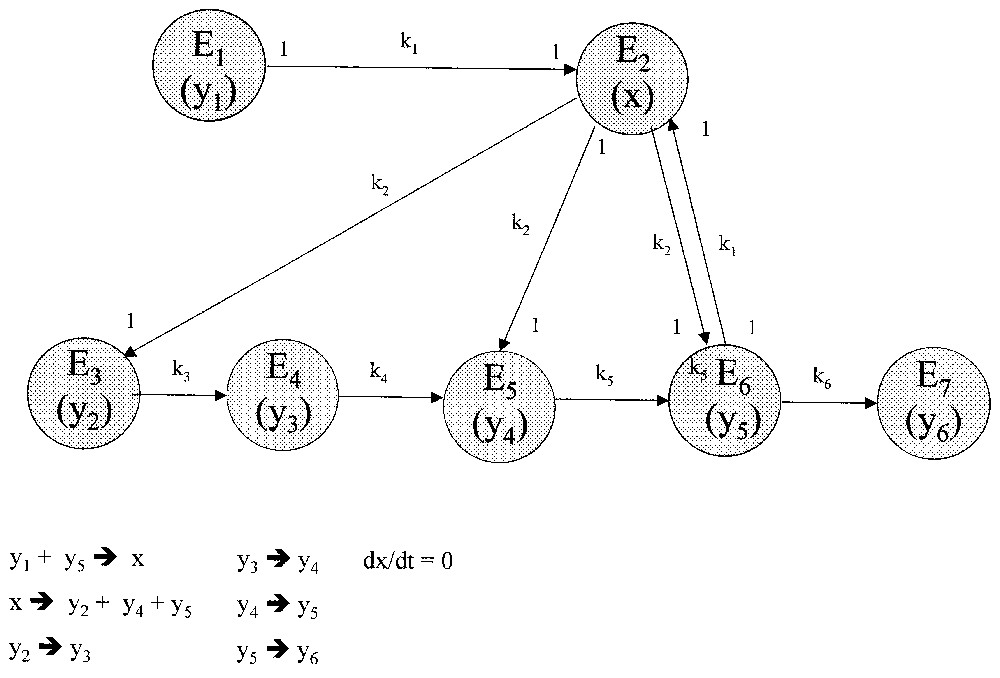
Système à cinq états cellulaires : trois états juvéniles (y₂,y₃,y₄), un état mature (y₅) et un état sénescent (y₆).

D'autre part, les points singuliers de la structure temporelle de Y(t)(calculés après ajustement par une logistique généralisée) correspondent, comme avec le système précédent, à ceux du gradient du potentiel de division défini par les ressources mitotiques actuelles, soit : pot.div.(t)=k₁(1−k₆)y₁(t)y₅(t).

5 Discussion

Le type de modèle présenté concerne le cas particulier d'une croissance d'une population en nombre d'éléments constitutifs. Il peut être étendu formellement à d'autres cas de croissance de population (individus par exemple). En outre, son application à d'autres types de croissance – dimensionnelle ou pondérale – (grandissement cellulaire, croissance d'organes ou d'organismes) peut également être envisagée. Dans ce cas, on ne traite pas des entités discrètes et dénombrables comme des effectifs cellulaires, mais des « éléments », de nature topologique, d'un ensemble physique continu. Rappelons le cas des modèles discrets fondés sur les grammaires formelles (comme les L-systèmes). Outre la multiplication cellulaire qui constitue leur champ principal d'investigation, le principe de ces modèles s'applique également, avec discrétisation spatiale, au grandissement cellulaire lui-même [16].

Notons brièvement une comparaison entre les L-systèmes et le modèle proposé ici. Le type de critère de structuration de la population est analogue (existence d'un nombre limité d'états cellulaires). Mais les transitions entre états sont formalisées différemment : « règles de production » avec discrétisation du temps pour les L-systèmes, ou équations différentielles de transformations pour notre modèle. Ces systèmes discrets ont fait l'objet de diverses applications (croissance d'algues filamenteuses et de méristèmes, par exemple [17]). Par rapport à ces « automates cellulaires », la particularité de notre modèle réside d'abord dans la prise en compte explicite du processus d'autocatalyse que nous couplons à un processus de compétition. Mais surtout notre modèle permet : (i) de quantifier cette notion de « potentiel de croissance » défini par les ressources mitotiques instantanées de la population ; (ii) de relier la cinétique « globale » d'une population au concept fondamental de « structure temporelle » de croissance.

Un autre aspect important est la flexibilité des courbes de croissance générées par notre modèle, correspondant à la diversité des sigmoı̈des dissymétriques observées (voir, par exemple, la croissance de l'hypocotyle de Lupinus albus [5, (p. 305, Fig. 4)]. Notre modèle met en relation ce caractère (souvent négligé quoique caractéristique de certaines croissances) avec les valeurs relatives des coefficients de transformations (Tableau 1).

L'introduction d'une source limitée de nutriments comme variable (sujette à déplétion) dans le cadre d'un système dynamique a été souvent exploitée pour modéliser une cinétique de croissance [18,19]. Elle rend compte évidemment du caractère sigmoı̈de variable de nombreuses courbes de population cellulaires, mais sans fournir, par elle-même, d'explication aux points singuliers du cursus. De leur côté, les diverses études de populations structurées [20] ignorent généralement la notion de structure temporelle de croissance. Notre propre analyse montre ce que peut apporter la conjonction de ces deux aspects. Elle souligne que l'explication d'une cinétique de croissance requiert de satisfaire les deux conditions suivantes : (i) quantifier correctement l'activité instantanée de croissance (ce qui implique de structurer la population) ; (ii) recourir à un formalisme, précis et de portée générale, pour l'autocatalyse en tant que processus de base de toute croissance.

6 Conclusion

1. La structure temporelle de la croissance logistique (au sens de la décomposition du cursus temporel en phases selon les valeurs du couple (V,Γ)) ne correspond pas à des caractéristiques particulières de la structure de la population (sa distribution en classes d'état). Son interprétation repose sur les variations du potentiel de division qui exprime les ressources mitotiques instantanées de la population. Celles-ci évoluent au cours de la croissance par le fait (i) du caractère limitant de la source conditionnant l'état limite en fin de processus, (ii) de la transition entre classes d'états qui détermine, à tout instant, la quantité de cellules aptes à se diviser.

2. Ceci nous apparaı̂t comme une base intéressante fournissant une interprétation, en termes biologiques, de la fonction logistique. Celle-ci ne doit plus être considérée comme un simple outil empirique d'ajustement, mais comme un modèle formel de population structurée sur un critère d'état et soumise au jeu conjoint autocatalyse + compétition. Par ailleurs, l'intérêt de la notion de structure temporelle d'un processus s'en trouve renforcé, puisque les caractéristiques de la suite de phases de croissance sont dépendantes des coefficients de transition entre classes d'état. D'où l'on peut envisager son application à d'autres types de croissance, monotone ou non.

Bibliographie

[1] J.A. Lockhart An analysis of irreversible plant cell elongation, J. Theor. Biol., Volume 8 (1965), pp. 264-275

[2] D. Cosgrove Biophysical control of plant cell growth, Annu. Rev. Plant Physiol., Volume 37 (1986), pp. 377-405

[3] R. Makany A theoretical basis for Gompertz's curve, Biom. J., Volume 33 (1991), pp. 121-128

[4] M.E. Turner; E.L. Bradley; K.A. Kirk; K.M. Pruitt A theory of growth, Math. Biosci., Volume 29 (1976), pp. 367-373

[5] R. Buis Models of growth kinetics in plants (H. Greppin; M. Bonzon; R. Degli Agosti, eds.), Some Physicochemical and Mathematical Tools for Understanding of Living Systems, université de Genève, 1993, pp. 295-318

[6] R. Buis Growth activity and structure at various organization levels in plants, Acta Biotheor., Volume 41 (1993), pp. 231-247

[7] R. Buis On the interpretation of the logistic law of growth: a new reading of the relationships between autocatalysis and growth, Acta Biotheor., Volume 45 (1997), pp. 251-266

[8] P. Delattre L'évolution des systèmes moléculaires, Maloine-Douin, Paris, 1971

[9] P. Delattre Une définition formalisée de l'autocatalyse, C. R. Acad. Sci. Paris, Sér. C, Volume 290 (1980), pp. 101-104

[10] P.F. Verhulst Recherches mathématiques sur la loi d'accroissement de la population, Nouv. Mém. Acad. Roy. Sci. et Belles-Lettres de Bruxelles, Volume 18 (1845), pp. 1-39

[11] F.J. Richards; J.A. Nelder The fitting of a generalization of the logistic curve, Biometrics, Volume 10 (1959), pp. 290-300

[12] R. Buis; M.-T. L'Hardy-Halos; C. Lambert Caractérisation des types cellulaires cladomophore et pleuridiophore chez la rhodophycée céramaciée Antithamnion plumula : apport de l'analyse des cinétiques de croissance, Can. J. Bot., Volume 78 (2000), pp. 1114-1123

[13] L. Demetrius Primitivity conditions for growth matrices, Math. Biosci., Volume 12 (1971), pp. 53-58

[14] H. Caswell Matrix Population Models, Sinauer Assoc. Sunderland, Mass, 1989 (p. 238)

[15] R. Buis; M.-T. L'Hardy-Halos; C. Lambert Characterization of the structure of a growth process, Acta Biotheor., Volume 44 (1996), pp. 359-375

[16] H.B. Lück; J. Lück Automata theoretical explanation of tissue growth, Proc. Int. Symp. Math. Topics Biol., Kyoto, 1978, pp. 174-185

[17] H.B. Lück; J. Lück Cell number and cell size in filamentous organisms (A. Lindenmayer; G. Rozenberg, eds.), Automata, Languages, Development, North-Holland, Amsterdam, 1976, pp. 109-124

[18] J. Monod Recherches sur la croissance de cultures bactériennes, Actualités scientifiques et industrielles, n^∘911, Hermann, Paris, 1942 (pp. 1–215)

[19] J.-R. Lobry; J.-P. Flandrois; G. Carret; A. Pavé Monod's bacterial growth model revisited, Bull. Math. Biol., Volume 54 (1992), pp. 117-122

[20] Lect. Notes Biomath., 68 (1980), pp. 1-511