Although the human genome project is yielding clues to thousands of new targets for drug development [1], selecting suitable targets is not easy, as we analyse here, and requires a systemic approach, i.e. one that recognizes that enzymes are organized into metabolic systems. Despite the triumphalism implicit in titles such as ‘Intelligent drug design’ [2] or ‘Drug discovery’ [3] for supplements in Nature and Science, there is now increasing recognition that intelligent drug design (or drug design tout court) remains something for the future, so that an industry analyst could recently write that ‘any regular reader cannot avoid being impressed by the startling failure of the pharmaceutical research effort’ [4]. Most currently prescribed antibiotics (and a good fraction of other drugs) are derivatives of agents in clinical use for 30 years or more [5], but this may appear less surprising when considered in the light of the low level of attention given to metabolism. The discovery of new classes of antibiotics has now virtually ceased—ten major classes discovered between 1935 and 1963; one class, the oxazolidones, since then—despite the urgent need for new antibiotics created by broad resistance to almost all existing ones by hospital-adapted pathogenic bacteria. In spite of genetic engineering, combinatorial chemistry, bioinformatics and so on, the impact of the human genome project on drug discovery has been disappointing.
Unfortunately ‘intelligent drug design’, at least as understood by authors who use the term, appears not to include the idea that what cells do is metabolism and a major thing drugs are supposed to do is to alter metabolism: of the 500 current targets 30% are enzymes and 45% are receptors [6]. To forget metabolism when discussing strategies for drug design [2] or drug discovery [3] (these two supplements barely mention metabolism) is a mistake.
Taking a broader view of biotechnology beyond the development of drugs, efforts to improve yields of industrial processes by overexpressing the enzymes thought to catalyse rate-limiting steps have been equally ineffective. As long ago as 1989 it was known from experiment that overexpressing phosphofructokinase in fermenting yeast by 250% had no perceptible effect on the flux to ethanol [7], a result subsequently confirmed in other organisms, but this knowledge did not prevent the investment of vast amounts of money in similarly fruitless quests. In 1989 one could perhaps have explained the absence of known examples of success in terms of commercial secrecy, but a decade later the only plausible explanation must be that no examples are known because no examples exist.
It is known from theoretical considerations [8] as well as experiments such as those in fermenting yeast [7] just mentioned, that increasing metabolic fluxes by significant amounts is very difficult. Decreasing them is easier, but still more difficult than one might hope. However, metabolite concentrations are much less stable than fluxes, and respond far more sensitively to perturbations in enzyme activities. This generalization is proving very helpful for probing the functions of supposedly silent genes [9] and it also suggests that pharmacological effects due to changes in metabolite concentration may be much easier to achieve than ones that require significant changes in fluxes. Significantly, ‘Roundup’ (N-phosphonomethylglycine), commercially by far the most successful of all herbicides, owes its effect to its capacity to raise the concentration of shikimate several hundredfold [10], and quinine, one of the more successful antimalarial drugs, likewise acts by increasing the concentration of haem in treated parasites to toxic levels [11]. Lithium, very effective in the treatment of manic depression, appears to exert its effect by decreasing the level of inositol [12]. Studying how such effects are brought about may offer a useful introduction to how intelligent drug design may one day become a reality. All three of the substances mentioned act by inhibiting enzymes, and all behave as uncompetitive inhibitors.
The common inhibition types are easily confused in experiments in the spectrophotometer, with the result that cases of mixed inhibition are frequently reported as competitive. However, steady-state experiments at substrate and product concentrations that are decided and fixed by the experimenter are very misleading as a model of inhibition in vivo, where concentrations are not fixed at all, and certainly not by an external agent such as an experimenter. For a typical enzyme that catalyses a reaction in the middle of a metabolic pathway it is a better approximation (though still not exact) to consider that the rate is fixed and that the substrate and products are adjusted by the enzymes that use them to whatever values will sustain the appropriate flux. In these conditions competitive and uncompetitive inhibition become very different from one another [13] and the uncompetitive component becomes the main determinant of the response of the system to a mixed inhibitor.
These points are illustrated in Fig. 1. When the inhibition is competitive (Fig. 1c), effects on both flux and metabolite concentrations are very slight, but all become much larger when the inhibition is uncompetitive (Fig. 1d). In the latter case, the slopes are small at very low inhibitor concentrations, but the significant curvature causes the lines to become rapidly much steeper as the inhibitor concentration increases. The essential point is that a molecule that competes with a substrate is a molecule that a substrate can compete with, and so the effect of a competitive inhibitor can be nullified by relatively minor adjustments of the concentrations of substrates and products around the inhibited enzyme. By contrast, effects of uncompetitive inhibitor are potentiated by the variations in substrate that they generate, and fairly modest levels of inhibition may therefore produce huge changes in substrate concentration. It is essentially this kind of effect that is exploited by Roundup, which inhibits 3-phosphoshikimate 1-carboxyvinyltransferase, uncompetitively with respect to 3-phosphoshikimate [10].
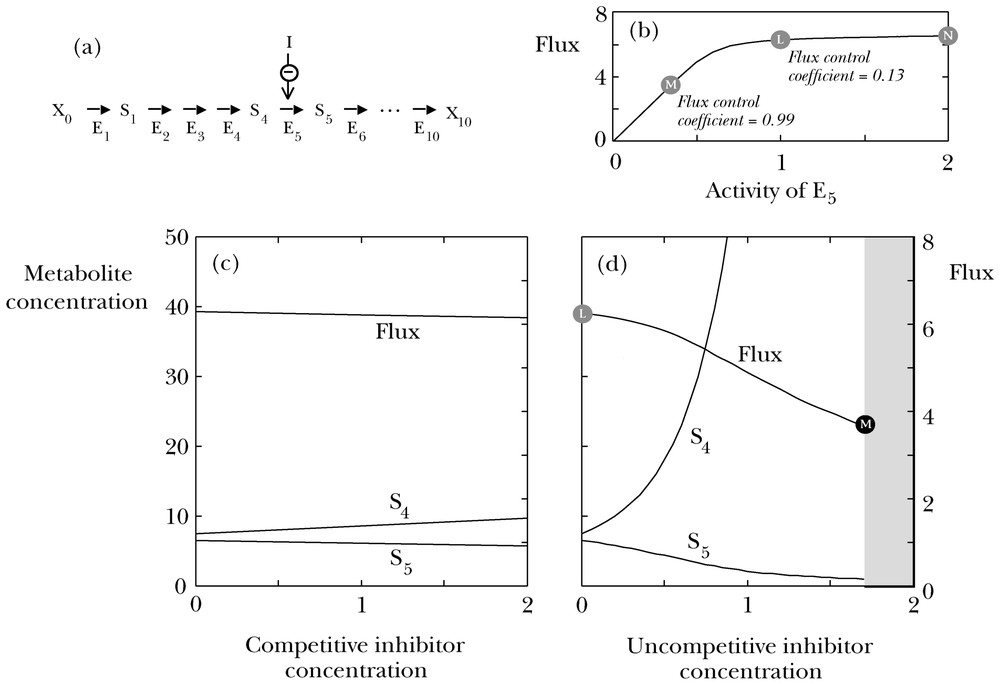
Effects of inhibition on an enzyme in the middle of a long pathway. Panel (a) shows a pathway of ten reactions converting a starting material X0 into a sink metabolite X10 via nine intermediates S1,S2,…,S9. The concentrations of X0 and X10 are assumed to be 10 and 0 (arbitrary units) respectively, and those of the intermediates are those necessary to achieve a steady state. Each enzyme apart from E5 is assumed to follow reversible Michaelis–Menten kinetics with limiting rate 10 in the forward direction, equilibrium constant 5 in favour of the forward direction, and Michaelis constants 1 and 5 for the forward and reverse reactions, respectively. In the case of E5, competitive inhibition was simulated by replacing the Michaelis constants for both directions by apparent values obtained by multiplying by a factor (1+[I]/Kic), where [I] is the inhibitor concentration and Kic=1; uncompetitive inhibition was simulated by replacing both limiting rates and Michaelis constants for both directions by apparent values obtained by multiplying by a factor (1+[I]/Kiu), where [I] is the inhibitor concentration and Kiu=1. Panel (b) shows the dependence of the flux through the pathway in the absence of inhibition on the activity of E5 relative to the basal state (point L). The point N illustrates how the flux would depend on enzyme activity if the basal activity were twofold higher. Panel (c) shows the effect of a competitive inhibitor on the flux through the pathway and on the concentrations of the substrate (S4) and product (S5) of E4. Metabolites earlier in the pathway behave like S4, and those later in the pathway like S5, but in both cases with smaller slopes. Panel (d) shows the corresponding effect of an uncompetitive inhibitor. No steady state could be reached in the grey region at inhibitor concentrations above 1.7. The point labelled L refers to the same state as the point labelled L in panel (b); the point labelled M refers to a state similar to that of the point labelled M in panel (b). The labelling of the left-hand ordinate axis in panel (c) applies also to panel (d), and the labelling of the right-hand ordinate axis in panel (d) applies also to panel (c). Note that although there is not a great difference between uncompetitive and competitive inhibition in vitro, the difference can be dramatic in vivo [13].
Fig. 1b shows the effects of varying enzyme activity without necessarily implying the presence of an inhibitor. In the basal state (point L on the curve), small variations in the activity of E5 are almost without effect: in relative terms, the effect on the flux is only 13% of the variation in enzyme activity. However, by the time the activity is decreased to about one-third (point M, corresponding approximately to the point in Fig. 1d, where the steady state is lost) changes in flux are almost exactly proportional to changes in enzyme activity. On the other hand, if the basal activity had been twofold higher (point N), the system could stand quite large changes in activity in either direction with almost no effect on the flux. This type of curve explains why organisms can usually tolerate quite large losses of activity of many enzymes with almost no effect on phenotype, as studied for example in the context of mitochondrial diseases [14,15].
Designing an inhibitor with significant uncompetitive character is a much more difficult task than designing a competitive inhibitor, because it cannot just be a substrate analogue. This difficulty is not an adequate reason for not attempting it, however, because solving a difficult task is likely to be more rewarding than solving an easy task if its solution is potentially useful and the solution to the easy problem potentially useless. Nonetheless, the systemic context of the inhibition always needs to be considered because there are at least two circumstances where uncompetitive inhibition may not be much more effective than competitive.
The first of these is that some enzymes do act in vivo in environments resembling the constant-concentration conditions of the spectrophotometer: an enzyme that acts on glucose at the beginning of a minor pathway, for example, will have very little effect on the glucose concentration in any ordinary conditions, because that is determined by controls on the major glucose-using pathways like glycolysis and glycogen synthesis; such an enzyme can therefore be treated like an enzyme in a spectrophotometer, and will respond to competitive inhibition as readily as to uncompetitive inhibition, unless feedback loops ensure that its activity responds to demand for the product of the minor pathway, in which case it may largely ignore any kind of inhibitor.
The second point is that as an uncompetitive inhibitor can only have an important effect in vivo if the metabolite concentrations can increase by a large amount, in practice many potential targets may not fulfil this requirement because of stoichiometric constraints: a metabolite concentration can only show a large response to changes in the activities of enzymes that consume it or produce it if it is largely free from stoichiometric constraints. Some constraints are obvious from inspection: for example, in a cell with a fixed total NAD concentration the concentrations of neither reduced nor oxidized NAD can exceed the fixed total. However, much more complicated constraints may also exist, and identifying these may require stoichiometric analysis by computer.
Glycolysis in Trypanosoma brucei (Fig. 2), illustrates all of these points. It not only provides an example of a stoichiometric relationship that one would be unlikely to discover by inspection, but it is also a very attractive system to model in the computer for several other reasons. T. brucei is responsible for a disease of major economic importance, African sleeping sickness, and is thus a major focus of research into tropical diseases. Its bloodstream form has possibly the simplest metabolism of any known organism, glycolysis accounting for nearly all of its metabolic activity, with glucose its only energy source [16,17]. There is therefore some hope that it may be possible to model essentially the whole of its metabolism in the computer with experimentally determined parameters for all the enzymes. Not only that, but most of the currently available kinetic data come from a single research group working to high standards, so variations due to arbitrary differences between the conditions used in different laboratories are largely avoided. All of this allowed the construction of a computer model [18,19] that is about 60% complete, in the sense that it includes about 60% of the experimentally determined values that an ideal model would contain. With the possible exception of models of the human erythrocyte [20] no other metabolic model even approaches this degree of completeness.

The glycolytic pathway in bloodstream form Trypanosoma brucei. There are four compartments, labelled Host blood, Cytosol, Glycosome and Mitochondrion. Dihydroxyacetone phosphate and glycerol 3-phosphate diffuse between the glycosome and the cytosol, but the two transport steps are not explicitly shown; glycerol 3-phosphate is reoxidized under aerobic conditions to dihydroxyacetone phosphate on the membrane of the mitochondrion. ‘GROWTH’ represents all of the steps in the rest of metabolism that are driven by dephosphorylation of ATP. Each of the metabolites labelled is counted once in the stoichiometric constraint discussed in the text; each of those labelled is counted twice. Of the potential targets for a drug, the step labelled ‘Pyruvate transporter’ is the only one that escapes elimination for the reasons discussed in the text.
Although at first sight the model in Fig. 2 suggests numerous potential targets for drug design, metabolic simulations have shown that the real number of useful targets is much smaller: in practice only one, the pyruvate transporter. Computer analysis of the model in Fig. 2 revealed four distinct stoichiometric constraints on the metabolite concentrations. (The matrix algebra necessary to arrive at the stoichiometric relationships systematically is explained elsewhere [21].) Three of these—the sums of the concentrations of oxidized and reduced NAD in the glycosome, of adenine nucleotides in the glycosome, and of adenine nucleotides in the cytosol—are obvious from inspection, but the fourth, involving the metabolites marked by asterisks in the scheme, is not. It includes most of the transferable phospho groups in the glycosome, but not all of them: 3-phosphoglycerate is not involved, and 1,3-bisphosphoglycerate is counted only once even though it has two transferable phospho groups; it also includes cytosolic dihydroxyacetone phosphate and glycerol 3-phosphate (but not other cytosolic molecules, such as cytosolic ATP). Once recognized, this relationship can be rationalized as representing that part of the glycosomal phosphate pool that is not accounted for by uptake of inorganic phosphate and export of 3-phosphoglycerate.
The existence of the stoichiometric constraints may appear to be of purely academic interest, but they have a practical importance as well, because they place severe restrictions on the possible targets of an inhibitor intended to destroy the trypanosome by acting in a similar way to Roundup in plants. As the four constraints involve nearly all of the metabolites in the glycosome, they rule out many of the enzymes as useful targets for uncompetitive inhibition. Of the few that remain, all but the pyruvate transporter are ruled out by other considerations [19], so that instead of the wealth of potential targets suggested by visual inspection of Fig. 2 there is in reality just one. Until recently we overlooked a paper that bears directly on this point, and suggested the pyruvate transporter as a good target on the basis of theoretical analysis [19] without mentioning the experimental observation that inhibiting it in vivo does indeed cause the pyruvate concentration to rise, followed by osmotic shock and, probably, death [22].
A frequent difficulty in simulations of metabolic pathways is the absence of experimentally determined kinetic parameters for reverse reactions, especially for reactions considered to be irreversible. Normally the researcher has to choose between guessing the parameters for the reverse reaction from the equilibrium constant, or treating the reaction as irreversible. When the equilibrium constant is very high, as with pyruvate kinase, one may expect it not to matter one way or the other, but when simulating the T. brucei model we found that it did. The distribution of flux control was quite different in the two cases, with pyruvate transport, a step with no control at all with pyruvate kinase irreversible, becoming the second most important step when pyruvate kinase was allowed to be reversible. This was a surprising result, and although resolving it was not very important for the T. brucei model as such, it was desirable to study the general implication that all metabolic models would need to be composed entirely of reversible steps if they were to give valid predictions.
The explanation [23] of this apparent anomaly proved to be quite simple, and relates more to the practices of biochemists than to the underlying biochemistry. There is no fundamental reason why an irreversible reaction should be insensitive to its product, as one may readily see from the reversible form of the Michaelis–Menten equation [24]:
| (1) |
In the case of the model of glycolysis in T. brucei, making pyruvate kinase subject to inhibition by pyruvate (but still irreversible) proved sufficient to render the behaviour indistinguishable from that with a fully reversible equation for this enzyme [23]. Thus the absence of product inhibition and not of reversibility was responsible for the anomaly noted earlier [19]. What is important is transfer through the pathway of information about the concentrations of metabolites: adequate regulation of any metabolic pathway requires mechanisms for enzymes early in the pathway to receive information about the concentrations of metabolites at the end [23]. The simplest mechanism is provided by serial product inhibition of all the enzymes in the system, but although this can regulate fluxes quite adequately it is very unsatisfactory for living systems because variations in flux are accompanied by huge variations in metabolite concentrations. In practice, therefore, living organisms virtually always obtain a more direct transfer of information by incorporating cooperative feedback inhibition [25].
The human genome project is suggesting as many as 30 000 human gene products as research targets for drug development. Testing all these will be extremely expensive, with operation on a very large scale, and it will be essential to make efforts to restrict the number of targets to ones with a real chance of success. Metabolic simulation, as discussed here, can help enormously to reduce the costs.



