Fuelwood harvesting in Niger and a generalization of Faustmann's formula

Nicolas Bacaër; Alassane Bah; Ali Mahamane

doi:10.1016/j.crvi.2004.10.017

Biological modelling / Biomodélisation

Fuelwood harvesting in Niger and a generalization of Faustmann's formula
[Récolte de bois de feu au Niger et une généralisation de la formule de Faustmann]

Présenté par : Pierre Auger

Nicolas Bacaër ¹ ; Alassane Bah ² ; Ali Mahamane ³

¹ Institut de recherche pour le développement (IRD), 32, avenue Henri-Varagnat, 93143 Bondy cedex, France
² DGI–SMA, École supérieure polytechnique, université Cheikh-Anta-Diop de Dakar, BP 15915 Dakar-Fann, Sénégal
³ Département de biologie, faculté des sciences, université Abdou-Moumouni de Niamey, BP 10662 Niamey, Niger

Comptes Rendus. Biologies, Volume 328 (2005) no. 4, pp. 379-385.

Résumés

Anglais
Français

In some forests of Niger where ‘controlled rural markets’ have been organized, fuelwood is harvested following a policy of the form: every T year, cut the dead trees and those live trees which have a diameter greater than D. Dead trees generally form the main part of the harvest. In this paper, we present a simple continuous time model for the management of these uneven-aged stands subject to a high natural death rate α, and we derive a formula for the cycle length and the diameter optimizing the discounted income over an infinite horizon. Faustmann's classical formula for even-aged stands corresponds to the limit $α \to 0$ and $D = 0$ (clear-cut).

Dans certaines forêts du Niger où ont été établis des « marchés ruraux contrôlés », le bois de chauffe est récolté suivant une politique de la forme : tous les T années, couper les arbres morts et les arbres vivants d'un diamètre supérieur à D. Les arbres morts constituent en général la majeure partie de la récolte. Dans cet article, on présente un modèle simple en temps continu pour la gestion de ces parcelles forestières inéquiennes sujettes à un taux de mortalité α élevé, et on obtient une formule pour le cycle et le diamètre de coupe optimisant le revenu actualisé avec un horizon infini. La formule classique de Faustmann pour les parcelles équiennes correspond à la limite $α \to 0$ et $D = 0$ (coupe claire).

Métadonnées

Reçu le : 2004-02-20
Accepté le : 2004-10-19
Publié le : 2005-02-05

PMID

DOI : 10.1016/j.crvi.2004.10.017

Keywords: Forest management, Uneven-aged stand, Modelling, Optimization, Fuelwood, Niger
Mot clés : Sylviculture, Forêt inéquienne, Modélisation, Optimisation, Bois de feu, Niger

Affiliations des auteurs :

Nicolas Bacaër ¹ ; Alassane Bah ² ; Ali Mahamane ³

@article{CRBIOL_2005__328_4_379_0,
     author = {Nicolas Baca\"er and Alassane Bah and Ali Mahamane},
     title = {Fuelwood harvesting in {Niger} and a generalization of {Faustmann's} formula},
     journal = {Comptes Rendus. Biologies},
     pages = {379--385},
     publisher = {Elsevier},
     volume = {328},
     number = {4},
     year = {2005},
     doi = {10.1016/j.crvi.2004.10.017},
     language = {en},
}

TY  - JOUR
AU  - Nicolas Bacaër
AU  - Alassane Bah
AU  - Ali Mahamane
TI  - Fuelwood harvesting in Niger and a generalization of Faustmann's formula
JO  - Comptes Rendus. Biologies
PY  - 2005
SP  - 379
EP  - 385
VL  - 328
IS  - 4
PB  - Elsevier
DO  - 10.1016/j.crvi.2004.10.017
LA  - en
ID  - CRBIOL_2005__328_4_379_0
ER  -

%0 Journal Article
%A Nicolas Bacaër
%A Alassane Bah
%A Ali Mahamane
%T Fuelwood harvesting in Niger and a generalization of Faustmann's formula
%J Comptes Rendus. Biologies
%D 2005
%P 379-385
%V 328
%N 4
%I Elsevier
%R 10.1016/j.crvi.2004.10.017
%G en
%F CRBIOL_2005__328_4_379_0

Nicolas Bacaër; Alassane Bah; Ali Mahamane. Fuelwood harvesting in Niger and a generalization of Faustmann's formula. Comptes Rendus. Biologies, Volume 328 (2005) no. 4, pp. 379-385. doi : 10.1016/j.crvi.2004.10.017. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2004.10.017/

Version originale du texte intégral

1 Introduction

In Niger, fuelwood is still the most important source of energy for cooking food. Because of drought, of a growing urban population, and of a partially uncontrolled access to the resource, pressure on forests around cities such as Niamey is high. Since 1989, a new governmental strategy has led to the protection of some forest areas, where harvesting is managed to ensure sustainability. The yield is then sold exclusively in neighboring state-approved markets. A differential tax system encourages traders to buy fuelwood from these structures instead of organizing the harvesting of uncontrolled forests [1].

Two management systems have been selected. In the ‘oriented rural markets’, only dead trees are harvested. In the ‘controlled rural markets’, apart from the dead trees, some live trees are also cut and the cutting is organized as a cycle to allow spatial rotation. A lower bound for the diameter of the live trees to be cut is sometimes fixed. It may take several cycles for a live tree to reach this diameter, so that dead trees form in general the main part of each harvest. Typically, cycle length is fixed between 5 and 10 years.

The harvesting policy in these ‘controlled rural markets’ is therefore quite similar to the selective logging practised in uneven-aged forests of other parts of the world. But the importance of the dead trees is rather unusual because of the destination (dead wood is more appropriate than recently cut green wood for cooking food), the absence of transformation, and its availability (the Sahelian climate induces a high death rate for the trees).

Despite the large literature dealing with various extensions of Faustmann's classical formula [2,3] for the optimal rotation problem ([4], and over 300 papers listed in [5]), no simple closed formula has been proposed for the optimal cutting cycle and diameter of uneven-aged stands subject to a high natural death rate, where dead trees form the main part of the harvest to be used as fuelwood. In [6], a closed formula was derived but for even-aged stands subject to a low catastrophic death rate such as fire. The model used continuous time, and the formula was found using the theory of renewal reward processes. It should be emphasized that for high natural death rate, isolated trees die from time to time and there may be a delay before they are cut during the next planned harvest. On the contrary, for a catastrophic death rate such as fire, the whole forest is affected almost instantly and the trees are removed shortly after. In the first case, simple spatial rotation can be maintained while in the second case, as stressed in [6], it cannot.

In [7], a closed formula generalizing Faustmann's formula to uneven-aged stands was derived, but the model focused only on the economics and did not consider any particular biological growth model. In [8], this formula was used in combination with a discrete-time matrix model similar to [9,10] for the growth, but no simple formula for the optimal cutting cycle could be found so that the results had to rely on simulations. Many references such as [11,12] stress the fact that Faustmann's model and many of its generalizations are particular examples of Markov decision processes, for which dynamic programming techniques can be used. The focus is then more on numerical algorithms than on simple closed formulas. In all these references, little attention was generally paid to natural death rate, because in the European or North-American context, it is rather negligible compared to several other factors.

The goal of this paper is therefore to derive – in the framework of a simple model for uneven-aged stands subject to a high natural death rate – a closed formula for the optimal cycle length and cutting diameter. The optimization criterion will be the same as in Faustmann's model, namely the discounted income over an infinite horizon. The interest is mainly theoretical since obviously, despite [13], much field work is still needed to obtain sufficient data to calibrate the model for the forests of Niger. However, as more and more ‘controlled rural markets’ are being organized in Niger and in the whole Sahelian region, more data may become available and the interest may shift from ‘how to manage the forest’ to ‘how to optimize the management’. The model is also intended to serve as the basis for the development of more complex and more realistic models, to take into account, for example, the price fluctuations reported in [14].

The plan of the paper is the following. In Section 2, the notations of the model are introduced. In Section 3, a formula is derived for the optimal cutting cycle and diameter, and it is discussed using a simple mathematical expression for the trees' growth curve. In Section 4, it is shown that Faustmann's classical formula corresponds to the limit of a negligible death rate ( $α \to 0$ ) and of a cutting diameter $D = 0$ (clear-cut). It is also shown that the formula for the average yield of even-aged stands subject to a low but catastrophic death rate such as fire given in [6] corresponds to the limit of a cutting cycle length $T \to 0$ with a discounting factor $β \to 0$ . Further extensions of the formula – to an age-dependent death rate and to a possible difference in price between dead trees and recently cut green trees – are also presented. They may be useful in other contexts.

2 A simple model

Suppose that a stand of trees has a fixed number N of spots for trees to grow (N is large). Suppose that $V (x)$ is the volume of a tree with age x, and that $V (0) = 0$ . Suppose that the price P per unit volume of the wood is constant. Let c be the cost of preparation for the growth of one new tree, and $c^{'}$ be a fixed cost per harvest. Let α be the death rate of the trees: during a short interval of time dt, $α d t$ is the percentage of the trees which die (if we think about the model as being deterministic), or the probability for one tree of dying (if we think about the model as being stochastic). For the moment, α is supposed to be independent of age, but this assumption will be relaxed in Section 4.

Suppose that the length of the cutting cycle is T and that every T year, the harvest consists of all dead trees and of those live trees which have a diameter greater than D. Let X be the age at which trees reach the diameter D. Regeneration is supposed to be purely artificial: trees that have been cut are replaced without delay by new trees with age 0, so that the total number of trees stays constant. Natural regeneration is supposed to be negligible during one rotation. Finally, let β be a discounting factor such that income at time $t = n T$ is weighted by the factor $e^{- β n T}$ in the optimization criterion. The problem is to choose T and X in order to optimize the expected discounted income over all future harvests.

Formally, if $p (x, t)$ is the expected age-specific population density of live trees at time t, if $q (x, t)$ is the expected age-specific population density of dead trees at time t (when they die, trees stop aging), and if $K_{n}$ is the expected income of the harvest at time $t = n T$ , then the problem can be formulated as a system of partial differential equations with impulse control. Recall that these partial differential equations are just the continuous-time equivalent of the discrete-time age-structured matrix models. Such an approach was adopted, for example, in [15,16], but for steady instead of periodic harvesting of forests. Between the harvests ( $n T < t < (n + 1) T$ ), the functions satisfy

\frac{\partial p}{\partial t} + \frac{\partial p}{\partial x} + α p (x, t) = 0

\frac{\partial q}{\partial t} = α p (x, t)

and

p (0, t) = 0

. If

n T^{-}

and

n T^{+}

mean, respectively, ‘just before

t = n T

’ and ‘just after

t = n T

’, then

p (x, n T^{+}) = [\int_{0}^{\infty} q (ξ, n T^{-}) d ξ + \int_{X}^{\infty} p (ξ, n T^{-}) d ξ] δ_{x = 0} + p (x, n T^{-}) 1_{x \in (0, X)}

and

q (x, n T^{+}) = 0

. Here,

δ_{x = 0}

stands for Dirac's mass at

x = 0

, and

1_{x \in (0, X)}

for the characteristic function of the interval

(0, X)

. The expected income at

t = n T

K_{n} = \int_{0}^{\infty} q (x, n T^{-}) [P V (x) - c] d x + \int_{X}^{\infty} p (x, n T^{-}) [P V (x) - c] d x - c^{'}

and the objective is to maximize with respect to T and X the expected discounted income over all future harvests

\sum_{n = 1}^{\infty} e^{- β n T} K_{n}

The functions

p (x, t)

and

q (x, t)

also satisfy some initial conditions such that

\int_{0}^{\infty} [p (x, 0) + q (x, 0)] d x = N

. When

α = 0

and

X = 0

, this model is equivalent to Faustmann's classical model for the optimal rotation problem.

3 Optimal cutting cycle and diameter

Whatever the age structure of the initial conditions, it can be easily realized that the age specific densities $p (x, t)$ and $q (x, t)$ converge after a certain number of years to T-periodic solutions $\hat{p} (x, t)$ and $\hat{q} (x, t)$ which satisfy

\hat{p} (x, n T^{-}) = N \frac{1 - e^{- α T}}{1 - e^{- i α T}} \sum_{k = 1}^{i} e^{- k α T} δ_{x = k T}

\hat{q} (x, n T^{-}) = N \frac{1 - e^{- α T}}{1 - e^{- i α T}} α e^{- α x} 1_{x \in (0, i T)}

\hat{p} (x, n T^{+}) = N \frac{1 - e^{- α T}}{1 - e^{- i α T}} \sum_{k = 0}^{i - 1} e^{- k α T} δ_{x = k T}

and

\hat{q} (x, n T^{+}) = 0

, where for convenience we set

i = [X / T] + 1

(and

[X / T]

is the integer part of

X / T

). Notice that if

X < T

(so that

i = 1

), all the live trees reaching

t = n T^{-}

have the same age (even-aged stand) and are all harvested at

t = n T

together with the dead trees (clear-cut). On the contrary, if

X > T

(so that

i ⩾ 2

), live trees reaching

t = n T^{-}

have ages

T, 2 T, \dots, i T

(uneven-aged stand) and only those aged iT are harvested at

t = n T

together with the dead trees (selection). Hence, the integer i represents the number of cycles a tree can continue growing before being harvested – unless it dies before, in which case the tree is harvested during the first harvest following its death. The dead trees harvested at

t = n T

give the income

N \frac{1 - e^{- α T}}{1 - e^{- i α T}} \int_{0}^{i T} α e^{- α x} [P V (x) - c] d x

The live trees harvested at

t = n T

are those aged iT. They give the income

N \frac{1 - e^{- α T}}{1 - e^{- i α T}} e^{- i α T} [P V (i T) - c]

The total income at

t = n T

is therefore (after integration by parts)

K_{n} = N \frac{1 - e^{- α T}}{1 - e^{- i α T}} [P \int_{0}^{i T} e^{- α x} V^{'} (x) d x - c] - c^{'}

Finally, the expected discounted income over all future harvests is

\frac{1}{e^{β T} - 1} {N \frac{1 - e^{- α T}}{1 - e^{- i α T}} [P \int_{0}^{i T} e^{- α x} V^{'} (x) d x - c] - c^{'}}

(1)

for which the maximum is to be found with respect to T and X. Equivalently, the maximum is to be found with respect to T and the integer

i = [X / T] + 1

. This is the generalization of Faustmann's classical formula for the policy considered (as will be shown in the next section). To reduce the number of parameters for the discussion, let us rewrite this formula as

N P V_{\infty} \frac{1}{e^{β T} - 1} {\frac{1 - e^{- α T}}{1 - e^{- i α T}} [\int_{0}^{i T} e^{- α x} \frac{V^{'} (x)}{V_{\infty}} d x - \frac{c}{P V_{\infty}}] - \frac{c^{'}}{N P V_{\infty}}}

where

V_{\infty}

is the maximum volume a tree can reach during its lifetime. Notice that

c / (P V_{\infty})

is the ratio between the cost of cutting and replanting one tree and the maximum value of a tree, whereas

c^{'} / (N P V_{\infty})

is the ratio between the fixed cost per harvest and the maximum value of the stand.

To discuss the formula, consider a simple mathematical expression for the growth curve of the trees $V (x)$ , or equivalently for its derivative $V^{'} (x)$ , for example,

V^{'} (x) = V_{\infty} \frac{{(γ / τ)}^{γ + 1}}{Γ (γ + 1)} x^{γ} e^{- γ x / τ}

where Γ is the usual Gamma function. This function – which is supposed to represent the growth speed – increases from 0 to a maximum reached at

x = τ

, and then decreases to 0 as

x \to \infty

. So

V (x) = \int_{0}^{x} V^{'} (ξ) d ξ

is an increasing function which is convex for

x < τ

and concave for

x > τ

. The parametrization also stresses the maximum volume of a tree

V_{\infty} = \lim_{x \to \infty} V (x)

Fig. 1 illustrates how the expected discounted income can vary as a function of the length T of the cutting cycle for different values of the cutting diameter (corresponding to $i = 1 \dots 4$ ). The curve most to the right is the one for $i = 1$ (clear-cutting and even-aged management). The optimal strategy is obtained with $T^{*} ≃ 9.5$ and $i = 2$ , i.e., by cutting every $T^{*}$ years the dead trees and the live trees aged $2 T^{*}$ or more. Notice that all curves become negative when T approaches 0 because of the nonzero fixed cost per harvest. The parameter values used for this figure are $α = 0.05$ per year (life expectation of $1 / α = 20$ years for the trees), $τ = 10$ years (age at which the growth is the fastest) and $γ = 2$ for the growth curve, a discounting factor $β = 0.03$ per year, costs $c / (P V_{\infty}) = 0$ and $c^{'} / (N P V_{\infty}) = 0.1$ , and a normalized maximum forest value $N P V_{\infty} = 1$ .

Fig. 1
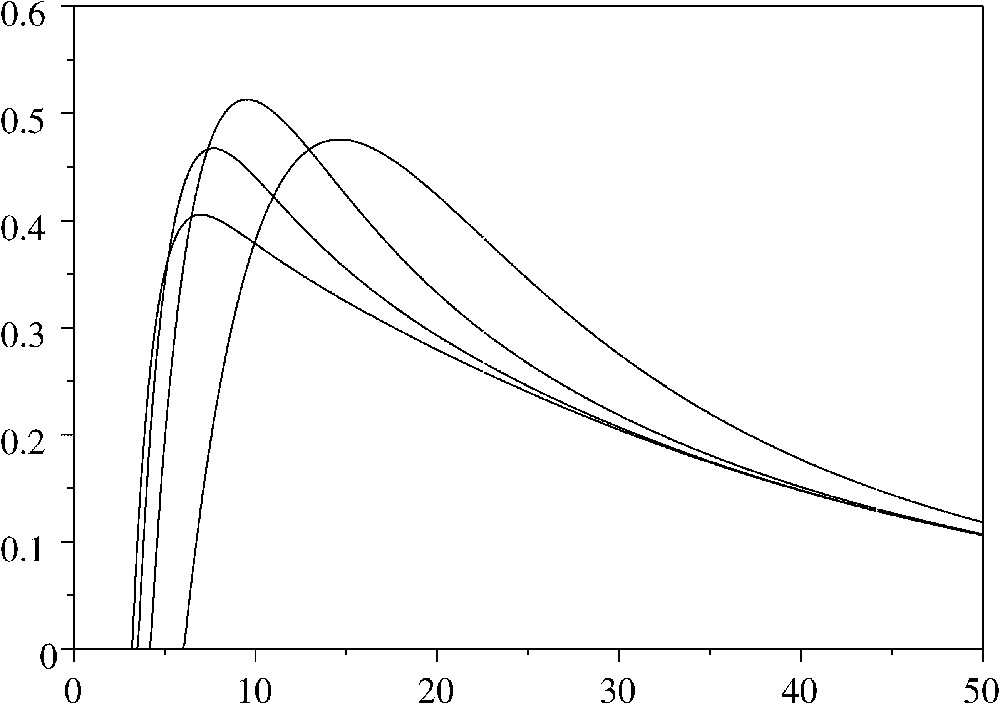
Expected discounted income as a function of the cutting-cycle length T for different values of the cutting diameter (corresponding to i=1…4).

Fig. 2 illustrates how the optimal cutting cycle and diameter can change when the death rate α, the discounting factor β, and the fixed cost per harvest $c^{'}$ vary. The values for the fixed parameters are the same as for Fig. 1. As can be expected, uneven-aged management with a short cutting cycle (represented by areas labelled $i = 2$ and $i = 3$ ) appears more profitable than even-aged management ( $i = 1$ ) when the death rate is high (top-left and top-right diagram), when the discounting factor is high (top-left and bottom diagram), or when the fixed cost per harvest is low (top-right and bottom diagram). Notice from the top-left (respectively, top-right) diagram that even in the limit $α \to 0$ (the case of Faustmann's model), uneven-aged management becomes more profitable than even-aged management if the discounting factor (respectively, fixed cost per harvest) is above (respectively, below) a certain threshold value.

Fig. 2
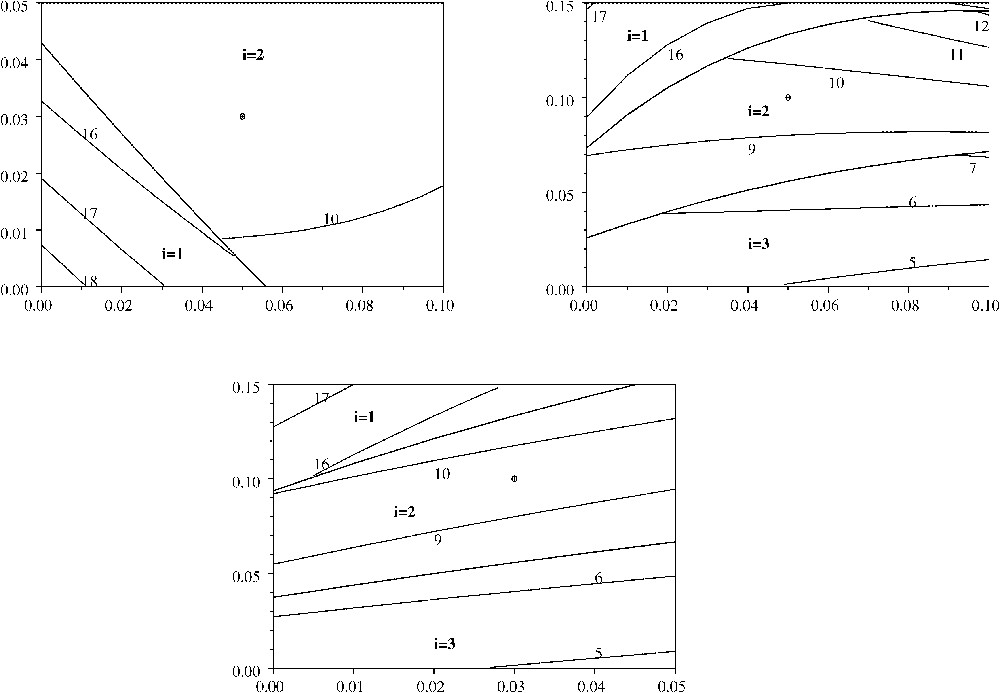
Optimal cutting cycle and diameter when the death rate α, the discounting factor β and the fixed cost per harvest $c^{'}$ vary. Top left: (α,β) plane. Top right: $(α, c^{'} / N P V_{\infty})$ plane. Bottom: $(β, c^{'} / N P V_{\infty})$ plane. The bold lines separate the areas labelled i=1 (where even-aged forest management is optimal) from i=2 and i=3 (where uneven-aged forest management is optimal). The other lines are level curves of the optimum length of the cutting cycle. In each case, a point reminds of the parameter values of Fig. 1.

Fig. 2 also shows the level curves of the optimum length of the cutting cycle. Notice that there is no simple relationship between the optimal length of the cutting cycle and the death rate: the former may be an increasing or a decreasing function of the latter, depending on parameter values, as in the top-right diagram.

4 Limit cases, extensions

If one sets the critical diameter D to cut the live trees to 0 (clear-cut), then the corresponding age is $X = 0$ . So $i = 1$ , and formula (1) reduces to

\frac{1}{e^{β T} - 1} {N [P \int_{0}^{T} e^{- α x} V^{'} (x) d x - c] - c^{'}}

If moreover the fixed cost per harvest

c^{'}

and the death rate α are negligible, the formula reduces further to Faustmann's formula [2,3]

N \frac{P V (T) - c}{e^{β T} - 1}

Another limiting case is obtained by letting the discounting factor β and the cutting cycle length T tend to 0, which corresponds to looking at the average income with a permanent screening of the forest to harvest dead trees and live trees aged over X. Recalling the relationship between average income per year and discounted income over all future harvests

\lim_{ν \to \infty} \frac{1}{ν T} \sum_{n = 1}^{ν} K_{n} = \lim_{β \to 0} β \sum_{n = 1}^{\infty} e^{- β n T} K_{n}

and keeping

c^{'} = 0

, formula (1) then leads to the average income

N α \frac{P \int_{0}^{X} e^{- α x} V^{'} (x) d x - c}{1 - e^{- α X}}

(2)

and the age-specific densities

p (x, t)

and

q (x, t)

converge to the steady solutions

\hat{p} (x) = N \frac{α e^{- α x}}{1 - e^{- α X}} 1_{x \in (0, X)}

and

\hat{q} (x) = 0

. Formula (2) is the same as the one given in [6] for the average income in forests subject to the risk of catastrophic fire. Indeed, when

T \to 0

, there is no delay between the death of the tree and its harvesting as in [6]. So it is normal for the average income to be the same. However, the synchronization of the deaths in the case of fire induces a difference for the expression of the discounted income.

Extensions. Suppose now that the death rate, instead of being constant, depends on age. Set $Δ (x) = \exp (- \int_{0}^{x} α (ξ) d ξ)$ . Suppose that the price of dead wood is Q, which can differ from the price of recently cut green wood P. The expected discounted income over all future harvests is then

\frac{1}{e^{β T} - 1} {N (\frac{Δ (i T) [P V (i T) - c]}{\sum_{n = 0}^{i - 1} Δ (n T)} - \frac{\int_{0}^{i T} Δ^{'} (x) [Q V (x) - c] d x}{\sum_{n = 0}^{i - 1} Δ (n T)}) - c^{'}}

where again

i = [X / T] + 1

. Formula (1) corresponds to a constant α – so that

Δ (x) = \exp (- α x)

– and to

Q = P

. In the limit

β \to 0

and

T \to 0

, this formula (with

c^{'} = 0

) leads to the average income

N \frac{Δ (X) [P V (X) - c] - \int_{0}^{X} Δ^{'} (x) [Q V (x) - c] d x}{\int_{0}^{X} Δ (x) d x}

a formula which was given in [6] in the context of forests under the risk of fire with possible salvage of the burnt wood.

5 Conclusion

In the framework of a simple model, a formula for the optimal cutting cycle and diameter was derived when the harvesting policy consists in cutting every T year the dead trees and the live trees with a diameter greater than a fixed value D. The model was designed for forests subject to a high natural death rate, where dead trees form the main part of the harvest and are used as fuelwood. It was seen that uneven-aged management was more profitable under such circumstances. For a low natural death rate, a low discounting factor, or a high fixed cost per harvest, even-aged management can be more profitable.

Forest management in Niger and in other Sahelian countries is still in its early phase. Rotation has been introduced only a decade ago. Field data are still very limited. Though a considerable amount of research has been accumulated during more than 150 years concerning the optimal rotation problem in developed countries, adaptation to local conditions is necessary. In this study, we focused on only one specific aspect, namely the high natural death rate. Hopefully, this microeconomic model will be combined with the macroeconomic models [17–19] to provide a more complete modelling tool to decision makers.

Acknowledgments

The second author would like to thank Édith Perrier (IRD), Alain Bertrand, Martine Antona, Christophe Le Page (CIRAD) and Aboubacar Ichaou (Environment Department of Niger). This paper is dedicated to the memory of Ovide Arino.

Bibliographie

[1] J.M. d'Herbès; J.M.K. Ambouta; R. Peltier Fonctionnement et gestion des écosystèmes forestiers contractés sahéliens, John Libbey Eurotext, Paris, 1997

[2] M. Faustmann Berechnung des Wertes welchen Waldboden sowie noch nicht haubare Holzbestände für die Waldwirtschaft besitzen, Allg. Forst- und Jagd-Z., Volume 15 (1849), pp. 7-44 (English transl. J. Forest Econ., 1, 1995)

[3] C.W. Clark Mathematical Bioeconomics: The Optimal Management of Renewable Resources, John Wiley & Sons, New York, 1990

[4] D.H. Newman, The optimal forest rotation: a discussion and annotated bibliography, USDA Forest Service, Technical Report SE-48, Ashville, OH, USA, 1988

[5] D.H. Newman Forestry's golden rule and the development of the optimal forest rotation literature, J. Forest Econ., Volume 8 (2002), pp. 5-27

[6] W.J. Reed; D. Errico Assessing the long-run yield of a forest stand subject to the risk of fire, Can. J. For. Res., Volume 15 (1985), pp. 180-190

[7] S.J. Chang Determination of the optimal growing stock and cutting cycle for an uneven-aged stand, For. Sci., Volume 27 (1981), pp. 739-744

[8] S. Sanchez Orois; S.J. Chang; K. von Gadow Optimal residual growing stock and cutting cycle in mixed uneven-aged maritime pine stands in Northwestern Spain, For. Policy Econ., Volume 6 (2004), pp. 145-152

[9] M.B. Usher A matrix approach to the management of renewable resources, with special reference to the selection forests, J. Appl. Ecol., Volume 8 (1966), pp. 355-367

[10] J. Buongiorno; B.R. Michie A matrix model of uneven-aged forest management, For. Sci., Volume 26 (1980), pp. 609-625

[11] J. Buongiorno Generalization of Faustmann's formula for stochastic forest growth and prices with Markov decision process models, For. Sci., Volume 47 (2001), pp. 466-474

[12] J. Buongiorno; J.K. Gilless Decision Methods for Forest Resource Management, Academic Press, Boston, 2003

[13] A. Ichaou, Dynamique et productivité des structures forestières contractées des plateaux de l'ouest nigérien, PhD thesis, University Toulouse-3, France, 2000

[14] A. Manvell; G. Shepherd Woodfuel in Niger: crisis or adaptation in the last ten years? http://www.handels.gu.se/econ/EEU/cifor.html (Overseas Development Institute, 2001)

[15] C. Rorres; W. Fair Optimal age specific harvesting policy for a continuous-time population model (T.A. Burton, ed.), Modeling and Differential Equations in Biology, Marcel Dekker, New York, 1980, pp. 239-254

[16] R. Goetz; A. Xabadia Applications of distributed optimal control in economics – the case of forest management http://www2.fundacion-centra.org/pdfs/E200337.pdf (Working paper, 2003)

[17] CSFD Pour une gestion viable des ressources ligneuses péri-urbaines : analyse et modélisation des impacts des règles et des pratiques coutumières sur divers milieux naturels sahéliens et sahélo-soudaniens au Niger et au Mali http://www.csf-desertification.org/projets/projet3.php

[18] J. Woodwell Fuelwood and land use in West Africa: understanding the past to prepare for the future http://www.dec.org/pdf_docs/PNACQ877.pdf (Report, 2002)

[19] MARGE Le modèle GLOBUS http://www.marge.fr

Commentaires - Politique

Ces articles pourraient vous intéresser

Access to drinking water and health of populations in Sub-Saharan Africa

Julien Ntouda; Fondo Sikodf; Mohamadou Ibrahim; ...

C. R. Biol (2013)

Towards a statistical mechanics of cities

Luís M.A. Bettencourt

C. R. Phys (2019)