A simple framework to describe the regulation of gene expression in prokaryotes

Filipa Alves; Rui Dilão

doi:10.1016/j.crvi.2005.01.009

Biological modelling / Biomodélisation

A simple framework to describe the regulation of gene expression in prokaryotes
[Un cadre simple décrivant l'expression génique chez les procaryotes]

Présenté par : Pierre Auger

Filipa Alves ¹ ; Rui Dilão ¹

¹ Non-Linear Dynamics Group, Instituto Superior Técnico, Department of Physics, Av. Rovisco Pais, 1049-001 Lisboa, Portugal

Comptes Rendus. Biologies, Volume 328 (2005) no. 5, pp. 429-444.

Résumés

Anglais
Français

Based on the bimolecular mass action law and the derived mass conservation laws, we propose a mathematical framework in order to describe the regulation of gene expression in prokaryotes. It is shown that the derived models have all the qualitative properties of the activation and inhibition regulatory mechanisms observed in experiments. The basic construction considers genes as templates for protein production, where regulation processes result from activators or repressors connecting to DNA binding sites. All the parameters in the models have a straightforward biological meaning. After describing the general properties of the basic mechanisms of positive and negative gene regulation, we apply this framework to the self-regulation of the trp operon and to the genetic switch involved in the regulation of the lac operon. One of the consequences of this approach is the existence of conserved quantities depending on the initial conditions that tune bifurcations of fixed points. This leads naturally to a simple explanation of threshold effects as observed in some experiments.

En partant de la loi d'action de masse bimoléculaire et des lois dérivées de conservation de masse, nous proposons un cadre mathématique permettant de décrire la régulation de l'expression génique chez les procaryotes. On montre que les modèles dérivés possèdent tous les propriétés qualitatives des mécanismes régulatoires d'activation et d'inhibition observés expérimentalement. La construction basique considère les gènes comme des modèles types pour la production de protéines, pour lesquels les processus de régulation résultent d'activateurs or de répresseurs connectant les sites de liaison de l'ADN. Tous les paramètres de ces modèles ont une signification biologique manifeste. Après avoir décrit les propriétés générales des mécanismes basiques de la régulation positive et négative des gènes, nous appliquons ce cadre à l'autorégulation de l'opéron trp et à la mutation génétique impliquée dans la régulation de l'opéron lac. Une des conséquences de cette approche est l'existence de quantités conservées dépendant des conditions initiales qui commandent les bifurcations de points fixes. Ceci conduit naturellement à une explication des effets de seuil observés dans quelques expériences.

Métadonnées

Reçu le : 2004-11-23
Accepté le : 2005-01-25
Publié le : 2005-02-19

PMID

DOI : 10.1016/j.crvi.2005.01.009

Keywords: Genetic regulatory networks, Mathematical modelling of genetic regulatory networks, trp operon, lac operon
Mot clés : Réseaux de régulation, Modélisation mathématique de réseaux de régulation génétique, Opéron trp, Opéron lac

Affiliations des auteurs :

Filipa Alves ¹ ; Rui Dilão ¹

¹ Non-Linear Dynamics Group, Instituto Superior Técnico, Department of Physics, Av. Rovisco Pais, 1049-001 Lisboa, Portugal

@article{CRBIOL_2005__328_5_429_0,
     author = {Filipa Alves and Rui Dil\~ao},
     title = {A simple framework to describe the regulation of gene expression in prokaryotes},
     journal = {Comptes Rendus. Biologies},
     pages = {429--444},
     publisher = {Elsevier},
     volume = {328},
     number = {5},
     year = {2005},
     doi = {10.1016/j.crvi.2005.01.009},
     language = {en},
}

TY  - JOUR
AU  - Filipa Alves
AU  - Rui Dilão
TI  - A simple framework to describe the regulation of gene expression in prokaryotes
JO  - Comptes Rendus. Biologies
PY  - 2005
SP  - 429
EP  - 444
VL  - 328
IS  - 5
PB  - Elsevier
DO  - 10.1016/j.crvi.2005.01.009
LA  - en
ID  - CRBIOL_2005__328_5_429_0
ER  -

%0 Journal Article
%A Filipa Alves
%A Rui Dilão
%T A simple framework to describe the regulation of gene expression in prokaryotes
%J Comptes Rendus. Biologies
%D 2005
%P 429-444
%V 328
%N 5
%I Elsevier
%R 10.1016/j.crvi.2005.01.009
%G en
%F CRBIOL_2005__328_5_429_0

Filipa Alves; Rui Dilão. A simple framework to describe the regulation of gene expression in prokaryotes. Comptes Rendus. Biologies, Volume 328 (2005) no. 5, pp. 429-444. doi : 10.1016/j.crvi.2005.01.009. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2005.01.009/

Version originale du texte intégral

1 Introduction

Genome sequencing is producing huge amounts of data and modern experimental techniques are enabling large scale gene expression analysis (see, for example, [1–5]).

Mathematical modelling of gene expression can provide interpretation of experimental results, help to focus new experiments on critical missing data, and predictions can be made about results that are difficult to obtain in vivo. Mathematical modelling can still be used to explore and predict properties of a given system, testing the behaviour of different network structures and parameter values. On the other hand, the inferential power of modelling can be used to deal with ambiguous or unknown information in experiments.

Several theoretical strategies are being used to approach the modelling of gene regulation networks [6–9]. For example, several authors have developed simple representations of real genetic networks and have explored its basic properties [10,11]. Some models are built starting from simplified views of known regulatory networks and then the model parameters are adjusted in order to find results close to the patterns of gene expression observed in vivo [12,13]. Another approach is to infer unknown regulatory mechanisms from known experimental data [14–18]. A different strategy is the design of simple in vivo artificial genetic networks that have specific properties to be tested under several conditions [19–25].

From the mathematical point of view, there are several methodologies to describe genetic regulatory networks. Some authors use discrete models, building, for example, boolean or bayesian networks [26–32]. Others, use several types of continuous models, as differential equations, difference equations and reaction-diffusion equations [33–38]. All these models aim to describe the real system with different levels of detail.

Here we propose a simple mathematical framework in order to build models of gene regulatory interactions using differential equations. Our approach is based on the operon model of Jacob and Monod [39], as a paradigm of the mechanisms of gene regulation in bacteria. The description of these mechanisms starts by establishing a basic model for the quantitative description of protein production. The action of the activators and repressors regulating the expression of each gene are the building blocks of these mathematical models.

We consider that genes are templates for protein production, and regulation occurs due to the interconversion between the activated and the repressed states of the genes. We also assume that both transcriptional and translational mechanisms are described by one overall rate constant. As a consequence, we are able to describe genetic regulatory systems where the control of the protein production is associated with ‘on’ and ‘off’ states of the gene expression. The resulting gene expression patterns predicted by these mathematical models can be compared with the real experimental system in order to be validated and calibrated. A similar strategy can also be used to infer some unknown gene interactions from known expression patterns.

One of our concerns has been to maintain this mathematical framework as simple as possible, enabling the derivation of the qualitative properties of the models, as well as the possibility of constructing simple computer programs for the derivation and integration of the equations for the temporal evolution of protein concentrations. From the methodological point of view, this construction is based on the bi-molecular mass action law and the basic mechanisms do not introduce ad hoc regulatory functions, as is in general used in the mathematical modelling of gene expression [7,13,40–42]. As a consequence, the modelling strategy proposed here is close to the basic principles of chemical kinetics, and do not introduces neither ad hoc threshold effects, nor Michaelis-Menten type functional forms. However, threshold effects will be found as a consequence of the conservation laws associated to the mass action law.

In Section 2, we introduce the basic simplifying assumptions for the construction of the differential equations describing genetic regulatory networks, and we analyze the basic mechanism of protein production resulting from gene expression, without any regulatory mechanism. From Sections 3 to 6, we analyze the simplest cases of positive and negative regulation. It is shown that the proposed models have all the qualitative properties of the regulatory mechanisms analyzed in experiments. Therefore, if a biological mechanism in prokaryotes is described by a known genetic network, in principle, the formalism developed here is a good candidate to describe the most important qualitative features of the biological process under analysis.

In Section 7, as an illustrative example, we apply this framework to model of the negative self-regulation of the trp operon. In Section 8, we analyze the genetic switch involved in the regulation of the lac operon, responsible for the control of the lactose metabolism in Escherichia coli. Finally, in Section 9, we discuss the main conclusions of this paper.

2 The basic model for protein production from a DNA template

The simplest model of protein production from a DNA template without any regulation mechanism can be described by the kinetic diagram:

(1)

where G, M and P represent the gene, the mRNA and the protein, respectively, C₁ and C₂ are catalysts not consumed in the reactions;

k_{1}^{'}

,

k_{2}^{'}

,

d_{1}

and

d_{2}

are rate constants.

In chemical kinetics, diagrams of type (1) represent the collision between molecules and subsequent chemical transformation. In a chemical process of type (1), after the production of one molecule of protein P, the gene template, the mRNA and the catalysts become free, and new transcription and translation processes can be initiated. If the collisional interactions that initiates these processes occur randomly in the media, the time evolution of the several components is described by the mass action law, [43,44]. To be more specific, we consider several substances, $A_{j}$ , $j = 1, \dots, m$ , involved in the n kinetic diagrams:

ν_{i 1} A_{1} + \dots + ν_{i m} A_{m} \overset{k_{i}}{\to} μ_{i 1} A_{1} + \dots + μ_{i m} A_{m} i = 1, \dots, n

(2)

where

ν_{i j}

and

μ_{i j}

are integer stoichiometric coefficients, and the constants

k_{i}

measure the rates of the transformations. From a master equation approach [43, pp. 166–172], it follows that the concentrations of the

A_{j}

evolve in time according to the equations:

\frac{d A_{j}}{d t} = \sum_{i = 1}^{n} k_{i} (μ_{i j} - ν_{i j}) A_{1}^{ν_{i 1}} \dots A_{m}^{ν_{i m}} j = 1, \dots, m

(3)

In the following, Eq. (3) calculated from diagrams (2), will be simply called mass action law.

Applying the mass action law to the kinetic diagram (1), the time evolution of the concentrations of G, M and P is described by the differential equations:

(4)

where we use the same notation to represent a specific substance or its concentration.

To simplify the model diagram (1) and Eq. (4), we assume that the concentrations of C₁ and C₂ are not limiting factors of the reactions in (1), that is, C₁ and C₂ do not degrade. We also assume that during transcription the mRNA (M) concentration is constant, implying that, by (4), $M = k_{1}^{'} {GC}_{1} / d_{1}$ . Under these conditions, we substitute the mechanism (1) by the simpler diagram:

(5)

In this case, the equations for the time evolution of the concentrations is:

(6)

Comparing (4) with (6), we obtain

k = k_{1}^{'} k_{2}^{'} C_{1} C_{2} / d_{1}

. As we are concerned with the regulation of protein production, in the following we will use the simplified model form (5) to represent both transcriptional and translational mechanisms. Under these conditions, the concentrations of catalysts will affect the rate constant k.

The general solution of (6) is:

(7)

As far as protein is being produced at a constant rate k, by (7) and in the limit

t \to \infty

, the concentration level of protein attains the equilibrium value

P = k G (0) / d

. If protein production is interrupted at some time

t = t^{*}

, the level of protein production decays as

P (t) = P (t^{*}) e^{- d t}

, where

P (t^{*})

is the amount of protein at time

t^{*}

.

In this simple model for protein production, the use of the mass action law relies on the hypothesis that DNA templates, mRNA molecules and proteins are well distributed inside the cell and that the collisional interaction mechanisms are essentially random. The rate constants k and d are effective velocity constants multiplied by catalysts, nucleotides and aminoacids concentrations. In order to simplify the models, we will always avoid the explicit introduction of other species than gene templates (DNA) and proteins, being the gene concentration always a conserved quantity.

In the following, in order to describe the binding of transcription factors that account for activation and repression of proteins, we associate binding sites or operons to genes where transcription factors (transcriptional activators and repressors) can bind in order to promote or repress protein production, Fig. 1. This approach follows the operon model of Jacob and Monod [39].

Fig. 1
Jacob and Monod operon model for the regulation of protein production in bacteria. The transcriptional regulators bind to the binding sites of the gene and transcription is activated or repressed. We can consider different binding sites for different transcription factors or, in the competitive case, the same binding site can be occupied by an activator or a repressor.

We will now consider the basic cases of protein production by positive and negative regulation. The interaction between the regulators and inducer or corepressor molecules will not be taken into account in these models. We will only consider the interaction between activator or repressor molecules and the respective DNA binding sites. These interactions obey the mass action law (see, for example, [45]) and this approach will be followed in the next sections.

3 Positive regulation

3.1 The activator total concentration is constant

In the mechanism of protein production by positive regulation, an activator binds to an operator site in the DNA and transcription and consequent protein production (translation) is initiated. Representing the activator concentration in the cell by A, the concentration of template gene by G, and the concentration of binded DNA-activator complex by $G_{A}$ , the basic mechanism for protein production is:

(8)

We are assuming that genes can be measured in units of concentration (number of molecules or gene templates per unit of volume). This applies to batch cultures where we have several copies of the same gene, and to tissues where we have several copies of identical cells. For cells with only one expressing gene, we can introduce an ergodic argument, and assume that for a time scale larger than the characteristic time of protein production, the protein production is also described by a mass action law mechanism. In fact, this ergodic argument is on the very foundation of the mass action law, in the derivation of Eqs. (3) from molecular mechanisms (2) [46, pp. 89, 291–294]; [43, pp. 166–172].

Applying the mass action law to the above reactions, we obtain the following system of differential equations:

(9)

The evolution equations in (9) are not independent, obeying the conservation laws,

(10)

where,

A (0)

,

G (0)

and

G_{A} (0)

denote initial concentrations, and

c_{1}

and

c_{2}

are positive constants. By (10), we can eliminate G and

G_{A}

from the system of Eqs. (9), obtaining the set of equations describing protein production:

(11)

Knowing the time solutions

A (t)

and

P (t)

of the system of Eqs. (11), by (10), we have,

G (t) = A (t) - c_{1} + c_{2}

and

G_{A} (t) = c_{1} - A (t)

.

The system of Eqs. (11) has the two fixed points in phase space:

(A_{p}, P_{p}) and (A_{n}, P_{n})

(12)

where

(13)

and the indexes p and n stand for positive and negative signs, respectively. Note that

(0, 0)

is a fixed point of Eq. (11) if and only if

c_{1} = 0

. In this case, there is no protein production because the activator A is absent. The only fixed point that corresponds to meaningful asymptotic solutions of Eq. (11) is

(A_{p}, P_{p})

, which is a stable node provided

a > 0

,

d > 0

,

k_{1} > 0

and

k_{2} > 0

. In this case, the Jacobian matrix of Eq. (11) calculated at

(A_{p}, P_{p})

has eigenvalues

λ_{1} = - k_{1} s < 0

and

λ_{2} = - d < 0

, where s is square root term in (13). The same analysis shows that

(A_{n}, P_{n})

is an (unstable) saddle point with eigenvalues

λ_{1} = k_{1} s > 0

and

λ_{2} = - d < 0

.

As the first equation in (11) is independent of P, integration by quadratures gives:

(14)

where

A_{0} = A (0)

. The transient behaviour of protein depends on the reaction and degradation rates as well as on the conservation laws through (13) and (10). This is a typical behaviour in reaction kinetics where, in the presence of conservation laws, the parametric behaviour of transients, fixed points and phase space structure of orbits change with the initial concentration of the agents involved in the reactions. This effect has been pointed out by Travers [45], in the context of the control of the cell cycle by transcriptional switching.

In Fig. 2, we show the time solution (14) as a function of the time t, for a particular choice of parameters and initial conditions. For $t < 10$ , the activator concentration is zero, and there is no protein production. At $t = 10$ , the activator is introduced, and the concentration of protein increases with the usual sigmoidal growth form. The first conclusion we derive from this model is that the amount of produced protein (at equilibrium) is determined by the initial concentration of the activator, the initial concentration of the gene, the rates at which the activator binds and unbinds to the DNA template and the production and degradation rates. Comparing the quantitative behaviour of activated protein production with the non regulated production model derived in Section 2, depending of the activator concentration, in the asymptotic limit, positive regulation leads eventually to higher protein concentrations than the nonactivated simple model for protein production.

Fig. 2
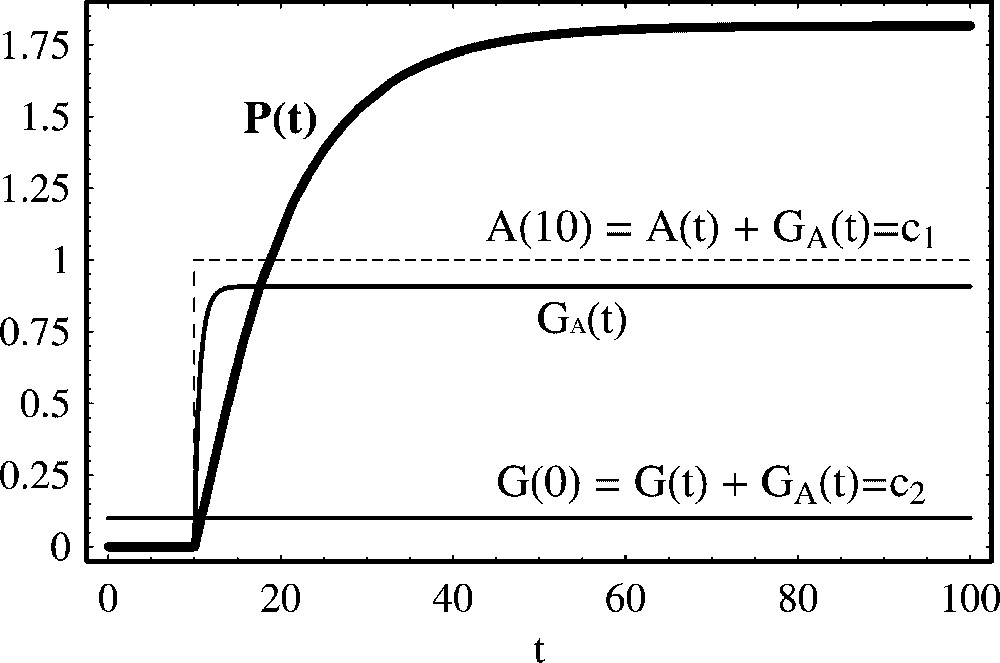
Positive regulation of protein production with constant activator total concentration. We show the temporal evolution of protein concentration calculated from (11). From t=0 to t=10, the activator is absent, A(t)=0.0. In this case, by (10), $c_{1} = 0$ and there is no protein production. At time t=10, we have changed the activator concentration for $A (10) = 1.0 = c_{1}$ . Other parameter values are: $k_{1} = 1.0$ , $k_{2} = 0.1$ , a=0.2 and d=0.1. Initial concentrations are: A(0)=0.0, A(10)=1.0, P(0)=0.0, $G (0) = 0.1 = c_{2}$ and $G_{A} (0) = 0.0$ . After the introduction of the activator at t=10, the equilibrium solutions of the free activator and protein are $(A_{p}, P_{p}) = (0.092, 1.817)$ .

3.2 The activator degrades

In the simple model (8), the activator does not degrade in the process. If the activator A is itself a protein, we must consider an extra mechanism accounting for the activator degradation:

A \overset{d_{A}}{\to}

(15)

Therefore, the first equation in (9) is now:

\frac{dA}{d t} = - k_{1} A G + k_{2} G_{A} - d_{A} A

(16)

In this case, we have only the second conservation law in (10), and the equations for protein production are:

(17)

where we have eliminated

G_{A}

owing to the second conservation law in (10).

Eq. (17) has one stable fixed point with coordinates $(A^{*}, G^{*}, P^{*}) = (0, G (0) + G_{A} (0), 0) = (0, c_{2}, 0)$ , and the asymptotic time solution converge to this fixed point. In Fig. 3, we show the time solution (17) as a function of t for the same parameter values of Fig. 1, with a small degradation rate $d_{A}$ . In this case, the concentration of the free activator protein decreases very fast in time and the produced protein, after attaining a maximum value, has a slow decaying rate. Numerical analysis shows that the maximum value of protein concentrations depends on the magnitude of the degradation rate $d_{A}$ . If $d_{A} \to 0$ , Eq. (17) converges to Eq. (11), with an additional conservation law. At the asymptotic time limit the system ends up with the same amount of initial gene template, without protein and activator.

Fig. 3
Positive regulation of protein production with a degrading activator. We show the temporal evolution of protein concentration calculated from (17), for the same parameter values and initial concentrations of Fig. 1. Initially, the activator is absent and there is no protein production. At t=10, we have introduced the activator with the initial value A(10)=1.0, and the degradation rate of the activator protein has been set to $d_{A} = 0.1$ . The equilibrium values of the activator, gene template and protein are $(A^{*}, G^{*}, P^{*}) = (0, 0.1, 0)$ .

3.3 Self-activation

An important case occurs when the produced protein activates its own production. For this situation, the activation mechanism is:

(18)

and by the mass action law, we obtain the following system of differential equations:

(19)

As we have the conservation law,

G + G_{P} = G (0) + G_{P} (0) = c_{2}

, the independent set of equations describing the time evolution of the process (18) is:

(20)

Eqs. (20) have two steady states with coordinates,

(G^{(1)}, P^{(1)}) = (c_{2}, 0)

and

(G^{(2)}, P^{(2)}) = (\frac{d k_{2}}{a k_{1}}, \frac{a c_{2} k_{1} - d k_{2}}{d k_{1}})

Calculating the Jacobian matrix of Eq. (20) at the fixed points, if

k_{2} d < k_{1} c_{2} a

, the fixed point

(G^{(1)}, P^{(1)})

is of saddle type, and

(G^{(2)}, P^{(2)})

is a stable node. As the determinant of the Jacobian matrices calculated at

(G^{(1)}, P^{(1)})

and

(G^{(2)}, P^{(2)})

have opposite signs, if

k_{2} d > k_{1} c_{2} a

,

(G^{(1)}, P^{(1)})

is stable and

(G^{(2)}, P^{(2)})

is unstable. Note that, in this last case,

P^{(2)}

is negative.

In Fig. 4, we show the temporal evolution of the concentration of a self-activating protein, for two different initial protein concentrations.

Fig. 4
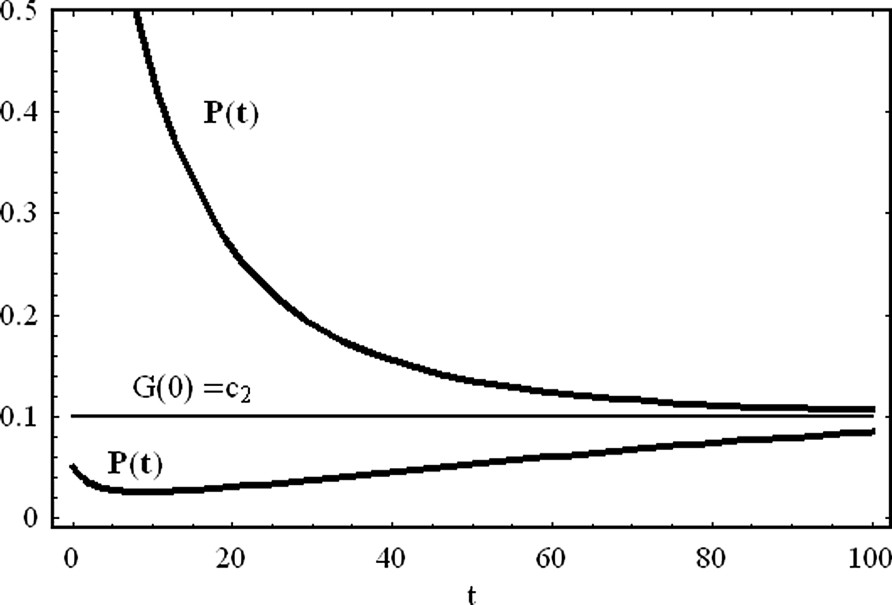
Self-activation of protein production. We show the temporal evolution of protein concentration calculated from (20), for protein initial concentrations P(0)=1.0 and P(0)=0.05. At t=0, the protein concentration is larger than zero, and the gene has no additional activating mechanisms. If the initial concentration of gene templates available for protein production is above some definite threshold value defined by $k_{1} c_{2} a > k_{2} d$ , where $c_{2} = G (0) + G_{P} (0)$ , in the limit t→∞, the protein attains a constant value. The parameter values of the simulation are: $k_{1} = 1.0$ , $k_{2} = 0.1$ , a=0.2 and d=0.1, and the initial concentrations of the gene template is $G (0) = 0.1 = c_{2}$ . If $k_{1} c_{2} a < k_{2} d$ , the final protein concentration goes to zero.

If $k_{1} c_{2} a > k_{2} d$ , a self-activating protein mechanism leads to a nonzero asymptotic protein concentration. As $c_{2} = G (0) + G_{P} (0)$ , having initially enough gene templates, the equilibrium values of the produced protein depend on the reaction rates of the processes involved in the transcriptional mechanisms, and on the concentrations of the gene template. If the initial concentration of the gene template is below a certain threshold, asymptotically in time, the protein concentration decays to zero. In this case, the conservation law derived from the mass action law implies the existence of a threshold effect. In Fig. 5, we have ploted the steady state value of the protein concentration as a function of the conserved quantity $c_{2} = G (0) + G_{P} (0)$ . The threshold occurs for $c_{2} = d k_{2} / a k_{1}$ .

Fig. 5
Threshold effect for positive regulation with a self-activator, for the parameter values $k_{1} = 1.0$ , $k_{2} = 0.1$ , a=0.2 and d=0.1. When the conserved quantity $c_{2}$ is below $d k_{2} / a k_{1}$ , the equilibrium value (t→∞) of the protein concentration is $P_{eq} = P^{(1)} = 0$ . If, $c_{2} ⩾ d k_{2} / a k_{1}$ , then $P_{eq} = P^{(2)} = (a c_{2} k_{1} - d k_{2}) / d k_{1}$ , and the threshold occurs for $c_{2} = d k_{2} / a k_{1}$ .

4 Negative regulation

4.1 The repressor total concentration is constant

In negative regulation of protein production, an inhibitor binds to an operator site and mRNA transcription is not initiated. Representing by R the concentration of the repressor, the template gene by G, and the binded complex by $G_{R}$ , the basic mechanism of protein production is now:

(21)

Applying the mass action law to the above reactions, we obtain the following set of differential equations:

(22)

and the conservation laws:

(23)

where

R (0)

is the initial concentration of the protein inhibitor, and

e_{1}

and

e_{2}

are positive constants. Introducing the conservation laws (23) into (22), the independent set of equations describing protein inhibition is:

(24)

As in the case of activation, the system of Eqs. (24) has two fixed points with coordinates:

(R_{p}, P_{p}) and (R_{n}, P_{n})

(25)

where,

(26)

and the indexes p and n stand for positive and negative signs, respectively. The fixed point

(R_{p}, P_{p})

is a stable node and

(R_{n}, P_{n})

is a (unstable) saddle point.

The solution of the system of Eqs. (24) is:

(27)

where

R_{0} = R (0)

. Comparing (24) with (13), for the inhibition and the activation mechanisms the time solutions are analytically similar.

In Fig. 6, we plot the time evolution of protein production as a function of time. In order to compare the effect of activation and repression agents, we have taken the same parameter values as in the case of Fig. 1. In this case, there exists protein production in the absence of repressor, but when we connect the repression mechanisms, the production process stops and asymptotically in time, the steady state of the protein reaches a low value but away from zero.

Fig. 6
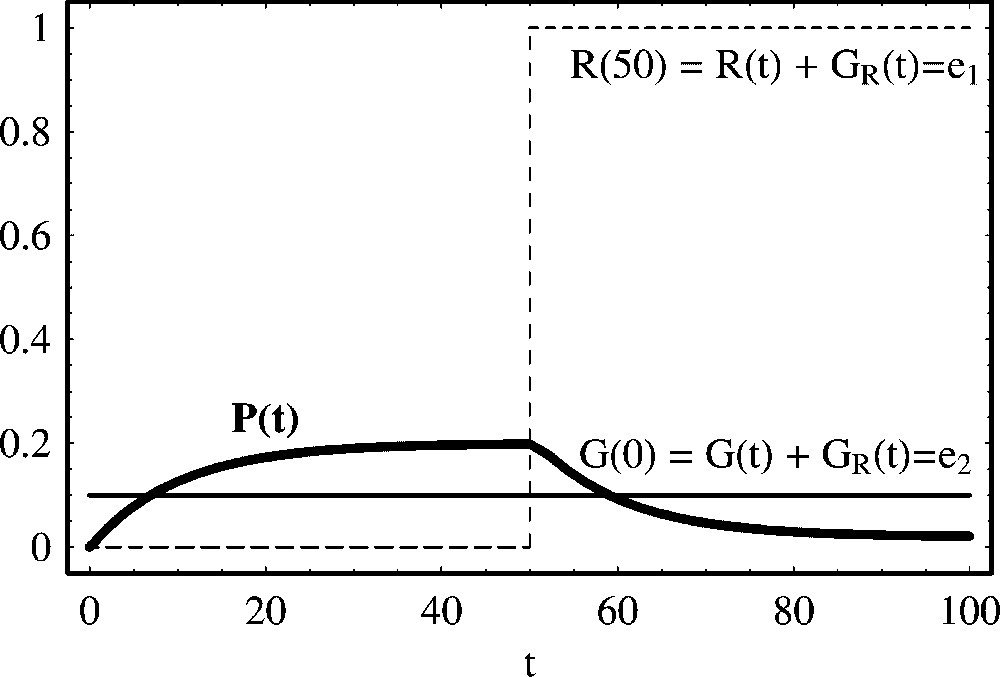
Negative regulation of protein production with constant repressor concentration. We show the temporal evolution of protein concentration calculated from (27). From t=0 to t=50, the repressor is absent (R(0)=0.0) and, therefore, protein production is initiated. At time t=50, we have introduced a repressor R(50)=1.0 and protein decay is initiated. After the introduction of the repressor, asymptotically in time, the protein concentration attains a low equilibrium value, $(R_{p}, P_{p}) = (0.910, 0.020)$ . Parameter values of the simulation are: $k_{3} = 1.0$ , $k_{4} = 0.1$ , a=0.2 and d=0.1. Initial concentrations are: P(0)=0.0, G(0)=0.1 and $G_{R} (0) = 0.0$ .

4.2 The repressor degrades

In the simple model (21), the repressor does not degrade during the process. If the repressor R is itself a protein, we must consider the extra mechanism accounting for repressor degradation,

R \overset{d_{R}}{\to}

(28)

Therefore, the first equation in (22) is now:

\frac{dR}{d t} = - k_{3} R G + k_{4} G_{R} - d_{R} R

(29)

In this case, we have only the second conservation law in (23), and the equations for protein production are:

(30)

where we have eliminated

G_{R}

due to the second conservation law in (23). The system of Eqs. (30) has one stable fixed point with nonnegative coordinate

(R^{*}, G^{*}, P^{*}) = (0, e_{2}, a e_{2} / d) = (0, G (0) + G_{R} (0), a (G (0) + G_{R} (0)) / d)

, where the constant

e_{2}

is given by (23).

In the case of a repressor agent that degrades during time, the asymptotic protein concentration assumes a positive value, $P^{*} = a (G (0) + G_{R} (0)) / d$ . This contrasts with the case of a degrading activator, where protein concentration goes to zero, asymptotically in time.

4.3 Self-repression

An important case is when the produced protein represses its own production. For these situations, the mechanism is:

(31)

and by the mass action law, we obtain the following system of differential equations,

(32)

As we have the conservation law,

G (t) + G_{P} (t) = G (0) + G_{P} (0) = c_{1}

, the independent set of equations describing the time evolution of the process (31) is:

(33)

If $c_{1} > 0$ , the system of Eqs. (33) has one stable steady state, with coordinates:

(G^{*}, P^{*}) = (\frac{- d k_{4} + \sqrt{d^{2} k_{4}^{2} + 4 a c_{1} d k_{4}}}{2 a k_{3}}, \frac{- d k_{4} + \sqrt{d^{2} k_{4}^{2} + 4 a c_{1} d k_{4}}}{2 d k_{3}})

(34)

For a zero initial concentration of protein and

c_{1} > 0

, asymptotically in time, the protein concentration attains the value

P^{*}

, given by (34), Fig. 7. This case can be compared with the solution of nonregulated protein production in (7). With

k_{3} \to 0

and

c_{1} = G (0)

, we obtain the same asymptotic state as in (7). As expected, protein self-repression makes protein production less efficient. For the same parameter values, the equilibrium value of protein concentration is lower in the case of self-repression, but this equilibrium state is reached faster than for the nonregulated case of protein production.

Fig. 7
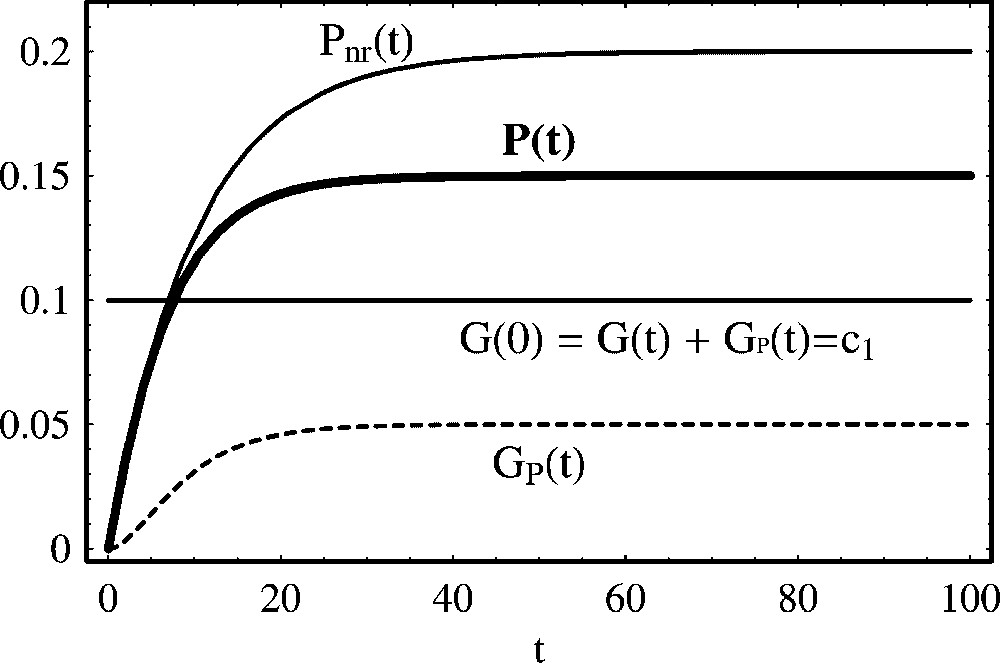
Self-repression of protein production. P(t) represents the temporal evolution of a self-repressing protein as described by mechanism (31). $P_{nr} (t)$ represents the temporal evolution of a nonregulated protein according to mechanism (5). Parameter values are: $k_{3} = 1.0$ , $k_{4} = 0.1$ , a=0.2 and d=0.1. Initial concentrations are: P(0)=0.0 and G(0)=0.1.

5 Positive and negative regulation with the regulators binding the same operator

We now extend this model to the case where the template DNA has overlapping binding site where an activator or an inhibitor can bind, leading to the activation or repression of protein production. This can be seen as the case of competition by the same binding site.

Adopting the same strategy of the preceeding sections, we now have:

(35)

where protein production only occurs when the operon binding site of the DNA template is occupied by an activator. We can now proceed by applying mass action law to diagram (35), obtaining:

(36)

Eqs. (36) have the conservation laws:

(37)

Solving Eqs. (37) in order to get G,

G_{A}

and

G_{R}

, and eliminating these dependent variables from (36), we obtain:

(38)

The first two equations in (38) are independent of P, and we can determine their fixed points. Equating $\frac{dA}{d t}$ and $\frac{dR}{d t}$ to zero, and solving in order to get R and A, respectively, we obtain the equations for the nullclines:

(39)

The nullclines (39) are monotonic functions in the first quadrant of the

(A, R)

phase space and intersect at only one point, say,

(A^{*}, R^{*})

. The phase space point

(A^{*}, R^{*})

is the only fixed point with positive coordinates of system (38). Calculating the Jacobian matrix at

(A^{*}, R^{*})

of the first two equations in (39), we obtain:

M = (\begin{matrix} - k_{1} A^{*} - \frac{k_{2} f_{2}}{A^{*}} & - k_{1} A^{*} \\ - k_{3} R^{*} & - k_{3} R^{*} - \frac{k_{4} f_{3}}{R^{*}} \end{matrix})

As,

Det M = A k_{1} k_{4} f_{3} / R + k_{2} k_{4} f_{2} f_{3} / AR + R k_{2} k_{3} f_{2} / A > 0

, and

Tr M < 0

, the fixed point

(A^{*}, R^{*})

is always asymptotically stable and the system of Eqs. (38) has a unique stable steady state with positive coordinates.

In the simulation of Fig. 8, we show that when a repressor is present, even in small concentrations, and competes for the same binding site as the activator, its effect is to decrease the equilibrium value of the produced protein.

Fig. 8
Competition of a positive and a negative regulator for the same binding site. We show the temporal evolution of protein concentration calculated from (38). From t=0 to t=10, both the activator and the repressor are absent. From t=10 to t=50, the activator A is present. From t=50 to t=100, both the activator A and the repressor R are present. From t=100 to t=150, only the repressor R is present. Other parameter values of the simulation are: $k_{1} = 1.0$ , $k_{2} = 0.1$ , $k_{3} = 1.0$ , $k_{4} = 0.1$ , a=1.0 and d=0.1. Initial concentrations are: P(0)=0.0, G(0)=0.1 and $G_{A} (0) = G_{R} (0) = 0.0$ .

6 Positive and negative regulation with the regulators binding different operators

For the case where the template DNA has two operon sites, one for the activator and another for the inhibitor, the reaction mechanisms are:

(40)

where protein production only occurs when the operon binding site of the DNA template is occupied by an activator and the repressor binding site is free. We can now proceed by applying mass action law to diagram (40), obtaining:

(41)

Eqs. (41) obey the conservation laws:

(42)

Solving Eqs. (42) in order to get

G_{A}

,

G_{R}

and

G_{A, R}

, and eliminating the dependent variables from (41), we obtain:

(43)

where

G_{A} = g_{1} - g_{3} - G + R

,

G_{R} = g_{1} - g_{2} + A - G

and

G_{A, R} = g_{2} - g_{1} + g_{3} - A - R

.

In the simulation of Fig. 9, we show that when the activator and the repressor have different binding sites, the effect of the repressor is more pronounced when compared with the competitive case of Fig. 8.

Fig. 9
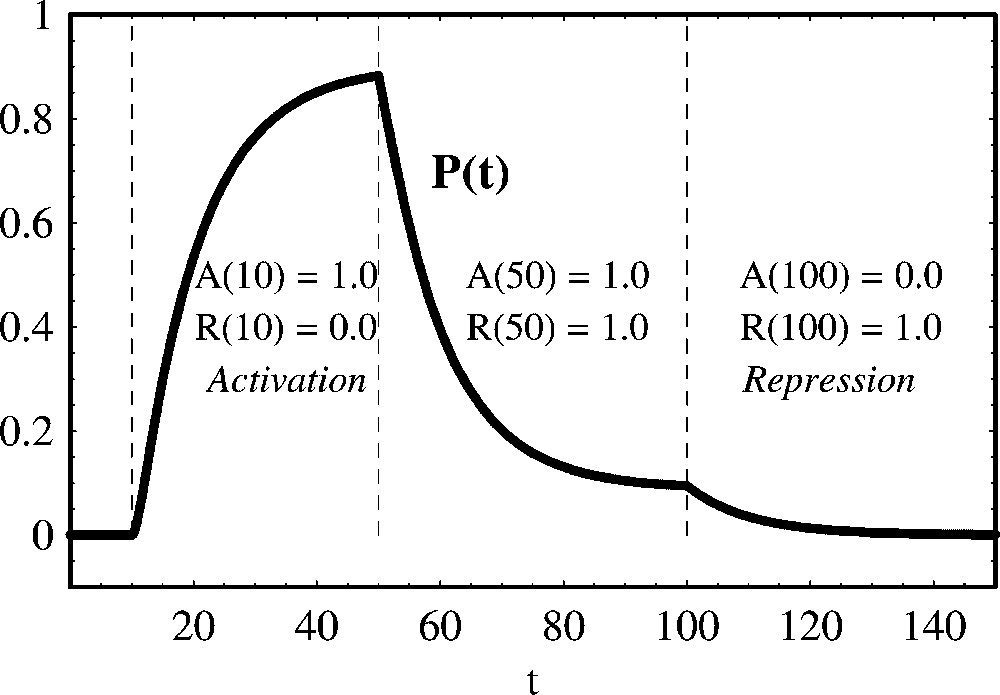
Positive and negative regulation of protein production with the regulators binding different operators. We show the temporal evolution of protein concentration calculated from (43). From t=0 to t=10 both the activator and the repressor are absent. From t=10 to t=50 the activator A is present. From t=50 to t=100 both an activator A and a repressor R are present. From t=100 to t=150 only the repressor R is present. Parameter values are: $k_{1} = k_{3} = k_{5} = k_{7} = 1.0$ , $k_{2} = k_{4} = k_{6} = k_{8} = 0.1$ , a=1.0 and d=0.1. Initial concentrations are: P(0)=0.0, G(0)=0.1, $G_{A} (0) = G_{R} (0) = G_{A, R} (0) = 0.0$ .

7 The negative regulation of the trp operon

The tryptophan (trp) operon is an example of a repressible system. The mRNA coded by the trp operon is translated into five polypeptides that assemble the enzymes responsible for the biosynthesis of the aminoacid tryptophan. Both the synthesis and the activity of these enzymes are controlled by the level of tryptophan in the cell. The cell also produces a repressor protein (R) that is only active if bounded to a tryptophan molecule ( $R_{trp}$ ). If the levels of tryptophan are low inside the cell, the gene of the trp operon (G) is expressed by default. When the tryptophan accumulates in the cell, the repressor protein is activated and the expression of the genes controlled by the trp operon are inhibited. There are other mechanisms involved in the regulation of the tryptophan synthesis, as transcriptional attenuation and feedback regulation of the enzymes activity. For another model, using ad hoc regulatory functions, see [13]. Here we are focusing only on the mechanism of negative regulation. This situation is similar to the general case presented in Section 4.3 with two additional mechanism. One mechanism accounts for the induction of the repressor, and the other mechanism is a simplified representation of the biosynthesis of the aminoacid trp. The simplified kinetics of this regulation mechanism is,

(44)

where G represents the gene of the trp operon,

G_{R}

is the repressed trp operon (

R_{trp}

bounded to the trp operon), and

P_{trp}

represents the enzymes and precursors responsible for trp biosynthesis. By the mass action law, we obtain the following system of differential equations,

(45)

with the conservation laws,

(46)

Solving Eqs. (46) in order to get $G_{R}$ and $R_{trp}$ , and eliminating the dependent variables from (45), we obtain,

(47)

where

G_{R} = h_{2} - G

, and

R_{trp} = h_{1} - h_{2} + G - R

.

The system of Eqs. (47) has two fixed points in phase space. If $h_{1} > 0$ and $h_{2} > 0$ , one of the fixed points has positive coordinates and is stable. The other fixed point has negative coordinates. At the steady state, the level of the aminoacid trp depends on the initial concentration of the nonrepressed gene, and on the rate at which trp is transcribed and degraded. In Fig. 10, we show the time evolution of the concentration of the aminoacid tryptophan from two different initial conditions. One initial condition is zero and the other is positive. For low trp initial concentration, the aminoacid is continuously produced, reaching a steady state. For higher concentrations, the repressor protein inhibits its production, and the same steady state is reached. The proposed mechanism shows how self-repression maintains stable levels of trp inside de cell.

Fig. 10
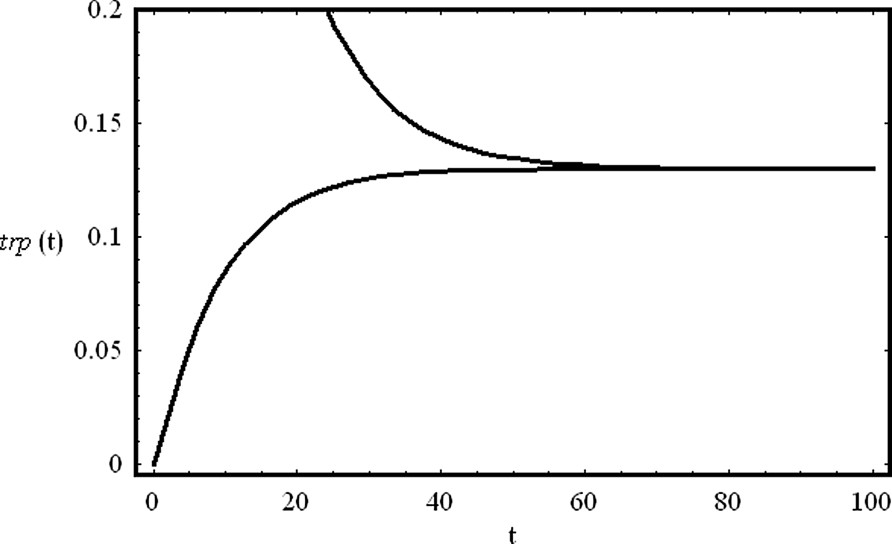
The negative regulation of the trp operon. We show the temporal evolution of the concentrations of the aminoacid trp from two different initial conditions (trp(0)=0.0 and trp(0)=1.0). The production of the aminoacid tryptophan is self-repressed as described by the mechanism (44). Parameter values are: $k_{1} = 1.0$ , $k_{2} = 0.1$ , $k_{3} = 1.0$ , $k_{4} = 0.1$ , $k_{5} = 1.0$ , a=0.2 and $d_{1} = d_{2} = 0.1$ . Initial concentrations are: G(0)=0.1, R(0)=0.1 and $P_{trp} (0) = 0.0$ .

8 The genetic switch in the regulation of the lac operon

In Escherichia coli the main source of carbon is glucose. Lactose is only used as an alternative in the absence of glucose. The lac operon controls the expression of a set of genes that code for proteins involved in the metabolism of the disaccharide lactose. In the presence of glucose, the lac operon is off and the genes under its control are not transcribed. The lac operon (G) is controlled by a transcriptional activator, the ‘catabolite activator protein’ (CAP), and a transcriptional repressor, the ‘lac repressor’ (REP), binding different operators. A decrease in glucose concentration inside the cell leads to the rise of CAP induced by cAMP ( ${CAP}_{i}$ ). In this form, ${CAP}_{i}$ is able to bind the DNA and the lac operon can then be turned on. If the glucose concentration increases, cAMP decreases and CAP cannot bind to the DNA, turning the lac operon off. The ‘lac repressor’ binds to the lac operon in the absence of lactose, turning off the operon, even if ${CAP}_{i}$ is bound. The presence of lactose induces the increase in allolactose concentration that binds to the lac repressor protein, removing it from the DNA. ${CAP}_{i}$ can only turn on the lac operon if the lac repressor is not repressing it. This means that lac operon is turned on only if glucose is absent and lactose is present. Under the control of the lac operon the main genes that are turned on encode permease and β-galactosidase enzymes, responsible for the lactose transport and hydrolysis.

In this framework, the regulation of the lac operon is described by the mechanism:

(48)

Protein production only occurs when the operon has a binded activator, but not a repressor (

G_{{CAP}_{i}}

). Comparing (48) with (40), with the identification,

{CAP}_{i} = A

,

REP = R

, the evolution equations of concentrations are the same as Eqs. (41), with the conservation laws:

(49)

The simulations in Fig. 11 show that the lac operon behaves like an ‘on/off soft switch’: the operon is turned on only when the concentration of ${CAP}_{i}$ is high and the concentration of REP is low. These conditions only occur if glucose is absent and lactose is present. In Fig. 12 we show the steady state value of protein concentration as a function of the initial concentration of the repressor REP.

Fig. 11
The regulation of the lac operon. This is a case of positive and negative regulation of protein production, with the regulators binding different operators. We show the temporal evolution of protein concentration for different initial concentrations of the activator ${CAP}_{i}$ and the repressor REP. Parameter values are: $k_{1} = k_{3} = k_{5} = k_{7} = 1.0$ , $k_{2} = k_{4} = k_{6} = k_{8} = 0.1$ , a=1.0 and d=0.1. Initial concentrations are: P(0)=0.0, G(0)=0.1 and $G_{{CAP}_{i}} (0) = G_{REP} (0) = G_{{CAP}_{i}, REP} (0) = 0.0$ . It is clear that the lac operon is significantly activated only when the concentration of the activator is at least about ten times higher than the concentration of the repressor.

Fig. 12
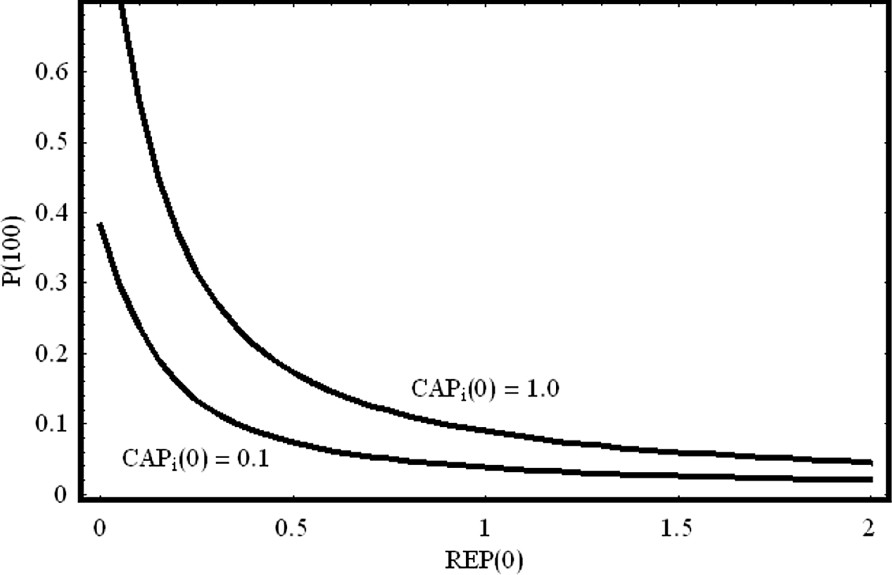
On/off switch of the lac operon. We have plotted the protein concentration for t=100 as a function of the initial concentration of the repressor REP. For fixed activator initial concentration, as the repressor concentration increases linearly, the equilibrium value of the produced protein decreases exponentially. We have chosen two different initial conditions for the activator ${CAP}_{i}$ . The other parameter values are the same as in Fig. 11.

9 Discussion and conclusions

We have developed a class of differential equation models describing the basic biological mechanisms of regulation of gene expression. The models are easy to handle, enabling a straightforward comparison with experiments in order to be validated and calibrated. The basic assumptions in the construction of this simple framework are the following:

– (1) genes are considered as templates for protein production;
– (2) gene transcription is activated or repressed by transcriptional regulators binding to the regulator sites of the gene;
– (3) all the mechanisms are bi-molecular and derived from the mass action law;
– (4) both transcriptional and translational mechanisms are described in time by the same rate constants.

In this approach, the interactions between regulators and inducer or co-repressor molecules, cooperative effects, and multimerization of regulatory proteins are not taken into account. However, these mechanisms can also be described using this mathematical framework.

We have explored and explained the quantitative behaviour of basic simple gene regulatory mechanisms. For example, when we compare nonregulated protein production with activated protein production, the equilibrium protein values become dependent of the activator initial concentration, and therefore, are not only limited by the rate constants of the production mechanisms. In the case of nonregulated protein production, the equilibrium values are limited by the rate at which production and degradation mechanisms occur.

If the protein activator concentration degrades during time, the produced protein, after reaching a maximum concentration value, decays to zero. This contrasts with the case of protein self-activation, where the equilibrium values of the produced protein depend on the reaction rates of the processes involved in the production mechanisms and on the concentrations of the gene template. In this last case, if the concentration of the gene template is bellow a certain threshold, protein concentration decays to zero.

When the protein is produced by default and exists a negative regulation mechanism, the equilibrium value of the protein concentration is lower in the presence of the repressor and depends on the repressor initial concentration. If in addition the repressor molecules degrade, the resulting protein concentration reaches a higher asymptotic positive value. In the case of self-repression, the produced protein reaches lower equilibrium values when compared with the nonregulated case. Without regulation, protein concentration at equilibrium only depends on the reaction rates of the reactions.

It follows from these simple models that the threshold effect observed in some experimental systems is associated with the existence of conserved quantities derived from the mass action law. In general, the conserved quantities change the position of fixed points in phase space and, in some cases, leads to bifurcation of equilibria. In particular, in the case of protein production by self-activation, depending on the initial concentration of the gene, different asymptotic states of the protein are reached (Fig. 5).

We have also analyzed the two cases where both an activator and a repressor are regulating the production of the same protein. In the simulation of Fig. 8, we can see that when a repressor is present, and competes for the same binding site of the activator, its effect is to decrease the equilibrium value of the produced protein. When the activator and the repressor have different binding sites, Fig. 9, the effect of the repressor is more pronounced, leading to even lower protein concentrations.

The models of positive and negative regulation of protein production are the building blocks for more complex mechanisms of gene regulatory interactions, as we have shown in the cases of the trp and the lac operon. Analyzing the mechanism of self-repression of the tryptophan synthesis, we have shown how this process contributes for the regulation of the aminoacid concentration inside the cell. It is shown that the regulation mechanism of the lac operon behaves like a soft on/off switch, and we have analyzed the dependence on the concentrations of the activator and the repressor.

These models depend on biologically relevant parameters, are robust to the variation of the parameters and have low computational cost. For complex networks of gene regulation, the approach developed here enables the construction of general computer programs for the derivation and integration of the equations describing the temporal (and spatial) evolution of the protein concentrations. The predicted gene expression patterns can then be compared with the real experimental system in order to be validated and calibrated.

Acknowledgments

This work has been partially supported by Fundação para a Ciência e a Tecnologia (Portugal), under the framework of POCTI project C/FIS/13161/1998, and by the grant PRAXIS XXI/BD/18379/98.

Bibliographie

[1] S. Fields; Y. Kohara; D.J. Lockhart Functional genomics, Proc. Natl Acad. Sci. USA, Volume 96 (1999), pp. 8825-8826

[2] A.M. Huerta; H. Salgado; D. Thieffry; J. Collado-Vides RegulonDB: a database on transcriptional regulation in Escherichia coli, Nucl. Acids Res., Volume 26 (1998), pp. 55-59

[3] M. Kanehisa; S. Goto KEGG: Kyoto encyclopedia of genes and genomes, Nucl. Acids Res., Volume 28 (2000), pp. 27-30

[4] P.D. Karp; M. Riley; M. Saier; I.T. Paulsen; J. Collado-Vides; S.M. Paley; A. Pellegrini-Toole; C. Bonavides; S. Gama-Castro The EcoCyc database, Nucl. Acids Res., Volume 30 (2002), pp. 56-58

[5] A.V. Spirov; T. Bowler; J. Reinitz HOX Pro: a specialized database for clusters and networks of homeobox genes, Nucl. Acids Res., Volume 28 (2000), pp. 337-340

[6] J. Hasty; D. McMillen; F. Isaacs; J.J. Collins Computational studies of gene regulatory networks: in numero molecular biology, Nat. Rev. – Genetics, Volume 2 (2001), pp. 268-279

[7] H.D. Jong Modelling and simulations of genetic regulatory systems: a literature review, J. Comput. Biol., Volume 9 (2002), pp. 67-103

[8] P. Smolen; D.A. Baxter; J.H. Byrne Mathematical modelling of gene networks, Neuron, Volume 26 (2000), pp. 567-580

[9] M.A. Savageau Design principles for elementary gene circuits: elements, methods, and examples, Chaos, Volume 11 (2001), pp. 142-159

[10] D.E. Koshland; A. Goldbeter; J.B. Stock Amplification and adaptation in regulatory and sensory systems, Science, Volume 217 (1982), pp. 220-225

[11] M.A. Savageau Design of gene circuitry by natural selection: analysis of the lactose catabolic system in Escherichia coli, Biochem. Soc. Trans., Volume 27 (1999), pp. 264-270

[12] M. Ronen; R. Rosenberg; B.I. Shraiman; U. Alon Assigning numbers to the arrows: parameterizing a gene regulation network by using accurate expression kinetics, Proc. Natl Acad. Sci. USA, Volume 99 (2002), pp. 10555-10560

[13] M. Santillán; M.C. Mackey Dynamic regulation of the tryptophan operon: a modelling study and comparison with experimental data, Proc. Natl Acad. Sci. USA, Volume 98 (2001), pp. 1364-1369

[14] J.-M. Claverie Computational methods for the identification of differential and coordinated gene expression, Human Mol. Genet., Volume 8 (1999), pp. 1821-1832

[15] H. Herzel; D. Beule; S. Kielbasa; J. Korbel; C. Sers; A. Malik; H. Eickhoff; H. Lehrach; J. Schuchhardt Extracting information from cDNA arrays, Chaos, Volume 11 (2001), pp. 98-107

[16] T.E. Ideker; V. Thorsson; R.M. Karp Discovery of regulatory interactions through perturbation: inference and experimental design, Pac. Symp. Biocomput., Volume 5 (2000), pp. 302-313

[17] D.M. Mutch; A. Berger; R. Mansourian; A. Rytz; M.A. Roberts The limit fold change model: a practical approach for selecting differentially expressed genes from microarray data, BMC Bioinformatics, Volume 3 (2002), pp. 17-27

[18] D. Thieffry; H. Salgado; A.M. Huerta; J. Collado-Vides Prediction of transcriptional regulatory sites in the complete genome sequence of Escherichia coli K-12, Bioinformatics, Volume 14 (1998), pp. 391-400

[19] A. Becskei; B. Seraphin; L. Serrano Positive feedback in eukaryotic gene networks: cell differentiation by graded to binary response conversion, EMBO J., Volume 20 (2001), pp. 2528-2535

[20] M.B. Elowitz; S. Leibler A synthetic oscillatory network of transcriptional regulators, Nature, Volume 403 (2000), pp. 335-338

[21] T.S. Gardner; C.R. Cantor; J.J. Collins Construction of a genetic toggle switch in Escherichia coli, Nature, Volume 403 (2000), pp. 339-342

[22] J. Hasty; F. Isaacs; M. Dolnik; D. McMillen; J.J. Collins Designer gene networks: towards fundamental cellular control, Chaos, Volume 11 (2001), pp. 207-220

[23] J. Hasty; D. McMillen; J.J. Collins Engineered gene circuits, Nature, Volume 420 (2002), pp. 224-230

[24] H.H. McAdams; A. Arkin Gene regulation: towards a circuit engineering discipline, Curr. Biol., Volume 10 (2000), p. R318-R320

[25] M.A. Savageau Rules for the evolution of gene circuitry, Pac. Symp. Biocomput., Volume 3 (1998), pp. 54-65

[26] T. Akutsu; S. Miyano; S. Kuhara Inferring qualitative relations in genetic networks and metabolic pathways, Bioinformatics, Volume 16 (2000), pp. 727-734

[27] T. Akutsu; S. Miyano; S. Kuhara Algorithms for inferring qualitative models of biological networks, Pac. Symp. Biocomput., Volume 5 (2000), pp. 290-301

[28] H.H. McAdams; L. Shapiro Circuit simulation of genetic networks, Science, Volume 269 (1995), pp. 650-656

[29] D. Thieffry From global expression data to gene networks, BioEssays, Volume 21 (1999), pp. 895-899

[30] D. Thieffry; D. Romero The modularity of biological regulatory networks, BioSystems, Volume 50 (1999), pp. 49-59

[31] D. Thieffry; R. Thomas Qualitative analysis of gene networks, Pac. Symp. Biocomput., Volume 3 (1998), pp. 77-88

[32] A. Wuensche Genomic regulation modeled as a network with basins of attraction, Pac. Symp. Biocomput., Volume 3 (1998), pp. 89-102

[33] A. Arkin; P. Shen; J. Ross A test case of correlation metric construction of a reaction pathway from measurements, Science, Volume 277 (1997), pp. 1275-1279

[34] T. Chen; H.L. He; G.M. Church Modelling gene expression with differential equations, Pac. Symp. Biocomput., Volume 4 (1999), pp. 29-40

[35] P. D'Haeseleer Linear modelling of mRNA expression levels during CNS development and injury, Pac. Symp. Biocomput., Volume 4 (1999), pp. 41-52

[36] E. Mjolsness; T. Mann; R. Castaño; B. Wold From coexpression to coregulation: an approach to inferring transcriptional regulation among gene classes from large-scale expression data, Adv. Neural Inform. Process. Syst., Volume 12 (2000), pp. 928-934

[37] D.C. Weaver; C.T. Workman; G.D. Stormo Modelling regulatory networks with weight matrices, Pac. Symp. Biocomput., Volume 4 (1999), pp. 112-123

[38] D.A. Drew A mathematical model for prokaryotic protein synthesis, Bull. Math. Biol., Volume 63 (2001), pp. 329-351

[39] F. Jacob; J. Monod Genetic regulatory mechanisms in the synthesis of proteins, J. Mol. Biol., Volume 3 (1961), pp. 318-356

[40] R.D. Bliss; P.R. Painter; A.G. Marr Role of feedback inhibition in stabilizing the classical operon, J. Theor. Biol., Volume 97 (1982), pp. 177-193

[41] D.M. Wolf; F.H. Eeckman On the relationship between genomic regulatory element organization and gene regulatory dynamics, J. Theor. Biol., Volume 195 (1998), pp. 167-186

[42] T.A. Carrier; J.D. Keasling Investigating autocatalytic gene expression systems through mecanistic modeling, J. Theor. Biol., Volume 201 (1999), pp. 25-36

[43] N.G. Van Kampen Stochastic Processes in Physics and Chemistry, Elsevier, Amsterdam, 1992

[44] A.I. Volpert; V.A. Volpert; V.A. Volpert Traveling Wave Solutions of Parabolic Systems, American Mathematical Society, Providence, RI, 1994

[45] A. Travers Transcriptional switches: the role of the mass action, Phys. Life Rev., Volume 1 (2004), pp. 57-69

[46] H. Haken Synergetics. An Introduction, Springer-Verlag, Berlin, 1983

Commentaires - Politique