The effect of hormones on bone growth is mediated through mechanical stress

Xavier Wertz; Damien Schoëvaërt; Habibou Maitournam; Philippe Chassignet; Laurent Schwartz

doi:10.1016/j.crvi.2005.10.005

Physiology / Physiologie

The effect of hormones on bone growth is mediated through mechanical stress
[La croissance osseuse est régulée par les hormones via les contraintes mécaniques]

Présenté par : Huy Duong Bui

Xavier Wertz ¹ ; Damien Schoëvaërt ² ; Habibou Maitournam ³ ; Philippe Chassignet ¹ ; Laurent Schwartz ⁴

¹ Laboratoire d'informatique, École polytechnique, 91128 Palaiseau, France
² Laboratoire d'analyse d'images en pathologie cellulaire, Institut universitaire d'hématologie, hôpital Saint-Louis, 1, av. Claude-Vellefaux, 75010 Paris, France
³ Laboratoire de mécanique des solides, École polytechnique, 91128 Palaiseau, France
⁴ Service de radiotherapie, hôpital de la Pitié-Salpêtrière, bd de l'Hôpital, 75013 Paris, France

Comptes Rendus. Biologies, Volume 329 (2006) no. 2, pp. 79-85.

Résumés

Anglais
Français

Mechanical stresses play a key role in regulating cell growth and cell differentiation. Using mechanical and physiological data available in the literature, we are able to construct a growth curve of a child, which we compare to the standard curve. It appears likely that the impact of hormones on pubertal growth rate sprout followed by growth arrest can be solely explained by increased mechanical stresses. The uptake of hormones by the muscles results in increased mechanical stress on the chondrocyte before and at the puberty, resulting in a peak in growth followed by growth cessation.

Les contraintes mécaniques jouent un rôle prépondérant dans la croissance et la différenciation cellulaire. À partir des données mécaniques et physiologiques colligées dans la littérature, nous construisons une courbe de croissance d'un enfant, que nous comparons à la courbe standard. Il est vraisemblable que l'action des hormones sur le pic de croissance et la fin de l'ossification puisse être expliquée par la variation des contraintes mécaniques. Les hormones induisent un anabolisme musculaire, responsable d'une augmentation de la contrainte exercée sur le cartilage de conjugaison. Ceci explique vraisemblablement le pic de croissance prépubertaire suivi de l'arrêt de la croissance.

Métadonnées

Reçu le : 2005-07-09
Accepté le : 2005-11-10
Publié le : 2005-12-27

PMID

DOI : 10.1016/j.crvi.2005.10.005

Keywords: Bone growth, Cartilage, Growth rate, Hormones, Mechanical stresses
Mot clés : Ossification, Cartilage, Taux de croissance, Hormones, Contraintes mécaniques

Affiliations des auteurs :

Xavier Wertz ¹ ; Damien Schoëvaërt ² ; Habibou Maitournam ³ ; Philippe Chassignet ¹ ; Laurent Schwartz ⁴

@article{CRBIOL_2006__329_2_79_0,
     author = {Xavier Wertz and Damien Scho\"eva\"ert and Habibou Maitournam and Philippe Chassignet and Laurent Schwartz},
     title = {The effect of hormones on bone growth is mediated through mechanical stress},
     journal = {Comptes Rendus. Biologies},
     pages = {79--85},
     publisher = {Elsevier},
     volume = {329},
     number = {2},
     year = {2006},
     doi = {10.1016/j.crvi.2005.10.005},
     language = {en},
}

TY  - JOUR
AU  - Xavier Wertz
AU  - Damien Schoëvaërt
AU  - Habibou Maitournam
AU  - Philippe Chassignet
AU  - Laurent Schwartz
TI  - The effect of hormones on bone growth is mediated through mechanical stress
JO  - Comptes Rendus. Biologies
PY  - 2006
SP  - 79
EP  - 85
VL  - 329
IS  - 2
PB  - Elsevier
DO  - 10.1016/j.crvi.2005.10.005
LA  - en
ID  - CRBIOL_2006__329_2_79_0
ER  -

%0 Journal Article
%A Xavier Wertz
%A Damien Schoëvaërt
%A Habibou Maitournam
%A Philippe Chassignet
%A Laurent Schwartz
%T The effect of hormones on bone growth is mediated through mechanical stress
%J Comptes Rendus. Biologies
%D 2006
%P 79-85
%V 329
%N 2
%I Elsevier
%R 10.1016/j.crvi.2005.10.005
%G en
%F CRBIOL_2006__329_2_79_0

Xavier Wertz; Damien Schoëvaërt; Habibou Maitournam; Philippe Chassignet; Laurent Schwartz. The effect of hormones on bone growth is mediated through mechanical stress. Comptes Rendus. Biologies, Volume 329 (2006) no. 2, pp. 79-85. doi : 10.1016/j.crvi.2005.10.005. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2005.10.005/

Version originale du texte intégral

1 Introduction

Growth and maturation of bones is a highly predictable phenomenon [1]. Growth is fast (about 20 cm per year) during early childhood and then slows down. A peak in growth is followed by growth cessation at puberty (Fig. 1, after [2]). The reason for this highly reproducible pattern is unknown. This paper aims at suggesting that this pattern can be explained by the mechanical constraints exerted on the chondrocyte.

Fig. 1
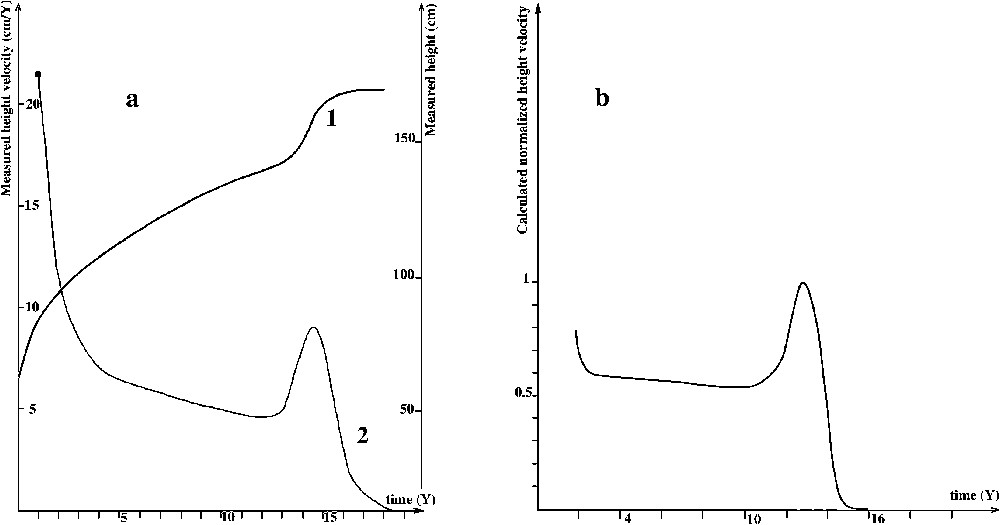
(a) 1 Height curve, 2 Height velocity. (b) Height velocity calculated in this work (see also Fig. 5b).

During embryogenesis, bones are formed on an initial cartilaginous model. Cartilage is later replaced by bone; this process is called ‘enchondral ossification’ [3]. Long bones end near the joint in a separate epiphysis, which is ossified later. During childhood, epiphyses undergo a characteristic series of events: central calcification, absorption of cartilage and enchondral ossification [3]. At puberty, epiphysis becomes fused with the shaft of the bone (diaphysis), resulting in growth arrest [3].

Cartilage and bone are subjected to mechanical stresses; the greatest load comes from the muscle [4]. Collagen secretion is not isotropic, but directional [5]. Its direction is ruled by main loading directions [6]. These constraints appear to play a key role in the growth and the transformation of cartilage into bone. In the embryo and later in life, ossification of the cartilage starts in parallel with active movement of the feet by muscle contraction [7,8]. Mechanical stress resulting from the contraction of the muscles seems to guide enchondral ossification patterns [7,9–11].

Extensive mechanical constraints, like the use of rigid fixation for fracture, can result in growth arrest. For example, epiphyses plated for a year show increased bone differentiation, premature closure, and growth arrest [12]. Similarly, heavily trained gymnasts [13] or swimmers [14] experience attenuated growth during their years of training, followed by catch-up growth during reduced training schedule or the months following the end of extensive training.

Hormones have a well-known effect on cartilage growth and on the differentiation of cartilage into bone. They induce prepubertal bone growth followed by a subsequent bone arrest. The question is whether the effect of hormones are mediated by the androgen receptor located at the surface of the chondrocyte or by changes in mechanical constraints.

The effect of hormones on the development of muscles is well known. The muscle load increases around puberty. The most intense force development occurs between 12 and 15 years of age in boys [15]. Treatment with testosterone of young boys prior to puberty increases both muscle mass and bone growth [16].

Common measurement made in order to predict children's final height are built on the evolution of growth speed with time (Fig. 1a₂). An example of such a curve is given by Despert [2]. The question is about phenomena taking place, leading to such a behaviour of growth speed.

This paper aims at suggesting that a peak in growth followed by growth cessation at puberty is mediated at least in part by increased mechanical constraints.

We will show that the height velocity (the derivative function on time of a height curve) can be calculated (Fig. 1b) using mechanical sollicitations and physiological data on cartilage.

We use the following experimental data:

– the evolution of muscle strength with age;
– a growth curve allowing to calculate the evolution of long-bone section with age;
– the evolution of chondrocyte synthesis according to mechanical loadings;
– the evolution of cartilage volume with age (measured from a bone age atlas);

and we construct the curve of the evolution of collagen synthesis by cartilage with age, which is an equivalent to a height-velocity curve.

2 Material and methods

We have retrieved data on human growth [17], bone cells [11], and muscles [18] from the literature, as well as informations on the effects of mechanical constraints on cartilage and the anabolic effects of hormones on muscles [18].

2.1 Correlation between muscle strength and time

The evolution of the relationship between muscle strength and time is given in the curve in Fig. 2a (from Clarke, cited in [18]). In this work, a correlation between the strength of leg muscles and time among young boys is observed.

Fig. 2
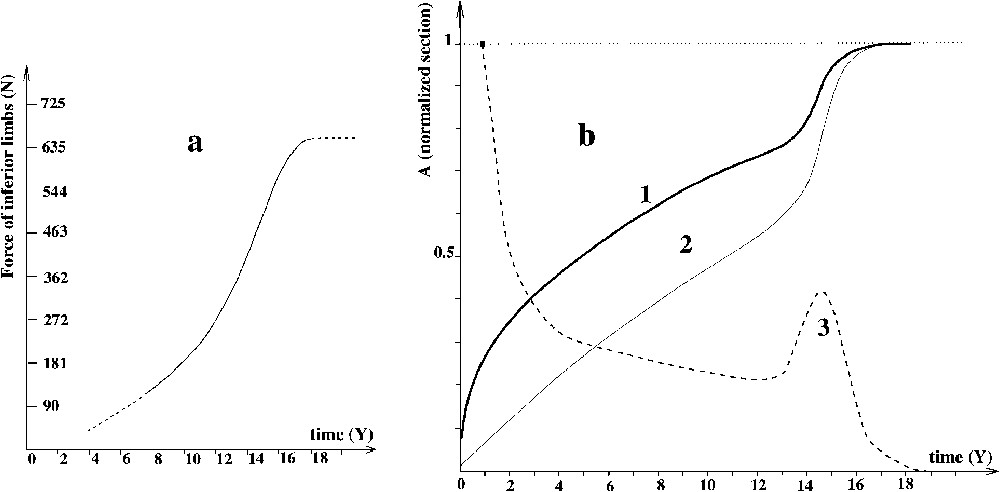
(a) Evolution of muscle strength versus time t [18]. (b) Normalized evolution versus time t of: (1) standard height curve h(t); (2) standard normalized long bone section $A \propto h^{2} (t)$ ; (3) height velocity $\dot{h} (t)$ .

2.2 Correlation between bone section, cartilage volume and time

Bone section increases during childhood. We have calculated the normalized bone section versus time (homothetic growth, see [5]). This curve is thus qualitatively identical to the square of the growth curve, in function of time (growth curve after Kumar and Clark [19]). Normalization is done: normalized section = current section/final section. Actually, this curve is similar to the normalized square of a height–time curve [19]. This provides the curve of the evolution of the surface as a function of time (Fig. 2b₂). As bones grow in a homothetic way [5], the curve is similar for every bone.

2.3 Response of chondrocytes according to mechanical loadings

Experimentation by Klein-Nulend et al. [20] and Tanck et al. [21] show the influence of mechanical stress on ossification. Wong and Carter conceived an ‘osteogenic index’ [22] that rules ossification in the case of a cyclic loading and whose analytical expression is:

I = \sum_{i = 1}^{c} n_{i} (τ_{i} + λ P_{i})

(1)

with:

– I the osteogenic index;
– $n_{i}$ is the number of cycles of load case i;
– c is the number of load cases;
– $τ_{i}$ is related to maximum octahedral shear stresses in load case i and actually, proportional to the Von Mises equivalent stress;
– $P_{i}$ is related to the peak cyclic hydrostatic stresses in load case i;
– λ is a constant which ranges from 0.3 to 1.0 and could be 0.5, according to Wong and Carter [22].

They used this formula to simulate ossification by a finite element method, but studies made by Tanck et al. [21] seems to show that hydrostatic pressure might be the prevailing cause. Ossification means chondrocytes death and subsequent end of collagen synthesis by these cells.

The response $S_{i}$ in synthesis of an individual chondrocyte to a mechanical prompting is completed by experimental data [23] in order to obtain the complete behaviour (Fig. 3a).

Fig. 3
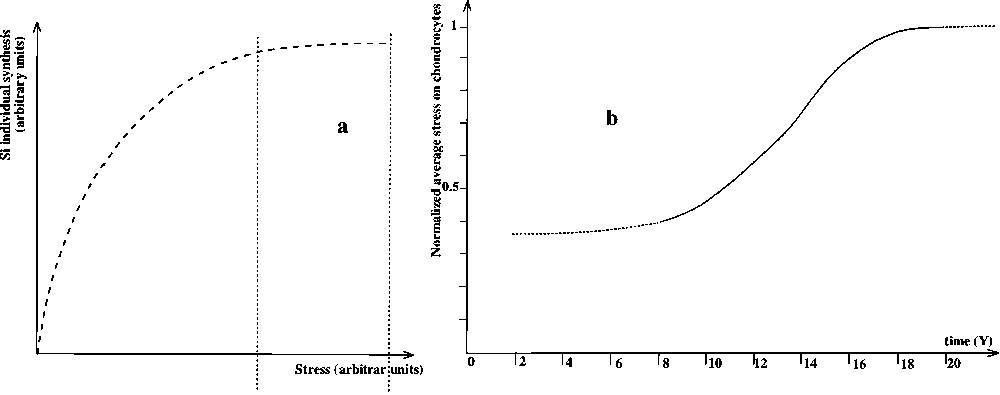
(a) Evolution of synthesis $S_{i}$ of a single chondrocyte versus σ after Yoshihida et al. [24]. (b) Evolution of the stress σ on chondrocytes versus time t.

2.4 Methods

Our goal is to compute growth rate as a function of time using physiological and mechanical data.

Mechanical stress exerted on a chondrocyte is estimated as the ratio $σ = \frac{F}{A}$ of the force F applied to the bone on $A$ , the area of the bone section that passes through this chondrocyte, perpendicular to the axis of the diaphysis, with σ the average stress, and F the macroscopic force.

We use this definition of mechanical stress to establish the evolution of average stress exerted on chondrocytes as a function of time. This is achieved using curve 2a for the force and curve 2b₂ for the surface. We obtain Fig. 3b.

We then studied growth of cartilage during childhood. From the literature, it appears likely that the number of chondrocytes per unit of cartilage is constant during childhood [5,25]. Density of chondrocytes has been reported to be constant in the different cartilages of the body [5,25]. Nevertheless, the remaining articular cartilage has a lower chondrocyte density. The volume of cartilage during childhood has never been precisely measured. For our study, we need to know the extent of cartilage and its evolution during childhood. We know that growth of bones is homothetic [5]. The total height of the child is proportional to the length of the thumb. We confirmed this assumption by serial measurements of the femur and compared them to the measurements of the thumb (data not shown).

Atlases of standardized radiographies of the hand are available [26]. These atlases were developed by pediatricians to measure the bone age in order to assess the growth retardation of a sick child.

We measured the amount of cartilage of the thumb during childhood. Bone is visible on radiographies, cartilage is transparent.

In order to plot the evolution curve of the volume of cartilage against time, we draw a cylinder around the two diaphyses on each side of the articulation, and subsequently inside each part of the cartilage we are dealing with (as the transversal section of the cartilage is always bigger than the section of the diaphysis, in metacarpals and phalanges). The diameter of this cylinder grows homothetically with the whole (bone + cartilage) unit. We assume that the evolution on radiographies of the dark area inside the cylinder – which is actually cartilage – is representative of the evolution of the total volume of cartilage. This is not absolutely true, as the secondary ossification develops first inside the cylinder (never far from the axis) and later outside the cylinder. We assume that epiphyses are axisymmetrical. It is then possible to measure their average diameter. When divided by the diameter, a computed measurement of the area of the dark surface of the cylinder projection provides the average height of the dark part of the cylinder. Knowing diameter and average height is sufficient to calculate the volume of the cartilage (see Fig. 4).

Fig. 4
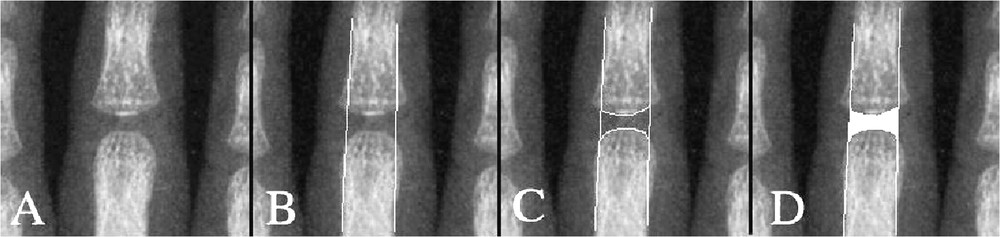
Evaluation of cartilage volume using radiographies of the hand: drawing of the cartilage projection surface. A: Initial picture; B: With cylinder tangent to diaphyses; C: The outer bound of the cartilage contained in the cylinder; D: The measured surface.

The computed image analysis is made with the Samba image analysis software (manufacturer: Sambatechnologies¹) through the following process: first, bounds of areas are reproduced on a calque paper. These images are numerated with 131.3 μm for one pixel, into a gray-scale picture. A ‘top-hat’ filter is applied to these images in order to obtain closed boundaries. The surfaces of these objects are calculated by the software. Then, the cylinder volume is calculated following the method described above, using average height and diameter.

The fact that radiographies are taken from different children leads us to our obtaining a non-realistic curve of the evolution of cartilage volume in these bones: at a given age, children do not all have the same height, nor the same bone size. A non-normalized curve of the volume according to the child's own bone size leads to a curve that is more representative of children's disparity in size, rather than of the evolution of cartilage volume. This is the reason why we normalize volume data by dividing them by the cubic diameter of the diaphysis.

We then obtain Fig. 5a₂.

Fig. 5
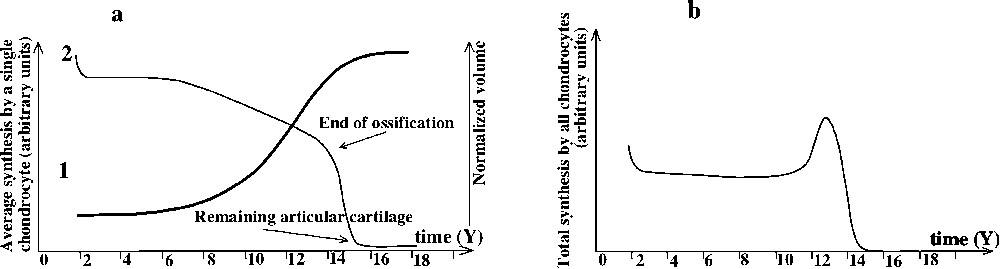
(a) Evolution of: 1 of synthesis by a single chondrocyte, 2 normalized cartilage volume. (b) Evolution of synthesis by cartilage, cartilage versus time.

The radiological analysis provides us with the evolution of the amount of cartilage during childhood. As we know the number of chondrocytes per volume, we can calculate the number of chondrocytes present at a given time (Fig. 5a₁). As secretion of extracellular matrix by chondrocytes is function of mechanical stresses, we can deduce the amount synthesized by one chondrocyte as a function of time:

S_{i} (t) = S_{i} (σ (\frac{F (t)}{A (t)}))

(2)

then we multiply by the number of chondrocytes and calculate:

S_{t} (t) = N_{chondro} (t) \times S_{i} (σ (t))

(3)

the total synthesis

S_{t}

of chondrocytes (Fig. 5b) which is an equivalent to height velocity (Fig. 1b).

3 Results

3.1 Prepubertal period

During this phase, sexual hormone concentration (e.g., testosterone) in blood is low and constant [17]. The development of muscles is slow and linear [18]. The lowest mechanical stimulation of the chondrocytes is situated were the synthesis is the highest: $S_{i}$ is low but chondrocytes are numerous such as the total synthesis is important. There is a feedback equilibrium between muscles and cartilage. The evolution of growth speed is linear, but slowly decreases. The slowing of growth rate results from progressive ossification of epiphysis, which reduces the relative amount of cartilage.

3.2 Puberty and growth peak

Puberty is a time when sexual hormones are massively secreted. This results in accelerated muscle development and strengthening [18].

Stress σ exerted on chondrocytes increases very swiftly, and synthesis $S_{i}$ of chondrocytes reaches the saturation point: chondrocytes synthesis is situated in the area where stresses are maximal. Growth is maximal.

3.3 End of ossification and growth arrest

As testosterone continues to increase, muscles strengthen [18], resulting in growth arrest (Fig. 1).

As chondrocytes synthesis reaches saturation, $S_{y}$ , and then $A$ cannot increase fast enough to restore its equilibrium with F, contrary to what occurs during the prepubertal period. Stresses are over the ossification threshold. The ossification front progresses rapidly. The number of active chondrocytes decreases, and growth slows down, until the growth plate disappears, resulting in growth cessation.

4 Discussion and conclusion

This paper proves that cell growth and cell differentiation is the result of physical constraints. This is confirmed by in vitro experiments [8]. Chondrocytes are known to sense and respond to the mechanical stimuli by multiple regulatory pathways: upstream signalling transcription, translation, post-translational modifications, and vesicular transport [6]. Fluid induced shear causes chondrocytes to elongate and align [27]. Chondrocytes respond to shear stress by an increased secretion of an extra cellular matrix, namely collagen and proteoglycan [6], as well as the modification of metabolism [27].

The importance of mechanical constraints is not unique to cartilage. The development of every organ is constrained by internal and external limitations [28]. The effect of shear stress on endothelial cells is another example. Shear stresses are responsible for vascular network formation, fractal organization of arterial and venous trees, as well as the unavoidable tropism of arteries toward capillaries and then veins [29]. At the cellular level, shear stress induces cell proliferation. Similarly, mechanical deformation of foetal rat lung cells simulating foetal respiratory movements increases cellular replication [30]. Rhythmic deformation also increases intestinal epithelial cell proliferation in a frequency-dependent manner [31].

The role played by mechanical forces is major in regulating bone growth. During childhood and adolescence, there is a constant strengthening of muscles and increase in body length. These increased mechanical stresses appear to explain the prepubertal peak in growth followed by a subsequent growth arrest. Section of muscles during trauma result in bone-growth delay or cessation. Similarly, in microgravity stresses are decreased, resulting in dwarfism [17]. Two main symptoms of dwarfism are a weakness of muscles and a failure in the growth of long bones [32]. On the contrary, testosterone supplementation increases both muscle strength and premature closing of the growth plate [17].

As said Donald Insber speaking about cells fate, “There's mechanics as well as chemistry” [33].

Acknowledgements

We are indebted to Pr. H.D. Bui and Pr. J.-M. Steyaert for their constant support and advice.

¹ http://www.sambatechnologies.com.

Bibliographie

[1] C.B. Graham Assessment of bone maturation-methods and pitfall, Radiol. Clin. North Am., Volume 10 (1972), pp. 185-202

[2] F. Despert Prise en charge du retard de croissance et de puberté, Encyclopédie Médico-Chirurgicale, Encyclopédie pratique de médecine 3-0670, Elsevier, Paris, 1998

[3] R. Cancedda; P. Castagnola; F.D. Cancedda; B. Dozin; R. Quarto Development control of chondrogenesis and osteogenesis, Int. J. Dev. Biol., Volume 44 (2000), pp. 707-714

[4] H. Schiessl; H.M. Frost; W.S. Jee Estrogen and bone-muscle strength and mass relationships, Bone, Volume 22 (1998), pp. 1-6

[5] R. Coujard; J. Poirier; J. Racadot Précis d'histologie humaine, Masson, Paris, 1980

[6] M. Jim; E.H. Frank; T.M. Quinn; E.B. Hunziker; A.J. Grodzinsky Tissue shear deformation stimulates proteoglycan and protein biosynthesis in bovine cartilage explants, Arch. Biochem. Biophys., Volume 395 (2001), pp. 41-48

[7] E.H. Burger; J. Klein-Nulend; J.P. Veldhuijzen Modulation of osteogenesis in fetal bone rudiments by mechanical stress in vitro, J. Biomech., Volume 24 (1991) no. Suppl. 1, pp. 101-109

[8] L. Schwartz; H. Maitournam; C. Stolz; J.-M. Steyaert; M.-C. Ho Ba Tho; B. Halphen Growth and cellular differentiation: a physico-biochemical conundrum? The example of the hand, Med. Hypotheses, Volume 61 (2003) no. 1, pp. 45-51

[9] D'Arcy Thompson On Growth and Form, Cambridge University Press, Cambridge, 1917

[10] D.R. Carter; M. Wong; T.E. Orr Musculoskeletal ontogeny, phylogeny and functional adaptation, J. Biomech., Volume 24 (1991) no. Suppl. 1, pp. 3-16

[11] C.H. Turner; F.M. Pavalko Mechanotransduction and functional response of the skeleton to physical stress: The mechanisms and mechanics of bone adaptation, J. Orthop. Sci., Volume 3 (1998), pp. 346-355

[12] L.A. Opperman; D.B. Drake; P. Kang; S.M. Nakeeb; M. Gammas; R.F. Morgan A pilot study of short and long term sequelae to rigid fixation across metaphyseal physes in a baboon model, Ann. Plast. Surg., Volume 44 (2000)

[13] D. Caine; R. Lewis; P. O'Connor; W. Howe; S. Bass Does gymnastics training inhibit growth of female, Clin. J. Sport Med., Volume 11 (2001), pp. 260-270

[14] G. Wawryniak Biological age in children who practise swimming, Antropol. Anz., Volume 59 (2001), pp. 149-156

[15] E. Backman Methods for measurement of muscle function. Methodological aspects, reference values for children, and clinical applications, Scand. J. Rehabil. Med., Volume S20 (1998), pp. 9-95

[16] A.T. Soliman; M.M. Khadir; M. Asfour Testosterone treatment in adolescent boys with constitutional delay of growth, Metabolism, Volume 44 (1995), pp. 1013-1015

[17] H. Bricaire; E. Baulieu; J. Leprat Glandes Endocrines, Flammarion, Paris, 1980 (p. 27)

[18] J.H. Wilmore; D.L. Costil Physiology of Sport and Exercise, De Boek, 1999, pp. 527-540

[19] P. Kumar; M. Clark Clinical Medicine, W.B. Saunders Co., Elsevier Science Ltd., Paris, London, 2002 (p. 1032)

[20] J. Klein-Nulend; J.P. Veldhuijzen; E.H. Burger Increased calcification of growth plate cartilage as a result of compressive force in vitro, Arthritis and Rheumatism, Volume 29 (1986) no. 8, pp. 1002-1009

[21] E. Tanck; W.D. van Driel; J.W. Hagen; E.H. Burger; L. Blankevoort; R. Huiskes Why does intermittent hydrostatic pressure enhance the mineralization process in fetal cartilage?, J. Biomech., Volume 32 (1999), pp. 153-161

[22] M. Wong; D.R. Carter Theoretical stress analysis of organ culture osteogenesis, Bone, Volume 11 (1990), pp. 127-131

[23] M.D. Buschman; Y.A. Gluzband; A.J. Grodzinsky; E.B. Hunziker Mechanical compression modulates matrix biosynthesis in chondrocyte/agarose culture, J. Cell Sci., Volume 108 (1995), pp. 1497-1508

[24] U. Yoshihisa; I. Toshihiro; Y. Takeshi; K. Masashi; M. Shoji Five jumps per day increase bone mass and breaking force in rats, J. Bone Miner. Res., Volume 12 (1997), pp. 1480-1485

[25] P.L. William; R. Warwick Gray's Anatomy, W.B. Saunders Co., Philadelphia, PA, USA, 1980, pp. 230-270

[26] J.M. Tanner; R.H. Whitehouse; N. Cameron; W.A. Marshall; M.J.R. Healy; H. Goldstein Assessment of Skeletal Maturity and Prediction of Adult Height (TW2 Method), Academic Press, London, 1983

[27] R.L. Smith; B.S. Dolon; M.K. Gupta; M. Mohtai; P. Das; D.R. Carter; J. Cook; G. Gibbon; N. Hutchinson; D.J. Schurman Effects of fluid-induced shear stress on articular chondrocytes morphology and metabolism in vitro, J. Orthop. Res., Volume 13 (1995), pp. 824-831

[28] P.F. Davie; S.C. Tripathi Mechanical stress mechanisms and the cell, Circ. Res., Volume 72 (1993), pp. 239-245

[29] V. Fleury; L. Schwartz D.L.A. from shear stresses as a simple model of vasculogenesis, Fractals, Volume 7 (1999), pp. 33-39

[30] M. Liu; J. Xu; A.K. Transwell; M. Post Inhibition of mechanical strain-induced fetal rat lung cell proliferation by gadolinium, a stretch-activated channel blocker, J. Cell Physiol., Volume 161 (1994), pp. 501-507

[31] M. Murnin; A. Kumar; G. Li; M. Brown; B.E. Sumpio; M.D. Basson Effects of glutamine isomers on human(Caco-2)intestinal epithelial proliferation, strain responsiveness and deformation, J. Gastrointest. Surg., Volume 4 (2000), pp. 435-442

[32] V. Perraudin; H. Lefebvre; J.-M. Kuhn Insuffisance antéhypophysaire, Encyclopédie Médico-Chirurgicale, Elsevier, Paris, 1992 (10-019-A-10)

[33] H. Pearson, Stretching changes stem cell's fate, Nature Science, Update 13th December 2003