How was the French BSE epidemic underestimated?

Virginie Supervie; Dominique Costagliola

doi:10.1016/j.crvi.2005.12.004

Medical sciences / Sciences médicales

How was the French BSE epidemic underestimated?
[Comment l'épidémie d'ESB a-t-elle été sous-estimée en France ?]

Présenté par : Jean Rosa

Virginie Supervie ^1,² ; Dominique Costagliola ^1,²

¹ INSERM, U 720, 56, bd Vincent-Auriol, BP 335, 75013 Paris, France
² Université Pierre-et-Marie-Curie, 4, place Jussieu, 75252 Paris cedex 05, France

Comptes Rendus. Biologies, Volume 329 (2006) no. 2, pp. 106-116.

Résumés

Anglais
Français

In a previous study, we showed that estimates of the BSE epidemic in France were censored by cattle mortality and by a lack of diagnosis. Indeed, we estimated that 51 300 cattle were infected by the BSE agent between 1987 and 1997, whereas only 103 clinical BSE cases were detected by the passive surveillance system up to June 2000. The question thus arises as to the part played by each form of censorship in this underestimation. Here, using an updated cattle survival distribution, we estimated that 44 800 cattle were infected by the BSE agent between 1987 and 1997, and that 7100 of them showed clinical signs of BSE up to June 2000, showing the low efficiency of the surveillance system. Moreover, between 2087 and 5980 ‘infectious’ cattle, with clinical or preclinical BSE, entered the human food chain before July 1996, the date of the ban on specified bovine offal.

Dans une étude précédente, nous avons montré que l'épidémie d'ESB en France avait été censurée par la mortalité des bovins et par un défaut de diagnostic. En effet, nous estimions que 51 300 bovins avaient été infectés par l'agent de l'ESB entre 1987 et 1997, alors que seulement 103 cas cliniques d'ESB avaient été détectés par le système de surveillance passif jusqu'en juin 2000. Quelle part chaque forme de censure a joué dans cette sous-estimation ? Ici, en utilisant une distribution de survie des bovins mise à jour, nous avons estimé que 44 800 bovins ont été infectés par l'ESB entre 1987 et 1997, dont 7100 ont présenté des signes cliniques d'ESB jusqu'en juin 2000, ce qui montre la faible efficacité de la surveillance passive. De plus, entre 2087 et 5980 bovins « infectieux », au stade clinique ou préclinique, sont entrés dans la chaîne alimentaire humaine avant juillet 1996, la date d'implémentation du retrait des matériaux à risque spécifié.

Métadonnées

Reçu le : 2005-09-01
Accepté le : 2005-12-13
Publié le : 2006-01-18

PMID

DOI : 10.1016/j.crvi.2005.12.004

Keywords: Back-calculation, Bovine spongiform encephalopathy, Epidemiology, Survival, Under-reporting
Mots-clés : Rétrocalcul, Encéphalopathie spongiforme bovine, Épidémiologie, Survie, Sous-notification

Affiliations des auteurs :

Virginie Supervie ^{1, 2} ; Dominique Costagliola ^{1, 2}

¹ INSERM, U 720, 56, bd Vincent-Auriol, BP 335, 75013 Paris, France
² Université Pierre-et-Marie-Curie, 4, place Jussieu, 75252 Paris cedex 05, France

@article{CRBIOL_2006__329_2_106_0,
     author = {Virginie Supervie and Dominique Costagliola},
     title = {How was the {French} {BSE} epidemic underestimated?},
     journal = {Comptes Rendus. Biologies},
     pages = {106--116},
     publisher = {Elsevier},
     volume = {329},
     number = {2},
     year = {2006},
     doi = {10.1016/j.crvi.2005.12.004},
     language = {en},
}

TY  - JOUR
AU  - Virginie Supervie
AU  - Dominique Costagliola
TI  - How was the French BSE epidemic underestimated?
JO  - Comptes Rendus. Biologies
PY  - 2006
SP  - 106
EP  - 116
VL  - 329
IS  - 2
PB  - Elsevier
DO  - 10.1016/j.crvi.2005.12.004
LA  - en
ID  - CRBIOL_2006__329_2_106_0
ER  -

%0 Journal Article
%A Virginie Supervie
%A Dominique Costagliola
%T How was the French BSE epidemic underestimated?
%J Comptes Rendus. Biologies
%D 2006
%P 106-116
%V 329
%N 2
%I Elsevier
%R 10.1016/j.crvi.2005.12.004
%G en
%F CRBIOL_2006__329_2_106_0

Virginie Supervie; Dominique Costagliola. How was the French BSE epidemic underestimated?. Comptes Rendus. Biologies, Volume 329 (2006) no. 2, pp. 106-116. doi : 10.1016/j.crvi.2005.12.004. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2005.12.004/

Version originale du texte intégral

Le texte intégral ci-dessous peut contenir quelques erreurs de conversion par rapport à la version officielle de l'article publié.

1 Introduction

Clinical identification of cases of infectious diseases, whether human or non-human, is often the only way of tracking an epidemic. However, when the incubation period is long and variable, as in the acquired immunodeficiency syndrome (AIDS), variant Creutzfeldt–Jacob disease (vCJD) and bovine spongiform encephalopathy (BSE), the reported clinical incidence does not reflect trends in the spread of the infection. Brookmeyer and Gail [1,2] proposed a method known as back-calculation for estimating the incidence of human immunodeficiency virus (HIV) infection from AIDS incidence data and for obtaining short-term projections of the incidence of AIDS. This method relies on the principle that the known number of clinical cases results from an unknown past number of cases of infection and a known incubation period, defined as the time between infection and initial clinical onset. In order to obtain an unbiased estimate of the epidemic dynamics of an infection, the back-calculation method must be applied to accurate disease incidence data over time. Sometimes, however, the epidemiological characteristics of infectious disease and/or the characteristics of the study population result in biased disease incidence data.

In addition to a long and variable incubation period and age-dependent susceptibility/exposure, two other features have to be taken into account when studying the epidemic of BSE infection. First, one must consider under-reporting of BSE clinical cases and variations in the degree of under-reporting during the course of the epidemic. Up to June 2000, the surveillance of BSE was solely based on clinical surveillance through a mandatory reporting system (passive surveillance), in which veterinary practitioners and farmers were required to report animals with clinical signs of BSE. The difficult clinical diagnosis of BSE probably accounts for some under-reporting. In addition, between the description of the first clinical BSE case diagnosed in 1986 in the United Kingdom and the realization in 1996 that the most likely explanation for vCJD was exposure to the BSE agent [3–5], the BSE epidemic had no economic consequences for farmers and no known health consequences for humans. The reporting rate may thus have varied as awareness of the gravity of the disease grew. The second characteristic we must take into account is the particular demography of cattle. Indeed, as a result of human eating habits, many cattle are slaughtered young. Thus, the average survival time is shorter than the average BSE incubation period. This implies that some BSE-infected animals are selectively excluded from the passive surveillance system, as they die before the infection is diagnosed. Also, some animals die before being infected. Thus, both natural mortality and that resulting from slaughter must be taken into account. In our previous study [6], we adapted the back-calculation method by taking these epidemiological and demographic characteristics into account, and this allowed us to estimate longitudinal trends in the incidence of BSE infection in France on the basis of reported BSE clinical cases. We showed that estimates of the BSE infection epidemic in France were censored by cattle mortality and clinical under-reporting. We estimated that 51 300 cattle were infected by the BSE agent between July 1987 and June 1997, whereas only 103 clinical cases were detected by the passive surveillance system up to June 2000. Although we assumed that the French BSE epidemic started in 1980, in this analysis, we focused on estimates between July 1987 and June 1997, in order to avoid uncertainties as to what actually occurred in the 1980s. We asked: “How could 51 300 cattle infected by the BSE agent go unnoticed?” and “How was the French BSE epidemic underestimated?” Of course, not all cattle infected by the BSE agent had clinical signs of BSE, but what was the share of each form of censorship in the underestimation? And what was the risk for the French consumer?

Here, after studying the sensitivity of our previous results to variations in the model parameters, such as cattle mortality and the distribution of the incubation period, we estimated the parts played by cattle mortality and under-reporting of clinical cases in the underestimation of the French BSE epidemic. We estimated the number of infected cattle that developed clinical signs and the number of infected cattle that died before developing clinical signs. We also determined how many infectious cattle, in the clinical or preclinical stage of BSE, entered the human food chain.

2 The back-calculation method

2.1 The extended back-calculation method

We adapted the back-calculation method described by Becker and Marschner [7], taking the effect of age into account, in order to include the survival distribution of cattle and a time-dependent reporting rate of clinical BSE cases. The age covariate carries information about the incubation period of an individual when the infection rate depends on age, and permits the use of an incubation period distribution that is dependent on age at infection. In our adaptation of the back-calculation method, the age covariate was used to simultaneously estimate a time-dependent incidence of infection and a risk of infection for animals of different ages. The incubation period distribution was assumed to be independent of age at infection.

Let $N_{a, t}$ and $Y_{a, t}$ be the random numbers of newly infected animals and new clinical cases among animals of age a at time t, and let $E (N_{a, t})$ , $E (Y_{a, t})$ be their expectations. Assuming that the incubation period distribution has a density $f (t)$ , that $S (a | a^{'})$ represents the probability that an animal will survive to age a, knowing that the same animal was alive at age $a^{'}$ (the age at infection), and that $Λ (t)$ is a time-dependent probability that a given clinical case is actually reported at time t, the model becomes:

E (Y_{a, t}) = \int_{0}^{t} E (N_{a - t + s, s}) f (t - s) S (a | a - t + s) d s Λ (t)

Age a varies between 1 and A, where A is the age of the oldest cattle, and time t varies between 1 and T, where T is the last date at which the clinical case count is considered reliable.

In our model, survival is conditional on being alive at the time of infection. Indeed, only some cattle were exposed to the risk of contracting BSE agent, as others died or were slaughtered shortly after birth. It was therefore necessary to consider survival among animals that were alive at the time of infection. We assumed that the survival distribution was independent of time.

The unknown time- and age-specific number of infections was modelled by using the multiplicative model

E (N_{a, t}) = π_{a} α_{a} λ_{t}

(1)

where

π_{a}

, considered known from demographic data, is the proportion of animals in the population that are of age a, and

α_{a}

reflects the susceptibility/exposure of animals of age a. We assumed that these two parameters were independent of time. In addition, we assumed that no further infections occurred after age A, and therefore fixed

α_{a}

at 0 for all

a > A

.

To avoid an identifiability problem in model (1), we imposed the constraint

\sum_{a = 1}^{A} π_{a} α_{a} = 1

With this constraint, $λ_{t}$ represents the overall intensity of infection.

2.2 Parameter estimation

Assuming that the age- and time-specific numbers of newly infected animals $N_{a, t}$ are independent Poisson variates, then the age- and time-specific numbers of new clinical cases $Y_{a, t}$ are also independent Poisson variates. This gave the likelihood function corresponding to the age- and time-specific numbers of observed clinical BSE cases $y_{a t}$ :

L = L (α, λ | y) = \prod_{t = 1}^{T} \prod_{a = 1}^{A} \frac{μ_{a t}^{y_{a t}} \exp (- μ_{a t})}{y_{a t}!}

where

μ_{a, t} = E (Y_{a, t}) = \int_{0}^{t} π_{a - t + s} α_{a - t + s} λ_{s} f (t - s) S (a | a - t + s) d s Λ (t)

(2)

Instead of assuming a parametric family of curves for α and λ, we used a non-parametric form and obtained maximum-likelihood estimates of age at infection and of the time-dependent risk of infection by using the EM algorithm [8]. However, when a large number of parameters are involved, the resulting EM estimates will tend to fluctuate implausibly. One simple remedy is to add a smoothing $(S)$ step to each iteration of the EM algorithm, as in the so-called EMS algorithm [9].

Of course, when a smoothing step is added, the procedure no longer maximizes the likelihood; instead, the process is related to maximization of a penalized likelihood [7]. There is thus no compelling reason to use a convergence criterion based on the value of the likelihood. It is logical to use a convergence criterion based on the values of the parameters of interest. We chose small positive values for $ɛ_{1}$ and $ɛ_{2}$ , and stopped the iteration when both the following conditions were met:

\frac{‖ α^{new} - α^{old} ‖}{‖ α^{old} ‖} < ɛ_{1} and \frac{‖ λ^{new} - λ^{old} ‖}{‖ λ^{old} ‖} < ɛ_{2}

2.3 Model-selection criterion

When estimating the age- and time-specific numbers of newly infected animals with the back-calculation method, all other model epidemiological parameters need to be known. This means that sufficient data must be available from other sources for accurate estimation. If such data sources are not available, flexible functions should be attributed to these parameters; sensitivity analyses should then be performed and a selection criterion should be defined to choose the best model. Here, as we lacked independent data from which to estimate the time-dependent clinical BSE case reporting function and the incubation period distribution, we assumed flexible functions for these parameters, performed sensitivity analyses, and chose the best model on the basis of Akaike's information criterion (AIC) [10], as follows:

AIC(model) = - 2 \log L + 2 K

where L is the model likelihood and K is the number of estimated parameters. We used the empiric rule of Burnham and Anderson [10], which retains a model if

(AIC (model) - \min AIC ⩽ 2)

, where

\min AIC

is the minimum AIC, i.e. the AIC of the best model.

The parameters regarding the demography of French cattle ( $S (a | a^{'})$ and $π_{a}$ ) were estimated from independent data supplied by the ‘Direction générale de l'alimentation’ (DGAL).

2.4 Confidence intervals

The usual asymptotic properties of maximum-likelihood estimates do not apply in the present context, because of the large number of parameters. Following the method of Becker and Marschner [7], we used bootstrap estimates of precision. In this procedure we first use the EM algorithm to obtain the maximum-likelihood estimates of ${\hat{μ}}_{a t}$ . These are given by ${\hat{μ}}_{a t} = μ_{a t} (\hat{λ}, \hat{α})$ , where $\hat{α}$ and $\hat{λ}$ are the maximum-likelihood estimates obtained from the EM algorithm and $μ_{a t}$ is given by (2). The ${\hat{μ}}_{a t}$ are then used to generate a large number of age-specified BSE data sets, using the independence of Poisson variates $Y_{a t}$ . Then, the EMS procedure is applied to each simulated data set, each giving an estimate of α and λ. The B estimates $(\hat{α}, \hat{λ})$ give a frequency distribution for $(\hat{α}, \hat{λ})$ , which can be used to calculate confidence intervals or standard errors. To assign 95% confidence intervals, we used the percentile method [11]. The confidence intervals for the simulation studies and applications described below are based on $B = 1000$ simulated BSE datasets.

3 Application

3.1 The French BSE history and the high-risk period for French consumers

In France, BSE became a notifiable disease in June 1990. In December 1990, a mandatory passive surveillance system was set up, in which veterinary practitioners and farmers were required to report animals with clinical signs. The first case of BSE identified by this surveillance system was detected in 1991. A total of 103 cases were identified by passive surveillance between 1991 and June 2000. From mid-2000 to July 2001, the surveillance system underwent several changes. From mid-2000, in addition to the mandatory reporting system, a pilot study of rapid testing was implemented on cattle at risk (dead-on-farm, emergency-slaughtered and euthanatized cattle). Then, from January 2001, systematic screening was extended to all cattle over 30 months of age entering the food chain, and this age was reduced to 24 months in July 2001. Implementation of active surveillance revealed the inefficiency of passive surveillance, both in France and elsewhere. In France, comparison of the results of the passive and active surveillance systems between July 2001 and June 2002 showed that only 20% of BSE cases were identified by passive surveillance. This implied considerable BSE case under-reporting throughout the epidemic.

Only animals slaughtered for consumption late in the incubation period and, above all, animals in the clinical stage, are likely to be infectious. Consequently, regarding the exposure of the French human population to the BSE agent via the French BSE epidemic, the period at risk was situated before the implementation of rapid tests. In addition, only the period before July 1996 was at high risk, i.e. the period before the French ban on high-risk bovine tissues (‘specified offal’) from all cattle entering the human food chain.

3.2 Data

For the above reasons and because of the above-mentioned changes in the French BSE monitoring system, our analysis was restricted to clinical cases detected before July 2000, i.e. the 103 cases identified by passive surveillance between 1991 and June 2000 [6]. All the animals were cows aged between 4 and 9.5 years at clinical onset; the median age was 5.5 years and the interquartile range was $[4.8; 6.6]$ .

The assumption of independence regarding the number of new clinical cases is reasonable (Section 2.2), as only 3 of the 103 clinical cases of BSE detected up to June 2000 were secondary cases.

3.3 BSE epidemiological characteristics and cattle demographics

Epidemiological data on clinical onset by age, assuming a long incubation period, suggest that most infections occur shortly after birth. This means that the infection rate depends on age. We therefore took the effect of age into account by estimating an age-dependent susceptibility and/or exposure to infection, as available data did not allow us to discriminate between the two. As the data did not allow estimating a susceptibility/exposure per year of age, we estimated susceptibility/exposure per age class. We considered six susceptibility/exposure groups (in years): ]0–0.5], ]0.5–1], ]1–2], ]2–3], ]3–5], ]5–30]. The smoothing step was not appropriate for age-dependent susceptibility/exposure to infection, because of the small number of groups.

We explored two incubation period distributions – a gamma distribution and a distribution derived from a mechanistic model.

When assuming the gamma distribution, the probability density function of the incubation period $f (t)$ was:

f (t) = {\begin{matrix} 0 & \forall t ⩽ 2 \\ \frac{q^{p} {(t - 2)}^{p - 1} \exp (- q (t - 2))}{Γ (p)} & \forall t > 2 \end{matrix}

In order to reproduce the observed incubation period of at least two years before clinical onset, we assumed that the probability of a BSE incubation period of two years or less was nil. The distribution mean was

(p / q + 2)

years and the distribution variance was

p / q^{2}

. By varying the distribution parameters, we varied the mean incubation period between 4 and 6 years and the variance between 1 and 3 years² by steps of 0.1.

Another assumed incubation period distribution arises from a mechanistic model of disease pathogenesis [12]. The underlying model assumes that the prion density grows exponentially, at rate $γ_{1}$ from an initial dose $d_{0}$ , causing the onset of clinical signs when it reaches a critical level. Arbitrarily setting this critical level at 1 and assuming that the initial dose arises from the distribution $h (d_{0})$ , the incubation period conditional on the initial dose is:

u = \frac{- \log d_{0}}{γ_{1}}

and the distribution of incubation period is given by:

f (u) = - h [d_{0} (u)] \frac{d d_{0}}{d u} = - h [\exp (- γ_{1} u)] γ_{1} \exp (- γ_{1} u)

An initial delay in the incubation period distribution can be obtained if the initial dose distribution peaks at doses far below the critical level. Assuming that the initial doses arise from a gamma distribution, we obtain the following incubation period distribution

f (u) = \frac{γ_{1}}{Γ (γ_{3})} {[γ_{2} \exp (- γ_{1} u)]}^{γ_{3}} \exp [- γ_{2} \exp (- γ_{1} u)]

where u represents the incubation period and

γ_{2}

and

γ_{3}

determine the parameters of the gamma distribution of the initial dose. Analytic expressions of the mean and of the variance do not exist for this distribution. Therefore, in order to vary the mean and the variance, we varied

γ_{1}

from 0.70 to 2 with steps of 0.05,

γ_{2}

from 0 to 0.030 with steps of 0.001 and

γ_{3}

from 0 to 0.002 with steps of 0.00005, then we selected the values of

γ_{1}

,

γ_{2}

and

γ_{3}

for which the mean incubation period was between 4 and 6 years and the variance was between 1 and 3 years². In addition, several combinations of

γ_{1}

,

γ_{2}

and

γ_{3}

can lead to the same values of the mean and variance of this distribution.

The sharp increase in the incidence of BSE noted when the first systematic screening program was instigated revealed the inefficiency of passive surveillance. Thus, a time-dependent BSE case reporting function had to be introduced. A logistic shape was assumed for the time-dependent reporting function, starting in June 1990, with zero reporting before this date (no monitoring system existed):

Λ (t) = {\begin{matrix} \frac{\exp (θ + β (June 2000 - t))}{1 + \exp (θ + β (June 2000 - t))} & \forall t ⩾ 1990 \\ 0 & \forall t < 1990 \end{matrix}

The logistic function depended on two parameters, namely β the shape parameter and θ the parameter determining the reporting probability in June 2000. Let $Λ (June 2000)$ be the probability of a clinical case being reported in June 2000, then

θ = \ln (\frac{Λ (June 2000)}{1 - Λ (June 2000)})

By varying β, we explored a wide range of reporting shapes, from constant reporting throughout the epidemic $(β = 0)$ to a reporting function with very low reporting probabilities in the early stages of the epidemic and an abrupt increase in the recent past $(β = - 1)$ . We varied β by steps of 0.1. As only about 20% of all BSE cases were identified by passive surveillance between July 2001 and June 2002, we used an upper limit of 20% for the reporting probability in June 2000, but we also ran the model assuming a reporting probability of 99% in June 2000. Therefore, by varying the second parameter θ, we varied the reporting probability in June 2000 between 5% and 20%, and 99%. However, in the absence of independent data on reporting probabilities, it is impossible to fit a time-dependent probability of reporting across the entire epidemic, as the reporting rate is confounded with the time-varying risk of infection. Only temporal changes in these probabilities can be estimated. All the reporting probabilities in June 2000 that we tested were compatible with a good fit (similar AICs). Thus, external data were needed to establish the reporting probability in June 2000. For this purpose, we compared annual predictions of clinical BSE cases with observed clinical BSE cases. Then, to select the value of the shape parameter of the reporting function, and to select all unknown parameters of the model, we used the AIC.

Data on cattle demography were obtained from the French reference database for bovine identification (‘Base de données nationale d'identification’, BDNI). Launched in 2000, this system is administered by the DGAL, a department of the Ministry for Agriculture, Food and Fisheries. It allows cattle to be followed from birth to death. We obtained data on the age-specific numbers of cattle alive on 1 January 2002 and on 1 January 2003, and on the age-specific numbers of cattle sent to the abattoir and rendered in 2002 and 2003. The comparison of estimates between 2002 and 2003 showed no change, and allowed us to assume that these demographic parameters were stationary. We used the demographic data for 2002 to estimate the survival distribution (Fig. 1, ▴), the age-specific risk of death, and the age-specific proportion of cattle mortality resulting from slaughter. 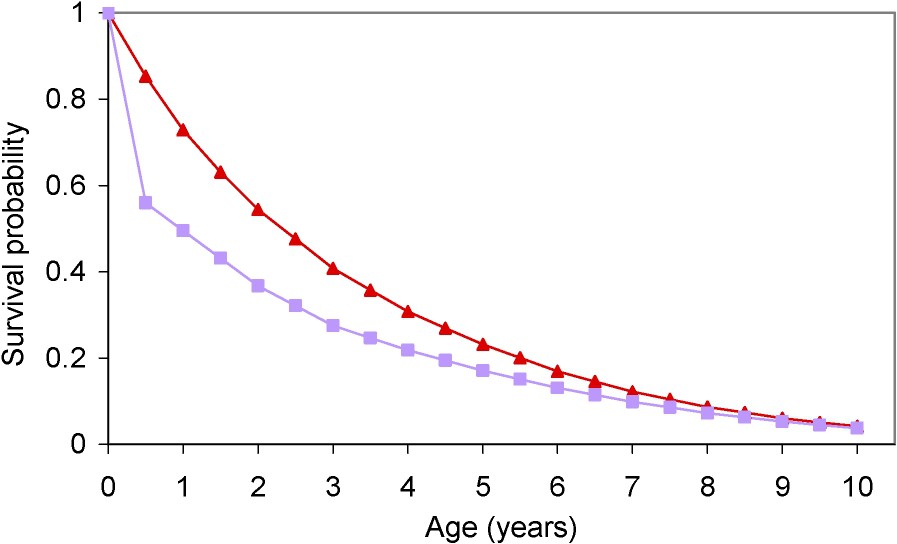The median survival was 2.3 years and the interquartile range was $[0.9; 4.8]$ . In our previous study [6], we reconstructed a survival distribution from three data sources (Fig. 1, ■), as the above data were not available. Survival probabilities estimated in the present study were higher than in our previous study. Below, we performed analyses using the survival distribution estimated from DGAL data and discussed the impact of using different survival distributions.

Fig. 1
Estimated survival distributions of French cattle in our previous study (■) [6] and in the present study (▴).

3.4 Estimates of BSE infections, preclinical and clinical cases, and predictions

The time-dependent intensity of infection $λ_{t}$ was estimated annually up to 1996. Years were defined so that, for example, 1996 consisted of the period between 1 July 1996 and 30 June 1997. As we considered cases of BSE detected up to June 2000, we could not estimate the BSE infection rate beyond June 1997. Indeed, because of the long BSE incubation period, BSE incidence data offer little information on the number of animals most recently infected. In addition, as in our previous study, we assumed that the French BSE epidemic began in 1980. However, in our previous study, the confidence intervals of our estimate of the epidemic were very large in the 1980s and only the estimate between July 1987 and June 1997 was informative. So, in this study, even if we assumed that the BSE epidemic started in 1980, only the period between July 1987 and June 1997 is described, in order to simplify the comparison of the results of our two studies.

From the estimated number of cattle infected by the BSE agent, we ascertained by simulation the fate of each infected animal in order to determine the number of cattle that developed clinical signs of BSE (clinical BSE cases), the number that died or were slaughtered before clinical onset (preclinical BSE cases), and the number of ‘infectious’ animals that entered the human food chain (infectious preclinical BSE cases). We defined as ‘infectious’ an animal infected by the BSE agent that was slaughtered at the abattoir within the year before clinical onset. For each infected animal, we randomly assigned an age at infection, an incubation period, and a lifetime, given that the animal was alive at the age of infection. We thus obtained the number of infected cattle between times s and $s + Δ$ aged between a and $a + Δ$ at infection, with an incubation period between d and $d + Δ$ , and a lifespan between $a^{'}$ and $a^{'} + Δ$ . Using the age-specific proportion of cattle mortality resulting from slaughter, we were then able to deduce the number of infected cattle slaughtered between ages $a^{'}$ and $a^{'} + Δ$ , between times t and $t + Δ (t = s + (a^{'} - a))$ and between times x and $x + Δ$ before clinical onset $(x = d - (a^{'} - a))$ .

The number of new BSE clinical cases at time t was predicted by:

\int_{0}^{A} E (Y_{a t}) d a = \int_{0}^{A} \int_{0}^{t} E (N_{a - t + s, s}) f (t - s) S (a | a - t + s) d s Λ (t) d a

Up to June 1997, we used estimates of

E (N_{a, t})

, while beyond June 1997 we assumed that no new infections occurred. Regarding the time-dependent reporting function, beyond June 2000 we assumed that the reporting probability of clinical cases was 20%.

3.5 Results

Table 1 shows estimates that minimized the AIC according the reporting probability in June 2000 and the distribution of the incubation period. The gamma distribution always fitted the data slightly better, based on the AIC, than the distribution derived from the mechanistic model (Table 1). We therefore assumed a gamma distribution in subsequent calculations. Except for a reporting probability of 99% in June 2000, whatever the reporting probability in June 2000, the best models suggested that the average BSE incubation period was about 5.6 yr, that the variance was about 2.6 yr², that 99% of infections occurred between 0.5 and 1 year of age, and that the value of the shape parameter of the reporting function, β, was −0.5. The model assuming a reporting probability of 99% fitted the data less well than the other models. Similar AICs were obtained for all other assumed reporting probabilities in June 2000, so the Burnham and Anderson empiric rule did not allow us to select one value rather than another. To establish the reporting probability in June 2000, as in our first study we compared estimated annual numbers of clinical BSE cases with observed clinical cases for the periods July 2000 to June 2001 and July 2001 to June 2002. Passive surveillance detected 134 clinical BSE cases between July 2000 and June 2001 and 60 clinical BSE cases between July 2001 and June 2002; in addition, respectively 75 and 161 BSE cases were detected among cattle at risk. We also reported the number of BSE cases detected among cattle at risk, because a retrospective clinical investigation [13] suggested that the vast majority of BSE cases detected among cattle at risk should have been included in the mandatory reporting system (passive surveillance), as the animals concerned had clinical signs of BSE. This implied that the numbers of clinical BSE cases estimated by the model should be at least equal to the number detected by passive surveillance, in order to be consistent with reality, i.e. 134 clinical BSE cases between July 2000 and June 2001 and 60 between July 2001 and June 2002. Using a reporting probability of 5% in June 2000, we estimated that roughly 154 and 94 clinical cases would have been detected by the passive surveillance system for the periods from July 2000 to June 2001 and July 2001 to June 2002, respectively, compared to 76 and 47 clinical cases if the reporting probability was 10%. Thus, the assumed reporting probability of 10% or more in June 2000 underestimated the true situation. When using a reporting probability above 6%, estimated numbers of clinical BSE cases were lower than observed numbers. In addition, when using a reporting probability under 4%, estimated numbers of clinical BSE cases were higher than the sum of observed numbers of BSE cases detected by passive surveillance and among at risk cattle. It was not possible to select a value between 4% and 6% for the reporting probability, for example with the mean square criterion, as we did not know how many cattle would have been detected by passive surveillance. Nevertheless, in subsequent calculations we assumed that the reporting probability in June 2000 was 5%.

	Reporting probability in June 2000: $Λ (June 2000)$
	0.05	0.10	0.15	0.20	0.99
Gamma incubation period distribution
AIC	326.2	326.2	326.1	326.1	331.8
Shape parameter of the reporting curve (β)	−0.5	−0.5	−0.5	−0.5	−0.7
Mean of the incubation period (years)	5.6	5.6	5.6	5.7	6
Variance of the incubation period (years²)	2.6	2.6	2.6	2.7	2.7
Distribution of age of infection (years)
]0–0.5]	≈0	≈0	≈0	≈0	≈0
]0.5–1]	0.99	0.99	0.99	0.99	0.95
]1–2]	≈0	≈0	≈0	≈0	0
]2–3]	0	0	0	0	0
]3–5]	0	0	0	0	0.04
]5–30]	0	0	0	0	0
Mechanistic incubation period distribution
AIC	328.3	328.3	328.2	328.2	334.0
Shape parameter of the reporting curve (β)	−0.5	−0.5	−0.5	−0.5	−0.9
Mean of the incubation period (yr)	5.5	5.5	5.5	5.5	5.8
Variance of the incubation period (yr²)	2.9	2.9	2.9	2.9	2.8
Distribution of age of infection (yr)
]0–0.5]	0	0	0	0	≈0
]0.5–1]	0.99	0.99	0.99	0.99	≈0.95
]1–2]	≈0	≈0	≈0	≈0	0
]2–3]	≈0	≈0	≈0	≈0	0
]3–5]	≈0	≈0	≈0	≈0	≈0.05
]5–30]	0	0	0	0	0

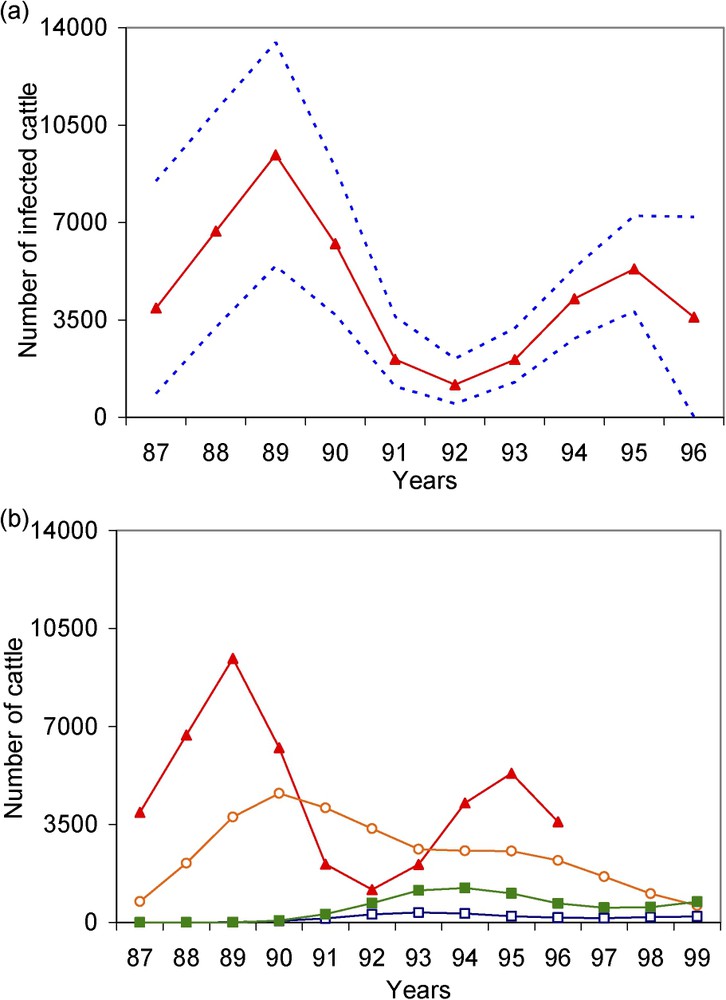
Under the assumptions of the best model, we estimated that 44 800 cattle (95% confidence interval $(CI) = [22 700 – 70 700]$ ) were infected by the BSE agent between July 1987 and June 1997. The infection dynamics are shown in Fig. 2a. The number of infections rose between 1987 and 1989, then fell between 1989 and 1992; the period 1992–1995 saw another, smaller rise and, finally, a new fall occurred after 1995.

Fig. 2
(a) Estimated (▴) annual incidence of BSE infection with 95% bootstrap confidence intervals (- - - -); (b) Incidence of clinical BSE cases (■), preclinical BSE cases (○) and ‘infectious’ preclinical BSE cases (□) obtained by simulation from the estimated incidence of BSE infection. We defined clinical BSE cases as infected cattle that had clinical signs of BSE, preclinical cases as infected cattle that died or were slaughtered before clinical onset, and ‘infectious’ preclinical BSE cases as infected cattle slaughtered at the abattoir within the year before clinical onset. Estimates and simulations were obtained by assuming a reporting probability of 5% in June 2000 and parameter β of the reporting curve =−0.5. Masquer
(a) Estimated (▴) annual incidence of BSE infection with 95% bootstrap confidence intervals (- - - -); (b) Incidence of clinical BSE cases (■), preclinical BSE cases (○) and ‘infectious’ preclinical BSE cases (□) obtained by simulation from the estimated incidence of BSE ... Lire la suite

In our previous study [6], in which we used a different cattle survival distribution (Fig. 1, ■), the best model suggested that the average BSE incubation period was 5 yr, the variance was 1.8 yr², that 86% of infections occurred between 0.5 and 1 yr of age and 8% between 1 and 2 years of age, that the value of the shape parameter of the reporting function, β, was −0.6 and that the reporting probability in June 2000 was 5%. We estimated that 51 300 cattle $(CI = [24 300 – 84 700])$ were infected by the BSE agent between July 1987 and June 1997.

The values retained in this study for the shape parameter of the reporting curve and for the parameters of the incubation period distribution were slightly higher than in our previous study. The number of BSE infections estimated in the present study was slightly lower than in our previous study. However, the confidence intervals of the estimate of the number of BSE infections were compatible in the two studies. Fig. 3 shows the dynamics of the BSE infection epidemic obtained in our two studies, under the assumptions of the best model. Up to the beginning of the 1990s, the curve estimated in the present study is above the curve estimated in the previous study, and then it is the other way round.

Fig. 3
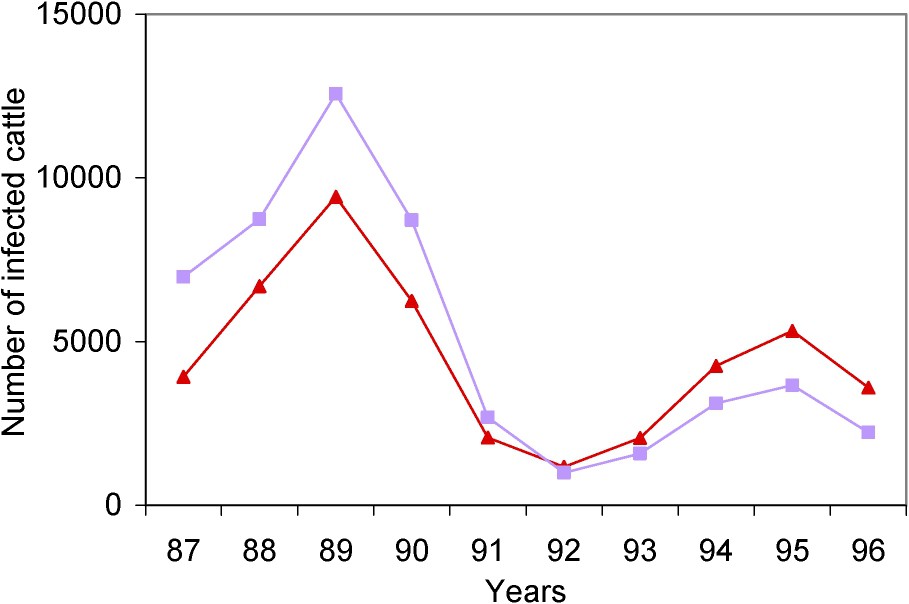
Estimated annual incidence rates of BSE infection obtained in the present study (▴) and in our previous study (■) [6], under the assumptions of the best model.

We also simulated the fate of cattle estimated to have been infected by the BSE agent in France in the present study. Fig. 2b illustrates the dynamics of the BSE infection epidemic between July 1987 and June 1997 obtained in the present study, and the numbers of the preclinical, ‘infectious’ preclinical and clinical BSE cases resulting from this epidemic. To assess the proportion of cattle estimated to be infected by the BSE agent that should have been detected by the passive surveillance system, we focused on what happened before July 2000, the date of implementation of rapid tests. To assess the risk for the consumer, we focused on cattle that entered the human food chain before July 1996, when high-risk bovine tissues (‘specified offal’) were banned from human consumption.

Based on the estimated 44 800 cattle $(CI = [22 700 – 70 700])$ infected by the BSE agent between July 1987 and June 1997, we estimated that, up to June 2000, 34 900 cattle $(CI = [17 800 – 54 900])$ (78%) were slaughtered or died before showing clinical signs (preclinical cases) and that 7100 cattle $(CI = [3700 – 11 200])$ (16%) had clinical signs (clinical cases); beyond June 2000, we estimated that 2800 infected cattle $(CI = [1100 – 4600])$ (6%) died, were slaughtered, or were detected by the passive surveillance. Until June 2000, only 103 clinical BSE cases were actually detected by clinical surveillance among the estimated 7100 cattle $(CI = [3700 – 11 200])$ that had clinical signs.

Until June 1996, we estimated that 4600 cattle $(CI = [2200 – 7400])$ had clinical signs (clinical cases) and that 1400 $(CI = [700 – 2300])$ infected cattle were slaughtered for human consumption within the year before clinical onset, representing ‘infectious’ preclinical cases. Only 20 clinical BSE cases were detected by passive surveillance up to June 1996.

4 Discussion

Some cattle, infected by the BSE agent, were not reported in France, either because of death from competing causes before disease onset or because the disease went undiagnosed. In this study, after having examined the sensitivity of our estimates to cattle mortality and to the incubation period distribution, we assessed the part played by each form of censorship in the under-estimation of the French BSE epidemic, and the risk for the consumer.

In contrast to our previous study [6], here we used an updated survival distribution. Indeed, newly available data from a single accurate source allowed us to estimate the survival distribution, whereas in our previous study we pooled data from three sources. The survival probabilities estimated in the present study were higher than in our previous study. Nevertheless, as explained in Section 2.1, both models considered conditional survival. The conditional survival probabilities markedly were less different than the unconditional survival probabilities.

In the two studies, we obtained the same reporting probability of BSE clinical cases in June 2000 (5%), and a similar distribution of age at infection. In this study, we estimated that 99% of infections occurred between 6 and 12 months of age, compared to 87% in our previous study. Slight shifts occurred in the values retained for the shape parameter of the reporting function (−0.5 in this study versus −0.6 in the previous study), and in the mean and variance of the incubation period (5.6 yr and 2.6 yr² versus 5 yr and 1.8 yr²). When comparing the dynamics of the BSE infection epidemic in our two studies, we observed that the curve obtained in the present study was above the curve obtained in our previous study, and that the situation then reversed. The value of the shape parameter of the reporting function only influences the dynamics of the curve in the 1980s (results not shown). The fact that the curve obtained in the present study is above the curve obtained in our previous study from 1992 (Fig. 3) results from the lengthening of the mean incubation period in the present study. Indeed, the longer the incubation period, the smaller the number of infections early in the epidemic and the larger the number of infections in the recent past. In the present study, the mean estimate of the number of infected cattle for the period July 1987 to June 1997 is slightly lower than in the previous study (44 800 versus 51 300). Nevertheless, the ranges of these estimates were similar: 22 700 to 70 700 cattle in the present study and 24 300 to 84 700 in the previous study. Finally, the use of a higher survival distribution results in slightly different estimates of certain parameters (such as the mean incubation period and the reporting rate of clinical cases of BSE) and in a lower estimate of the number of infected cattle. It is not possible to determine whether the age of slaughter varied following changes in consumer habits, or whether the data used for our previous study were inadequate to accurately reconstruct the survival distribution. The longer the survival time, the smaller the number of infections required to observe the reported number of clinical cases of BSE.

In both studies the best-fit model suggested that almost all BSE infections occurred between 6 and 12 months of age. Our results confirm those of Anderson et al. [14] and Ferguson et al. [12] regarding the British BSE epidemic, but differ from those of Arnold and Wilesmith [15], who concluded that the risk of infection was highest during the first 6 months of life. The best model in the present study suggested that the mean incubation period was 5.6 yr, compared to 5 yr in our previous study. These values are compatible with the estimates of 5 yr, 4.75–5.00 yr and 5.5 yr obtained respectively by Anderson et al. [14], Ferguson et al. [12], and Arnold and Wilesmith [15]. Contrary to Ferguson et al. [12], we found that the gamma distribution fitted the data slightly better than the distribution derived from the mechanistic model.

Overall, it can be considered that BSE infection in cattle occurs during the first year of life, and that the incubation period lasts between 4.75 and 5.6 yr.

We estimated that 44 800 cattle $(CI = [22 700 – 70 700])$ were infected by the BSE agent in France between July 1987 and June 1997, whereas up to June 2000, only 103 clinical cases of BSE had actually been identified. Although we assumed that the French BSE epidemic started in 1980, in this analysis we focused on estimates between July 1987 and June 1997, in order to avoid uncertainties as to what actually occurred in the 1980s. To understand how 44 700 cattle infected by the BSE agent could go undiagnosed, we simulated the fate of cattle estimated to have been infected by the BSE agent. We focused on the period before the implementation of rapid tests, in July 2000, to assess what proportion of these BSE-infected animals should have been detected by the passive surveillance system. Among cattle infected by the BSE agent that were detected or slaughtered or died up to June 2000, we estimated that 34 900 $(CI = [17 800 – 54 900])$ (83%) died or were slaughtered before clinical onset (BSE preclinical cases) and that 7100 $(CI = [3700 – 11 200])$ (17%) developed clinical signs (BSE clinical cases). These 7100 cattle should have been detected by passive surveillance. However, up to June 2000, only 103 clinical cases of BSE (1.5%) had actually been identified. Many cattle infected by the BSE agent could not be detected by clinical surveillance, as they died before developing clinical signs. However, any such cattle that entered the human food chain represented a lower risk for the consumer than cattle that had clinical BSE but escaped detection by the clinical surveillance system and also entered the human food chain.

Regarding the risk for the French consumer represented by French bovine products, only the period before the exclusion of high-risk bovine tissues (‘specified offal’) from human consumption in June 1996 was at high risk. Therefore, we focused on the number of ‘infectious’ preclinical and clinical BSE cases entering the human food chain before this date. Up to June 1996, we estimated that 1400 infected cattle $(CI = [700 – 2300])$ were slaughtered for human consumption within the year before clinical onset (‘infectious’ BSE preclinical cases), and that 4600 cattle $(CI = [2200 – 7400])$ developed clinical signs (BSE clinical cases). Up to June 1996 the passive surveillance system detected 20 clinical BSE cases. The fate of the estimated 4580 clinical BSE cases which were not detected by clinical surveillance is uncertain. Most were probably classified as cattle at risk (dead-on-farm, emergency-slaughtered or euthanatized). Dead-on-farm and euthanatized cattle are considered unfit for human consumption, but emergency-slaughtered cattle were only eliminated from the human food chain in February 2001. In addition, some were no doubt sent to the abattoir for human consumption. Indeed, a retrospective clinical survey of BSE cases detected after the implementation of screening tests [13] showed that 36% of all animals testing positive at the abattoir had possible, probable or definite clinical signs of BSE before death, and that this was the case of 92% of animals testing positive among at-risk cattle. By applying these proportions to the cases of BSE detected by each surveillance system (at the abattoir and among at-risk cattle), we were able to deduce the total number of clinical cases of BSE, and concluded that about 15% of cattle with clinical BSE were probably sent to the abattoir. This is a lower limit, as these surveys suffered from an information bias; indeed, interviews were conducted knowing that the animals were BSE-positive, and diseased animals are not allowed to be sent to the abattoir. In addition, these surveys were carried out after implementation of rapid testing, in July 2000. Rapid tests can detect all clinical cases of BSE, and this may have modified the fate of cattle with clinical signs of BSE that were sent to the abattoir.

To simplify the following discussion, we defined late-stage cattle as cattle slaughtered within 12 months of clinical onset, thus including clinical BSE cases and ‘infectious’ preclinical cases. In the best-case scenario, i.e. if only 15% of cattle with clinical BSE that were not detected by passive surveillance were sent to the abattoir, 2087 $(1400 + 687)$ late-stage cattle entered the human food chain before June 1996. In the worse-case scenario, if all cattle with clinical BSE that were not detected by passive surveillance were sent to the abattoir, 5980 $(1400 + 4580)$ late-stage cattle entered the human food chain before June 1996. We emphasize that few French late-stage cattle entered the human food chain in France before 1990 (Fig. 2b).

Another source of exposure of the French human population to the BSE agent was imported British bovine products. We focused on the period before November 1989, when the British specified-offal ban was implemented. In 1997, Ferguson et al. [12] estimated that 954 000 British cattle had been infected by the BSE agent. Of these, only 8000 late-stage cattle entered the British human food chain before November 1989. In 2003, in an updated study, Ferguson and Donnelly [16] estimated that 4 000 000 British cattle had been infected by BSE, but did not report the number of late-stage animals slaughtered for human consumption. In order to obtain a rough idea of this number, we used the same ‘late-stage/infected’ ratio as in the first study by Ferguson et al. [12]. We thus estimated that 27 673 late-stage cattle entered the British human food chain before November 1989. Exposure of the French human population via imported British bovine products was estimated to represent between 5% and 10% of the exposure level of the British population [17]. Based on the last study by Ferguson and Donnelly [16], between 1384 and 2767 late-stage cattle entered the French human food chain before November 1989, while based on the first study by Ferguson et al. [12] between 400 and 800 late-stage cattle did so. Consequently, exposure of the French human population to the BSE agent via French bovine products was not negligible. In addition, exposure of the French human population to the BSE agent via French bovine products occurred later than exposure via imports of British bovine products. Consequently, keeping in mind that the incubation period of vCJD is 15 years [18], exposure of the French human population to the BSE agent via French bovine products from 1990 could lead to an increase of the number of French cases of vCJD from 2005. This is supported by the observed number of the definite or probable cases of vCJD in France: 1 in 1996, 1 in 2000, 1 in 2001, 3 in 2002, 2 in 2004 and 5 in 2005.

This study shows how the French BSE epidemic was underestimated and that the risk for the French consumer from French bovine products was not negligible compared to the risk from imported British products. Not only was clinical surveillance inefficient, but the BSE epidemic also went unnoticed because of the particular demography of French cattle. Therefore, when estimating the size and kinetics of an epidemic, it is important to consider not only the epidemiological characteristics of the disease but also the characteristics of the study population. This applies not only to the BSE epidemic but also to other infectious diseases such as AIDS and hepatitis C: as effective treatments artificially lengthen the ‘incubation period’, deaths due to competing causes can no longer be ignored.

Acknowledgements

This work was funded by a grant from GIS ‘Infection à Prions’. We are grateful to DGAL (‘Direction générale de l'alimentation’) for providing demographic data on cattle.

Bibliographie

[1] R. Brookmeyer Reconstruction and future trends of the AIDS epidemic in the United States, Science, Volume 253 (1991), pp. 37-42

[2] R. Brookmeyer; M.H. Gail A method for obtaining short-term projections and lower bounds on the size of the AIDS epidemic, J. Am. Stat. Assoc., Volume 83 (1988), pp. 301-308

[3] M.E. Bruce; R.G. Will; J.W. Ironside; I. McConnell; D. Drummond; A. Suttle; L. McCardle; A. Chree; J. Hope; C. Birkett; S. Cousens; H. Fraser; C.J. Bostock Transmissions to mice indicate that ‘new variant’ CJD is caused by the BSE agent, Nature, Volume 389 (1997), pp. 498-501

[4] A.F. Hill; M. Desbruslais; S. Joiner; K.C.L. Sidle; O. Gowland; J. Collinge The same prion causes vCJD and BSE, Nature, Volume 389 (1997), pp. 448-450

[5] R.G. Will; J.W. Ironside; M. Zeidler; S.N. Cousens; K. Estibeiro; A. Alperovitch; S. Poser; M. Pocchiari; A. Hofman; P.G. Smith A new variant of Creutzfeldt–Jakob disease in the UK, Lancet, Volume 347 (1996), pp. 921-925

[6] V. Supervie; D. Costagliola The unrecognised French BSE epidemic, Vet. Res., Volume 35 (2004), pp. 349-362

[7] N.G. Becker; I.C. Marschner A method for estimating the age-specific relative risk of HIV infection AIDS incidence data, Biometrika, Volume 80 (1993), pp. 165-178

[8] A.P. Dempster; N.M. Laird; D.B. Rubin Maximum likelihood from incomplete data via the EM algorithm (with discussion), J. R. Stat. Soc. B, Volume 39 (1977), pp. 1-38

[9] B.W. Silverman; M.C. Jones; J.D. Wilson; D.W. Nychka A smoothed EM approach to indirect estimation problems, with particular reference to stereology and emission tomography, J. R. Stat. Soc. B, Volume 52 (1990), pp. 271-324

[10] K. Burnham; D. Anderson Model Selection and Inference: A Practical Information-Theoretic Approach, Springer-Verlag, New York, 1998

[11] B. Efron The Jackknife, the Boostrap and other Resampling Plans, Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 1982 (p. 82)

[12] N.M. Ferguson; C.A. Donnelly; M.E. Woolhouse; R.M. Anderson The epidemiology of BSE in cattle herds in Great Britain. II. Model construction and analysis of transmission dynamics, Phil. Trans. R. Soc. B, Volume 352 (1997), pp. 803-838

[13] G. Cazeau; C. Ducrot; E. Collin; G. Desjouis; D. Calavas Questionnaire analysis of BSE cases in France detected by active surveillance and the reasons for non-notification, Vet. Rec., Volume 154 (2004), pp. 133-136

[14] R.M. Anderson; C.A. Donnelly; N.M. Ferguson; M.E. Woolhouse; C.J. Watt; H.J. Udy; S. MaWhinney; S.P. Dunstan; T.R. Southwood; J.W. Wilesmith; J.B. Ryan; L.J. Hoinville; J.E. Hillerton; A.R. Austin; G.A. Wells Transmission dynamics and epidemiology of BSE in British cattle, Nature, Volume 382 (1996), pp. 779-788

[15] M.E. Arnold; J.W. Wilesmith Estimation of the age-dependent risk of infection to BSE of dairy cattle in Great Britain, Prev. Vet. Med., Volume 66 (2004), pp. 35-47

[16] N.M. Ferguson; C.A. Donnelly Assessment of the risk posed by bovine spongiform encephalopathy in cattle in Great Britain and the impact of potential changes to current control measures, Proc. R. Soc. Lond. B Biol. Sci., Volume 270 (2003), pp. 1579-1584

[17] Agence française de sécurité sanitaire des produits de santé (AFSSAPS), Révision des mesures de réduction du risque de transmission des ESST par les produits sanguins, in : AFSSAPS Documents [on line]

[18] P.-Y. Boelle; G. Thomas; J.-Y. Cesbron; R. Will; A.J. Valleron Modelling the epidemic of vCJD in the UK based on age characteristics: An update and detailed analysis, Stat. Methods Med. Res., Volume 12 (2003), pp. 221-233

Commentaires - Politique