Abridged English version
Introduction
The study of molecular networks by ‘high-throughput’ techniques is based on coupling in-silico modelling and experimental validation. This interdisciplinary approach leads us to revisit the model–experimentation cycle by integrating computing for the formulation of assumptions. The interaction, resulting from the need to treat automatically a large amount of biological data, gives rise to new problems focused on the conception of computational frameworks for biological modelling. Hence, the question is to correctly interpret data by these formal models, in accordance with methods, biological observations, and possible therapeutic applications. The interpretation may lead to a better understanding of biological functions. Thus, computational models formulate an explanation of biological functions by characterizing the role of the interaction network and of its agents, either in the context of its environment, or within a global network.
How is it possible to get insights into the role played by molecular agents in the achievement of a biological function from interactions and their dynamics? It turns out that the problem is to bridge the gap from data to functional knowledge. A possible approach consists in expressing the role of each agent as a ‘goal to achieve’. Thus, the function would be explained by the synergy of each agent's goal. The validity of the explanation is based on the coherence of the synergy in the model.
It becomes interesting to consider models used in other disciplines that describe complex interactions. Game theory constitutes a privileged framework for this type of modelling. With game theory, it is possible to study how players (or agents) make their choice (or strategy), evolve according to the game, with the aim of maximizing their own expected profit (or payoff). In this game-based modelling, interactions are identified to a game, and biological equilibria are equivalent to game equilibria (Nash equilibria).
Nevertheless, biological systems complexity is partially covered by game theory. More specifically, some concepts, as locality and modularity, are missing. In order to deal with these various concepts, we propose an original extension of game theory: the game networks' theory.
Game theory
The strategic game theory describes situations where a set of agents (or players) interact together. Agents choose, once and for all, and simultaneously, a strategy. The attribution of a strategy to each agent defines a game configuration from which the payoff is fixed. In strategic games, each agent is considered as being rational – it aims at maximizing its payoff – and perfectly informed of other agents' payoffs.
The Nash equilibrium is a major concept in game theory. To some extent, Nash equilibria can be considered as stable configurations of a strategic game. A Nash equilibrium is reached when the strategy played by each agent is the best possible response to other players' strategies. Hence, no agent can unilaterally deviate from a Nash equilibrium without decreasing its payoff.
Biological games. In biology, strategic games represent interactions between biological agents (proteins, genes...). The strategies of the agents characterize their possible experimentally observable states (degrees of affinity, levels of expression, concentrations, conformations...). Payoffs are set to each games configuration and quantifies the relevance of this configuration in comparison with the states of the various agents.
Game theory is used in order to characterize biological equilibria of the system from the interactions, by the computation of Nash equilibria. Obviously, this computation is highly connected to the payoffs. Considering strategies as states of agents, the highest payoff will be set to the most stable strategy of an agent in comparison with possible states (strategies) of other agents. Indeed, maximizing one's payoff means converge towards one's most stable state, according to the configuration determined by other players.
Game networks' theory
Biological systems are often composed of a large amount of interacting agents. In order to deal with the staggering complexity of the interaction, one must put the emphasis on the locality of interactions where few agents are in tight interaction. Such behaviours, frequently encountered in biological cases studies, can not be straightly modelled by game theory. It needs to equip the theory with some features that capture these notions.
Basically, the game networks' theory is developed to deal with large biological networks by taking advantage of locality of interactions. A game network is a network of games and agents where agents can play several games simultaneously, but it only plays one strategy for all the games it depends on. A game network enlarges the definition of equilibria by considering two levels of equilibria, local and global ones. Local equilibria correspond to usual Nash equilibria for each game, whereas a global equilibrium is a configuration at the scale of the network. Global equilibria are obtained by combining various local equilibria. Given a game, local equilibria only depend on interactions described by one game. But global equilibria depend on all the interactions of the network (because all the agents must be in a situation of local equilibrium). Thus, local and global equilibria allow us to scale up: from local interactions, we determine a global behaviour, identified by equilibria at the scale of the network.
Modelling biological systems. The modelling of biological systems can be described in the following way. Experiments enable us to describe the evolution of the system, to determine a relation between various configurations of this system (i.e. to establish that a configuration is more stable than another, for example). From these experiments, a relation on payoffs is defined (given an agent, the more stable the configuration it participates to, the higher its payoff). Theoretical research of global equilibria allows us to identify the states of equilibria of the biological system.
Modules. Discovering modular activity in a biological network is a challenging problem, because a module refers to a functional unit having an independence with regard to other system components. These modules would constitute the ‘basic building blocks’ that compose the system and could explain the complex biological functions as an ‘assembly’ of modules.
The game networks' theory naturally associates modules with the games that compose the network. However, it is necessary to specify that these modules are identified by considering the dynamics of the interactions and not simply the structure of the network.
Conclusion
We used the game networks' theory to model genetic networks and a part of the Plasminogen Activator system (PAs), which is involved in the migration of cancer cells. The results highlighted the central role of the Plasminogen Activator Inhibitor, PAI-1, as well as the presence of two global equilibria corresponding to two characteristic biological states – a non-migratory state and a pro-migratory state. These results were confirmed by experiments.
1 Introduction
L'étude des réseaux moléculaires par des techniques dites de haut débit se fonde sur le couplage entre modélisation in silico et validation expérimentale. Cette approche interdisciplinaire actualise le cycle modèle–paillasse en intégrant l'informatique pour la formulation d'hypothèses. Cette interaction, issue du besoin de traiter automatiquement de grandes masses de données biologiques, pose de nouveaux problèmes centrés sur la conception de cadres calculables de modélisation biologique. Il s'agit ici d'interpréter correctement les données grâce à ces modèles informatiques, au regard des méthodes, des observations biologiques ainsi que des applications thérapeutiques éventuelles. Une meilleure compréhension des fonctions biologiques est au cœur de cet enjeu. Ainsi, le modèle informatique formulerait une explication des fonctions biologiques en caractérisant le rôle du réseau d'interactions et de ses agents, soit dans le contexte de son environnement, soit au sein d'un réseau global.
Comment, à partir des interactions et de leur dynamique, est-il possible d'extraire des renseignements sur le rôle joué par les agents moléculaires dans l'accomplissement d'une fonction biologique ? En fait, l'interprétation des interactions pose le problème de les rendre intelligibles, c'est-à-dire d'extraire une connaissance fonctionnelle à partir des données. Une approche possible consiste à exprimer le rôle de chaque agent comme un « but à accomplir ». Ainsi, la fonction s'expliquerait par la synergie des buts ou rôles de chacun. La validité de l'explication par le modèle repose sur la cohérence de cette synergie.
Il devient alors intéressant de se pencher sur les modèles utilisés dans d'autres disciplines qui décrivent les enjeux des interactions. Dans cette perspective, la théorie des jeux constitue un cadre privilégié pour ce type de modélisation. Elle permet d'étudier comment des joueurs (ou agents) voient évoluer leur choix (ou leur état) en fonction de la nature des interactions (le jeu), dans le but de maximiser leur gain propre. La modélisation de réseaux biologiques assimile les interactions à un jeu. Les équilibres biologiques équivalent dans ce modèle aux équilibres du jeu (les équilibres de Nash).
Néanmoins, la théorie des jeux ne traduit que partiellement le caractère complexe des systèmes biologiques ; il manque, en particulier, des notions telles que la localité et la modularité. C'est dans le but de permettre l'examen de ces différentes notions que nous proposons une extension originale de la théorie des jeux stratégiques, la théorie des réseaux de jeux.
2 Théorie des jeux
Nous présentons ici les principales notions de la théorie des jeux. Nous nous intéressons ensuite à la modélisation de systèmes biologiques, et plus particulièrement aux réseaux de régulation génétique. Le lecteur pourra se référer à [1] pour avoir un vision plus complète de la théorie des jeux.
2.1 Théorie des jeux stratégiques
2.1.1 Jeux stratégiques
Introduite par Von Neumann et Morgenstern en 1944 [2], la théorie des jeux stratégiques propose un modèle d'interactions où les agents choisissent, simultanément et une fois pour toute, une stratégie. De plus, chaque agent est rationnel – il cherche à maximiser son gain – et parfaitement informé des gains des autres agents. Formellement, un jeu stratégique se définit de la manière suivante :
Un jeu stratégique Γ est un triplet où :Définition 2.1 Jeu stratégique
2.1.2 Représentation par tableau
Les jeux stratégiques – 2 joueurs ayant chacun 2 stratégies – sont souvent utilisés en théorie des jeux pour en présenter les notions. Un tel jeu est habituellement représenté par un tableau où les stratégies du premier joueur sont en lignes et celles du second joueur en colonnes. Ainsi, dans l'exemple de la Fig. 1, si le joueur x joue sa stratégie off et le joueur y sa stratégie on, un gain de 0 est attribué au joueur x et un gain de 2 au joueur y.

Circuit représentant une inhibition mutuelle.
2.1.3 Équilibre de Nash
Un concept central en théorie des jeux est la notion d'équilibres de Nash [3] :
Soit un jeu stratégique. Un équilibre de Nash est une configuration du jeu telle que :Définition 2.2 Équilibre de Nash
où correspond à la configuration dans lequel le joueur i joue sa stratégie (plutôt que ).
Les équilibres de Nash permettent de capturer les configurations stables d'un jeu stratégique. En effet, dans un équilibre de Nash, la stratégie jouée par l'agent i est la meilleure réponse possible aux stratégies des autres joueurs. L'agent i n'a donc pas d'intérêt à changer, seul, de stratégie.
2.2 Jeux biologiques
En biologie, les jeux permettent de représenter des interactions entre agents biologiques (protéines, gènes...). Les stratégies des agents caractérisent alors leurs différents états observables (degré d'affinité, niveaux d'expression, concentrations, conformations...). Les fonctions de gains attribuent à chaque configuration du jeu une valeur spécifique, appelée gain, qui quantifie la pertinence de cette configuration au regard des états des différents agents.
La régulation génétique, le contrôle de l'expression du taux de transcription des gènes, est habituellement représentée par un réseau de régulation, ou graphe. Les gènes, ou produits de gènes, interagissant sont reliés par un arc étiqueté « + » dans le cas d'une activation et « – » dans le cas d'une inhibition.
L'exemple de la Fig. 1 présente un circuit à deux gènes où chaque gène s'inhibe mutuellement (le gène x inhibe le gène y et y inhibe x). Dans ce jeu biologique de régulation, les deux agents sont x et y. On considère deux stratégies par agent : la stratégie « off » représente le cas où le gène ne s'exprime pas et la stratégie « on » le cas où le gène s'exprime. La fonction de gain nous permet de modéliser la dynamique du système : si x joue sa stratégie off (x ne s'exprime pas), alors x n'a pas d'influence négative sur y, et le meilleur état pour y est on (y s'exprime) plutôt que l'état off. Si x joue sa stratégie on, alors x a une influence négative sur y, et le meilleur état pour y est off plutôt que l'état on. Selon les stratégies de x (resp. y), on peut alors ordonner les gains de y (resp. x) : le gain de y pour est inférieur à son gain pour , et le gain de y pour est supérieur à son gain pour .
2.3 Équilibres de Nash et équilibres biologiques
La modélisation par les jeux stratégiques permet de caractériser les équilibres biologiques du système à partir des interactions, par le calcul des équilibres de Nash. L'attribution des gains relatifs aux stratégies conditionnent évidemment ce calcul. Si l'on considère que les stratégies correspondent aux états des agents, le gain le plus élevé sera attribué à l'état le plus stable d'un joueur au regard des états (stratégies) possibles des autres agents. De fait, maximiser son gain signifie converger vers son état le plus stable en fonction de la configuration déterminée par les autres joueurs. En situation d'équilibre de Nash, le système entier (tous les joueurs) se trouve alors en état d'équilibre. Pour un même jeu, plusieurs équilibres de Nash sont possibles ; chacun représente un état différent du système biologique. Ainsi, dans l'exemple de la double inhibition de la Fig. 1, on trouve deux équilibres de Nash qui correspondent à l'expression du gène x (resp. y) et à l'absence d'expression du gène y (resp. x).
Cette approche suppose que les équilibres de Nash correspondent à des états stables d'une classe de systèmes dynamiques décrivant la dynamique des réseaux biologiques. Mathématiquement, cette classe existe. Elle correspond notamment à une branche de la théorie des jeux appelée jeux évolutionnaires [4], qui comprend, entre autres, les équations des réplicateurs [5].
3 Théorie des réseaux de jeux
Nous nous intéressons ici à la théorie des réseaux de jeux, extension de la théorie des jeux, qui permet de prendre en compte la localité des interactions intervenant dans les processus biologiques.
3.1 Biologie et réseaux de jeux
Les systèmes biologiques présentent habituellement un grand nombre d'agents (molécules, gènes...) interagissant les uns avec les autres. Cependant, ces interactions n'interviennent pas entre tous les agents. On observe, par exemple, des situations où les agents exercent une action uniquement sur leurs proches voisins. On parle alors de localité des interactions. De tels comportements ne sont pas modélisables à l'aide de la théorie des jeux. En effet, dans un jeu, tous les joueurs jouent ensemble. C'est pour prendre en compte les interactions locales, fréquentes en biologie, que nous développons la théorie des réseaux de jeux.
Dans un réseau de jeux, un agent peut participer à plusieurs jeux, et ce de manière simultanée. Cependant, l'agent doit jouer la même stratégie, quel que soit le jeu auquel il participe. Formellement, un réseau de jeux se définit de la manière suivante :
Un réseau de jeux est un triplet où :Définition 3.1 Réseau de jeux
Il n'est pas nécessaire dans les jeux de rappeler l'ensemble des stratégies d'un agent, car celles-ci sont identiques pour tous les jeux auxquels il participe. Elles sont donc associées à l'agent plutôt qu'au jeu.
3.1.1 Représentation graphique
Les réseaux de jeux peuvent se représenter sous forme de graphes bipartis, comme dans l'exemple de la Fig. 2. Dans un tel graphe, les agents sont représentés par un cercle qui contient leur nom et les jeux par des rectangles. Les agents sont reliés aux jeux auxquels ils participent. Dans les cas de la Fig. 2, on indique directement dans les rectangle le tableau de gains du jeu.

Réseau de régulation et réseau de jeux.
3.1.2 Exemple sur un réseau de régulation
La Fig. 2 présente un exemple de réseau de régulation à trois agents : y participe à la fois à une inhibition mutuelle avec x et à une activation mutuelle avec z. La modélisation sous forme de réseau de jeux se fait naturellement en faisant participer y à deux jeux, l'un avec x pour décrire leurs inhibitions (identique au jeu de la Fig. 1) et l'autre avec z pour décrire leurs activations.
3.2 Équilibres locaux, équilibres globaux
Un jeu stratégique modélise un ensemble d'interactions entre tous ses joueurs. Dans un réseau de jeux, les interactions deviennent plus complexes. Un agent donné va interagir avec certains joueurs (ils participent alors au même jeu), mais pas avec d'autres. Cependant, l'état de cet agent peut avoir une influence sur tous les joueur du réseau de jeux. Pour prendre en compte ce phénomène, nous définissons deux niveaux d'équilibres :
- – les équilibres locaux correspondent aux équilibres de Nash de chacun des jeux qui constituent le réseau. Ils permettent de définir des zones d'équilibre biologique entre agents. Dans l'exemple de la Fig. 2, on trouve ainsi deux équilibres locaux pour le jeu – et – et deux équilibres locaux pour le jeu – et ;
- – les équilibres globaux correspondent à une situation d'équilibre tenant compte de tous les jeux du réseau. Les équilibres globaux sont calculés en deux temps : tout d'abord en calculant les équilibres locaux de chaque jeu, puis en combinant et sélectionnant ces équilibres locaux pour qu'ils soient compatibles entre eux. Un équilibre global existera uniquement si chaque agent possède une stratégie lui permettant de se trouver en situation d'équilibre local pour tous les jeux auxquels il participe. Dans l'exemple de la Fig. 2, y peut avoir la stratégie off ou on. Il existe ainsi deux équilibres globaux : et .
3.3 Modélisation et modules
La modélisation d'un système biologique par la théorie des réseaux de jeux peut se décrire de la manière suivante. Des expériences nous permettent de décrire l'évolution du système, de déterminer une relation entre différentes configurations de ce système (d'établir qu'une configuration est plus stable qu'une autre, par exemple). D'après ces expériences, on est alors capable de définir une relation sur les gains à attribuer aux différents agents du système (les gains d'un agent sont d'autant plus élevés que la configuration à laquelle il participe est stable). La recherche, théorique, des équilibres globaux du réseau de jeux créé permet alors d'identifier les états d'équilibres du système biologique.
Une notion importante en biologie est celle de module [6–8], car elle fait référence à une unité fonctionnelle possédant une certaine indépendance vis-à-vis des autres composants du système. Ces modules constitueraient les « briques de base » composant le système et permettraient d'expliquer les fonctions biologiques complexes comme un « assemblage » de modules. La théorie des réseaux de jeux associe naturellement les modules aux jeux qui composent le réseau. Toutefois, il est nécessaire de préciser que ces modules s'identifient en considérant la dynamique des interactions et non simplement la structure du réseau. Nous proposons dans la référence [9] un algorithme permettant ce découpage en jeux élémentaires qui s'appuie sur les interactions entre agents.
4 Conclusion
Nous avons présenté la théorie des réseaux de jeux comme un outil de modélisation des systèmes biologiques. Cette théorie, qui est une extension de la théorie des jeux, nous permet de prendre en compte la localité des interactions ainsi que la modularité de ces systèmes.
Nous avons utilisé la théorie des réseaux de jeux pour modéliser différents réseaux génétiques ainsi qu'une partie du système activateur du plasminogène ou PAs (Fig. 3) [10]. Le système PAs est impliqué, entre autres, dans la migration des cellules cancéreuses. La modélisation par réseaux de jeux a mis en évidence le rôle central de l'inhibiteur de l'activateur du plasminogène, PAI-1. Deux équilibres globaux ont été calculés, et correspondent à deux états biologiques caractéristiques du système PAs – un état non migratoire et un état pro migratoire – qui ont été retrouvés expérimentalement [11].
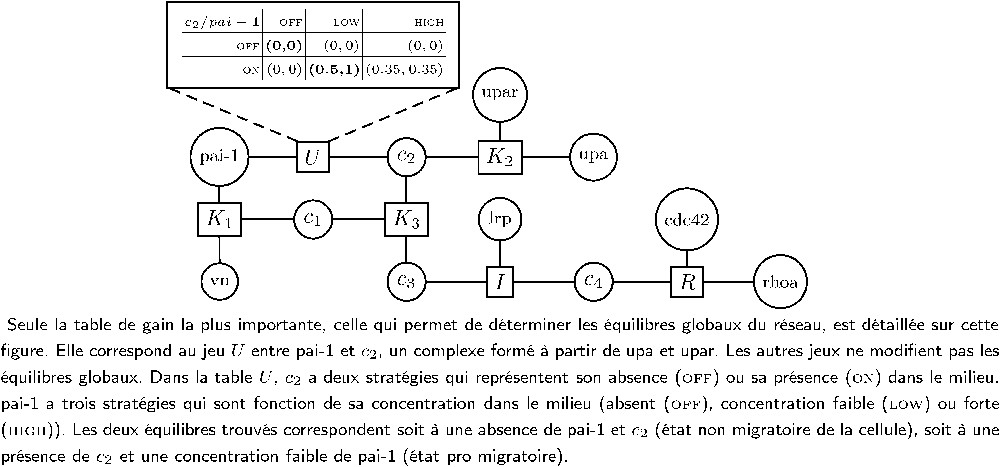
Réseau de jeux modélisant le système PAs et table de gain définissant les équilibres globaux.


