Spatial distribution and inbreeding in <i>Tetranychus urticae</i>

Guillaume Le Goff; Anne-Catherine Mailleux; Claire Detrain; Jean-Louis Deneubourg; Gwendoline Clotuche; Thierry Hance

doi:10.1016/j.crvi.2009.06.002

Ethology / Éthologie

Spatial distribution and inbreeding in Tetranychus urticae
[Distribution spatiale et consanguinité chez Tetranychus urticae]

Présenté par : Pierre Buser

Guillaume Le Goff ¹ ; Anne-Catherine Mailleux ² ; Claire Detrain ² ; Jean-Louis Deneubourg ² ; Gwendoline Clotuche ¹ ; Thierry Hance ¹

¹ Unité d'écologie et de biogéographie, Biodiversity Research Centre, université catholique de Louvain, 4-5, place Croix du Sud, B-1348 Louvain-la-Neuve, Belgium
² Service d'écologie sociale, université libre de Bruxelles, campus de la plaine, boulevard du Triomphe, B-1050 Bruxelles, Belgium

Comptes Rendus. Biologies, Volume 332 (2009) no. 10, pp. 927-933.

Résumés

Anglais
Français

In group living, species spatial distribution results from responses to environmental heterogeneity and/or mutual interactions between individuals. These mutual interactions can be regulated by genetic and/or epigenetic factors. In this study, we focus on genetic factors and investigate how the spatial distribution of some individuals colonizing a new environment is influenced by inbreeding.

Our biological model is Tetranychus urticae, a phytophagous mite considered as a major pest of many cultivated plants. Groups of T. urticae were composed of individuals from successive inbreeding (sister–brother sib-mating). Our results show that the inter-individual distances increase with inbreeding. Indeed, inbreeding level seems to be an important factor affecting the intra-plant spatial distribution of mites. These results confirm that mites have the capability to discriminate their kin and, moreover, that they are able to accurately perceive differences between close relatives from sib-mating lines.

La distribution spatiale d'individus peut être le résultat de réponses à des hétérogénéités environnementales et/ou à des interactions interindividuelles. Dans cette étude, nous nous intéressons aux facteurs génétiques pouvant influencer ces interactions et étudions comment la distribution spatiale d'individus colonisant un nouvel environnement peut être influencée par leur proximité génétique.

Notre modèle biologique est Tetranychus urticae, c'est un acarien phytophage considéré comme un ravageur majeur dans beaucoup de culture. Les groupes d'acariens testés sont composés d'individus issus de générations consanguines successives (accouplement frère–soeur).

Les résultats montrent une distribution spatiale influencée par la consanguinité du groupe ainsi qu'une augmentation de la distance inter-individuelle avec le taux de consanguinité. Il apparaît donc que le lien génétique entre individus est un facteur capable d'influencer la distribution spatiale de T. urticae. Ce qui signifie également que ces acariens sont capables de discriminer des individus issus de lignées consanguines et donc très proches.

Métadonnées

Reçu le : 2009-02-13
Accepté le : 2009-06-29
Publié le : 2009-08-19

PMID

DOI : 10.1016/j.crvi.2009.06.002

Keywords: Tetranychus urticae, Spatial distribution, Sib-mating line
Mot clés : Tetranychus urticae, Distribution spatiale, Consanguinité, Lignées consanguines

Affiliations des auteurs :

Guillaume Le Goff ¹ ; Anne-Catherine Mailleux ² ; Claire Detrain ² ; Jean-Louis Deneubourg ² ; Gwendoline Clotuche ¹ ; Thierry Hance ¹

@article{CRBIOL_2009__332_10_927_0,
     author = {Guillaume Le Goff and Anne-Catherine Mailleux and Claire Detrain and Jean-Louis Deneubourg and Gwendoline Clotuche and Thierry Hance},
     title = {Spatial distribution and inbreeding in {\protect\emph{Tetranychus} urticae}},
     journal = {Comptes Rendus. Biologies},
     pages = {927--933},
     publisher = {Elsevier},
     volume = {332},
     number = {10},
     year = {2009},
     doi = {10.1016/j.crvi.2009.06.002},
     language = {en},
}

TY  - JOUR
AU  - Guillaume Le Goff
AU  - Anne-Catherine Mailleux
AU  - Claire Detrain
AU  - Jean-Louis Deneubourg
AU  - Gwendoline Clotuche
AU  - Thierry Hance
TI  - Spatial distribution and inbreeding in Tetranychus urticae
JO  - Comptes Rendus. Biologies
PY  - 2009
SP  - 927
EP  - 933
VL  - 332
IS  - 10
PB  - Elsevier
DO  - 10.1016/j.crvi.2009.06.002
LA  - en
ID  - CRBIOL_2009__332_10_927_0
ER  -

%0 Journal Article
%A Guillaume Le Goff
%A Anne-Catherine Mailleux
%A Claire Detrain
%A Jean-Louis Deneubourg
%A Gwendoline Clotuche
%A Thierry Hance
%T Spatial distribution and inbreeding in Tetranychus urticae
%J Comptes Rendus. Biologies
%D 2009
%P 927-933
%V 332
%N 10
%I Elsevier
%R 10.1016/j.crvi.2009.06.002
%G en
%F CRBIOL_2009__332_10_927_0

Guillaume Le Goff; Anne-Catherine Mailleux; Claire Detrain; Jean-Louis Deneubourg; Gwendoline Clotuche; Thierry Hance. Spatial distribution and inbreeding in Tetranychus urticae. Comptes Rendus. Biologies, Volume 332 (2009) no. 10, pp. 927-933. doi : 10.1016/j.crvi.2009.06.002. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2009.06.002/

Version originale du texte intégral

1 Introduction

In social biology, the spatial distribution of individuals is an important issue that determines the organization of groups. In many species, individuals form aggregates, increasing local population density much more than in the surrounding environment [1,2]. Forming such aggregates has many advantages both for the individual and the group as it provides easier access to food and mates as well as protection against predators [3,4]. It also presents disadvantages as forming aggregates means sharing food, mates and living space, and therefore may result in inter-individual conflicts [3]. Although group formation is of critical importance for the survival of many species, few studies have been done on the parameters modulating spatial distribution, especially in non-eusocial arthropods such as Tetranychus urticae [5,6].

T. urticae is considered as a major pest of many cultivated plants (more than 200 host-plants listed [7]). Consequently, research has focused mainly on the management and control of this species, whereas its behaviour, especially its social behaviour, has often been disregarded. However, T. urticae is a very good biological model with which to study group formation, as this species builds a collective web by weaving silk threads, cooperating in its enlargement and repair [8]. The web is used like a shield protecting mites from rain [9], pesticides [10] and predators [11], and it seems to be a prevailing factor inducing the formation of mite aggregates observed in the field from leaf to leaf or plant to plant [12,13].

Another crucial factor that modulates spatial distribution is the individual genetic background [1,2,14–18]. Aggregate with kin may help individuals avoid predators by diluting each individuals' risk of being attacked (dilution hypothesis [19]) [1,2,16], whereas kin avoidance can be a mechanism to avoid kin mating and so maintain a high level of genetic diversity in the population [15,17]. In insects [1,18,20–22] and arachnids [23], chemical cues such as specific cuticular hydrocarbon may mediate kin recognition. Many arthropod species have the ability to discriminate between kin and non-kin odors and often choose to form an aggregate with close relatives [1,18,21,24]. In T. urticae, females (sisters or non-sisters) coming from inbred and outbred population are able to modify their offspring sex-ratio according to the genetic relatedness of the group (Roeder [25]). Therefore, T. urticae mites have the ability to discriminate individuals differing by their original populations and environments. Do mites still display such discriminative abilities when they face very close relatives? In other words, are they able to perceive tiny genetic differences between close relatives coming from sib-mating lines? Such questions are very important for the study of T. urticae socio-ecology. Indeed, in the field, the probability of inbreeding is very high in groups living on the same plant due to the low mobility exhibited by mites (increasing the likelihood of interactions among kin) and to their mating systems (parthenogenesis and haplo-diploidy) [26,27].

How inbreeding influences the spatial distribution of mites is also unknown. Previous studies on this topic have mainly focused on insects [1,2,18,20,22] while mites have been disregarded. In order to address this question, we studied the spatial distribution within small groups of mites during the colonization of a new leaf through successive generations of inbred individuals. Our results will be discussed in the context of T. urticae ecology.

2 Materials and methods

We tested the relation between inbreeding and spatial distribution by using a red form of T. urticae provided by Dr. Lebdi Grissa (Institut National Agronomique, Tunis). The strain was reared on bean leaves placed on damp cotton (Phaseolus vulgaris) in Petri dishes [28]. Breeding stocks were maintained in a climate room at 26 °C, 50–60% RH, 16:8 (L:D).

2.1 Establishment of sib-mating lines

Founding sib-mating lines is a basic and essential tool for investigating the influence of inbreeding [29]. Three sib-mating lines were established; each was initiated from a virgin female isolated at the deutonymph stage and placed with three unrelated males on a bean leaf for 48 h. Mated females were then isolated on a new bean leaf. Their offspring was subsequently used for sib-mating for four generations to form a highly related line. In each line, three females of the first generation (G1) were fertilized by their brothers. The other females of this first generation were used in aggregation experiments and were called G1. Three females of the second generation were also fertilized by their brothers. Their sisters were also used for the test and were called G2. The above manipulations were repeated in order to obtain many individuals of known age for four generations (G1 to G4). Generation after generation, inbreeding increased. Data obtained using G3 are not presented in this paper because of a lack of replication.

2.2 Spatial distribution tests

Experiments were performed in a climate room at 26 °C, 50–60% RH, 16:8 (L:D). Ten virgin females belonging to the same sib-mating line, of the same generation and less than 48 hours old (number of replicates: G1: $n = 14$ ; G2: $n = 13$ ; G4: $n = 25$ ) were placed one by one in the centre of a bean leaf disc ( $\emptyset 5 mm$ ). The time taken to placed the individuals never exceeded 8 min. Bean leaf discs were placed on damp cotton, to prevent mite escape. These bean leaves were freshly cut before the experiment and were chosen to minimize heterogeneity due to veins. A numeric camera (Panasonic WV-CP450/G) with a macroscopic lens (1:1.2/12.5–75) and a magnifying lens (1.2×) was focused on the leaf disc and recorded female behaviour.

We started recording 15 minutes after the last individual was placed on the leaf to avoid stress behaviour. One picture was taken every 30 seconds for 15 minutes. These pictures were analysed using a data processing program called Fourmilier V3.3 (software creator, Jean-Michel Hudry (jm.hudry@ifrance.com)) [30], which attributed spatial coordinates to each individual and thus allowed further analyses and quantification of the spatial distribution of individuals.

In order to link the inbreeding and the spatial distribution, three parameters were measured:

Fig. 1
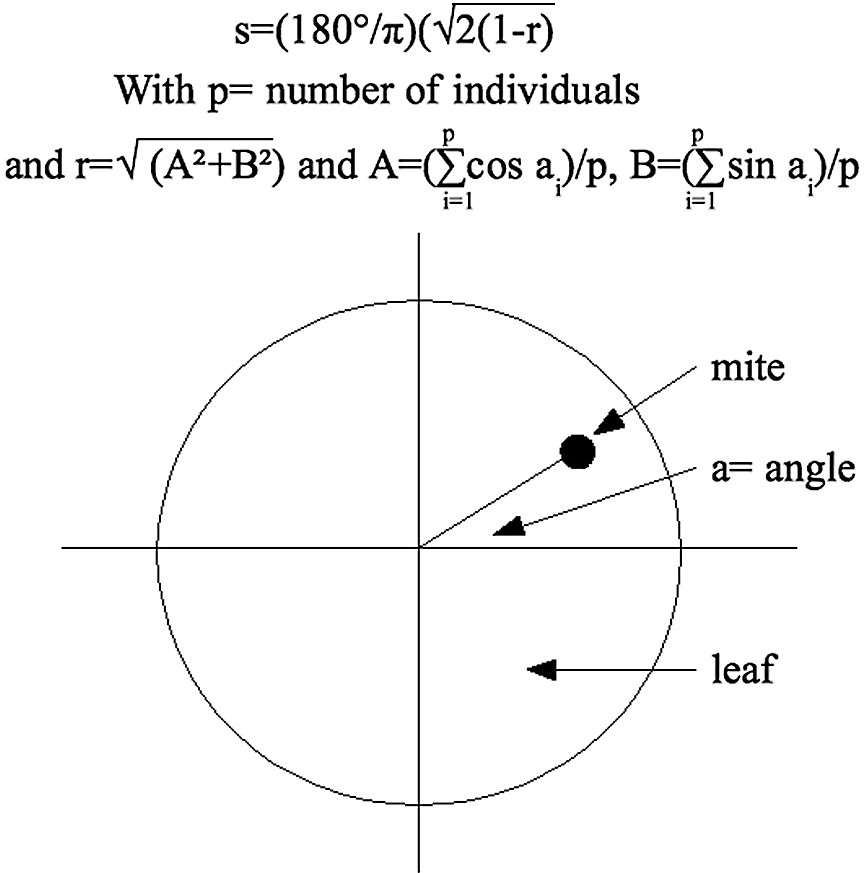
Calculation of the mean angular deviation.

These three parameters were measured for each individual, for each generation and each sib-mating line.

2.3 Statistical tests

Friedman tests were used to test whether the three measured indicators (the angular distribution, the radial distribution, the mean distance between individuals) changed according to time. Kruskal Wallis tests of variance (KW) and Dunn post test were also used to compare changes in angular distribution, radial distribution and distances between individuals and between generations. Tests were performed using GraphPad Prism version 5.01 for Windows, GraphPad Software, San Diego, California, USA (http://www.graphpad.com). All tests were applied under two-tailed hypotheses and the significance level p was set at 0.05.

3 Results

The three measured indicators (the angular distribution, the radial distribution, the mean distance between individuals) did not change according to time since the beginning of the recording in any tested generation (Friedman test for the angular distribution: G1: $Fr = 40.32$ , $P > 0.05$ ; G2: $Fr = 32.14$ , $P > 0.05$ ; G4: $Fr = 28.49$ , $P > 0.05$ ; for the radial distribution, G1: $Fr = 25.77$ , $P > 0.5$ ; G2: $Fr = 42.82$ , $P > 0.05$ ; G4: $Fr = 28.49$ , $P > 0.05$ ; the mean distances between individuals: G1: $Fr = 38.23$ , $P > 0.05$ ; G2: $Fr = 37.18$ , $P > 0.05$ ; G4: $Fr = 26.86$ , $P > 0.05$ ). That is why the results presented here focused on the final state of the mite group (31st picture).

3.1 The mean angular distribution “s”

The mean s (°) values for G1, G2, and G4 were not statistically different but (G1 ± Standard Error $(S.E.) = 51.91 \pm 3.46$ , $G 2 \pm S.E. = 54.54 \pm 3.15$ , $G 4 \pm S.E. = 54.15 \pm 3.58$ ; $KW = 30.41$ , $df = 3$ ; $P > 0.5$ ; Dunn: G1 vs. G2: $P > 0.05$ , G1 vs. G4: $P > 0.05$ , G2 vs. G4: $P > 0.05$ ) (Fig. 2) for each generation, s was statistically different from the reference value i.e. the expected H values of randomly distributed individuals ( $KW = 30.41$ , $df = 3$ , $P < 0.001$ ; Dunn: G1 vs. H: $P < 0.001$ , G2 vs. H: $P < 0.001$ , G4 vs. H: $P < 0.001$ ) (Fig. 2). This result showed that mites were non-randomly distributed at the end of the experiments.

Fig. 2
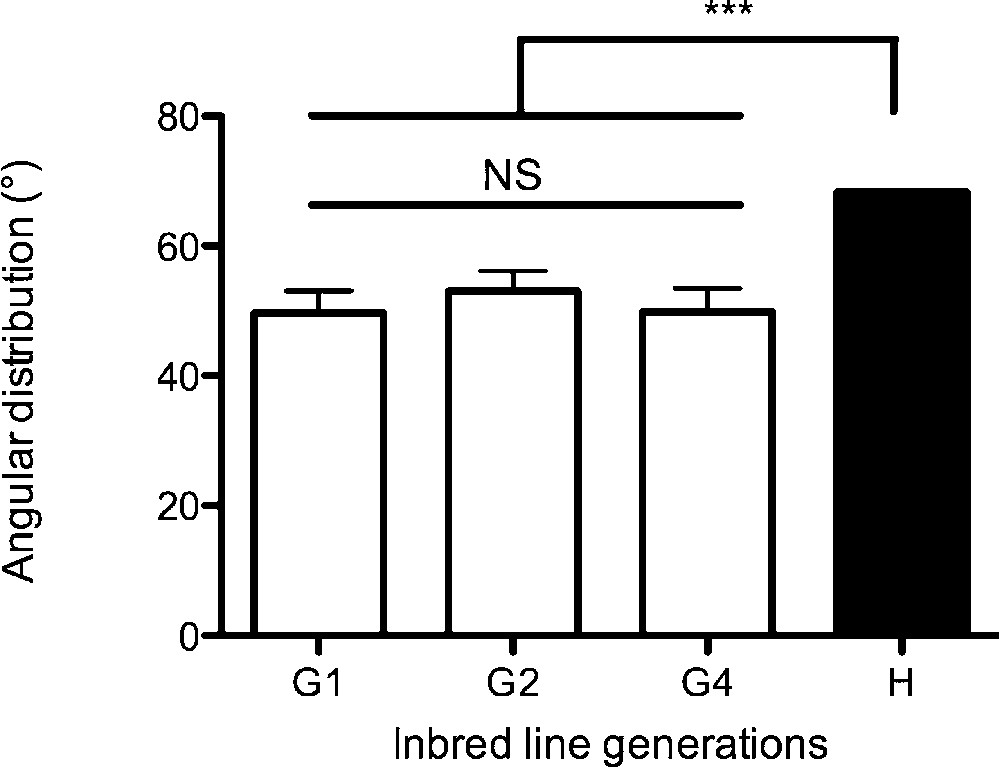
Mean angular distribution “s” (°) of individuals for each generation (G1, n = 14; G2, n = 13; G4, n = 25) ± S.E. at the end of experiments (30 min). H is the reference for ten randomly distributed individuals, and was obtained from 50 000 simulations of ten individuals that were randomly distributed in a circular area.

3.2 The radial distribution of the mites

The mean values of the radial distribution differed between successive generations: In the central ring, the highest density of mites was observed at G1 ( $density \pm S.E. = 0.07 \pm 0.02 individual / {mm}^{2}$ ) and G2 ( $density \pm S.E. = 0.08 \pm 0.04 individual / {mm}^{2}$ ), whereas the lowest density was observed at G4 ( $density \pm S.E. = 0.006 \pm 0.006 individual / {mm}^{2}$ ). The difference was statistically significant ( $KW = 8.23$ , $df = 2$ ; $P < 0.05$ ; Dunn: G1 vs. G2: $P > 0.05$ , G1 vs. G4: $P < 0.05$ , G2 vs. G4: $P > 0.05$ ) (Fig. 3). In terms of mite population fraction, 7% of G1 individuals and 0.4% of G4 individuals were found in the central ring.

Fig. 3
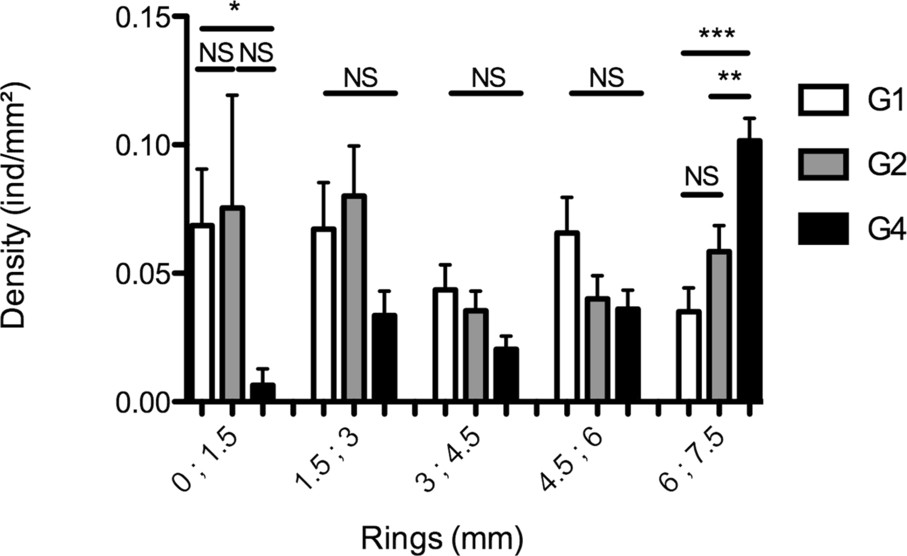
Mean radial distribution of individuals: density of individuals for each generation (G1, n = 14; G2, n = 13; G4, n = 25) (mean number of $ind / {mm}^{2} + S.E.$ ) in the five rings (0 represents the centre of the leaf disc) at the end of the experiment (30 min).

On the other hand, in the external ring, the highest mite density was observed at G4 ( $density \pm S.E. = 0.10 \pm 0.009 individual / {mm}^{2}$ ), whereas the lowest density was observed at G1 ( $density \pm S.E. = 0.04 \pm 0.009 individual / {mm}^{2}$ ). The difference was statistically significant ( $KW = 19.37$ , $df = 2$ ; $P < 0.001$ ; Dunn: G1 vs. G2: $P > 0.05$ , G1 vs. G4: $P < 0.001$ , G2 vs. G4: $P < 0.01$ ) (Fig. 3). In other words, 23% of G1 individuals and 68% of G4 individuals were found in the external ring.

No difference across generations was found in the other rings (1.5; 3: $KW = 5.46$ , $df = 2$ , $P > 0.05$ ; 3; 4.5: $KW = 5.52$ , $df = 2$ , $P > 0.05$ ; 4.5; 6: $KW = 3.81$ , $df = 2$ , $P > 0.05$ ).

3.3 The mean distance between individuals

The mean distance between individuals (mm) increased significantly across generations from $4.53 mm \pm 0.13 (S.E.)$ in G1 to $6.14 \pm 0.13 (S.E.)$ in G4 ( $KW = 44.72$ , $df = 2$ ; $P < 0.001$ ; Dunn: G1 vs. G2: $P < 0.001$ , G1 vs. G4: $P < 0.001$ , G2 vs. G4: $P > 0.05$ ) (Fig. 4). After four inbred generations, the mean distance between individuals increased by about 1.6 mm. This result showed that inbreeding lowered mutual attraction among spider mites. The higher the inbreeding level, the higher the inter-individual distances.

Fig. 4
Mean distance (mm) between individuals for each generation (G1, n = 14; G2, n = 13; G4, n = 25) ± S.E. at the end of experiments (30 min).

4 Discussion

In group-living species spatial distribution results from responses to environmental heterogeneity [35–37] and/or to mutual interactions between individuals [38]. During this study, we showed that the level of inbreeding and environmental heterogeneity influence mite distribution during the colonization of a new leaf.

Indeed the results of mean angular distribution are about 50° for all generation of sib-mating and each of them is different from the reference value $H = 68.3 °$ for ten individuals randomly distributed. Therefore individuals are not randomly distributed in our experiments, they are so attracted each other or/and to a same place. For each generation our results showed a difference of about 27% between empirical and theoretical distribution of s. In our experimental set up, leaf disc has been chosen to minimize heterogeneities due to vein. We can thus imagine that in more natural condition there would be more unevenness like veins to initiate web spinning (personal observation) and aggregation, and so we would have a lower level of angular distribution, and a higher level of aggregation.

We also observed that after 4 generations of sib-mating, the mean distance between T. urticae mites increased of about 1.6 mm which means three times the size of an individual. These results confirm that mites have the capability to discriminate their kin [25,39,40] and to perceive tiny differences between very close relatives.

These differences between generations suggest that inbreeding should increase the tendency to leave the patch or, at least, increase the inter-individual distance. What could be the benefit of such avoidance of close relatives? Increasing inter-individual distance may decrease competition for food, mates and space between relatives [41,42]. This may also decrease the probability of mating with relatives [17,43] and thereby may prevent, at least partly, inbreeding depression and its negative physiological consequences [44].

In addition, the spatial distribution of mites is influenced by environmental heterogeneity such as the borders of the experimental set-up. The trend to follow the leaf border increases with inbred generations. This suggests that individuals has a higher probability of leaving the leaf disc but are limited to it. That demonstrated link between radial distribution and inbreeding emphasizes the role of inbreeding in the spatial distribution of T. urticae.

Previous papers showed that spatial distribution results from social interactions mediated by visual, auditory and tactile stimuli [1,4]. The web in combination with social interactions mediated by pheromones could favor the initiation of clustering in a particular site or reinforce gregariousness [45]. Like many species of gregarious arthropods, spider mites are probably able to produce aggregative pheromones [4,46] that may be contact pheromones that are adsorbed on the cuticle [47,48], deposited on the leaf surface and/or on the silk [49,50]. They might also exert a remote aggregating effect as volatile pheromones attracting at short or long distances [1,51]. No aggregation pheromone has yet been found in T. urticae but such a pheromone has clearly been identified in families other than Tetranychidae [52,53]. These studies suggest the possible existence of an aggregation pheromone in this mite.

Our work contributes to the understanding of spatial organization in spider mites during the colonization of a new leaf. This study shows that with 10 individuals, the spatial distribution is influenced by the genetic background of the group. The following step in this study should be to test with different numbers and density of individuals, different stases, with a higher level of inbreeding. Identifying aggregative pheromones and studying their interplay with the web structure could also help to draw a coherent picture of the mechanisms involved in the spatial distribution of mites and to open new applied perspectives in the control of this worldwide pest.

Acknowledgements

We are very grateful to Dr. Lebdi Grissa Kaouthar who supplied the red form of Tetranychus urticae used in our experiments and to George van Impe for the useful discussions about Tetranychus urticae. We would like to thank Marie Pairon, Gregory Sempo and all the team of the “Unité d'écologie et biogeographie” for their help in data analysis. The authors are also indebted to the National Fund for Scientific Research (FNRS, Belgium) for funding through the Fund for Fundamental and Collective Research (FRFC, convention 2.4622.06). A.C. Mailleux is financially supported by IRSIB (Institut d'encouragement de la Recherche Scientifique et de l'Innovation de Bruxelles). This publication is number BRC140 of the Biodiversity Research Center.

Bibliographie

[1] C. Rivault; A. Cloarec; L. Sreng Cuticular extracts inducing aggregation in the German cockroach, Blattella germanica (L.), J. Insect Physiol., Volume 44 (1998), pp. 909-918

[2] J.-M. Ame; C. Rivault; J.L. Deneubourg Cockroach aggregation based on strain odor recognition, Anim. Behav., Volume 68 (2004), pp. 793-801

[3] E. Ranta; H. Rita; H. Lindström Competition vs. cooperation: Success of individuals foraging alone and in groups, Am. Nat., Volume 142 (1993), pp. 42-58

[4] B. Wertheim Evolutionary ecology of communication signals that induce aggregative behaviour, Oikos, Volume 109 (2005), pp. 117-124

[5] G.F. Millar, Aggregation and development of the gorse spider mite Tetranychus lintearius, Dufor (Acari: Tetranychidae), Masters thesis, University of Canterbury, Christchurch, 1993

[6] W.B. Strong; B.A. Croft; D.H. Slone Spatial aggregation and refugia of the mites Tetranychus urticae and Neoseiulus fallacies (Acari: Tetranychidae, Phytoseiidae) on hop, Environ. Entomol., Volume 26 (1997), pp. 859-865

[7] G. Van Impe, Contribution à la conception de stratégies de contrôle de l'acarien tisserand commun, Tetranychus urticae Koch (Acari : Tetranychidae), Ph.D. thesis, Université Catholique de Louvain, 1985, 283 pp

[8] G. Clotuche, G. Le Goff, A.C. Mailleux, J.L. Deneubourg, C. Detrain, T. Hance, How to visualize spider-mite silk? Microsc. Res. Techniq., in press

[9] D.W. Davis Influence of population density on Tetranychus multisetis, J. Econ. Entomol., Volume 45 (1952), pp. 652-654

[10] J.L. Ashley, Toxicity of selected acaricides on Tetranychus urticae Koch (Tetranychidae: Acari) and Orius insidiosus Say (Hemiptera: Anthocoridae) life stages and predation studies with Orius insidiosus, M.Sc. thesis, Faculty of the Virginia Polytechnic Institute, USA, 2003

[11] J.A. McMurtry; C.B. Huffaker; M. Van de Vrie Ecology of Tetranychid mites and their natural enemies: A review. I. Tetranychidae enemies: Their biological characters and the impact of spray practices, Hilgardia, Volume 40 (1970), pp. 331-390

[12] F.J. Alatawi; G.P. Opit; D.C. Margolies; J.R. Nechols Within-plant distribution of two-spotted spider mites (Acari: Tetranychidae) on Impatiens: Development of a presence–absence sampling plan, J. Econ. Entomol., Volume 98 (2006), pp. 1040-1047

[13] G.P. Opit; D.C. Margolies; J.R. Nechols Within-plant distribution of two-spotted spider mite, Tetranychus urticae Koch (Acari: Tetranychidae), on Ivy geranium: Development of a presence–absence sampling plan, J. Econ. Entomol., Volume 96 (2003), pp. 482-488

[14] D.C. Queller Unrelated helpers in a social insect, Nature, Volume 405 (2000), pp. 784-787

[15] S.C. Banks; S.J. Ward; D.B. Lindermayer; G.R. Finlayson; S.J. Lawson; A.C. Taylor The effects of habitat fragmentation on the social kin structure and mating system of the agile antechinus, Antechinus agilis, Mol. Ecol., Volume 14 (2005), pp. 1789-1801

[16] M.J. Keough Kin-recognition and the spatial distribution of larvae of the bryozoan Bugula neritina (L.), Evolution, Volume 38 (1983), pp. 142-147

[17] A. Stow; A. Beattie Chemical and genetic defenses against disease in insect societies, Brain Behav. Immun., Volume 22 (2008), pp. 1009-1013

[18] C. Rivault; A. Cloarec Cockroach aggregation: Discrimination between strain odors in Blattella germanica, Anim. Behav., Volume 55 (1998), pp. 177-184

[19] T. Caraco; H.R. Pulliam Sociality and survivorship in animals exposed to predation (P.W. Price; C.N. Slobodchikoff; W.S. Gaud, eds.), A New Ecology: Novel Approaches to Interactive Systems, Wiley–Interscience, New York, 1984, pp. 279-309

[20] R.K. Vandermeer; M.D. Breed; M. Winston; K.E. Espelie Pheromone Communication in Social Insects, Westview Press, Boulder, CO, 1998

[21] T.L. Singer Roles of hydrocarbons in the recognition systems in insects, Am. Zool., Volume 38 (1998), pp. 394-405

[22] A. Lenoir; D. Fresneau; C. Errard; A. Hefetz Individual and colonial identity in ants: The emergence of the social representation concept (C. Detrain; J.L. Deneubourg; J.M. Pasteels, eds.), Information Processing in Social Insects, Birkhauser, Bale, 1999, pp. 219-237

[23] R.W. Howard; G.J. Blomquist Ecological behaviour and biochemical aspect of insect hydrocarbons, Annu. Rev. Entomol., Volume 50 (2005), pp. 371-393

[24] A.C. Mailleux; F. Robert; F. Saffre; B. Krafft; J.L. Deneubourg How non-nestmates affect the cohesion of swarming groups in social spiders, Insect. Soc., Volume 55 (2008), pp. 355-359

[25] C. Roeder; R. Harmsen; S. Mouldey The effects of relatedness on progeny sex ratio in spider mites, J. Evol. Biol., Volume 9 (1996), pp. 143-151

[26] W. Hussey; W.J. Parr Dispersal of the glasshouse red spider mite Tetranychus urticae Koch (Acarina, Tetranychidae), Ent. Exp. Appl., Volume 6 (1963), pp. 207-214

[27] S. Carbonnelle; T. Hance; A. Migeon; P. Barret; S. Cros-Arteil; M. Navajas Microsatellite markers reveal spatial genetics structure of Tetranychus urticae (Acari: Tetranychidae) populations among a latitudinal gradient in Europe, Exp. Appl. Acarol., Volume 41 (2007), pp. 225-241

[28] W.P.J. Overmeer Rearing and handling (W. Helle; M.W. Sabelis, eds.), Spider Mites, Their Biology, Natural Enemies and Control, vol. 1B, Elsevier, 1985, pp. 161-170

[29] Y. Saito; K. Sahara; K. Mori Inbreeding depression by recessive deleterious genes affecting female fecundity of a haplo–diploid mite, J. Evol. Biol., Volume 13 (2000), pp. 668-678

[30] S. Depickère; D. Fresneau; J.L. Deneubourg A basis for spatial and social patterns in ant species: Dynamics and mechanisms of aggregation, J. Insect Behav., Volume 17 (2004), pp. 81-97

[31] E. Batschelet Circular Statistics in Biology, Academic Press, London, 1981

[32] J.H. Zar Biostatistical Analysis, Prentice–Hall, New Jersey, 1999

[33] M. Dambach; B. Goehlen Aggregation density and longevity correlate with humidity in first instar nymphs of the cockroach (Blattella germanica L., Dictyoptera), J. Insect Physiol., Volume 45 (1999), pp. 423-429

[34] A.J. Catana The wandering quarter method of estimating population density, Spring, Volume 44 (1968), pp. 349-360

[35] R. Ceuster, Social homeostasis in colonies of Formica polyctena (Hymenoptera: Formicidae): Nestform and temperature preferences, in: Proceedings of 8th International Congress IUSSI, Wageningen, 1977, pp. 111–112

[36] R. Jeanson; C. Rivault; J.L. Deneubourg; S. Blanco; R. Fournier; C. Jost; G. Theraulaz Self-organized aggregation in cockroaches, Anim. Behav., Volume 69 (2005), pp. 169-180

[37] J.L. Deneubourg; A. Lioni; C. Detrain Dynamics of aggregation and emergence of cooperation, Biol. Bull., Volume 202 (2002), pp. 262-267

[38] J.K. Parrish; L. Edelstein-Keshet Complexity, pattern, and evolutionary trade-offs in animal aggregation, Science, Volume 284 (1999), pp. 99-101

[39] F. Faraji; A. Janssen; P.C.J. Van Rijn; M.W. Sabelis Kin recognition of the predatory mite Iphiseius degenerans: Discrimination among own, conspecific and heterospecific eggs, Ecol. Entomol., Volume 25 (2000), pp. 147-155

[40] Y. Saito Sociality and kin selection in Acari (J.C. Choe; B.J. Crespi, eds.), The Evolution of Social Behaviour in Insects and Arachnids, Cambridge University Press, Cambridge, 1997, pp. 443-457

[41] X. Lambin; J. Aars; S.B. Piertney Dispersal, intraspecific competition, kin competition and kin facilitation: A review of the empirical evidence (J. Clobert; A.A. Dhont; J.D. Nichols, eds.), Dispersal, Oxford University Press, Oxford, 2001, pp. 110-122

[42] D. Charlesworth; B. Charlesworth Inbreeding depression and its evolutionary consequences, Annu. Rev. Ecol. Syst., Volume 18 (1987), pp. 237-268

[43] J. Ridley; W.J. Sutherland Kin competition within groups: The offspring depreciation hypothesis, Proc. R. Soc. B, Volume 269 (2002), pp. 2559-2564

[44] W. Helle Inbreeding depression in an arrhenotokous mite (Tetranychus urticae Koch), Entomol. Exp. Appl., Volume 8 (1965), pp. 299-304

[45] G. Le Goff, A.C. Mailleux, C. Detrain, J.L. Deneubourg, G. Clotuche, T. Hance, Web as a meeting point in the two spotted spider mite Tetranychus urticae, in: Proceedings of 5th Meeting Ecology and Behaviour, Lyon, http://serl2009.univ-lyon1.fr/IMG/pdf/abstracts-2.pdf, 2009, pp. 119–120

[46] S. Ishii; Y. Kuwahara An aggregation pheromone of the German cockroach Blattella germanica L. (Orthoptera: Blattellidae). Site of the pheromones production, Appl. Entomol. Zool., Volume 2 (1967), pp. 203-217

[47] S. Ishii; Y. Kuwahara Aggregation of German cockroach Blattella germanica nymphs, Experientia, Volume 24 (1968), pp. 88-89

[48] O. Prouvost; M. Trabalon; M. Papke; S. Schulz Contact sex signals on web and cuticle of Tegenaria atrica (Araneae Agelenidae), Arch. Insect Biochem. Physiol., Volume 40 (1999), pp. 194-202

[49] T.A. Evans; B.Y. Main Attraction between social crab spiders: Silk pheromones in Diaea socialis, Behav. Ecol., Volume 42 (1993), pp. 99-105

[50] J.L. Deneubourg; J.C. Gregoire; E. Le Fort Kinetics of larval gregarious behaviour in the bark beetle Dendroctonus micans (Coleoptera: Scolytidae), J. Insect Behav., Volume 3 (1990), pp. 169-182

[51] Y. Kuwahara; L. Thi My Yen; Y. Tominaga; K. Matsumoto; Y. Wada 1,3,5,7-Tetramethyldecyl formate, lardolure: Aggregation pheromone of the acarid mite, Lardoglyphus konoi (Sasa and Asanuma) (Acarina: Acaridae), Agric. Biol. Chem., Volume 46 (1982), pp. 2283-2291

[52] K. Nishimura; N. Shimizu; N. Mori; Y. Kuwahara Chemical ecology of astigmatid mites. LXIV. The alarm pheromone neral functions as an attractant in Schwiebea elongata (Banks) (Acari: Tetranychidae), Appl. Entomol. Zool., Volume 37 (2002), pp. 13-18

[53] D.E. Sonenshine Pheromones and other semiochemicals of the acari, Ann. Rev. Entomol., Volume 30 (1985), pp. 1-28