Evaluation of the genetic trend of milk yield in the multiple ovulation and embryo transfer populations of dairy cows, using stochastic simulation

Navid Ghavi Hossein-Zadeh

doi:10.1016/j.crvi.2010.07.001

Résumé

Stochastic modeling of dairy cattle populations using multiple ovulation and embryo transfer (MOET) was used to compare 15-year genetic responses with an artificial insemination (AI) program. MOET and AI techniques were simulated in four populations, two with 100 breeding females each and two with 400 breeding females. The selection goal was to maximize genetic progress in milk yield. The reduction in genetic variation due to inbreeding and linkage disequilibrium was accounted for in the simulation process. All four MOET breeding schemes studied achieved larger genetic responses than the realized and theoretical genetic gains from the current AI progeny testing populations. Strict restriction against inbred matings slowed genetic progress significantly in the small population but would not be consequential in the larger population. However, allowing inbred matings in the smaller population caused a rapid accumulation of inbreeding. Linkage disequilibrium was as important as inbreeding in reducing genetic variation. Genetic drift variance was much smaller in the larger population.

1 Introduction

The application of reproductive techniques has had a major impact on the structure of breeding programs, the rate of genetic gain and the dissemination of genetic gain in livestock production. In essence, the most basic effect of reproductive technologies is to increase fecundity. This means that fewer parents are needed to produce a given number of offspring.

Reproductive management has received increased attention in recent years as new technologies and programs have been developed to aid dairy managers in efficiently breeding cows and heifers. Efficient breeding of cows and heifers has become increasingly difficult as fertility has decreased because of a correlated negative response with milk yield [1].

The first reproductive technique that had a major impact on animal breeding schemes was artificial insemination (AI). Rendel and Robertson [2] proposed a progeny-testing scheme to make efficient use of the possibilities offered by AI. Since then, progeny-testing schemes have been widely adopted in dairy cattle breeding. Although AI technology is still being improved and refined, breakthroughs in male reproductive technology with substantial consequences for breeding programs or dissemination of genetic progress are no longer expected. Use of embryo transfer (ET) technologies could enhance cattle production at several levels in both dairy and beef industries.

Nearly all studies indicated that breeding schemes employing multiple ovulation and embryo transfer (MOET) techniques promised a greater rate of genetic response than current AI progeny testing programs. This conclusion was based on the argument that MOET would lead to shortened generation intervals, more progeny from genetically superior females, and higher intensity in selecting cows for replacements [3,4]. However, the effective use of MOET in the bovine is limited by many problems. The main limitations of MOET are the low average and high variability of embryo numbers per female [5]. These limitations can be overcome by non-surgical harvesting of ova from females and subsequent in vitro maturation and in vitro fertilization which can yield larger numbers of transferable embryos. Among the early studies of the genetical implications of MOET were those by Land and Hill [6] for beef cattle and Nicholas and Smith [7] for dairy cattle. The general conclusion from these studies was that MOET could produce substantial increases in genetic improvement. However, it was noted that the rate of inbreeding would also be substantially increased. Realistic biological and managerial situations in a MOET dairy operation were closely approximated by simulating the occurrence of breeding decisions and events, including the selection and stocking of semen and embryo banks, on a monthly basis.

The aim of this study was to evaluate genetic changes in small closed populations of dairy cattle as the result of applying breeding programs that utilize MOET techniques with milk yield as the selection goal. A stochastic simulation model was used to generate results from MOET schemes and comparison with conventional AI breeding programs based on progeny testing.

2 Materials and methods

2.1 Model description

Briefly, dynamic programming is a mathematical technique which divides a multi-stage problem into a series of independently soluble single-stage problems and pictures the multi-stage problem as developing a guideline for dairy cows of varying size and production over a certain planning horizon. The objective of using a dynamic model for this study was to mimic the biology and management of a herd of individual youngstock and cows over time, with emphasis on reproduction and lifetime. The inclusion of stochastic functions generates variability in the performance of animals. This consequently results in realistic variability in the herd performance.

Microsoft Visual Basic^® 6.0 was used to simulate the MOET breeding schemes and conventional AI populations of dairy cows. Four MOET breeding schemes in the closed dairy cattle herds were simulated over 15-year period. Prior to the onset of each of the MOET breeding schemes, an unselected base population was established by simulating random mating. In all four schemes, the selection goal was genetic improvement in milk production. The structures of four MOET breeding schemes were as follows: a total of six males and 100 females were included in the population of MOET 1 and no restrictions were imposed to avoid inbred matings. Population size of MOET 2 was as in MOET 1, but matings resulting in offspring with inbreeding coefficient greater than 0.0625 were not allowed. A total of 25 males and 400 females were in the MOET 3 and no restrictions were imposed to avoid inbred matings. Population size of MOET 4 was as in MOET 3, and restriction on inbreeding was the same as in MOET 2.

Input parameters used in all four MOET breeding schemes are shown in Table 1. The simulated trait was milk yield in the first lactation. Sex of the calf was determined by a U (0, 1) random variable. Bull calves make up 52% of all calves born [8]. Number of embryos per superovulation follows a Poisson distribution with mean of 5. The results in each of the 15-year period were used to calculate average genetic trend and genetic drift, which were compared to expected genetic change from a conventional AI progeny testing program in a large population. Theoretical annual genetic gain in a conventional AI population for milk yield was 0.02 of population average [7], i.e., 160 kg/yr. Realized genetic gain was assumed to be a third of the theoretical gain, i.e., 53 kg/yr [9,10]. Therefore, cows and heifers were bred to sires with milk genetic trend of 53 and 160 kg/yr.

Parameter	Value
Number of replications	30
Average milk yield in base population (kg)	8000
Simulation period (yr)	15
Phenotypic standard deviation in base population (kg)	1500
Conception rate (%)	0.7
Survival rate (from birth to breeding age)	0.7
Minimum number of embryos in embryo bank	50
Maximum number of transferable embryos per selected male	50
Mortality rate, % per mo among cows older than 14 mo age	2
Genetic variance of milk (kg²)	292,852
Residual variance of milk (kg²)	757,000

2.2 Simulation of records

Records of milk production were generated by assuming an infinitesimal additive genetic model as y_i =μ + a_i + e_i where y_i = phenotypic lactation milk record of the animal i; μ = population mean; a_i = additive genetic effect of the animal i; and e_i = random residual effect. The breeding value of animal i, a_i, was generated by a_i = zσ_a, if parents were unknown, where z is an independent random normal deviate and σ_a is the assumed additive genetic standard deviation. If parents were known, this was generated by a = 0.5(a_i(s) + a_i(d)) + M, where $a_{i (s)}$ and $a_{i (d)}$ are true breeding values of the sire and dam of animal i and M is a deviation due to random Mendelian sampling, which was generated as $M = z {(0.5 (1 - \bar{F}))}^{\frac{1}{2}} σ_{a}$ , where $\bar{F}$ was the average inbreeding of the parents, and $0.5 (1 - \bar{F})$ accounted for the reduction of genetic variation due to inbreeding. Also, the residual effect, e_i, was generated as e_i = zσ_e, where σ_e as the assumed residual standard deviation. The additive breeding values were generated, at the birth, and if the animal was female, a phenotypic milk record was generated 10 months after calving.

2.3 Simulation of base population

For each of the four MOET breeding schemes, the base populations were considered as random samples from a large unselected dairy population. A base population was generated with a uniform age distribution ranging from 1 to 23 months and in gametic phase equilibrium state [11]. Five females in MOET 1 and MOET 2 (or 20 in MOET 3) were generated per each month of age, and a fixed number of sires (seven in MOET 1 and MOET 2 and 28 in MOET 3 and MOET 4) was used in the time period for establishing a base population.

The initial founder animals in a base population did not have lactation records, and selection could not be applied immediately. Therefore, animals in a base population were randomly mated for 13 months in order to obtain records for evaluation and selection. Female animals that were 14 months or older were mated. Father to daughter matings were avoided in base populations for all four MOET breeding schemes. All births resulted in females, and no mortality was allowed. At the conclusion of the 13 months, age would range from 1 to 36 months. Starting from the 14th month, and for each of the succeeding 180 months, selection of animals was based on their predicted breeding values from an animal model. The number of founder animals in a base population determined the size of subsequent breeding population and was kept constant.

2.4 Evaluation, selection, mating and culling of animals

Breeding values were evaluated every month based on the lactation records using an animal model:

y = μ 1 + Za + e

where y is a vector of the lactation records; μ is the fixed lactation mean; a is a vector of random effects of additive breeding values for all animals in the herd, male and female; e is a vector of random residuals; and 1 and Z are incidence matrices corresponding to μ and a, respectively. The (co)variances were:

var [\begin{array}{c} y \\ a \\ e \end{array}] = [\begin{array}{c} Z A Z^{'} σ_{a}^{2} + I σ_{e}^{2} & Z A σ_{a}^{2} & I σ_{e}^{2} \\ A Z^{'} σ_{a}^{2} & A σ_{a}^{2} & 0 \\ I σ_{a}^{2} & 0 & I σ_{e}^{2} \end{array}]

where A is an additive relationship matrix for all animals in a including inbreeding coefficients. Mixed model equations were constructed using the parameter value for

\frac{σ_{e}^{2}}{σ_{a}^{2}}

and the solution for a was used as the selection criterion.

The best young bull of 14 months of age was selected each month. His semen was stored in a semen bank and used to fertilize no more than 50 transferable embryos. This restriction should reduce generation interval and the accumulation of inbreeding. Then, the best bull semen in storage was used to breed the selected donors. The number of donors selected was dependent on the number of embryos available in the embryo bank, which was kept at a minimum of 50. The assumption was that the number of embryos per each superovulation averaged five following a Poisson distribution. If the bank had 50 embryos or more, still one donor was selected to ensure the availability of superior genetic potential in a given month. The selection intensity on either males or females was impossible to enumerate but was a function of size of the semen and embryo banks, number of embryos per superovulation, number of bulls and donors selected, and number of transferable embryos per bull, all of which varied from month to month.

In all the MOET breeding schemes, matings were planned to maximize genetic gain in milk yield. However, in MOET 2 and 4, matings that would have resulted in progeny with inbreeding coefficients greater than 0.0625 were excluded. This was accomplished by computing the inbreeding coefficients of offspring of all possible matings among selected males and donors and then allowing only those producing the highest expected breeding values but with inbreeding coefficients less than 0.0625. Those donors were flushed, and recovered embryos were stored in the embryo bank. All embryos were ranked by their predicted breeding values, i.e., average of sire's and dam's breeding values. Then, the top ranked embryos were transferred each month to open cows and heifers that were ready to be bred.

The linkage disequilibrium (LD) at time t was defined as the proportional variation left in the population under linkage disequilibrium after accounting for reduction due to inbreeding, and was expressed as follows:

L D = \frac{σ_{g (t)}^{2}}{(1 - \bar{F}) σ_{g (t_{0})}^{2}}

where

σ_{g (t)}^{2}

, was the genetic variance at time t;

σ_{g (t_{0})}^{2}

was the initial genetic variance in the base population and

\bar{F}

was the average inbreeding coefficient in the population at time t. Therefore, selection would lead to a reduction in genetic variance. The random genetic drift was computed as the standard deviation of genetic means over the replicates.

Involuntary culling was imposed on those cows that failed to conceive after three consecutive breedings. Also, a monthly 2% mortality rate due to diseases and accidents was imposed on cows after completion of first lactation. Voluntary culling was then practiced to keep the number of breeding females in the populations constant. When population size exceeded capacity, open cows in second or greater lactations were culled first. If further culling was needed, heifers were culled. Within each category of females, culling was done by the magnitude of predicted breeding values in ascending order. Young bulls not selected at 14 mo of age were culled as well as selected ones having produced 50 transferable embryos. After the stochastic process in each of the four MOET populations was simulated over the course of 180 months and repeated for 30 times, inbreeding, linkage disequilibrium, and genetic response with random genetic drift variation were calculated for each month.

3 Results and discussion

One consequence of inbreeding is decreased production due to inbreeding depression. The model used in this study did not include nonadditive genetic effects and thus did not consider inbreeding depression. Another consequence is reduced genetic variation in direct proportion to the average inbreeding coefficient in the population. If genetic variance is reduced due to inbreeding, the loss would not be recovered unless foreign genetic material is introduced. The accumulation of inbreeding over 15-year period in the four MOET populations simulated is presented in Fig. 1. The MOET 1 population with 100 breeding females without restriction on inbreeding accumulated 21.7% inbreeding over 15 year, but MOET 3 with 400 breeding females without restriction on inbreeding accumulated 19.8% inbreeding. The MOET 2 and MOET 4 populations both with restriction on inbreeding reached 4.5 and 3.6% inbreeding, respectively. If MOET 1 and MOET 3 populations be continued beyond 15 years, inbreeding would soon reach the point where selection would be ineffective due to severe loss of additive genetic variation. In MOET 2 and MOET 4 populations, genetically superior animals might not be selected due to the restriction on inbreeding, thus hindering genetic progress in the populations. The breeding scheme in both MOET 2 and MOET 4 was the same, but MOET 4 had a lower rate of inbreeding due to a larger population size. The rate of inbreeding in all four MOET populations followed approximately a linear trend. Quinton and Smith [12] reported to balance the short and long-term response, a restriction on the rate of inbreeding is required.

Fig. 1
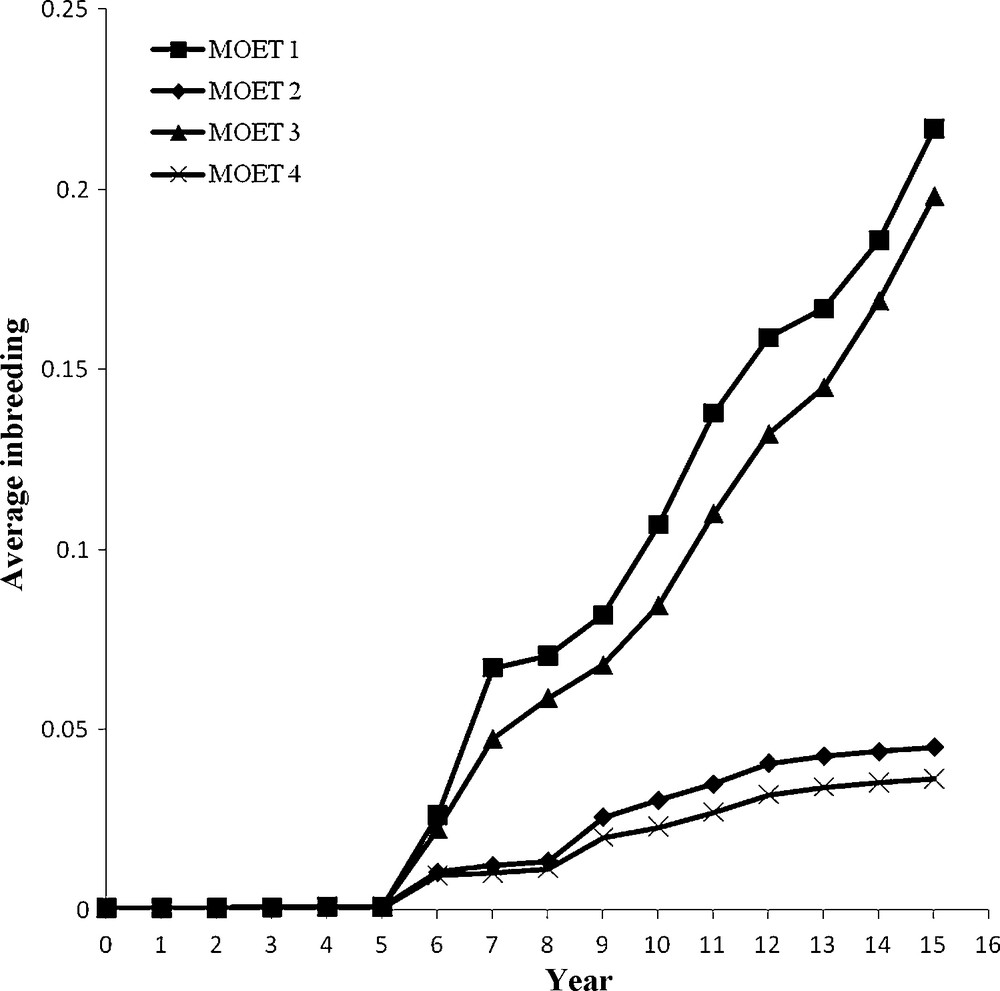
Annual average of inbreeding coefficients of newborn animals in each of the four MOET populations.

Selection of parents reduces variance in progeny generation from gametic phase disequilibrium or linkage disequilibrium [13]. With increasing selection intensity, reduction of genetic variance due to linkage disequilibrium is expected to be larger. The MOET 3 and 4 populations had the largest number of breeding animals, which allowed higher selection intensity on males than MOET l and MOET 2. This resulted in the largest reduction of genetic variance (22.5 and 22.0%, respectively) due to linkage disequilibrium for MOET 3 and 4. The linkage disequilibria in MOET l and MOET 2 were 17 and 16.8%, respectively. Even in conventional AI breeding schemes, appreciable loss in genetic response was caused by linkage disequilibrium [14]. The amount of genetic variation and the corresponding SD varied over time as shown in Fig. 2. In MOET 2 and MOET 4, if top ranking bulls could not be used because of restriction on inbreeding in the progeny, bulls were used from previous generations, which might not be as intensively selected, leading to more genetic variation among progeny. This should explain why MOET 2 and MOET 3 showed more fluctuation in genetic variation over time than MOET 1 and MOET 4.

Fig. 2
Changes in genetic variation in the four MOET populations.

The genetic changes from the four MOET schemes were compared with both theoretical and realized genetic progress from a conventional progeny testing AI population. The genetic trend over 15 years is shown in Figs. 3–6. At the end of year 15, the genetic gain in MOET l (2342 kg) was significantly larger than that in MOET 2 (1525 kg) (P < 0.05), which was due to restriction on inbreeding in MOET 2. The genetic gain in MOET 4 (2302 kg) was also significantly larger than that in MOET 2 (P < 0.05), which was due to difference in population size. In addition, the genetic trend of milk yield in MOET 3 (2749 kg) was significantly larger than other MOET schemes (P < 0.05), which was due to the no restriction on inbreeding and larger population size in MOET 3. The genetic means of MOET l and 3 populations followed a smooth linear trend and fluctuated less than those of MOET 2 and MOET 4. This was due to the absence of restriction on inbreeding in MOET 1 and 3, allowing the best genetic material to be used each month. Selection of the best animals was not always possible in MOET 2 because of the restriction on inbreeding, thereby hindering genetic progress. The same restriction on inbreeding was imposed in MOET 4 population, but its genetic trend was similar to that of MOET l. Due to the larger population size, MOET 4 population was less affected by the inbreeding restriction and had higher probability of selecting animals that were less related. The rate of genetic progress in all of MOET populations was significantly greater than both theoretical and realized genetic gains from the current AI progeny testing population (P < 0.05).

Fig. 3
Annual genetic means with genetic drift variation as the genetic standard deviation (GSD) in MOET 1.

Fig. 4
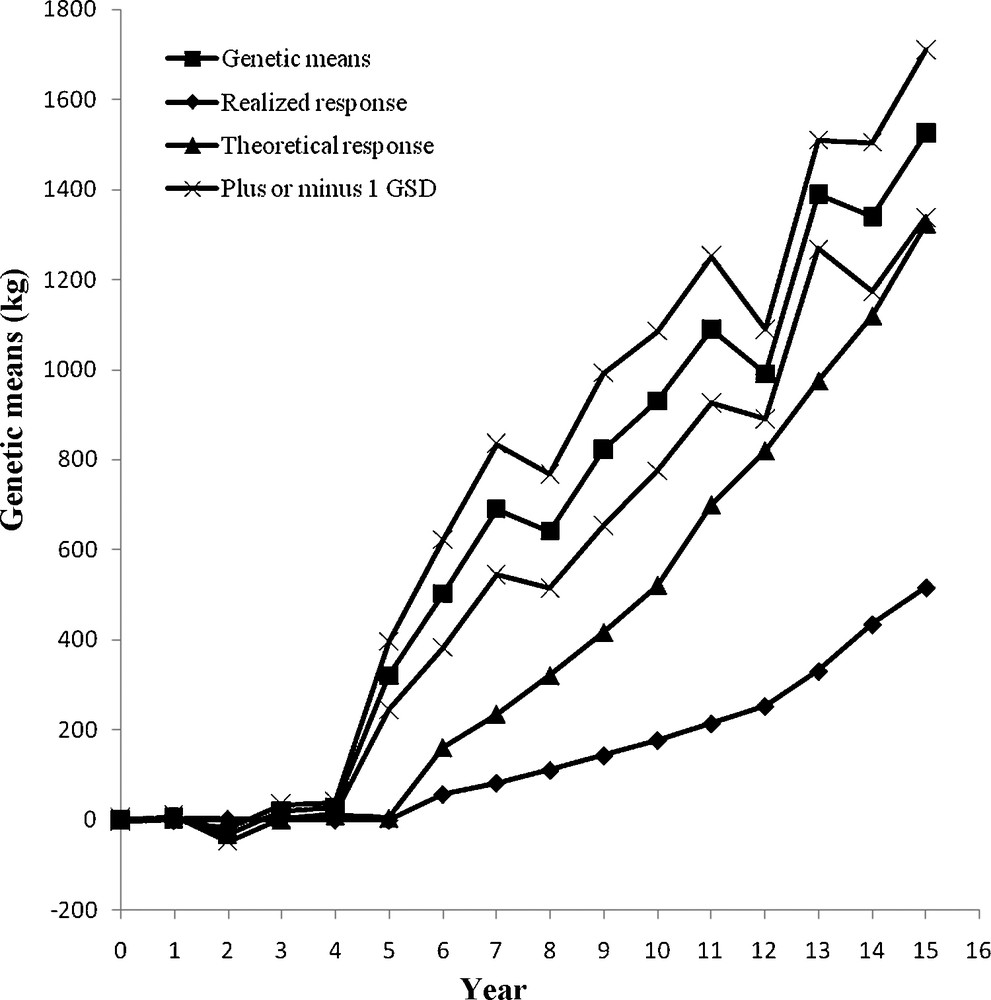
Annual genetic means with genetic drift variation as the genetic standard deviation (GSD) in MOET 2.

Fig. 5
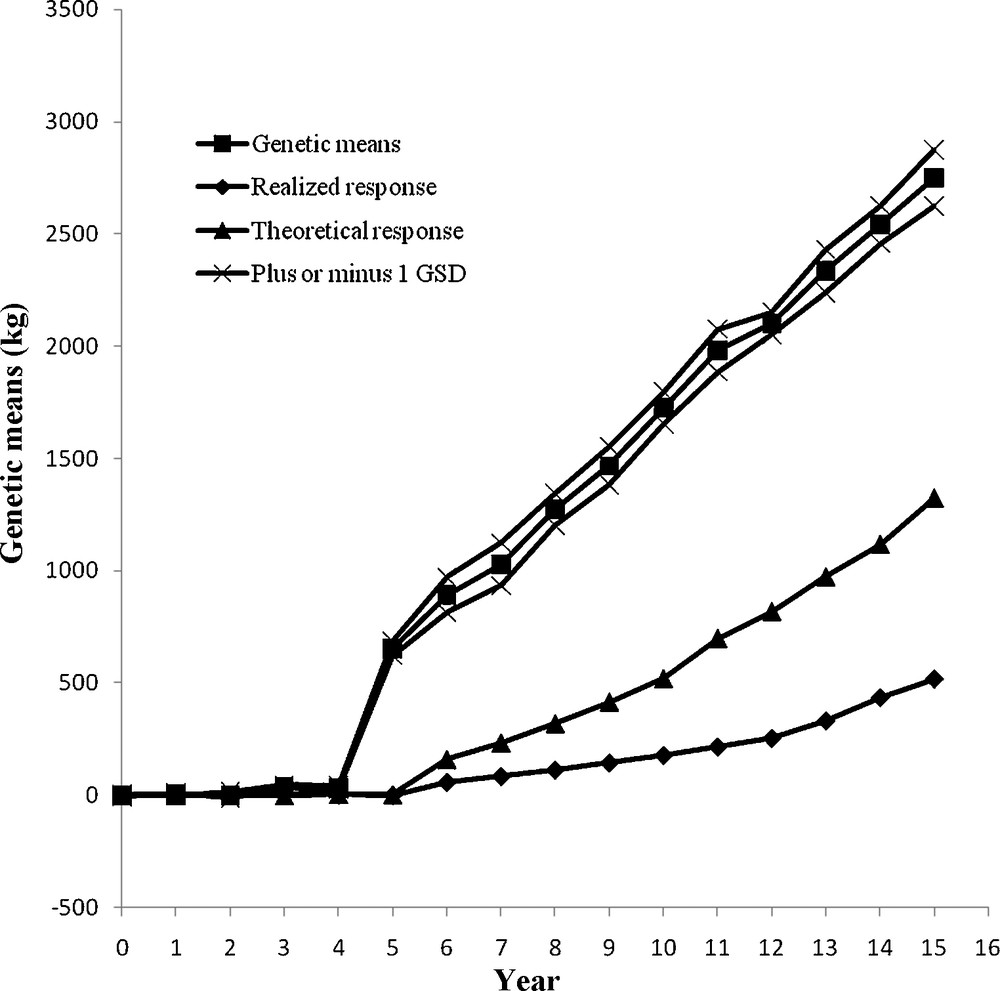
Annual genetic means with genetic drift variation as the genetic standard deviation (GSD) in MOET 3.

Fig. 6
Annual genetic means with genetic drift variation as the genetic standard deviation (GSD) in MOET 4.

The random genetic drift was expressed as the standard deviation of genetic means and was also shown in Figs. 3–6. Many factors contribute to random genetic drift, but it is mainly related to effective population size. Imposing higher selection intensity on highly heritable traits for a fixed number of generations would require a smaller population size. However, for fixed intensity and heritability, relatively large population size would be required. Hence, after 15 years of selection, the coefficient of variation (CV) of genetic response in MOET 3 population was the smallest, 3.24%, and those in MOET 1, MOET 2 and MOET 4 were 8.54, 10.79 and 9.84%, respectively. In MOET 2 and MOET 4, the selection intensity was lower than those in MOET l and MOET 3 due to inbreeding restriction and smaller size, which resulted in the highest CV of genetic response. Colleau et al. [15] reported asymptotic rate of genetic gain for Monte Carlo simulations were about 10 and 7% lower for juvenile and adult MOET schemes, respectively, but still higher (20%) than the predicted value for the corresponding conventional scheme. Montaldo et al. [4] concluded that use of IVEP (in vitro embryo production) techniques to obtain more progeny per donor female, could increase the rates of genetic response in MOET nucleus herds of dairy cattle, but inbreeding rates need to be limited. Peixoto et al. [16] reported there was a positive genetic trend for milk yield in the MOET nucleus of Guzerat herds at low inbreeding coefficients due to the increased accuracy and estimated genetic merit, but no changes in the average milk yield were observed.

4 Conclusions

All four MOET breeding schemes studied achieved larger genetic responses than the realized and theoretical genetic gains from the current AI progeny testing populations. This progress was accomplished in spite of their small sizes, the closed schemes, and restrictions on inbreeding in some cases. The small population without restrictions on inbreeding accumulated a high level of inbreeding. Such restrictions did not appear to be worthwhile in terms of genetic gain for the time horizon studied. Beyond that, however, selection would become ineffective due to reductions in genetic variation caused by inbreeding. Higher selection intensity regardless of population size led to a higher degree of linkage disequilibrium. The reduction in genetic variation due to linkage disequilibrium was as important as that due to the accumulation of inbreeding. Large population size did lead to lower random genetic drift.