Plan
Comptes Rendus
no. 4

Biological modelling/Biomodélisation
Niche invasion, competition and coexistence amongst wild and domestic Bolivian populations of Chagas vector Triatoma infestans (Hemiptera, Reduviidae, Triatominae)
[Invasion de niche, compétition et coexistence entre populations boliviennes sauvages et domestiques du vecteur de la maladie de Chagas Triatoma infestans (Hemiptera, Reduviidae, Triatominae)]
Frédéric Lardeux1
1 Institut de recherche pour le développement (IRD), BP 64501, 34394 Montpellier cedex 5, France
Comptes Rendus. Biologies, Volume 336 (2013) no. 4, pp. 183-193.

Résumés

The model developed for human parasites by Bottomley et al. (2007) [52] has been adapted to the dynamics of triatomines to better understand the processes of niche invasion, competition among species and coexistence. In Bolivia, both wild and domestic populations of Triatoma infestans exist. Their ecological niches are normally separated and the two populations do not interbreed, behaving as two distinct species. However, it has been suggested that the two populations may compete, highlighting therefore the potential risk of wild populations invading human dwellings. The model revealed the importance of the basic reproduction rates R0 of triatomine colonies for the risk of invasion. This depends not only on life traits such as survival and fecundity, but also on (1) the density-dependence phenomenon that limits triatomine establishment, (2) on house exposure to infection and (3) on the correlation between house susceptibility to domestic T. infestans and house susceptibility to wild T. infestans. Competition and coexistence amongst the two groups of T. infestans may occur under particular conditions, but are very unlikely.

Le modèle mis au point pour les parasites humains par Bottomley et al. (2007) [52] a été adapté à la dynamique des Triatomes afin de mieux comprendre les processus d’invasion de niche, de compétition entre espèces et de coexistence. En Bolivie, il existe des populations sauvages et domestiques de Triatoma infestans. Leurs niches écologiques sont normalement séparées, les deux populations ne s’hybrident pas et se comportent donc comme deux espèces distinctes. Toutefois, il a été suggéré que les deux populations pourraient entrer en compétition, soulignant ainsi un risque potentiel d’invasion des habitations humaines par des populations sauvages. Pour l’invasion de niche, le modèle met en évidence l’importance des taux de reproduction de base R0 des colonies de Triatomes, qui dépendent non seulement de traits de vie tels que la survie et la fécondité, mais aussi (1) de phénomènes de densité-dépendance qui limitent l’implantation des Triatomes, (2) du taux d’exposition de la maison à l’infection et (3) de la corrélation entre la susceptibilité d’une maison aux populations domestiques de T. infestans et sa susceptibilité aux populations sauvages. La compétition et la coexistence entre les deux groupes de T. infestans sont possibles dans des conditions particulières, mais sont très peu probables.

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crvi.2013.05.003
Keywords: Triatominae, Invasion, Competition, Coexistence, Domiciliation, Chagas
Mot clés : Triatominae, Invasion, Compétition, Coexistence, Domiciliation, Chagas
Frédéric Lardeux 1

1 Institut de recherche pour le développement (IRD), BP 64501, 34394 Montpellier cedex 5, France 
@article{CRBIOL_2013__336_4_183_0,
     author = {Fr\'ed\'eric Lardeux},
     title = {Niche invasion, competition and coexistence amongst wild and domestic {Bolivian} populations of {Chagas} vector {\protect\emph{Triatoma} infestans} {(Hemiptera,} {Reduviidae,} {Triatominae)}},
     journal = {Comptes Rendus. Biologies},
     pages = {183--193},
     publisher = {Elsevier},
     volume = {336},
     number = {4},
     year = {2013},
     doi = {10.1016/j.crvi.2013.05.003},
     language = {en},
}
TY  - JOUR
AU  - Frédéric Lardeux
TI  - Niche invasion, competition and coexistence amongst wild and domestic Bolivian populations of Chagas vector Triatoma infestans (Hemiptera, Reduviidae, Triatominae)
JO  - Comptes Rendus. Biologies
PY  - 2013
SP  - 183
EP  - 193
VL  - 336
IS  - 4
PB  - Elsevier
DO  - 10.1016/j.crvi.2013.05.003
LA  - en
ID  - CRBIOL_2013__336_4_183_0
ER  - 
%0 Journal Article
%A Frédéric Lardeux
%T Niche invasion, competition and coexistence amongst wild and domestic Bolivian populations of Chagas vector Triatoma infestans (Hemiptera, Reduviidae, Triatominae)
%J Comptes Rendus. Biologies
%D 2013
%P 183-193
%V 336
%N 4
%I Elsevier
%R 10.1016/j.crvi.2013.05.003
%G en
%F CRBIOL_2013__336_4_183_0
Frédéric Lardeux. Niche invasion, competition and coexistence amongst wild and domestic Bolivian populations of Chagas vector Triatoma infestans (Hemiptera, Reduviidae, Triatominae). Comptes Rendus. Biologies, Volume 336 (2013) no. 4, pp. 183-193. doi : 10.1016/j.crvi.2013.05.003. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2013.05.003/

Version originale du texte intégral

1 Introduction

Chagas disease is an endemic parasitic anthropozoonosis from the American continent caused by Trypanosoma cruzi, a flagellate protozoan that can infect a wide range of wild and domestic mammals as well as humans[1]. Human infections can occur through blood transfusion, congenital transmission, oral route, organ transplant etc., but the most important route is by far through insect vectors (> 80% of the cases) [2]. Insect vectors are hematophagous bugs (Hemiptera, Reduviidae, Triatominae) [3] that acquire the infection by sucking blood from an infected mammal and may retransmit the parasite during the next blood meal, not through the bite itself but by defecating while sucking blood. The trypanosomes are in the faeces and therefore can penetrate the skin using any mucus membrane or any wound. In the infected host, the disease tends quickly towards a chronic presentation, the parasite causing not immediately apparent but irreversible lesions in the cardiac, digestive and nervous system, frequently leading to the death of the host.

Most species of Triatominae occupy predominantly wild habitats that offer shelter from climatic extremes along with easy access to a blood source: bird nests or rodent burrows are common examples. However, some species can also invade and colonise peridomestic habitats such as hen houses or goat corrals, and some have successfully colonised human dwellings. This tendency to colonize houses is important in terms of disease transmission to humans. Transmission is dependent on various factors and for triatomines, the most significant are, among others, the blood trophic preference, the rapidity to which the insect can defecate shortly after blood-feeding and therefore leaving T. cruzi close to possible body entries [4], and even the density of the insects in a house [5]. However, the most important parameter is by far the tendency of the species to live close to human dwellings (i.e., its degree of domesticity) and therefore to enter frequently in contact with him [6]. Indeed, major vectors of Chagas disease such as Triatoma infestans, Rhodnius prolixus, T. dimidiata or T. brasiliensis are among the species that have successfully colonized human dwellings in which they now accomplish their life cycle and develop colonies [6]. The “domiciliation process” of Triatominae [2,7] is of major importance in transmission dynamics. Interrelationships between wild (i.e., “sylvatic”), peridomestic and domestic populations of Triatominae (from the same or from different species) should therefore be carefully studied to propose efficient vector control strategies [8, among others].

Unfortunately, the existence of interspecific interactions between triatomine species capable of domiciliation is not yet well documented. A particular species has two ways of being successful in colonizing habitats: it may be very good at colonizing open sites, or it may be very good at displacing other species from a given site. Between these two extremes, species may coexist if none of them have too superior a combination of both traits [9]. For triatomines, colonizing open sites, and in particular human dwellings, may occur when humans enter new territories. Such a process is observed in Bolivia for R. stali [10], T. sordida, Eratyrus mucronatus [11] or Panstrongylus rufotuberculatus [12], and in Argentina for T. guasayana [6]. Another scenario would be when a pest-control campaign empties such an ecological niche. Then some new species may colonize the empty niche from the wild environment [13,14] or the same species may re-colonize the niche from the peridomestic environment, which is generally less well controlled by pesticides [15–19]. Despite these examples of the struggle for domiciliation, there is no clear record of coexistence of colonies of two different species in the same house. Apart of very infrequent observations [20], only one single species is generally present in one type of ecotope [21, among others]. It seems that there exists competitive exclusion, which specifies that two different species cannot share the same ecological niche: one of the two competitors will always win over the other. The loser will either become extinct or will shift towards a different ecological niche by means of evolution or behaviour [22]. This principle might also explain a third scenario of domiciliation which consists of species displacements, such as those observed with T. infestans, which appears to be a strong competitor to other species [6,15,23–25].

In Bolivia, T. infestans is well domiciled and is the main vector of T. cruzi. Domiciled populations are numerous and widely distributed. There also exist space-limited wild foci which have been identified not only in Bolivia [26–30], but also in Argentina [31–34], Paraguay [35], Brazil [36] and Chile [37,38]. In these countries, wild foci of T. infestans were observed in the Chaco region and the Andean cordillera, which represent only a small part of the geographic distribution of the species in Latin America. Wild and domestic populations belong to the same species and probably wild populations have had domestic ones as ancestors [28,39–41]. However, unlike, for example, the case of T. dimidiata [42], the two entities do not mix. They behave as two different “species” without or with limited gene flow [28,41,43–45] and can be morphologically distinguished [44,46]. However, although reinvasion of the domestic environment after insecticide treatment seems to be the fact of residual domestic T. infestans populations [46–49, among others], the possibility that wild populations may re-invade empty human dwellings cannot be discarded [50]. This would be a complication in terms of vector control strategy, which therefore would have to take into account the role of wild populations as a potential reservoir for human dwelling reinvasion.

Therefore, it is crucial to better understand:

  • • how different species (or different populations that do not interbreed) can compete for colonization;
  • • if they can manage it, which one is likely to succeed (i.e., what are the key factors for a successful establishment of a species in human dwellings, in particular if another species is already there?);
  • • if two species can coexist in the same ecological niche.

Two hypotheses can be suggested:

  • • the two species (or separated “groups”) can really share the same ecological niche and in that case invasion, competition and coexistence are part of the natural ecological processes that the two groups may undergo;
  • • the two groups cannot share the same niche because they do not have exactly the same ecological needs. In that case, the species cannot interact and there is no possibility of competition or coexistence.

The second hypothesis deals, for example, with characteristics such as trophic preferences, microclimatic preferences, behavioural characteristics or any other genetically driven characteristic that would impede one species from colonizing the niche of the other one. This hypothesis will be discussed in a subsequent article for wild and domestic populations of T. infestans.

In the present paper, two initial hypotheses will therefore be taken into account:

  • • as stated above, the two groups of T. infestans may share the same ecological niche;
  • • the two populations (wild and domestic) are supposed not to interbreed and can thus be considered as two different species.

These hypotheses enable competition and therefore, a more general theoretical framework to explore the population dynamics of two competing species of triatomines colonizing human dwellings. In this framework, a new modelling approach for these disease vectors can be proposed: Triatomines can be assimilated to “macroparasites” and human dwellings to “hosts” in a similar manner as for human parasitic diseases modelling [51]. Therefore the mathematical model developed for macroparasites colonizing human populations by Bottomley et al. [52] can be adapted to “triatomines colonizing houses”. The model enables to point out the importance of some life traits of the triatomine species for successful invasion, competition or coexistence. The model's results, although general in the framework of Triatomine dynamics, are discussed in the light of the problem of wild/domestic populations of T. infestans in Bolivia and the possible establishment of wild populations in place of domestic ones.

2 Material and methods

The model's initial hypothesis is that the two populations, i.e. wild and domestic ones, can live in the same biotopes and do not interbreed. Both populations may colonize a domestic environment (inside houses) or a wild environment, as described in Noireau [53]: rupiculous or arboreal environments consisting in marsupial or rodent burrows, rocky outcrops, hollow trees etc. Model parameters appear in Table 1 and are explained thereafter.

Table 1

Model parameters and variables.

Parameter Description
n Number of human dwellings considered
F Size of the population of triatomines with the potential of colonizing a house (i.e., “fertilized females” which are seeking for a human dwelling)
m F Mean number of “fertilized females”
μ F Per capita rate of mortality of “fertilized females”
C i Number of triatomines colonies (of one species) in the house i (burden of triatomine colonies for house i)
m C Mean number of triatomine colonies in a house
μ C Per capita rate of disappearance of triatomine colonies
Гi Contact rate of a house i with “fertilized females”
mΓ (σГ2) Mean (and variance) for contact rate of houses with triatomines
v Γ vΓ = σΓ/mΓ coefficient of variation of the rate of exposure which measures the degree of heterogeneity of exposure of houses to triatomine colonization
r Rate of production of newborns by a colony
P Probability of development of a newborn to the status of “fertilized female”
δ = r P = rate at which a colony produces new “fertilized females”
η and ηij Density-dependent parameter. It is the “per-colony reduction in probability of starting a new colony when other colonies are already established and therefore, (1 – η Ci) = probability that a new female survives to start a colony”. Therefore, the maximum number of colonies harbored by a house is 1/η
In the two-species model, ηij represents the effect of species i on the probability of establishment of species j. Therefore, (1 – η11 C1 – η21 C2) (and equivalent terms for species 2) is the probability of establishment of a fertilized female of species 1 in a house where C1 colonies of species 1 and C2 colonies of species 2 are already present
σГC Covariance between exposure to house infestation and the burden of colonies in houses
ρ Correlation between house susceptibility to species 1 and house susceptibility to species 2

2.1 Model for domiciliation of a single species

A colony of triatomines will be defined as “all the insects from the same mother living in one house”. From all the triatomines living in an area, the population with the potential to colonize a house and start a colony are fertilized females. This population is of size F. These females may belong to a colony already established in a house and fertilized there, or may come from another house (by flight for example) and may be already fertilized or will be fertilized in this new house. Thereafter, these insects will be referred to as “fertilized females” for simplicity. The number of houses that can be colonized is n. In one house i, there are Ci colonies of triatomines of one single species. F and Ci are random variables.

The rate of production of new females by a colony is r. If the probability that a newborn female develop to the status of “fertilized female” is P, then the colonies in the n houses produce fertilized females at a rate δ   ∑i=1nCi, where δ = r P.

In one house, “fertilized females” in colonies are lost either through natural mortality μF or through emigration to another house (intending to start a new colony). The rate at which fertilized females are lost through house colonization can be computed as ∑i=1nΓi F, where the product Γi F represents the contact rate of one house i with fertilized females.

Houses may harbour large colonies of T. infestans, but generally less than the apparent carrying capacity (i.e., the number of adequate places to breed), because populations undergo strong density-dependence effects that limit the number of triatomines in one house. These density-dependence relationships are related to the availability of hosts for blood-feeding [5,54–58] and hiding places availability [59]. Therefore, the model should take into account a kind of density-dependent establishment, and it can be assumed that the probability of a “fertilized female” surviving and starting a new colony in a house i is lowered by the number of yet established colonies Ci. This probability can therefore be formulated as (1 – ηCi), where η is the “per-colony reduction in probability of starting a new colony”. In the model, whenever (1 – ηCi) becomes negative, it is set to zero.

For model completion, some hypothesis should be formulated on the dynamics of both triatomine colonies and houses. A colony can disappear at a per capita rate μC and a house at a per capita rate μH. However, it is assumed that the number of houses is maintained at size n (i.e., each time a house disappears, it is replaced by a new one that can be infected by triatomines). If a house disappears, the colonies in this house disappear as well.

The model can then be formulated in terms of increasing or decreasing number of fertilized females and triatomine colonies following a n + 1-dimensional Markov process:

  • • the number of fertilized females increases by one at a rate δ∑i=1nCi;
  • • the number of fertilized females decreases by one at a rate (μF+∑i=1nΓi) F;
  • • the number of colonies in one house increases by one at a rate F Γi(1−ηCi);
  • • the number of colonies in one house decreases by one at a rate μC Ci;
  • • the number of colonies in a house is set to 0 at a rate μH.

2.1.1 Model when house exposures to infestation are identical

In a first approach, it is assumed that each house has the same contact rate with “fertilized females”, i.e., Γi = Γ for all i. Following the analysis of Bottomley et al. [52], the random variable F (size of the population of “fertilized females”) is replaced by its mean mF for simplification and it is therefore possible to derive differential equations for the mean number of “fertilized females” mF(t), the mean number of colonies mC(t) and its variance σ2C(t). It is reasonable to consider that the life duration of the “fertilized female” stage (which corresponds to the house-seeking phase) is shorter than the duration of its corresponding colony. Therefore dmF/dt can be set to zero and the model simplifies to the two following equations for the mean number of colonies and its variance (see Bottomley et al. [52] for details):

dmC/dt=δ′mC1−η mC−μC+μHmC(1)
dσC2/dt=δ′mC1−η2σC2+mC+μCmC+μHmC2−2μC+μHσC2(2)
where δ′ = δ Γ n/(μL + Γ n) represents the product of δ, the rate at which a colony produces new “fertilized females”, and the probability Γ n/(μL + Γ n) of survival of a “fertilized female” to start a colony.

In a mathematical sense, mC(t) and σ2C(t) are limiting values of the mean number of colonies and variance when the number of houses tends to infinity. However, these terms also well describe large but finite populations (i.e., > 100 houses), as observed in field situations.

Epidemiologists define the basic reproduction number (R0) of a disease as the expected number of secondary infections arising from a single individual during his entire infectious period, in a population of susceptible individuals where there is no immunity and in the absence of interventions to control the infection [60]. The R0 concept has also been widely used in ecology where it measures individual reproductive success under ideal conditions (i.e., the mean number of offspring produced over the lifetime of an individual) [61]. From these definitions, it emerges that when R0 < 1, each individual (or infected individual if a disease is concerned) produces, on average, less than one new (infected) individual, and therefore the population (or the disease) will not grow. If R0 > 1, the population will grow (or, from the disease's point of view, the “pathogen” is able to invade the susceptible population of hosts). This threshold notion is one of the most important and useful characteristic of the R0 concept. This concept can be applied to the development of triatomine colonies (= the “pathogen”) in the population of houses (= the “hosts”). In the present triatomine model, the basic reproduction number for the mean number of colonies can be computed from Eq. (1) as:

R0=δ′/μC+μH=δ ΓnμL+Γn/μC+μH(3)

When R0 < 1, the triatomine species is unable to establish itself in the houses and therefore, mC = 0. This value is a stable point. When R0 > 1, the point mC = 0 is unstable and the number of colonies can increase, up to an equilibrium point where mC = (1/η) (1 – R0−1). The mean number of triatomine colonies is therefore dependent on the basic reproduction number R0 and on the strength of density-dependence η (i.e., the “per-colony reduction in probability of starting a new colony when other colonies are already established”). At this equilibrium, assuming that the rate of disappearance of houses μH is much smaller than the other rates, the variance to mean ratio becomes R0−1. Indeed, when equating Eqs. (1) and (2) to zero at equilibrium, and equating R0 = δ′/(μC + μH) ≈ δ′/μC, straightforward calculations give σ2C/mC = R0−1. Then, if R0 > 1 (which enables triatomine colonies to grow in number), then σ2C/mC < 1, which implies that the distribution of the number of triatomine colonies across the houses is distributed more evenly than at random. However, field observations prove that triatomine bugs are generally aggregated amongst houses, and therefore some houses harbour more colonies than others [62].

2.1.2 Model when there is heterogeneity in house exposure to infestation

The model should therefore be modified to take into account the aggregated distribution of triatomines and therefore to enable σ2C/mC > 1. Several mechanisms can generate such heterogeneity; among them, ecological factors that make some habitats less suitable than others. For example, triatomine establishment can be limited if triatomine refuge quantity and quality diminish [62] or when house walls are improved (this can be assimilated to a kind of “immunity” of the houses). Another likely mechanism is the heterogeneous exposure of houses to colonization which can also mimic the above mechanisms. Among various factors that can influence heterogeneous exposure, one can think for example to close favourable infested peridomestic habitats that can generate higher domestic exposure in the vicinity [18,47]. In the model, heterogeneity can be achieved by enabling a random contact rate of houses with “fertilized females”, i.e. replacing in the model the contact rate Γ, which was fixed, by independent and identically distributed random variables Γi (i = 1 to n) with mean mΓ and variance σ2Γ (and therefore a coefficient of variation of the exposure rate of vΓ = σΓ2/mΓ that measures the degree of heterogeneity). In that case, the model's development gives the following equation for the mean number of colonies at stable equilibrium:

mC=12ηvΓ2−1vΓ2−1+2R0−1−vΓ2−12+4vΓ2R0−2, if   vΓ>1(4a)
and
mC=12η1−R0−1,  if   vΓ=1(4b)
where R0 = δ′/(μC + μH) and δ′ = n δ mΓ/(μF + n mΓ).

Again, when R0 < 1, the triatomine species cannot invade the environment and when R0 > 1, colonies tend to a non-zero equilibrium given by Eqs. (4a) and (4b).

These equations indicate that at equilibrium, the mean number of triatomine colonies is, as before, dependent on:

  • • the basic reproduction number R0 of the colonies;
  • • the strength of density-dependence η, and now also on;
  • • the degree of heterogeneity vΓ, through which the aggregative distribution of triatomine colonies within houses can be mimicked.

More precisely, Eq. (4a) indicates that the mean number of colonies increases as the degree of heterogeneity σΓ decreases. In fact, no house can harbour more than 1/η colonies, and even houses with very high rates of exposure cannot have a corresponding high number of triatomine colonies. On the contrary, houses with rates of exposure close to zero will harbour a very low number of colonies. Thus, the mean number of colonies decreases as heterogeneity in exposure increases. The maximum number of colonies mCmax = (1/η) (1 – R0−1) is reached when σΓ = 0, and mC ≈ 0 when σΓ → ∞.

2.2 Model for two competing species or populations

Two species (or two independent populations as it seems to be the case for wild and domestic populations of T. infestans) can compete for domiciliation only if they are both able to colonize the same ecotope. Clearly, there exist species of triatomines that cannot invade houses because they cannot encounter their ecological preferences in human dwellings. On the contrary, there may exist situations where continuous exchanges between wild and domestic populations take place, as it is the case, for example with R. prolixus [63]. In the present model, it is assumed that the two “species” can evenly colonize both ecotopes. Therefore, if the two species can mix, they may compete for resources such as blood sources [5] or even space [18,64]. The latter can be indirectly the consequence of house improvement for example, which limit shelters for T. infestans populations.

The model for one single species can be extended to two competing species, considering that the probability that a “fertilized female” starts a colony in one house depends, as before, on the number of colonies of its own species (as in the single species model), but also now on the number of colonies of the other species already established. Therefore, one house i may then be colonized at time t by C1i colonies of species 1 and C2i colonies of species 2 respectively. The “one species model” can then be modified by replacing δ, Ci, Γi, μF, F, μC in the transition rates of the Markov process by δ1, C1i, Γ1i, μF1, F1, μC1 for species 1 and δ2, C2i, Γ2i, μF2, F2, μC2 for species 2. Only the transition rate for increasing the number of colonies by one is modified to take into account species competition, modifying the parameter η for each species (per-colony reduction in probability of starting a new colony when other colonies are already established), by the parameter ηjk (j,k = 1,2) which represents the effect of species j on the probability of establishment of species k.

Therefore, the Markov process for species 1 (and similarly for species 2) is:

  • • the number of fertilized females (species 1) increases by one at a rate δ1∑i=1nC1i;
  • • the number of fertilized females (species 1) decreases by one at a rate (μF1+∑i=1nΓ1i)F1;
  • • the number of colonies of species 1 in one house increases by one at a rate F1Γ1i(1 – η11C1i – η21C2i). Whenever this rate becomes less than 0, it is set to zero. The term (1 – η11C1i – η21C2i) represents the probability of establishment of an “infective female” of species 1 in a house where C1 colonies of species 1 and C2 colonies of species 2 are already present;
  • • the number of colonies (species 1) in one house decreases by one at a rate μC1 C1i;
  • • the number of colonies in a house is set to 0 at a rate μH.

2.2.1 Model when house exposures to infestation by every species are identical

Following the same approach as for the one species model, and first considering that exposure to each species is the same for all houses (i.e., Γ1i = Γ1 and Γ2i = Γ2 for i = 1 to n) and setting dmF1/dt = dmF2/dt = 0 (i.e., life expectancy of “fertilized females” is much smaller than that of a colony), the mean number of colonies for species 1 and species 2 can be modelled as:

dmC1/dt=δ1′mC11−η11mC1−η21mC2−μC1+μHmC1(5)
dmC2/dt=δ2′mC21−η22mC2−η12mC1−μC2+μHmC2(6)
where δ′i = δi Γi n/(μFi + n Γi) i = 1, 2 is the product of the rate at which potentially “infective females” are produced by a colony and the probability that an “infective female” survives to colonize a house.

Theses equations are symmetrical in regard to species 1 or 2, and are generalizations of Eq. (1).

Once again, the behaviour of the system is dependent on the basic reproduction numbers of the two species colonies and the inter- and intra-specific interactions parameters (i.e., the ηij). For colonies of species i, the basic reproduction number is R0i = δ’i/(μCi + μH). As in the “one-species model”, the mean number of colonies of species i will grow if the reproductive number R0i > 1. If reproductive numbers for both species are greater than 1, then two scenarios are possible:

  • • the exclusion of one species by the other and therefore the system approaches a single-species equilibrium, or;
  • • the coexistence of both species in a mixed equilibrium.

As a first approach, the probability of establishment of both species can be considered as dependent on the availability of resources in the house (blood access and space). In other words, the effect of species i (i = 1, 2) on the establishment of species i or species j is the same. Therefore in the model, η11 = η12 and η22 = η21. With this assumption, competitive exclusion and coexistence can be understood by analysis of Eqs. (5) and (6) in the plane (mC1, mC2) (Fig. 1). In this plane, points P1, P2, P3 and P4 are computed as: P1 = (1/η21)(1 – R01−1); P2 = (1/η22)(1 – R02−1); P3 = (1/η11)(1 – R01−1); and P4 = (1/η12)(1 – R02−1).

Fig. 1

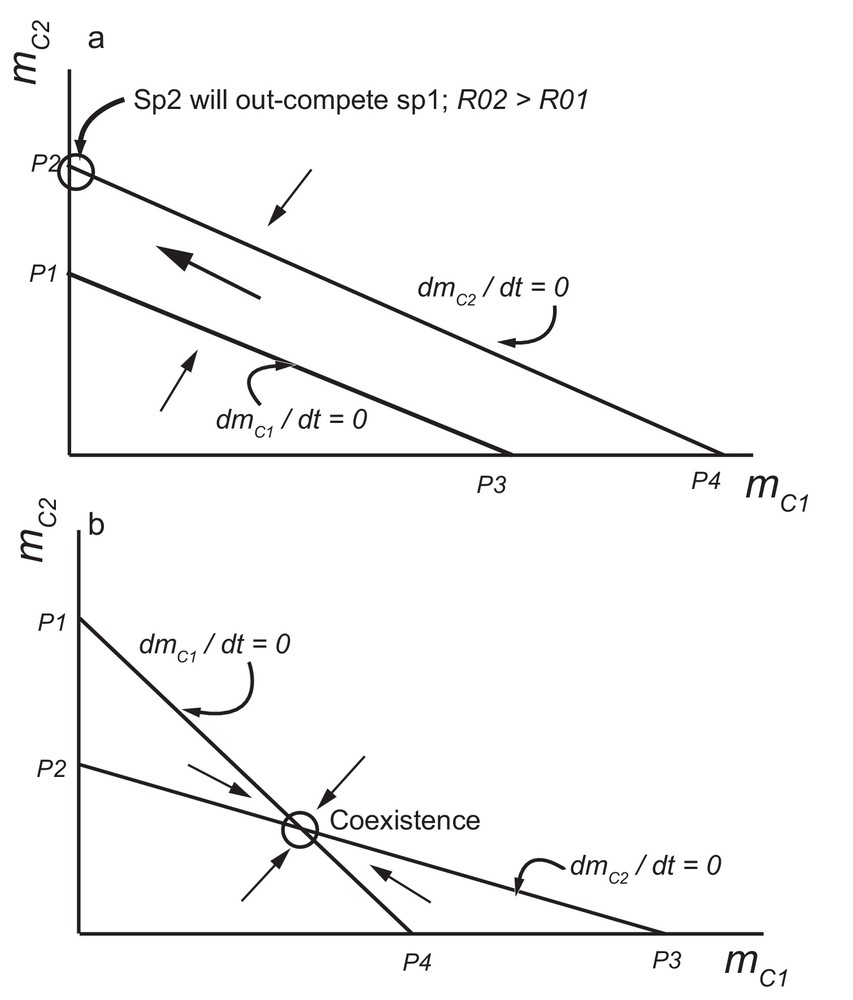
Phase plane analysis based on Eq. (7) for two competing species. The point P1 = (1/η21)(1 – R01−1) correspond to the mean number of colonies of species 2 (C2) when the isoclines dmC2/dt = 0 crosses the Y-axis. Equivalently, P2 = (1/η22)(1 – R02−1); P3 = (1/η11)(1 – R01−1); and P4 = (1/η12)(1 – R02−1) are defined as for P1: a: corresponds to competition between the two species for a limiting resource, with parameters η11 = η12 and η22 = η21 (equality of effects of species 1 (2) on the establishment of its own species or of species 2 (1)). Species 2 will exclude species 1 if R02 > R01 since this implies that P2 > P1; b: the two species will coexist if P1 > P2 and P3 > P4.

P1 corresponds to the mean number of colonies of species 2 (i.e., mC2) when the isocline dmC1/dt = 0 crosses the y-axis (mC2). P2 corresponds to the mean number of colonies of species 2 (i.e., mC2) when the isocline dmC2/dt = 0 crosses the y-axis (mC2). P3 corresponds to the mean number of colonies of species 1 (i.e., mC1) when the isocline dmC1/dt  =  0 crosses the x-axis (mC1). P4 corresponds to the mean number of colonies of species 1 (i.e., mC1) when the isocline dmC2/dt = 0 crosses the x-axis (mC1).

Fig. 1a describes competition of the two species under the assumption η11 = η12 and η22 = η21 (equality of effects of species 1 (2) on the establishment of its own species or of species 2 (1)). The two isoclines dmC2/dt = 0 and dmC1/dt = 0 are parallel and therefore a mixed equilibrium cannot exist. The species with the highest basic reproduction number will exclude the other. In the figure, species 2 will exclude species 1 if R02 > R01, since this implies that P2 > P1. This dynamics of competitive exclusion, based on the relative importance of the R0, has been well described in other biological systems [65,66, for example].

Fig. 1b describes the second scenario, i.e., coexistence. This scenario is possible if species i affects the establishment of its own species more than the other species j. In the model, this implies that η11 > η12 and η22 > η21. In the phase plane analysis, coexistence is achieved when P1 > P2 and P4 > P3.

2.2.2 Model when there is heterogeneity in house exposure to infestation

However, as for the one species model, heterogeneity in house exposure to infestation should be taken into account. Following Bottomley et al. [52], the model can be slightly modified and therefore, the variation with time of the mean number of colonies mci (i = 1,2) is:

dmC1/dt=δ′1mC11−η11σΓ1c1mΓ1+mC1−η21σΓ1c2mΓ1+mC2−μ′c1mC1(7)
dσΓ1C1/dt=δ′1.mc1σ2Γ1mΓ1−1−η11σΓ1C1σ2Γ1+mc1mΓ1−η21σΓ1C2σ2Γ1+mC2mΓ1−μ′C1.σΓ1C1(8)
dσΓ1C2/dt=δ′2.mc2σΓ1Γ2mΓ2−1−η22(σΓ1C2σΓ1Γ2+mc2mΓ2)−η12(σΓ1C1σΓ1Γ2+mC1mΓ2)−μ′C2⋅σΓ1C2(9)
with δ′1=mΓ1n/μF1+mΓ1n   δ1 and μ′Ci=μCi+μH.(i = 1, 2). Similar equations can be derived for mc2, σΓ2C2 and σΓ2C1 of species 2.

As in the single species model, the Eq. (7) describing the colony burden of species 1 in one house (and similarly for species 2) now also depends on the covariance between exposure to house infestation and the burden of colonies in houses (σΓiCj).

Coexistence appears when mutual invadability is possible, i.e., when each species can invade an equilibrium where only the other species is present [67]. Conditions of coexistence can therefore be derived from the model as follows: considering equilibrium e1 and e2 of each species, mutual invadability implies that e1 and e2 must be unstable to permit invasion of one species by the other. At e2, if few “infective females” of species 1 start (few) colonies and as such disturb the equilibrium, invasion will be successful if after some time the mean number of colonies of species 1 (mC1) is growing. In a mathematical sense, dmC1/dt (Eq. (7)) > 0. At the beginning of the process, the number of colonies of the invading species 1 is small as compared to species 2 and therefore, from Eq. (7), the rate of increase of species 1 is:

r1=δ′11−η21σΓ1c2mΓ1+mc2−μ′c1

When r1 > 0, equilibrium (2) is unstable, enabling the establishment of species 1. In the same way, r2 determines the stability of equilibrium 1. The effective reproductive numbers of species 1 and 2 at equilibrium e2 and e1 respectively are: R1 = R01 r1 and R2 = R02 r2, where R0i = (δ′i/μ′c) (i = 1,2). Therefore, the condition for coexistence is R1 > 1 and R2 > 1.

The two effective reproductive numbers R1 and R2 can be reformulated taking into account that at ei (i = 1, 2), the maximum possible value of the mean number of colonies for species i is attained when vГi (the coefficient of variation for the rate of exposure of species i) is zero. Then, this maximum value is mcimax = (1/ηii) (1 – R0i−1). Now, introducing ρ = σΓ1 Γ2/σΓ1 σΓ2 (the correlation between house susceptibility to species 1 and house susceptibility to species 2) and developing r1 and r2, the effective reproductive numbers R1 and R2 at equilibrium e2 and e1, respectively, can be expressed as:

R1=R011−η21ρνΓ1νΓ2mc2max−mc2+mc2(11)
R2=R021−η12ρνΓ2νΓ1mc1max−mc1+mc1(12)

These effective reproductive numbers appear to be the product of the basic reproductive number (R0) and of a term representing the probability of establishment. This probability depends on the burden of resident triatomines in a house (mcmax – mc) and also on the covariance between the burden of the resident species and the susceptibility of the house to the invading species.

These equations indicate that at each respective equilibrium, the effective reproductive numbers are a decreasing function of ρ (the correlation between house susceptibility to species 1 and house susceptibility to species 2). Therefore, intuitively, decreasing the correlation between exposure rates will encourage coexistence.

When heterogeneity is the same for both species (i.e., νГ1 = νГ2 = νГ), then Ris are increasing functions of vГ for ρ < 1 and, therefore, increasing the heterogeneity in house exposure to both species of triatome will facilitate coexistence. From these equations, it may also be the case that if νГ1 >> νГ2 (i.e., heterogeneity in house exposure to species 1 is high compared to heterogeneity in house exposure to the other species), then R1 will be small because νГ1/νГ2 >> 1, and it will be very difficult for species 1 to establish itself. Therefore, coexistence is unlikely to succeed when the degree of heterogeneity in house exposure greatly differs between the two species of triatomine.

3 Results and discussion

A model has been developed to simulate the invasion and colonization of houses by triatomines. The model is a general framework that can describe all situations where one species of triatomine attempts to invade a particular ecotope, or where two species compete to colonize a particular ecotope. The model has been developed in the framework of T. infestans dynamics where individuals may colonize houses, or where two groups (domestic vs. wild) may compete or coexist. In that case, it was assumed that the two groups behaved as two different species, with no interbreeding.

3.1 Single-species invasion and mean number of triatomine colonies per house

3.1.1 Importance of R0 of triatomine colonies

The model captures the observation that the mean number of triatomine colonies in a house is dependent on the basic reproduction number R0 of colonies, the strength of density-dependence processes (which govern, for example, access to blood sources and/or shelter for triatomes), and the degree of heterogeneity (i.e., the degree of exposure of houses to infestation by triatomines), through which the aggregative distribution of triatomine colonies within houses can be mimicked. Introducing mechanisms that can generate aggregation is of crucial importance in T. infestans dynamics, because field observations indicate clearly the existence of such a phenomenon [2,5,54,61,68].

3.1.2 Density-dependence processes and heterogeneity of colonization exposure

The model reveals that if density-dependence processes are strong, it will be difficult for a new colony to start. Triatomine dynamics are dependent on the R0 value, which is:

  • • directly proportionate to the rate at which a colony produces new “fertilized females” and the probability of survival of “fertilized females” of starting a colony, and;
  • • inversely proportionate to the per capita rate of disappearance of a colony.

Thus, demographic parameters are of importance, in particular, as one might expect intuitively, fecundity and survival [69,70]. However, these parameters are offset by density-dependence processes. In the model, the mean number of colonies decreases as heterogeneity in exposure increases. Heterogeneity of exposure can be understood in terms of an infested peridomicile or an infested nearby house or structure which can be a source of infestation for a house. Indeed, as heterogeneity increases, there are more houses with very high and very low rates of exposure. However, since the number of colonies in a house is limited (as assumed in the model), houses with very high rates of exposure cannot have a corresponding high number of colonies. Thus, in total, the mean number of colonies decreases as heterogeneity increases. In the field, T. infestans exhibit such an aggregative distribution with highly infested houses and low infested ones, but always with a limited maximum number of colonies per house. Moreover, when the peridomestic environment is infested (i.e., high exposure rate for the house), and if the “immunity” of the house is low (i.e. if triatomines can find shelter and accessible blood sources inside) [62], the house also hosts domestic populations of triatomines.

A partial concluding remark would be that for a species to invade and colonize an ecotope, the model points out the predominant role of intuitive parameters such as the survival of “infective females”, the survival of a colony, a good contact rate (exposure of that ecotope to triatomines) and a good fecundity of colonies producing “infective females”.

3.2 Competition and coexistence of two species

The model has been extended to two “species” of triatomines (i.e., true species or distinct groups of a same species not interbreeding). The basic hypothesis in the model is that the two “species” have the same ecological needs and therefore, can theoretically share the same niche.

3.2.1 Competitive exclusion

In the model, competitive exclusion or coexistence can be described. They depend on the R0 values of both species colonies and the values of the γii and γij, i.e., the “effects” of each species on the establishment of other individuals of its own species and the establishment of individuals of the other species. Generally, the species with the highest basic reproduction number (R0 for colonies) will exclude the other, but coexistence may also occur in particular conditions (see below). Therefore, because R0s are directly dependent on fecundity and mortality rates, it would be interesting to compare these life traits between the two species.

3.2.2 Coexistence

Coexistence may occur if one species affects the establishment of its own species more than the other species. Indeed, the phase plane analysis of Fig. 1b demonstrated that the two species will coexist if P1 > P2 and P4 > P3 [i.e., γ11 (1 – R02−1) > γ12 (1 – R01−1) and γ22 (1 – R01−1) > γ21 (1 – R02−1)]. The developed formulas indicate that for R01 >> 1 and R02 >> 1, coexistence will exist when interspecific effects are weaker than intra-specific ones. Interspecific effects might be weaker than intra-specific ones if, for example, there is site segregation between the two species within human dwellings. Such situations have been observed for the peridomestic distribution of Triatoma garciabesi and Triatoma guasayana in northwest Argentina [21]. The two species have slightly different ecotopes in the peridomicile and, therefore, coexistence situations have been described. At a larger geographic scale, it has also been described for Rhodnius neglectus and R. nasutus [71] and for Triatoma sordida and T. garciabesi [72]. As for T. infestans however, it does not seem that R0 values are >> 1, and there is no evidence that one group (domestic for example) may affect its proper establishment more than that of the other group if this latter enters the same site (house, in this case). Even if coexistence is possible, a species may still exclude another one if the R0 of the competitively inferior species is sufficiently close to 1. In that case, for various situations where the R0s of the triatomine species are low and species are in low densities, the competitive advantage of one species on the other will vary as R0 values change between situations. Then, it might appear that in one site, one competitor will be present exclusively, while in another site, it will be the other one.

3.2.3 The domestic/wild T. infestans populations

The model clearly shows that the colonization of houses by wild T. infestans populations is unlikely. Personal field observations by the mark–release–recapture technique indicate that T. infestans individuals do not move easily between wild and domestic ecotopes, even if they are close (50 m for example). Therefore, mutual exposure (i.e., exposure of houses to wild triatomines and exposure of sylvatic environment to domestic triatomines) seems to be close to zero while exposure of each type of ecotope by each respective “species” is high and homogenous. If so, the model indicates that (see Eqs. (11) and (12)) it is hard for a wild population of T. infestans for which host heterogeneity in exposure is high (i.e., a low value of exposure for houses and a high value for a wild environment) to invade the already established domestic population where host heterogeneity is relatively low. For example, for the wild species invading a house, Eq. (11) indicates that its reproductive number will be small because νΓ1/νΓ2 >> 1. Invasion will therefore be very hard. Coexistence of wild and domestic populations of T. infestans is possible, but very unlikely to occur. Indeed, the model demonstrates that coexistence may occur if one species affects the establishment of its proper species more than the other species when both share the same site. For wild/domestic populations, this is unlikely as each group seems to have slightly different ecological needs and thus occupies different ecological niches. Genetics studies tend to distinguish two groups which do not mix [40]. However, a recent study indicated that gene flows can exist between the two groups [41], but, as stated, may represent invasion of sylvatic habitats by domestic populations finding here refuges after insecticide sprayings of houses. In that case, there is no competition, but invasion of an empty niche followed by intra-specific movements of dispersion as one might expect. Conversely, if domestic individuals have survived vector control actions and still occupy their houses, the model tends to minimize the possible role of wild population in invading such a “not totally empty” niche.

Wild populations of T. infestans are mostly found close to the domestic/peridomestic environment (Brenière, comm. pers.) and the definition of “wild” is indeed difficult. Blood meal sources may help in defining a “wild” population which then feed on wild animals. However, at present, the wild foci of T. infestans discovered are mostly under human influence, close to human settlings, except maybe in the Chaco region of Bolivia. For most of these foci, then, it seems that the domestic–peridomestic populations of T. infestans have invaded the wild environment and our model can account for such behaviour. If so, a new category of triatomine environment could be proposed: the “PARA-domestic” environment, in addition to the “domestic”, “peridomestic” and “sylvatic” terms yet in use. The para-domestic environment is then under the influence of the domestic–peridomestic environments, with some different characteristics (such as blood sources for triatomines that may be mainly of wild origin) and may permit population to undergo some level of differentiation.

When two groups are considered for coexistence or competition, our model assumption is that they do not interbreed (i.e., are real species). Below this working hypothesis, our model indicates that coexistence of wild and domestic populations of T. infestans is still possible, but very hard to achieve. If so, the colonization of domestic habitats by wild populations is unlikely. However, if further studies indicated that gene flows amongst wild and domestic T. infestans are significant (i.e., that they interbreed and mix), other models should be used to describe their interactions. Models taking into account source-sink dynamics [73] or better, ecological traps [74,75] should then be of great value and would likely explain the present heterogeneities observed amongst wild and close domestic T. infestans populations, such as genes and phenotypic differences or insecticide resistance. If gene flows exist amongst the two groups, then the population is single and the main question would be to identify likely source-sink dynamics where wild groups cannot persist without close domestic ones (and then without threats for vector control) or to identify mechanisms that enable the persistence of wild populations jeopardizing vector control. If so, distant wild populations without any anthropogenic influence should also be found.

Disclosure of interest

The author declares that he has no conflicts of interest concerning this article.

Acknowledgements

The author acknowledges the support of (1) the French “Agence nationale de la recherche” (ANR), under grant ALTERNATIVE (ANR–2010 CESA 018 01) “What alternatives to the chemical control of Triatoma infestans?” and (2) OMS-TDR/IDRC under grant EBS-LAC no A90281 “An eco-bio-social approach to implement integrated techniques to control T. infestans in Bolivian poor communities”; he also thanks Sam Featherston for correcting the English spelling.

Bibliographie

[1] A.M. Jansen; A.L.R. Rodrigues Domestic and wild mammalian reservoirs (J. Telleria; M. Tibayrenc, eds.), American Trypanosomiasis Chagas Disease. One Hundred Years of Research, Elsevier, London, 2010, pp. 248-276

[2] C.J. Schofield Triatominae. Biology and control, Eurocommunica Pub. Bognor Regis, UK, 1994

[3] H. Lent; P. Wygodzinsky Revision of the Triatominae (Hemiptera, Reduviidae), and their significance as vector of Chagas Disease, Bull. Am. Museum Nat. Hist., Volume 163 (1979), pp. 1-520

[4] R. Zeledon Epidemiology, modes of transmission and reservoir hosts of Chagas disease (K. Elliot; M. O’Connor; G.E.W. Wolstenholme, eds.), Trypanosomiasis and Leishmaniasis. Ciba Foundation Symposium 20, Elsevier, North Holland, 1974, pp. 52-85

[5] C.J. Schofield; N.G. Williams; C. Marshall Density-dependent perception of triatominae bugs bites, Ann. Trop. Med. Parasitol., Volume 80 (1986), pp. 351-358

[6] J.P. Dujardin; C.J. Schofield; F. Panzera Les vecteurs de la maladie de Chagas. Recherches taxonomiques, biologiques et génétiques, Acad. R. Sci. Outre-Mer Mem in 8, Volume 24NS (2000), pp. 1-162

[7] C.J. Schofield; L. Diotaiuti; J.P. Dujardin The process of domestication in Triatominae, Mem. Inst. Oswaldo Cruz, Volume 94 (1999), pp. 375-378

[8] S. Gourbière; E. Dumonteil; J.E. Rabinovich; R. Minkoue; F. Menu Demographic and dispersal constraints for domestic infestation by non-domiciliated Chagas disease vectors in the Yucatan Peninsula, Mexico, Am. J. Trop. Med. Hyg., Volume 78 (2008), pp. 133-139

[9] A. Hastings Disturbance, coexistence, history and competition for space, Theor. Pop. Biol., Volume 18 (1980), pp. 363-373

[10] A. Matias; J. De la Riva; E. Martinez; M. Torrez; J.P. Dujardin Domiciliation process of Rhodnius stali (Hemiptera: Reduviidae) in Alto Beni, La Paz, Bolivia, Trop. Med. Int. Health, Volume 8 (2003), pp. 264-268

[11] F. Noireau; M.F. Bosseno; R. Carrasco; J. Telleria; F. Vargas; C. Camacho; N. Yaksic; S. Brenière Sylvatic triatomines (Hemiptera: Reduviidae) in Bolivia: trends toward domesticity and possible infection with Trypanosoma cruzi (Kinetoplastida: Trypanosomatidae), J. Med. Entomol., Volume 32 (1995), pp. 594-598

[12] F. Noireau; M.F. Bosseno; F. Vargas; S. Brenière Apparent trend to domesticity observed in Panstrongylus rufotuberculatus Champion, 1899 (Hemiptera: Reduviidae), Bolivia, Res. Rev. Parasitol., Volume 54 (1994), pp. 263-264

[13] J. Gamboa Dispersion de Rhodnius prolixus en Venezuela, Bol. Inf. Dir. Malar. Sanid. Ambient., Volume 3 (1962), pp. 262-272

[14] M.E. Bar; E.B. Oscherov; M.P. Damborsky Presencia de Triatoma sordida Stal (1859) en ecotopos urbanos de la ciudad de Corrientes, Argentina, Rev. Saude Pub., Volume 27 (1993), pp. 117-122

[15] M.B. Aragão Sôbre a dispersão do Triatoma infestans, Rev. Soc. Bras. Med. Trop., Volume 5 (1971), pp. 183-191

[16] R.E. Gürtler; R.M. Petersen; M.C. Cecere; N.J. Schweigmann; R. Chuit; J.M. Gualtieri; C. Wisnivesky-Colli Chagas disease in north-west Argentina: risk of domestic reinfestation by Triatoma infestans after a single community – wide application of deltamethrin, Trans. R. Soc. Trop. Med. Hyg., Volume 88 (1994), pp. 27-30

[17] J. Costa The synanthropic process of Chagas disease vectors in Brazil, with special attention to Triatoma brasiliensis Neiva, 1911 (Hemiptera, Reduviidae, Triatominae) population, genetical, ecological, and epidemiological aspects, Mem. Inst. Oswaldo Cruz, Volume 94 (1999), pp. 239-241

[18] M.C. Cecere; G.M. Vazquez-Prokopec; R.E. Gürtler; U. Kitron Spatio-temporal analysis of reinfestation by Triatoma infestans (Hemiptera: Reduviidae) following insecticide spraying in a rural community in northern Argentina, Am. J. Trop. Med. Hyg., Volume 71 (2004), pp. 803-810

[19] G.M. Vazquez-Prokopec; M.C. Cecere; D.M. Canale; R.E. Gürtler; U. Kitron Spatiotemporal patterns of reinfestation by Triatoma guasayana (Hemiptera: Reduviidae) in a rural community of northwestern Argentina, J. Med. Entomol., Volume 42 (2005), pp. 573-581

[20] H.N. Espinola; R.J. Tonn; E. Moca; J. Jimenez; T.D. Gonzalez Colonization and competition of Rhodnius prolixus, Rhodnius pictipes, and Triatoma maculata (Hemiptera: Reduviidae, Triatominae) in experimental chicken houses in Venezuela, Bull. Soc. Vector Ecol., Volume 8 (1983), pp. 43-50

[21] D.M. Canale; M.C. Cecere; R. Chuit; R.E. Gürtler Peridomestic distribution of Triatoma garciabesi and Triatoma guasayana in north-west Argentina, Med. Vet. Entomol., Volume 14 (2000), pp. 383-390

[22] G. Harding The competitive exclusion principle, Science, Volume 131 (1960), pp. 1292-1297

[23] M.E. Bar; E.B. Oscherov; M.F. Damborsky; E.A. Porcel; B. Mabel Interacción entre poblaciones de Triatoma infestans y Triatoma sordida, Rev. Saud. Publ., Volume 28 (1994), pp. 59-68

[24] F. Noireau; S. Brenière; L. Cardozo; M.F. Bosseno; F. Vargas; C. Peredo; M. Medinacelli Current spread of Triatoma infestans at the expense of Triatoma sordida in Bolivia, Mem. Inst. Oswaldo Cruz, Volume 91 (1996), pp. 271-272

[25] M.H. Pereira; N.F. Gontijo; A.A. Guarneri; R.V. Maurıcio; M.R.V. Sant’Anna; L. Diotaiuti Competitive displacement in Triatominae: the Triatoma infestans success, Trends Parasitol., Volume 22 (2006), pp. 516-520

[26] R.A. Torrico Hallazgo de Eratyrus mucronatus, infestacion natural de “vinchucas” de cerro y Eutriatoma sordida en Cochabamba, Ann. Lab. Central Cochabamba, Volume 1 (1946), pp. 19-23

[27] M. Borda Contribución al estudió del T. infestans en Bolivia y su distribución geográfica, Rev. Salud Publ. Boliv., Volume 7 (1967), pp. 6-10

[28] J.P. Dujardin; M. Tibayrenc; E. Venegas; P. Maldonado; P. Desjeux; F.J. Ayala Isozyme evidence of lack of speciation between wild and domestic Triatoma infestans (Heteroptera: Reduviidae) in Bolivia, J. Med. Entomol., Volume 24 (1987), pp. 40-45

[29] H. Bermúdez; F. Balderrama; F. Torrico Identification and characterization of wild foci of Triatoma infestans in Central Bolivia, Am. J. Trop. Med. Hyg., Volume 49 (1993), p. 371

[30] M. Rojas; L. Emperaire; R.V. Piccinali; R.E. Gürtler; F. Torrico; A.M. Jansen; F. Noireau Sylvatic Triatoma infestans (Reduviidae, Triatominae) in the Andean valleys of Bolivia, Acta Trop., Volume 102 (2007), pp. 47-54

[31] S. Mazza Comprobaciones de Triatoma platensis, Eutriatoma oswaldoi, Panstrongylus seai, y Psammolestes coreodes en la provincia de Santiago del Esteros, todos ellos sin infestación por S. cruzi. Otros datos sobre infestación esquizotripanósica natural silvestre de Triatoma infestans, Prensa Med. Argent., Volume 30 (1943), pp. 1-23

[32] J.F.R. Berajano Estado selvático de T. infestans y otros aspectos a tener en cuenta para la eliminación de la enfermedad de Chagas, 2nd J. Entomo-epidemiol. Argent., Volume 3 (1967), pp. 171-196

[33] M.J. Viana; D.J. Carpintero Aporte al conocimiento de los triatominos en la Argentina. Primera comunicación, Rev. Museo Argent. Cienc. Nat. Bernardina Rivadavia, Volume 5 (1977), pp. 161-174

[34] L.A. Ceballos; R.V. Piccinali; I. Berkunsky; U. Kitron; R.E. Gürtler First finding of melanic sylvatic Triatoma infestans (Hemiptera: Reduviidae) colonies in the Argentine Chaco, J. Med. Entomol., Volume 46 (2009), pp. 1195-1202

[35] C.J. Velasquez; G. González Aspectos de la enfermedad de Chagas en Paraguay, Rev. Goiana Med., Volume 5 (1959), pp. 357-373

[36] M.P. Barretto; F. Ferrioli Estudos sôbre reservatorios e vetores silvestres do Trypanosoma cruzi. IV. Infecçao natural do Triatoma infestans encontrado em ecotopos silvestres por tripanossomo semelhante ao T. Cruzi, Rev. Inst. Med. Trop. Sao Paulo, Volume 6 (1964), pp. 219-224

[37] A. Bacigalupo; J.A. Segura; A. Garcia; J. Hidalgo; S. Galuppo; P.E. Cattan First finding of Chagas disease vectors associated with wild bushes in the Metropolitan Region of Chile, Rev. Med. Chil., Volume 134 (2006), pp. 1230-1236

[38] A. Bacigalupo; F. Torres-Perez; V. Segovia; A. García; J.P. Correa; L. Moreno; P. Arroyo; P.E. Cattan Sylvatic foci of the Chagas disease vector Triatoma infestans in Chile: description of a new focus and challenges for control programs, Mem Inst. Oswaldo Cruz, Volume 105 (2010), pp. 633-641

[39] F.A. Monteiro; R. Perez; F. Panzera; J.P. Dujardin; C. Galvaõ; D. Rocha; F. Noireau; C. Schofield; C.B. Beard Mitochondrial DNA variation of Triatoma infestans populations and its implication on the specific status of T. melanosoma, Mem. Inst. Oswaldo Cruz, Volume 94 (1999), pp. 229-238

[40] R.V. Piccinali; P.L. Marcet; F. Noireau; U. Kitron; R.E. Gürtler; E.M. Dotson Molecular population genetics and phylogeography of the Chagas disease vector Triatoma infestans in South America, J. Med. Entomol., Volume 46 (2009), pp. 796-809

[41] L.A. Ceballos; R.V. Piccinali; P.L. Marcet; G.M. Vazquez-Prokopec; M.V. Cardinal; J. Judith Schachter-Broide; J.P. Dujardin; E.M. Dotson; U. Kitron; R.E. Gürtler Hidden sylvatic foci of the main vector of Chagas disease Triatoma infestans: Threats to the vector elimination campaign?, PLoS Negl Trop Dis, Volume 5 (2011) no. 10, p. e1365 | DOI

[42] C.J. Ramirez; C.A. Jaramillo; M.P. Delgado; N.A. Pinto; G. Aguilera; F. Guhl Genetic structure of sylvatic, peridomestic and domestic populations of Triatoma dimidiata (Hemiptera: Reduviidae) from an endemic zone of Boyaca, Colombia, Acta Trop., Volume 93 (2005), pp. 23-29

[43] J.P. Dujardin; M. Tibayrenc Etudes isoenzymatiques du vecteur principal de la maladie de Chagas Triatoma infestans (Hemiptera: Reduviidae), Ann. Soc. Belge Med. Trop., Volume 65 (1985), pp. 165-169

[44] J.P. Dujardin; H. Bermúdez; C. Casini; C.J. Schofield; M. Tibayrenc Metric differences between sylvatic and domestic Triatoma infestans (Hemiptera: Reduviidae) in Bolivia, J. Med. Entomol., Volume 34 (1997), pp. 544-551

[45] L. Carlier; M. Muñoz; J.P. Dujardin RAPD Protocol for Triatominae (C.J. Schofield; J.P. Dujardin; J. Jurberg, eds.), Proceedings of the International Workshop on Population Genetics and Control of Triatominae, Santo Domingo de los Colorados, Ecuador, INDRE, Mexico City, 1996, pp. 81-83

[46] J.P. Dujardin; L. Cardozo; C.J. Schofield Genetic analysis of Triatoma infestans following insecticidal control interventions in central Bolivia, Acta Trop., Volume 61 (1996), pp. 263-266

[47] M.C. Cecere; R.E. Gürtler; D. Canale; R. Chuit; J.E. Cohen The role of the peridomiciliary area in the elimination of Triatoma infestans from rural Argentina communities, Pan. Am. J. Publ. Health, Volume 1 (1997), pp. 273-279

[48] L.A. Cebalos; G.M. Vazquez-Prokopec; M.C. Cecere; P.L. Marcet; R.E. Gürtler Feeding rates, nutritional status and flight dispersal potential of peridomestic populations of Triatoma infestans in rural northwestern Argentina, Acta Trop., Volume 95 (2005), pp. 149-159

[49] K. McGwire; E.L. Segura; M. Scavuzzo; A.A. Gomez; M. Lamfri Spatial pattern of reinfestation by Triatoma infestans in Chancani, Argentina, J. Vector Ecol., Volume 31 (2005), pp. 17-28

[50] F. Noireau; M.R. Cortez; F.A. Monteiro; A.M. Jansen; F. Torrico Can wild Triatoma infestans foci in Bolivia jeopardize Chagas disease control efforts?, Trends Parasitol., Volume 21 (2005), pp. 7-10

[51] R.M. Anderson; R.M. May Infectious Diseases of Humans: Dynamics and Control, Oxford University Press, Oxford and New York, 1991

[52] C. Bottomley; V. Isham; M.G. Basañez Population biology of multispecies helminth infection: competition and coexistence, J. Theor. Biol., Volume 244 (2007), pp. 81-95

[53] F. Noireau Wild Triatoma infestans, a potential threat that needs to be monitored, Mem. Inst. Oswaldo Cruz, Volume 104 (2009) no. Suppl. I, pp. 60-64

[54] C.J. Schofield The role of blood intake in density regulation of populations of Triatoma infestans (Klug) (Hemiptera: Reduviidae), Bull. Entomol. Res., Volume 72 (1982), pp. 617-629

[55] J. Piesman; I.A. Sherlock; H.A. Christensen Host availability limits population density of Panstrongylus megistus, Am. J. Trop. Med. Hyg., Volume 32 (1983), pp. 1445-1450

[56] D.E. Gorla; C.J. Schofield Population dynamics of Triatoma infestans under natural climatic conditions in Argentina, Med. Vet. Entomol., Volume 3 (1989), pp. 127-140

[57] R.E. Gürtler; M.C. Cecere; D.N. Rubel; N.J. Schweigmann Determinants of the domiciliary density of Triatoma infestans, vector of Chagas disease, Med. Vet. Entomol., Volume 6 (1992), pp. 75-83

[58] M.C. Cecere; R.E. Gürtler; R. Chuit; J.E. Cohen Factors limiting the domestic density of Triatoma infestans in north-west Argentina: a longitudinal study, Bull. WHO, Volume 76 (1998), pp. 373-384

[59] M.C. Cecere; M. Delmi; D.M. Canale; R.E. Gürlter Effects of refuge availability on the population dynamics of Triatoma infestans in central Argentina, J. Appl. Ecol., Volume 40 (2003), pp. 742-756

[60] J.A.P. Heesterbeek A brief history of R0 and a recipe for its calculation, Acta Biotheret., Volume 50 (2002), pp. 189-204

[61] D. Smith; N. Keyfitz, Mathematical Demography: Selected Papers, Biomathematics, vol. 6, Springer, Berlin, 1977

[62] C.J. Schofield Population dynamics and control of Triatoma infestans, Ann. Soc. Belge Med. Trop., Volume 65 (1985), pp. 149-164

[63] S. Fitzpatrick; M.D. Feliciangeli; M.J. Sanchez-Martin; F.A. Monteiro; M.A. Miles Molecular genetics reveal that sylvatic Rhodnius prolixus do colonize rural houses, PLoS Negl. Trop. Dis., Volume 2 (2008), p. e210 | DOI

[64] J.C. Gomez-Núñez Desarrollo de un Nuevo método para evaluar la infestación intradomiciliaria por Rhodnius prolixus, Acta Cient. Venezol., Volume 16 (1965), pp. 26-31

[65] R. Armstrong; B. MacGehee Competitive exclusion, Am. Nat., Volume 115 (1980), pp. 151-170

[66] O. Diekmann; J.A.P. Heesterbeek Mathematical Epidemiology of Infectious Diseases. Model Building, Analysis and Interpretation, John Wiley & Son, Ltd, NewYork, 2000

[67] V. Hutson; K. Schmitt Permanence and the dynamics of biological systems, Math. Biosci., Volume 111 (1992), pp. 1-71

[68] C.J. Schofield Density regulation of domestic populations of Triatoma infestans in Brazil, Trans. R. Soc. Trop. Med. Hyg., Volume 74 (1980), pp. 761-769

[69] M.B. Castañera; J.P. Aparicio; R.E. Gürtler A stage-structured stochastic model of the population dynamics of Triatoma infestans, the main vector of Chagas disease, Ecol. Model., Volume 162 (2003), pp. 33-53

[70] E.B. Oscherov; M.P. Damborsky; M.E. Bar; G. Avalos; B.M. Alvarez; H. Presman; C. Wisnivesky-Colli Interactions between Triatoma infestans and Triatoma sordida (Hemiptera: Reduviidae) in artificial ecotopes: population growth and age structure, J. Med. Entomol., Volume 38 (2001), pp. 214-217

[71] T.A. Batista; R. Gurgel-Gonçalves Ecological niche modelling and differentiation between Rhodnius neglectus Lent, 1954 and Rhodnius nasutus Stål, 1859 (Hemiptera: Reduviidae: Triatominae) in Brazil, Mem. Inst. Oswaldo Cruz, Volume 104 (2009) no. 8, pp. 1165-1170

[72] J.B. Gurgel-Gonçalves; C. Ferreira; A.F. Rosa; M.E. Bar; C. Galvao Geometric morphometrics and ecological niche modelling for delimitation of near-sibling triatomine species, Med. Vet. Entomol., Volume 25 (2011), pp. 84-93

[73] H.R. Pulliam Sources, sinks, and population regulation, Am. Nat., Volume 132 (1988), pp. 652-661

[74] B.A. Robertson; R.L. Hutto A framework for understanding ecological traps and an evaluation of existing evidence, Ecology, Volume 87 (2006), pp. 1075-1085

[75] M.A. Schlaepfer; M.C. Runge; P.W. Sherman Ecological and evolutionary traps, Trends Ecol. Evol., Volume 17 (2002), pp. 474-480

Commentaires - Politique

Ces articles pourraient vous intéresser

Analysis of spermiogenesis like a tool in the study of the triatomines of the Brasiliensis subcomplex

Kaio Cesar Chaboli Alevi; Priscila Pasqüetto Mendonça; Nathália Paiva Pereira; ...

C. R. Biol (2013)

Digestive cells in the midgut of Triatoma vitticeps (Stal, 1859) in different starvation periods

Lamara Laguardia Valente Rocha; Clóvis Andrade Neves; José Cola Zanuncio; ...

C. R. Biol (2010)