Sur l’extinction des populations avec plusieurs types dans un environnement aléatoire

Nicolas Bacaër

doi:10.1016/j.crvi.2018.01.009

Résumés

Français
Anglais

On étudie le taux d’extinction d’une population modélisée par un processus de branchement à plusieurs types en temps continu dans un environnement aléatoire. Des calculs numériques dans un exemple particulier inspiré d’un modèle épidémique suggèrent une formule explicite pour ce taux d’extinction, mais seulement pour certaines valeurs des paramètres.

This study focuses on the extinction rate of a population that follows a continuous-time multi-type branching process in a random environment. Numerical computations in a particular example inspired by an epidemic model suggest an explicit formula for this extinction rate, but only for certain parameter values.

1 Introduction

Supposons que l’environnement, noté k, oscille de manière aléatoire entre un nombre fini d’états 1, …, K selon une chaîne de Markov en temps continu. Pour k≠ ℓ, la probabilité pour que l’environnement bascule de ℓ vers k est Q_k,ℓ dt pendant chaque intervalle de temps infinitésimal dt, avec Q_k,ℓ ≥ 0. Introduisons la matrice $Q = (Q_{k, ℓ})$ telle que Q_ℓ,ℓ = − ∑_k≠ℓQ_k,ℓ pour tout ℓ ; c’est la matrice transposée du générateur infinitésimal de la chaîne [1].

Considérons, par ailleurs, une population d’individus qui peuvent être de I types différents et qui évoluent dans l’environnement aléatoire que l’on vient de décrire. Supposons qu’il y ait au moins un individu dans la population au temps initial t = 0. Un individu de type i dans l’environnement k a une probabilité $c_{i}^{(k)} d t$ de subir quelque événement pendant chaque intervalle de temps infinitésimal dt, avec $c_{i}^{(k)} > 0 .$ Si l’événement se produit, on trouve à la place de cet individu n_j individus de type j, pour 1 ≤ j ≤ I, avec une probabilité $π_{i}^{(k)} (n_{1}, \dots, n_{I}) .$ Autrement dit, entre deux sauts de l’environnement, chaque individu a un temps de vie aléatoire qui suit une loi exponentielle de paramètre $c_{i}^{(k)};$ au bout de ce temps, la loi de reproduction est donnée par $(π_{i}^{(k)} (n_{1}, \dots, n_{I})),$ indépendamment des autres individus. Il s’agit donc d’un processus de branchement en temps continu à plusieurs types [2].

Notons p^(k) (t, n₁, …, n_I) la probabilité que la population soit composée de n_i individus de type i pour 1 ≤ i ≤ I et que l’environnement soit k au temps t. Ordonnons les états (k, n₁, …, n_I) du système par groupes selon le nombre total d’individus n = n₁ + … + n_I, de manière à avoir un vecteur colonne infini p(t). On observe dans la section 2 que p(t) est solution d’un système linéaire d’équations différentielles $\frac{d p}{d t} = Z p (t),$ où Z est une matrice infinie de la forme

(\begin{array}{c} Z_{0,0} & Z_{0,1} & 0 & \dots & 0 & \dots \\ 0 & Z_{1,1} & Z_{1,2} & ⋱ & ⋮ \\ 0 & Z_{2,1} & Z_{2,2} & ⋱ & 0 \\ ⋮ & ⋮ & ⋮ & ⋱ & Z_{n - 1, n} & ⋱ \\ 0 & Z_{n, 1} & Z_{n, 2} & ⋱ & Z_{n, n} & ⋱ \\ ⋮ & ⋮ & ⋮ & ⋱ & ⋮ & ⋱ \end{array})

(1)

et les blocs Z_m,n sont eux-mêmes des matrices de tailles différentes. On voit sur la structure de cette matrice que, lorsqu’un individu subit un événement, le nombre total d’individus ne peut décroître que d’une unité, mais qu’il peut croître de plusieurs unités. De plus, la classe des états avec zéro individu est absorbante : elle correspond à l’extinction de la population. On se restreint dans la suite au cas sous-critique où la population s’éteint presque sûrement ; un résultat de [3] relatif aux modèles en temps discret permet de déterminer à quelle condition il y a extinction dans notre modèle en temps continu. L’objectif est alors d’essayer de déterminer le taux d’extinction de la population.

Les articles [4–6] ont calculé ce taux d’extinction dans un modèle analogue mais en temps discret, où les environnements successifs sont aléatoires, indépendants et identiquement distribués. Les deux premières références donnent une formule simple pour le taux d’extinction, mais avec des conditions assez restrictives sur les différents environnements (les matrices moyennes doivent avoir un vecteur propre commun). Vatutin et Wachtel [6] donnent une formule moins explicite, mais avec des hypothèses plus générales, en restant néanmoins dans le cas fortement sous-critique.

Le taux d’extinction dépend des propriétés spectrales de la sous-matrice infinie extraite de (1) avec Z_1,1 dans son coin supérieur gauche. Notons

M_{i, j}^{(k)} = c_{j}^{(k)} (\sum_{n_{1}, \dots, n_{I} \geq 0} n_{i} π_{j}^{(k)} (n_{1}, \dots, n_{I}) - δ_{i, j}),

(2)

où δ_i,j = 1 si i = j, δ_i,j = 0 sinon. Soit M^(k) la matrice $(M_{i, j}^{(k)})$ . Notons diag(M⁽¹⁾, …, M^(K)) la matrice diagonale par blocs avec M⁽¹⁾, …, M^(K) sur la diagonale. Notons ω₁ la borne spectrale, c’est-à-dire la valeur propre de plus grande partie réelle, de la matrice

W^{[1]} = Q \otimes I + diag (M^{(1)}, \dots, M^{(K)}),

où I est la matrice identité d’ordre I et Q ⊗ I est le produit tensoriel des deux matrices. Les calculs de la section 2 suggèrent que ω₁ serait le taux d’extinction de la population pour certaines valeurs des paramètres. Cela reste néanmoins une conjecture.

Dans la section 3, on considère tout d’abord le cas particulier des processus de naissance et de mort à plusieurs types, puis on se restreint aux populations avec seulement deux types d’individus. On présente un exemple où l’on compare la valeur numérique de ω₁ avec la limite α₁ quand n → ∞ de la borne spectrale de la sous-matrice finie de (1) avec Z_1,1 dans son coin supérieur gauche et Z_n,n dans son coin inférieur droit. Les résultats numériques suggèrent l’égalité de ces deux nombres pour certaines valeurs des paramètres, mais pas pour toutes, comme d’ailleurs dans le cas où il n’y a qu’un seul type d’invidu [7]. On conjecture par ailleurs que la limite α₁ est bien le taux d’extinction de la population, défini, par exemple, comme étant la limite

\lim_{t \to + \infty} \frac{1}{t} \log p^{(k)} (t, n_{1}, \dots, n_{I}) .

D’après [8] (section 4.5), cette limite (appelée paramètre de Kingman) ne dépend ni de k, ni de (n₁, …, n_I) pourvu que n₁ + … + n_I ≥ 1, ni des conditions initiales (environnement et nombre d’individus des différents types).

2 Cas général

2.1 Le système d’équations différentielles

Notons n = (n₁, …, n_I) et 0 = (0, …, 0) le vecteur dont les I composantes sont égales à 0. Convenons que n ≥ 0 signifie que n_i ≥ 0 pour tout i. Notons u_j = (0, …, 0, 1, 0, …, 0) le vecteur avec le 1 en j^e position. Les hypothèses du modèle impliquent que

\frac{d p^{(k)}}{d t} (t, n) = - \sum_{j = 1}^{I} n_{j} c_{j}^{(k)} p^{(k)} (t, n) + \sum_{ℓ = 1}^{K} Q_{k, ℓ} p^{(ℓ)} (t, n)

+ \sum_{j = 1}^{I} \sum_{r + s = n} (r_{j} + 1) c_{j}^{(k)} p^{(k)} (t, r + u_{j}) π_{j}^{(k)} (s),

(3)

où r = (r₁, …, r_I) ≥ 0 et s = (s₁,… s_I) ≥ 0 sont des vecteurs de nombres entiers positifs ou nuls. En effet, s’il y a n individus dans l’environnement k au temps t, alors il y a pendant chaque intervalle de temps infinitésimal dt une probabilité $n_{j} c_{j}^{(k)} d t$ qu’un événement survienne pour l’un des n_j individus de type j, et aussi une probabilité −Q_k,k dt que l’environnement bascule dans un autre état. Si, en revanche, il y a n individus dans un environnement ℓ ≠ k, il y a une probabilité Q_k,ℓ dt que l’environnement bascule vers l’état k. Enfin, s’il y a r + u_j individus dans l’environnement k, un événement survient chez l’un des (r_j + 1) individus de type j avec une probabilité $(r_{j} + 1) c_{j}^{(k)} d t,$ et l’on retrouve à sa place s individus des différents types avec une probabilité $π_{j}^{(k)} (s);$ si r + s = n, on se retrouve avec n_i individus de type i pour tout i. Le système (3) a bien la structure (1).

2.2 Le système d’équations aux dérivées partielles

Notons 1 = (1, …, 1) et x = (x₁, …, x_I). Introduisons les fonctions génératrices

f^{(k)} (t, x) = \sum_{n \geq 0} p^{(k)} (t, n) x_{1}^{n_{1}} \dots x_{I}^{n_{I}},

où les x_i sont des nombres complexes et les indices n_i des entiers. Puisque $\sum_{k} \sum_{n_{i} \geq 0} p^{(k)} (t, n_{1}, \dots, n_{I}) = 1$ , le domaine de convergence de ces séries inclut l’ensemble $\{(x_{1}, \dots, x_{I}); |x_{i}| < 1 pour tout i\}$ [9] (chapitre IV). Notons

g_{j}^{(k)} (x) = \sum_{n \geq 0} π_{j}^{(k)} (n) x_{1}^{n_{1}} \dots x_{I}^{n_{I}} .

On a $g_{j}^{(k)} (1) = 1 .$ Alors

\frac{\partial f^{(k)}}{\partial x_{j}} (t, x) = \sum_{r \geq 0} (r_{j} + 1) p^{(k)} (t, r + u_{j}) x_{1}^{r_{1}} \dots x_{I}^{r_{I}} .

\frac{\partial f^{(k)}}{\partial t} (t, x) = \sum_{n \geq 0} \frac{d p^{(k)}}{d t} (t, n) x_{1}^{n_{1}} \dots x_{I}^{n_{I}} .

Avec le système (3), on obtient

\frac{\partial f^{(k)}}{\partial t} = \sum_{ℓ = 1}^{K} Q_{k, ℓ} f^{(ℓ)} + \sum_{j = 1}^{I} c_{j}^{(k)} (g_{j}^{(k)} (x_{1}, \dots, x_{I}) - x_{j}) \frac{\partial f^{(k)}}{\partial x_{j}} .

(4)

C’est une généralisation du système (3) dans [7], qui correspond à I = 1.

2.3 Le vecteur des espérances

Introduisons les espérances

E_{i}^{(k)} (t) = \frac{\partial f^{(k)}}{\partial x_{i}} (t, 1) = \sum_{n \geq 0} n_{i} p^{(k)} (t, n) .

Comme $g_{j}^{(k)} (1) = 1$ , on déduit de l’équation (4), en prenant sa dérivée partielle par rapport à x_i puis en prenant x = 1, que

\frac{d E_{i}^{(k)}}{d t} = \sum_{ℓ = 1}^{K} Q_{k, ℓ} E_{i}^{(ℓ)} + \sum_{j = 1}^{I} M_{i, j}^{(k)} E_{j}^{(k)},

où

M_{i, j}^{(k)} = c_{j}^{(k)} (\frac{\partial g_{j}^{(k)}}{\partial x_{i}} (1) - δ_{i, j})

(5)

comme dans l’introduction, et on suppose que

M_{i, j}^{(k)} < + \infty

pour toutes les valeurs des indices. C’est la généralisation de l’équation (4) de [7], qui correspondait à I = 1. Soit E le vecteur colonne

(E_{1}^{(1)}, \dots, E_{I}^{(1)}, \dots, E_{1}^{(K)}, \dots, E_{I}^{(K)}) .

Alors $\frac{d E}{d t} = W^{[1]} E,$ avec

W^{[1]} = (\begin{array}{c} Q_{1,1} I + M^{(1)} & Q_{1,2} I & \dots & Q_{1, K} I \\ Q_{2,1} I & Q_{2,2} I + M^{(2)} & ⋱ & ⋮ \\ ⋮ & ⋱ & ⋱ & Q_{K - 1, K} I \\ Q_{K, 1} I & \dots & Q_{K, K - 1} I & Q_{K, K} I + M^{(K)} \end{array})

comme dans l’introduction. Rappelons que ω₁ est la borne spectrale de cette matrice, c’est-à-dire la valeur propre de plus grande partie réelle. Comme Q_k,ℓ ≥ 0 pour k≠ ℓ et $M_{i, j}^{(k)} \geq 0$ pour i ≠ j, on remarque, en effet, que W^[1] est une matrice dont les coefficients en dehors de la diagonale sont tous ≥ 0. D’après un corollaire du théorème de Perron et Frobenius, W^[1] a bien une valeur propre réelle dominante, c’est-à-dire supérieure à la partie réelle de toutes les autres valeurs propres.

Supposons, pour simplifier, que la matrice Q soit irréductible : pour tout k ≠ ℓ , il existe une suite (k₀, …, k_N) telle que k₀ = k, k_N = ℓ , et $Q_{k_{n}, k_{n + 1}} > 0$ pour tout n. Supposons de plus que les matrices M^(k) soient toutes irréductibles. Alors, la matrice $W^{[1]}$ est elle aussi irréductible. Puisque E(0) ≠ 0, on a

\frac{1}{t} \log ∥E (t)∥ \underset{t \to + \infty}{\to} ω_{1}

et ω₁ est le taux de croissance ou de décroissance du vecteur des espérances E(t).

2.4 Le cas sous-critique

Considérons une suite fixée d’environnements engendrés par la chaîne de Markov en temps continu de matrice Q : l’environnement est d’abord k₀ pour t₀ < t < t₁ avec t₀ = 0, puis k₁ pour t₁ < t < t₂, etc. Entre deux sauts de l’environnement, la population évolue selon un processus de branchement en temps continu à plusieurs types dans un environnement constant. À notre processus en temps continu, on peut donc associer un processus en temps discret qui ne considère que l’état de la population aux instants t_n où l’environnement bascule. Les deux processus sont simultanément surcritiques, critiques ou sous-critiques.

Le vecteur des espérances e(t)=(e₁(t), …, e_I(t)) des populations de chaque type, sachant que l’environnement est k_n pour t_n < t < t_n+1, est solution de $\frac{d e}{d t} = M^{(k_{n})} e (t)$ pendant cet intervalle de temps. Notons τ_n = t_n+1 − t_n. Alors, $e (t_{n + 1}) = \exp (τ_{n} M^{(k_{n})}) e (t_{n}) .$ D’après [3] (section∼4), la suite

\frac{1}{n} \log ∥\exp (τ_{n} M^{(k_{n})}) \dots \exp (τ_{0} M^{(k_{0})})∥

(6)

converge presque sûrement vers une limite indépendante de la suite particulière d’environnements ; de plus, la population dans le processus en temps discret s’éteint presque sûrement dans le cas sous-critique où λ₁ < 0 et ne s’éteint pas avec une probabilité > 0 lorsque λ₁ > 0. Ainsi, le processus en temps continu dans notre modèle de départ est aussi sous-critique quand λ₁ < 0. Si T est la limite de t_n/n quand n → +∞, on remarque que λ₁/T est l’exposant de Lyapounoff du système différentiel pour e(t).

Notons enfin que la borne spectrale ω₁ de la section précédente peut être positive alors que λ₁ est négatif ; c’est déjà possible lorsqu’il n’y a qu’un seul type d’individus [10].

2.5 Les valeurs propres dans le cas régulier

Cherchons des solutions du système (4) de la forme $f^{(k)} (t, x) = e^{ω t} F^{(k)} (x)$ avec des fonctions F^(k) (x) qui ne sont pas toutes identiquement nulles. Ainsi,

ω F^{(k)} (x) = \sum_{ℓ = 1}^{K} Q_{k, ℓ} F^{(ℓ)} (x) + \sum_{j = 1}^{I} c_{j}^{(k)} (g_{j}^{(k)} (x) - x_{j}) \frac{\partial F^{(k)}}{\partial x_{j}} (x) .

(7)

En prenant x = 1, on voit que

ω F^{(k)} (1) = \sum_{ℓ = 1}^{K} Q_{k, ℓ} F^{(ℓ)} (1) .

Ou bien F^(k) (1) = 0 pour tout k, ou bien ω est une valeur propre de la matrice Q.

Si les fonctions F^(k) (x) sont analytiques dans un voisinage de x = 1 (c’est le cas régulier), alors on voit, comme dans la section 2.3, en dérivant l’équation (7) par rapport à x_i et en prenant x = 1, que

ω ϕ_{i}^{(k)} = \sum_{ℓ = 1}^{K} Q_{k, ℓ} ϕ_{i}^{(ℓ)} + \sum_{j = 1}^{I} M_{i, j}^{(k)} ϕ_{j}^{(k)},

où $ϕ_{i}^{(k)} = \frac{\partial F^{(k)}}{\partial x_{i}} (1) .$ Donc ou bien $\frac{\partial F^{(k)}}{\partial x_{i}} (1) = 0$ pour tout i et tout k, ou bien ω est une valeur propre de $W^{[1]}$ .

Pour tout entier n ≥ 1, pour toute suite d’indices $(i_{1}, \dots, i_{n}) \in {\{1, \dots, I\}}^{n},$ notons

ϕ_{i_{1}, i_{2}, \dots, i_{n}}^{(k)} = \frac{\partial^{n} F^{(k)}}{\partial x_{i_{1}} \partial x_{i_{2}} \dots \partial x_{i_{n}}} (1) .

Soit n ≥ 2. Supposons que $ϕ_{i_{1}, i_{2}, \dots, i_{m}}^{(k)} = 0$ pour tous les indices 1 ≤ k ≤ K, 1 ≤ m < n et $(i_{1}, \dots, i_{m}) \in {\{1, \dots, I\}}^{m} .$ Dérivons l’équation (7) par rapport à $x_{i_{1}}, \dots, x_{i_{n}}$ et prenons x = 1. À cause de l’hypothèse sur les dérivées partielles d’ordre < n et puisque $g_{j}^{(k)} (1) = 1,$ il ne reste que les termes suivants :

ω ϕ_{i_{1}, i_{2}, \dots, i_{n}}^{(k)} = \sum_{j = 1}^{I} [M_{i_{1}, j}^{(k)} ϕ_{j, i_{2}, \dots, i_{n}}^{(k)} + \dots + M_{i_{n}, j}^{(k)} ϕ_{i_{1}, i_{2}, \dots, j}^{(k)}] + \sum_{ℓ = 1}^{K} Q_{k, ℓ} ϕ_{i_{1}, i_{2}, \dots, i_{n}}^{(ℓ)}

(8)

pour tout $(i_{1}, \dots, i_{n}) \in {\{1, \dots, I\}}^{n}$ et 1 ≤ k ≤ K. Donc, ou bien $ϕ_{i_{1}, i_{2}, \dots, i_{n}}^{(k)} = 0$ pour tous les indices i₁, …, i_n et k, ou bien ω est une valeur propre de la matrice carrée $W^{[n]}$ d’ordre K × Iⁿ définie par les équations linéaires (8).

En résumé, on conclut que si les fonctions propres F^(k) (x) associées à la valeur propre ω sont analytiques dans un voisinage de x = 1, alors, ou bien ω est une valeur propre de la matrice Q, ou bien ω est une valeur propre d’une matrice $W^{[n]}$ pour un certain n ≥ 1. En effet, si tel n’était pas le cas, on aurait F^(k) (1) = 0 et $ϕ_{i}^{(k)} = 0$ pour tous les indices. D’après ce qui précède, on en déduirait par récurrence que $ϕ_{i_{1}, \dots, i_{n}}^{(k)} = 0$ pour tous les indices avec n ≥ 2. D’après le principe du prolongement analytique [9] (chapitre∼IV), l’application F(x) serait identiquement nulle, ce qui n’est pas possible.

Remarque. Pour I = 1, on note plus simplement

ψ_{n}^{(k)} = \frac{\partial^{n} F^{(k)}}{\partial x_{1}^{n}} (1), M^{(k)} = c_{1}^{(k)} (\frac{\partial g_{1}^{(k)}}{\partial x_{1}} (1) - 1) .

L’équation (8) s’écrit alors

ω ψ_{n}^{(k)} = \sum_{ℓ = 1}^{K} Q_{k, ℓ} ψ_{n}^{(ℓ)} + n M^{(k)} ψ_{n}^{(k)} .

On en déduit que ω est une valeur propre de la matrice Q ou d’une matrice $Q + n d i a g (M^{(1)}, \dots, M^{(K)})$ avec n ≥ 1. La section 4.2 de [11] avait déjà remarqué ce cas particulier pour les processus linéaires de naissances et de mort à un seul type.

2.6 La matrice tronquée

Notons Y_n la sous-matrice finie de la matrice (1) avec Z_1,1 dans son coin supérieur gauche et Z_n,n dans son coin inférieur droit. Sa borne spectrale μ_n est telle que μ_n ≤μ_n+1 ≤ 0. En effet, comme dans la proposition 2 de [11], notons 1 le vecteur ligne (1, …, 1) de taille convenable. Alors 1Y_n ≤ 0 = 0 · 1. Donc μ_n ≤ 0 (voir par exemple [12] [théorème 30.1]). Soit v_n ≠ 0 un vecteur colonne tel que Y_nv_n = μ_nv_n et v_n ≥ 0. Soit w_n le vecteur colonne (v_n, 0). Alors Y_n+1w_n ≥ μ_nw_n puisque les matrices Z_n+1,1, …, Z_n+1,n sont toutes à coefficients ≥ 0. On en déduit que μ_n+1 ≥ μ_n d’après [12] (théorème 30.3). De ceci, il résulte aussi que la limite α₁ de μ_n quand n → ∞ existe bien.

3 Cas particuliers

3.1 Les processus de naissance et de mort

Pour chaque environnement k, on se donne comme dans [13] trois matrices de même taille : une matrice de naissance $A^{(k)} = (A_{i, j}^{(k)})$ à coefficients ≥ 0, une matrice de transfert $T^{(k)} = (T_{i, j}^{(k)})$ telle que $\sum_{i} T_{i, j}^{(k)} = 0$ pour tout j et $T_{i, j}^{(k)} \leq 0$ pour tout i ≠ j, et une matrice diagonale de sortie $S^{(k)} = (S_{i, j}^{(k)})$ avec $S_{j, j}^{(k)} \geq 0$ pour tout j. Autrement dit, chaque individu de type j qui se trouve dans l’environnement k a, pendant chaque intervalle de temps infinitésimal dt, une probabilité $A_{i, j}^{(k)} d t$ de donner naissance à un nouvel individu de type i, une probabilité $- T_{i, j}^{(k)} d t$ de se transformer en un individu de type i pour i ≠ j, et une probabilité $S_{j, j}^{(k)} d t$ de mourir ou de sortir de la population. Ainsi,

c_{j}^{(k)} = \sum_{i} A_{i, j}^{(k)} + T_{j, j}^{(k)} + S_{j, j}^{(k)}

g_{j}^{(k)} (x_{1}, \dots, x_{I}) = [\sum_{i} A_{i, j}^{(k)} x_{i} x_{j} + S_{j, j}^{(k)} - \sum_{i \neq j} T_{i, j}^{(k)} x_{i}] / c_{j}^{(k)} .

Posons $B_{i, j}^{(k)} = T_{i, j}^{(k)} + S_{i, j}^{(k)}$ . Alors, l’équation (4) s’écrit

\frac{\partial f^{(k)}}{\partial t} = \sum_{ℓ = 1}^{K} Q_{k, ℓ} f^{(ℓ)} + \sum_{i = 1}^{I} \sum_{j = 1}^{I} [x_{i} - 1] [A_{i, j}^{(k)} x_{j} - B_{i, j}^{(k)}] \frac{\partial f^{(k)}}{\partial x_{j}},

(9)

qui est la généralisation de l’équation présentée dans la section 2 de [14] au cas d’un environnement aléatoire, ou encore la généralisation de l’équation (5) de [11] au cas de plusieurs types. En distinguant le cas où i = j de celui où i ≠ j, on montre facilement que $M_{i, j}^{(k)}$ , défini par l’équation (5), est donné par $M_{i, j}^{(k)} = A_{i, j}^{(k)} - B_{i, j}^{(k)} .$ La population est sous-critique lorsque la limite λ₁ de (6) est < 0.

3.2 Deux types d’individus

Prenons le cas d’un processus de naissance et de mort où il n’y a que I = 2 types, ce qui permet d’ordonner facilement les différents états de la population. Introduisons les matrices diagonales

C_{j} = d i a g (c_{j}^{(1)}, \dots, c_{j}^{(K)}), A_{i, j} = d i a g (A_{i, j}^{(1)}, \dots, A_{i, j}^{(K)}),

T_{i, j} = d i a g (T_{i, j}^{(1)}, \dots, T_{i, j}^{(K)}), S_{j, j} = d i a g (S_{j, j}^{(1)}, \dots, S_{j, j}^{(K)}) .

Ordonnons les fonctions p^(k) (t,n₁,n₂) selon le nombre total n₁ + n₂ d’individus, et ce nombre fixé, par le nombre d’individus de type 1 puis par l’environnement. Avec cet ordre, on considère le vecteur colonne infini

\begin{array}{l} p (t) = & (p^{(1)} (t, 0,0), \dots, p^{(K)} (t, 0,0), \\ p^{(1)} (t, 1,0), \dots, p^{(K)} (t, 1,0), \\ p^{(1)} (t, 0,1), \dots, p^{(K)} (t, 0,1), \\ p^{(1)} (t, 2,0), \dots, p^{(K)} (t, 2,0), \\ p^{(1)} (t, 1,1), \dots, p^{(K)} (t, 1,1), \\ p^{(1)} (t, 0,2), \dots, p^{(K)} (t, 0,2), \dots) . \end{array}

Alors le système (3) s’écrit aussi dp/dt = Zp(t), où :

–Z est la matrice infinie tridiagonale par blocs

(\begin{array}{c} Z_{0,0} & Z_{0,1} & 0 & \dots & 0 & \dots \\ 0 & Z_{1,1} & Z_{1,2} & ⋱ & ⋮ \\ 0 & Z_{2,1} & Z_{2,2} & ⋱ & 0 \\ ⋮ & ⋱ & ⋱ & ⋱ & Z_{n - 1, n} & ⋱ \\ 0 & \dots & 0 & Z_{n, n - 1} & Z_{n, n} & ⋱ \\ ⋮ & ⋱ & ⋱ & ⋱ \end{array})

et les zéros sont des matrices nulles de la taille qui convient ;

–Z_n,n est la matrice carrée d’ordre (n + 1)K tridiagonale par blocs qui décrit les transitions lorsque le nombre total d’individus est n et lorsque celui-ci ne change pas (saut de l’environnement ou individu transféré dans l’autre des deux types)

(\begin{array}{c} Q - n C_{1} & - T_{1,2} & 0 & \dots & 0 \\ - n T_{2,1} & Q - (n - 1) C_{1} - C_{2} & - 2 T_{1,2} & \dots & 0 \\ 0 & - (n - 1) T_{2,1} & Q - (n - 2) C_{1} - 2 C_{2} & ⋱ & ⋮ \\ ⋮ & ⋮ & ⋱ & ⋱ & - n T_{1,2} \\ 0 & 0 & \dots & - T_{2,1} & Q - n C_{2} \end{array})

et Z_0,0 = Q ;

–Z_n−1,n est la matrice rectangulaire à nK lignes et (n + 1)K colonnes qui n’a que deux bandes de blocs non nuls et qui décrit les transitions où le nombre total d’individus passe de n à n − 1 (morts ou sorties)

(\begin{array}{c} n S_{1,1} & S_{2,2} & 0 & \dots & 0 \\ 0 & (n - 1) S_{1,1} & 2 S_{2,2} & ⋱ & ⋮ \\ ⋮ & ⋱ & ⋱ & ⋱ & 0 \\ 0 & \dots & 0 & S_{1,1} & n S_{2,2} \end{array});

–Z_n+1,n est la matrice rectangulaire à (n + 2)K lignes et (n + 1)K colonnes, également avec deux bandes de blocs non nuls, qui décrit les transitions où le nombre total d’individus passe de n à n + 1 (naissances)

(\begin{array}{c} n A_{1,1} & 0 & 0 & \dots & 0 \\ n A_{2,1} & (n - 1) A_{1,1} + A_{1,2} & 0 & ⋮ \\ 0 & (n - 1) A_{2,1} + A_{2,2} & ⋱ & ⋮ \\ ⋮ & ⋱ & ⋮ \\ ⋮ & ⋱ & A_{1,1} + (n - 1) A_{1,2} & 0 \\ ⋮ & ⋱ & A_{2,1} + (n - 1) A_{2,2} & n A_{1,2} \\ 0 & \dots & \dots & 0 & n A_{2,2} \end{array}) .

3.3 Exemple

Comme exemple de processus avec deux types d’individus, considérons le cas du modèle épidémique linéaire de [14], où les individus de type 1 sont les personnes infectées, mais pas encore infectieuses (c’est-à-dire dans la phase latente), et les individus de type 2, autrement dit ceux qui sont infectieux. Le cas linéaire sous-critique correspond par exemple à la situation où la maladie est importée dans un environnement aléatoire défavorable à sa propagation. Alors

T^{(k)} = (\begin{array}{c} τ & 0 \\ - τ & 0 \end{array}), A^{(k)} = (\begin{array}{c} 0 & β^{(k)} \\ 0 & 0 \end{array}), S^{(k)} = (\begin{array}{c} 0 & 0 \\ 0 & γ \end{array}) .

Le paramètre τ est le taux auquel les personnes dans la phase latente deviennent infectieuses, indépendamment de l’environnement. Le paramètre β^(k) est le taux selon lequel les personnes infectieuses infectent de nouvelles personnes au début d’une épidémie ; il dépend de l’environnement à cause de l’influence du climat sur la probabilité de transmission. Le paramètre γ est le taux de guérison des personnes infectieuses. Ainsi,

M^{(k)} = (\begin{array}{c} - τ & β^{(k)} \\ τ & - γ \end{array}) .

Supposons de plus qu’il n’y ait que K = 2 environnements différents et posons :

Q = (\begin{array}{c} - q_{1} & q_{2} \\ q_{1} & - q_{2} \end{array}) .

Le système (9) s’écrit

\frac{\partial f^{(1)}}{\partial t} = q_{2} f^{(2)} - q_{1} f^{(1)} + τ (x_{2} - x_{1}) \frac{\partial f^{(1)}}{\partial x_{1}} + [β^{(1)} (x_{1} - 1) x_{2} - γ (x_{2} - 1)] \frac{\partial f^{(1)}}{\partial x_{2}}

\frac{\partial f^{(2)}}{\partial t} = q_{1} f^{(1)} - q_{2} f^{(2)} + τ (x_{2} - x_{1}) \frac{\partial f^{(2)}}{\partial x_{1}} + [β^{(2)} (x_{1} - 1) x_{2} - γ (x_{2} - 1)] \frac{\partial f^{(2)}}{\partial x_{2}} .

On a choisi les valeurs numériques suivantes, utilisées dans [14] pour la rougeole : 1/τ = 8 jours, 1/γ = 5 jours. Quant à β^(k), supposons que β⁽¹⁾ = 4ɛ par mois (avec un mois de 30 jours) et que β⁽²⁾ = 8ɛ par mois ; dans [14], le coefficient β variait de manière périodique entre 4 et 8 par mois pour avoir un bon ajustement avec la courbe épidémique. Le paramètre ɛ est destiné à varier. Supposons enfin que q₁ = q₂ = 1, de sorte que l’environnement passe en moyenne la moitié du temps dans chacun des deux états.

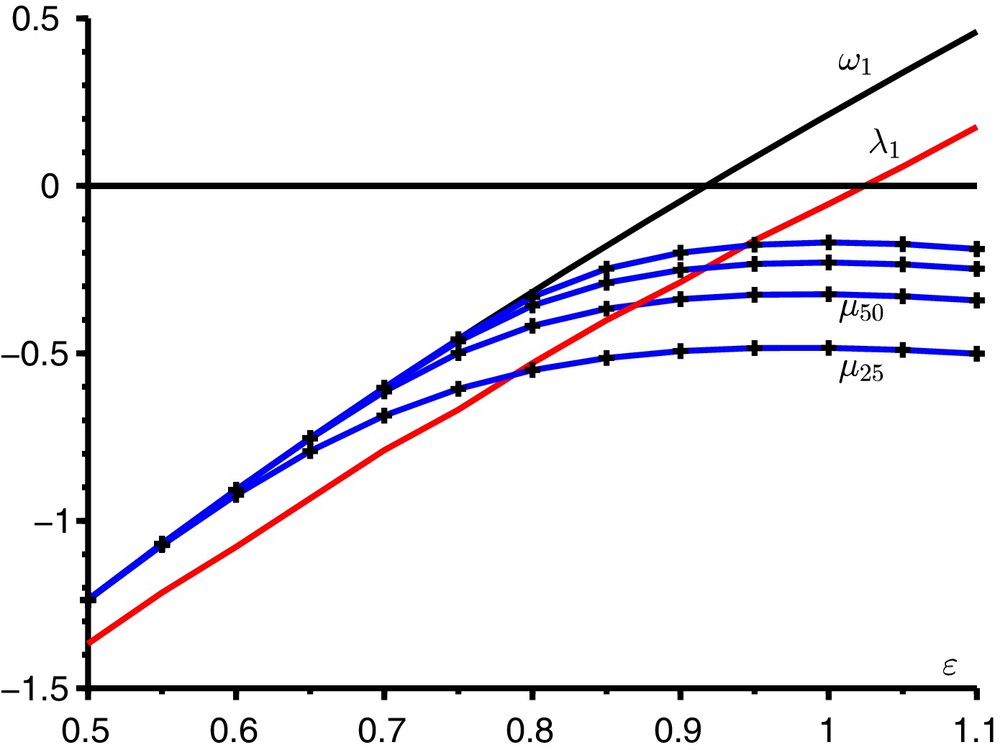
Avec une méthode itérative qui tire avantage de la structure tridiagonale par blocs [15], on estime la borne spectrale μ_n de la sous-matrice finie Y_n de Z lorsque n vaut successivement 25, 50, 100 et 200. Cette sous-matrice carrée est d’ordre $2 K + 3 K + \dots + (n + 1) K = n (n + 3) K / 2 .$ On estime, par ailleurs, le paramètre critique λ₁ lié à l’exposant de Lyanounoff en utilisant par exemple 5000 sauts de l’environnement. Les résultats sont exposés sur la Fig. 1. Notons que si l’environnement était constant, le processus serait sous-critique pour β < γ.

Fig. 1
Le paramètre critique λ₁ (en rouge), la borne spectrale ω₁ (en noir) et la borne spectrale μ_n (en bleu avec des croix pour $n \in \{25, 50, 100, 200\}$ de bas en haut) en fonction de ɛ. Notons que α₁, qui doit être le taux d’extinction, est la limite de μ_n quand n → ∞.

La figure suggère qu’on a α₁ = ω₁ lorsque ɛ est petit, en particulier tant que β⁽¹⁾ < γ et β⁽²⁾ < γ, ce qui équivaut à $\frac{8 ε}{30} < \frac{1}{5}$ ou ɛ < 0,75. Mais α₁ < ω₁ dans une zone où λ₁ reste < 0. Malheureusement, on n’est pas parvenu à déterminer α₁ plus explicitement. On s’attend à ce que α₁ = 0 lorsque λ₁ = 0. Rappelons que, lorsqu’il n’y a qu’un seul type d’individus (I = 1), les matrices M^(k) sont en fait des nombres scalaires M^(k), et Bacaër [7] tendait à montrer dans ce cas que

α_{1} = \min_{0 \leq θ \leq 1} s (Q + θ d i a g (M^{(1)}, \dots, M^{(K)})),

où $s (\cdot)$ désigne la borne spectrale. L’analogue de cette formule lorsqu’il y a plusieurs types d’individus reste à déterminer. Dyakonova [4,5] et Vatutin et Wachtel [6] n’y étaient pas non plus parvenus dans le cadre des modèles en temps discret. Sans doute une meilleure compréhension du comportement des fonctions F^(k) (x) près du point singulier x = 1 dans le système (7) permettrait de progresser.