Sur la taille finale des épidémies dans un environnement périodique

Nicolas Bacaër

doi:10.1016/j.crvi.2019.07.001

Résumé

Il est difficile de prédire la taille finale d’une épidémie comme celle de dengue qui sévit actuellement à la Réunion, d’autant qu’il faut tenir compte de la saisonnalité. Dans cet article, on se propose d’étudier d’un point de vue théorique comment, dans le cadre d’un modèle très simple de type S–I–R pour une maladie à transmission directe, un environnement saisonnier périodique peut modifier la taille finale d’une épidémie. On obtient des résultats analytiques en supposant que l’amplitude de la saisonnalité est faible.

1 Introduction

Une épidémie de dengue sévit actuellement sur l’île de la Réunion, dans l’océan Indien. Plus de 5 000 cas ont été confirmés biologiquement entre janvier et juin 2018, et plus de 16 000 cas évocateurs de la dengue ont été signalés (Figure 1). Fin juin, du fait de l’arrivée de l’hiver austral, mais aussi de la lutte antivectorielle, l’épidémie recule. Cependant, il est difficile de prévoir si le nombre d’infections diminuera suffisamment pour empêcher une seconde vague épidémique à la fin 2018, lorsque les conditions climatiques seront plus favorables aux moustiques vecteurs de la maladie. C’est cette deuxième vague qui, en 2006, avait infecté presqu’un tiers de la population avec le chikungunya.

Fig. 1
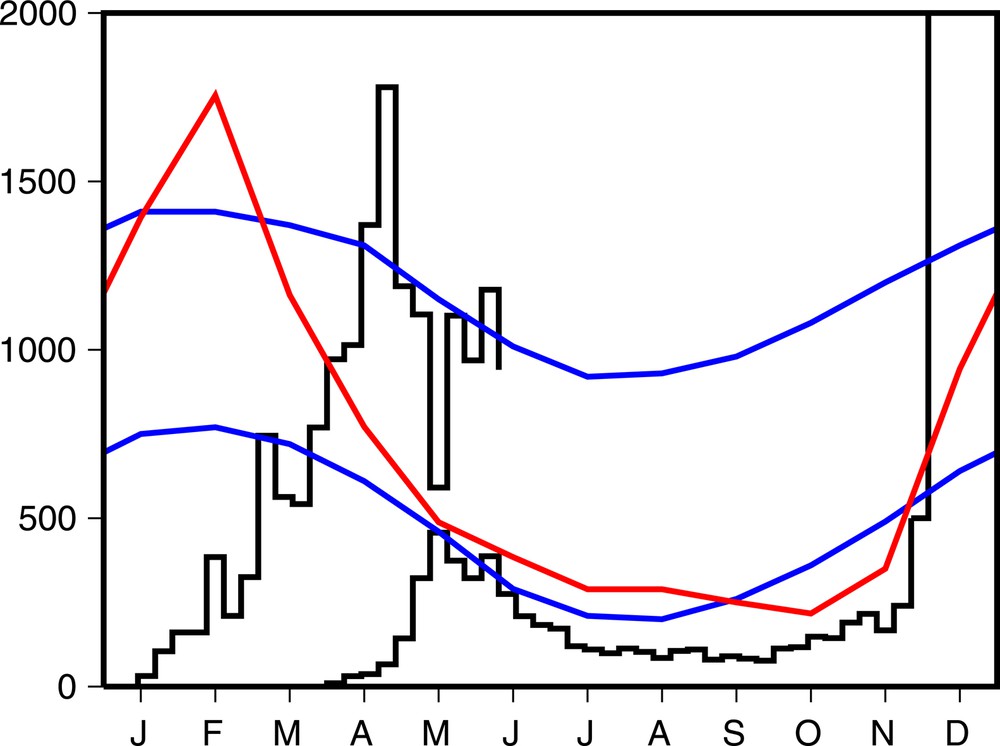
Courbe en noir du haut (échelle sur l’axe vertical de gauche) : estimation du nombre de cas hebdomadaires évocateurs de la dengue à la Réunion entre janvier et juin 2018, d’après [1]. Courbe en noir du bas (même échelle) : cas hebdomadaires de chikungunya en 2005, avant le grand pic de la fin 2005 et du début de 2006 [2]. Données climatiques à la station de l’aéroport de la Réunion, d’après [3] : en bleu, température minimale (de 18,0 à 23,7^oC) et température maximale (de 25,2 à 30,1^oC) ; en rouge, précipitations mensuelles (de 43 à 351 mm).

Il serait tentant de modéliser mathématiquement la propagation de la dengue de manière réaliste tout en limitant la complexité du modèle pour n’avoir que quelques paramètres inconnus, comme on a essayé de le faire pour le chikungunya dans [2]. Mais les incertitudes qui pèsent sur ces paramètres et sur leur dépendance par rapport aux variables climatiques sont si grandes que les résultats numériques risquent fort d’être assez douteux [4]. On se contentera ci-dessous d’un modèle épidémique extrêmement simplifié à transmission directe et non vectorielle, qui ne prétend donc pas pouvoir être appliqué au cas de la dengue à la Réunion. Cela n’aurait pas vraiment de sens de vouloir ajuster ses paramètres aux données épidémiques. L’objectif est plutôt d’attirer l’attention sur la question de la taille finale d’une épidémie dans un environnement saisonnier périodique, qui a été peu étudiée d’un point de vue théorique.

Même les modèles mathématiques les plus simples qui tiennent compte de la saisonnalité présentent de nombreuses difficultés. On sait depuis longtemps que pour les modèles de maladies endémiques, un coefficient périodique peut engendrer des oscillations avec une période différente, voire des oscillations chaotiques [5]. Dans l’étude [2], inspirée de l’épidémie de chikungunya à la Réunion, on a vu par ailleurs que même la notion classique de reproductivité (notée R₀ à la suite de Lotka [6]) dans les modèles périodiques devait être définie avec quelques précautions pour que l’inégalité R₀ > 1 traduise bien l’instabilité de la situation sans épidémie ; la difficulté apparaît notamment pour les modèles avec au moins deux compartiments infectés.

Dans [7], on a abordé le modèle S–I–R périodique, simple généralisation du modèle classique de Kermack et McKendrick [8, p. 75] :

\frac{d S}{d t} = - a (t) \frac{S I}{N}, \frac{d I}{d t} = a (t) \frac{S I}{N} - b I, \frac{d R}{d t} = b I,

(1)

où N est la taille de la population, S(t) le nombre de personnes susceptibles d’être infectées, I(t) le nombre de personnes infectées, R(t) le nombre de personnes guéries, a(t) le taux de contact infectieux et b le taux de guérison. Les conditions initiales sont S(t₀) = s = N − i avec 0 < i < N, I(t₀) = i et R(t₀) = 0. La fonction a(t) est périodique, de période T. Après avoir posé

R_{0} = \frac{1}{b T} \int_{0}^{T} a (t) d t

, on a montré que la propriété de seuil épidémique se traduisait de la manière suivante : si R₀ < 1, alors la taille finale R(∞) de l’épidémie tend vers 0 si i tend vers 0 ; si, au contraire, R₀ > 1, alors R(∞) > N(1 − 1/R₀), quel que soit 0 < i < N. Cette propriété s’étend d’ailleurs des modèles avec une transmission directe, comme le système (1), aux modèles avec une transmission vectorielle, comme pour la dengue. Dans [10, figure 1], on a étudié numériquement comment la taille finale R(∞) de l’épidémie dépend de l’instant initial t₀ et de l’amplitude du taux de contact infectieux a(t). On a observé que R(∞) pouvait varier du simple au double pour une même valeur de la reproductivité R₀.

En combinant méthodes numériques et méthodes analytiques, on étudie ici plus attentivement la taille finale de l’épidémie dans le cas particulier où

a (t) = a_{0} (1 + ɛ ϕ (t))

avec une fonction ϕ(t) (disons continue par morceaux) qui est périodique de période T et de moyenne nulle, et avec un paramètre ɛ qui est petit, de sorte que l’environnement n’est que faiblement saisonnier. Notons S_ɛ(t), I_ɛ(t) et R_ɛ(t) les solutions correspondantes, mais avec toujours la même condition initiale (N − i, i, 0). On montre dans la section 2 que

R_{ɛ} (\infty) = R_{0} (\infty) + N c ɛ + o (ɛ)

quand ɛ → 0, où R₀(∞) est la taille finale de l’épidémie dans un environnement constant. Le coefficient correcteur c peut être positif ou négatif.

Si ϕ(t) = cos(ωt), si le nombre de personnes infectées au départ est petit devant la taille de la population (i ≪ N) ; si R₀ = a₀/b > 1 avec R₀ proche de 1 et si i/N ≪ (R₀ − 1)², alors on détermine analytiquement le coefficient correcteur c en fonction des paramètres N, i, a₀, b, t₀ et ω du modèle. On trouve que l’environnement périodique augmente la taille finale de l’épidémie (c > 0) si le taux de contact infectieux vérifie a(t₀ + τ) > a₀, où t₀ + τ est le moment où l’épidémie atteindrait son pic dans un environnement constant.

2 Formule exacte pour le coefficient correcteur

Rappelons tout d’abord qu’à partir du système différentiel (1), on montre que: S_ɛ(t) + I_ɛ(t) + R_ɛ(t) = N pour tout t ≥ t₀ ; S_ɛ(t) > 0, I_ɛ(t) > 0 et R_ɛ(t) ≥ 0 pour tout t ≥ t₀ ; S_ɛ(t) est une fonction décroissante qui tend vers une limite S_ɛ(∞) ; R_ɛ(t) est une fonction croissante qui tend vers une limite R_ɛ(∞) ; I_ɛ(t) tend vers une limite qui ne peut être que 0 [7]. Intégrons la troisième équation différentielle de t₀ à l’infini : cela donne $R_{ɛ} (\infty) = b \int_{t_{0}}^{\infty} I_{ɛ} (t) d t$ . Par ailleurs, la première équation différentielle s’écrit $\frac{1}{S_{ɛ}} \frac{d S_{ɛ}}{d t} = - a (t) I_{ɛ} (t) / N$ . Intégrons de même pour obtenir

log \frac{S_{ɛ} (\infty)}{N - i} = - \frac{a_{0}}{N} \int_{t_{0}}^{\infty} I_{ɛ} (t) d t - \frac{a_{0}}{N} ɛ \int_{t_{0}}^{\infty} I_{ɛ} (t) ϕ (t) d t .

On peut remplacer la première intégrale et tenir compte de ce que S_ɛ(∞) = N − R_ɛ(∞) pour obtenir l’équation implicite

log \frac{N - R_{ɛ} (\infty)}{N - i} + \frac{a_{0}}{b} \frac{R_{ɛ} (\infty)}{N} + \frac{a_{0}}{N} ɛ \int_{t_{0}}^{\infty} I_{ɛ} (t) ϕ (t) d t = 0,

(2)

qui est de la forme F(R_ɛ(∞), ɛ) = 0. Lorsque ɛ = 0, le dernier terme à droite disparaît et on reconnaît l’équation classique pour la taille finale de l’épidémie dans un environnement constant [8, p. 76]. D’après le théorème des fonctions implicites [9, p. 892], la fonction qui à ɛ associe R_ɛ(∞) est continûment dérivable au voisinage de ɛ = 0, de sorte que R_ɛ(∞) = R₀(∞) + N c ɛ + o(ɛ) pour ϵ → 0, avec

N c = - \frac{\partial F}{\partial ɛ} (R_{0} (\infty), 0) / \frac{\partial F}{\partial R} (R_{0} (\infty), 0) .

On trouve ainsi

c = \frac{a_{0} / N}{\frac{N}{N - R_{0} (\infty)} - \frac{a_{0}}{b}} \int_{t_{0}}^{\infty} I_{0} (t) ϕ (t) d t .

(3)

Rappelons comme dans l’introduction que R₀(∞) > N(1 − b/a₀). Donc le dénominateur de la formule (3) est strictement positif et en particulier non nul. Le coefficient c a le même signe que l’intégrale

\int_{t_{0}}^{\infty} I_{0} (t) ϕ (t) d t

On peut évaluer numériquement cette intégrale. On utilise d’abord un logiciel de calcul numérique (tel que Scilab et sa fonction << ode >>, voir www.scilab.org/fr) pour résoudre le système différentiel (1) avec ɛ = 0). On obtient ainsi (S₀(t), I₀(t), R₀(t)) pour un ensemble discret de valeurs de t, avec un petit pas de temps. On en déduit en particulier la valeur R₀(∞). Puis on calcule l’intégrale avec cette même discrétisation du temps. On en déduit la valeur du coefficient c.

Prenons un exemple. Supposons que ϕ(t) = cos(ωt) avec ω = 2π/T, N = 10 000, i = 1, T = 12 mois, a₀ = 10/mois et b = 5/mois. Alors la reproductivité est R₀ = 2 ; la taille finale de l’épidémie dans un environnement constant est R₀(∞) ≃7 968. La Figure 2 montre comment R_ɛ(∞) varie en fonction de ɛ (0 ≤ ɛ ≤ 1) lorsque t₀ prend trois valeurs différentes, qui correspondent à trois moments différents d’introduction du premier cas infecté dans la population : 0,5 mois, 2 mois ou 3 mois. La figure montre aussi l’approximation R₀(∞) + N c ɛ pour ɛ petit, avec le coefficient correcteur c calculé selon la formule (3). On observe que le coefficient c peut être positif ou négatif, de sorte que la taille finale de l’épidémie peut être plus grande ou plus petite que dans un environnement constant. On observe aussi que pour t₀ = 3 mois, la fonction R_ɛ(∞) varie en fonction de ɛ de manière plus compliquée que pour les deux autres valeurs de t₀ : en particulier, cette fonction n’est décroissante que tant que ɛ < 0,3.

Fig. 2
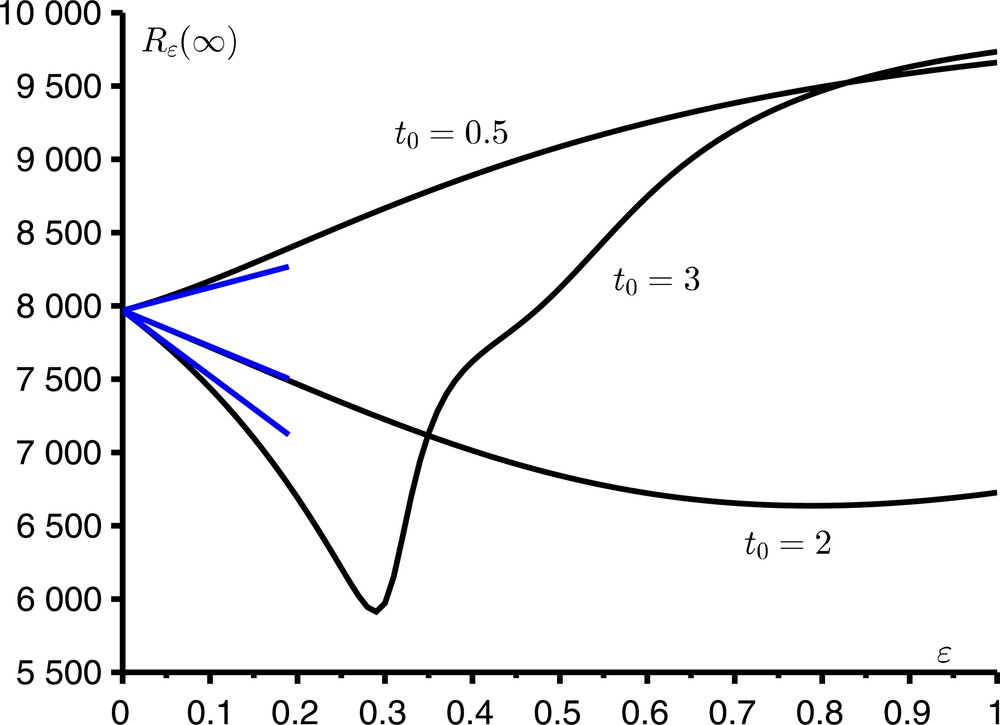
La taille finale de l’épidémie en fonction de ɛ pour trois valeurs différentes de t₀. En bleu : l’approximation R₀(∞) + N c ɛ.

3 Formules approchées

Kermack et McKendrick ont trouvé (voir par exemple [11, §2] ou [12, p. 235]) une approximation pour I₀(t) à partir de l’équation exacte dR₀/dt = b(N − s e^{−a₀R₀/(Nb)} − R₀) vérifiée par R₀(t). Un développement limité de l’exponentielle e^−x = 1 − x + x²/2 + o(x²) tronqué à l’ordre 2 conduit à une équation de Ricatti résoluble pour R₀(t) et à une courbe en cloche symétrique pour I₀(t),

I_{0} (t) ≃ \frac{N X}{{ch}^{2} (Y (t - t_{0}) - Z)}

pour tout t > t₀, où

X = \frac{b^{2} N W^{2}}{2 a_{0}^{2} s}, Y = \frac{b W}{2}, th (Z) = \frac{\frac{a_{0} s}{b N} - 1}{W},

W = \sqrt{{(\frac{a_{0} s}{b N} - 1)}^{2} + 2 \frac{s i}{N^{2}} \frac{a_{0}^{2}}{b^{2}}} .

Ici, ch(·) et th(·) désignent le cosinus et la tangente hyperboliques. Rappelons que s = N − i. L’approximation pour I₀(t) est d’autant meilleure que a₀R₀(∞)/(Nb), la valeur maximale du terme dans l’exponentielle, est petit devant 1. Alors

c ≃ \frac{a_{0} X}{\frac{N}{N - R_{0} (\infty)} - \frac{a_{0}}{b}} \int_{t_{0}}^{\infty} \frac{ϕ (t)}{{ch}^{2} (Y (t - t_{0}) - Z)} d t .

(4)

Supposons plus précisément que R₀ = a₀/b → 1 avec R₀ > 1 et que (i/N)/(R₀ − 1)² → 0 ; autrement dit, R₀ est proche de 1 et i/N ≪ (R₀ − 1)². Alors i → 0 et on a bien R₀(∞) → 0 d’après l’équation (2) avec ɛ = 0. Comme on a aussi i/N ≪ (R₀ − 1), on trouve que

W \sim \frac{a_{0}}{b} - 1, X \sim \frac{{(1 - b / a_{0})}^{2}}{2}, Y \sim \frac{a_{0} - b}{2}

1 - th (Z) \sim \frac{i / N}{{(b / a_{0} - 1)}^{2}}

. Donc Z → +∞ et 1 − th(Z) ∼ 2 e^−2Z, ce qui donne

Z \sim \frac{1}{2} log \frac{2 {(b / a_{0} - 1)}^{2}}{i / N} .

Posons τ = Z/Y; c’est en t = t₀ + τ que l’approximation de I₀(t) atteint son pic. Notons que Y → 0 et que τ → +∞. Après le changement de variable t = t₀ + τ + u, on remarque que la fonction 1/ch²(Yu) est presque nulle en dehors du voisinage de u = 0, de sorte que

\int_{- τ}^{\infty} \frac{ϕ (t_{0} + τ + u)}{{ch}^{2} (Y u)} d u ≃ \int_{- \infty}^{\infty} \frac{ϕ (t_{0} + τ + u)}{{ch}^{2} (Yu)} d u .

Cette dernière intégrale se calcule explicitement lorsque ϕ(t) = cos(ωt). En effet,

\int_{- \infty}^{\infty} \frac{cos (ω (t_{0} + τ + u))}{{ch}^{2} (Y u)} d u = cos (ω (t_{0} + τ)) \int_{- \infty}^{\infty} \frac{cos (ω u)}{{ch}^{2} (Y u)} d u

puisque l’intégrale avec la fonction impaire sin(ωu) s’annule. D’après la formule dans l’appendice de [13], on a

\int_{- \infty}^{\infty} \frac{cos (ω u)}{{ch}^{2} (Y u)} d u = \frac{\frac{π ω}{Y^{2}}}{sh (\frac{π ω}{2 Y})},

où sh(·) désigne le sinus hyperbolique. Avec les équivalents de X et Y déjà obtenus, on arrive finalement à

c ≃ \frac{cos (ω (t_{0} + τ))}{\frac{N}{N - R_{0} (\infty)} - \frac{a_{0}}{b}} \frac{\frac{2 π ω}{a_{0}}}{sh (\frac{π ω}{a_{0} - b})} .

(5)

On voit que le signe de c est le même que celui de cos(ω(t₀ + τ)). Donc l’environnement périodique augmente la taille finale de l’épidémie si a(t₀ + τ) > a₀, où t₀ + τ est le moment où l’épidémie atteindrait son pic dans un environnement constant.

Comme exemple, prenons les mêmes valeurs des paramètres que dans la Figure 2, sauf que a₀ = 6/mois pour avoir R₀ = 1,2 plus proche de 1 ; [12, p. 240] indique d’ailleurs que l’approximation en cloche symétrique de Kermack et McKendrick n’est satisfaisante que pour R₀ < 1,5. La Figure 3 compare l’expression exacte (3) du coefficient correcteur c avec les approximations (4) et (5). Avec nos valeurs numériques, ces deux dernières approximations sont indiscernables. Elles sont d’autant plus proches de la valeur exacte que R₀ est proche de 1. Notons qu’ici i/N = 10⁻⁴ ≪ (R₀ − 1)² = 0,04. La figure s’interprète comme ceci : si l’épidémie démarrait à t₀ = 0, les valeurs des paramètres conduiraient à un pic de l’épidémie environ τ ≃ 6,3 mois plus tard dans un environnement constant ; or, l’environnement périodique sera défavorable à ce moment (on sera dans le creux du facteur cos ωt) ; donc, la taille finale de l’épidémie sera moindre et c < 0.

Fig. 3
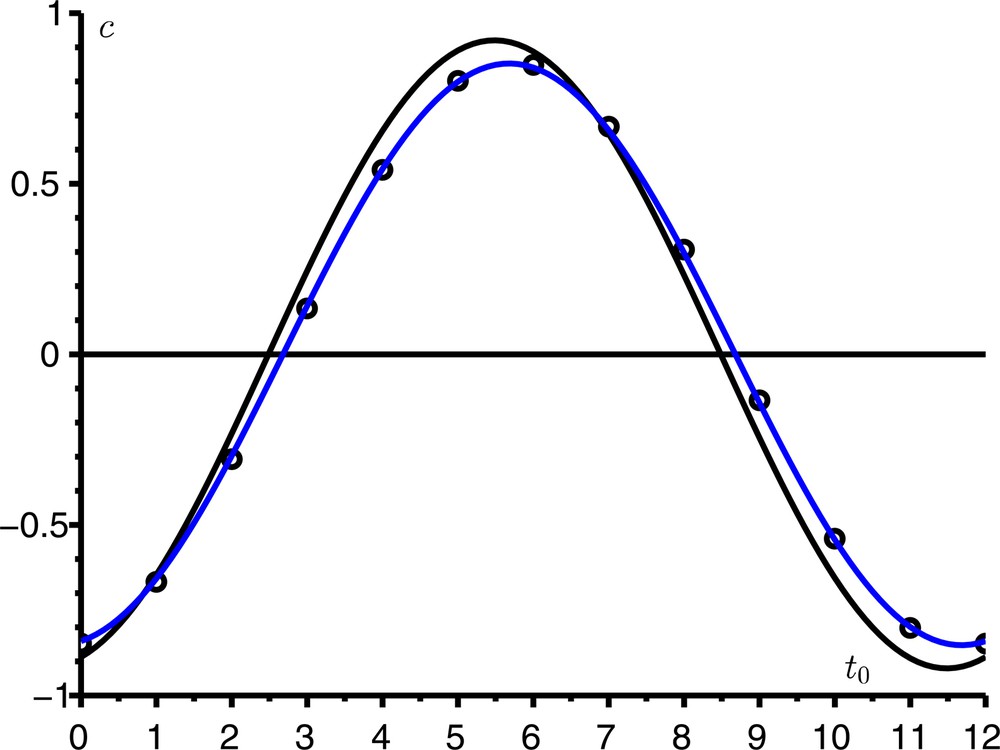
Le coefficient correcteur c pour la taille finale de l’épidémie en fonction de t₀, l’instant du début de l’épidémie. Comparaison de l’expression exacte (3) [en noir] avec les approximations (4) [points] et (5) [en bleu].

4 Remarque

On peut adapter la formule exacte (3) pour le coefficient correcteur c à des modèles plus complexes. Supposons par exemple que l’épidémie se propage entre deux populations (comme des hommes et des vecteurs) suivant le schéma S–I–R, avec N₁ = S₁(t) + I₁(t) + R₁(t) et N₂ = S₂(t) + I₂(t) + R₂(t) :

\frac{d S_{1}}{d t} = - a (t) S_{1} \frac{I_{2}}{N_{2}}, \frac{d I_{1}}{d t} = a (t) S_{1} \frac{I_{2}}{N_{2}} - b_{1} I_{1}, \frac{d R_{1}}{d t} = b_{1} I_{1},

\frac{d S_{2}}{d t} = - a (t) I_{1} \frac{S_{2}}{N_{2}}, \frac{d I_{2}}{d t} = a (t) I_{1} \frac{S_{2}}{N_{2}} - b_{2} I_{2}, \frac{d R_{2}}{d t} = b_{2} I_{2} .

Supposons aussi que a(t) = a₀(1 + ɛ ϕ(t)), comme précédemment. Notons S_1,ɛ(t), I_1,ɛ(t), etc., les solutions. Posons i₁ = I₁(t₀) et i₂ = I₂(t₀). On trouve facilement l’équivalent de l’équation (2), qui est un système :

log \frac{N_{1} - R_{1, ɛ} (\infty)}{N_{1} - i_{1}} + \frac{a_{0}}{b_{2}} \frac{R_{2, ɛ} (\infty)}{N_{2}} + \frac{a_{0}}{N_{2}} ɛ \int_{t_{0}}^{\infty} I_{2, ɛ} (t) ϕ (t) d t = 0

log \frac{N_{2} - R_{2, ɛ} (\infty)}{N_{2} - i_{2}} + \frac{a_{0}}{b_{1}} \frac{R_{1, ɛ} (\infty)}{N_{2}} + \frac{a_{0}}{N_{2}} ɛ \int_{t_{0}}^{\infty} I_{1, ɛ} (t) ϕ (t) d t = 0 .

Ce système a des solutions de la forme R_k,ɛ(∞) = R_k,0(∞) + N_k c_k ɛ + o(ɛ) pour k = 1 ou 2. Avec le théorème des fonctions implicites, on trouve que

(\begin{array}{c} N_{1} c_{1} \\ N_{2} c_{2} \end{array}) = {(\begin{array}{c} \frac{1}{N_{1} - R_{1,0} (\infty)} & - \frac{a_{0}}{b_{2} N_{2}} \\ - \frac{a_{0}}{b_{1} N_{2}} & \frac{1}{N_{2} - R_{2,0} (\infty)} \end{array})}^{- 1} (\begin{array}{c} \frac{a_{0}}{N_{2}} \int_{t_{0}}^{\infty} I_{2,0} (t) ϕ (t) d t \\ \frac{a_{0}}{N_{2}} \int_{t_{0}}^{\infty} I_{1,0} (t) ϕ (t) d t \end{array}) .

Il n’est cependant pas possible de poursuivre comme dans la section 3, car on ne dispose pas de formules approchées explicites pour I_1,0(t) et I_2,0(t).

5 Conclusion

On a déterminé de manière analytique comment la taille finale de l’épidémie était influencée par un taux de contact infectieux périodique de faible amplitude, lorsque la reproductivité R₀ reste proche de 1. Il s’agit d’un petit progrès par rapport aux études précédentes, qui étaient soient qualitatives comme dans [7], soit purement numériques comme dans [10, figure 1]. Les hypothèses sont néanmoins assez restrictives. Elles évitent en particulier les cas où plusieurs pics épidémiques se produisent, puisque l’on reste proche de la situation à un seul pic des environnements constants. Or ce sont justement ces cas qui risquent de se présenter avec l’épidémie de dengue à la Réunion.