1 Introduction
Habitat fragmentation alters population viability mainly through the concomitant processes of decrease in habitat availability and increasing isolation of each remaining habitat patch. The decrease of habitat area affects local population viability by reducing population size (small population paradigm [1]), whereas isolation affects viability by reducing immigration from other populations, thus impeding demographic rescue effects (metapopulation paradigm [2,3]). Habitat fragmentation implies also genetic consequences as small population size favours genetic drift and inbreeding, both processes resulting in the erosion of genetic diversity and alteration of fitness [4]. The respective effects of habitat destruction and isolation are usually not distinguishable in natural landscapes because habitat patch isolation most frequently results from habitat destruction. When habitat is progressively destroyed the relationship between habitat loss and habitat patch isolation appears theoretically as a non-linear process with a strong threshold effect [5]. However, despite the great interest of such a relationship for conservation actions, establishing such a threshold effect in situ is a difficult task and investigating the connectivity of the landscape remains one of the current challenges of conservation biology.
Habitat fragmentation does not result exclusively from the anthropogenic management of natural habitats. The populations of most species have been spatially structured by natural fragmentation of their habitats for long periods. The ability of dispersing across the matrix of unfavourable environment that surrounds habitat patches thus appears as an evolutionary response to habitat fragmentation allowing the avoidance of inbreeding and crowding [6]. The costs of movements between two habitat patches are probably not linearly proportional to the distance to be covered, but are modulated by the resistance of the habitat matrix (matrix resistance) [7–9]. This resistance could be evaluated by physiological costs and/or by mortality risks. Physiological costs involve specific energy demand of movement (for a ground-dweller to cross a corrugated ploughed field is more costly than to cross a flat meadow) or specific physiological stress (scarcity of food, constraints on water metabolism). Mortality risks are linked to the lack of refuges against predators or to demographic sinks such as roads. Each landscape patch can thus be attributed a cost-benefit score for a given type of animal (species, sex, age) that can influence both direction, speed, and propensity of movements.
Because the study of dispersal mechanisms will remain a difficult task for the coming years, it could be convenient to undertake a landscape-based approach by means of simulations. Despite their putative nature, simulations can prove useful in identifying crucial parameters and stimulating empirical researches. Such an approach can take advantage of Geographic Information Systems (GIS) that make it possible to relate spatial information to animal movements for modelling dispersal explicitly. Neutral models may be used for analysing the biological connectivity of a landscape. They derive from percolation theory and thus consider the individuals as “particles” that follow random walks constrained by patch quality and patch boundaries [10–13].
Amphibians offer several advantages for the empirical approach of the relationships between landscape structure and conservation because of the ground-dweller habits of most species that expose them directly to a great variety of connectivity breakdowns. Large rivers, canals, highways and human buildings constitute absolute barriers to amphibian movements. Cultivated fields and vineyards can dramatically increase the resistance of the landscape to movements, while the roads act as demographic sinks. The movements of amphibians across the landscape result from both complex life cycles and dispersal. Complex life cycles imply the use of two different habitats at a local scale. Breeding occurs usually in an aquatic habitat whereas the other activities take place on land. Breeding migrations connect the terrestrial home range to the aquatic breeding place at each breeding occasion. The scale of dispersal is wider as it concerns movements from one population to another, or from a breeding place to another.
Most authors suspect dispersal to be mainly achieved by juveniles because of high site fidelity of adults. Several studies indeed revealed the high propensity of adult amphibians to be faithful to a given breeding sites [14–20]. However, phylopatry is not a general trait as nomadism has also been detected in several species [20–23]. From optimality theory we suspect that the distances that separate terrestrial residence sites from breeding sites are the shortest as possible. However, this distance probably results from a trade off between costs of migration and local resource availability (food, shelter, microclimate, competition avoidance). Breeding migration can reach up to 5 km in the common toad [24]. Studies on orientation during the breeding migrations have shown that the movements of most individuals follow a straight line. The orientation mechanisms involved in migrations can explain this directionality of movements since they consist in pilotage toward goal emanating cues [25] and magnetic compass [26]. As a consequence the abundance of breeding individuals at a pond mainly depends on the width of the “migration sector” constituted by low friction landscape patches [27].
From these biological considerations it results that one of the present challenges of amphibian conservation is to delineate buffer zones around wetlands and ponds for allowing the animals to achieve their life cycles [28]. Another is to evaluate the efficiency of corridors for connecting isolated populations. The aim of the present paper is an attempt to explicitly define migration zones for the common toad (B. bufo) in a floodplain by taking into account both energetic costs and mortality risks.
2 Materials and methods
2.1 Principle
The approach combined population-based concepts (population viability, costs of movements) and landscape-based concepts (landscape analysis, connectivity assessment) in using diffusion model in a GIS [12,13]. In the present work, we focused on breeding migrations by attributing a potential migration energy (PME) to each individual, which decreases as the animal moves (we assume that the focal species does not forage during breeding migrations). The decrease rate depends on both the covered distance and the resistance of the crossed habitat. If the whole migration takes place in the less resistant habitat, the animal covers the maximum migration distance (MMD). The distance that an individual can travel is the ratio of MMD on friction costs.
2.2 Friction maps
Landscape structure and habitat types were established using Arcview (ESRI Inc., USA). BDCarto (Institut Géographique National, France) provided a basic cartographic background (rivers, inhabited zones, forests, railways, roads). We used aerial photographs for mapping land use by agriculture (cultivated lands, meadows, poplar growing, marshes). The Rhone National Company (which is in charge of civil engineering and power production) provided data for the areas under its management. Field visits were also performed to complete information on land use when the interpretation of photographs was not possible. The areas above 300 m elevation were not included in the analysis because outside the floodplain. We attributed to each habitat type a resistance coefficient based on current knowledge of habitat use by the focal species [13]. The costs varied from 5 to 80 (Table 1). The lowest cost was attributed to forested areas since forested grounds are the usual habitats of the common toad. Higher costs were attributed to more open habitats as desiccation effects are expected to be stronger in these habitats. Roads are considered as an open habitat the crossing of which is not very costly but dangerous (see below for mortality risks). Highest costs were attributed to habitats where substratum unevenness involves high movement costs and where the animal is in direct contact with the soil (arable lands). Absolute barriers (such as large rivers) received a resistance coefficient that exceeds the migration potential of the species. We thus obtained a friction map of the studied landscape by using the function “Merge” on a rasterised version of the map (function “Convert to grid” in the Spatial Analyst extension of ArcView) with a 10 m resolution. The friction map presents the potential costs of crossing each cell of this matrix.
Resistance coefficients of each habitat type
| Urbanised areas and vineyards | 80 |
| Cultivated fields | 45 |
| Pebble beds | 45 |
| Roads and railways | 45 |
| Meadows and marshes | 25 |
| Poplar growing fields | 15 |
| Forested areas | 5 |
2.3 Mortality risks
In the present study, we considered only mortality by road traffic. The relationship between traffic and mortality was established using data from [29] and Berthoud (pers. comm.) (Fig. 1). We attributed a 0.9 survivorship to the small roads for which no information was available (the administrative services in charge of roads only establish statistics for high traffic roads).
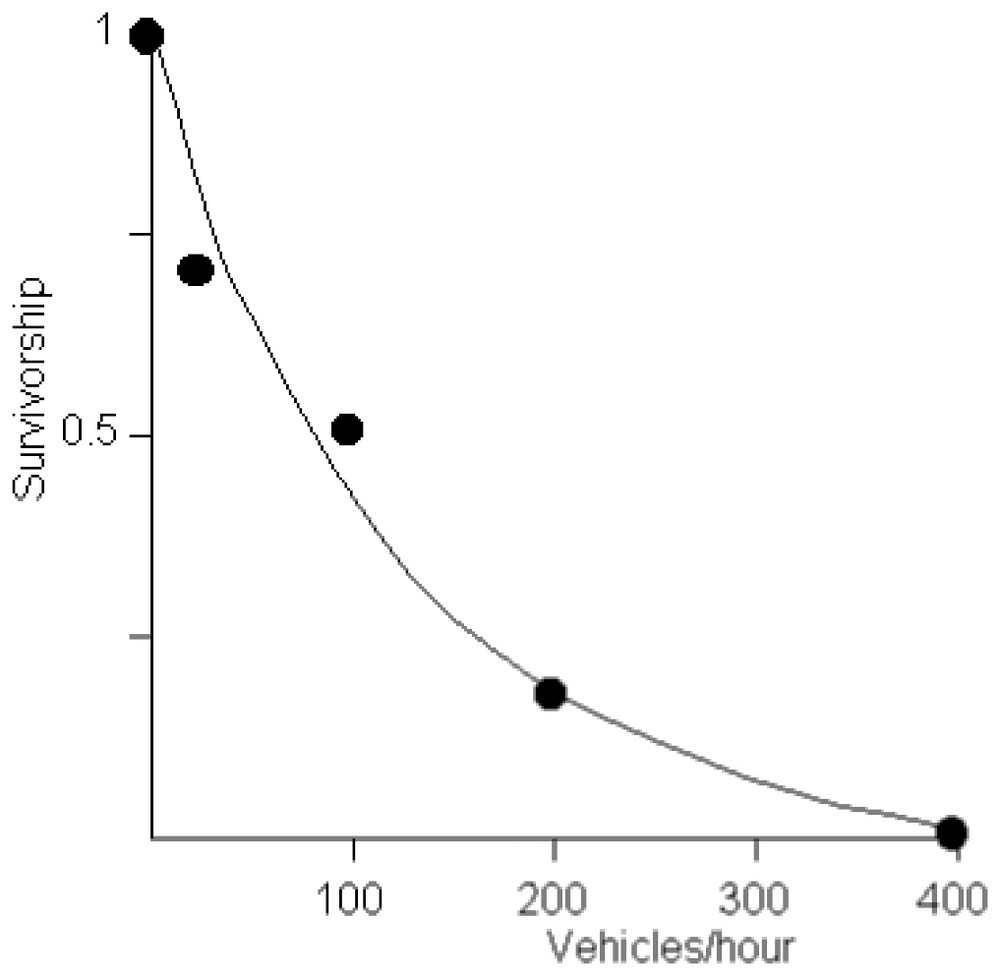
Relationship between road traffic and survivorship of toads crossing a road when migrating. Data from [1] and Berthoud (pers. comm.)
2.4 Migration zones
Each pond was considered as a potential breeding site around which a migration zone can be modelled. We assumed that each individual can migrate in all directions with an equal probability. The shape of the migration zone then depends on resistance variation of the landscape matrix. The standard ArcView Cost Distance function was used to compute the migration zones. The spreading function stopped when the PME is consumed. The movements did not necessarily followed straight lines but low cost trajectories. We attributed to each pond a potential population of 1000 individuals for modelling a first density map that only took into account the resistance of the habitat matrix. We then considered mortality risks by attributing to each road a probability to be safely crossed (survivorship) depending on the traffic.
2.5 Study site
The study site is a sector of the Rhone floodplain approximately 80 km upstream from Lyon near Bregnier-Cordon and Les Avennières. We defined a 7.5×7.5 km area (56.3 km2) which encompassed a river bend. Eighteen ponds are distributed in the vicinity of the river. Some of them are natural dead arms while others are man-made gravel pits and other ponds.
2.6 Focal species
The focal species is the common toad (Bufo bufo). We selected this species because it is widely distributed in the study region but occurs only in half of the ponds in the floodplain suggesting that its presence there is constrained by ecological factors. The life cycles of B. bufo are typically biphasic with breeding in an aquatic habitat (usually a pond), and both feeding and hibernation occurring on land in forested habitats. Breeding migration distances are usually from a few meters to 2–3 km.
3 Results
The habitat map was composed of 9 habitat types (Fig. 2). We then build the friction map by computing the resistance coefficients of each habitat type in a rasterised version of the habitat map (grid-based with each cell measuring 10×10 m) (Fig. 2).
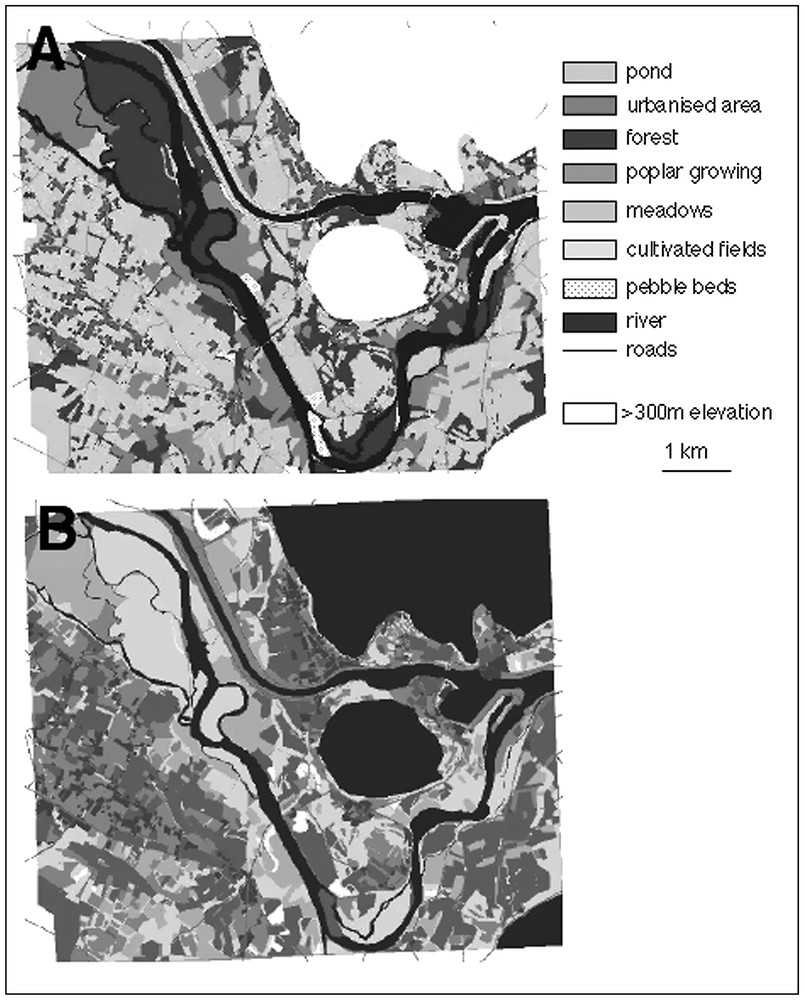
Habitat map (A) and friction map (B) of the studied area. In (B), darker shading corresponds to higher habitat resistance against toad movements. Habitats with elevation exceeding 300 m were not considered in this study.
For simulating the migration zones, we first considered a potential migration distance of 3 km in the less resistant habitat (forest with resistance=5). The potential energy costs of the migration was thus 3×5=15. This energy amount decreases proportionally to the resistance of the habitats crossed by the toad. The cells where PME becomes null determine the border of the migration zone. An example of such a migration zone is given by Fig. 3. We attributed to each pond a toad population of 1000 individuals for including mortality risks from road traffic. This virtual population allowed us to draw density maps including both migration costs and mortality risks (Fig. 3). In such maps, presence probability of a toad in some areas within the migration range may be nullified because of high mortality risks.
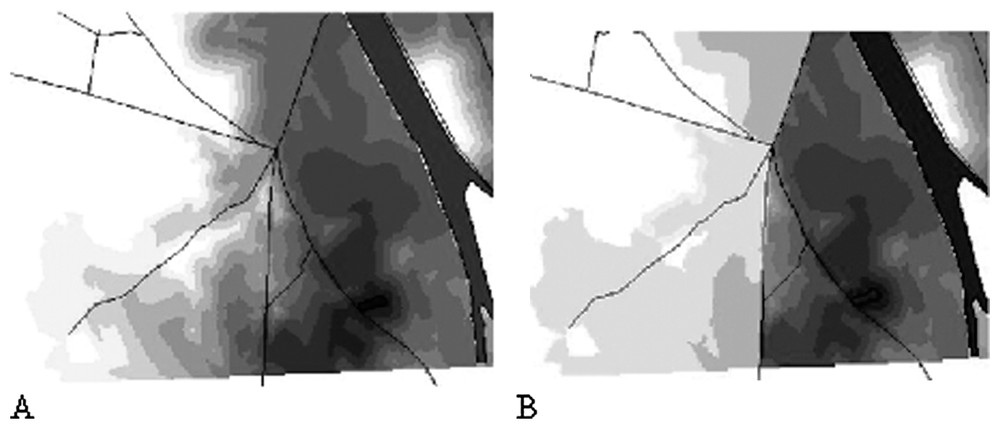
Example of modelling a migration zone around a pond. (A): modelling density on the only basis of habitat resistance. (B): modelling density including mortality risks by the roads.
Computing the simulation on the whole studied area made it possible to visualise the zones of potential highest density where ponds are surrounded by permeable land habitats (Fig. 4). When the migration zones of two ponds overlap, expected densities are added. The map thus expresses the cumulative effects of pond clumping (independently of any putative metapopulation functioning). Such high density areas suggest that between-pond movements of adult toads are possible. The deleterious impacts of roads are clearly perceptible.
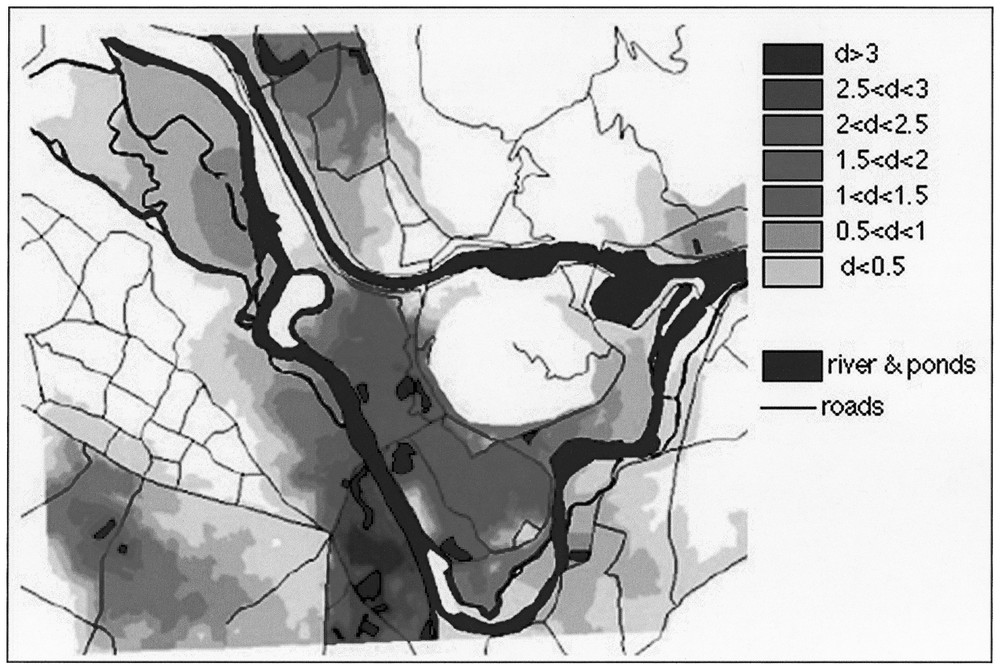
Connectivity map for the whole studied area. The overlap between several migration zones determines higher density.
4 Discussion
The present work shows how a GIS package can be used to build a tool for simulating connectivity variation of the landscape matrix for a ground-dwelling species. Such simulations could be of great interest for the management of the landscape for the maintenance of biodiversity. Networks of preserved areas can indeed be designed by following such an approach. The connectivity map makes it also possible to identify the ways by which population isolation can be broken.
The present work will nevertheless remain exploratory since several validations are not performed. Under our assumptions, the area of the migration zone should be the best predictor of the presence of a breeding population in a pond. The first way of validation will be to compare the reliability of this prediction with that of more conventional approaches based on pond ecology or composition of pond environment. Because we focused primarily on landscape influence, we considered that all the ponds of the floodplain are equally suitable for the reproduction of the common toad. Probably this species makes this assumption quite acceptable as it is preserved from fish predation by repellents. The presence of fish in ponds is indeed one of the main factors structuring the amphibian community of the floodplain [30]. The influence of ecological factors in the breeding sites has, however, to be considered and investigated.
Because the resistance coefficients of each habitat type represent the hard core of the model, a particular attention has to be paid to their estimation. It will remain difficult to estimate variation of the costs of movement according to habitat. Because of multiple exchanges of water through their skin, amphibians do not allow the use of labelled water for measuring metabolism. It will be also difficult to recreate habitat conditions in indoor respirometers. Behavioural tests of habitat selection during migration would probably be the best way of investigation of the relationship between individual trajectories and habitat quality. In the same way, a sensitivity analysis has to be performed to investigate the respective influences of the parameters that are used in modelling. Another way of refining the resistance coefficients could lie in the calibration of their values to fit the observed data, and then to test experimentally their biological significance.
The present work deals essentially with breeding migration. The scale of the life cycles of adult individuals (local scale) is important as it focuses on the conditions of reproductive success of a population. However, the broader scale of dispersal among local populations is also of great importance as it determines the long-term persistence of the species at a regional scale through rescue effects and colonisation of new habitat patches. In the common toad, dispersal is mainly ensured by juvenile individuals that are able to roam during two or three years before reaching sexual maturity. Dispersal remains a black box, as no satisfactory individual marking is available for such small organisms. Behavioural experiments have to be performed to establish the rules of decision making when toadlets are dispersing.
Diffusion models offer a convenient way of assessing landscape connectivity by using current GIS package. Individual-based models could produce more refined predictions especially on extinction probabilities, but their implementation needs specialised programming and they require that many biological parameters are accurately established. Moreover their predictions can not be immediately validated. We thus consider that diffusion-percolation modelling can reveal useful to managers of natural landscapes because of suitable accessibility and possibility of validation.
Acknowledgements
This study was supported by the French Environment Ministry (programme Espaces Protégés). We thank the Compagnie Nationale du Rhone for providing data on land use in the areas under its concession.


