Using wood creep data to discuss the contribution of cell-wall reinforcing material

Joseph Gril; David Hunt; Bernard Thibaut

doi:10.1016/j.crvi.2004.08.002

Plant biology and pathology / Biologie et pathologie végétales

Using wood creep data to discuss the contribution of cell-wall reinforcing material
[Utilisation de données de fluage du bois pour discuter la contribution des constituants de la paroi cellulaire.]

Présenté par : Michel Thellier

Joseph Gril ¹ ; David Hunt ² ; Bernard Thibaut ³

¹ Laboratoire de mécanique et génie civil, université Montpellier-2, place Eugène-Bataillon, CC048, 34095 Montpellier cedex 05, France
² South Bank University, London, UK
³ CNRS, Cayenne, French Guyana

Comptes Rendus. Biologies, Volume 327 (2004) no. 9-10, pp. 881-888.

Résumés

Anglais
Français

Longitudinal four-point creep bending tests were performed on small clear-wood spruce specimens having various microfibrillar angles. Cell-wall compliance was deduced from macroscopic data by accounting for porosity. Time-dependent compliance was converted into complex compliance and rigidity using the value and the slope of the compliance versus logarithm of time. Complex rigidity plots of all specimens, for the time range 10³–10⁶ s, could be superimposed by a horizontal shift depending on the microfibrillar angle. The shape of complex trajectories allowed a decomposition of the cell-wall relaxation modulus as the sum of an elastic contribution function of the microfibrillar angle and a time-dependent term unrelated to it, and suggested a discussion on the contribution of the various cell-wall layers to the observed relaxation process.

Des essais de fluage en flexion quatre points longitudinale ont été réalisés sur des petits échantillons de bois d'épicéa, d'angles microfibrillaires variés. La complaisance pariétale est déduite des données macroscopiques, en tenant compte de la porosité. La complaisance différée est convertie en complaisance et rigidité complexes en utilisant la valeur et la pente des courbes donnant la complaisance en fonction du logarithme du temps. Les graphes de rigidité complexe, dans la fenêtre temporelle 10³–10⁶ s, peuvent être superposés moyennant une translation horizontale qui est fonction de l'angle microfibrillaire. L'allure des trajectoires complexes permet une décomposition du module de relaxation pariétale comme la somme d'une contribution élastique dépendant de l'angle microfibrillaire et d'un terme différé n'en dépendant pas, et suggère une discussion sur la contribution des différentes couche de la paroi cellulaire au processus de relaxation observé.

Métadonnées

Reçu le : 2004-01-26
Accepté le : 2004-08-09
Publié le : 2004-09-01

PMID

DOI : 10.1016/j.crvi.2004.08.002

Keywords: wood, creep, microfibrillar angle, cell wall
Mot clés : bois, fluage, angle des microfibrilles, paroi cellulaire

Affiliations des auteurs :

Joseph Gril ¹ ; David Hunt ² ; Bernard Thibaut ³

¹ Laboratoire de mécanique et génie civil, université Montpellier-2, place Eugène-Bataillon, CC048, 34095 Montpellier cedex 05, France
² South Bank University, London, UK
³ CNRS, Cayenne, French Guyana

@article{CRBIOL_2004__327_9-10_881_0,
     author = {Joseph Gril and David Hunt and Bernard Thibaut},
     title = {Using wood creep data to discuss the contribution of cell-wall reinforcing material},
     journal = {Comptes Rendus. Biologies},
     pages = {881--888},
     publisher = {Elsevier},
     volume = {327},
     number = {9-10},
     year = {2004},
     doi = {10.1016/j.crvi.2004.08.002},
     language = {en},
}

TY  - JOUR
AU  - Joseph Gril
AU  - David Hunt
AU  - Bernard Thibaut
TI  - Using wood creep data to discuss the contribution of cell-wall reinforcing material
JO  - Comptes Rendus. Biologies
PY  - 2004
SP  - 881
EP  - 888
VL  - 327
IS  - 9-10
PB  - Elsevier
DO  - 10.1016/j.crvi.2004.08.002
LA  - en
ID  - CRBIOL_2004__327_9-10_881_0
ER  -

%0 Journal Article
%A Joseph Gril
%A David Hunt
%A Bernard Thibaut
%T Using wood creep data to discuss the contribution of cell-wall reinforcing material
%J Comptes Rendus. Biologies
%D 2004
%P 881-888
%V 327
%N 9-10
%I Elsevier
%R 10.1016/j.crvi.2004.08.002
%G en
%F CRBIOL_2004__327_9-10_881_0

Joseph Gril; David Hunt; Bernard Thibaut. Using wood creep data to discuss the contribution of cell-wall reinforcing material. Comptes Rendus. Biologies, Volume 327 (2004) no. 9-10, pp. 881-888. doi : 10.1016/j.crvi.2004.08.002. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2004.08.002/

Version originale du texte intégral

Version française abrégée

Les excellentes performances mécaniques du bois trouvent leur source dans une structuration multi-échelles sophistiquée de composants polymériques. Du fait de sa structure en nid d'abeille, le module d'Young longitudinal peut être directement relié à la rigidité de la paroi, elle-même principalement déterminée par l'angle moyen des microfibrilles cristallines de cellulose par rapport à la direction des fibres (AMF). À partir d'un jeu de données de fluage obtenues sur des échantillons de bois d'angles microfibrillaires variés, nous espérons identifier un comportement viscoélastique de la matière constitutive des parois et proposer des éléments de discussion quant à l'organisation ultrastructurale de la paroi.

Des essais de fluage en flexion quatre points dans la direction longitudinale ont été réalisés sur de petits échantillons de bois d'épicéa, possédant des angles microfibrillaires variés. Dans un premier temps, la complaisance pariétale est déduite des données macroscopiques en tenant compte de la porosité. La complaisance différée est alors convertie en complaisance complexe en utilisant la valeur et la pente des courbes donnant la complaisance en fonction du logarithme du temps. Nous obtenons ainsi, pour chaque essai de fluage réalisé, une trajectoire dans le plan complexe donnant la partie imaginaire de la complaisance complexe en fonction de sa partie réelle. Plus l'AMF est élevé, plus la courbe traduit des complaisances instantanée et différée plus grandes, ce qui est conforme à ce que l'on peut attendre, du fait de la contribution grandissante des zones amorphes de la paroi. Toutefois, lorsque la complaisance complexe est convertie en rigidité complexe, un résultat plus inattendu est observé : les portions de trajectoire de rigidité complexe correspondant à la fenêtre temporelle 10³–10⁶ s peuvent être superposées moyennant une translation horizontale, qui est fonction de l'angle microfibrillaire. Nous en déduisons la possibilité de décomposer le module de relaxation longitudinal de la paroi comme la somme de deux termes : (i) une contribution élastique dépendant de l'angle microfibrillaire et (ii) un terme différé n'en dépendant pas.

Nous pouvons ensuite émettre des hypothèses sur la forme géométrique dans laquelle s'inscrivent les trajectoires obtenues. Reprenant l'idée, antérieurement soutenue par Huet, de mécanismes de relaxation paraboliques, nous nous attendons à observer dans le plan complexe des portions de cercle. La forme observée pouvant effectivement être considérée comme le début d'un arc de cercle, nous sommes à même d'obtenir directement, par observation des courbes obtenues, les paramètres d'un modèle viscoélastique solide à trois éléments, constitué d'un ressort de rigidité $E_{2}$ , fonction de l'AMF, en parallèle avec un ressort de rigidité $E_{1}^{0}$ en série avec un l'amortisseur parabolique de temps caractéristique $τ_{1}$ et d'ordre $p_{1}$ . Le nombre $p_{1}$ est inférieur à 1, la valeur 1 correspondant à un ressort linéaire habituel. Les valeurs ainsi identifiées sont les suivantes : $E_{2}$ (GPa) $\approx 39, 4$ – $1, 1 ϕ$ , l'AMF ϕ étant exprimé en degrés ; $E_{1}^{0} \approx 28 GPa$ , $p_{1} \approx 0, 28$ , $\log τ_{1}$ (s) ≈7 à 8.

Ce résultat appelle des commentaires. Tout d'abord, la représentation du comportement ainsi identifié suggère inévitablement une interprétation en termes de contribution des différentes couches de la paroi, disposées en parallèle par rapport à la direction longitudinale. C'est ainsi que le ressort (2) pourrait représenter la contribution de la couche S2, et l'ensemble (1) celle des autres couches. S'il en était ainsi, cela voudrait dire que la couche S2, dans la fenêtre expérimentale envisagée (bois sec, fenêtre temporelle de la fraction d'heure à quelques années), ne serait pas responsable de la viscoélasticité du matériau, celle-ci étant principalement prise en charge par les autres couches.

Toutefois, cette interprétation n'est pas cohérente avec ce que l'on peut attendre comme contribution respective des deux couches. En effet, la couche S2 étant de loin la plus importante, tant en terme d'épaisseur que de rigidité, les valeurs obtenues de 35–15 GPa pour $E_{2}$ sont trop faibles par rapport aux 28 GPa trouvés pour $E_{1}^{0}$ . On peut donner à cela deux types d'explication. Tout d'abord, la branche (2) pourrait ne pas représenter toute la couche S2, mais seulement les lamelles de S2 contenant les microfibrilles, les zones de lignines de S2 contribuant alors à la branche (1). Ensuite, l'évaluation faite de $E_{1}^{0}$ est tributaire d'hypothèses fortes sur la forme des trajectoires, c'est-à-dire à l'extrapolation sur le long terme des processus de relaxation viscoélastique. C'est ainsi que, sur la base d'essais du même type, nous avons proposé dans d'autres travaux des prédictions à long terme basées sur des extrapolations complètement différentes. Quoi qu'il en soit, d'autres choix de modèles auraient pu aboutir à des valeurs de $E_{1}^{0}$ bien inférieures et, de ce fait, plus compatible avec l'interprétation structurelle proposée.

1 Introduction

The exceptional mechanical performance of wood, used as a structural material both by the stems of living trees as well as by human engineers, relies on a sophisticated, multiscale arrangement of polymeric components [1]. The ‘microfibrillar angle’ (MFA), mean orientation of the crystalline zones in the dominant S2 layer within the cell wall, plays an essential biomechanical function by controlling the level of maturation strain at the latest stage of wood formation. It is also commonly recognized as a key factor for wood quality [2]. Due to the honeycomb-like structure of wood, its longitudinal elastic modulus $(E_{L})$ can be directly related to the longitudinal elastic modulus of the cell wall $(E_{Lw})$ through the following equation:

\frac{E_{L}}{ρ} \approx \frac{E_{Lw}}{ρ_{w}}

(1)

where ρ is the wood density and

ρ_{w}

the cell-wall density. Since

ρ_{w}

is close to a constant 1500 kg m⁻³, estimates of the cell-wall rigidity can be directly obtained from macroscopic data [3–6]. In our previous works, this use of Eq. (1) was extended to time-dependent moduli obtained from creep or vibrations tests [7,8]. Using sets of viscoelastic data obtained with specimens having different MFA, we tried to characterize an intrinsic behaviour of the cell wall material. Such approach is heavily relying on the model used to explain the observed behaviour of the cell wall, made of various layers differing in their chemical composition and microfibrillar orientation. In this paper, we will address this question from a different angle. We will, again, consider a set of creep data for specimens of varying MFA. However, instead of using a structural model with partially unknown constants to fit to the results, we will simply proceed to the rheological analysis and then discuss the implication of these results, in terms of structural organisation of the cell wall.

2 Material and methods

2.1 Material

Specimens of dimensions $R = 8 mm \times T = 3.2 mm \times L = 170 mm$ were cut at various radial positions between the pith and growth-ring number 35 from a tree of European spruce (Picea abies) of age more than 40 years, supplied by INRA-Nancy, France; the latewood proportion is not listed here, but generally fell between 15% and 19%. All surfaces were sanded to minimise surface damage. The specimens were then characterised by measuring (i) the S2 microfibril angle, using the Cave X-ray diffraction method [9–11] on latewood samples with $R = 1 mm \times T = 3 mm$ , with the X-ray beam in the radial direction and some checks by the iodine-staining optical method, on thin tangential sections, and (ii) the density and Young's modulus, both of which were measured at 30% RH and 23 °C. Table 1 lists values of growth ring, density $(ρ)$ , microfibril angle (MFA), the ratio of longitudinal Young's modulus to density $(E_{L} / ρ)$ and a calculated value $(- Δ E_{2})$ , whose meaning will be introduced later.

Spec. No.	Growth ring pos.	ρ (kg m⁻³)	MFA (°)	$E_{L} / ρ$ (MN × m kg⁻¹)	$- Δ E_{2}$ (GPa)
7	10.5	409	17.7	34.1	12
27	6.1	452	13.1	33.3	13.5
33	27.2	439	6.6	41.5	0.2
34	30.5	414	6.3	40.0	3
36	31.2	462	6.5	42.1	0
39	9.1	424	7.2	36.4	8
47	7.0	458	7.5	41.6	0.4
49	16.2	403	9	39.8	3
50	10.1	392	23.7	28.6	19.8
67	5.4	474	12.7	31.8	15.3

2.2 Creep at controlled humidity

The bending-creep experiments were made in an environmental chamber maintained at $62 \pm 1 %$ RH and $19.5 \pm 0.1$ °C. The testing machines applied longitudinal four-point bending with a nominal stress of 7.5 MPa in the central part of the specimen, and bending axis in R direction, and were described in [12], together with the experimental techniques.

2.3 Analysis method

For each specimen tested, the original data was listed in a table $(t_{k}, d_{k})$ of the bending deflection $d_{k}$ measured at increasing times $t_{k}$ . The following steps of analysis are performed [13].

(1) The deflection values $d_{k}$ are extrapolated to 1 s by plotting in a $\log (t)$ scale, converted into relative creep, and into compliance $J_{k}$ using the evaluation of elastic rigidity obtained by preliminary static tests.
(2) The $J_{k}$ values are smoothed by searching for the best-fitting parabola approximating J versus $x = \log (t)$ around increasing values of x, and interpolated for these chosen x values. At the same time, we obtain an estimate of the slope of J vs x for these x values.
(3) The interpolated (J, $d J / d x$ ) are used to evaluate the components of the complex compliance $J^{*} = J^{'} + i J^{″}$ using the Alfrey approximation [14]:
(2)
(4) The specimen compliance is converted into an estimated longitudinal cell-wall compliance using the specimen density ρ and the cell-wall density $ρ_{w}$ (the latter taken as 1500 kg m⁻³):
$J_{w}^{'} = J^{'} (ρ / ρ_{w}); J_{w}^{″} = J^{″} (ρ / ρ_{w})$ (3)
(5) The complex rigidity $E^{*} = 1 / J^{*} = E^{'} - i E^{″}$ is deduced from $J^{'}$ and $J^{″}$ by:
(4)
The analysis is based on a visual assessment of the trajectories in the complex planes $(J^{'}, J^{″})$ or $(E^{'}, E^{″})$ , hoping that they will suggest appropriate rheological models to describe the behaviour of the samples [15–18].

3 Results

3.1 Smoothing and interpolation

The successive stages of the analysis are illustrated in Figs. 1 and 2, in the case of specimen No. 27. In Fig. 1a, the experimental data have been replaced by a few values equally spread in a log time scale: $\log t = 0, 0.5 \dots 6$ . In Fig. 1b, the values have been used to evaluate the real and imaginary part of the compliance (Eq. (2)) and these have been converted into cell-wall values taking into account the specimen porosity (Eq. (3)). Fig. 2a shows the resulting complex compliance ( $J^{″}$ vs $J^{'}$ ) and Fig. 2b the complex rigidity ( $E^{″}$ vs $E^{'}$ ), calculated by Eq. (4).

Fig. 1
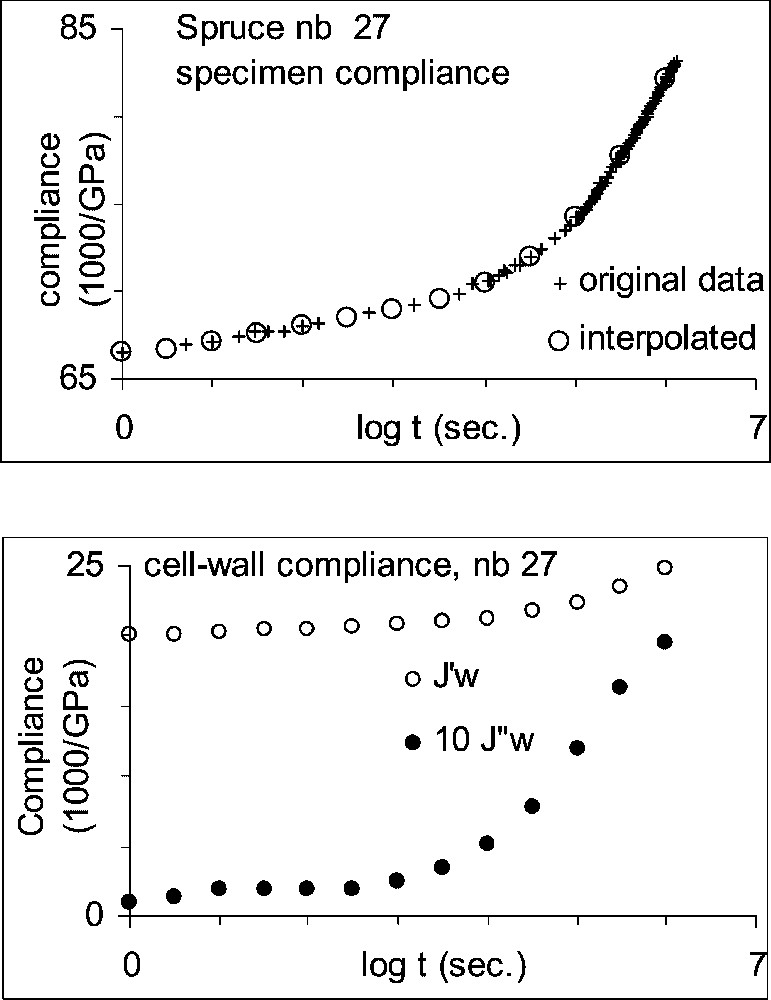
Smoothing–interpolation procedure applied to specimen No. 27: (a) interpolated compliance compared with the original data; (b) estimated components of the complex cell-wall compliance.

Fig. 2
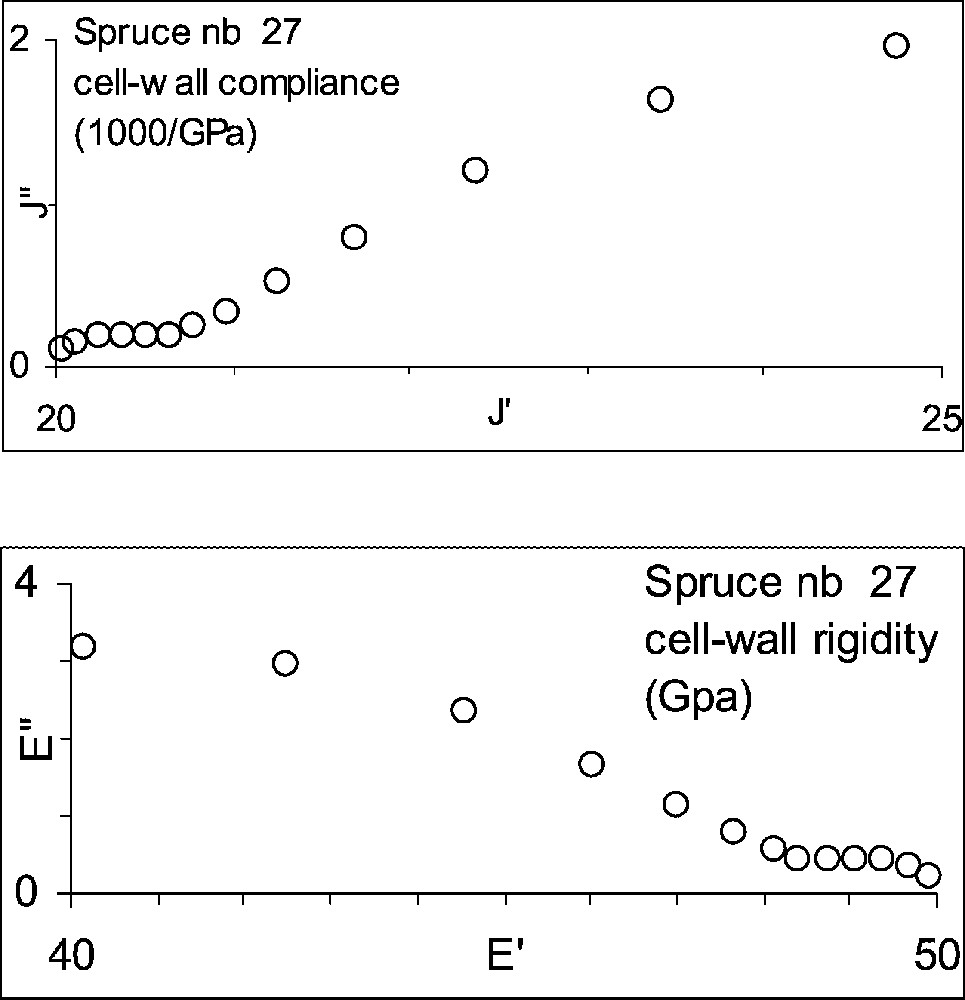
Representation of the results in the complex planes based on Fig. 1b: (a) compliance; (b) rigidity.

3.2 Complex plots and influence of the microfibrillar angle

Fig. 3 shows the complex plots of the whole set of specimens tested during this experiment. In two cases (specimens Nos. 7 and 50), the transducers became ‘sticky’ after a few days, so that we had to remove the two last points from the curves, corresponding to $\log t = 5.5$ and 6. In the compliance plots of Fig. 3a, each curve represents a creep test, starting from the left, close to the x-axis, and aiming to the right. We observe here a well-known trend: the higher the instantaneous compliance (the intercept of the trajectory with the x-axis), the higher the amount of creep during a given time (the horizontal extent of the curve). However, once the compliance has been transformed into rigidity in Fig. 3b, we observe a rather surprising phenomenon: the size of the trajectories does not depend on the specimen in any clear way, as if they could be deduced from each other by a translation along the x-axis.

Fig. 3
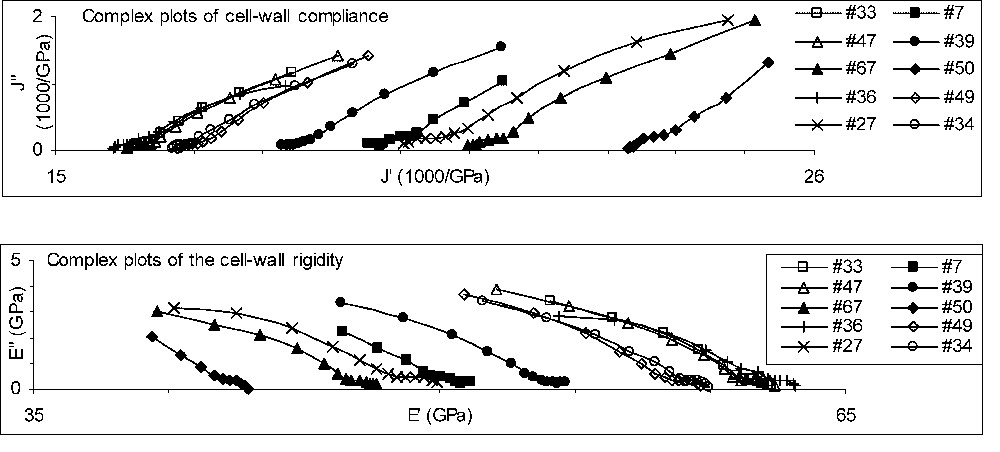
Complex plots for the whole set of specimens tested. (a) Compliance; (b) rigidity.

In Fig. 4a we have applied a horizontal shift to all curves except that of specimen No. 36, which exhibited the highest rigidity values. The amount of shift applied is given in Table 1 as $- Δ E_{2}$ . For each curve, it has been tuned manually, to reach a rather good superposition during the major relaxation process of the test between $\log t = 3$ and 6. The minor relaxation process evidenced in Figs. 3a or 3b for all specimens at the lower time scale, $\log t = 1$ to 3, is subject to more discrepancy. Fig. 4b shows that the horizontal shift $- Δ E_{2}^{″}$ increases with the MFA of the specimen, the reference specimen being also that with the smallest measured MFA. This is consistent with previous observations of more relaxation, creep or damping for higher MFA. In our sampling, other structural factors could have also influenced the behaviour, such as the higher growth ring curvature of specimens closer to pith, or varying proportion of latewood. Moreover, our MFA value might not be completely relevant for each specimen, since we did not check MFA differences between latewood and earlywood, or between radial and tangential walls. Therefore, in Fig. 4b, the MFA ϕ should be considered as a parameter expressing the structural variation within the sampling.

Fig. 4
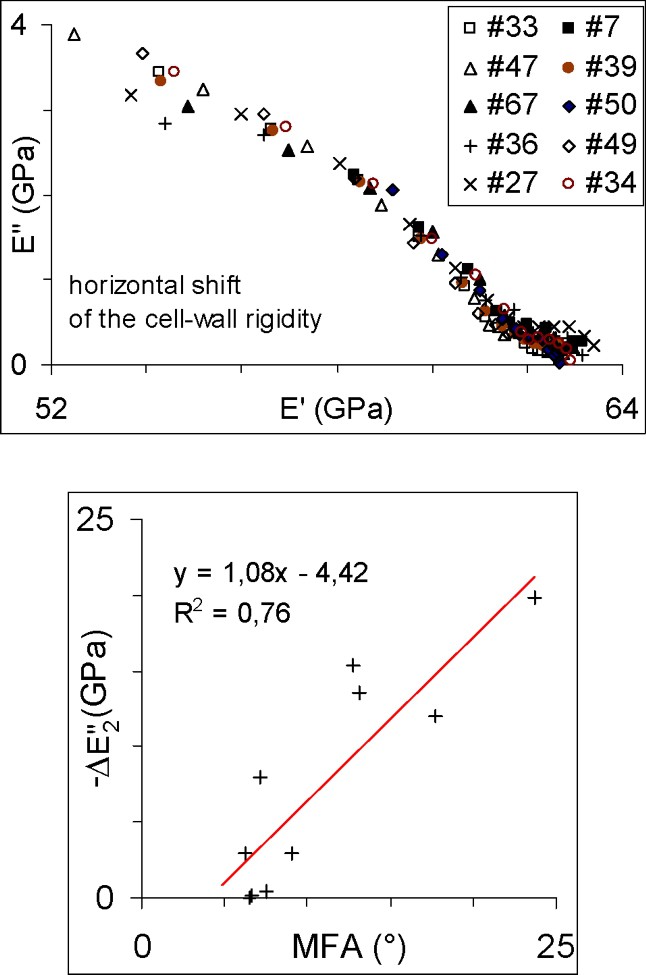
Superposition of the complex rigidity by a horizontal shift: (a) plots for all specimens, specimen No. 34 being taken as reference; (b) amount of shift as a function of the microfibrillar angle.

4 Discussion

4.1 Construction of a predictive model

In Fig. 5 the data of Fig. 4a have been redrawn at a wider scale, with equal units for the x- and y-axes. Excluding the points corresponding to the earliest stage of the relaxation process ( $t < 1000 s$ ), the remaining points could be considered as a portion of circle, plotted as a dotted line. As explained by Huet [15], a portion of circle in the complex plane indicates the possibility to use a parabolic model to represent the rheological behaviour of a viscoelastic material like wood. The parameters of the parabolic link can be evaluated by visual assessment of the graph: the rigidity of the link $E_{1}^{0}$ is given by the horizontal extent of the circle portion, the parabolic order $p_{1}$ by the ratio of the vertical extent to half the horizontal extent, and the characteristic time $τ_{1}$ by the time needed to reach the highest point. In the case of the circle portion shown in Fig. 5, we have $E_{1}^{0} \approx 28 GPa$ , $p_{1} \approx 0.28$ , $\log τ_{1}$ (s) ≈7 to 8. For $τ_{1}$ , this is a very rough estimate, since obviously the peak has not been reached during the test. The total relaxation function given by this model would be of the form $E_{1} (t) + E_{2}$ , where $E_{2}$ is the left intercept with the x-axis of the circle portion; in this case, $E_{2} = 35 GPa$ . For all specimens but No. 36, the horizontal shift should be accounted for, giving an $E_{2}$ value depending on the specimen, but an unchanged $E_{1} (t)$ . The plot of Fig. 4b suggests that $E_{2}$ could be considered, as a rough approximation, as a linear function of the MFA $(ϕ)$ :

E_{2} (ϕ) \approx 35 - (1.1 ϕ - 4.4) \approx 39.4 - 1.1 ϕ (ϕ in °, E_{2} in GPa)

This would result in a rather simple model of the longitudinal relaxation function, as:

E (t) = E_{1} (t) + E_{2} (ϕ) = E_{1}^{\infty} R_{p1} (t / τ_{1}) + E_{2} (ϕ)

where

R_{p1}

is a function of the reduced time

t / τ_{1}

, giving the relaxation response of a parabolic link of unit rigidity and parabolic order

p_{1}

. If necessary for practical computation,

R_{p1} (t / τ_{1})

can be replaced by a sum of Maxwell functions of the form

A_{1k} \exp [- t / τ_{1k}]

, with the

τ_{1k}

equally spread along a logarithmic scale around

τ_{1}

, and the sum of the

A_{1k}

normalised to 1 [13].

Fig. 5
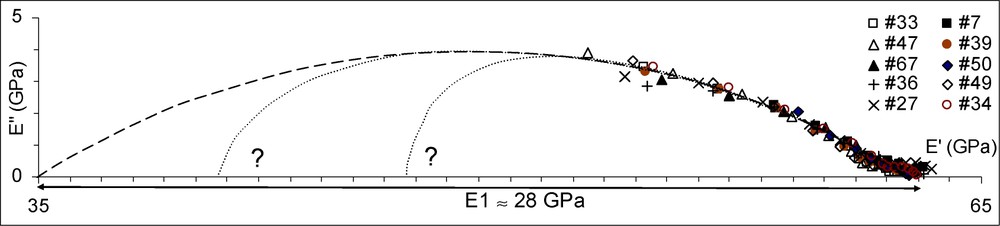
Construction of a parabolic model.

4.2 Physical interpretation

The rheological representation of the model proposed is drawn in Fig. 6, with two parallel links. The first link is represented by a spring of rigidity $E_{1}^{0}$ in series with a parabolic dashpot, characterised by $τ_{1}$ and $p_{1}$ . The second link is purely elastic, with a rigidity $E_{2}$ depending on ϕ. The image carried by this representation is that the cell wall would be made of two regions, labelled (1) and (2), arranged in parallel with respect to the fibre direction, characterised by the instantaneous rigidities $E_{1}^{0}$ and $E_{2}$ , respectively. ‘Instantaneous’, in the present case, must be understood as a rough time order of 100–1000 s. In the experimental window considered here (range of time observed), no viscoelastic process occurs in region (2), while it is starting to occur in region (1). At small times, the region (1) supports a part of the load given by $E_{1}^{0}$ , while that supported by (2) is given by $E_{2}$ . At an intermediate time t, the region (1) supports a part of the load given by $E_{1} (t)$ . After an infinite time, the region (1) is fully relaxed and supports no more load, while all is supported by (2) – provided no new relaxation process has started.

Fig. 6
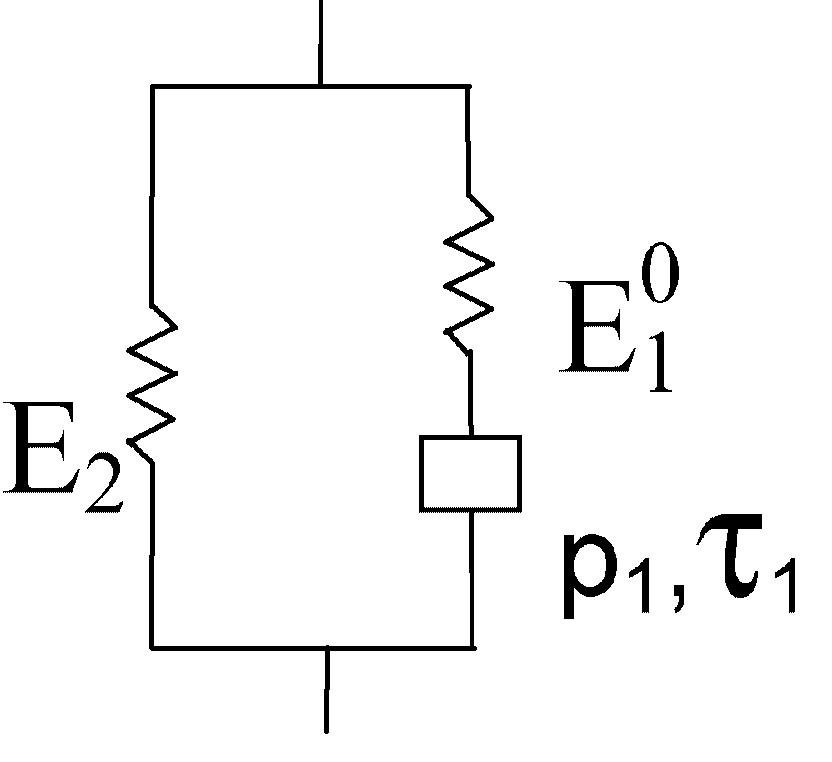
Analogical representation of the rheological behaviour.

Since ϕ is the mean microfibrillar angle of the S2 layer, and only E2 seems to depend on it, it is tempting to assimilate the region (2) to the S2 layer, and the region (1) to S3, S1, P and the middle lamella, considered as a single set. Provided, of course, that our results be confirmed by more extensive experimental data, they would mean that, contrarily to common intuition, the S2 layer is not directly involved in the relaxation process of air-dry wood, at least in the experimental window considered here ( $t > 1000 s$ ).

However, there is a default with this interpretation. In the MFA range considered here, 6 to 24°, the value of $E_{2}$ decreases from 35 to 15 GPa, in the same order as the value of 28 GPa obtained for $E_{1}^{0}$ . If the two links were corresponding to the two parts of the cell wall, as suggested previously, we would have expected a much higher contribution of S2 to the overall rigidity. Two explanations can be proposed to maintain the interpretation proposed. First, link No. 2 could be considered to represent, not exactly the contribution of the whole of S2, but of the lamellae of S2 containing microfibrils; lamellae of lignin disposed between sub-lamellae of microfibrils, would be contributing to link No. 1. Second, the evaluation of $E_{1}^{0}$ made in Fig. 5 is heavily relying on the assumption that the viscoelastic processes are parabolic. In a previous work, a very different type of extrapolation was proposed based on similar experimental data [19]. Anyway, other models could have suggested other extrapolations, like those indicated on the graph with a question mark. They could result in significantly lower estimates for $E_{1}^{0}$ , more compatible with the proposed physical interpretation.

Acknowledgment

We thank Dr Jean-Michel Leban from INRA–Nancy for kindly supplying us with the test material.

Bibliographie

[1] B. Thibaut; J. Gril; M. Fournier Mechanics of wood and trees: some new highlights for an old story, C. R. Acad. Sci., Ser. IIb, Volume 329 (2001) no. 9, pp. 701-716

[2] B.G. Butterfield Microfibril angle in wood, Int. Assoc. Wood Anatomists Publ., Chicago, 1998

[3] D.R. Cowdrey; R.D. Preston Elasticity and microfibrillar angle in the wood of Sitka spruce, Proc. R. Soc. Lond., Ser. B, Volume 166 (1966) no. 1004, pp. 245-272

[4] I.D. Cave Modelling the structure of the softwood cell wall for computation of mechanical properties, Wood Sci. Technol., Volume 10 (1976), pp. 19-28

[5] L. Salmen; A. de Ruvo A model for the prediction of fiber elasticity, Wood Fiber Sci., Volume 17 (1985) no. 3, pp. 336-350

[6] M. Norimoto; F. Tanaka; T. Ohogama; R. Ikimune Specific dynamic Young's modulus and internal friction of wood in the longitudinal direction, Wood Res. Tech. Notes, Volume 22 (1986), pp. 53-65

[7] J. Gril, Une modélisation du comportement hygro-rhéologique du bois à partir de sa microstructure, PhD thesis, University Paris-6, France, 1988

[8] D. Hunt; J. Gril Estimation of cell-wall compliance from creep measurements (B.G. Butterfield, ed.), Proc. Int. Conf. on the Significance of Microfibril Angle to Wood Quality, Wesport, New Zealand, 21–26 November 1997, 1998, pp. 397-409

[9] I.D. Cave Theory of X-ray measurement on microfibril angle in wood, For. Prod. J., Volume 16 (1966), pp. 37-42

[10] B.A. Meylan Measurement of microfibril angle by X-ray diffraction, For. Prod. J., Volume 17 (1967) no. 5, pp. 51-58

[11] H. Yamamoto; T. Okuyama; M. Yoshida Method of determining the mean microfibril angle of wood over a wide range by the improved Cave's method, Mokuzai Gakkaishi, Volume 39 (1993) no. 4, pp. 375-381

[12] D.G. Hunt The mechano-sorptive creep susceptibility of two softwoods and its relation to some other materials properties, J. Mater. Sci., Volume 21 (1986), pp. 2088-2096

[13] J. Gril; D. Hunt Analysing wood creep at constant moisture using phase diagrams (P. Navi, ed.), Proc. 1st Int. Conf. of the European Society for Wood Mechanics, Lausanne, Switzerland, 19–21 April 2001, 2002, pp. 73-81

[14] T. Alfrey Mechanical behaviour of high polymers, Interscience Publishers, New York, 1948

[15] C. Huet Représentation des modules et complaisances complexes dans les plans complexes arithmétique et logarithmique, Cah. Groupe Fr. Rhéol., Volume 5 (1967) no. 1, pp. 237-258

[16] C. Huet Some aspects of the thermo-hygro-viscoelastic behaviour of wood (P. Morlier, ed.), Eur. Conf. on Mechanical Behaviour of Wood, Bordeaux, France, 8–9 June, 1988, pp. 104-118

[17] C. Huet; P. Navi Multiparabolic multitransition model for thermo-viscoelastic behaviour of wood, ASME Winter Annual Meeting, Dallas, Texas, USA, 1990, pp. 17-24

[18] S. Bardet; J. Gril Modelling the transverse viscoelasticity of green wood using a combination of two parabolic elements, C. R. Mecanique, Volume 330 (2002) no. 8, pp. 549-556

[19] D. Hunt Strain rate versus strain plots and creep-limit studies (P. Navi, ed.), 1st Int. Conf. of the European Society for Wood Mechanics, Lausanne, Switzerland, 19–21 April 2001, 2002

^☆ A tribute to Bernard Monties, who played a significant role in the development of academic wood research in France, through his strong involvement in many discussions and policy decisions, his wide culture, his energy.

Commentaires - Politique