1 Introduction
Comparison of biological macromolecules has become an everyday task for biologists, for extremely diverse purposes such as genomic sequencing, structural modelling, functional inference, phylogenetic reconstruction, allelic or mutational analyses, etc. In all cases, comparison methods rely on a fundamental postulate that one can simply state as: “the closer in the evolution, the more alike and reversely, the more alike, probably the closer in the evolution” [1]. Numerous computer-based tools are used to estimate the proximity of protein sequences [2]. Alignment of two sequences is typically done by maximizing (or minimizing) a given quantity, named score, which reflects the shared features of the two biological entities. Global alignment algorithms [3] are not accurate to assess homology of domains in modular proteins [4]; local alignments are better suited [5,6]. They use scoring matrices to maximize the summed scores of compared residues and find optimal local alignments, computed with a dynamic programming procedure [2–6]. Scoring matrices have been found to be similarity matrices as well [2,4,6]. Many similarity matrices are available [7–10] and evaluation studies led to the conclusion that those based on a log-odds ratio, like BLOSUM 62 [8], over performed the others [9]. BLOSUM 62 was computed using blocks of aligned sequences with
| (1) |
Karlin and Altschul [11] have shown that substitution matrices depend on a particular set of data in which amino acids are paired with frequencies that correspond to the matrices' target frequencies. If the set of data is made up of aligned homologous sequences, then the matrix is usable to distinguish distant local homologies, from similarities due to chance [12]. Using information theory, Altschul [12] have further reported that substitution matrices can be evaluated using the average information they contained. This average information, known as the relative entropy of Shannon (1948) [13], was computed as
| (2) |
Given a probability law P that characterizes a random variable, the Hartley self-information h [15] is defined as the amount of information one gains when an event i occurs:
| (3) |
| (4) |
| (5) |
If the occurrence of one of the two events makes the second impossible, mutual information is equal to −∞. If the two events are fully independent, mutual information is null.
Recently, we rigorously demonstrated that the score between two amino acids was the mutual information, in the sense of Hartley, between the two considered amino acid (Bastien et al., submitted), that is to say:
| (6) |
Whereas the BLOSUM model is efficient in most cases, it fails to estimate satisfactorily the alignment between two proteins of very different amino acid composition [16–18]. A major reason lies in Eq. (1) that does not account for the distinct sequences where the amino acids i and j are sampled. This can be of importance when compared proteins are from very different cell environments (like soluble or membrane-bound proteins) or of strongly different amino acids composition [18–21]. In a pioneering study addressing this problem, Müller et al. [22] introduced a non-symmetric substitution matrices model for the comparison of homologous trans-membrane proteins and showed that this kind of matrices had a larger discrimination power, i.e. specificity. We reformulated this model for the comparison of biased and non-biased genomes ([16] and the present work).
Considering the general case of genome comparison with distinct global amino acid compositions, we used mutual information theory to construct non-symmetric substitution matrices dedicated to the detection of homologous sequences. An important application is the computing of non-symmetric matrices for the comparison between complete proteomes with deep differences in their composition in amino acids. Comparison of Arabidopsis thaliana and Plasmodium falciparum proteomes is given as a case study.
2 Methods
2.1 Nomenclature for sequences databases (query, subject, Species 1 and 2) and for the non-symmetric DirSp1Sp2 matrices
In molecular alignments, we used the standard nomenclature for homology searches methods, i.e. query for a known probing sequence (or database of sequences) that is compared to another sequence (or database of sequences), termed subject. The family of non-symmetric matrices computed here were dedicated to the comparison of a query sequence from a first species (termed Species1) with a subject database, or a single sequence, from a second species (termed Species2). The family of amino acid substitution matrices referred to as DirSp1Sp2 (Species1 → Species2) were designed to be implemented in the conventional BLASTP alignment algorithm: columns correspond to the query (or Species1) and rows to the subject (or Species2) entries.
2.2 Identification of a non-redundant set of homologous proteins between Arabidopsis thaliana and Plasmodium falciparum
As a source of genomic sequence material, we selected the annotated sequences from Arabidopsis thaliana and Plasmodium falciparum from Internet databases, respectively the National Center for Biotechnology Information server (ftp://ftp.ncbi.nih.gov) and the Plasmodb genome resource (http://plasmodb.org/). The massive annotation resulting from collaborative efforts, genomic annotations contain errors. We selected therefore annotated sequences that were judged trustworthy at the downloading date in the respective Internet-available databases, i.e. 25 545 sequences from A. thaliana as of December 2002, 5334 from P. falciparum as of December 2002. According to a method describe previously [18], the two proteomes were used to identify a non-redundant set of homologous proteins using the BLASTP program and the Smith–Waterman algorithm [5,6], implemented in the Biofacet software package (Gene-IT, France, [23]). To remove the similarity redundancies from P. falciparum and A. thaliana protein-sequence databases, for each proteome, we built up a random proteome database containing an identical number of protein sequences, of identical size and amino acid distribution, in which each sequence was an obligate shuffling of a corresponding sequence from the original database. Each real protein of a given organism was compared to all the sequences of the random database using BLASTP algorithm; the best alignment P-value was collected. From the distribution of the self x random P-values, a 5-percentile was set to define a cut-off. Then, for each species, the calculated cut-off was used as a criterion to partition the proteome owing to the single-linkage clustering method. Eventually, the longest sequence was drawn from each similarity cluster to build up non-redundant proteomes. All proteins from the A. thaliana non-redundant proteome were compared to the P. falciparum non-redundant proteome, using the SW algorithm. For each alignment, a Z-value was computed and a Z-value-cut-off of 8 was used to create clusters of aligned P. falciparum × A. thaliana sequences, owing to the single-clustering method. In this paper, this set was termed ‘automatic training set’. Clusters were examined manually to select pairs of sequences whose functional annotation appeared analogous. This set was termed ‘manual training set’ (see table in [18]).
2.3 Initial construction of a database of protein blocks, from pairs of aligned sequences from Species1 and Species2 (or query and subject)
As described by [24], local alignments can be represented as ungapped blocks with each row a different protein segment and each column an aligned residue position. In the particular case described here, blocks can be simply derived as ungapped segments in pairs of aligned sequences. These 2-line blocks were ordered so that the first sequence always belongs to the same genome. Substitutions of a given amino acid from a first sequence (Species1 or query) with another amino acid from a second (Species2 or subject) were counted in all pairs of matching amino acids in each blocks in the database and then summed. The substitution frequency table is used to calculate matrices representing the odd ratio between these observed frequencies and those expected by chance.
2.4 Families of similarity matrices computed from blocks filtered by segment clustering
Closely related blocks in blocks databases exhibit a high percentage of identity, up to 100% when no amino acid substitution is observed in aligned sequences. Evolutionary divergence is marked by a decrease in the identity percentage. Thus, the distribution of the identity percentages within a block database can lead to a biased calculation of substitution matrices, that over- or underscores alignments of close or distant sequences. Therefore, for each matrix computing, the training set of blocks was filtered using a clustering percentage, so that sequence segments that were identical for at least that percentage of amino acid were kept for the substitution frequency counting. This filtering is an alternative definition of the clustering percentage described by [8], in which the multiple contribution of segments that were identical for at least that percentage, were averaged in calculating pair frequencies. In both cases, the decrease in the clustering percentage implies a decrease in the contribution of the blocks which percentage of identity is higher than the clustering percentage. Like for the BLOSUM family of matrices, varying the clustering percentage leads to a family of matrices.
2.5 Iterative process in the computation of non-symmetric matrices
Construction of DirSp1Sp2 matrices was stepwise. Frequency tables, matrices, and programs for UNIX machines were primarily designed using the Biofacet multipurpose package (Gene-IT, Rueil-Malmaison, [23]. The initial training set of pairs of sequences derived from alignments using the Smith–Waterman algorithm implemented with BLOSUM 62. For a given clustering percentage, an initial non-symmetric matrix was computed, and indexed 1: DirSp1Sp21. The initial training set was then re-aligned using the Smith–Waterman algorithm implemented with this first non-symmetric matrix. From these alignments, ungapped segments were selected and filtered owing to the defined clustering percentage, and used as a new database of Blocks to compute a new non-symmetric matrix indexed 2: DirSp1Sp22. The process was iterated, outputting a convergent family of matrices DirSp1Sp2,3, DirSp1Sp2,4, …DirSp1Sp2,n. The stable matrices where referred to as un-indexed DirSp1Sp2.
3 Results and discussion
3.1 Question of the mutual information between two homologous sequences of distinct amino acid distributions
The physical environment of proteins, (pH, water solubility or association to membranes), the codon use that is required for their synthesis or nucleotidic compositional trends are constraints that can lead to very uncommon amino acid distributions in some families of protein or even in complete proteomes [16–18,22]. Although biased amino acid distributions affect the performance of protein comparison tools built for ‘average’ amino acid distributions, they can bring useful information to discriminate homologous proteins. To that purpose, we considered two kinds of sequences, or set of sequences, the first named query, the second subject. For example, query sequence can be from a first species, called Species1 (such as Arabidopsis thaliana; with an average nucleotidic −55% A+T− and amino acid distribution) and the subject sequence from a second species, called Species2 (such as Plasmodium falciparum; which nucleotidic bias −82% A+T− leads to a biased compositional proteome).
We can consider two kinds of events: given the amino acids i in the subject sequence and given the amino acids j in the query sequence (as an application, X can be defined in a given species such as Arabidopsis thaliana and Y in another such as Plasmodium falciparum). The self-information h, for the occurrence of a given amino acid does not have the same signification in the context of each sequence:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
| (12) |
3.2 Training sets to compute non-symmetrical substitution matrices
Determining sets of homologous sequences is a difficult question. Here, we examined the possibilities of an automatic or manual selection of a training set of pairs of similar sequences, in the given example of Arabidopsis thaliana and Plasmodium falciparum proteomes, obtained after an all-against-all comparison of non-redundant protein sequence databases. We selected genomic sequences from A. thaliana (25 545 annotated sequences as of December 2002) and P. falciparum (5334 annotated sequences as of December 2002). The strong nucleotidic bias of the P. falciparum genome (82% AT) strikingly affects the amino acid distribution within encoded proteins (Fig. 1). Six amino acids (N, K, I, L, E, and S) account for 51% of the total amino acid content in proteins. Fig. 1 shows that the amino acid distribution in A. thaliana is strongly divergent, with a more balanced contribution of individual amino acids to the overall composition of proteins. On top of the very strong amino acid bias found in P. falciparum, the protein sequences exhibit a very low complexity, marked by long stretches of repeated amino acids. It is still not known whether the very low complexity is solely due to the amino acid bias or if a generic mechanism dedicated to the insertions of amino acid repeats would contribute to this striking occurrence of repeated amino acid portions in proteins. For an in-depth discussion of the biological rational of P. falciparum bias as compared to A. thaliana, see [18]. We selected a training set of similar sequences, which was either directly used for matrices' calculations (automatic sampling) or with the restriction that the analogy of the protein function could be assessed by inspection of an expert curator (manual sampling). The advantage of the manual training set, described in [18], lies in its quality, but it is costly. Although one might question the quality of the automatic sample, the case study in the present paper proved that no major difference between the converging matrices calculated from the manual and the automatic training sets could be noticed. Because a model generalization and a pragmatic computation of matrices would benefit mostly from a fully automated method, we therefore detailed results obtained in that context.
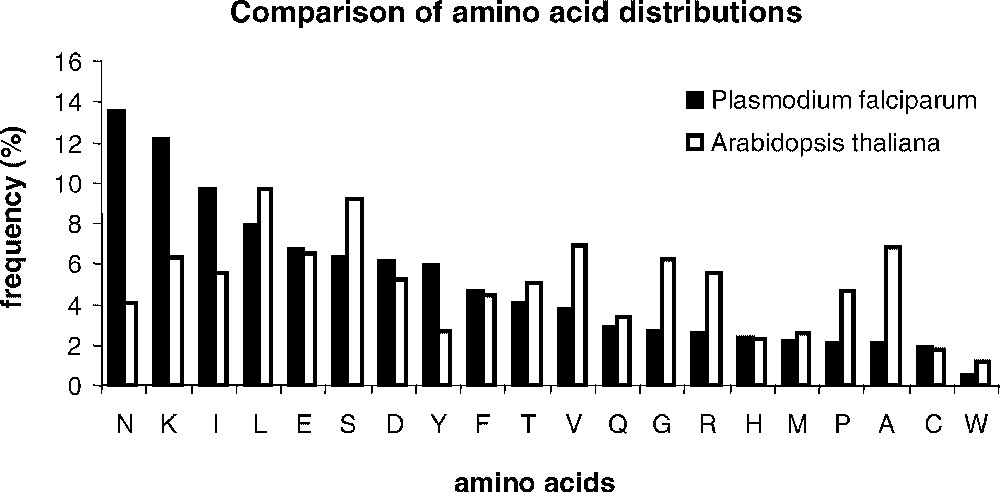
Comparison of the amino acid distribution in the Plasmodium falciparum and Arabidopsis thaliana proteomes. Frequencies were calculated using the set of 71 pairs of homologous sequences selected with the method described in [17] from the two complete proteomes (see material and methods). Amino acids were ranked owing to their frequencies in P. falciparum.
3.3 Convergence of the non-symmetric matrices obtained after iterative computation
Blocks used to calculate matrices were filtered as described in the Methods section, according to a clustering percentage. Matrices were termed dirSp1Sp2, with Sp1 being the query species, and Sp2 the subject species. The matrices devoted to the comparison of A. thaliana and P. falciparum are therefore called dirAtPf matrices. We generated matrices corresponding to eleven block clustering percentages (dirAtPf100n for a clustering percentage = 100% and n iterations, dirAtPf90n, …, dirAtPf50n). We analysed the evolution of the matrices obtained after each iterative round (summarized in Fig. 2). Fig. 3 shows the number of amino acids that are initially aligned by the generalist matrix BLOSUM 62 in the training set and after alignments using matrices computed after 1, 4, 7 and 9 iterations. From the very first matrix computation, one notice a decrease in the number of aligned amino acid, with a very rapid convergence, as early as ∼10 iterations. Interestingly, in the present result, convergence appears as a decrease in the number of amino acids ‘detected’ by the non-symmetrical matrices. That decrease would suggest that, in the case of well-assessed alignments, the non-symmetrical matrices are more specific. By contrast, although they converge to a close result, matrices computed with a manual training set exhibit an increase in the number of aligned amino acid along the training process. That increase would conversely suggest that in the case of hypothetical alignments, the non-symmetrical matrices would lead to a gain in sensitivity. Thus it appears that an apparent gain in selectivity and specificity would be obtained. To that extent, and as mentioned by Müller et al. [22], definition of a specificity/sensitivity gain when deriving substitution matrices is difficult to rigorously assess. The matrices obtained from automatic or manual samples exhibited identical trends for each terms: no opposite deviations were observed. For all clustering percentages, convergence was also observed for the number of detected blocks and the value of the matrices (data not shown).
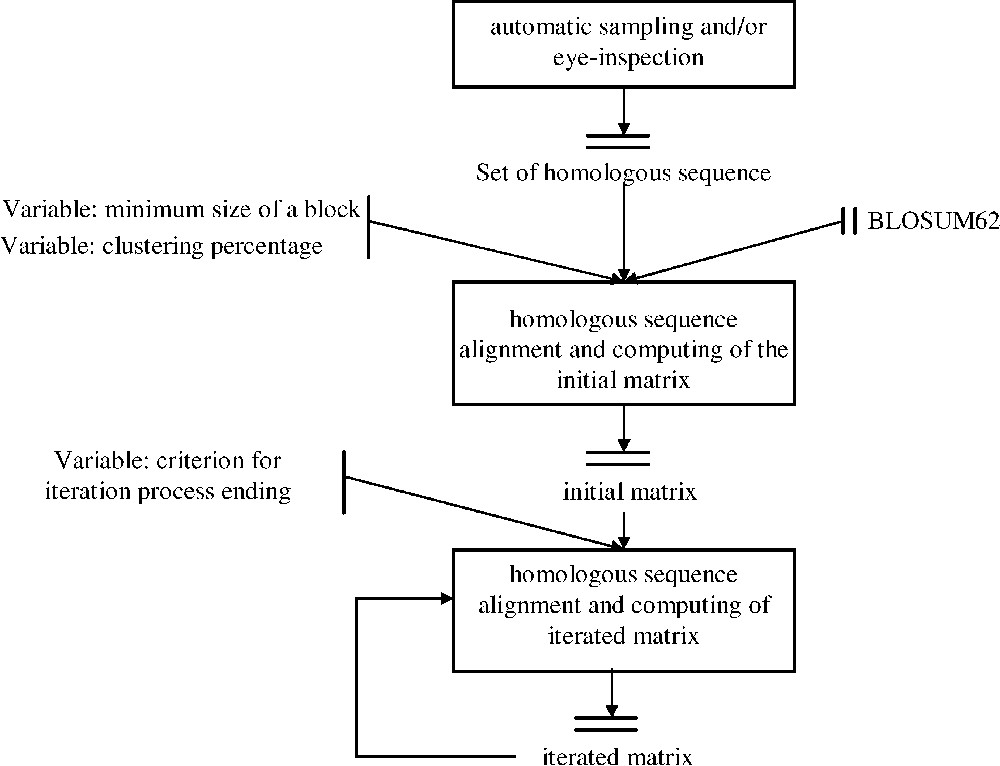
dirSp1Sp2 matrices iterative computing Workflow. After sampling a set of pairs of homologous sequences between Species1 and Species2, these sequences were primarily aligned using BLOSUM 62 in order to determine conserved block. BLOSUM 62 is therefore used as a way to initially ‘anchor’ homologous regions. These blocks are considered only if they have both the required minimum size and a maximum given percentage of identity, named clustering percentage. The first deduced matrix, called initial matrix, is then used to iterate the process and lead to a sequence of dirSp1Sp2 matrices. A convergence criterion is applied on the sequence dirSp1Sp2n so as to end the process.
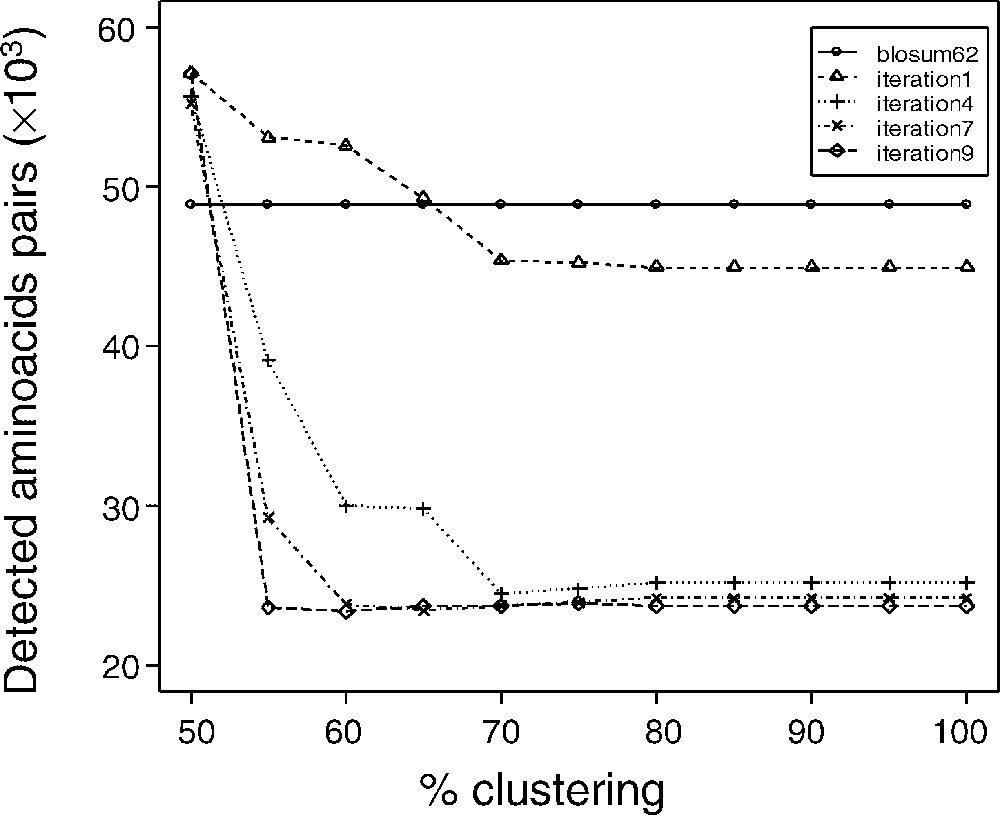
Convergence of the matrices computing iterating process. Convergence of the iterating process was studied according to the number of detected aligned amino acids pairs. For all clustering percentage, convergence was also observed for the number of detected blocks and the value of the matrices (data not shown). Except for the 50% clustering percentage, convergence leads to a number of aligned amino acids pairs lower than that obtained with the BLOSUM 62 matrix. As described by Müller et al. [22], non-symmetric matrices lead to an increase of the discrimination power of the matrices, an expression of a more accurate mutual information values.
3.4 Asymmetry of the DirSp1Sp2 matrices: case study of DirAtPf
We generated all the convergent dirAtPf matrices after a 10-iteration computation process dirAtPf10010, dirAtPf9010, …, dirAtPf5010, indistinctly called dirAtPf100, dirAtPf90, …, dirAtPf50. All the matrices we obtained were non-symmetric, as shown in Fig. 4 for dirAtPf100. In detail, the sub-matrices (N, R) × (N, R) giving the mutual information between all substitution available between Asparagines (N) and Arginines (R) stresses the different roles played by these two amino acids in the two proteomes, as recorded by Singer and Hickey [20] and Bastien et al. [17].

BLOSUM 62 and dirAtPf100 substitution matrices.
3.5 Analysis of the relative entropy H of the family of DirAtPf matrices
As described earlier for the family of BLOSUM matrices [8], the relative entropy H derived from Eq. (2) decreases with the blocks clustering percentage (Fig. 5). Interestingly, relative entropy values in dirAtPf matrices (0.5–1.5 bits) are slightly higher than those of the BLOSUM or PAM matrices (0.2–1.2 bits) [7,8]. Following the theory of information, this higher relative entropy would suggest a higher sensitivity of dirAtPf matrices as compared to symmetrical matrices.
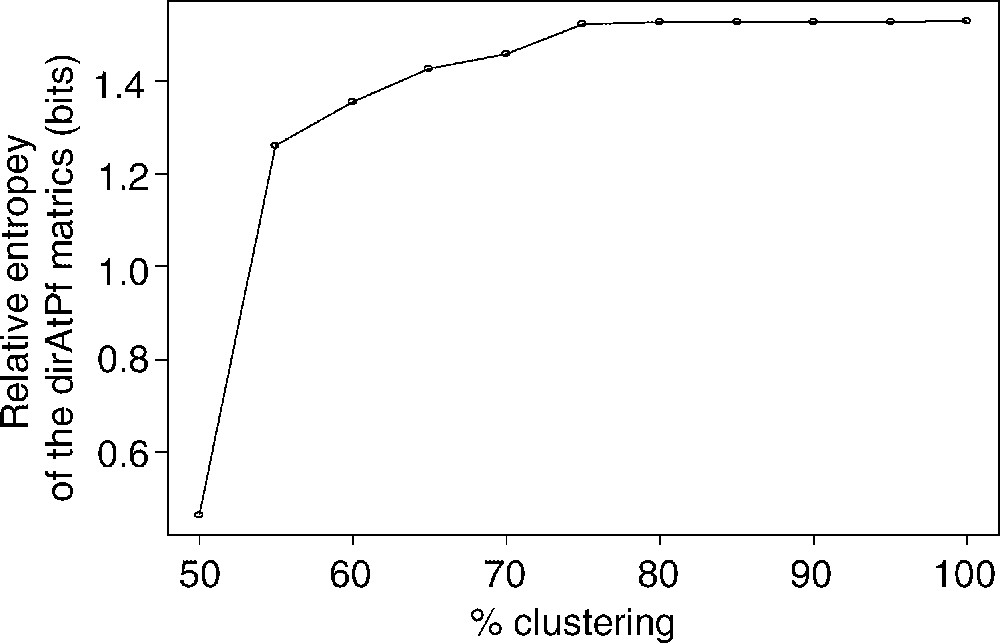
Evolution of the relative Entropy as a function of the clustering percentage. As intuitively predicted by Müller et al. [22], the better definition of the mutual information between aligned amino acids leads to a higher relative entropy than this of BLOSUM 62 (H≅0.69).
4 Conclusion
This article describes a method to compute a novel family of substitution matrices that are dedicated to the comparison of proteins, which amino acid composition deviates from the average distribution. They exhibit remarkable features such as (i) the possibility of computing reliable matrices from automatically selected pairs of similar sequences (automatic training sets), (ii) a rapidly convergent iterative process, and (iii) an increase in relative entropy. Still the selectivity/sensitivity gain is difficult to assess besides pragmatic use. Families of matrices for pairwise proteome comparisons including biased genomes such as that of Plasmodium flaciparum (AT rich) or Chlamydomonas reinhardtii (GC rich) are expected to be improved.


