Steady-state kinetic behaviour of two- or <i>n</i>-enzyme systems made of free sequential enzymes involved in a metabolic pathway

Guillaume Legent; Michel Thellier; Vic Norris; Camille Ripoll

doi:10.1016/j.crvi.2006.02.008

Biological modelling / Biomodélisation

Steady-state kinetic behaviour of two- or n-enzyme systems made of free sequential enzymes involved in a metabolic pathway
[Comportement cinétique en conditions stationnaires de systèmes bi- ou multienzymatiques constitués d'enzymes libres intervenant séquentiellement dans une voie métabolique]

Présenté par : Michel Thellier

Guillaume Legent ^1,² ; Michel Thellier ^1,² ; Vic Norris ^1,² ; Camille Ripoll ^1,²

¹ Laboratoire AMMIS (Assemblages moléculaire : modélisation et imagerie SIMS), FRE CNRS 2829, faculté des sciences de l'université de Rouen, 76821 Mont-Saint-Aignan cedex, France
² Epigenomic Project, Genopole®, 93, rue Henry-Rochefort, 91000 Évry, France

Comptes Rendus. Biologies, Volume 329 (2006) no. 12, pp. 963-966.

Résumés

Anglais
Français

The overall rate of functioning of a set of free sequential enzymes of the Michaelis–Menten type involved in a metabolic pathway has been computed as a function of the concentration of the initial substrate under steady-state conditions. Curves monotonically increasing up to a saturation plateau have been obtained in all cases. The shape of these curves is sometimes, but not usually, close to that of a hyperbola. Cases exist in which the overall rate of reaction becomes quasi proportional to the concentration of initial substrate almost up to the saturation plateau, which never occurs with individual enzymes. Increasing the number of enzymes sequentially involved in a metabolic pathway does not seem to generate any particularly original behaviour compared with that of two-enzyme systems.

La vitesse globale de fonctionnement d'un ensemble d'enzymes michaéliennes impliquées séquentiellement dans une voie métabolique a été calculée en fonction de la concentration du substrat initial en conditions stationnaires. Des courbes monotones croissantes jusqu'à un plateau de saturation ont toujours été obtenues. Ces courbes ont parfois, mais rarement, une forme proche de celle d'une hyperbole. Il arrive que la vitesse globale de réaction devienne quasi proportionnelle à la concentration du substrat initial pratiquement jusqu'au plateau de saturation, ce qui ne se produit pas lorsqu'une seule enzyme intervient. Il ne semble pas qu'augmenter le nombre d'enzymes différentes impliquées dans la transformation du substrat initial en produit final génère des comportements originaux par rapport aux systèmes à deux enzymes.

Métadonnées

Reçu le : 2006-01-09
Accepté le : 2006-02-28
Publié le : 2006-09-07

PMID

DOI : 10.1016/j.crvi.2006.02.008

Keywords: Enzyme kinetics, Metabolic pathways, Modelling, FDS
Mot clés : Cinétique enzymatique, Voies métaboliques, Modélisation

Affiliations des auteurs :

Guillaume Legent ^{1, 2} ; Michel Thellier ^{1, 2} ; Vic Norris ^{1, 2} ; Camille Ripoll ^{1, 2}

¹ Laboratoire AMMIS (Assemblages moléculaire : modélisation et imagerie SIMS), FRE CNRS 2829, faculté des sciences de l'université de Rouen, 76821 Mont-Saint-Aignan cedex, France
² Epigenomic Project, Genopole®, 93, rue Henry-Rochefort, 91000 Évry, France

@article{CRBIOL_2006__329_12_963_0,
     author = {Guillaume Legent and Michel Thellier and Vic Norris and Camille Ripoll},
     title = {Steady-state kinetic behaviour of two- or \protect\emph{n}-enzyme systems made of free sequential enzymes involved in a metabolic pathway},
     journal = {Comptes Rendus. Biologies},
     pages = {963--966},
     publisher = {Elsevier},
     volume = {329},
     number = {12},
     year = {2006},
     doi = {10.1016/j.crvi.2006.02.008},
     language = {en},
}

TY  - JOUR
AU  - Guillaume Legent
AU  - Michel Thellier
AU  - Vic Norris
AU  - Camille Ripoll
TI  - Steady-state kinetic behaviour of two- or n-enzyme systems made of free sequential enzymes involved in a metabolic pathway
JO  - Comptes Rendus. Biologies
PY  - 2006
SP  - 963
EP  - 966
VL  - 329
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crvi.2006.02.008
LA  - en
ID  - CRBIOL_2006__329_12_963_0
ER  -

%0 Journal Article
%A Guillaume Legent
%A Michel Thellier
%A Vic Norris
%A Camille Ripoll
%T Steady-state kinetic behaviour of two- or n-enzyme systems made of free sequential enzymes involved in a metabolic pathway
%J Comptes Rendus. Biologies
%D 2006
%P 963-966
%V 329
%N 12
%I Elsevier
%R 10.1016/j.crvi.2006.02.008
%G en
%F CRBIOL_2006__329_12_963_0

Guillaume Legent; Michel Thellier; Vic Norris; Camille Ripoll. Steady-state kinetic behaviour of two- or n-enzyme systems made of free sequential enzymes involved in a metabolic pathway. Comptes Rendus. Biologies, Volume 329 (2006) no. 12, pp. 963-966. doi : 10.1016/j.crvi.2006.02.008. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2006.02.008/

Version originale du texte intégral

1 Introduction

Proteins involved in metabolic pathways are often distributed non-randomly as multimolecular assemblies that may range from quasi-static, multi-enzyme complexes to transient, dynamic protein associations [1–6]. A functioning-dependent structure (FDS) is such an enzyme complex that forms and maintains itself as a result of its action in accomplishing a task [7]. Moreover, in the case of an extremely simplified model system, we have inferred that such FDSs may display unexpected kinetic properties under steady-state conditions [7]. Before endeavouring to build a complete theory of FDS functioning under realistic conditions, it was necessary to study the behaviour of free (i.e. non-engaged in a FDS) enzymes involved sequentially in a metabolic pathway. This is the aim of the present contribution, in which the calculations have been made according to the classical approach of enzyme kinetics [8].

2 The model of free sequential enzymes

A model of free sequential enzymes of the Michaelis–Menten type is represented in Fig. 1, in the case of a two-enzyme system catalysing the transformation of an initial substrate S₁ into a final product S₃. This model system is made of two reaction circuits, where the first and second circuits correspond to the activity of the first and second enzyme, E₁ and E₂, respectively. 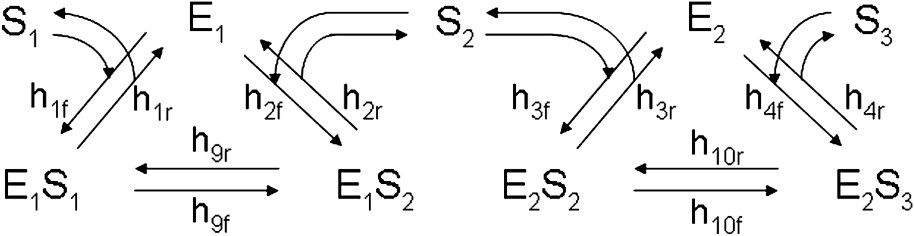Clearly, it would be easy to model three-, four-, …, n-enzyme systems by adding a third, fourth, …, nth reaction circuit corresponding to enzymes $E_{3}, E_{4}, \dots, E_{n}$ , respectively (not shown).

Fig. 1
The model of free sequential enzymes in the case of a two-enzyme system. The first enzyme, E₁, binds to the initial substrate, S₁, to form the enzyme–substrate complex, E₁S₁. Within this complex, E₁ transforms S₁ into its product, S₂, resulting in the transformation of E₁S₁ into E₁S₂, and then E₁S₂ liberates S₂, thus regenerating E₁. In similar manner, the second enzyme E₂ binds S₂; transforms S₂ into S₃ and finally liberates the final product, S₃. $h_{i f}$ and $h_{i r}$ are the forward and reverse rate-constants; their numbering, i, has been chosen in such a way as to be consistent with that for the FDSs (in preparation). Note that $h_{1 f}$ , $h_{2 f}$ , $h_{3 f}$ and $h_{4 f}$ are expressed in mol⁻¹ s⁻¹ m³, whereas all the other rate constants are expressed in s⁻¹.

3 Numerical simulations in the case of a two-enzyme system

The numerical simulations have consisted of studying the dependence of the rate, v, of the overall reaction of transformation of S₁ into S₃, on the concentration of S₁ for various values of the forward and reverse rate constants, $h_{i f}$ and $h_{i r}$ (see Fig. 1). In practise, we have used dimensionless expressions of all the variables and parameters. For the definition of these dimensionless quantities, see Appendix A. Independent steady-state equations have been obtained by writing down the mass balance of the species involved, i.e.

d e_{1} / d τ = k_{1 r} \cdot e_{1} s_{1} + k_{2 r} \cdot e_{1} s_{2} - (k_{1 f} \cdot s_{1} + k_{2 f} \cdot s_{2}) \cdot e_{1} = 0

(1)

d e_{2} / d τ = k_{3 r} \cdot e_{2} s_{2} + k_{4 r} \cdot e_{2} s_{3} - (k_{3 f} \cdot s_{2} + k_{4 f} \cdot s_{3}) \cdot e_{2} = 0

(2)

d s_{2} / d τ = k_{2 r} \cdot e_{1} s_{2} + k_{3 r} \cdot e_{2} s_{2} - (k_{2 f} \cdot e_{1} + k_{3 f} \cdot e_{2}) \cdot s_{2} = 0

(3)

e_{1} + e_{1} s_{1} = e_{1 t}

(4)

e_{2} + e_{2} s_{2} = e_{2 t}

(5)

In these equations, $k_{i f}$ , $k_{i r}$ , τ, $e_{1}$ , $e_{2}$ , $s_{1}$ , $s_{2}$ , $s_{3}$ , $e_{1} s_{1}$ , $e_{1} s_{2}$ , $e_{2} s_{2}$ and $e_{2} s_{3}$ are the dimensionless expressions of the forward and reverse rate constants, $h_{i f}$ and $h_{i r}$ , of the time, t, and of the concentrations of E₁, E₂, S₁, S₂, S₃, E₁S₁, E₁S₂, E₂S₂, and E₂S₃.

To write down the steady-state conditions of functioning of the system, we have assumed that external mechanisms supply S₁ and remove S₃ as and when they are consumed and produced, respectively, such that S₁ is maintained at a constant concentration $(s_{1} = constant)$ and S₃ at a zero concentration $(s_{3} = 0)$ . Under such steady-state conditions, v is measured indifferently by the rate of consumption of S₁ or the rate of production of S₃, i.e. for the dimensionless expression of v:

v = k_{1 f} \cdot e_{1} \cdot s_{1} - k_{1 r} \cdot e_{1} s_{1} = k_{4 r} \cdot e_{2} s_{3} - k_{4 f} \cdot e_{2} \cdot s_{3}

(6)

Moreover, two relationships have to be taken into account between the rate constants. One is imposed by how the dimensionless quantities have been defined (see Appendix A, Eq. (A.9)),

k_{1 r} \equiv 1

(7)

and the other is a consequence of the principle of detailed balance, i.e.:

k_{1 f} \cdot k_{2 r} \cdot k_{3 f} \cdot k_{4 r} \cdot k_{9 f} \cdot k_{10 f} / k_{1 r} \cdot k_{2 f} \cdot k_{3 r} \cdot k_{4 f} \cdot k_{9 r} \cdot k_{10 r} = K

(8)

in which K is the equilibrium constant of the overall reaction of S₁ into S₃.

The numerical simulations of the dependence of v on $s_{1}$ (with $s_{3} = 0$ ) for a variety of values of the rate constants have been carried out using the MAPLE software to solve the algebraic system (Eqs. (1) to (5)). We have always found, as expected from the calculation of the first derivative of v (not shown), that the ${s_{1}, v}$ curves were increasing monotonically up to a saturation plateau (see examples in Fig. 2A). Moreover, in these numerical simulations, we have never found any curve exhibiting one or several inflexion points. Sometimes, the shape of the curves was close to that of a hyperbola as shown by the fact that the corresponding curves in the system of coordinates ${v / s_{1}, v}$ (Fig. 2B) were close to straight lines (see curve b); however, most often this was not the case (see especially curves d and e). When adjusting straight lines to the computed curves in Fig. 2A, in the range of $s_{1}$ values from 0 to the abscissa, $s_{int}$ , of the point of intersection of the tangent at origin with the saturation plateau of each curve (see Eq. (B.5) in Appendix B for the determination of $s_{int}$ ), the values of the regression coefficient, $r^{2}$ , of these linear adjustments were 0.9608, 0.9682, 0.9843, 0.9991, and 0.9999 for curves (a) to (e), i.e. for $k_{2 f}$ -values varying from 10 (curve a) to 0.01 (curve e). This means that decreasing the value of $k_{2 f}$ tends to render the reaction rate, v, proportional to the concentration of initial substrate, $s_{1}$ ; moreover, with a $k_{2 f}$ value as low as 0.01, it appears that proportionality remains valid (curve e practically undistinguishable from its tangent at origin) almost up to the saturation plateau. It is also visible in the figure that the linear approximation thus observed at a low $k_{2 f}$ value extends far beyond the quasi-linear zone that is known to exist at the beginning ( $s_{1}$ close to zero) of a hyperbolic ${s_{1}, v}$ curve (compare curve (e) with the hyperbolic curve drawn in dotted line in Fig. 2A).

Fig. 2
Examples of computed curves in the case of a two-enzyme system with $s_{3} = 0$ . (A) Curves represented in the system of coordinates ${s_{1}, v}$ . The parameter values are $e_{1 t} = e_{2 t} = 0.5$ , K=100, $k_{1 f} = 10$ , $k_{2 r} = k_{3 f} = 100$ , $k_{9 f} = k_{10 f} = k_{3 r} = k_{4 r} = k_{9 r} = k_{10 r} = 1$ , $k_{1 r} \equiv 1$ (Eq. (7)), $k_{4 f}$ calculated according to Eq. (8), and $k_{2 f} = 10$ (curve a), 5 (curve b), 1 (curve c), 0.1 (curve d) and 0.01 (curve e). The straight, dashed line is the tangent at origin of curve (e). The curve in dotted line is the hyperbola with the same tangent at origin and the same plateau as curve (e). (B) Same data as in (A), expressed in the system of coordinates ${v / s_{1}, v}$ .

Increasing $k_{1 f} / k_{1 r}$ or $k_{4 f} / k_{4 r}$ and/or decreasing $k_{3 f} / k_{3 r}$ have the same effect as decreasing $k_{2 f} / k_{2 r}$ , i.e. this tends to favour the proportional response of v as a function of $s_{1}$ . Increasing $k_{10 f} / k_{10 r}$ tends to increase the value of the saturation plateau. In our present approach, the equilibrium constant, K, of the overall reaction of transformation of S₁ into S₃ is involved only in the calculation of $k_{4 f}$ from the other rate constants (Eq. (8)); since we have imposed $s_{3} = 0$ , the value of $k_{4 f}$ , and consequently that of K, has no effect on the result of the numerical simulations.

4 Numerical simulations in the case of an n-enzyme system

As an example of an n-enzyme system, we have studied the case of a system made of four free enzymes. We have always found ${s_{1}, v}$ curves (i) monotonically increasing up to a saturation plateau and (ii) sometimes exhibiting an extended region where v was proportional to $s_{1}$ . On total, the results were never qualitatively very different from those observed with two-enzyme systems.

5 Discussion and conclusion

With a system of two free sequential enzymes of the Michaelis–Menten type in a metabolic pathway, we have always observed in our numerical simulations that the ${s_{1}, v}$ curves were monotonically increasing up to a saturation plateau. Depending on the values of the rate constants, the curve shape varied from quasi-hyperbolic to extremely non-hyperbolic, including cases in which v became quasi proportional to $s_{1}$ almost up to the saturation plateau (which never occurs with individual enzymes). Choices of values of the rate constants either increasing the efficiency of enzyme E₁ in the transformation of S₁ to S₂ (high values of $k_{1 f} / k_{1 r}$ and low values of $k_{2 f} / k_{2 r}$ ) or decreasing the efficiency of enzyme E₂ in the transformation of S₂ to S₃ (low values of $k_{3 f} / k_{3 r}$ and high values of $k_{4 f} / k_{4 r}$ ) favoured the appearance of this quasi-proportional response. The behaviour of four-enzyme systems was qualitatively not very different from that of two-enzyme systems.

Acknowledgements

We thank Jean-Pierre Mazat for helpful comments.

Appendix A Definition of dimensionless quantities in the case of a two-enzyme system

Dimensionless quantities have been defined by normalising all concentrations (with [X] = concentration of X) to the sum of the total concentrations of E₁ and E₂, $[E_{1 t}] + [E_{2 t}]$ , and all time values to $1 / h_{1 r}$ . As a consequence, the molar fractions of enzymes E₁ and E₂ are:

e_{1 t} = [E_{1 t}] / ([E_{1 t}] + [E_{2 t}]) e_{2 t} = [E_{2 t}] / ([E_{1 t}] + [E_{2 t}]), with e_{1 t} + e_{2 t} = 1

(A.1)

the dimensionless concentrations of all the substances involved are

s_{1} = [S_{1}] / ([E_{1 t}] + [E_{2 t}]) s_{2} = [S_{2}] / ([E_{1 t}] + [E_{2 t}]) s_{3} = [S_{3}] / ([E_{1 t}] + [E_{2 t}])

(A.2)

e_{1} = [E_{1}] / ([E_{1 t}] + [E_{2 t}]) e_{2} = [E_{2}] / ([E_{1 t}] + [E_{2 t}])

(A.3)

e_{1} s_{1} = [E_{1} S_{1}] / ([E_{1 t}] + [E_{2 t}]) e_{1} s_{2} = [E_{1} S_{2}] / ([E_{1 t}] + [E_{2 t}])

(A.4)

e_{2} s_{2} = [E_{2} S_{2}] / ([E_{1 t}] + [E_{2 t}]) e_{2} s_{3} = [E_{2} S_{3}] / ([E_{1 t}] + [E_{2 t}])

(A.5)

the dimensionless expression, τ, of time, t, is

τ = t \cdot h_{1 r}

(A.6)

The dimensionless expression of constants

h_{1 f}

to

h_{4 f}

is:

k_{1 f} = (h_{1 f} / h_{1 r}) \cdot ([E_{1 t}] + [E_{2 t}])

k_{2 f} = (h_{2 f} / h_{1 r}) \cdot ([E_{1 t}] + [E_{2 t}])

k_{3 f} = (h_{3 f} / h_{1 r}) \cdot ([E_{1 t}] + [E_{2 t}])

and

k_{4 f} = (h_{4 f} / h_{1 r}) \cdot ([E_{1 t}] + [E_{2 t}])

(A.7)

while the dimensionless expression of

h_{9 f}

,

h_{10 f}

and all the reverse constants

h_{i r}

are

k_{9 f} = h_{9 f} / h_{1 r}, k_{10 f} = h_{10 f} / h_{1 r} and k_{i r} = h_{i r} / h_{1 r}

(A.8)

with, obviously,

k_{1 r} = h_{1 r} / h_{1 r} \equiv 1

(A.9)

Appendix B

The steady-state rate of transformation of S₁ into S₃ at saturation, $v_{\max}$ $(s_{1} = \infty)$ , and the slope at origin, $v^{'} (0)$ $(s_{1} = 0)$ , can be derived from Eqs. (1) to (5). Define Q by:

Q = k_{4 r} \cdot k_{10 f} \cdot (k_{2 r} + k_{9 f} + k_{9 r}) \cdot e_{2 t} - k_{2 r} \cdot k_{9 f} \cdot (k_{4 r} + k_{10 f} + k_{10 r}) \cdot e_{1 t}

(B.1)

If Q < 0, then v_{\max} = k_{4 r} \cdot k_{10 f} \cdot e_{2 t} / (k_{4 r} + k_{10 f} + k_{10 r})

(B.2)

If Q > 0, then v_{\max} = k_{2 r} \cdot k_{9 f} \cdot e_{1 t} / (k_{2 r} + k_{9 f} + k_{9 r})

(B.3)

and it is easily checked that the two

v_{\max}

values are identical to each other when

Q = 0

. Moreover, the slope at origin is written:

v^{'} (0) = k_{1 f} \cdot k_{2 r} \cdot k_{3 f} \cdot k_{4 r} \cdot k_{9 f} \cdot k_{10 f} \cdot e_{1 t} \cdot e_{2 t} / (k_{1 r} \cdot k_{2 f} \cdot k_{9 r} \cdot (k_{3 r} \cdot k_{4 r} + k_{3 r} \cdot k_{10 r} + k_{4 r} \cdot k_{10 f}) \cdot e_{1 t} + k_{3 f} \cdot k_{4 r} \cdot k_{10 f} \cdot (k_{1 r} \cdot k_{2 r} + k_{1 r} \cdot k_{9 r} + k_{2 r} \cdot k_{9 f}) \cdot e_{2 t})

(B.4)

Eventually, the concentration of initial substrate,

s_{int}

, which corresponds to the intercept of the tangent at origin with the saturation plateau, is written as:

s_{int} = v_{\max} / v^{'} (0)

(B.5)

Bibliographie

[1] J. Mowbray; V. Moses The tentative identification in Escherichia coli of a multi-enzyme complex with glycolytic activity, Eur. J. Biochem., Volume 66 (1976), pp. 25-36

[2] P.A. Srere Complexes of sequential metabolic enzymes, Annu. Rev. Biochem., Volume 56 (1987), pp. 21-56

[3] J. Ovádi; P. Tompa; B. Vértessy; F. Orosz; T. Keleti; G.R. Welch Transient time analysis of substrate channelling in interacting enzyme systems, Biochem. J., Volume 257 (1989), pp. 187-190

[4] T. Keleti; J. Ovádi; J. Batke Kinetic and physico-chemical analysis of enzyme complexes and their possible role in the control of metabolism, Prog. Biophys. Mol. Biol., Volume 53 (1989), pp. 105-152

[5] P.A. Srere; J. Ovádi Enzyme-enzyme interactions and their metabolic role, FEBS Lett., Volume 268 (1990), pp. 360-364

[6] B.S.J. Winkel Metabolic channelling in plants, Annu. Rev. Plant Biol., Volume 55 (2004), pp. 85-107

[7] M. Thellier; G. Legent; V. Norris; C. Baron; C. Ripoll Introduction to the concept of ‘functioning-dependent structures’ in living cells, C.R. Biologies, Volume 327 (2004), pp. 1017-1024

[8] J.-P. Mazat Cinétique enzymatique et contrôle des flux (P. Tracqui; J. Demongeot, eds.), Éléments de biologie à l'usage d'autres disciplines : de la structure aux fonctions, EDP Sciences, Les Ulis, France, 2003, pp. 175-206

Commentaires - Politique