Potential automata. Application to the genetic code III

Jacques Demongeot; Adrien Elena; Georges Weil

doi:10.1016/j.crvi.2006.07.010

Biological modelling / Biomodélisation

Potential automata. Application to the genetic code III
[Automates cellulaires potentiels. Application au code génétique]

Présenté par : Michel Thellier

Jacques Demongeot ^1,² ; Adrien Elena ¹ ; Georges Weil ¹

¹ TIMC-IMAG UMR CNRS 5525, faculté de médecine, université Joseph-Fourier, Grenoble, 38700 La Tronche, France
² Institut universitaire de France, 75005 Paris, France

Comptes Rendus. Biologies, Volume 329 (2006) no. 12, pp. 953-962.

Résumés

Anglais
Français

In previous notes, we have described both mathematical properties of potential (n-switches) and potential-Hamiltonian (Liénard systems) continuous differential systems, and also biological applications, especially those concerning primitive cyclic RNAs related to the genetic code. In the present note, we give a general definition of a potential automaton, and we show that a discrete Hopfield-like system already introduced by Goles et al. is a good candidate for such a potential automaton: it has a Lyapunov functional that decreases on its trajectories and whose time derivative is just its discrete velocity. Then we apply this new notion of potential automaton to the genetic code. We show in particular that the consideration of only physicochemical properties of amino-acids, like their molecular weight, hydrophobicity and ability to create hydrogen bonds suffices to build a potential decreasing on trajectories corresponding to the synonymy classes of the genetic code. Such an ‘a minima’ construction reinforces the classical stereochemical hypothesis about the origin of the genetic code and authorizes new views about the optimality of its synonymy classes.

Dans les notes précédant cet article, nous avons décrit des systèmes différentiels continus potentiels (de type « n-switches ») et potentiel-hamiltoniens (de type « systèmes de Liénard »), dont les équations étaient bien adaptées à la modélisation des systèmes dynamiques en biologie. Par exemple, un système différentiel potentiel défini sur $R^{n}$ est du type : $\forall i = 1, \dots, n$ , $d x_{i} / d t = - \partial P / \partial x_{i}$ , où P est une fonction réelle continûment différentiable sur $R^{n}$ . Nous donnons dans cet article une définition du même type pour les automates discrets et nous montrons, à titre d'exemple, un système de type Hopfield, déjà étudié par Goles et al., pour lequel il existe une fonction de Lyapunov décroissant le long des trajectoires. Nous montrons que la dérivée temporelle de cette fonction de Lyapunov est exactement la vitesse discrète de l'automate et nous appliquons cette nouvelle notion au code génétique. Nous montrons en particulier que l'on peut construire un potentiel uniquement à partir de propriétés physicochimiques simples des amino acides, comme leur poids moléculaire, leur hydrophobicité et leur capacité à créer des liaisons hydrogène, les orbites de l'automate potentiel correspondant n'étant autres que les classes de synonymie du code. Leur construction « a minima » renforce l'hypothèse classique stéréochimique quant à l'origine du code génétique et ouvre de nouvelles perspectives vers l'optimalité de ses classes de synonymie.

Métadonnées

Reçu le : 2006-03-03
Accepté le : 2006-07-10
Publié le : 2006-10-09

PMID

DOI : 10.1016/j.crvi.2006.07.010

Keywords: Potential automata, Lyapunov functional, Genetic code, Synonymy classes, Stereochemical hypothesis
Mot clés : Automate potentiel, Fonction de Lyapunov, Code génétique, Classes de synonymie, Hypothèse stéréochimique

Affiliations des auteurs :

Jacques Demongeot ^{1, 2} ; Adrien Elena ¹ ; Georges Weil ¹

¹ TIMC-IMAG UMR CNRS 5525, faculté de médecine, université Joseph-Fourier, Grenoble, 38700 La Tronche, France
² Institut universitaire de France, 75005 Paris, France

@article{CRBIOL_2006__329_12_953_0,
     author = {Jacques Demongeot and Adrien Elena and Georges Weil},
     title = {Potential automata. {Application} to the genetic code {III}},
     journal = {Comptes Rendus. Biologies},
     pages = {953--962},
     publisher = {Elsevier},
     volume = {329},
     number = {12},
     year = {2006},
     doi = {10.1016/j.crvi.2006.07.010},
     language = {en},
}

TY  - JOUR
AU  - Jacques Demongeot
AU  - Adrien Elena
AU  - Georges Weil
TI  - Potential automata. Application to the genetic code III
JO  - Comptes Rendus. Biologies
PY  - 2006
SP  - 953
EP  - 962
VL  - 329
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crvi.2006.07.010
LA  - en
ID  - CRBIOL_2006__329_12_953_0
ER  -

%0 Journal Article
%A Jacques Demongeot
%A Adrien Elena
%A Georges Weil
%T Potential automata. Application to the genetic code III
%J Comptes Rendus. Biologies
%D 2006
%P 953-962
%V 329
%N 12
%I Elsevier
%R 10.1016/j.crvi.2006.07.010
%G en
%F CRBIOL_2006__329_12_953_0

Jacques Demongeot; Adrien Elena; Georges Weil. Potential automata. Application to the genetic code III. Comptes Rendus. Biologies, Volume 329 (2006) no. 12, pp. 953-962. doi : 10.1016/j.crvi.2006.07.010. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2006.07.010/

Version originale du texte intégral

1 Introduction

A discrete dynamical system has the same definition as the continuous ones [1–9]. It involves a flow function f defined on $E \times T$ , where T is a discrete time space (in general N) and E a discrete state space ( ${0, 1}^{n}$ in the Boolean case and more generally a countable subset of $R_{+}^{n}$ ), $f (e, t)$ representing, for each state e and time t, the state reached after time t by the trajectory starting in state e at time 0. We denote in general $f (x (0), t)$ by $x (t) = (x_{i} {(t))}_{i = 1, \dots, n}$ , which permits to have a coherent notation for all the states of a trajectory. The set of such states is called the orbit of $x (0)$ . Following [10], we can now define the discrete time derivative for the state vector $(x_{i} {(t))}_{i = 1, \dots, n}$ of an automaton by: $Δ x_{i} / Δ t = (x_{i} (t + Δ t) - x_{i} (t)) / Δ t$ , which reduces to $x_{i} (t + 1) - x_{i} (t)$ , if $Δ t = 1$ . By using the same formula, we can also define:

– the space derivative: $Δ f (x) / Δ i = (f (x_{i + Δ i}) - f (x_{i})) / Δ i = f (x_{i + 1}) - f (x_{i})$ , if $Δ i = 1$
– the partial state derivative: $Δ f (x) / Δ x_{i} = (f (x_{i} + Δ x_{i}) - f (x_{i})) / Δ x_{i}$ .

A discrete automaton is defined by a transition function F: $Δ x_{i} / Δ t = (x_{i} (t + Δ t) - x_{i} (t)) / Δ t = F_{i} (x (t))$ , where $F_{i}$ depends only on coordinates $(x_{j} {(t))}_{j \in V (i)}$ , $V (i)$ being a neighbourhood of i in the space set S (in general the Manhattan – or $L_{1}$ – unit ball of $S \subseteq Z^{m}$ centred on i and having a radius equal to 1), with conditions defining V on the boundary of S (e.g., periodic) and with constraints on the discrete velocity ensuring that the flow remains in E.

The aim of the paper is to find a discrete analogous for the definition of a potential (or gradient) discrete dynamical system (called here potential automaton) similar to those known in continuous systems. Then we will study as biological application a potential automaton whose orbits are the synonymy classes of the genetic code, the potential deriving only from simple physicochemical properties of the amino-acids corresponding to these synonymy classes.

2 Definition of a potential automaton

A continuous potential differential equation on $R^{n}$ is defined by: $\forall i = 1, \dots, n$ , $d x_{i} / d t = - \partial P / \partial x_{i}$ , where P is a real continuously differentiable function (e.g., a polynomial with real coefficients) on $R^{n}$ . In the same way, a potential automaton on the discrete state space E is defined by:

x_{i} (t + 1) = h (- Δ P / Δ x_{i} + x_{i} (t))

(1)

where P is a real function (e.g., a polynomial with real coefficients) on E and h a function from

R

to E, with boundary conditions ensuring that the flow remains in E. For example, in the Boolean case, we will choose for h the Heaviside function H:

H (s) = 1

s > 0

, and

H (s) = 0

s ⩽ 0

. In the integer case (E subset of

N^{n}

), h will be the identity, if P has integer coefficients and if

\forall i = 1, \dots, n

Δ x_{i} \in {- 1, 0, 1}

. Then Eq. (1) rewritten as

Δ x_{i} / Δ t = h (- Δ P / Δ x_{i} + x_{i} (t)) - x_{i} (t)

can be considered as the discrete equivalent of

d x_{i} / d t = - \partial P / \partial x_{i}

Example

In the Boolean case, if $P (x) = \sum_{k} ({}^{t}x A_{k} x) x_{k} + {}^{t}x W x + B x$ , where $A = (a_{i j k})$ is an interaction tensor, with $A_{k} = {(a_{i j})}_{k}$ as marginal matrices and $a_{i i i} = 0$ , $W = (w_{i j})$ is an interaction matrix and $B = (b_{i})$ a threshold line vector, we have, for the partial space derivatives of P:

Δ P / Δ x_{i} = \sum_{j, k} (a_{i j k} + a_{j i k} + a_{j k i}) x_{j} x_{k} + \sum_{j} (w_{i j} + w_{j i}) x_{j} + b_{i} + [w_{i i} + \sum_{j \neq i} (a_{i j j} + a_{j i j} + a_{j j i}) x_{j}] Δ x_{i}

(2)

Then the potential automaton associated to P is defined by:

Δ x_{i} / Δ t = Δ x_{i} = - Δ P / Δ x_{i} = - \sum_{j, k} (a_{i j k} + a_{j i k} + a_{j k i}) x_{j} x_{k} - \sum_{j} (w_{i j} + w_{j i}) x_{j} - b_{i} - [w_{i i} + \sum_{j \neq i} (a_{i j j} + a_{j i j} + a_{j j i}) x_{j}] Δ x_{i}

Hence we have:

Δ x_{i} = - [\sum_{j, k} (a_{i j k} + a_{j i k} + a_{j k i}) x_{j} (t) x_{k} (t) + \sum_{j} (w_{i j} + w_{j i}) x_{j} (t) + b_{i}] / [1 + w_{i i} + \sum_{j \neq i} (a_{i j j} + a_{j i j} + a_{j j i}) x_{j} (t)]

and

x_{i} (t + 1) = H (Δ x_{i} + x_{i} (t)) = H (- Δ P / Δ x_{i} + x_{i} (t))

, where H is the Heaviside function. From (2), we derive:

x_{i} (t + 1) = H (- [\sum_{j, k} (a_{i j k} + a_{j i k} + a_{j k i}) x_{j} (t) x_{k} (t) + \sum_{j} (w_{i j} + w_{j i}) x_{j} (t) + b_{i}] / [1 + w_{i i} + \sum_{j \neq i} (a_{i j j} + a_{j i j} + a_{j j i}) x_{j} (t)] + x_{i} (t))

(3)

3 Properties of a potential automaton

Proposition 1

Let us suppose that the state space E equals $N^{n}$ and that P is defined on E by: $\forall x \in E$ , $P (x) = \sum_{k} ({}^{t}x A_{k} x) x_{k} + {}^{t}x W x + B x$ , where A, W, B are respectively an integer tensor, an integer matrix and an integer line vector. Let suppose also that: $\forall i = 1, \dots, n$ , $Δ x_{i} \in {- 1, 0, 1}$ . Consider now the potential automaton defined by: $x_{i} (t + 1) = - Δ P / Δ x_{i} + x_{i} (t)$ , if $x_{i} (t) > 0$ , and by boundary conditions $x_{i} (t + 1) ⩾ 0$ , if $x_{i} (t) = 0$ , such that the flow remains in E.

Then, if the tensor A is symmetrical with vanishing diagonal (i.e. if $\forall i, j, k = 1, \dots, n$ , $a_{i j k} = a_{i k j} = a_{k i j} = a_{j k i} = a_{j i k} = a_{k j i}$ and $a_{i i k} = 0$ ), and if each sub-matrix on any subset J of indices in ${1, \dots, n}$ of $A_{k}$ and of W is non-positive with vanishing diagonal, P decreases on the trajectories of the potential automaton, for any mode of implementation of the dynamics (sequential, block sequential and parallel). Hence the stable fixed configurations of the automaton correspond to the minima of its potential P.

Proof

We have:

P (x (t + 1)) - P (x (t)) = 3 \sum_{k} \sum_{i, j} a_{i j k} Δ x_{i} Δ x_{j} x_{k} (t) + \sum_{i, j, k} a_{i j k} Δ x_{i} Δ x_{j} Δ x_{k} + 3 \sum_{k} \sum_{i, j} a_{i j k} x_{i} (t) x_{j} (t) Δ x_{k} + \sum_{i} (\sum_{j \neq i} (w_{i j} + w_{j i}) x_{j} (t) Δ x_{i} + \sum_{j \neq i} w_{i j} Δ x_{i} Δ x_{j} + 2 w_{i i} x_{i} (t) Δ x_{i} + w_{i i} Δ x_{i}^{2}) + \sum_{i} b_{i} Δ x_{i}

In a potential automaton, we have

\forall i = 1, \dots, n

Δ x_{i} = - Δ P / Δ x_{i}

, hence:

Δ x_{i} = - [\sum_{j, k} (a_{i j k} + a_{j i k} + a_{j k i}) x_{j} x_{k} + \sum_{j} (w_{i j} + w_{j i}) x_{j} + b_{i}] - [w_{i i} + \sum_{j \neq i} (a_{i j j} + a_{j i j} + a_{j j i}) x_{j}] Δ x_{i}

(1) In the sequential updating, only one component $x_{k}$ changes its value between t and $t + 1$ , hence:

P (x (t + 1)) - P (x (t)) = 3 (\sum_{i \neq k} a_{i k k} Δ x_{k}^{2} x_{i} (t) + \sum_{i, j} a_{i j k} x_{i} (t) x_{j} (t) Δ x_{k}) + \sum_{j} (w_{k j} + w_{j k}) x_{j} (t) Δ x_{k} + w_{k k} Δ x_{k}^{2} + b_{k} Δ x_{k} = Δ x_{k} (- Δ x_{k}) = - Δ x_{k}^{2} ⩽ 0

(2) In the block-sequential updating, let denote by J the subset of ${1, \dots, n}$ reached by the sequential iteration. Then only the $x_{k}$ 's for k in J can change their value between t and $t + 1$ , hence:

P (x (t + 1)) - P (x (t)) = 3 \sum_{k} \sum_{(i, j) \in J \times J} a_{i j k} Δ x_{i} Δ x_{j} x_{k} (t) + \sum_{(i, j, k) \in J \times J \times J} a_{i j k} Δ x_{i} Δ x_{j} Δ x_{k} + 3 \sum_{k \in J} \sum_{i, j} a_{i j k} x_{i} (t) x_{j} (t) Δ x_{k} + \sum_{i \in J} \sum_{j} (w_{i j} + w_{j i}) x_{j} (t) Δ x_{i} + \sum_{(i, j) \in J \times J} w_{i j} Δ x_{i} Δ x_{j} + \sum_{i \in J} b_{i} Δ x_{i} = \sum_{i \in J} Δ x_{i} [3 \sum_{j, k} a_{i j k} x_{j} (t) x_{k} (t) + 3 \sum_{j \in J, k} a_{i j k} Δ x_{j} x_{k} (t) + \sum_{(j, k) \in J \times J} a_{i j k} Δ x_{j} Δ x_{k} + \sum_{j} (w_{i j} + w_{j i}) x_{j} (t) + \sum_{j \in J} w_{i j} Δ x_{j} + b_{i}] = \sum_{i \in J} Δ x_{i} [- Δ x_{i} (1 + w_{i i} + 3 \sum_{j \neq i} a_{i j j} x_{j} (t)) + \sum_{j \in J} Δ x_{j} (w_{i j} + 3 \sum_{k} a_{i j k} x_{k} (t)) + \sum_{(j, k) \in J \times J} a_{i j k} Δ x_{j} Δ x_{k}] = - \sum_{i \in J} Δ x_{i}^{2} (1 + w_{i i}) + \sum_{(i, j) \in J \times J} w_{i j} Δ x_{i} Δ x_{j} + 3 \sum_{(i, j) \in J \times J, k} a_{i j k} Δ x_{i} Δ x_{j} x_{k} (t) + \sum_{(i, j, k) \in J \times J \times J} a_{i j k} Δ x_{i} Δ x_{j} Δ x_{k} = - \sum_{i \in J} Δ x_{i}^{2} (1 + w_{i i}) + \sum_{(i, j) \in J \times J} w_{i j} Δ x_{i} Δ x_{j} + 3 \sum_{(i, j) \in J \times J, k \notin J} a_{i j k} Δ x_{i} Δ x_{j} x_{k} (t) + 2 \sum_{(i, j, k) \in J \times J \times J} a_{i j k} Δ x_{i} Δ x_{j} x_{k} (t) + \sum_{(i, j, k) \in J \times J \times J} a_{i j k} Δ x_{i} Δ x_{j} (x_{k} (t) + Δ x_{k})

From the hypotheses of the present proposition and from the positivity of

x_{k} (t)

and

x_{k} (t + 1) = x_{k} (t) + Δ x_{k}

, we deduce that

P (x (t + 1)) - P (x (t)) ⩽ 0

. □

Proposition 2

In the Boolean case, let us suppose that $A = 0$ , $P (x) = {}^{t}x W x + B x$ , with $w_{i i} = 1$ and each sub-matrix on any subset J of indices in ${1, \dots, n}$ of W is non-positive. Then P decreases on the trajectories of the potential automaton defined by $x_{i} (t + 1) = H (- Δ P / Δ x_{i} + x_{i} (t))$ for any mode of implementation of the dynamics (sequential, block sequential, and parallel). This automaton is a Hopfield-like neural network, whose stable fixed configurations correspond to the minima of P.

Proof

It is easy to check that from (2): $Δ P / Δ x_{i} = \sum_{j} (w_{i j} + w_{j i}) x_{j} + b_{i} + w_{i i} Δ x_{i}$ , and from (3) and from $w_{i i} = 1$ :

x_{i} (t + 1) = H (- Δ P / Δ x_{i} + x_{i} (t)) = H (- [\sum_{j} (w_{i j} + w_{j i}) x_{j} (t) + b_{i}] / [1 + w_{i i}] + x_{i} (t)) = H (- \sum_{j \neq i} (w_{i j} + w_{j i}) x_{j} (t) - b_{i})

Then, for the block sequential iteration:

P (x (t + 1)) - P (x (t)) = - \sum_{i \in J} Δ x_{i}^{2} (1 + w_{i i}) + \sum_{(i, j) \in J \times J} w_{i j} \times Δ x_{i} Δ x_{j} ⩽ 0

, the result coming from the non-positivity of the sub-matrices of W or from [9]. □

The interest of Proposition 2 is to show that the Hopfield-like automaton, defined by:

\forall i = 1, \dots, n, x_{i} (t + 1) = H (- \sum_{j \neq i} (w_{i j} + w_{j i}) x_{j} (t) - b_{i})

has not only P as Lyapunov function, as proved in [9], but more it can be considered as a potential automaton with a potential equal to P, because the opposite of the gradient of P is the velocity of the automaton, which is quite different in general for a system with simply a Lyapunov function (Fig. 1).

Fig. 1
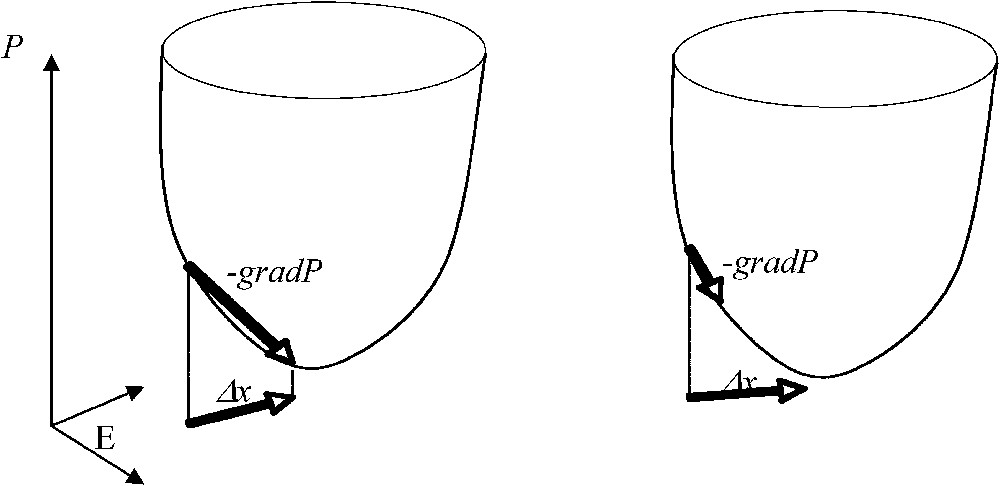
Potential automaton with Δx=−gradP (on the left) and automaton with a Lyapunov function decreasing on its trajectories (on the right).

4 Application to the genetic code

We will now use the notion of potential automaton introduced above in order to show what kind of biological significance can have the attraction basins of the stable fixed configurations (i.e. corresponding to the minima of the potential) of such an automaton (see also [11]).

The stereochemical hypothesis belongs to a theory about the origin of the genetic code for which the first complexes between amino-acids (AA) and nucleic acids (NA) have been the start of the autopoietic origin of life. This theory claims that, from a physicochemical similarity on three (dependent) dimensions: (i) the ability L of binding (in particular through hydrogen bounds), (ii) the hydrophobicity H, and (iii) the molecular weight P, codons are associated in an unique and degenerate way to their AA [13,14]. This correspondence can be summarized in Fig. 2, in which the variables H, L and P are given for each amino-acid showing a structure into synonymy classes with sizes from 1 to 6.

Fig. 2
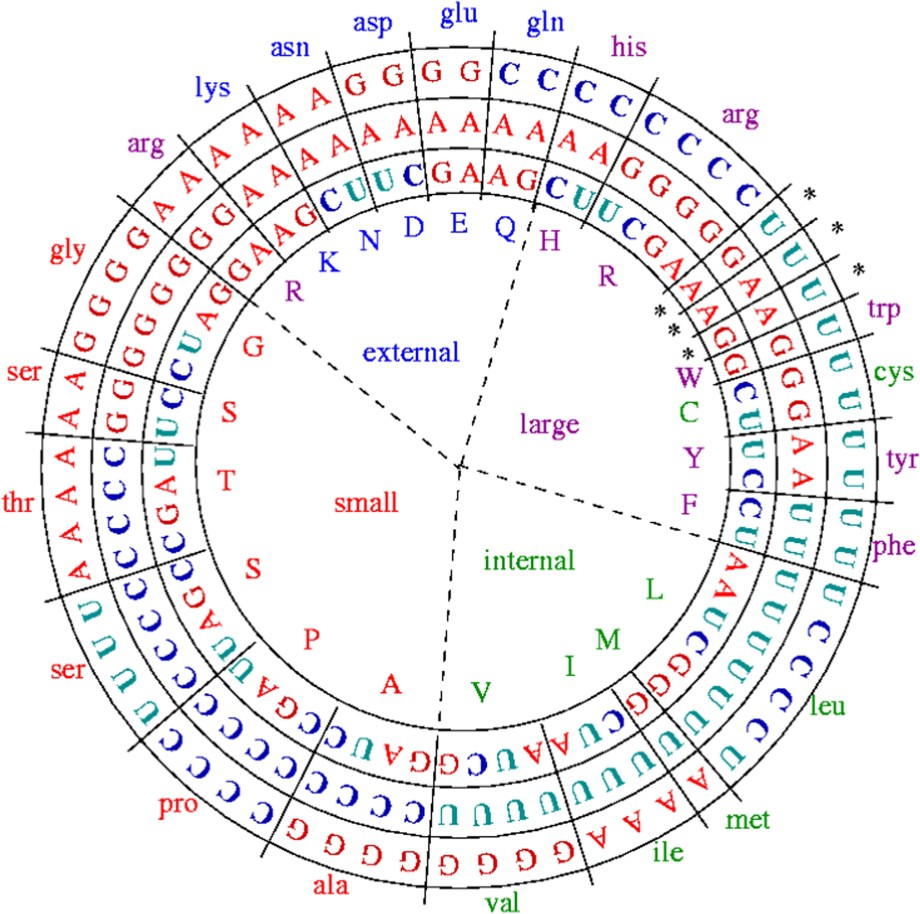
Repartition of the amino-acids and of their codons following two criteria, size (small or large) and hydrophobicity (high/internal and low/external) (after [12]).

According to the wobble hypothesis by Crick, the first two bases of a codon are essential for its affectation to a given amino-acid: we observe that the second base permits to share the codon space into classes (Fig. 3) associated with hydrophobic AA (central base uridine U or cytosine C) or heavy AA (central base U or adenine A), or able of binding AA (central base C or guanine G). Then we could represent each base by a Boolean number of three binary digits (e.g., 110 for U, the first 1 for the hydrophobicity, the second 1 pour the heavy weight and the last 0 for a weak ability of binding), summarizing their characteristics on the H, L and P axes. For the sake of simplicity, we will in the following reduce the coding to two binary digits, retaining only hydrophobicity and steric volume, redundant with P and L. We will show that it will suffice to explain the essential of the degeneracy of the genetic code, by taking into account optimality properties of the genetic code [15] and using a classical coding for the nucleic bases [1], i.e. $U = 11$ , $C = 10$ , $A = 01$ et $G = 00$ . We will also define a potential automaton SUSY (SUrrogate SYstem), linking codons and AA having similar physicochemical properties like hydrophobicity $H ⩾ 0$ (resp. hydrophily $H < 0$ ) et big (resp. small) steric volume, positively correlated to P and L.

Fig. 3
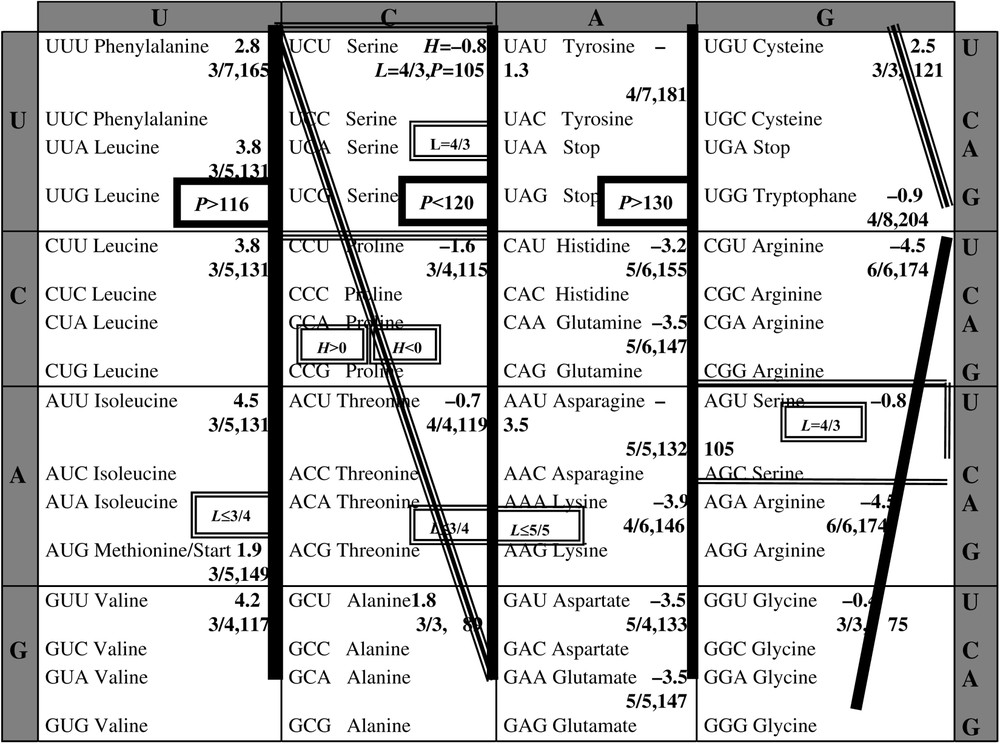
Table of the genetic code, indicating the hydrophobicity H, the maximal number L of possible hydrogen bounds divided by the length of the longest carbonate chain and molecular weight P, for each amino-acid of a synonymy class of codons.

Let us define, for each configuration W in ${0, 1}^{6}$ , the set of Boolean numbers of six binary digits, the subset $V (W) = {X; S (X, W) ⩾ 10$ and $D (X, W) ⩽ 3 / 32}$ :

– where D is the Hamming distance, weighted following the Crick's wobble, which defines the codons ordering O (given in Fig. 3 from 1 to 64, for the Ws varying between 111111 and 000000):
$\forall X, Y \in {0, 1}^{6} D (X, Y) = | x_{3} - y_{3} | + | x_{4} - y_{4} | / 2 + | x_{1} - y_{1} | / 4 + | x_{2} - y_{2} | / 8 + | x_{5} - y_{5} | / 16 + | x_{6} - y_{6} | / 32,$
– S is a similarity function between codons X and Y: $S (X, Y) = \sum_{i = 1, 5} a_{i} (x_{i}, y_{i}) x_{i} y_{i} + b_{i} (x_{i}, y_{i}) (1 - x_{i}) (1 - y_{i})$ ,
– coefficients $a_{i}$ and $b_{i}$ are fixed by electrostatic (hydrophobicity H) and steric (molecular weight P and ability of binding L) properties of the amino-acids [16]:
$a_{1} (1, 1) = 2, a_{2} (1, 1) = 2, a_{3} (1, 1) = 3,$
$a_{4} (1, 1) = 2, a_{5} (1, 1) = 2,$
$b_{1} (0, 0) = 2, b_{2} (0, 0) = 3, b_{3} (0, 0) = 2,$
$b_{4} (0, 0) = 3, b_{5} (0, 0) = 3 .$

Then the potential automaton SUSY is defined on ${0, 1}^{6}$ by:

O (W (t + 1)) = O (W (t)) + H (O (W (t) - O ({Min}_{O} V (W (t))))),

where for the ordering O,

O (W)

is the rank of the Boolean number W and

{Min}_{O} V (W (t))

denotes the minimum of the subset

V (W (t))

, H being the Heaviside function. The potential P is defined by:

P (W) = O (W) - O ({Min}_{O} V (W))

. P decreases along trajectories and has for attraction basins the first part of the states chains linked below by an arrow, the last state of a chain being a stable fixed configuration:

(111111) \Rightarrow (111110), (111101) \Rightarrow (111100)

(101111, 101110, 101101) \Rightarrow (101100)

(011111) \Rightarrow (011110) (011101) \Rightarrow (011100)

(001111, 001110, 001101) \Rightarrow (001100)

(111011, 111010, 111001) \Rightarrow (111000)

(101011, 101010, 101001) \Rightarrow (101000)

(011011, 011010, 011001) \Rightarrow (011000)

(001011, 001010, 001001) \Rightarrow (001000)

(110111) \Rightarrow (110110), (110101) \Rightarrow (110100)

(100111) \Rightarrow (100110), (100101) \Rightarrow (100100)

(010111) \Rightarrow (010110), (010101) \Rightarrow (010100)

(000111) \Rightarrow (000110), (000101) \Rightarrow (000100)

(110011) \Rightarrow (110010), (110001) \Rightarrow (110000)

(100011, 100010, 100001) \Rightarrow (100000)

(010011) \Rightarrow (010010), (010001) \Rightarrow (010000)

(000011, 000010), (000001) \Rightarrow (000000) .

The attraction basins can be identified in the framework of the genetic code table in Fig. 4.

Fig. 4
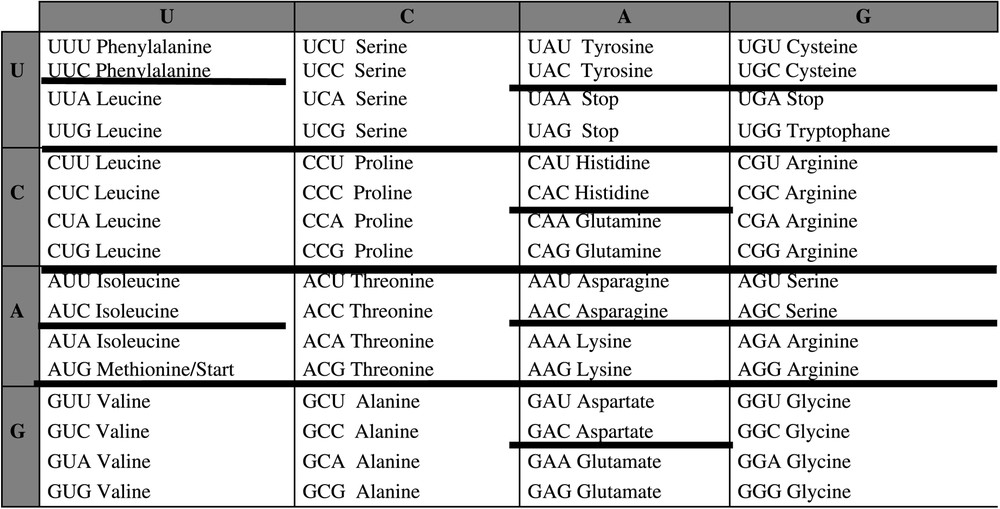
Identification of the attraction basins of the automaton SUSY in the genetic code table.

If we except codon 111100, whose similarity $S = 10$ with 101100, the only codons having an incorrect affectation [17,18] are:

• 011101, to relate to the block $(011111, 011110)$ ( $S = 9$ ),
• 110001, to relate to the block $(110101, 110100)$ ( $S = 9$ ),
• 010000, whose block has to be related to those of 100000 ( $S = 8$ ),
• 010011, whose block has to be related to those of 111011 ( $S = 7$ ).

For the two last codons above, the three digits coding with a complement of similarity equal to 1 for the equality between the third digit of the two first bases of a codon would relate 010001001 to the block of 101001001 ( $S = 9$ ) and 010001110 to the block of 110101110 ( $S = 9$ ). In any case of incorrect affectation we would be then very near to the above critical threshold of 10 defined for the similarity between the five first digits, in coherence with the stereochemical hypothesis and with the previous observations of the Gray code regularities [12,19,20].

5 Variational properties of the system

The automaton SUSY not only maximizes a similarity function, but it gives final synonymy classes verifying two other variational properties, one based on a maximal information principle and the second showing a maximal congruence with present nucleic ‘fossils’ existing in many types of cells.

5.1 A maximal information principle

The easy way shown above to obtain a sketch of the synonymy classes through the potential automaton SUSY reinforces the stereochemical hypothesis. Apart from the amino-acids with six codons, the result is particularly convincing for the amino-acids the most frequent both in the Miller experiment and in the human genome as recalled in the table in Fig. 5 [21,22]. The mutual benefit taken by the RNA and AA worlds from a possible primitive direct association as predicted by the stereochemical theory (four out of the AA in Fig. 5, Leu, Glu, Val and Arg have preferential affinities with their codons and anti-codons [24]) is compatible with their Darwinian co-evolution well summarized by de Duve [25]: “The theory considered most likely today supposes a historical, co-evolutionary process in which the anticodons and the corresponding amino-acids were progressively recruited together under the control of natural selection. Several arguments support this hypothesis. The most convincing lies in the structure of the code, which, far from being random, happens to be such as to minimize the deleterious consequences of mutations.”

Fig. 5
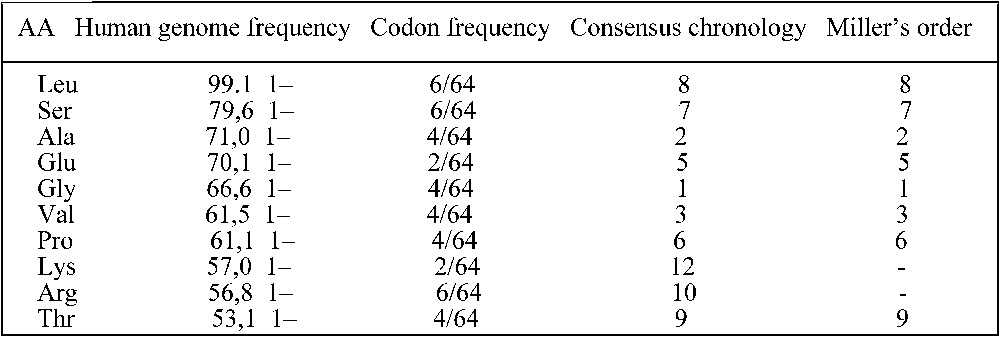
Table giving the frequencies of occurrences of the AA in human genome [23] and in the genetic code, and giving their rank in a consensus chronology [22] and in the Miller experiment [22].

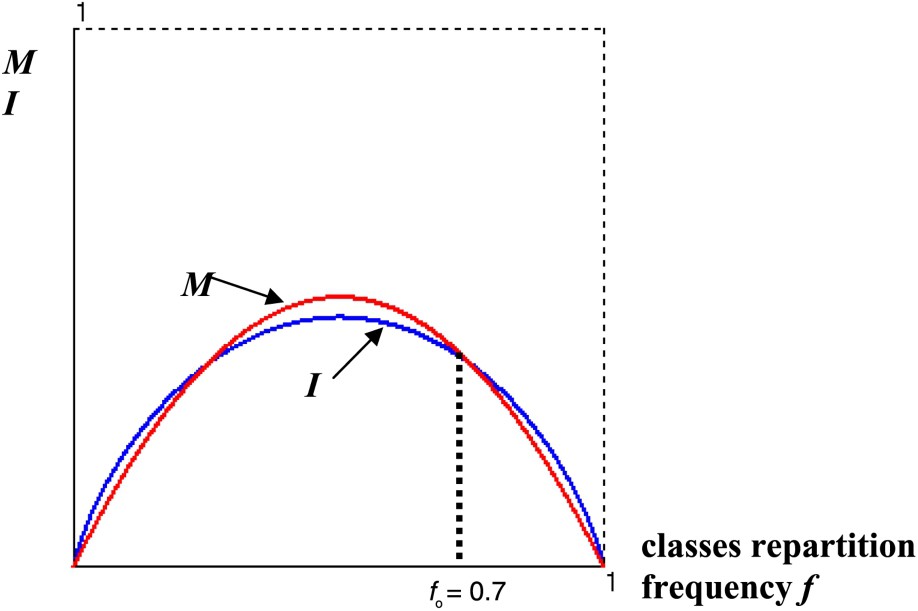
We can interpret in a very schematic way this progressive adaptation by using a simple variational criterion, based on the dual principle of the minimization of the mutation function M and of the maximization of the genetic code information I.

Fig. 6 gives the optimal classes repartition frequency $f_{o} \approx 2 / 3$ for a code with 2 AA, obtained at the intersection of the graphs of the functions

M (f) = 2 f (1 - f) and I (f) = (- f \ln f - (1 - f) \ln (1 - f)) \int_{0}^{1} M (x) d x / \int_{0}^{1} H (x) d x,

where

H (x) = - x \ln x - (1 - x) \ln (1 - x)

. The frequency of an amino-acid AA_i class being equal to

n_{i} / 64

, where

n_{i}

is its size, the mutation function

M = E / 64

is the expectation

E = \sum_{i = 1, 2} (64 - n_{i}) n_{i} / 64

of the deleterious mutations (causing the exit of a synonymy class) divided by the number of codons. The information I is equal to the entropy of the distribution of the AA classes frequencies normalized such as M and I have the same mean value on

[0, 1]

Fig. 6
Graph of the mutation function M and of the information I showing the optimal frequency $f_{o}$ .

If now we renormalize the repartition of the genetic code in 21 synonymy classes or clusters: 3 of 6 codons, 5 of 4, 2 of 3, 9 of 2 and 2 of 1, following at each step the rule such as we roughly respect the optimal proportion $f_{o} \approx 2 / 3$ for one of the bigger renormalized class, we get a coherent tree (Fig. 7), satisfying at each bifurcation the above variational criterion. For example, the first renormalization concerns clusters of size 1 and 2, we combine for obtaining clusters of size 3 and 4 (see the bottom line of the tree) and secondly with clusters of size 4 and 6 for obtaining the third line from the bottom, which corresponds to the affectation of codons to only 8 amino-acids (e.g., the 8 first in Miller's experiment). This short proof explains the classical properties of resistance to the mutations shown by the genetic code [26,27] compatible with the stereochemical hypothesis used in the automaton SUSY.

Fig. 7
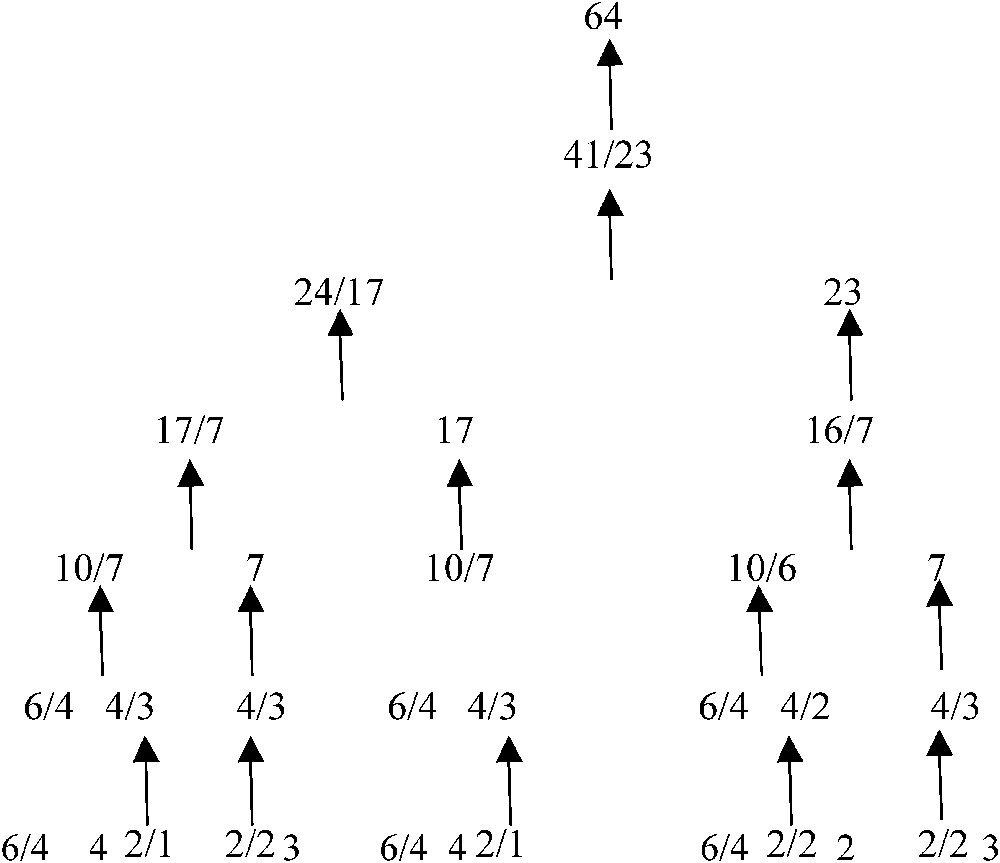
Renormalization tree respecting the optimal frequency $f_{o}$ for the synonymy classes of the genetic code.

5.2 A maximal congruence with present nucleic ‘fossils’

Some RNA relics exist in practically all eukaryote and prokaryote cells: tRNAs and miRNAs represent such fossils preserved during the evolution. We have already proved [1,2] that the most conserved part of tRNAS (their loops) were similar to primitive circular RNAs made of 1 and only 1 representative of each codon class, obtained by maximizing their affinity to AAs and minimizing their length. In the presently known functional miRNAS, we have the same similarities. For example, there is 222 known human miRNAs, plus 76 supplementary human miRNAs recently discovered [28], similar to a primitive circular RNA called AB: CAAGACUAUGAAUGGUGCCAUU, with a significativity p less than 21 – as shown in Fig. 8, which presents consensus sequences for these 76 miRNAs.

Fig. 8
Similarities between miRNA consensus sequences and a circular primitive RNA called AB.

Fig. 8 presents also consensus sequences for miARNs coming from bacteria and plants [29,30] showing the same similarities. Further statistical studies [31] confirm this fact and the miRNA world can then be considered as a fossil reservoir coming from primitive RNAs built with respect to the synonymy classes obtained from the automaton SUSY.

6 Conclusion

We have introduced in this paper the notion of potential automaton, which gives a natural framework to previous discrete systems like Hopfield neural networks, well studied in the past for the existence of Lyapunov energy functions. In a further study, we will introduce the notion of Hamiltonian automaton and propose new directions of research towards the potential-Hamiltonian decomposition of discrete dynamical systems (cf. [5,6] for the continuous case). An application of this new notion of potential automaton concerns the genetic code for which we proved that the degeneracy in synonymy classes of codons can be partly explained by the action of a potential automaton based on the stereochemical properties of both the amino-acids and their codons.

Acknowledgements

We are very indebted to L. Segel and J. Maynard-Smith (died in 2004) for inviting us to pursue researches in the field of theoretical biology and for showing and signalling the road.

Bibliographie

[1] J. Demongeot; J. Besson Code génétique et codes à enchaînement I, C. R. Acad. Sci. Paris, Ser. III, Volume 296 (1983), pp. 807-810

[2] J. Demongeot; J. Besson Genetic code and cyclic codes II, C. R. Acad. Sci. Paris, Ser. III, Volume 319 (1996), pp. 520-528

[3] J. Demongeot; F. Leitner Compact set valued flows I: Applications in medical imaging, C. R. Acad. Sci. Paris, Ser. IIb, Volume 323 (1996), pp. 747-754

[4] J. Demongeot; P. Kulesa; J.D. Murray Compact set valued flows II: Applications in biological modelling, C. R. Acad. Sci. Paris, Ser. IIb, Volume 324 (1997), pp. 107-115

[5] J. Demongeot, N. Glade, L. Forest, Liénard systems and potential-Hamiltonian decomposition. I: Methodology, C. R. Mathématique, in press

[6] N. Glade, L. Forest, J. Demongeot, Liénard systems and potential-Hamiltonian decomposition. II Applications in biology, C. R. Biologies, in press

[7] E. Goles; F. Fogelman Soulié; D. Pellegrin Decreasing energy functions as a tool for studying threshold networks, Discrete Appl. Math., Volume 12 (1985), pp. 261-277

[8] F. Fogelman Soulié; E. Goles; S. Martinez; C. Mejia Energy function in neural networks with continuous local functions, Complex Syst., Volume 3 (1989), pp. 269-293

[9] M. Cosnard; E. Goles Discrete states neural networks and energies, Neural Networks, Volume 10 (1997), pp. 327-334

[10] F. Robert Discrete Iterations: A Metric Study, Springer, Berlin, 1986

[11] O. Cinquin; J. Demongeot High-dimensional switches and the modeling of cell differentiation, J. Theor. Biol., Volume 233 (2005), pp. 391-411

[12] R. Swanson A unifying concept for the amino acid code, Bull. Math. Biol., Volume 46 (1984), pp. 187-203

[13] J.E. Blalock; K. Bost Binding of peptides that are specified by complementary RNAs, Biochem. J., Volume 234 (1986), pp. 679-683

[14] S. Mitaku; T. Hirokawa; T. Tsuji Amphiphilicity index of polar amino-acids as an aid in the characterization of AA preference at membrane–water interfaces, Bioinformatics, Volume 18 (2002), pp. 608-616

[15] D. Gilis; S. Massar; N. Cerf; M. Rooman Optimality of the genetic code with respect to protein stability and amino-acids frequencies, Genome Biol., Volume 2 (2001), pp. 1-12

[16] G. Trinquier; Y.H. Sanejouand Which effective property of amino acids is best preserved by the genetic code?, Protein Eng., Volume 11 (1998), pp. 153-169

[17] M. Magini; J.E.M. Hornos A dynamical system for the algebraic approach to the genetic code, Braz. J. Phys., Volume 33 (2003), pp. 825-830

[18] J.E.M. Hornos; L. Braggion; M. Magini; M. Forger Symmetry preservation in the evolution of the genetic code, Life, Volume 56 (2004), pp. 125-130

[19] D. Bosnacki; H. ten Eikelder; P. Hilbers Genetic code as a Gray code revisited, Proc. Int. Conf. on Mathematics and Engineering Techniques in Medicine and Biological Sciences METMBS'03, Las Vegas, NV, USA, CSREA Press, 2003, pp. 447-456

[20] M. He; S. Petoukhov; P. Ricci Genetic code, Hamming distance and stochastic matrices, Bull. Math. Biol., Volume 66 (2004), pp. 1405-1421

[21] A. Sciarrino A mathematical model accounting for the organization in multiplets of the genetic code, BioSystems, Volume 69 (2003), pp. 1-13

[22] E. Trifonov; J. Sussman The pitch of chromatin DNA is reflected in nucleotide sequence, Proc. Natl Acad. Sci. USA, Volume 77 (1980), pp. 3816-3820

[23] M.K. Hobish; N.S.M.D. Wickramasinghe; C. Ponnamperuma Direct interaction between amino-acids and nucleotides as a possible physico-chemical basis for the origin of the genetic code, Adv. Space Res., Volume 15 (1995), pp. 365-375

[24] I. Majerfeld; D. Puthenvedu; M. Yarus RNA affinity for molecular l-histidine; genetic code origins, J. Mol. Evol., Volume 61 (2005), pp. 226-235

[25] C. de Duve Life Evolving, Oxford University Press, Oxford, UK, 2002

[26] A. Figureau; M. Pouzet Genetic code and optimal resistance to the effects of mutations, Orig. Life, Volume 14 (1984), pp. 579-588

[27] J.M. Labouygues New mathematical model of genetic code with passive resistance to mutations or buccion and complementary dynamic protective mechanisms against noise at genome level, Agressologie, Volume 17 (1976), pp. 329-335

[28] I. Bentwich; A. Avniel; Y. Karov; R. Aharonov; S. Gilad; O. Barad; A. Barzilai; P. Einat; U. Einav; E. Meiri; E. Sharon; Y. Spector; Z. Bentwich Identification of hundreds of conserved and non-conserved human μRNAs, Nat. Genet., Volume 17 (2005), pp. 766-770

[29] S. Gottesman Micros for microbes: noncoding regulatory RNA in bacteria, Trends Genet., Volume 21 (2005), pp. 399-404

[30] B.H. Zhang; X.P. Pan; Q.L. Wang; G. Cobb; T. Anderson Identification and characterization of new plant μRNAs using EST analysis, Cell Res., Volume 15 (2005), pp. 336-360

[31] J. Demongeot, A. Moreira, Fossil tRNAs and miRNAs, and ancestral RNAs, PLOS Biol., submitted for publication

Commentaires - Politique

Ces articles pourraient vous intéresser

About a low complexity class of cellular automata

Pierre Tisseur

C. R. Math (2008)

Asymptotic aspects of Schreier graphs and Hanoi Towers groups

Rostislav Grigorchuk; Zoran Šunik´

C. R. Math (2006)

Prefixes of the Fibonacci word that end with a cube

Narad Rampersad

C. R. Math (2023)