1 Introduction
Individual assignment to species or population of origin is an important task in systematics (e.g., [1,2]), conservation biology (e.g., [3]), and ecology (e.g., [4,5]). Recent studies have shown that individual assignments based on morphological characters alone often underestimate the existing biodiversity (e.g., [6]). Therefore, molecular techniques are often necessary for accurately determining species and population of origin. However, these methods require specific skills and resources that are often not available to ecologists or wildlife managers working in the field. Furthermore, molecular methods may be difficult to perform when the quality of preservation of genetic material varies, such as in the case of museum specimens, and may also fail to recognize significant components of biodiversity (e.g., [7,8 and references therein]). Therefore, while the use of morphological characters to assign individuals to species or populations was a common practice before the use of molecular techniques, this approach still offers a great advantage if at least a few distinct characters or measurements could be used to determine the origin of individuals, especially when alternative molecular methods are unavailable. In addition, when applied to large museum collections, morphological methods can be useful to pinpoint individuals of interest, such as a potential representative of a cryptic lineage, to be further investigated using molecular methods. However, before morphological characters and assignment methods could be accurately applied, their validity and sensitivity to error need to be assessed. This is especially important when the number of shape variables is larger than the sample size, because assignment to groups both depends on the distinctiveness between groups and on the sample size itself.
In this study, we use geometric morphometric methods and a cross-validation calculation to evaluate the robustness of the morphometric assignment of individuals that were previously genotyped, and therefore of known origin, to two distinct tortoise lineages [9]. As it is often the case for field sampling studies, especially on endangered organisms, our dataset consisted of more variables (in this case three-dimensional landmark coordinates) than individuals. We here present a protocol to select the optimal number of shape variables when the reference sample is small and individual assignment is to be achieved. The setting used in this study also allows us to estimate the effect of sex as a confounding variable on taxonomic group assignment after taking into account allometries.
We further apply this approach to obtain the best assignment of the origin of museum tortoises to our previously genotyped reference dataset described above. The museum specimens here analyzed most likely come from the same island of the reference dataset, but it is so far unknown whether they belong to one or both of these two lineages.
2 Materials and methods
2.1 Data acquisition
In our study, we use two genetically very distinct lineages (Cerro Fatal and La Reserva) of Galápagos tortoises (Chelonoidis nigra) inhabiting the Island of Santa Cruz [9,10]. These lineages are phylogenetically recovered to have relatively deep genetic divergence ([11]; for additional information on these two lineages, see [9,10,12]). These tortoises have different, even if apparently very similar, domed shell morphology ([9,12]). The existing morphological data set of 60 Galápagos tortoises belonging to two genetically distinct lineages and already studied for morphological differences ([9,12]) was pruned of the seven juveniles to avoid possible confounding effects due to different carapace shape between juveniles and adults (see [9]). Subdivision of juveniles and adults was done as in our former study on these animals [9]. The final dataset consisted of 27 (11 males and 16 females) and 26 (10 males and 16 females) individuals for Cerro Fatal and La Reserva, respectively. This dataset was combined with 14 newly sampled museum specimens from the same island for which the sex is known [13]. Galápagos tortoise museum specimens were sampled in March and April 2009 at the California Academy of Sciences (CAS, San Francisco, USA). Digital images used for 3D carapace reconstruction and for the camera calibration were obtained with a Pentax K200D (pixel resolution of 3872 × 2592) following [14]. Information about the accuracy of the reconstructions can be found in [14]. Three-dimensional reconstructions were carried out with PhotoModeler® Pro 5.2.3 (Eos System Inc.) and were scaled to the “real” animal size as described in [12] and [14] (see also Fig. 1). The 14 newly sampled museum specimens were part of the 25 individuals sampled in Santa Cruz in 1905 during the California Academy of Sciences expedition [13] (landmark coordinates for these tortoises are available with the voucher information at the museum). We excluded for our analyses individuals that had carapace deformities or were either juveniles or embryos. Between 10 and 12 digital images were used for each 3D carapace reconstruction.
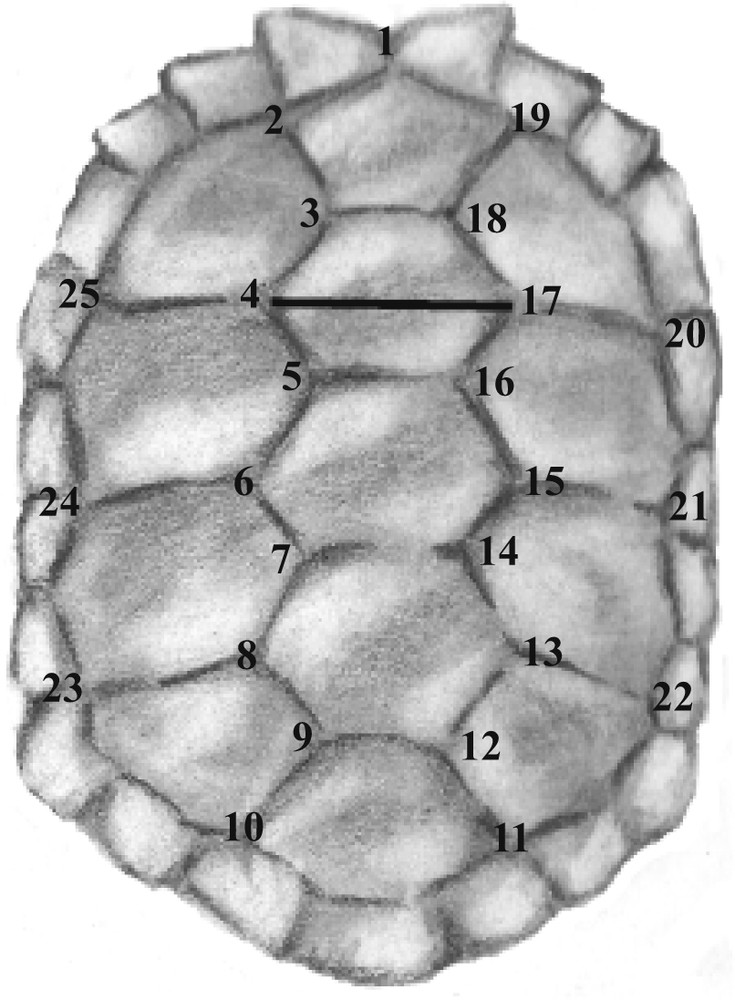
Carapace of a Galápagos tortoise with indicated by numbers the landmarks used for this study. The horizontal line between landmarks 4 and 7 represents the linear measurement used to scale the animal to its “real” size (see [12] and [14] for additional explanations).
2.2 Morphometric analyses
Geometric morphometric analyses were carried out on the total dataset of 67 tortoises using the R software and environment v. 2.6.0. [15] on 25 landmarks (Fig. 1). Missing landmarks occurring in 16 out of the 53 tortoises sampled in the wild were estimated by symmetry as described in [12]. A partial-generalized Procrustes superimposition ([16,17]) was applied to all configurations of landmarks to decompose the studied form into shape components and size. Size was estimated as the centroid size, while shape was given by the coordinates of the superimposed landmarks. Because our dataset included more variables than individuals (75 versus 53, respectively), shape coordinates were summarized by 52 principal components (PCs) having non-null eigenvalues.
To achieve a correct morphological assignment, a balance between the number of shape variables and the number of reference specimens needs to be respected. Furthermore, to be meaningful, discriminant analyses need to be cross-validated (see [18] and references therein). The rate of successful posterior assignment to taxonomic groups may increase as the number of variables used increases (see [18] for a review on this). However, if the number of variables is larger than or close to the number of individuals, predictive approaches, such as predictive linear discriminant analysis used for individual assignments, can become very sensitive to sampling size, producing non-robust posterior probabilities assignment. The trade-off between using more or less variables for the analyses is that when more variables are considered, posterior probabilities for assigning an individual to a group will be higher (but see [19]). However, if variables are in excess in comparison to the number of observations, the prediction is that the assignation will be probably sample dependent and therefore not robust enough. Therefore, to estimate the best number of shape variables to use, an optimal balance between shape information and sampling size needs to be assessed. We here evaluate, using a jackknife approach, the rate of incorrect assignment depending on the selection of an increasing number of shape variables (here identified by PCs). Therefore, to select the optimal number of free shape components that allows lower misclassification of the 53 tortoises of known origin and sex, we ran predictive discriminant analyses (PDA) by using two groups (the two lineages) on progressively adding an increasing number of free shape components with the “leave one individual out” cross-validation (jackknife) computation. The “leave one individual out” cross-validation (jackknife) approach means that each individual is iteratively excluded from the analysis to see how re-sampling the dataset affects the assignment estimation. This approach avoids the circularity of classifying individuals using functions based on those same individuals (as in the case of not-cross-validated discriminant analyses). Individuals included in this analysis vary in size and sexes [9], which can represent a confounding effect in taxonomic assignment. A Burnaby correction [20] was applied to remove possible shape differences due to allometric growth. We considered four different growth curves accounting for the two sexes per two lineages of Santa Cruz tortoises sampled in the wild. The predictive discriminant analysis was applied from the first to the 48th allometry free shape components (48 shape components correspond to 52 non null shape components–4 allometric corrections). The first allometry free shape components were added sequentially according to their rank in this iteration. Due to the confounding effects of sexual differences on the carapace shape, we also run a predictive discriminant analysis after the sex effect on shape was removed. To do this, we considered the shape residuals after shape variation related to sex was removed. The confounding effect of a possible interaction between sex and lineage does not need to be taken into account as it has already been shown [9,12] that this interaction was not significant once nuisance effects due to allometric growth are removed. Sex predictions based on the reference specimens were used. For this analysis, we considered the 47th allometry and sex free shape components (52 non null shape components–1 sex effect–4 allometric corrections). To assign individual museum specimens to the lineage of origin, a predictive discriminant analysis was then performed on the shape components of the entire dataset (including individuals sampled in the wild and at the California Academy of Sciences). Due to the fact that this approach may be sample dependent, the number of selected PCs was established on the reference sample that provided the lowest assignment error rate according to the two assignment strategies (with and without sex effects removed). Finally, because it is possible that the museum specimens may belong to another lineage, we checked whether the projection of the museum specimens felt into the variation of the reference specimens by performing a linear discriminant analysis (LDA) on all the reference individuals using four groups (two sexes per two lineages). For this checking analysis, we used the number of allometry free shape components assuring the lower incorrect classification according to the results of the above analyses.
3 Results
The correct assignment rate for the lineage of origin significantly depends on the number of allometry free shape components used (Fig. 2). The predictive discriminant analysis ran with a cross-validation calculation on two groups (the two lineages) shows best lineage assignment rate (8%, 4 individuals) with two or six shape components (Fig. 2). Incorrect classification occurs for the same two (a female from Cerro Fatal classified as La Reserva and a male from La Reserva assigned to Cerro Fatal) out of the four badly assigned individuals. Higher percentage of wrong lineage assignment is instead obtained with a high (43–48) and a low (one) number of allometry free shape components (Fig. 2).
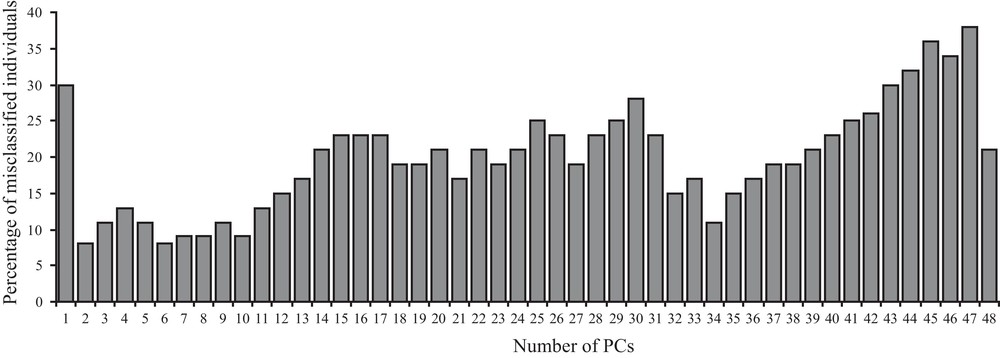
Bar-plot graph of the percentage of the estimated misclassified individuals (y-axes) according to the different number of first allometry free shape components (x-axes) taken into account (see Materials and methods for further explanations) after predictive discriminant analysis on two distinct groups (two lineages) with cross-validation calculation. Percentage of misclassification are rounded to the closest higher (if > 0.5) or lower (if < 0.5) value.
When confounding sex effects are filtered out and when the best shape components are taken into account (for 34, 35, 39, and 42 shape components, Fig. 3), the number of misclassified individuals decreases to only two. One of the two misclassified individuals is always the same when using 34, 35, 39, but not 42 shape components (4% misclassification). This individual is still misclassified when using 37, 38 (6% misclassification) or 6 (9% misclassification) shape components.
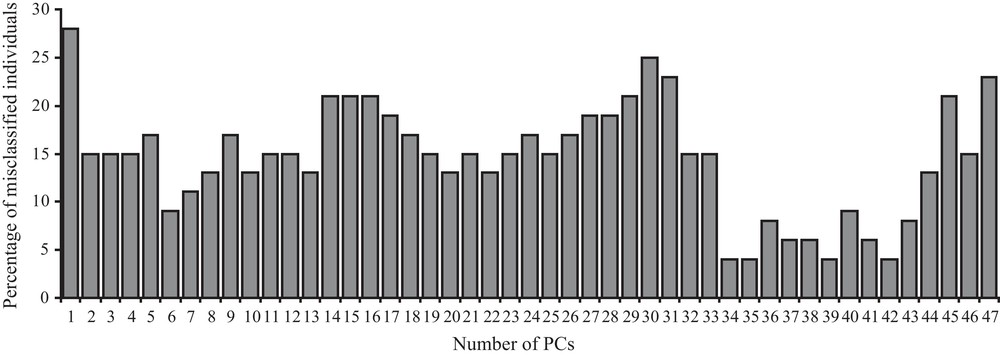
Bar-plot graph of the percentage of the estimated misclassified individuals (y-axes) according to the different number of first allometry free shape components (x-axes) taken into account (see Methods for further explanations) after linear discriminant analysis on two distinct groups (two lineages) after sex effects are removed and cross-validation calculation was applied. Percentage of misclassification are rounded to the closest higher (if > 0.5) or lower (if < 0.5) value.
Assignment of the museum tortoises to their lineage of origin is the same for six out of 14 individuals analyzed when the different allometry free shape components are used without removing confounding sex effects (Table 1a). The rate of identical assignment highly improves when these effects are removed. In fact, assignment of the museum tortoises is always the same for nine out of the 14 specimens analyzed (Table 1b). Furthermore, assignment of most individuals to one or the other lineage changes depending on the optimal or sub-optimal number of shape components used when confounding sex effects are not taken into account (Table 1a). Instead, most of the specimens are always assigned to La Reserva lineage with a very high posterior probability independently on the number of shape components used, while only one is always assigned to Cerro Fatal when the confounding sex effects are corrected for (Table 1b).
Individual assignment test run on two groups (the two lineages) for the 14 museum tortoises to assign the lineage of origin (Cerro Fatal or La Reserva) on the best shape variables. Percentage of assignment, rounded to the closest higher (if > 0.5) or lower (if < 0.5) value, is indicated. Percentages correspond to probabilities of belonging to one category. CF and Res indicate Cerro Fatal and La Reserva, respectively. LDA estimation corresponds to the assignment obtained with the discriminant analysis by using a different number of allometry free shape components (chosen as the one with the lower incorrect assignment percentage as in Figs. 2 and 3) without (a) and with (b) removing confounding sex effects. Assignment rates correspond to the ones reported in Figs. 2 and 3. CAS number indicates the voucher number for each museum specimen analyzed here. In bold are highlighted the samples that were always assigned to the same lineage, independently of the number of shape variables used.
| Number of shape components (a) | ||||||||||||||||
| Assignment rate | 8 % | 8 % | 9 % | 9 % | 9 % | |||||||||||
| Number of shape components | 2 | 6 | 7 | 8 | 10 | |||||||||||
| CAS voucher # | CF | Res | CF | Res | CF | Res | CF | Res | CF | Res | ||||||
| 8274 | 45 | 55 | 54 | 46 | 28 | 72 | 32 | 68 | 16 | 84 | ||||||
| 8276 | 74 | 26 | 68 | 32 | 30 | 70 | 35 | 65 | 44 | 56 | ||||||
| 8277 | 39 | 61 | 57 | 43 | 34 | 66 | 31 | 69 | 20 | 80 | ||||||
| 8279 | 39 | 61 | 41 | 59 | 36 | 64 | 39 | 61 | 21 | 79 | ||||||
| 8280 | 78 | 22 | 59 | 41 | 10 | 90 | 10 | 90 | 4 | 96 | ||||||
| 8281 | 99 | 1 | 91 | 9 | 44 | 56 | 47 | 53 | 35 | 65 | ||||||
| 8382 | 9 | 91 | 23 | 77 | 26 | 74 | 31 | 69 | 42 | 58 | ||||||
| 8383 | 53 | 47 | 32 | 68 | 10 | 90 | 11 | 89 | 4 | 96 | ||||||
| 8384 | 1 | 99 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | ||||||
| 8385 | 1 | 99 | 1 | 99 | 2 | 98 | 2 | 98 | 3 | 97 | ||||||
| 8386 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | ||||||
| 8287 | 8 | 92 | 21 | 79 | 4 | 96 | 5 | 95 | 2 | 98 | ||||||
| 8288 | 16 | 84 | 25 | 75 | 2 | 98 | 1 | 99 | 1 | 99 | ||||||
| 8290 | 3 | 97 | 41 | 59 | 40 | 59 | 40 | 60 | 76 | 24 | ||||||
| Number of shape components (b) | ||||||||||||||||
| Assignment rate | 4 % | 4 % | 4 % | 4 % | 6 % | 6 % | 6 % | 9 % | ||||||||
| Number of shape components | 34 | 35 | 39 | 42 | 37 | 38 | 41 | 6 | ||||||||
| CAS voucher # | CF | Res | CF | Res | CF | Res | CF | Res | CF | Res | CF | Res | CF | Res | CF | Res |
| 8274 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 67 | 33 |
| 8276 | 0 | 100 | 0 | 100 | 100 | 0 | 100 | 0 | 0 | 100 | 0 | 100 | 100 | 0 | 75 | 25 |
| 8277 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 63 | 37 |
| 8279 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 42 | 58 |
| 8280 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 74 | 26 |
| 8281 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 86 | 14 |
| 8382 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 17 | 83 |
| 8383 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 15 | 85 |
| 8384 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 |
| 8385 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 1 | 99 |
| 8386 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 |
| 8287 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 26 | 74 |
| 8288 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 | 15 | 85 |
| 8290 | 100 | 0 | 100 | 0 | 100 | 0 | 0 | 100 | 100 | 0 | 100 | 0 | 0 | 100 | 23 | 77 |
Finally, when applying a four group (two sexes, two lineages) linear discriminant analysis on reference specimens and projecting museum specimens on the two first linear discriminant axes, carapace shape variation of the museum specimens falls into the range of variation obtained for the two sampled lineages, suggesting that these tortoises do not represent a third, unknown morphological group (Fig. 4). Linear discriminant analysis well divides the two lineages and the two sexes along the first and second axes. However, partial overlap especially between the two sexes is observed and four individuals are misclassified as lineage. Also, according to this analysis, most of the museum specimens seem closer in shape to the La Reserva lineage than to Cerro Fatal.
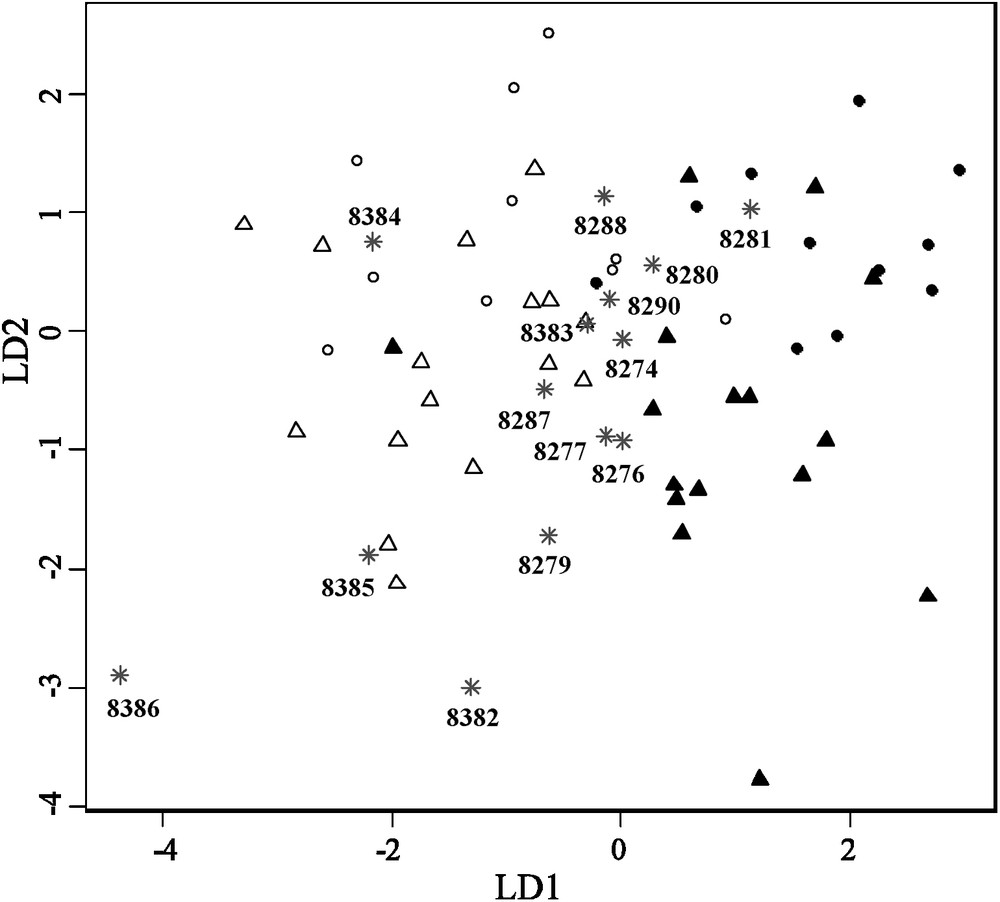
Linear discriminant analysis on four groups along the first and second discriminant axes (LD1 and LD2, respectively) on the first 6th principal components (PC) shape coordinates after removing allometric growth. Discriminant power associated with the first axis was 74%, while the one associated with the second axis was 20%. Black circles: Cerro Fatal males. White circles: La Reserva males. Black triangles: Cerro Fatal females. White triangles: La Reserva females. Grey stars and numbers: California Academy of Sciences specimens with voucher number.
4 Discussion
Morphological assignment by morphometric analyses to identify the lineage of origin has been and it is widely used on different organisms for distinct purposes (e.g., see references in the Introduction). Recently, Will and Rubinoff [21] stated the limits of DNA barcoding in comparison to morphology for identification and classification of living organisms. However, to be widely used, an assignment method needs to be reliable, without being affected by sampling bias, and repeatable. Morphological assignment methods are more recently used in combination with other data (e.g., ecological or genetics), so that assignments are based on concordance among data, without further testing the performance of these methods (e.g., see references in the Introduction). However, morphological assignment methods are often applied without a previous evaluation on their accuracy. In a recent study, 39 shell measurements were applied to assign the population of origin of wild individuals of the radiated tortoise (Astrochelys radiata, [22]). While this approach aided in identifying the origin of the sampled tortoises, the successful rate of assignment was not higher than 77% (average of assignment 63%), indicating the possible existence of a significant margin of error. Furthermore, the sampled individuals were not genotyped and except for the sampling locality (seven localities used), no other information was available to confirm the accuracy of the assignment results. Sheets et al. [4] comparing the rates of correct cross-validation assignment test of two approaches of dimensionality reduction–the first of which utilizes a variable number of PC axes and the second is the classical approach of using a fixed number of PC axes–observed a better performance of the former versus the latter. Our results indicate that morphological assignment may be strongly sensitive to the number of individuals (tested by applying the cross-validation test) and the number of shape component used for the analyses. According to our results, misleading results can be obtained when too many or too little shape components are applied for the analyses and indicate that it is not possible to know “a priori” the optimal number of shape component to apply. We therefore suggest checking the robustness of predictive analyses before using these tools to assign individuals to taxonomic groups.
In Galápagos tortoises, morphological differences in carapace shape have been identified among distinct lineages for which genetic data on their origin were previously available ([9,12,23]). However, when carapace shape is used to assign the lineage of origin in Galápagos tortoises, our results indicate that geometric morphometric methods on carapace shape cannot be reliably used to this purpose without a prior evaluation of the optimal number of shape components, at least for individuals with apparently very similar carapace morphology. In this study, tortoises have been previously genotyped–lineage of origin is already known–allowing the percentage of misclassification associated with the different number of shape variables to be evaluated. Our data show that incorrect lineage assignment rate varies depending on the number of allometry free shape components used for the discriminant analysis with cross-validation. Thanks to our setting, we could chose to use the number of allometry free shape components associated with the lowest percentage of lineage misclassification to provide the more robust assignment for individuals of unknown origin (the museum specimens). Most of the 14 museum specimens analyzed here were always recovered to belong to the La Reserva lineage independently of the number of shape variables used when confounding sex effects were taken into account. According to van Denburgh's report of the sampling of the museum tortoises [13], sampling was carried during few days by people visiting distinct sites. It is therefore possible that during the field sampling, individuals belonging to both lineages were collected. For five out of 14 of the museum tortoises, lineage assignment is not always the same when applying distinct number of shape component and taking into account sex effects on shape. However, this may also be due to the known morphological overlapping in carapace shape between the two lineages ([9,12], and current data) and the possible existence of hybrids between the two lineages. Finally, when the sex effect was filtered out from the reference group, the accuracy of the assignment rate increased and the assignment of museum individuals changed less depending on the number of shape components used. This highlights how filtering out sources of variation can increase the robustness of the analysis, especially when confounding factors operate on similar shape components and do not interact with the factor under study (here the lineage). Indeed, removing shape variation that can be caused by confounding effects forces the discriminant analysis to be based only on characters that are affected by the factor under study.
To conclude, our approach can be generalized whenever one needs to perform a predictive discriminant analysis. For such an aim, we suggest that the user should first manage to gather the largest available reference dataset and to identify all possible confounding effects. Once relationship between shape component selection and correct assignment rate are established, this optimal selection can be used for increasing the robustness of the prediction. Our protocol adds shape components according to their rank, even if a more exhaustive selection (in trying all possible combinations) can be thought to increase the robustness. We, however, believe that the strategy of adding shape components according to their rank remains a good heuristic approach. In fact, considering that high ranked shape components could bear less information, it is more likely that in this case the repeatability could become impeded and even more sample dependent.
Disclosure of interest
The authors declare that they have no conflicts of interest concerning this article.
Acknowledgments
We are very thankful to the staff of the California Academy of Sciences, and especially to Alan Leviton, Robert Drewes, Jens Vindum, Jefferey Wilkinson, Ricka Stoelting, and Hallie Brignall for their support on this work and help with the museum sampling. We are grateful to the EOS support for the irreplaceable help with PhotoModeler®. Scott Glaberman, Adalgisa Caccone and Edgar Benavides provided useful comments on a preliminary version of this manuscript. We are thankful to Andrea Cardini and to an anonymous reviewer for their useful suggestions on this work. This project has been supported by the Brett C. Stearns Award for Chelonian Research to YC. This is the publication ISEM # 2011-147.


