Plan
Comptes Rendus
no. 2

Influence de l’énergie interne sur la réactivité de l’ion Fe(CO)2+ avec le diméthyléther, étudiée dans un spectromètre de masse FT–ICR
Sophie Le Caër1  ; Pascal Pernot1 ; Michel Heninger1 ; Hélène Mestdagh1
1 Laboratoire de chimie physique (UMR 8000), bât. 350, université Paris-Sud, 91405 Orsay, France
Comptes Rendus. Chimie, Volume 5 (2002) no. 2, pp. 119-125.

Résumés

L’influence de l’énergie interne sur la réactivité de l’ion Fe(CO)2+ avec le diméthyléther, CH3OCH3 (noté DME) a été étudiée à l’aide d’un spectromètre de masse de résonance cyclotronique ionique (ICR) à trois cellules. Après une brève introduction de la technique expérimentale et de la méthode d’analyse des données, nous présenterons en détail les résultats expérimentaux obtenus. En effet, la réactivité est très sensible à l’énergie interne des ions Fe(CO)2+ réactants : avec des ions thermalisés, seules deux substitutions successives d’un ligand CO par une molécule de DME se produisent, alors que des réactions de rupture (homolytique ou avec réarrangement) de la liaison C–O sont observées lorsque les ions sont excités. Un mécanisme permettant de rendre compte de l’activation de la liaison C–O est alors proposé.

The influence of the internal energy on the reactivity of iron carbonyl cations with dimethylether CH3OCH3 (DME) has been studied using a triple cell Fourier Transform Ion Cyclotron Resonance mass spectrometer. The experimental set-up as well as the data analysis are briefly presented before being detailed on the example of the reactivity of Fe(CO)2+. The strong energy dependence upon the reactivity of the ion is shown: when working with thermalised ions, the only channels observed are the two successive substitutions of a CO ligand by one DME molecule, whereas other channels are opened up for excited ions (the cleavage of the C–O bond may be homolytic or due to a rearrangement). A reaction mechanism of the C–O bond activation is then proposed.

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/S1631-0748(02)01360-7
Mot clés : phase gazeuse, fer pentacarbonyle, réactions ion–molécule, spectrométrie de masse, résonance cyclotronique ionique, activation de la liaison C–O
Keywords: gas phase, iron carbonyl, ion–molecule reactions, mass spectrometer, ion cyclotron resonance, C–O bond activation

Sophie Le Caër 1 ; Pascal Pernot 1 ; Michel Heninger 1 ; Hélène Mestdagh 1

1 Laboratoire de chimie physique (UMR 8000), bât. 350, université Paris-Sud, 91405 Orsay, France 
@article{CRCHIM_2002__5_2_119_0,
     author = {Sophie Le Ca\"er and Pascal Pernot and Michel Heninger and H\'el\`ene Mestdagh},
     title = {Influence de l{\textquoteright}\'energie interne sur la r\'eactivit\'e de l{\textquoteright}ion {Fe(CO)\protect\textsubscript{2}\protect\textsuperscript{+}} avec le dim\'ethyl\'ether, \'etudi\'ee dans un spectrom\`etre de masse {FT{\textendash}ICR}},
     journal = {Comptes Rendus. Chimie},
     pages = {119--125},
     publisher = {Elsevier},
     volume = {5},
     number = {2},
     year = {2002},
     doi = {10.1016/S1631-0748(02)01360-7},
     language = {fr},
}
TY  - JOUR
AU  - Sophie Le Caër
AU  - Pascal Pernot
AU  - Michel Heninger
AU  - Hélène Mestdagh
TI  - Influence de l’énergie interne sur la réactivité de l’ion Fe(CO)2+ avec le diméthyléther, étudiée dans un spectromètre de masse FT–ICR
JO  - Comptes Rendus. Chimie
PY  - 2002
SP  - 119
EP  - 125
VL  - 5
IS  - 2
PB  - Elsevier
DO  - 10.1016/S1631-0748(02)01360-7
LA  - fr
ID  - CRCHIM_2002__5_2_119_0
ER  - 
%0 Journal Article
%A Sophie Le Caër
%A Pascal Pernot
%A Michel Heninger
%A Hélène Mestdagh
%T Influence de l’énergie interne sur la réactivité de l’ion Fe(CO)2+ avec le diméthyléther, étudiée dans un spectromètre de masse FT–ICR
%J Comptes Rendus. Chimie
%D 2002
%P 119-125
%V 5
%N 2
%I Elsevier
%R 10.1016/S1631-0748(02)01360-7
%G fr
%F CRCHIM_2002__5_2_119_0
Sophie Le Caër; Pascal Pernot; Michel Heninger; Hélène Mestdagh. Influence de l’énergie interne sur la réactivité de l’ion Fe(CO)2+ avec le diméthyléther, étudiée dans un spectromètre de masse FT–ICR. Comptes Rendus. Chimie, Volume 5 (2002) no. 2, pp. 119-125. doi : 10.1016/S1631-0748(02)01360-7. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/S1631-0748(02)01360-7/

Version originale du texte intégral

1 Introduction

La spectrométrie de masse est un outil analytique de choix pour l’identification des molécules et de leur structure, par exemple dans le cas des clusters métalliques 〚1〛. C’est également un moyen efficace d’étudier les réactions ion–molécule en phase gazeuse, en particulier avec des ions organométalliques. Ces études sur des espèces isolées permettent en effet de s’affranchir du rôle de solvant, et donc d’étudier spécifiquement l’interaction métal–ligand.

La chimie des ions métalliques M+ nus en phase gazeuse a été et est l’objet de nombreuses études expérimentales 〚2〛 ou théoriques 〚3〛. Les premiers travaux ont concerné la réactivité des cations des métaux de transition de la première ligne de la classification périodique, et en particulier de l’élément le plus largement répandu, le fer. Différents groupes ont ainsi étudié la réactivité de l’ion Fe+ avec diverses molécules organiques oxygénées comme les alcools 〚4〛, les cétones et les éthers 〚5〛, les peroxydes 〚6,7〛...

Concernant les cations métalliques porteurs de ligands, une part non négligeable des travaux porte sur la détermination des énergies de liaison métal–ligand 〚8〛. En effet, la connaissance de ces grandeurs thermodynamiques est importante, dans la mesure où ces données sont parfois transférables en phase condensée, et peuvent être comparées aux résultats des études théoriques. Les complexes porteurs de ligands fortement liés au centre métallique ont ainsi été étudiés, par exemple sur des complexes du fer 〚9〛. Ainsi, l’équipe de Schwarz s’est intéressée à la réactivité de FeO+ avec le méthane 〚10〛. En revanche, la réactivité des complexes pour lesquels les ligands sont moins fortement liés au centre métallique a été moins étudiée 〚11,12〛. Leur réactivité reste en effet difficile à prévoir, car les ligands autour du centre métallique peuvent être spectateurs, groupes partants ou même participer directement à la réaction par formation ou par rupture de liaison. Par ailleurs, peu de travaux ont porté sur l’effet de l’énergie interne sur la réactivité.

L’approche proposée ici allie un spectromètre de masse original à un outil de traitement des données performant. Pour pouvoir contribuer à une meilleure compréhension des effets de ligands et du rôle de l’énergie interne sur la réactivité, plusieurs systèmes ont été abordés dans notre laboratoire. Les réactions des différents cations du fer carbonyle Fe(CO)n+ (n = 1–5) avec le méthanol 〚13〛 et l’oxygène 〚14〛 ont été étudiées.

2 Technique expérimentale : le « tricyclotron »

2.1 Principe de la FT–ICR

La technique utilisée est la spectrométrie de masse de résonance cyclotronique ionique à transformée de Fourier (FT–ICR ou FT–MS) 〚15〛. C’est une technique basée sur le mouvement d’un ion soumis à l’action simultanée de champs électrique et magnétique croisés. Dans ces conditions, l’ion décrit une trajectoire hélicoïdale, superposition d’un mouvement de translation le long de l’axe du champ magnétique et d’un mouvement circulaire autour de cet axe de fréquence νc = q B/(2 π m), caractéristique du rapport q/m (ou charge sur masse) de l’ion.

Pour des ions d’un rapport masse sur charge donné, le mouvement cyclotron peut être excité à l’aide d’un champ électrique radiofréquence résonant (dont la fréquence est égale à la fréquence cyclotron). Les ions tournent alors en phase, sur une orbite dont le rayon croît linéairement avec le temps. Si la durée de l’excitation est assez grande, ils se neutralisent sur les électrodes de la cellule. Si l’excitation est interrompue avant, ils continuent à tourner en phase sur des orbites de grand rayon, et induisent un courant image dans le circuit de détection. Ce signal est une somme de sinusoïdes dont l’analyse, effectuée par transformée de Fourier, permet de déterminer, en fonction de la masse, l’abondance de tous les ions présents.

Pour l’étude des réactions ion–molécule, la FT–ICR présente les avantages suivants :

  • • le suivi des réactions chimiques peut être effectué sur une large gamme de temps de réactions, de quelques millisecondes à plusieurs secondes ;
  • • peu d’énergie cinétique est communiquée aux ions réactants, ce qui permet leur étude à énergie thermique.

2.2 Dispositif expérimental

L’appareil construit et utilisé au laboratoire (le Tricyclotron) comporte trois cellules montées en série. Ces trois cellules sont placées dans la région homogène du champ magnétique (électroaimant de 1.5 T). Chaque cellule possède sa propre enceinte à vide et son groupe de pompage. Deux cellules adjacentes communiquent via un « entonnoir » à ions. Les entonnoirs sont des réductions homothétiques de la cellule. Ils assurent le transfert des ions d’une cellule à l’autre, tout en limitant le passage des molécules neutres. La combinaison des entonnoirs et du pompage différentiel assure un gradient de pression de l’ordre de 250 entre deux cellules adjacentes.

La première cellule (ou cellule de production) est utilisée pour générer les ions, soit par impact électronique (IE), soit par ionisation chimique (CI). La seconde cellule est utilisée pour relaxer ou détecter les ions (cellule de relaxation/détection). La pression résiduelle est maintenue très basse (10–9 torr) dans cette cellule, car la relaxation radiative ainsi que la détection doivent s’effectuer dans les meilleures conditions de vide possible. En effet, les collisions entraînent une décroissance du signal en fonction du temps d’observation : c’est un signal transitoire. Ce signal ne peut donc être observé que s’il y a aussi peu de collisions que possible. La dernière cellule (cellule de réaction) sert de réacteur chimique. L’intérêt de séparer spatialement la réaction (troisième cellule) et la détection (deuxième cellule) des ions est de travailler avec des pressions de gaz « statiques », donc parfaitement connues, ce qui est une condition indispensable pour les études cinétiques.

2.3 Mode opératoire

Deux types d’expériences ont été réalisés au cours de ce travail : des études de réactivité et une étude de relaxation.

2.3.1 Études cinétiques

Les ions sont formés dans la première cellule par impact électronique sur Fe(CO)5 gazeux à une pression d’environ 10–6 torr, avec une énergie des électrons de 20 eV. Dans ces conditions expérimentales, les ions Fe(CO)+ et Fe(CO)2+ sont majoritaires. Ici, l’ion à étudier, Fe(CO)2+, est sélectionné en masse par éjection sélective de tous les ions indésirables. En effet, les ions Fe(CO)2+ excités et Fe(CO)+ conduisent tous deux à l’ion Fe(DME)+. L’éjection dans la première cellule permet donc d’étudier spécifiquement et précisément la réactivité de l’ion Fe(CO)2+ seul. Les ions sont ensuite transférés dans la troisième cellule, soit directement, soit après avoir été relaxés par collision sur de l’argon.

Ils réagissent pendant une durée variable avec le gaz neutre (ici le DME), présent à une pression d’environ 10–6 torr, avant d’être ramenés dans la deuxième cellule pour y être détectés.

2.3.2 Relaxation radiative

Le mode de fabrication et de sélection des ions est identique. Les ions sont ensuite piégés dans la deuxième cellule, en l’absence de gaz (donc en l’absence de collisions), pendant un temps variable. Ils sont ensuite introduits dans la cellule de réaction où ils réagissent avec le DME à pression et temps de réaction constants. Enfin, ils sont détectés dans la deuxième cellule.

2.4 Traitement des données

L’acquisition des spectres correspondant aux différents temps de réaction est pilotée par un ordinateur. Les courbes cinétiques sont obtenues en portant l’abondance des différents ions en fonction du temps de réaction. À partir de ces courbes et de la masse des ions détectés, un premier schéma réactionnel regroupant les différentes réactions successives est proposé. Ce schéma est ensuite validé par des expériences complémentaires d’éjection sélective. Le spectre de référence est comparé au spectre obtenu en éjectant pendant le temps de réaction un des ions produits par la réaction. Les ions sont ainsi détruits avant d’avoir pu réagir sur le DME. L’étude des pics affectés ou non par cette éjection nous permet alors d’établir les filiations entre les différents ions.

La méthode d’analyse des données, permettant d’obtenir les constantes de vitesse des réactions avec leurs incertitudes et de savoir si ces constantes de vitesse sont déterminées précisément, est présentée en appendice.

3 Résultats

Par impact électronique, les ions sont fabriqués avec une distribution en énergie interne, dans un état excité, avec des durées de vie éventuellement longues, allant de la milliseconde à la seconde dans le cas de l’ion Fe+ nu 〚16,17〛. L’énergie interne de l’ion réactant peut modifier la réactivité (ouverture de nouvelles voies de réaction, modification des vitesses de réaction...), comme cela a été montré pour des ions métalliques nus sélectionnés en énergie électronique 〚18〛. Dans cette étude, nous avons travaillé avec des ions Fe(CO)2+ thermalisés par collisions sur des atomes d’argon, ainsi qu’avec des ions Fe(CO)2+ excités. Une étude de relaxation radiative nous donne des informations sur les durées de vie des états excités mis en jeu.

3.1 Étude cinétique

Lorsque les ions Fe(CO)2+ sont froids (relaxés), les seules réactions observées (Fig. 1) sont les deux substitutions successives d’un ligand CO par une molécule de DME, conduisant à l’ion terminal Fe(DME)2+.

Fig. 1

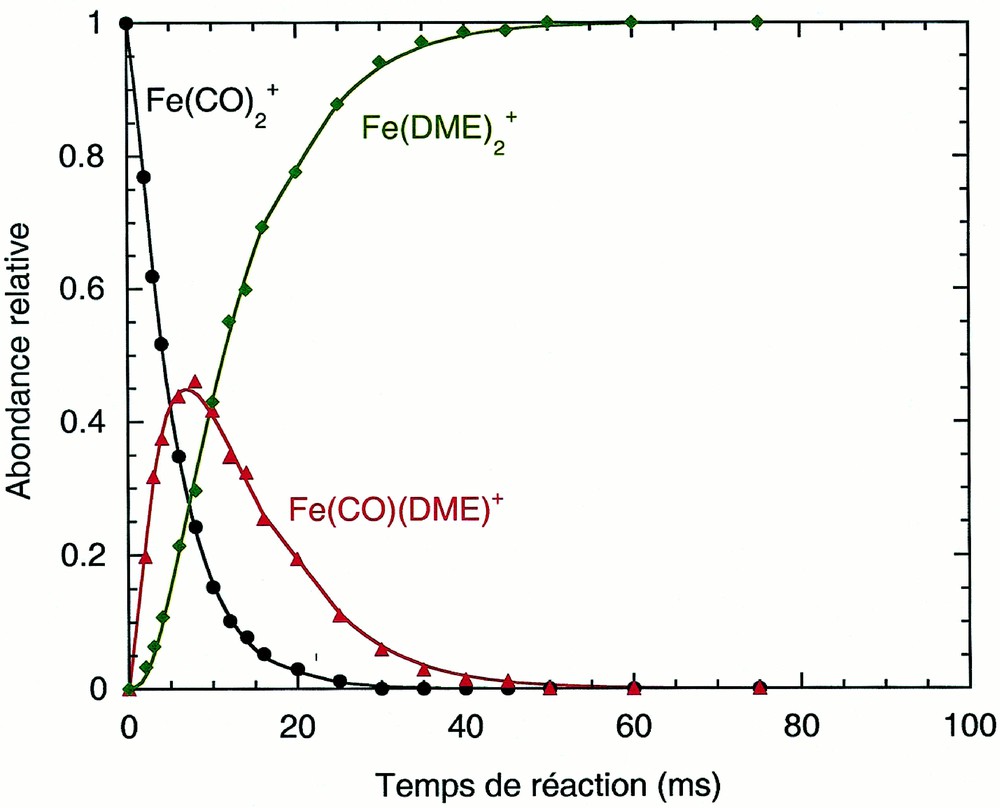
Évolution de la distribution des ions en fonction du temps de réaction, pour le système Fe(CO)2+ relaxé avec le DME (la pression du gaz réactant est de 6,1 10–6 torr) : m/z 112, Fe(CO)2+ (cercles noirs) ; m/z 130, Fe(CO)(DME)+ (triangles rouges) ; m/z 148, Fe(DME)2+ (losanges verts). Les lignes pleines sont les courbes ajustées sur les données expérimentales.

La réactivité est fortement modifiée lorsque les ions Fe(CO)2+ réagissent avec le DME (Fig. 2a aux temps longs et Fig. 2b aux temps courts) sans avoir été relaxés dans la deuxième cellule. Un nouvelle voie de réaction est ouverte puisque la réaction de Fe(CO)2+ sur le DME conduit maintenant à deux produits : l’ion Fe(CO)(DME)+, comme dans le cas précédent, et l’ion Fe(DME)+, après substitution simultanée de deux ligands CO par une molécule de DME.

Fig. 2

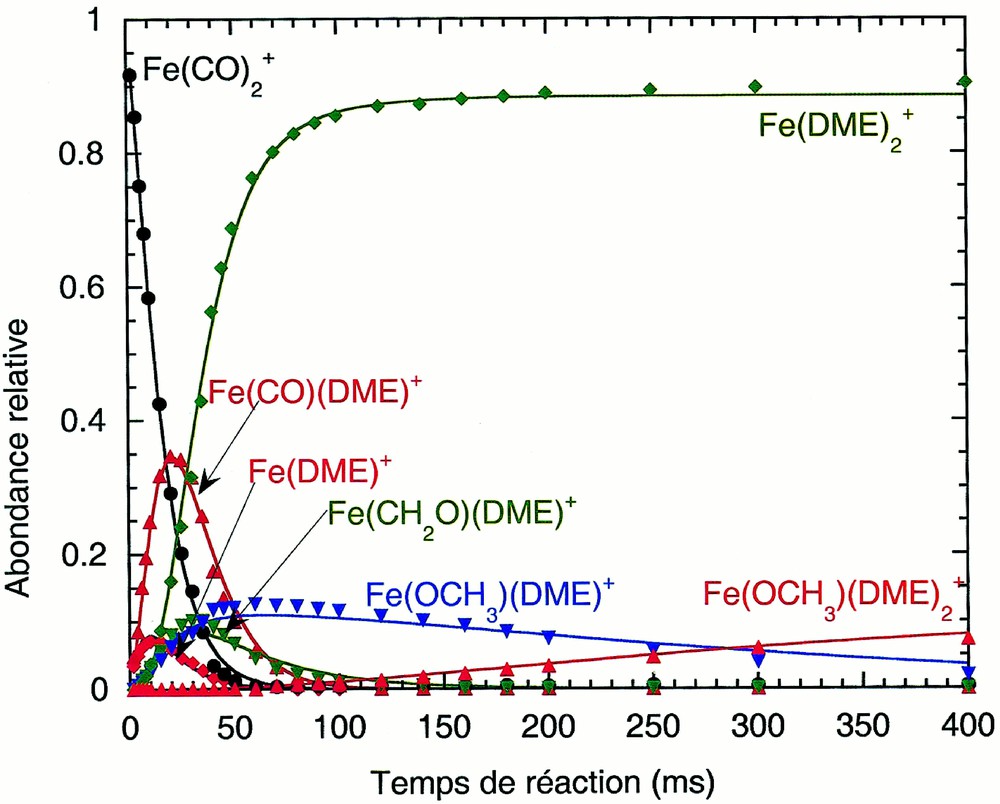
Évolution de la distribution des ions en fonction du temps de réaction pour le système Fe(CO)2+ non relaxé/DME (pression du gaz réactant : 2,6 10–6 torr) : m/z 102, Fe(DME)+ (losanges rouges) ; m/z 112, Fe(CO)2+ (cercles noirs) ; m/z 130, Fe(CO)(DME)+ (triangles rouges) ; m/z 132, Fe(OCH2)(DME)+ (triangles pointe en bas verts) ; m/z 133, FeOCH3(DME)+ (triangles pointe en bas bleus) ; m/z 148, Fe(DME)2+ (losanges verts) ; m/z 179, FeOCH3(DME)2+ (triangles rouges). Les lignes pleines sont les courbes ajustées sur les données expérimentales. (a) Longs temps de réaction ; (b) temps de réaction courts. L'ion Fe(CO)2+ n'a pas été représenté sur la Fig. 2b.

L’ion Fe(CO)(DME)+ conduit à la formation de l’ion Fe(DME)2+.

L’ion Fe(DME)+ réagit ensuite avec le DME pour former, après rupture de la liaison C–O, les ions Fe(CH2O)(DME)+ (avec perte d’une molécule de méthane) et Fe(OCH3)(DME)+ (avec perte d’un groupement méthyle).

3.2 Schéma cinétique

Le schéma cinétique global ainsi que les constantes de vitesse et les incertitudes obtenues en utilisant notre méthode d’analyse des données sont reportés sur la Fig. 3. L’incertitude expérimentale est beaucoup plus importante que celle calculée, puisqu’elle est de l’ordre de 20%. Elle est principalement due à la détermination de la pression.

Fig. 3

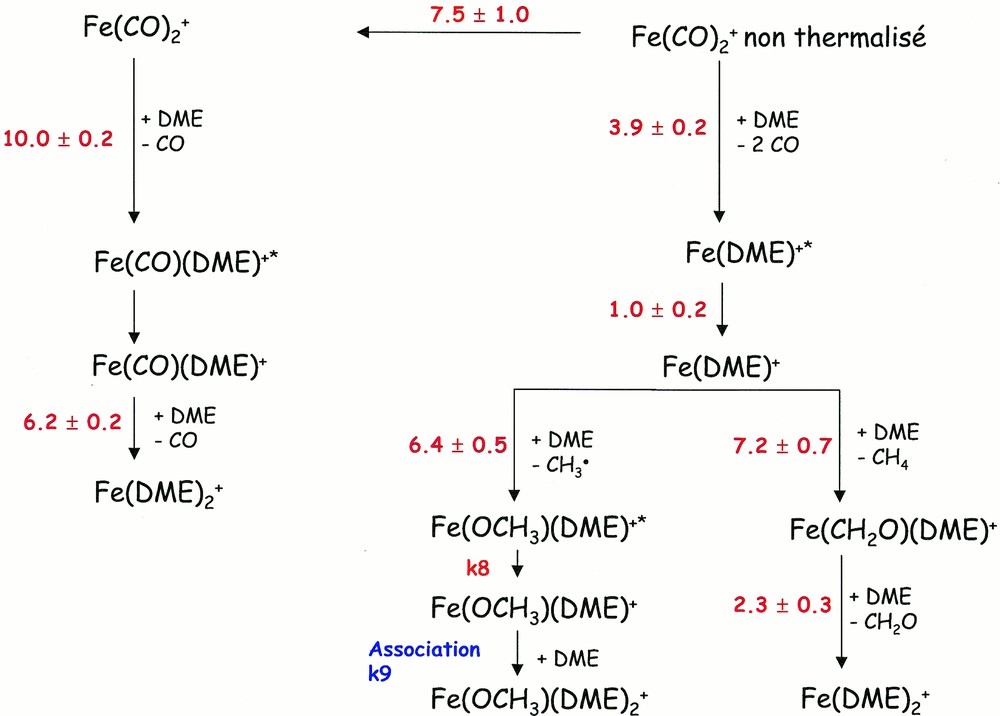
Schéma réactionnel pour le système Fe(CO)2+/DME. Les constantes de vitesse sont données sur les flèches de réaction avec les incertitudes calculées grâce à notre programme d'analyse de données. Elles sont exprimées en 10–10 cm3·s–1.

Les constantes de vitesse obtenues pour les deux substitutions successives sont grandes et elles ne dépendent pas de l’énergie interne des ions Fe(CO)2+. Il est intéressant de remarquer que l’accord entre les courbes expérimentales et les courbes ajustées a été amélioré en ajoutant, avant la seconde substitution, une étape de relaxation des ions Fe(CO)(DME)+, qui dépend donc de l’énergie interne des ions. En effet, la première substitution est exothermique et peut conduire à des produits eux-mêmes excités.

De même, la réaction d’association Fe(OCH3)(DME)+ + DME → Fe(OCH3)(DME)2+ doit être décrite en deux étapes. En effet, pour que la réaction d’association soit efficace, il est nécessaire que les réactants aient une énergie interne très faible. C’est pourquoi une étape de relaxation de l’ion Fe(OCH3)(DME)+* → Fe(OCH3)(DME)+ doit être introduite avant la réaction d’association. Enfin, ces deux constantes de vitesse n’ont pas pu être déterminées séparément, car elles sont fortement dépendantes l’une de l’autre.

3.3 Relaxation radiative

L’abondance relative des ions en fonction du temps de relaxation radiative (en absence de collisions) dans la seconde cellule est reportée sur la Fig. 4. Le temps de réaction dans la troisième cellule (12 ms) et la pression (2,4 10–6 torr) sont maintenus constants pendant toute l’expérience.

Fig. 4

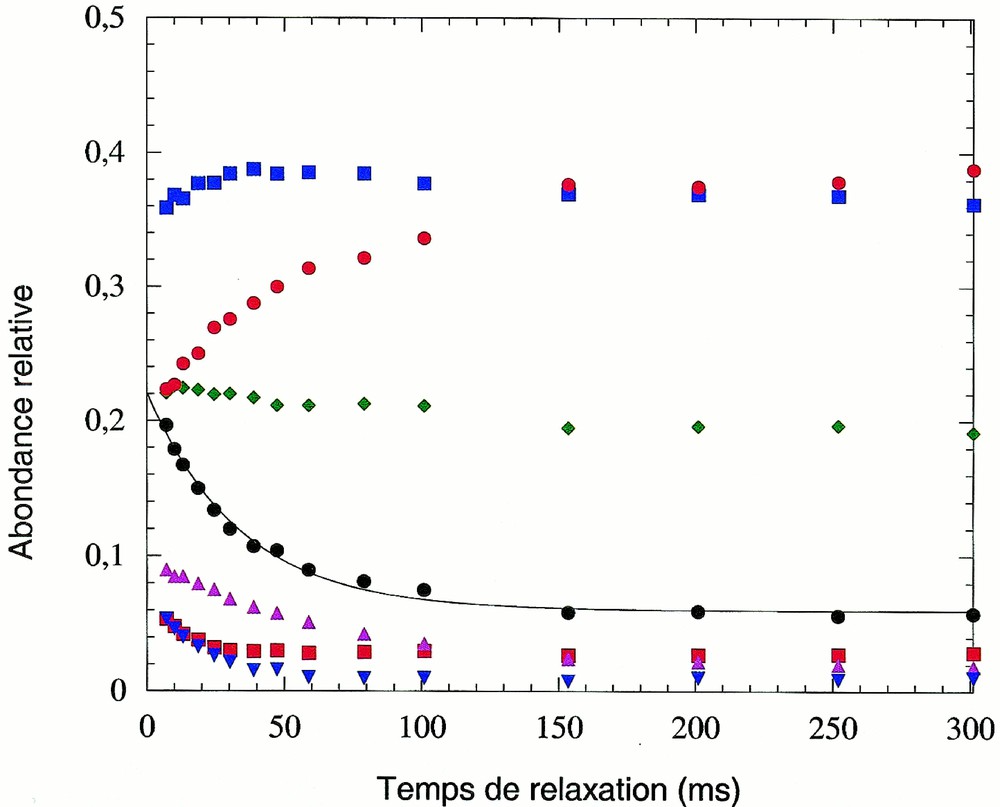
Relaxation radiative pour un temps de réaction de 12 ms, pour le système Fe(CO)2+/DME (pression du gaz réactant : 2,4 10–6 torr) : m/z 102, Fe(DME)+ (carrés rouges) ; m/z 112, Fe(CO)2+ (losanges verts) ; m/z 130, Fe(CO)(DME)+ (carrés bleus) ; m/z 132, Fe(OCH2)(DME)+ (triangles roses) ; m/z 133, FeOCH3(DME)+ (triangles pointe en bas bleus) ; m/z 148, Fe(DME)2+ (cercles rouges). La somme des ions Fe(DME)+, Fe(OCH2)(DME)+ ainsi que Fe(OCH3)(DME)+ est représentée à l'aide de cercles noirs. Cette somme est très bien ajustée grâce à une courbe (en trait plein sur la figure) d'équation A(t) = A0 + A1* exp(–t/τ), avec une durée de vie τ = 30 ms et des paramètres A0 = 0,06 et A1 = 0,16.

Aux temps de relaxation courts, les différents produits observés sur la courbe cinétique (Fig. 2a) sont présents. À partir de 150 ms, les ions Fe(CO)2+ sont relaxés, puisque nous n’observons plus que les deux substitutions successives des ligands CO par le DME. Par conséquent, le temps de demi-vie des états mis en jeu est inférieur à 100 ms. Ces temps sont caractéristiques d’états vibrationnels excités et/ou électroniques métastables. Cette différence de réactivité avec l’énergie disponible au niveau du centre métallique est compatible avec d’autres résultats expérimentaux sur les systèmes Fe+/NO 〚17〛 et avec des expériences de relaxation collisionelle de Fe+ avec divers atomes ou molécules 〚19〛.

L’ion Fe(DME)+ et ses produits de réaction Fe(OCH3)(DME)+ ainsi que Fe(OCH2)(DME)+ proviennent d’ions Fe(CO)2+ excités. Il n’est donc pas surprenant que leur intensité diminue lorsque le temps de relaxation augmente. En négligeant la transformation de Fe(OCH2)(DME)+ en Fe(DME)2+, qui est encore très limitée pour un temps de réaction de 12 ms, la somme de ces trois ions représente l’ensemble de l’ion Fe(DME)+ et de sa filiation. On peut alors vérifier que cette somme décroît exponentiellement, avec une constante de temps de l’ordre de 30 ms. Cette valeur peut être considérée comme la durée de vie moyenne des ions Fe(CO)2+ suffisamment excités pour pouvoir donner la double substitution.

On remarque que la décroissance de Fe(OCH3)(DME)+ est nettement plus rapide que celle de Fe(OCH2)(DME)+. Ceci suggère que les ions parents Fe(DME)+, issus d’ions Fe(CO)2+ très excités, donnent lieu à une plus forte proportion d’ions Fe(OCH3)(DME)+ que les ions Fe(DME)+ très peu énergétiques provenant d’ions Fe(CO)2+ peu excités, donc de plus longue durée de vie. D’autres résultats obtenus au laboratoire, en particulier avec le système Fe(CO)+/DME, confirment que le rapport de branchement Fe(OCH2)(DME)+/Fe(OCH3)(DME)+ entre les deux voies de la réaction de Fe(DME)+ sur le DME est effectivement très sensible à l’énergie des ions Fe(DME)+, et diminue quand celle-ci augmente.

3.4 Mécanisme réactionnel

Une proposition de mécanisme réactionnel conduisant de Fe(DME)+ à Fe(CH2O)(DME)+ et à Fe(OCH3)(DME)+ est reportée sur la Fig. 5.

Fig. 5

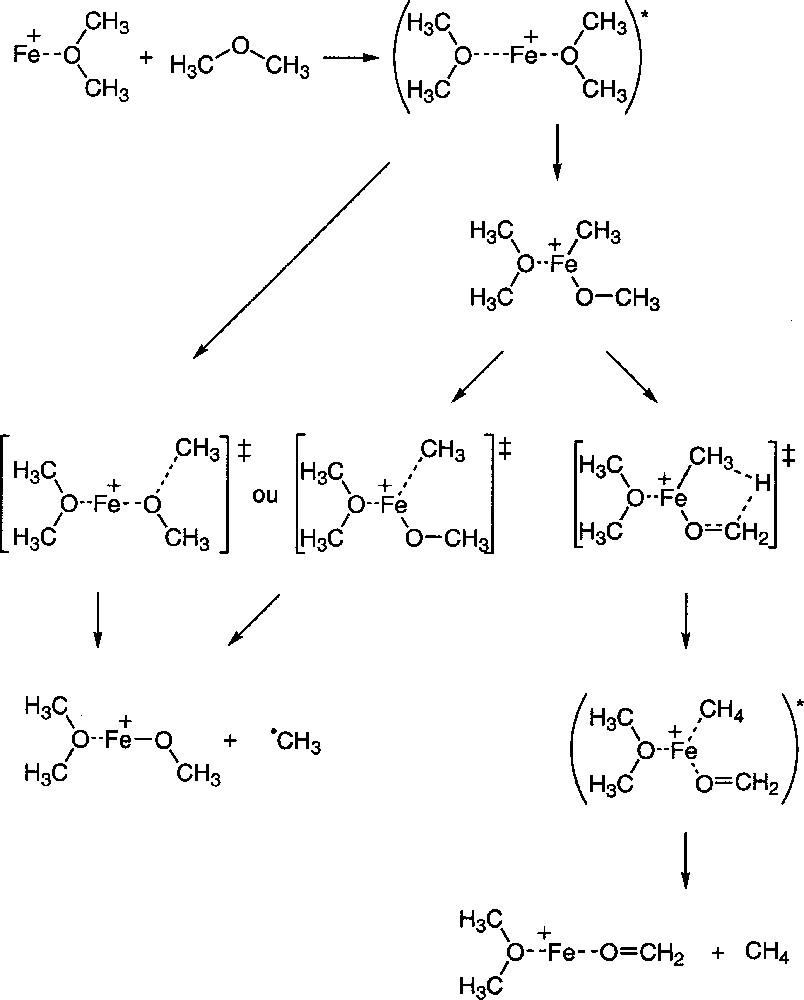
Proposition de mécanisme réactionnel expliquant les deux modes de rupture de la liaison C–O.

La formation du complexe Fe(OCH3)(DME)+ peut être expliquée, soit par rupture directe de la liaison C–O dans le DME complexé sur le centre métallique, de façon analogue au mécanisme proposé dans 〚6〛, soit par insertion du métal dans la liaison C–O du DME. Dans le second cas, la rupture de la liaison Fe+–CH3 dans le complexe Fe(CH3)(OCH3)(DME)+ conduit à l’ion Fe(OCH3)(DME)+. Ce mécanisme a été proposé dans le cas de la perte d’éthyle C2H5 (noté Et) dans la réaction de Fe(Et2O)+ avec Et2O 〚20〛.

En ce qui concerne la formation de l’ion Fe(CH2O)(DME)+, la première étape est l’insertion du métal dans la liaison C–O du DME. Dans le complexe ainsi formé, Fe(CH3)(OCH3)(DME)+, un atome d’hydrogène peut être transféré du ligand méthoxy vers le ligand méthyle, via un état de transition à plusieurs centres, pour conduire à l’ion Fe(CH2O)(DME)+ après décomplexation d’une molécule de méthane. Le transfert d’hydrogène à partir de Fe(OCH3)+ a déjà été décrit dans le cas du mécanisme d’interconversion de Fe(OCH3)+ en HFe(OCH2)+ 〚21〛. Un mécanisme analogue est proposé pour l’activation des alcanes par les métaux de transition 〚22〛, puisqu’un atome d’hydrogène est transféré, via un état de transition à plusieurs centres, vers un groupement M+(CH3) (où M est un métal de transition), ou pour l’oxydation du méthanol en méthanal sous l’action de FeO+ 〚23〛.

4 Conclusion

Dans le système Fe(CO)2+/DME, une forte influence de l’énergie interne des ions réactants sur la réactivité a été observée. Lorsque les ions Fe(CO)2+ sont thermalisés, les seules voies de réaction observées sont les deux substitutions successives d’un ligand CO par une molécule de DME. Lorsque les mêmes expériences sont menées avec des ions Fe(CO)2+ excités, d’autres voies de réaction sont ouvertes. En effet, deux ligands CO peuvent être substitués directement par une molécule de DME, pour former Fe(DME)+, qui réagit ensuite avec le DME selon deux modes de rupture de la liaison C–O : une rupture homolytique conduisant à Fe(OCH3)(DME)+ et une rupture suivie d’un réarrangement menant à l’ion Fe(OCH2)(DME)+. L’analyse des données permet ensuite de proposer un schéma cinétique complet, tenant compte, par le biais d’étapes de relaxation, de l’existence et de la production d’ions excités. Les incertitudes, calculées avec notre programme, sont également présentées avec le schéma cinétique. Les études de relaxation fournissent de plus des données nouvelles sur la durée de vie des états excités mis en jeu. Cependant, elles ne permettent pas de déterminer directement la nature de ces états. Pour préciser ces données, des expériences en phase gazeuse avec une source infrarouge intense et accordable sont prévues. Ces expériences, durant lesquelles plusieurs photons sont absorbés avant d’entraîner une dissociation au sein de la molécule, constituent une caractérisation structurale importante, dans la mesure où les fréquences infrarouges sont directement liées à la géométrie de la molécule. Ainsi, la géométrie de l’ion Fe(CO)2+ excité est différente de celle de l’ion dans son état fondamental. Ces expériences devraient donc permettre de déterminer directement si l’ion réactant est excité vibrationnellement et/ou électroniquement.

Appendice. Méthode d’analyse des données

Après avoir défini un schéma cinétique, il s’agit d’en estimer la validité en recherchant un jeu de paramètres autorisant le meilleur accord modèle/expérience. Les problèmes d’identifiabilité des paramètres, omniprésents en cinétique chimique, rendent cette tâche non triviale 〚24,25〛. Pour un traitement efficace, la méthode d’analyse doit permettre un ensemble de fonctions :

  • • prise en compte de contraintes sur les paramètres (information a priori) ;
  • • mise en évidence des problèmes d’identifiabilité des paramètres (optima multiples ou non localisés) ;
  • • calcul des propriétés statistiques des paramètres (intervalle de confiance...).

La méthode bayésienne d’analyse des données 〚26–28〛 répond particulièrement bien à ces exigences. Elle est basée sur l’évaluation et l’analyse de la distribution de probabilité conjointe de tous les paramètres conditionnellement aux données expérimentales, appelée aussi densité a posteriori. Cette distribution contient toutes les informations pertinentes pour la validation du schéma cinétique, l’identification et l’estimation des paramètres. Elle dépend à la fois d’un modèle statistique du bruit expérimental et de la densité a priori des paramètres. Cette densité a priori résulte en particulier de contraintes liées au sens physico-chimique des paramètres. Par exemple, une constante de vitesse ne peut pas être supérieure à la constante de capture kC du couple ion–molécule considéré. La densité a priori peut aussi résulter de l’analyse d’une autre expérience, ce qui permet le transfert d’informations sur les paramètres.

L’estimation des paramètres repose sur le calcul d’intégrales multiples de la densité a posteriori. Pour des systèmes un peu complexes, il n’est pas possible de traiter ce problème de manière analytique. La distribution jointe des paramètres est échantillonnée par simulation stochastique (méthode de Monte-Carlo par chaînes de Markov 〚29〛).

Après avoir exprimé pour chaque paramètre la densité a priori ou prior, le processus d’analyse se déroule ainsi :

  • • définition d’un modèle pour la densité a posteriori ; nous utilisons ici un modèle à bruit additif gaussien de moyenne nulle et de variance inconnue ; après élimination de cette variance par marginalisation, on aboutit à l’expression suivante :

pk|D∝χ 2 -N/2 prior k
où k représente l’ensemble des paramètres, D les données expérimentales, N le nombre de points expérimentaux et χ2 la somme des écarts quadratiques entre les valeurs expérimentales pour toutes les espèces et les valeurs correspondantes du modèle ;

  • • recherche de l’optimum global de la densité a posteriori dans l’espace des paramètres ; nous utilisons ici une minimisation locale à partir d’un ensemble de points de départ tirés au hasard ;
  • • itération d’une ou plusieurs chaînes de Markov pour échantillonner la densité a posteriori autour de l’optimum ;
  • • analyse de la densité a posteriori par calcul des densités marginales (densités déterminées dans un espace limité à des couples de paramètres) – les densités marginales révèlent sans ambiguïté les schémas de corrélation, linéaires ou non, entre les deux paramètres de chaque couple – ;
  • • calcul des valeurs moyennes et des incertitudes sur les paramètres.

Bibliographie

[〚1〛] B.F.G. Johnson; J.S. McIndoe Coord. Chem. Rev., 200–202 (2000), p. 901-901

[〚2〛] K. Eller; H. Schwarz Chem. Rev., 91 (1991), p. 1121-1121

[〚3〛] C.W. Bauschlicher; S.R. Langhoff; H. Partridge Organometallic Ion Chemistry (B.S. Freiser, ed.), Kluwer, Dordrecht, 1996, p. 47-47

[〚4〛] J. Allison; D.P. Ridge J. Am. Chem. Soc., 101 (1979), p. 4998-4998

[〚5〛] R.C. Burnier; G.D. Byrd; B.S. Freiser J. Am. Chem. Soc., 103 (1981), p. 4360-4360

[〚6〛] C.A. Schalley; R. Wesendrup; D. Schröder; T. Weiske; H. Schwarz J. Am. Chem. Soc., 117 (1995), p. 7711-7711

[〚7〛] C.A. Schalley; R. Wesendrup; D. Schröder; K. Schroeter; H. Schwarz J. Am. Chem. Soc., 117 (1995), p. 12235-12235

[〚8〛] P.B. Armentrout; B.L. Kickel Organometallic Ion Chemistry (B.S. Freiser, ed.), Kluwer, Dordrecht, 1996, p. 1-1

[〚9〛] L. Capron; H. Mestdagh; C. Rolando Coord. Chem. Rev., 178–180 (1998), p. 269-269

[〚10〛] D. Schröder; A. Fiedler; J. Hrusak; H. Schwarz J. Am. Chem. Soc., 114 (1992), p. 1215-1215

[〚11〛] J. Allison; D.P. Ridge J. Am. Chem. Soc., 98 (1976), p. 7445-7445

[〚12〛] M.S. Foster; J.L. Beauchamp J. Am. Chem. Soc., 97 (1975), p. 4808-4808

[〚13〛] M. Heninger; P. Pernot; H. Mestdagh; P. Boissel; J. Lemaire; R. Marx; G. Mauclaire Int. J. Mass Spectrom., 199 (2000), p. 267-267

[〚14〛] M. Heninger; P. Pernot; H. Mestdagh Chem. Phys. Lett., 333 (2001), p. 358-358

[〚15〛] A.G. Marshall; C.L. Hendrickson; G.S. Jackson Mass Spectrom. Rev., 17 (1998), p. 1-1

[〚16〛] J.V.B. Oriedo; D.H. Russell J. Phys. Chem., 96 (1992), p. 5314-5314

[〚17〛] J.V.B. Oriedo; D.H. Russel J. Am. Chem. Soc., 115 (1993), p. 8376-8376

[〚18〛] P.B. Armentrout Ann. Rev. Phys. Chem., 41 (1990), p. 313-313

[〚19〛] D.H. Russel; T. Solouki; J.V.B. Oriedo J. Am. Soc. Mass Spectrom., 6 (1995), p. 543-543

[〚20〛] S.K. Huang; J. Allison Organometallics, 2 (1983), p. 883-883

[〚21〛] A. Fiedler; D. Schröder; H. Schwarz; B.L. Tjelta; P.B. Armentrout J. Am. Chem. Soc., 118 (1996), p. 5047-5047

[〚22〛] S.S. Yi; M.R.A. Blomberg; P.E.M. Siegbahn; J.C. Weisshaar J. Phys. Chem. A, 102 (1998), p. 395-395

[〚23〛] K. Yoshizawa; Y. Kagawa J. Phys. Chem. A, 104 (2000), p. 9347-9347

[〚24〛] S. Vadja; H. Rabitz J. Phys. Chem., 92 (1988), p. 701-701

[〚25〛] S. Vajda; H. Rabitz J. Phys. Chem., 98 (1994), p. 5265-5265

[〚26〛] D.S. Sivia Data Analysis: a Bayesian Tutorial, Clarendon, Oxford University Press, 1996

[〚27〛] A. Gelman; J.B. Carlin; H.S. Stern; D.B. Rubin Bayesian Data Analysis, Chapman and Hall, London, 1995

[〚28〛] J.J.K.O. Ruanaidh; W.J. Fitzgerald Numerical Bayesian Methods Applied to Signal Processing, Springer, New York, 1996

[〚29〛] W.R. Gilks; S. Richardson; D.J. Spiegelhalter Markov Chain Monte Carlo in Practice, Chapman and Hall, London, 1996

Commentaires - Politique

Ces articles pourraient vous intéresser

Étude expérimentale et théorique de la cinétique de l’alcoolyse de la liaison P–N extracyclique du 2-diméthylamino-4,4,5,5-tétraméthyl-1,3-dioxaphospholane monocyclique

Outaf Fliss; Alia Mejri; Khaled Essalah; ...

C. R. Chim (2016)