1 Introduction
Recent studies of the non-planar distortions affecting the structures of sterically crowded porphyrins have shown that these macrocycles are considerably more flexible than originally suspected 〚1–3〛. This conformational flexibility may play an important role in controlling a wide range of physicochemical properties of the heme-cofactors present in hemeproteins. For instance, it has been observed recently that the electronic ground state of several ferric cytochromes c’ isolated from photosynthetic bacteria is, at pH 7.2, a quantum mechanical admixture of the high-spin (S = 5/2) and intermediate-spin (S = 3/2) states 〚4–6〛. This S = 5/2,3/2 admixed spin state (QMS state) has also been observed in plant peroxidases belonging to class III of the ‘plant peroxidase superfamily’ 〚7–10〛. Such a quantum mechanical S = 5/2,3/2 admixture has also been observed in the chloroiron(III) complexes of the sterically crowded 2,3,7,8,12,13,17,18-octamethyl-5,10,15,20-tetraphenylporphyrin (omtpp) and 2,3,7,8,12,13,17,18-octaethyl-5,10,15,20-tetraphenylporphyrin (oetpp). In one crystalline form of Fe(oetpp)Cl 5 and in Fe(omtpp)Cl, the magnetic properties indicate S = 3/2 admixtures of approximately 40 and 35%, respectively 〚11〛. In contrast, in the second crystalline form of Fe(oetpp)Cl 5’, in which the conformation of the porphyrin is only slightly less saddled than in 5, this S = 3/2 spin-admixture was found to lie only approximately between 4% (in frozen 2-MeTHF) and 10% (in frozen dichloromethane) 〚12〛. Cheng et al. 〚11〛 have proposed that the prime factor governing the occurrence of the quantum mechanical admixed S = 5/2,3/2 spin state (QMS state) observed in ferricytochrome c’ from photosynthetic bacteria is the saddle-shaped deformation of the hemes present in these proteins. Recent ETH and INDO calculations on a series of five-coordinate iron(III) porphyrin complexes have also indicated that the saddle distortion of a porphyrin, by decreasing the symmetry of the coordination sphere of the metal and by increasing the bonding interactions between this metal and the macrocycle, elevates the energy of the dx2-y2 orbital and therefore induces an admixture of the intermediate spin state (S = 3/2) into the high-spin (S = 5/2) ground state 〚13〛.
The crystal structures of several ferricytochromes c’ have been established 〚14–20〛. The hemes present in some of these molecules have been analysed by the normal-coordinate structural decomposition method (NSD) 〚9, 21–23〛. The results obtained indicate that they possess mainly saddled (sad) and ruffled (ruf) deformations, unlike the mitochondrial cytochromes c, which are primarily ruffled 〚24〛. However, the sad displacements found for the hemes of these molecules are quite small (only –0.4 to –0.5 Å) and sad is the dominant deformation only in Rhodospirillum molischanium cytochrome c’ 〚9〛. In Chromatium vinosum cytochrome c’, the NSD calculations show that the sad displacements are even smaller (only –0.2 (heme A) and –0.4 Å (heme B)) 〚23〛. A similar situation arises in the peroxidases, for which a predominately saddled (–1.4 to –0.4 Å) heme conformation is invariably observed in the crystal structures; however, the QMS state is found for only some of the plant peroxidases.
To study the relationship between non-planar distortions of the porphyrins and the S = 5/2,3/2 mixed spin states in ferric species, we have now investigated the X-ray crystal structures and EPR spectral properties of a series of chloroiron(III) porphyrin complexes in which steric constraints have been introduced at the porphyrin periphery and gradually increased by replacing the unsubstituted pyrrole rings of the tetraphenylporphyrin ligand by one, two, and three Cβ-diethyl substituted pyrroles. We have also analysed the conformation of the porphyrins present in the crystals of these compounds by NSD. We present here the results of these studies.
2 Experimental section
2.1 General procedures
All syntheses were performed using distilled and degassed solvents. Electronic absorption spectra were recorded on a Varian Cary 05E UV–visible–NIR spectrometer using dichloromethane as solvent.
2.2 Syntheses of the metal-free porphyrins
The metal-free porphyrins 2,3-diethyl-, H2(detpp) 2,3,7,8-tetraethyl-, H2(cis-tetpp), 2,3,12,13-tetraethyl-, H2(trans-tetpp) and the 2,3,7,8,12,13-hexaethyl-, H2(hetpp) and 5,10,15,20-tetraphenylporphyrins were prepared and purified according to published procedures 〚25, 26〛.
2.3 Syntheses of the chloroiron(III) porphyrin complexes
Metallation with iron of the free-base porphyrins was achieved under dry argon in THF containing 2,6-lutidine using iron(II) dichloride tetrahydrate FeCl2·4 H2O, following a method also outlined in the literature 〚27〛. Purification was carried out by chromatography on grade III alumina using dichloromethane containing methanol (0.5%) as eluent. The red–brown bands containing the iron(III) complexes were collected under vacuum and washed with 0.01 M HCl. These complexes, Fe(detpp)Cl (1), Fe(trans-tetpp)Cl (2), Fe(cis-tetpp)Cl (3) and Fe(hetpp)Cl (4), are depicted schematically in Fig. 1.
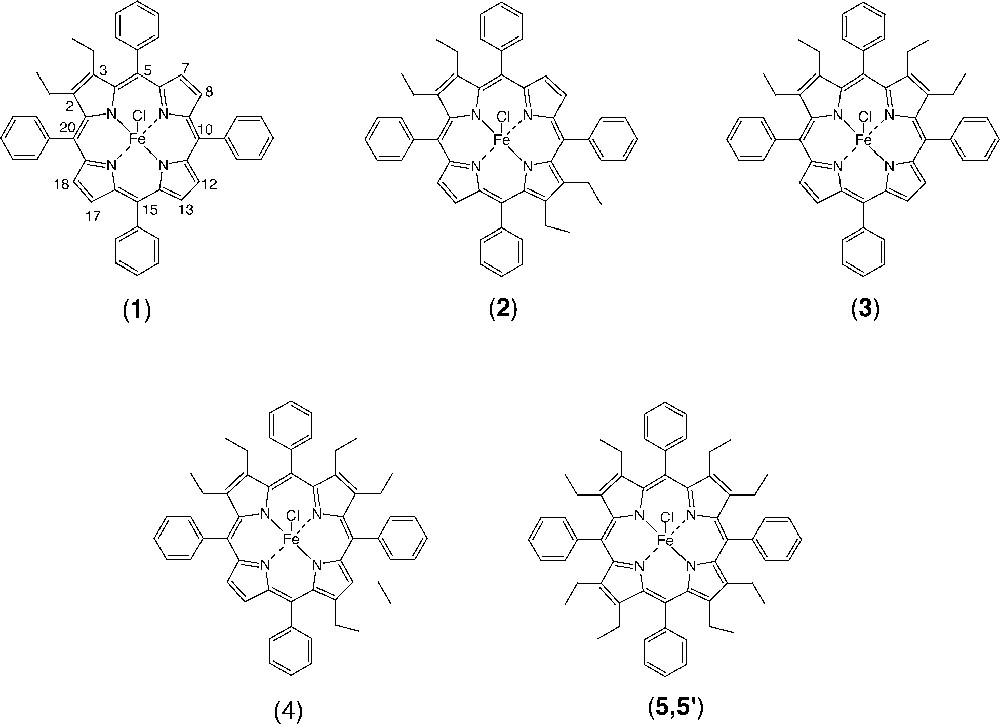
Schematic representation of the chloroiron(III) porphyrin complexes, Fe(detpp)Cl (1), Fe(trans-tetpp)Cl (2), Fe(cis(tetpp)Cl (3), Fe(hetpp)Cl (4) and Fe(oetpp)Cl (of crystal forms 5 and 5’).
The chloroiron(III) porphyrin complexes so obtained were characterised by UV–visible spectroscopy. λmax (ϵ in 10–3 M–1 cm–1), dichloromethane: 1 = 380(sh), 418(46.7), 513(6.4); 2 = 381(sh), 419(49.2), 515(6.2); 3 = 397(40.2), 426(43.5), 520(11.2); 4 = 396(40.2), 436(39.9), 520(11.2).
For the two crystalline forms of Fe(oetpp)Cl (5 and 5’) and for Fe(tpp)Cl: λmax (ϵ in 10–3 M–1 cm–1), dichloromethane: Fe(oetpp)Cl (5) = 396(59.8), 444(53.1) nm 〚11〛; Fe(oetpp)Cl (5’) = 395(40.5), 444(38.5), 535(16.6) nm 〚12〛; Fe(tpp)Cl = 377(20.4), 416.5(49.8), 519.5(6.0) nm 〚28〛.
2.4 X-ray data collection and processing
Single crystals of 1·C2H4Cl2, 2·C6H5Cl, 3 and 4·2 CHCl3, suitable for X-ray studies, were obtained by slow diffusion of n-heptane into 1,2-dichloroethane, chlorobenzene, or chloroform solutions containing the chloroiron(III) complexes 1, 2, 3 and 4, respectively. Data were collected on a Nonius Kappa CCD diffractometer at –100 °C, using Mo Kα graphite monochromated radiation (λ = 0.7107 Å), φ scans. Table 1 reports all pertinent crystallographic data for the four complexes. As frequent for porphyrin complexes, the diffraction power of the samples was low and their mosaic high leading to rather high R and Rw values. No absorption corrections were applied, but the determination of the scale factors between frames includes partially the absorption effects. The structures were solved using direct methods and refined against |F|. For 4, one of the solvent molecules is disordered over two positions. All non-hydrogen atoms were refined anisotropically apart from the atoms of the disordered solvent molecule of 4. The hydrogen atoms were introduced as fixed contributors ((dC–H = 0.95 Å, BH = 1.3Beqv(C)Å2), except the solvent protons for 1 and 2, and the proton of the disordered solvent molecule of 4. Final results are listed in Table 1. For all computations the OpenMoleN package was used 〚29〛.
Crystallographic data for 1, 2, 3 and 4.
| 1 | 2 | 3 | 4 | |
| Empirical formula | C50H40N4FeCl3 | C58H49N4FeCl2 | C52H44N4FeCl | C58H54N4FeCl7 |
| C48H36N4FeCl·C2H4Cl2 | C52H44N4FeCl•C6H5Cl | C56H52N4FeCl·2CHCl3 | ||
| FW | 859.11 | 928.82 | 816.26 | 1111.12 |
| Colour | dark red | dark blue | dark red | dark red |
| Space group | P21/n | P21/n | P21/c | |
| Crystal system | monoclinic | monoclinic | monoclinic | triclinic |
| a (Å) | 10.5548(5) | 18.6430(6) | 16.7383(2) | 10.0848(2) |
| b (Å) | 21.6454(9) | 13.9480(6) | 11.5905(2) | 12.2044(4) |
| c (Å) | 18.2467(9) | 19.2730(6) | 21.8371(4) | 23.7831(8) |
| α (deg) | 104.218(2) | |||
| β (deg) | 89.964(1) | 111.937(2) | 103.148(9) | 94.928(2) |
| γ (deg) | 104.678(2) | |||
| V (Å3) | 4168.7(6) | 4648.7(6) | 4125.5(3) | 2710.5(3) |
| Z | 4 | 4 | 4 | 2 |
| ρcalcd (g cm–3) | 1.37 | 1.33 | 1.31 | 1.36 |
| Crystal dimensions (mm) | 0.20 × 0.20 × 0.15 | 0.20 × 0.20 × 0.15 | 0.10 × 0.14 × 0.17 | 0.20 × 0.20 × 0.20 |
| μ (mm–1) | 0.595 | 0.484 | 0.472 | 0.665 |
| θmax (deg) | 30.6 | 30.5 | 28.6 | 32.5 |
| No. of meas. reflns | 28 083 | 30 508 | 30 376 | 20 185 |
| No. of ind. reflns | 12 449 | 13 592 | 8485 | 14 576 |
| Rint | 0.043 | 0.040 | 0.031 | 0.040 |
| No. of obs refln. | 5704 (I > 3 σ(I)) | 7408 (I > 3 σ(I)) | 6738 (I > 3 σ(I)) | 10716 (I > 3 σ(I)) |
| R(F)a | 0.074 | 0.060 | 0.038 | 0.065 |
| Rw(F)b | 0.097 | 0.070 | 0.061 | 0.081 |
| GOF | 1.60 | 1.09 | 1.30 | 1.14 |
3 Results
3.1 X-ray structures
The molecular structures of the chloroiron(III) porphyrin derivatives, Fe(detpp)Cl (1), Fe(trans-tetpp) (2), = Fe(cis-tetpp) (3) and Fe(hetpp)Cl (4) together with the labelling schemes used are displayed in Fig. 2, parts a–d, respectively. Fig. 3, parts a–d, bottom and top, show edge-on views of the skeletons of 1, 2, 3 and 4, with the phenyl rings removed for clarity (top) and underneath (bottom) linear displays in Å units of the skeletal displacements from the porphyrin-core mean planes (Pc). Table 2 lists selected bond distances and angles as well as some averages.
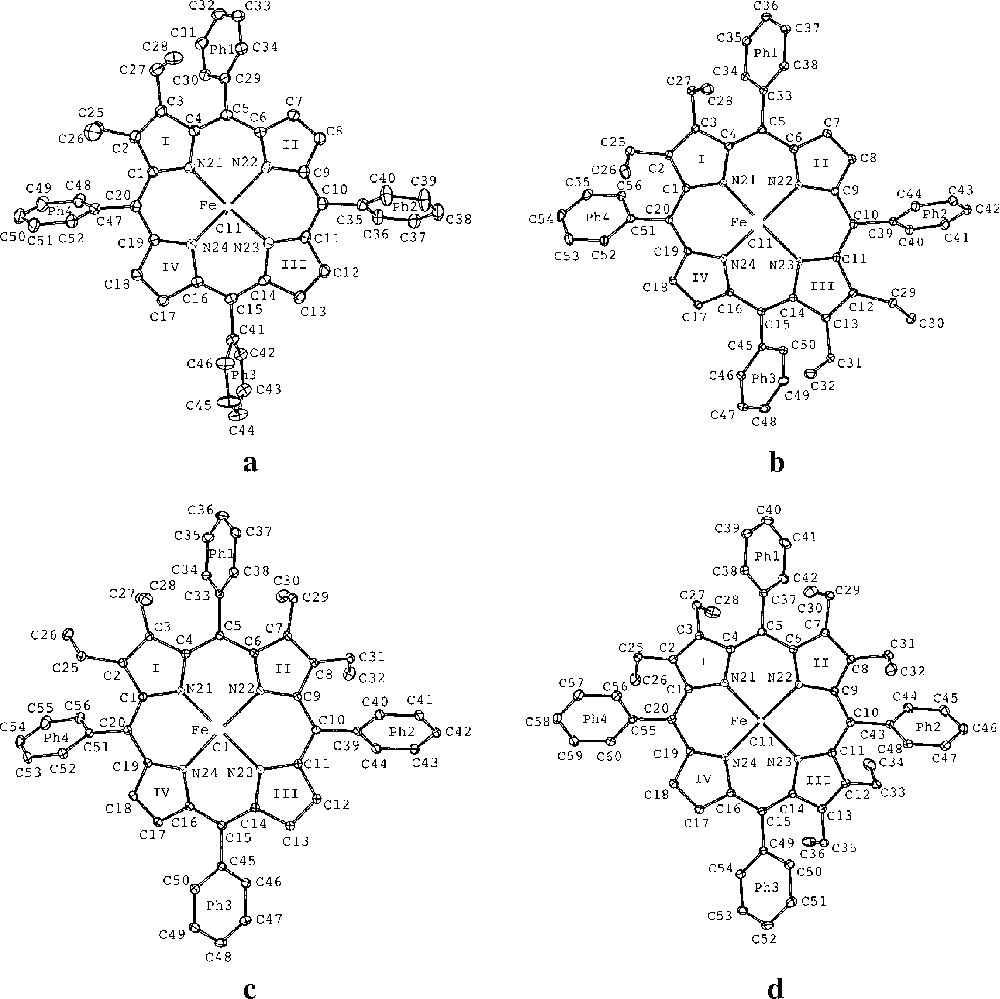
ORTEP drawings of the molecular structures of: (a) Fe(detpp)Cl (1), (b) Fe(trans-tetpp) (2), (c) Fe(cis-tetpp) (3), (d) Fe(hetpp)Cl (4), showing the numbering schemes used. Thermal ellipsoids are drawn at the 25% probability level.
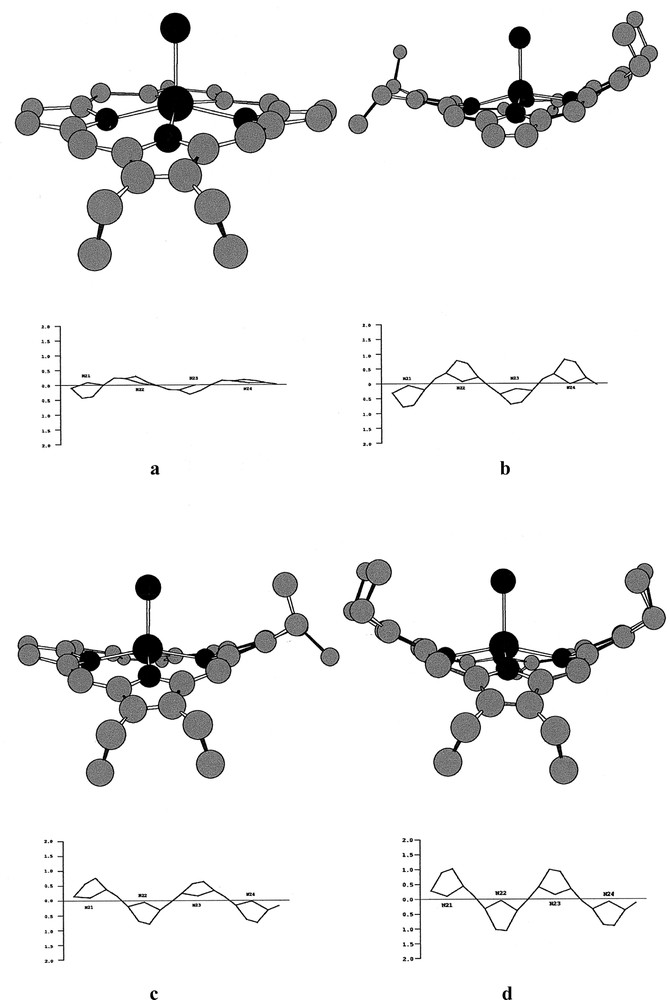
a–d, bottom and top: edge-on views of the skeletons of 1, 2, 3 and 4, with the phenyl groups removed for clarity, (top) and linear displays in Å units of the porphyrin-core atom displacements from the porphyrin-core mean planes (Pc) in 1, 2, 3 and 4 (bottom).
Selected bond distances (Å), angles (deg) and averages
| 1 | 2 | 3 | 4 | |
| Fe–Cl | 2.220(2) | 2.219(1) | 2.226(1) | 2.239(1) |
| Fe–N21 | 2.086(4) | 2.083(2) | 2.057(1) | 2.050(2) |
| Fe–N22 | 2.066(4) | 2.044(3) | 2.072(1) | 2.060(2) |
| Fe–N23 | 2.087(4) | 2.084(3) | 2.061(1) | 2.054(2) |
| Fe–N24 | 2.060(4) | 2.044(2) | 2.068(1) | 2.048(2) |
| <Fe–Np> | 2.075 | 2.064 | 2.065 | 2.053 |
| <Np–Cα> | 1.382 | 1.386 | 1.381 | 1.382 |
| <Cα–Cβ> | 1.434 | 1.446 | 1.446 | 1.449 |
| <Cβ–Cβ> | 1.341 | 1.355 | 1.361 | 1.366 |
| <Cm–Cα> | 1.400 | 1.400 | 1.402 | 1.404 |
| <Cm–Cp> | 1.497 | 1.495 | 1.494 | 1.493 |
| <Cp–Cp> | 1.378 | 1.387 | 1.387 | 1.387 |
| <Cα–Np–Cα> | 105.6 | 106.1 | 106.4 | 106.3 |
| <Np–Cα–Cβ> | 109.6 | 109.5 | 109.6 | 109.5 |
| <Cα–Cβ–Cβ> | 107.4 | 107.3 | 107.1 | 107.0 |
| <Cα–Cm–Cα> | 124.5 | 123.8 | 124.0 | 123.3 |
| <Cα–Cm–Cp> | 117 | 118 | 118 | 118 |
| <Np–Cα–Cm> | 125 | 124 | 124 | 123 |
| <Cp–Cp–Cp> | 120 | 120 | 120 | 120 |
Each one of the asymmetric units of the crystals of 1·C2H4Cl2 (monoclinic, space group P21/n), 2·C6H5Cl (monoclinic, space group P21/n), 3 (monoclinic, space group P21/c) and 4·2 CHCl3 (triclinic, space group ) contains one independent molecule of the chloroiron(III) porphyrin complex. One independent molecule of solvation is present in the asymmetric units of 1·C2H4Cl2 and 2·C6H5Cl and two in that of 4·2 CHCl3.
In all these chloroiron(III) porphyrin complexes, the five-coordinate iron atoms are bonded equatorially to the four pyrrole nitrogen atoms Np of the porphyrin ligand and to an axial chloride ion. It is known that non-planar saddle and ruffle distortions tend to shorten the M–Np bond distances. If there were significant doming of the porphyrin, this would have tended to increase these bond lengths. Probably, due to the increasing saddle distortions occurring in the porphyrins of these complexes (vide infra), the average Fe–Np bond distances decrease slightly from 2.075 Å in 1 to 2.053 Å in 4 (Table 2). In the two crystalline forms of Fe(oetpp)Cl (5 and 5’), in which the oetpp ring is more severely saddle-shaped, somewhat ruffled, and only slightly domed, the mean values of the Fe–Np bond distances are slightly smaller at 2.031(5) and 2.040(6) Å, respectively 〚11, 12〛. For the more planar Fe(tpp)Cl crystal structure, the average Fe–Np distance equals 2.070 Å 〚30〛.
As already observed in other metal complexes of sterically crowded tetraarylporphyrins 〚12, 25, 26〛, the four Fe–Np bond lengths are not completely equivalent; they always fall close to two slightly different values corresponding to two longer and two shorter distances that can be significantly different at the 3 σ level (Table 2). As shown by Senge and Kalish 〚25〛 for the nickel(II), copper(II) and zinc(II) complexes of a series of tetraphenylporphyrin complexes with graded degrees of Cβ-ethyl substitution, the shorter values of these bond distances correspond, in general, to the region of the porphyrin ring with little out-of-plane distortion, whereas the longer bonds correspond to regions where these distortions are more important. For example, for 1, the four Fe–Np bond distances adopt two mean values of 2.087(4) and 2.063(5) Å, which differ significantly at the 3 σ level. The longer values correspond to the Fe–Np bonds with N21 and N23 of pyrrole rings I and III, which deviate more strongly from the porphyrin-core mean plane than the shorter bonds with N22 and N24 belonging to the pyrrole rings II and IV, respectively. Indeed, the dihedral angles between the porphyrin-core mean plane and the mean planes of pyrrole rings I and III of 14.0 and 8.4 degrees, respectively, are larger than the corresponding angles of the mean planes of pyrrole rings II and IV of 7.8 and 2.8 degrees, respectively. Similar results are observable in 2, 3, and 4, although the values of the two sets of Fe–Np bonds lengths that can be defined for each compound are not always significantly different at the 3 σ level (see Table 2 and supplementary information).
The Fe–Cl bond distances observed in these four compounds are not significantly different, their mean value being 2.226(2) Å. Moreover, this value does not differ significantly from the mean value of 2.237(2) Å observed for the Fe–Cl bond distances in the two crystalline forms of Fe(oetpp)Cl (5 and 5’) 〚11, 12〛. In 1 to 4, the Fe–Cl bonds are almost perpendicular to the pyrrole nitrogen mean planes PN, the tilt angles of these bonds with respect to the normals to these mean planes PN being only 1.3(5)° (1), 4.1(3)° (2), 2.6(1)° (3) and 2.0(2)° (4).
A saddle distortion of S4 symmetry of a porphyrin ring can be characterised by the average displacement of the eight Cβ atoms relative to the porphyrin-core mean plane. To characterise an asymmetric distortion of this type, the average displacements above and below the porphyrin-core mean plane of the two geminal β-carbon atoms of the four adjacent pyrrole rings are necessary. Table 3 lists for each compound these displacements above (+) and below (–) the porphyrin-core mean plane as well as the mean values of these displacements above and below and their overall absolute averages. It is well known that, in tetraarylporphyrins with saddle distortions, the phenyl rings rotate into the porphyrin-core mean plane to minimize unfavourable contact distances with the Cβ-pyrrole substituents 〚26, 31–33〛. The values of these dihedral angles δ(Ph1/Pc), δ(Ph2/Pc), δ(Ph3/Pc) and δ(Ph4/Pc) (Pc = porphyrin-core mean plane) together with their mean values are displayed in Table 4. As usual, the nitrogen and carbon atoms of the non-substituted and substituted pyrrole rings are nearly planar, whereas the β-substituents are displaced out of the pyrrole mean planes. Relative to these mean planes, the average values of the absolute displacements of the Cα-atoms of the ethyl substituents are 0.322 Å in 1, 0.221 Å in 2, 0.190 Å in 3 and 0.236 Å in 4. The adjacent pyrrole rings are also tilted in a saddle distortion, the tilt angles increasing with the saddle-shape of the porphyrin. The dihedral angles δ occurring between the adjacent pyrrole rings (I/II, II/III, III/IV and IV/I) of the macrocycles present in these chloroiron(III) porphyrin complexes with graded degrees of Cβ-ethyl substitution are given in Table 5.
Average displacements in Å units of the Cβ atoms of the adjacent pyrrole rings above and below the porphyrin-core mean plane, their mean values (< + Cβ/Cβ > and < – Cβ/Cβ >) and their absolute averages (<Cβ/Cβ >) for each porphyrin ring present in 1, 2, 3, and 4.
| C2/C3 | C7/C8 | C12/C13 | C17/C18 | <+ Cβ/Cβ > | <– Cβ/Cβ > | <|Cβ/Cβ|> | |
| 1 | –0.414(6) | +0.202(6) | –0.256(6) | +0.157(6) | +0.179 | –0.335 | 0.257 |
| 2 | +0.758 (4) | –0.727(4) | +0.671(4) | –0.756(4) | +0.714 | –0.741 | 0.727 |
| 3 | +0.665(2) | –0. 742(2) | +0.603(2) | –0.694(2) | +0.634 | –0.718 | 0.676 |
| 4 | +0.958(3) | –1.042(3) | +0.955(3) | –0.887(3) | +0.956 | –0.964 | 0.960 |
Values in degrees of the dihedral angles δ occurring in 1, 2, 3 and 4 between the mean planes of the four phenyl rings (Ph1, Ph2, Ph3, Ph4) and the porphyrin-core mean plane (Pc) and their averages (<δ (Ph/Pc)>).
| δ(Ph1/Pc) | δ(Ph2/Pc) | δ(Ph3/Pc) | δ(Ph4/Pc) | <δ(Ph/Pc)> | |
| 1 | 58.7(2) | 78.1(2) | 70.9(2) | 65.1(2) | 68.2 |
| 2 | 52.3(1) | 63.9(1) | 51.8(1) | 50.6(1) | 54.6 |
| 3 | 62.2(1) | 58.1(1) | 49.2(1) | 60.9(1) | 57.6 |
| 4 | 47.0(1) | 48.8(1) | 54.7(1) | 44.9(1) | 48.8 |
Values of the dihedral angles δ in degrees of the adjacent pyrrole rings (I/II, II/III, III/IV, IV/I) and their mean value (<δ>) occurring in 1, 2, 3 and 4.
| δ (I/II) | δ (II/III) | δ (III/IV) | δ (IV/I) | <δ> | |
| 1 | 20.6(2) | 8.9(2) | 8.8(2) | 13.3(2) | 12.9 |
| 2 | 27.3(2) | 22.7(2) | 24.8(2) | 27.7(2) | 25.6 |
| 3 | 28.2(1) | 22.3(1) | 21.9(1) | 22.5(1) | 23.7 |
| 4 | 38.4(1) | 37.9(1) | 28.1(1) | 29.5(1) | 33.5 |
As indicated by the displacements of the meso-carbons Cm above and below the porphyrin-core mean plane (Pc), the porphyrins present in 1, 2, 3, and 4 are also slightly ruffled asymmetrically. The values of these Cm displacements observed in 1, 2, 3, and 4 are given in Å units in Table 6 together, for comparison, with those present in the oetpp rings of 5 and 5’.
Displacements in Å of the meso-carbon atoms, the mean values of the displacements above and below and the overall averages relative to the porphyrin-core mean planes of the macrocycles present in 1, 2, 3 and 4.
| C5/Pc | C10/Pc | C15/Pc | C20/Pc | <C10,C15/Pc> | <C10,C20/Pc> | <|Cm|/Pc> | Ref. | |
| 1 | +0.246(6) | –0.155(6) | +0.153(6) | –0.024(6) | +0.199 | –0.089 | 0.144 | this work |
| 2 | –0.166(4) | +0.101(4) | –0.150(4) | –0.046(4) | –0.158 | +0.073 | 0.115 | this work |
| 3 | +0.154(2) | –0.049(2) | +0.123(2) | –0.183(2) | +0.138 | –0.116 | 0.127 | this work |
| 4 | +0.099(3) | –0.012(3) | +0.070(3) | –0.137(3) | +0.084 | –0.074 | 0.079 | this work |
| 5 | +0.195(6) | –0.177(6) | +0.186(6) | –0.204(6) | +0.190 | –0.190 | 0.190 | 〚11〛 |
| 5’ | +0.220(8) | –0.212(8) | +0.220(8) | –0.212(8) | +0.220 | –0.212 | 0.216 | 〚12〛 |
The rings present in 1, 2, 3, and 4 are also slightly domed. Although, the mean planes of the four pyrrole nitrogens (PN) and of the porphyrin core (Pc) in these derivatives are, in general, not strictly parallel, the extent and orientation of the doming of these porphyrin ligands can be studied by the separations of these mean planes, PN–Pc, and by their sign (+ when the PN mean plane lies closer to the iron atom than the Pc mean plane, - in the reverse case). Table 7 lists the values observed in these compounds and in 5 and 5’ for comparison, together with the dihedral angles occurring between the PN and Pc mean planes.
Displacements (Ct–Fe) of the iron atoms of 1, 2, 3 and 4 relative to the four pyrrole nitrogen mean planes PN, the separations between the pyrrole nitrogen and the porphyrin-core mean planes (PN–Pc) and the dihedral angles (δ(PN/Pc) between these mean planes.
| Ct–Fe (Å) a | PN–Pc (Å) | δ(PN/Pc) (deg.) | Réf. | |
| 1 | 0.491(1) | +0.054(1) | 1.35(7) | this work |
| 2 | 0.494(1) | +0.050(1) | 2.11(6) | this work |
| 3 | 0.477(1) | +0.046(1) | 0.87(3) | this work |
| 4 | 0.490(1) | +0.029(1) | 0.87(4) | this work |
| 5 | 0.467(1) | –0.033(1) | 0.39(11) | 〚11〛 |
| 5’ | 0.477(2) | +0.003(2) | 0.00 | 〚12〛 |
The steric strain arising in these porphyrins between the Cβ-ethyl substituents and the meso-phenyl groups is in part released by a small opening of the Cα(et)–Cm–CPhe bond angles (Cα(et) = Cα of the Cβ-ethyl substituted pyrrole rings) relative to their non-substituted counterparts Cα(H)–Cm–CPhe. The mean value of the opening of this Cα(et)–Cm–CPhe angle relative to its counterpart Cα(H)–Cm–CPhe lies between 2 and 5° (see Table 2 and ‘Supplementary material’).
3.2 Normal-coordinate structural decomposition (NSD)
It has been shown recently that the porphyrin structure is often accurately described by displacements occurring only along the lowest-frequency normal-mode coordinates of each one of the symmetries (minimum basis), representing the normal deformations, even for highly distorted macrocycles 〚21, 22, 24〛. This recognition has led to a computational procedure, called the normal structural decomposition method (NSD), which projects out the contributions of all symmetric normal deformations to the total distortion. One can then simulate the out-of-plane and in-plane distortions of a porphyrin using only these lowest frequency deformations and compare the resulting simulated structure with that of the X-ray structure 〚21〛. The minimal basis of out-of-plane deformations required to simulate the out-of-plane structure of a porphyrin includes only the lowest frequency normal coordinate of each symmetry type; these modes have been named saddling (B2u), ruffling (B1u), doming (A2u), waving (Egx, Egy), and propelling (A1u), where their D4h symmetry classifications are indicated between parentheses. Table 8 lists in Å units the contributions of the saddle (sad), ruffle (ruf), dome (dom), wave (wav(x), wav(y)), and propeller (pro) components of the out-of-plane distortion ‘minimal basis’ for the porphyrin structures present in 1, 2, 3, 4, 5, and 5’. These six displacements serve to quantify approximately the distortions observed in these crystal structures.
Values of the saddle (sad), ruffle (ruf), doming (dom), waving (wav), and propelling (pro) out-of-plane displacements in Å, calculated by normal-coordinate structural decomposition of the crystal structures of 1, 2, 3, 4, 5, and 5’. (Dtsim = simulated total distortion, deviation).
| Total distortion and out-of-plane normal-coordinate deformations contained in the out-of-plane distortion of the macrocycle. | ||||||||
| Dtobs | a | sad | ruf | dom | wav(x) | wav(y) | pro | |
| 1 | 0.934 | 0.032 | 0.756 | –0.367 | –0.245 | –0.250 | 0.074 | –0.014 |
| 2 | 2.240 | 0.041 | 2.198 | –0.314 | 0.094 | –0.111 | –0.034 | –0.035 |
| 3 | 2.108 | 0.029 | 2.056 | –0.374 | –0.155 | –0.106 | 0.092 | –0.032 |
| 4 | 2.929 | 0.049 | 2.899 | –0.124 | 0.046 | –0.002 | 0.252 | –0.005 |
| 5 | 3.537b | 0.055 | 3.478 | –0.528 | –0.090 | 0.032 | 0.020 | –0.010 |
| 5’ | 3.486c | 0.063 | 3.401 | –0.657 | –0.014 | –0.000 | 0.000 | –0.027 |
3.3 EPR Studies
Fig. 4a shows the rhombic EPR spectrum of 3 in frozen 2-MeTHF solution measured at 10 K and Fig. 4b a spectrum simulated under the assumption of a Lorentzian line-shape. Since two slightly different average Fe–Np bond distances occur in all these complexes, the coordination environment of the iron centre cannot exceed C2v. Thus, the EPR spectra of these complexes can only be of rhombic symmetry. Although, small amounts of impurities were present in the spectra of 1, 2, and 4 (also measured in frozen 2-MeTHF at 10 K), the simulations of the main components of these spectra, as well as that of 3 (Fig. 4), yielded the effective g and E/D values listed in Table 9.
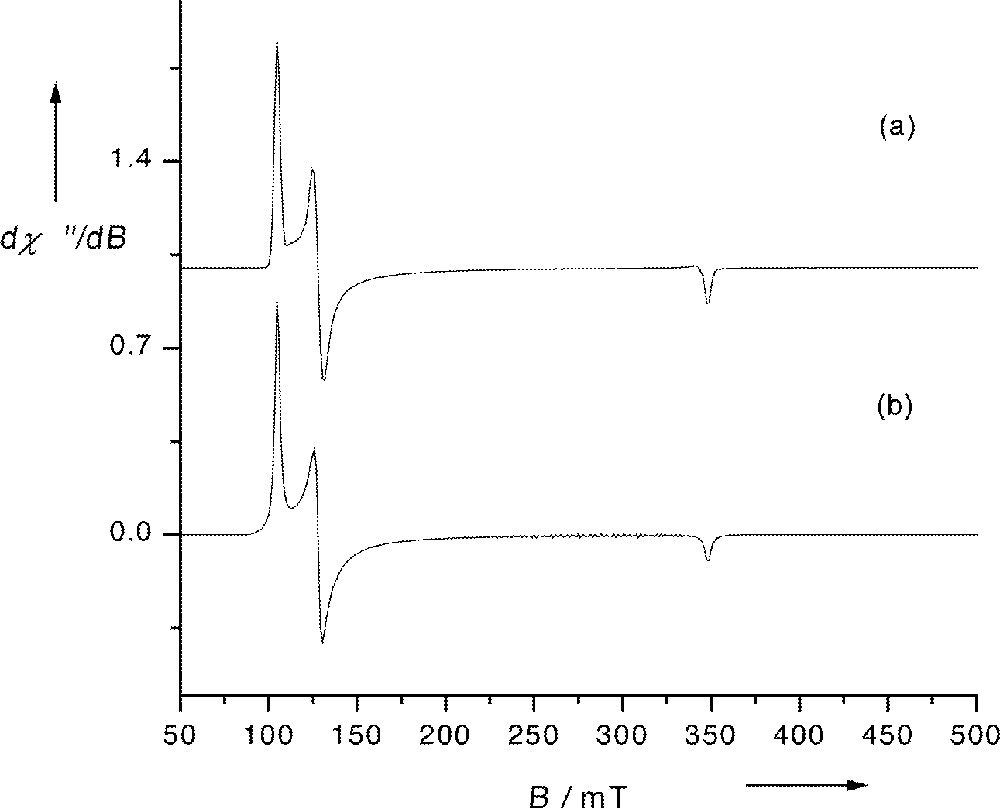
(a) EPR spectrum of 3 in frozen 2-MeTHF at 10 K; (b) spectrum simulated under the assumption of a Lorentzian line-shape with geffy=6.57, geffx=5.39 and geffz=1.98. Experimental conditions: microwave frequency 9.646 GHz, modulation frequency 100 kHz, modulation amplitude 5 G, microwave power 20 μW.
Effective g values and E/D values obtained by simulation of the EPR spectra of 1, 2, 3, 4, 5 and 5’ in frozen 2-MeTHF at T = 10 K.
| geffy | geffx | geffz=geff// | E/D | (a5/2)2 | %(3/2)a | Ref. | ||
| 1 | 6.31 | 5.69 | 2.00 | 6.00 | 0.013 | 1 | 0 | this work |
| 2 | 6.74 | 5.23 | 1.97 | 5.985 | 0.031 | 0.9925 | 0.75 | this work |
| 3 | 6.57 | 5.39 | 1.98 | 5.98 | 0.025 | 0.9880 | 1.20 | this work |
| 4 | 6.53 | 5.36 | 1.98 | 5.945 | 0.024 | 0.9725 | 2.75 | this work |
| 5 | 2.0 | 5.2 | 0.6 | 40 | 〚11〛 | |||
| 5’ | 6.55 | 5.28 | 1.98 | 5.915 | 0.025 | 0.9575 | 4.25 | 〚12〛 |
4 Discussion
The overall absolute mean values of the displacements of the Cβ atoms relative to the porphyrin-core mean planes of the macrocycles increase approximately from 0.26 to 0.96 Å in the order 1 < 3 < 2 < 4 (Table 3). The mean values of the dihedral angles between the phenyl mean planes and the porphyrin-core mean plane of each porphyrin ring decrease in the same order (Table 4), while the mean values of the dihedral angles occurring between the adjacent pyrrole rings increase in this order. These results show also that the saddle deformations occurring in the trans-substituted porphyrin complex, Fe(trans-tetpp)Cl (2) are slightly larger than in the cis-substituted porphyrin derivative, Fe(cis-tetpp)Cl (3). Moreover, these deformations appear to be clearly asymmetric in 1, but show a symmetry approaching C2, not only in the trans-substituted porphyrin ring of 2 but also in that of 3 and 4. Thus, in the crystalline state, the saddle deformations increase in the order 1 < 3 < 2 < 4. These deformations are smaller than those encountered in the structures of the two crystalline forms 5 and 5’ of Fe(oetpp)Cl 〚11, 12〛. The displacements and dihedral angles characterising the saddle distortions in the oetpp ring of 5 and 5’ are given in Table 10, parts a–c.
a. Displacements in Å of the Cβ atoms of the adjacent pyrrole rings above and below the porphyrin-core mean plane and their absolute averages (<Cβ/Cβ>). b. Values of the dihedral angles δ (in degrees) between the mean planes of the four phenyl rings (Ph1, Ph2, Ph3, Ph4) and the porphyrin-core mean planes (Pc) and their averages (<δ(Ph/Pc)>). c. The values of the dihedral angles δ (in degrees) of the adjacent pyrrole rings (I/II, II/III, III/IV, IV/I) and their mean values (<δ>) for the oetpp porphyrin rings present in the crystalline varieties of Fe(oetpp)Cl (5) and (5’).
| a | C2/C3 | C7/C8 | C12/C13 | C17/C18 | <|Cβ/Cβ|> | Ref. |
| 5 | –1.123(6) | +1.163(7) | –1.138(6) | +1.184(6) | 1.153 | 〚11〛 |
| 5’ | –1.138(8) | +1.127(8) | –1.138(8) | +1.127(8) | 1.132 | 〚12〛 |
| b | δ(Ph1/Pc) | δ(Ph2/Pc) | δ(Ph3/Pc) | δ(Ph4/Pc) | <δ(Ph/Pc)> | |
| 5 | 46.8(2) | 44.7(2) | 44.0(2) | 44.0(2) | 44.9 | 〚11〛 |
| 5’ | 43.9(3) | 45.1(3) | 43.9(3) | 45.1(3) | 44.5 | 〚12〛 |
| (c) | δ(I/II) | δ(II/III) | δ(III/IV) | δ(IV/I) | <δ> | |
| 5 | 39.7(3) | 41.5(3) | 41.3(3) | 42.2(3) | 41.2 | 〚11〛 |
| 5’ | 42.3(4) | 40.8(4) | 42.3(4) | 40.8(4) | 41.5 | 〚12〛 |
The values of the average displacements of the meso-carbon atoms relative to the porphyrin-core mean plane vary roughly from 0.14 to 0.08 Å (Table 6) in the order 1 < 3 < 2 < 4. They show that the smallest ruffling occurs in 4. As estimated by the meso-carbon displacements observed in 5 and 5’, relative to the Pc mean-planes, the ruffling of the porphyrins present in these compounds are slightly more important (Table 6) 〚11, 12〛.
As indicated by the PN–Pc separations between the pyrrole-nitrogen PN and porphyrin-core Pc mean planes which decrease from 0.054(1) to 0.029(1) Å (Table 7), the doming deformations observed in these compounds are generally small and seem to decrease from 1 to 4 as the number of Cβ-ethyl substituted pyrrole rings increases. The smallest doming occurs in 4. However, between 1 and 2, and 2 and 3, the values of the PN–Pc separations observed are not significantly different. In 5 the doming is smaller than in 4 and no doming at all is present in 5’, since for this compound the PN–Pc separation of 0.003(2) Å is not significant (Table 7) 〚11–12〛.
These measures of the saddling, ruffling, and doming deformations of the porphyrins are borne out by the NSD analyses of the crystal structures. The sad displacements determined by the structural decomposition method for the crystal structures of 1, 2, 3, and 4 confirm that the ordering of the saddle deformations of the porphyrins is 1 < 3 < 2 < 4, as determined by using the Cβ-atom displacements from the mean plane. The corresponding sad displacements of approximately 0.76 (1), 2.20 (2), 2.06 (3) and 2.90 Å (4) (Table 8) are rather large compared to those of –0.16 (heme A) and –0.35 Å (heme B) found by NSD analysis of the X-ray structure of Chromatium vinosum cytochrome c’〚23〛, but are typical of the peroxidases at the lowest range (the absolute signs of the displacements are not determined for synthetic porphyrins).
In the NSD analysis the asymmetry evident in these mainly sad structures is a consequence of the presence of contributions from other deformation types. The NSD calculations confirm that the smallest ruffling occurs in the porphyrin of 4, whereas between 1 and 3 the ruf displacements found vary in the order 1 ≈ 3 > 2 (Table 8). The ruf magnitudes of approximately 0.37 Å for 1 and 3 (Table 8) are not very different from that of 0.39 Å found in the structure of Chromatium vinosum cytochrome c’ 〚23〛. These NSD calculations also confirm that the smallest doming occurs in 4, and for the macrocycles of 1, 2, and 3, the calculated dom displacements, which vary between 0.10 (2) and 0.25 Å (1), are somewhat larger than those of 0.09 (heme A) and 0.05 Å (heme B), which are determined by NSD for the structure of ferricytochrome c’ from Chromatium vinosum 〚23〛. For the peroxidases, the magnitudes of the dom deformations vary from 0.02 to 0.37 Å 〚9〛. When the x and y symmetry is perturbed by the diethyl substitution pattern as is the case for complexes 1, 2, and 4, then we see large differences in the wav(x) and wav(y) displacements. On the other hand, when the x and y symmetry is approximately preserved as for the cis-tetpp and oetpp complexes, then the wav(x) and wav(y) contribution are nearly equal. Thus, even these small out-of-plane deformations seem to arise from substituent effects. Although the wave deformations are relatively small, nevertheless they are energetically significant because of the high frequencies of these normal modes. Similarly, although the pro deformations are small, they cannot be discounted in energetic considerations regarding the steric and crystal-packing forces.
The visible absorption spectra of the FeCl complexes studied here show increasing bathochromic shifts of the bands in the order 1 < 2 < 3 < 4 (see experimental section). This finding is in agreement with recent studies of the effects of non-planar cores on the visible absorption spectra of porphyrins and metalloporphyrins 〚1–3〛. These studies have shown that, due to the narrowing of the HOMO–LUMO gap, the bands forming the visible spectra of saddle-shaped free-base and metal porphyrins are red-shifted when compared to planar porphyrins 〚26〛. The red-shifts of the visible bands of the Fe(III)Cl complexes in dichloromethane solution investigated here suggest that the porphyrin rings present in these iron complexes also adopt non-planar conformations, in agreement with the solid state structures. It is possible however that the structures in solution might differ from those present in the solid state. The present data further supports the contention that the red shifts induced by non-planar distortion, which are mostly based on studies of porphyrin complexes with metals other than iron, are applicable to the Fe(III)Cl derivatives when the electronic structure of the Fe atom is not radically altered by the distortion.
The g-effective values obtained by the simulations of the EPR spectra are characteristic for an admixed S = 5/2,3/2 spin state with a positive zero-field splitting D and a small rhombicity (Table 9). According to Maltempo and Moss 〚4〛, the reduction of the average geff⊥ value due to a quantum-mechanical high-spin/intermediate spin (S = 5/2,3/2) admixture is given by geff⊥=6 (a5/2)2 + 4 (b3/2)2. Since (a5/2)2 + (b3/2)2 = 1, and the percentage of 3/2 spin admixture into the S = 5/2 ground state is given by 100 × (1 – (a5/2)2). The values found (Table 9) show that the electronic ground state of 1 is purely high-spin S = 5/2, that it consists of 0.75 and 1.20% of S = 3/2 and 99.25% and 98.80% of S = 5/2, in 2 and 3, respectively. Moreover, in 4, for which (a5/2)2 was found to be 0.9725, this ground state contains only 2.75% of S = 3/2 and 97.75% of S = 5/2. Thus, the 5/2,3/2 spin admixture increases in the order 1 < 2 < 3 <4. For porphyrins 2 and 3, this order is different from that deduced from the saddle deformations of the porphyrins in the solid state and is identical to that obtained by considering the red-shifts of the bands of the visible spectra in dichloromethane. Moreover, the present results are compatible with the degree of S = 5/2,3/2 admixture found to be 4.25% in Fe(oetpp)Cl 5’ in frozen 2-MeTHF (Table 9) 〚12〛.
In conclusion, to assess the effects of a gradual increase of the saddle deformations imposed on a porphyrin macrocycle and the basic spin state of chloroiron(III) complexes of such porphyrins, we have studied the structures and EPR spectral properties of the chloroiron(III) complexes of the 2,3-diethyl-(1), 2,3,12,13-tetraethyl-(2), 2,3,7,8-tetraethyl-(3) and 2,3,7,8,12,13-hexaethyl-(4) 5,10,15,20-tetraphenylporphyrins. As already observed by Senge and Kalish 〚25〛, the gradual steric crowding of the tetraphenylporphyrin ring by replacement of the unsubstituted pyrrole rings by 3,4-diethyl-substituted pyrroles leads to asymmetric non-planar distortions of the macrocycles present in these derivatives. Due to the gradual increase of the steric strain, the ligands present in these complexes display increased saddle distortions. The corresponding normal displacements calculated in these compounds by the normal-coordinate structural decomposition method are much larger than the sad displacements found in ferricytochrome c’ of Chromatium vinosum. Moreover, despite these large saddle-shaped deformations, the quantum mechanical S = 5/2,3/2 spin admixtures found in these compounds by analysis of their EPR spectra are quite small. The S = 3/2 admixture into the S = 5/2 high-spin state varies approximately between 0% in 1 to 3% in 4. These results indicate that the saddle distortions alone are probably not sufficient to cause the S = 5/2,3/2 spin admixture observed in the peroxidases nor the ferricytochromes c’ from Chromatium vinosum and other ferricytochromes c’ from photosynthetic bacteria. The five-coordinate iron atoms present in the cytochromes c’ for which the X-ray structures have been determined are bonded to four pyrrole nitrogens of a heme and to an axial imidazole ligand of a histidine residue. Moreover, it has been shown recently that the spin state of iron(III) meso-tetramesitylporphyrin monoimidazole complexes are quantum-mechanical admixtures of S = 3/2,5/2 〚34〛. It may be that saddling combined with other factors such as specific axial ligands and ligand geometries and specific combinations of non-planar deformations are necessary to realise the QMS state.
5 Supplementary material
Crystallographic data for the structural analysis have been deposited with the Cambridge Crystallographic Data Centre as Supplementary Publication n° CCDC 179324–179327 for compounds 1 to 4, respectively. Copies of the data can be obtained free of charge by application to CCDC, 12 Union Road, Cambridge, CN2 1EZ, UK (fax: +44-1223-336-033; e-mail: deposit@ccdc.cam.ac.uk or www: http://www.ccdc.cam.ac.uk).
Acknowledgements
We thank Sylvain Mérillon for the work done on these complexes and are very grateful to Professor Dr. A.X. Trautwein and Dr. V. Schünemann from the Institut für Physik of the Medizinische Universität von Lübeck (Germany) for the EPR spectral measurements and simulations. R.W. thanks Professor J.-M. Lehn, ‘Laboratoire de chimie supramoléculaire’, ISIS, University Louis-Pasteur (Strasbourg, France), for his kind hospitality. Sandia is a multiprogram laboratory operated by Sandia Corporation, a Lockheed Martin Company, for the United States Department of Energy, under Contract DE-AC04–94AL85000.



