1 Introduction
Rare-earth-doped glasses are of interest due to the many photonic applications that take advantage of the sharp f–f electronic transitions of trivalent rare-earth ions, as well as the transparency and formability of the host glasses. Nd-doped glasses with laser emission at 1060 nm have long been known 〚1〛. The success of Er-doped silica fibers in providing optical amplification at 1550 nm has stimulated research into the development of new rare-earth-doped glasses that could serve as fiber amplifiers in other portions of the telecommunications window, such as at 1300 nm or in the S (1450–1520 nm) and L (1565–1605 nm) bands. Although most recent studies have focused on Tm-doped glasses for S band amplification, much of the earlier work was directed towards the development of efficient host glasses for amplification at 1300 nm 〚2–5〛. The rare-earth dopant of choice for the latter application is Pr3+, as its 1G4 → 3H5 emission is peaked in the appropriate wavelength region, and it is not adversely affected by excited state absorption as is the 4F3/2→4I13/2 transition of Nd3+ 〚6〛. Despite this, the 1300-nm fluorescence of Pr3+ is only of practical intensity in nonoxide glasses that have sufficiently low maximum phonon energies, because of the likelihood of nonradiative decay arising from the small energy gap between the 1G4 upper laser level and the intermediate 3F4 level (ΔE ∼ 3000 cm–1). Optical amplification near 1300 nm has been demonstrated with Pr-doped fluoride glass fibers 〚7〛, but sulfide glass hosts are preferred for this application on account of the much more efficient luminescence that is ultimately due to the higher refractive index of these materials 〚8〛. In particular, GeAs sulfide glasses are potentially attractive host glasses on account of their good thermal stability, thereby minimizing the potential for devitrification during fiber fabrication.
However, rare-earth solubility is low in many chalcogenide glasses. The solubility limit of Er in vitreous As2S3 is well below 2000 ppm 〚9〛, while that of Pr in glassy GeS2 is only 400 ppm 〚4〛. Moreover, just as in the case of rare-earth-doped fused silica 〚10〛, rare-earth clustering is expected to limit fluorescence efficiency, even when the rare-earth-dopant concentration is kept below the solubility limit. Accordingly, in this paper, we examine rare-earth clustering in GeAs sulfide glasses using the fluorescence of Pr-doped glasses and, in particular, electron paramagnetic resonance (EPR) spectroscopy of Gd-doped glasses. We have chosen to concentrate on EPR, using Gd3+ as a probe ion due to its sharp EPR features even at room temperature. Furthermore, being trivalent, Gd3+ can be taken as a model for the structural behavior of the other trivalent rare-earth ions. The utility of EPR in investigating rare-earth clustering arises from the fact that, as rare-earth ions cluster, they begin to affect each other through a magnetic dipole–dipole interaction. Pake has shown that, for a random distribution of ion–ion directions relative to an applied magnetic field, the absorption spectrum due to dipolar broadening has a roughly Gaussian shape and is centered at approximately g = 2 〚11〛. Thus, if some proportion of the Gd dopant in the studied GeAs sulfide glasses is clustered, the EPR spectrum is expected to consist of a superposition of the so-called ‘U spectrum’, characteristic of isolated Gd ions and which has peaks at g-values of 6.0, 2.8 and 2.0 〚12〛, and a broad Gaussian absorption. This superposition will be manifest in the EPR spectrum as an increase in the width of the g ∼ 2 resonance, which, therefore, can be taken as a qualitative measure of rare-earth clustering.
2 Experimental
The glasses examined in this study were prepared by melting 10-g mixtures of the elements (≥ 99.9995% purity, metals basis). In the case of samples for EPR spectroscopy, each mixture contained 0.009 gm Gd2S3, corresponding to a nominal Gd concentration of about 690 ppm by weight (approximately 0.02 atomic% Gd). Samples for fluorescence spectroscopy were doped with 450-ppm Pr (approx. 0.015 atomic% Pr). These mixtures were loaded into fused silica ampoule,s which were subsequently evacuated to 10–6 Torr. In the case of I-containing batches, the ampoule was immersed in a liquid N2 dewar during evacuation in order to avoid sublimation. After flame-sealing, the ampoules were heated in a rocking furnace at 800 (As-rich glasses) or 925 °C (Ge-rich glasses) for at least 24 h. Cylindrical glass ingots were formed by quenching the hot ampoules into water. The samples were annealed by heating for about 1 hr at the glass transition temperature, after which they were cooled slowly to room temperature.
The Gd concentration of selected samples was measured by electron microprobe (JEOL 8900) using a GdPO4 standard. Fluorescence measurements of Pr-doped glasses were carried out by pumping 2-mm thick polished discs with a Ti-sapphire laser operating at 1060 nm (1G4→3H5 emission at 1300 nm) or with a RG4 rhodamine dye laser operating at 605 nm (1D2→1G4 emission at 1500 nm) and collecting the resultant fluorescence with a Ge detector. EPR spectra of powdered Gd-doped glass samples were recorded at room temperature with a Bruker spectrometer operating at 9.7 GHz. The width of the g ∼ 2 resonance was measured by determining the magnetic field difference between the sharp feature at ∼3380 G on the low field side of the g ∼ 2 resonance and the minimum at the high field side of the same transition. In glasses with very high degrees of Gd clustering, the 3380-G feature was not always clear and, in those cases, the EPR linewidth was arbitrarily taken to be the difference between the high-field minimum and 3380 G.
3 Results
3.1 Uncodoped glasses
Gd-doped Ge-rich (Ge:As = 2.5:1) and As-rich (Ge:As = 1:2) glasses were made with S contents varying from –50 to 40% of the stoichiometric amount. The actual Gd concentration (〚Gd〛) of these samples, as measured by electron microprobe, is listed in Table 1. For all As-rich glasses, 〚Gd〛 is well below the nominal concentration of 690 ppm, with the average 〚Gd〛 being little more than 200 ppm, and there seems to be no correlation between 〚Gd〛 and the S content of these glasses. In the case of Ge-rich glasses, only the most S-deficient glass (–50% S) has 〚Gd〛 equal to the nominal value, and there is an apparent increase in 〚Gd〛 with increasing S deficiency. In addition, 〚Gd〛 of Ge-rich glasses is typically higher than that of the corresponding As-rich glasses at any given S content: the average 〚Gd〛 for all S-deficient samples is about 240, 400 ppm for As-rich, Ge-rich glasses, respectively.
Gd content and EPR linewidth of uncodoped GeAsS glasses.
| Ge:As | % excess S | 〚Gd〛 (ppm) | EPR linewidth (gauss) |
| 1:2 | 40 | 60 | |
| 1:2 | 0 | 764 | |
| 1:2 | –10 | 380 | 884 |
| 1:2 | –20 | 270 | 927 |
| 1:2 | –30 | 20 | 678 |
| 1:2 | –40 | 120 | 712 |
| 1:2 | –50 | 420 | 755 |
| 2.5:1 | 40 | 1047 | |
| 2.5:1 | 0 | 921 | |
| 2.5:1 | –10 | 240 | 395 |
| 2.5:1 | –20 | 490 | 378 |
| 2.5:1 | –30 | 240 | 326 |
| 2.5:1 | –40 | 330 | 189 |
| 2.5:1 | –50 | 690 | 154 |
The spectrum of the 1G4→3H5 emission of a Pr-doped sample of the stoichiometric (0% excess S) Ge-rich glass Ge25As10S65 is shown in Fig. 1, along with that of the Ga-codoped analogue Ge25As9.8Ga0.2S65, which has a Ga:Pr ratio of 14:1 (atomic%). The intensity of this emission in the uncodoped glass is clearly much less than that in the Ga-codoped example, being reduced by more than an order of magnitude. Moreover, the emission lineshape is broader and peaked at 1350 nm instead of showing a sharp maximum at 1340 nm.
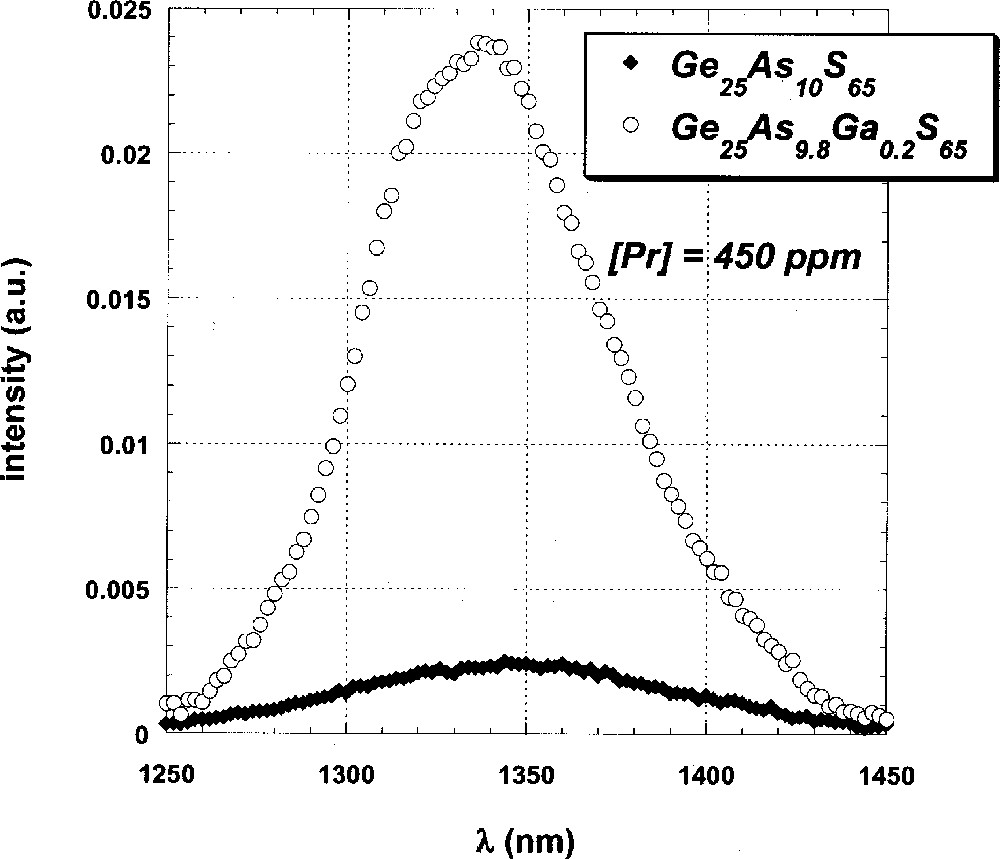
1G4 → 3H5 emission spectra of Pr-doped GeAs sulfide glasses with (open circles) and without (solid diamonds) Ga codopant.
The EPR spectrum of the stoichiometric Ge-rich glass, Ge25As10S65, is shown in Fig. 2, along with the spectra of two representative Ga-codoped glasses. Whereas the spectra of the latter show the prominent Gd U spectrum peaks, that of the uncodoped glass is relatively featureless, being dominated by a broad Gaussian absorption centered at g ∼ 2 (3600 G). The linewidth of the g ∼ 2.0 resonance for this and other uncodoped glasses is reported in Table 1. This quantity is large, ranging from 676 to 927 G, for all As-rich samples and, as with 〚Gd〛, there is no correlation between the EPR linewidth and the S content of the glass. For Ge-rich glasses, the EPR linewidth ranges from 1047 to 154 G, and clearly narrows with decreasing S content. Moreover, the EPR linewidth of all S-deficient Ge-rich glasses is much narrower than that of the corresponding As-rich glasses.
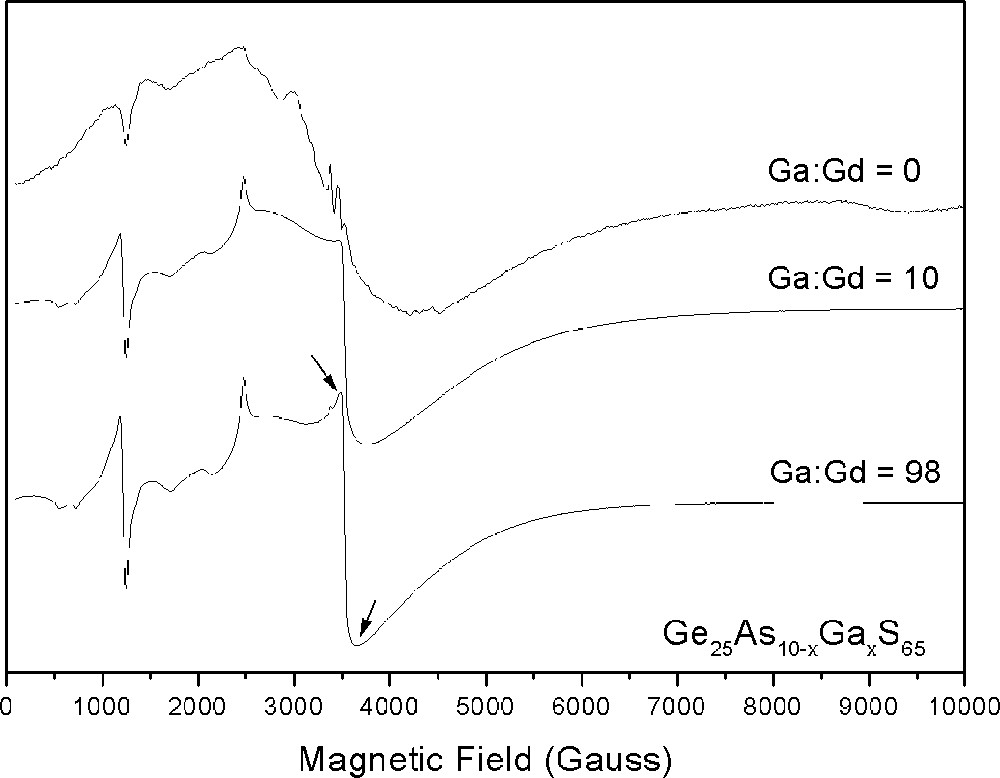
EPR spectra (9.7 GHz) of Gd-doped GeAs sulfide glasses with and without Ga codopant. Arrows delimit the reported g ∼ 2 resonance linewidth.
3.2 Codoped glasses
Gd-doped Ge-rich GeAsS glasses were codoped with Ga, In, P, Sn and I. In the case of the first three codopants, the compositional series investigated are represented by structural formulae of the type Ge25As10–xMxS65, where M = Ga, In, or P, i.e. the metallic codopant was progressively substituted for As. The Sn-codoped glasses were formulated as Ge25As10–xSnxS65–x/2, in view of the likelihood that most, if not all, Sn is divalent at these concentrations 〚13〛. For the I-containing glasses, the studied samples can be symbolized by formulae of the type Ge25As10S65–x/2Ix, in which S was progressively replaced by the non-metallic codopant I. Such substitutions ensured that the codoped glasses were stoichiometric, allowing for direct comparison with the 0% excess S glasses from the uncodoped sample set.
Fluorescence data for Ga- and P-codoped, Pr-doped glasses are given in Table 2 and illustrated in Fig. 3. In both cases, the data indicate a sharp increase in the intensity of the 1500 nm 1D2→1G4 emission band with increasing Ga or P concentration, as well as the previously described increase in the intensity of the 1340-nm 1G4 → 3H5 emission (Fig. 1). Furthermore, fluorescence intensity saturates for glasses in which the codopant:Pr ratio is greater than about 10:1, at which point it has increased by more than two orders of magnitude from that of uncodoped glasses.
Relative intensity of Pr3+ emission in codoped Ge-rich GeAsS glasses.
| Codopant | Codopant:Pr | Relative intensity (a.u.) |
| Ga | 0 | 3.5 |
| Ga | 1.2 | 13.5 |
| Ga | 2.4 | 25 |
| Ga | 3.6 | 65.5 |
| Ga | 6.7 | 175 |
| Ga | 13.5 | 366 |
| Ga | 29 | 354 |
| P | 2.7 | 3 |
| P | 6.4 | 1.5 |
| P | 12 | 10 |
| P | 61 | 20 |
| P | 123 | 20 |
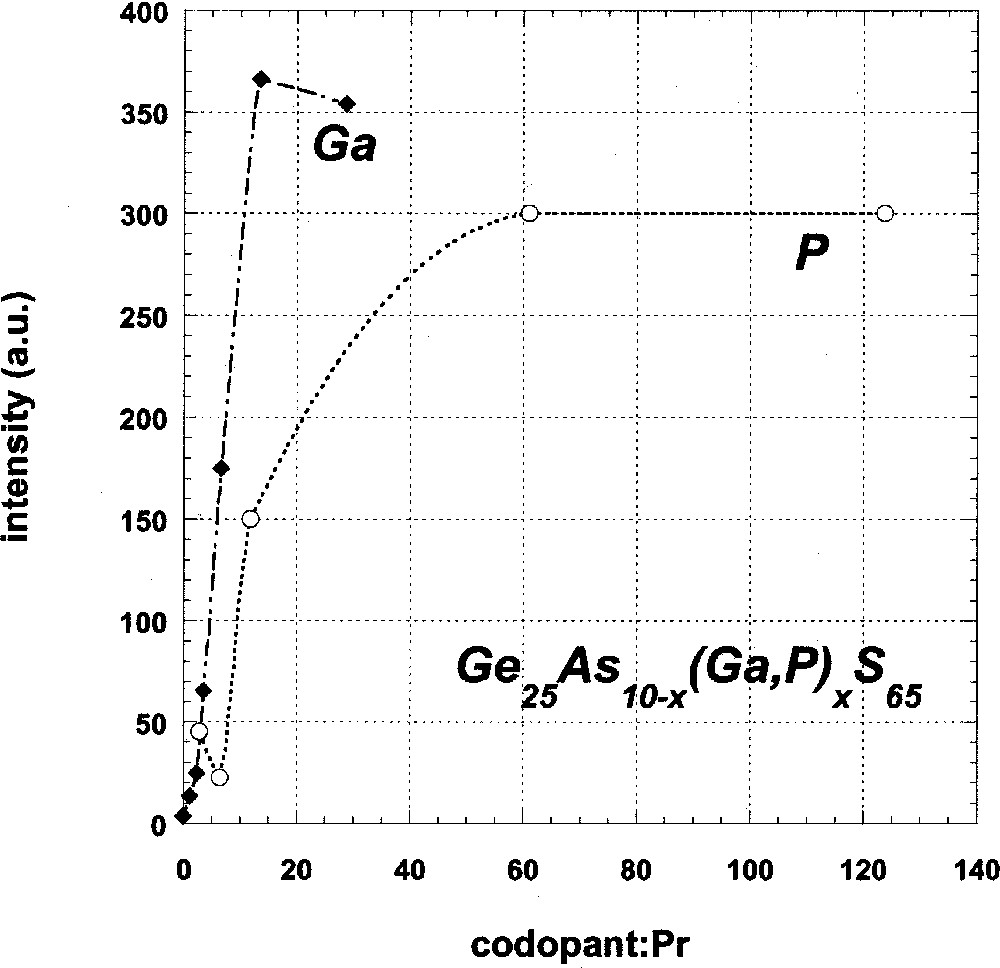
Relative intensity of fluorescence from the 1D2 level of Pr3+ in Ga- and P-codoped GeAs sulfide glasses as a function of the codopant:Pr ratio (solid diamonds: Ga; open circles: P).
The EPR spectra of two representative Ga-codoped are presented in Fig. 2. As noted above, these spectra show prominent resonances at magnetic field strengths of 1200, 2500 and 3600 G, corresponding to g values of 6, 2.8 and 2. This U spectrum is typical of isolated, non-interacting Gd3+ ions that occupy a single low symmetry site in glass 〚12〛; essentially the same features are observed whether the host glass is a silicate, borate, phosphate, fluoride or sulfide glass 〚14–17〛. With increasing Ga concentration, the EPR resonances become increasingly intense and narrow. EPR linewidth data for Ga-, In-, P-, Sn- and I-codoped Gd-doped Ge-rich glasses are presented in Table 3 and plotted in Fig. 4 as a function of the codopant:Gd ratio. For each codopant series, the base glass is the 0% excess S sample with Ge:As = 2.5:1 (i.e. Ge25As10S65) from Table 1, which is characterized by a very broad resonance with a linewidth of about 920 G. In the case of the Ga-codoped samples, the EPR linewidth is seen to narrow rapidly from 920 to 300 G as the Ga:Gd ratio increases from 0 to 10:1 (cf. also Fig. 2). Further increase in the Ga concentration results in a slower narrowing of the EPR linewidth, and a plateau value of about 170 G is attained in those samples where the Ga:Gd ratio is 40:1 or greater. Similar trends are also observed for glasses codoped with In or P, although, at a given codopant:Gd ratio, the EPR linewidth of these glasses is typically significantly broader than that of the analogous Ga-codoped samples. Sn-codoped glasses also show narrowed EPR resonances with increasing Sn concentration, but the line narrowing is even less than in the In-, P-codoped samples. Finally, I-codoped glasses show no resonance narrowing with increasing I concentration; the EPR linewidth of all samples in the studied range is essentially constant with an average breadth of about 960 G, which is hardly different from the 920 G linewidth of the uncodoped base glass.
EPR linewidth of codoped Ge-rich GeAsS glasses.
| Codopant | Codopant:Gd | EPR linewidth (gauss) |
| Ga | 2.5 | 865 |
| Ga | 65 | 730 |
| Ga | 10 | 303 |
| Ga | 44 | 202 |
| Ga | 98 | 180 |
| Ga | 197 | 169 |
| Ga | 296 | 169 |
| Ga | 396 | 157 |
| Ga | 496 | 169 |
| In | 1 | 853 |
| In | 10 | 753 |
| In | 25 | 382 |
| In | 50 | 303 |
| P | 2.2 | 725 |
| P | 5.1 | 705 |
| P | 9.4 | 661 |
| P | 49 | 279 |
| P | 99 | 225 |
| Sn | 5 | 991 |
| Sn | 10 | 938 |
| Sn | 50 | 725 |
| Sn | 100 | 299 |
| I | 25 | 973 |
| I | 50 | 973 |
| I | 100 | 987 |
| I | 150 | 938 |
| I | 200 | 938 |
| I | 250 | 938 |
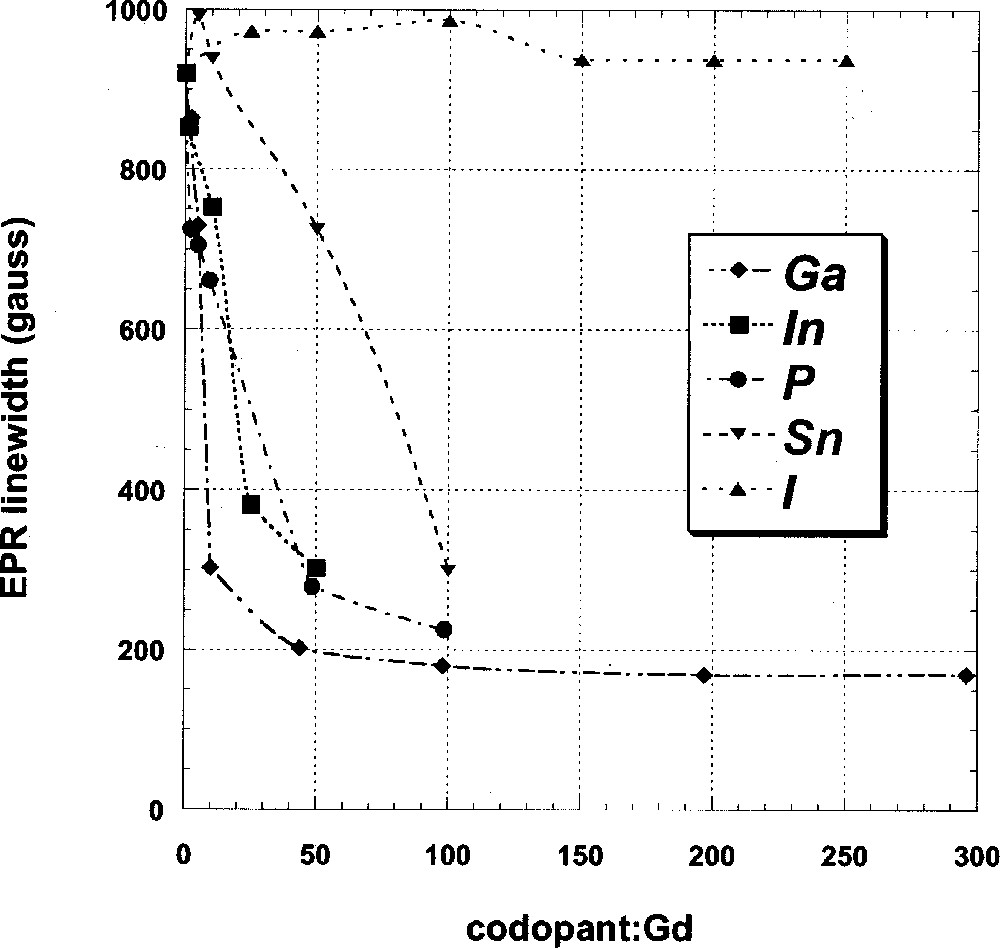
Linewidth of g ∼ 2 resonance of Gd3+ in Ga-, In-, P-, Sn- and I-codoped GeAs sulfide glasses as a function of the codopant:Gd ratio (diamonds: Ga; squares: In; circles: P; inverted triangles: Sn; triangles: I).
4 Discussion
The 〚Gd〛 microprobe data for the uncodoped glasses clearly indicate that the Gd solubility limit in most of these glasses, with the sole exception of the most S-deficient Ge-rich glass from the sample set, is much less than 700 ppm. Therefore, rare-earth ions can be expected to cluster in these glasses, and this expectation is indeed confirmed by both the Pr fluorescence and Gd EPR results. As shown by the data in Table 1 and Figs. 1 and 3, the intensity of the 1D2→1G4 and 1G4→3H5 emission bands of Pr3+ is reduced by as much as two orders of magnitude relative to that in Ga- or P-codoped glasses. As there is no concomitant increase in the maximum phonon energy of the uncodoped glasses relative to the codoped samples, which could decrease emission intensity by increasing the probability of multiphonon decay, the observed weak fluorescence of the uncodoped glasses is attributable to cross relaxation arising from rare-earth clustering. The 〚Gd〛 results further indicate that rare-earth solubility in uncodoped GeAs sulfide glasses is particularly low in As-rich glasses, increasing significantly with rising Ge:As ratio. In addition, rare-earth solubility is greatest for the most S-deficient Ge-rich glasses. This is in agreement with the data of Krasteva et al., who reported that 10 000 ppm of Pr were soluble in the S-deficient glass Ge43S57 〚18〛. Moreover, this trend is consistent with the EPR data, which similarly show that Gd clustering is most severe in As-rich glasses and that spectra typical of well-dispersed Gd atoms are only observed for S-deficient Ge-rich samples. Thus, in these network chalcogenide glasses, there appears to be a clear association of Gd and, hence, rare earths with Ge. Furthermore, based on previous Raman and EXAFS spectroscopic study, rare-earth-ion dispersal may possibly be correlated with an increased concentration of Ge–Ge bonds, as the latter have been shown to develop in Ge:As = 2.5:1 glasses when the S deficiency becomes greater than 20% 〚19〛. However, we have, as yet, no explanation for this relationship.
The rare-earth solubility limit in codoped GeAs sulfide glasses was, in general, not determined. However, given the above-described connection between low rare-earth solubility and clustering, it would seem reasonable to expect that rare-earth solubility in Ga-, In-, Sn- and P-codoped glasses would increase with increasing codopant concentration, as the EPR and fluorescence data clearly indicate that rare-earth clustering decreases with increasing codopant:rare earth ratio. This was corroborated by us for the case of Ga: the solubility limit of Pr in Ga-codoped Ge-rich GeAs sulfide glass (Ge25As8.3Ga1.7S65) was found to be about 5000 ppm (this study), corresponding to a Ga:Pr ratio of about 9:1. In contrast, as shown by the data in Table 1, the Gd solubility limit in the analogous Ga-free glass is only on the order of 200 ppm.
With regard to the EPR measurements and considering first the data for Ga-containing glasses, the progressively narrowed g ∼ 2 resonance linewidth with increasing Ga:Gd ratio demonstrates that Ga is an effective codopant in reducing the clustering tendency of rare earths in GeAs sulfide glasses. Furthermore, the fact that this linewidth narrowing becomes much less for Ga:Gd ratios of 10:1 or greater suggests that, in such glasses, the 700-ppm Gd present is fully dispersed. As shown in Fig. 5, the fluorescence data for the analogous Pr-doped glasses describe an identical trend: rapid increase in fluorescence intensity in the low Ga:rare earth regime where the decrease of the EPR linewidth is steepest, followed by an inflection point near Ga:rare earth = 10:1 in both curves. A similar mirroring of the fluorescence intensity and EPR linewidth versus composition trends is also seen for the P-codoped glasses, and thus provides support for our use of the EPR linewidth as a measure of rare-earth clustering.
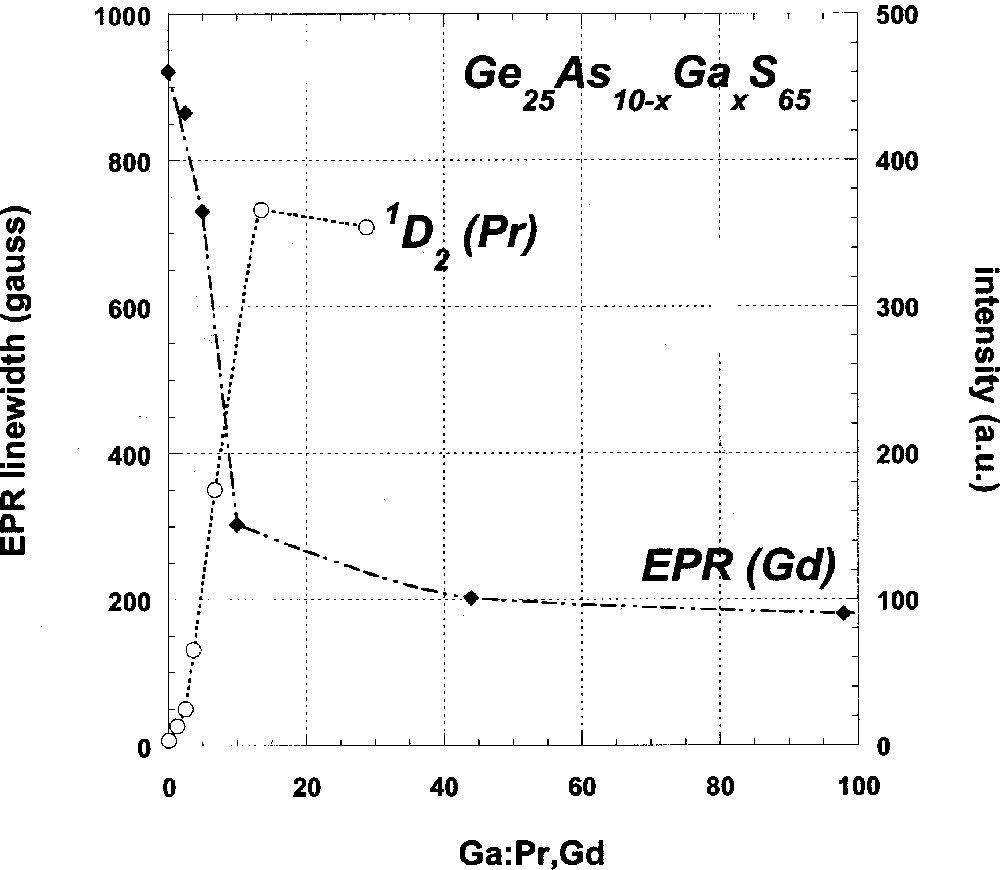
Gd3+ g ∼ 2 resonance linewidth (solid diamonds) and Pr3+ 1D2 emission relative intensity (open circles) of Ga-codoped GeAs sulfide glasses as a function of the Ga:rare earth dopant ratio. Note the inflection points in both curves near a Ga:rare earth dopant ratio of 10:1.
The EPR data for In-, P- and, to a lesser extent, Sn-codoped glasses indicate that addition of these elements to GeAs sulfide glasses also tends to reduce rare-earth clustering. However, at all but some of the lowest codopant:Gd ratios, the EPR linewidth for glasses codoped with P and In is broader than that of the corresponding Ga-codoped glass, indicating that Ga is the most efficient ‘declustering’ codopant of those studied. The even broader EPR linewidths of the Sn-containing glasses show that Sn is the least efficient codopant within the group of elements that have a measurable effect on reducing Gd clustering.
The results for the I-containing glasses show that, at least over the studied concentration range, I additions to these glasses have no tendency to suppress rare-earth clustering. As such, I-codoped GeAs sulfide glasses may represent an exception to the close connection between low rare-earth solubility and rare-earth clustering. Previous work on Ge–S–I glasses has shown that I additions to Ge-sulfide glasses resulted in enhanced Pr solubility 〚18〛. Therefore, it was reasonable to expect that Gd-doped I-substituted GeAs sulfide glasses might show evidence for EPR linewidth narrowing. However, whereas our I-codoped samples were stoichiometric, all of the I-substituted glasses studied by Krasteva et al. were anion-deficient, and it may have been this factor, rather than the presence of I, which contributed to increased Pr solubility. This would be consistent with our observations (cf. Table 1) that EPR-line narrowing and, hence, rare-earth dispersal occurs in S-deficient Ge-rich uncodoped glasses.
The fluorescence and EPR measurements of stoichiometric GeAs sulfide glasses reported above demonstrate that, in the absence of codopants, rare-earth dopants are relatively insoluble, although solubility does increase with rising Ge:As ratio. Moreover, the 200 ppm or so of rare earth that are soluble in such glasses are highly clustered, leading to poor luminescence efficiency, rendering these materials impractical for most photonic applications. Codoping these glasses with In, P and, in particular, Ga results in increased rare-earth solubility and, for a fixed rare-earth concentration, suppresses rare-earth clustering.
These features have led us to propose the following structural model of rare-earth-doped stoichiometric GeAs sulfide glasses. Firstly, rare-earth ions apparently concentrate in Ge-rich domains and, therefore, to a first approximation, the structure of vitreous GeS2 is used as a starting point. The IR and Raman spectroscopic study of Lucovsky et al. has shown that the latter can be regarded as a 3-dimensional network of corner- and edge-sharing GeS4/2 tetrahedra 〚20〛. In the case of uncodoped glasses, due to their low solubility, rare-earth dopants are believed to be located in poorly defined sites within the structural cavities formed by rings of tetrahedra. Within such rings, the rare earths are consequently clustered, as indicated by both the broad EPR linewidth and fluorescence quenching. As such, the rare-earth environment in uncodoped GeAs sulfide glasses is expected to resemble that in rare-earth-doped silica, where the NMR and EXAFS results of Sen indicated clustering of Nd at concentrations as low as 400 ppm 〚21〛.
The structural effect of codoping such glasses can be appreciated by considering the case of Ga. The latter element is well known to assume tetrahedral coordination with S in amorphous sulfides 〚22, 23〛 and is, therefore, expected to substitute randomly for Ge in the tetrahedral sites of GeS2 or, by extension, GeAs sulfide glass. Due to the lower charge of Ga relative to Ge, the S atoms that coordinate a substituting Ga are underbonded with respect to those that bridge solely GeS4/2 tetrahedra. Such underbonded S atoms can be stabilized by the donation of additional electron density and, thus, represent favorable sites for bonding with electron donors, such as rare earths. In other words, the rare-earth dopant can be viewed as acting as a charge-balancing cation for GaS4/2 tetrahedra, just as rare earths are also believed to play a similar role in Al-codoped silica by charge-balancing AlO4/2 tetrahedra 〚21〛. In this model, therefore, rare-earth dopants are believed to be spatially associated with the Ga codopant, specifically as next-nearest neighbours through Ga–S–rare earth linkages, as illustrated schematically in Fig. 6. The random distribution of Ga over the available tetrahedral sites of the glass structure thus ensures a well-dispersed distribution for the associated rare-earth dopant and, consequently, eliminates the ion–ion interactions that quench rare-earth luminescence in uncodoped glasses. The beneficial effect of In codoping on rare-earth dispersal can be explained in similar fashion, as In, like Ga, has a formal valence of +3 and is known to assume tetrahedral coordination in sulfides 〚24〛.
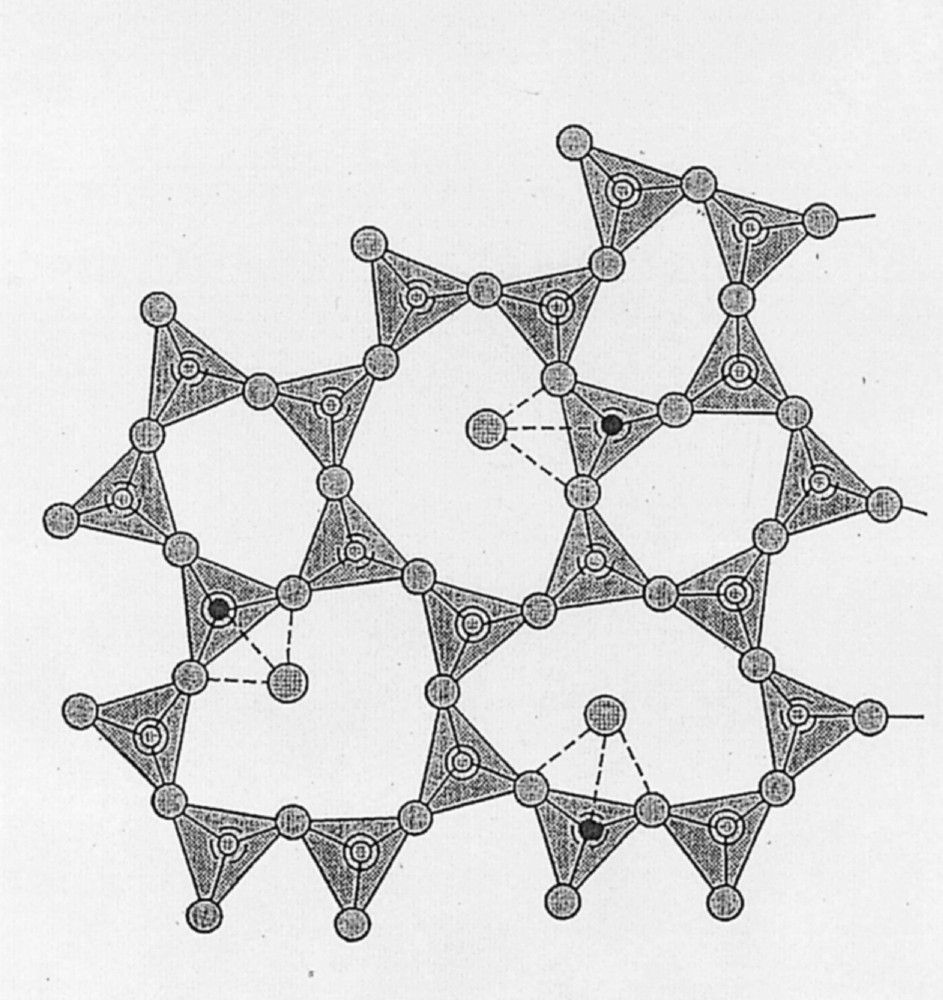
Idealized structure of rare-earth (large circles)-doped GeAs sulfide glass containing Ga, In or P codopants (small solid circles).
The case of P-codoping is interesting, because its effects mirror those observed in P-codoped silica glass 〚10〛. In the latter material, P occurs in O=PO3/2 groups (tetrahedra with one non-bridging doubly bonded oxygen) and analogous S=PS3/2 tetrahedra have been shown to be the dominant P species in stoichiometric P-containing GeAs sulfide glasses 〚25〛. Although the exact relationship between the rare-earth dopant and the P codopant is unknown in either case, one possibility is that the non-bridging anion may serve as the linkage to form a P–S,O–rare earth bond. The weaker codoping efficiency of P, relative to Ga, in GeAs sulfide glasses can then be rationalized by the fact that, even in stoichiometric glasses, a significant fraction of the P is also present as trigonal PS3/2 groups 〚25, 26〛, thereby reducing the concentration of tetrahedral P available to disperse the rare-earth dopant.
5 Conclusions
Rare-earth solubility is low in GeAs sulfide glasses, typically less than 500 ppm, although it increases with rising Ge:As ratio as well as decreasing S content. Moreover, fluorescence quenching and EPR resonance broadening indicate that, even at these reduced concentrations, rare earths are severely clustered, rendering such glasses impractical for photonic applications that require efficient luminescence. However, codoping these glasses with Ga, In or P, or to a lesser extent, Sn increases the solubility limit of rare earths and greatly suppresses their tendency to cluster. As a result, fluorescence intensity, e.g. of the 1G4 emission from Pr3+, can be increased by orders of magnitude. We suggest that rare-earth dopants and codopants are associated as next nearest neighbors in Ge-rich domains in these glasses, and that rare-earth clustering is eliminated by the ability of tetrahedrally-coordinated codopants such as Ga, In or P to randomly replace Ge in network sites in the glass.
Acknowledgements
The authors would like to thank M.L. Powley and D.H. Crooker for technical assistance in glass synthesis, F.A. Annunziata and K.T. Gahagan for fluorescence measurements, B.Z. Hanson for microprobe data, and B.L. Butler for EPR.



