1 Introduction
In the last two decades, a quite impressive development has been achieved in the field of molecule-based magnetic materials [1–7]. These materials are attractive not only for the challenge of learning how to use chemical methods for obtaining systems with predetermined physical properties, but also within the framework of the development of materials with revolutionary potential applications. The chemistry creative power has produced a significant number of new materials and processes for the transformation of matter. Therefore, as an obvious natural extension, a large number of chemists have moved their attention from the investigation of the properties of isolated molecules to the attempt of organising the molecules themselves in such a way that they can exhibit some predetermined bulk properties on a macroscopic scale. The basic approach seems rather clear since the chemistry postulate “molecular properties are determined by the molecular structure” may be obviously translated as “material properties are determined by material structure”. However, even if in theory there is no doubt that this analogy holds, in practice there are many differences, since control of molecular structure and control of self-assembly of molecules in condensed phases may involve enthalpy contributions of different orders of magnitude. Whenever these contributions are not too large, it is really difficult to predetermine the structure of a given material.
About 20 years ago, some researchers working in magnetochemistry conceived the dream of designing and synthesising molecule-based magnetic materials. This requires the utilisation of appropriate paramagnetic building blocks for assembling magnetically coupled networks with multidimensional extended topologies. Since the strength and sign (ferromagnetic or antiferromagnetic) of the magnetic coupling between the paramagnetic centres is strictly related to the structure of the solid, the major problem for chemists to surmount is the control of the tri-dimensional geometry of the building. This is not too difficult when strongly interacting inorganic particles are considered, but in this case the combinatory possibilities as well as the opportunities of tuning by means of molecular techniques, the magnetic properties are strongly limited. Organic chemistry in the recent past has developed the synthesis of several open shell molecules, i.e. mono- and poly-radicals, which in general are characterised by enhanced reactivity [8–11]. Although the number of these molecules has significantly increased in the last 20 years, their stabilisation requires the use of bulky substituents and the lack of electronegative elements that are necessary as far as the functionalisation of the radical is desired.
When the radicals can act as ligands towards transition metal ions, it is possible to take advantage of strong magnetic interactions. This is the basis of the so-called metal radical approach, which produced numerous interesting classes of molecular-based magnetic materials [2, 12]. This approach in principle allows the use of molecular chemistry techniques for tuning the chemical and physical properties of the systems and exploits the formation of metal complexes in order to reach the conformational definition of the system of paramagnetic centres. The use of different paramagnetic metal ions in addition allows the possibility of controlling the spin of the system. Finally, it must be recognised also that the coordination induces both kinetic and thermodynamic stabilisation of the open-shell radical ligand.
In order to give rise to extended systems, a need for bulk magnetic properties, this strategy requires that the radical may act as a bridging ligand towards two or more different metal ions. Therefore the molecule must contain not less than two donor atoms with appropriate topology. Nitronyl-nitroxides [13] and properly designed di- and tri-nitroxide ligands [14, 15] were found to be able to act as poly-monodentate ligands towards paramagnetic metal ions, whose Lewis acidity was increased by using hexafluoroacetylacetone as ancillary ligand. A large number of oligomeric and polymeric structures were found to characterise the resulting adducts, thus offering the possibility of investigating several different spin topologies.
Notwithstanding this success, the main chemical problem remains, since no structure showing a strong communication in more than one dimension has been obtained. The limitation of the approach can be easily understood considering that no more than two radical ligands may interact with the same metal ion and that the enthalpy difference existing between the intermolecular interactions of the adducts and the metal ligand interactions is too large. Small unforeseeable factors then play a determinant role. In this framework, the effort of the chemist in designing a predetermined multidimensional structure of paramagnetic building blocks vanishes.
A possible variation of the theme is that of using polyoxolene ligands. These, as we will show below, are much better ligands than nitronyl-nitroxides: they guarantee a priori a much better control of the chemical structures. Further they can be stable in different oxidation states, thus opening the possibility of obtaining bi- or multi-stable molecules, which might open the route to interesting applications. We wish to review here the results that we obtained in the effort to exploit polyoxolene ligands for the design of molecular based magnetic materials. We will start with simple o-dioxolene ligands, which provide the basic understanding of the metal radical interactions, then move to polydioxolenes, to polyiminosemiquinonates and finally to the so-called polynuclear valence tautomers. A final section will devote to conclusions and indications for the future.
2 O-Dioxolene ligand
Our attention to the o-dioxolene class of ligands (Fig. 1) fundamentally arose from the peculiar properties of these molecules, first of all their redox reactivity. In addition to organic chemistry reports on quinonoid systems, we wish to underline that excellent reviews concerning the coordination properties of these molecules have been published by Pierpont and co-workers during the last twenty years [16–19]. The simplest member of this family of compounds family i.e. 1, 2-dihydroxybenzene or catechol (CatH2), once deprotonated, is part of a three-member redox chain via two one-electron redox processes, yielding first the mononegative semiquinone (SQ) and then the neutral o-quinone ligand (Q). All these species may act as a ligand. The free-energy changes associated with the redox processes are relatively small and of the same order of magnitude as those accompanying the usual chemical reactions. Therefore, all the three dioxolene species can readily exist, either alone or stabilised via coordination to a metal ion.

As far as it concerns their use for designing paramagnetic building blocks, there is no doubt that the semiquinone, which is known to form stable complexes with all the transition-metal ions, is the most interesting one. Some of us recently showed that this property holds also for the elements of the f –block [20, 21]. The possibility of existence of a given metal-semiquinonato adduct is obviously determined by the redox properties of the two counterparts. As far one compares the redox potentials of the MIV/MIII and MIII/MII redox couples of 3d metal ions with those of the MIISQ/MIICat and MIIISQ/MIIICat couples, it is rather clear that Ti and V form MIV-semiquinonato complexes, whereas low oxidation states of the metal ions characterise the Ni and Cu semiquinonato derivatives. It is worth noting that the redox potentials of the 3d metal ions and dioxolene ligand cross in the region of the triad Mn–Fe–Co, thus indicating that the corresponding metal ions may yield derivatives in different oxidation states.
The complexes of 3d and 4f metal ions can be described with a well-defined charge distribution, the metal–ligand interaction being characterised by a low covalent character. Indeed the structural parameters of the three dioxolene oxidation states are extremely useful for the assessment of the charge distribution within a metal-o-dioxolene adduct. This in practice has the important consequence that, in contrast with dithiolenes and di-imino radical ligands, metal-semiquinonato complexes can be considered as localised, as far as the formal oxidation state of the metal acceptor is not too high.
The charge-localised description of metal-dioxolene derivatives allows a simple rationalisation of the magnetic properties of these complexes. In some cases, the same compound can be stable in two different electronic configurations, thus giving rise to the so-called valence tautomerism, to be discussed below.
The nature of the magnetic interactions in 1:1 metal-semiquinonato adducts can be easily predicted taking into account the symmetry of the magnetic orbitals (i.e. orbitals containing unpaired electrons) of the two counterparts [22]. Indeed, both the sign and the magnitude of the exchange coupling interaction between the paramagnetic centres is determined by the overlap between the magnetic orbitals: therefore, if the magnetic orbitals are orthogonal to each other, ferromagnetic coupling occurs, whereas if they have a non-zero overlap, antiferromagnetic coupling occurs. Since the magnetic orbital of the semiquinonato ligand is π*, we may predict that all the metal ions with filled dπ and partially filled dπ orbitals, like six-coordinate NiII and CuII, will yield ferromagnetically coupled metal–semiquinonato adducts. On the other hand, when the metal acceptor exhibits partially filled dπ orbitals, like VIII, CrIII, MnIV, etc., the metal–semiquinonato complex will be characterised by an electronic ground state arising from the antiferromagnetic coupling between the paramagnetic centres. It is generally found that when the electronic properties of a metal ion may allow both mechanisms to be operative. As an example for MnII and FeIII, the antiferromagnetic contribution dominates. However, some of us have recently shown how in some 1:1 hs-cobalt(II)-semiquinonato adducts the weak observed antiferromagnetic coupling suggests that the two contributions in practice cancel each other [23].
When more than one semiquinone ligand is present in a given molecule, magnetic interactions must be expected also between the organic radicals. For instance, in pseudo-octahedral bis- and tris- semiquinonato metal complexes, intramolecular ferromagnetic coupling is observed between the radical ligands [24–27]. Some years ago, we showed that the complex TiIV(Cat–N–SQ)2, where Cat–N–SQ is a dinegative diquinone tridentate Schiff-base radical ligand, exhibits a triplet ground state, the ferromagnetic exchange pathway being determined by the d orbitals of the metal ions [28, 29]. Again a simple qualitative picture predicts ferromagnetic coupling due to the orthogonality of the π* orbitals determined by the coordination around the metal ion. A DFT calculation supported this conclusion and provided a more complete picture of this molecular system [30]. Polarised neutron scattering experiments confirmed that the formally diamagnetic metal ion is involved in a superexchange mechanism [31]. In addition, the Zn(bpy)(DBSQ)2 and Ga(DBSQ)3 (DBSQ = 3,5-di-tert-butyl-semiquinonato) complexes were found to exhibit triplet and quartet ground states, respectively [27,32].
Though the Co(DBSQ)3 complex (DBSQ = 3,6-di-tert-butyl-semiquinonato) was found to be characterised by a doublet ground state [25], it has been recently found that two tris-iminosemiquinonato-cobalt complexes have a quartet ground state [33], in agreement with the results that we have recently found for a dinuclear tris-semiquinonato derivative (see below). These differences are believed to be due to the existence of both antiferromagnetic interligand and ferromagnetic metal-mediated exchange pathways, which in turn may dominate. A DFT study of these complexes is in progress in order to obtain a more accurate analysis of this intriguing phenomenon [34].
3 Polydioxolene metal complexes
The above radicals are certainly very well suited to investigate the fundamental nature of the interaction determining the magnetic coupling of dioxolene radical ligands with transition metal ions. However, if the final goal is that of designing molecular magnets, it is necessary to find radicals able to bridge at least two different metal ions.
The first ligand that we have considered some years ago was the 1,2,4,5-tetrahydroxybenzene (DHBQH4). This molecule, once deprotonated, may yield a five-term redox chain in which the trinegative and mononegative are radical anions. All the five terms may act as bis-bidentate ligands towards two different metal ions. Compounds of general formula MII(DHBQ) and MIII2(DHBQ)3.nH2O can be obtained by reaction of the ligand with divalent and trivalent 3d metal ions in basic solutions [35]. All these derivatives are presumably polymeric and were suggested to contain the dinegative diamagnetic dioxolene ligand. Though not supported by structural data, it is also suggested that all these complexes are six-coordinated with no more than two tetraoxolenes being coordinated to the same metal ion. Very unstable derivatives were obtained by using either oxidising or reducing agents in order to isolate solid compounds containing either the mononegative or the trinegative radical species. Because of their high reactivity, the complexes were not magnetically characterised, except a solid of formula Cr(DHBQ)·2 H2O obtained by the reaction of CrCl2 with an excess of the ligand. This compound has a triplet ground state, probably arising from the antiferromagnetic interaction between the S = 3/2 chromium(III) ion and the trinegative radical ligand. It is believed that also this complex is polymeric in nature.
The stabilisation and the characterisation of the tetraoxolene radical trianion was made using metal-tetraazamacrocycle acceptors [36]. Indeed, metal complexes of formula M2(CTH)2(DHBQ)Y3 (M = Cr, Fe; CTH = dl-5,7,7,12,14,14-hexamethyl-1,4,8,11-tetraazacyclotetradecane; Y = ClO4, PF6) were prepared and their physical properties showed that these compounds contain the radical species DHBQ3– bridging the tripositive metal ions. Their magnetic and ESR properties are consistent with a S = 5/2 and S = 9/2 ground state for chromium(III) and iron(III) derivatives, respectively, as a result of a strong antiferromagnetic coupling between the metal ions and the bridging radical. The observed J values (H = J SMet SRad) were 273 cm–1 and 372 cm–1 for chromium and iron, respectively.
The failure in synthesising crystalline polynuclear systems by using the above tetraoxolene ligand induced us to design another molecule in which two dioxolene rings were directly linked by a C–C bond. The bis-5,5′-tert-butyl-3,3′,4,4′-tetrahydroxybiphenyl may also yield a five-member redox chain, as shown in Fig. 2, in which all the members are able to act as bis-bidentate ligands. The electronic properties of this ‘ligand’ are expected to be strongly dependent on the dihedral angle between the dioxolene planes [10, 37–39]. Indeed, π conjugation is expected to be operative when the dihedral angle is different from 90°. In this case, the dinegative member is expected to be diamagnetic, but if the torsion angle reaches a value close to 90°, the molecule should be characterised by a triplet ground state. In addition, the mononegative Q–SQ and trinegative SQ–Cat are radical ligands and they can be classified as class-II or class-III mixed valence systems in the Robin and Day sense depending on the electronic coupling between the two ligand moieties [40]. This is particularly interesting since in the former case, they can be potentially used as molecular switches, whereas in the latter its use for the preparation of extended molecule-based magnetic materials or molecular wires can be proposed. With this in mind, we have synthesised the above ligand as well their dinuclear nickel(II), chromium(III) and cobalt(III) derivatives, using again the tetraazamacrocycle CTH as ancillary ligand. These complexes are postulated to contain dinuclear cations in which the metal ions are bridged by the bis-bidentate bis-dioxolene anion. The remaining coordination sites are occupied by the macrocyclic ligand, which assumes a folded conformation.
The magnetic properties of the Ni2(CTH)2(SQ–SQ)(PF6)2 complex show that the bis-dioxolene bridging ligand is diamagnetic, as expected [41]. Indeed, the χT value at room temperature is 2.1 emu K mol–1, as expected for two uncoupled S = 1 nickel(II) ions. With decreasing temperature, χT decreases, indicating a weak antiferromagnetic coupling between the two bis-dioxolene bridged metal ions. Similar conclusions can be drawn from the physical properties of the cobalt(III) and chromium(III) analogues, whose characterisation was limited to the respective solutions.
The redox properties of this bis-dioxolene ligand do not allow the easy isolation of dinuclear nickel(II) derivatives containing the trinegative SQ–Cat mixed-valence radical. This was obtained using metal acceptors with a higher formal oxidation state with respect to nickel(II), i.e. chromium(III) and cobalt(III). In addition to compounds of formula M2(CTH)2(Cat–Cat)(PF6)2, showing the expected properties of dinuclear complexes bridged by a diamagnetic ligand, complexes of formula M2(CTH)2(SQ–Cat)(PF6)3 were also obtained. Electrochemical data show that this compound is particularly stable towards disproportionation, the equilibrium constant for the equilibrium
The ESR spectrum of the cobalt complex in fluid solution is shown in Fig. 3. The spectrum consists of 17 equally spaced lines. We attributed this feature to the hyperfine coupling of the completely delocalized unpaired electron of the bridging ligand with two equivalent metal ions and with two equivalent 1H atoms. A good simulation was obtained by assuming giso = 2.00, aCo = 4.2 G, and and aH = 2.6 G. The observed cobalt coupling constant is approximately the half of those observed for similar mononuclear cobalt(III)-semiquinonato adducts. The ESR spectrum of the chromium(III) complex is consistent with a S = 5/2 ground state (see below).
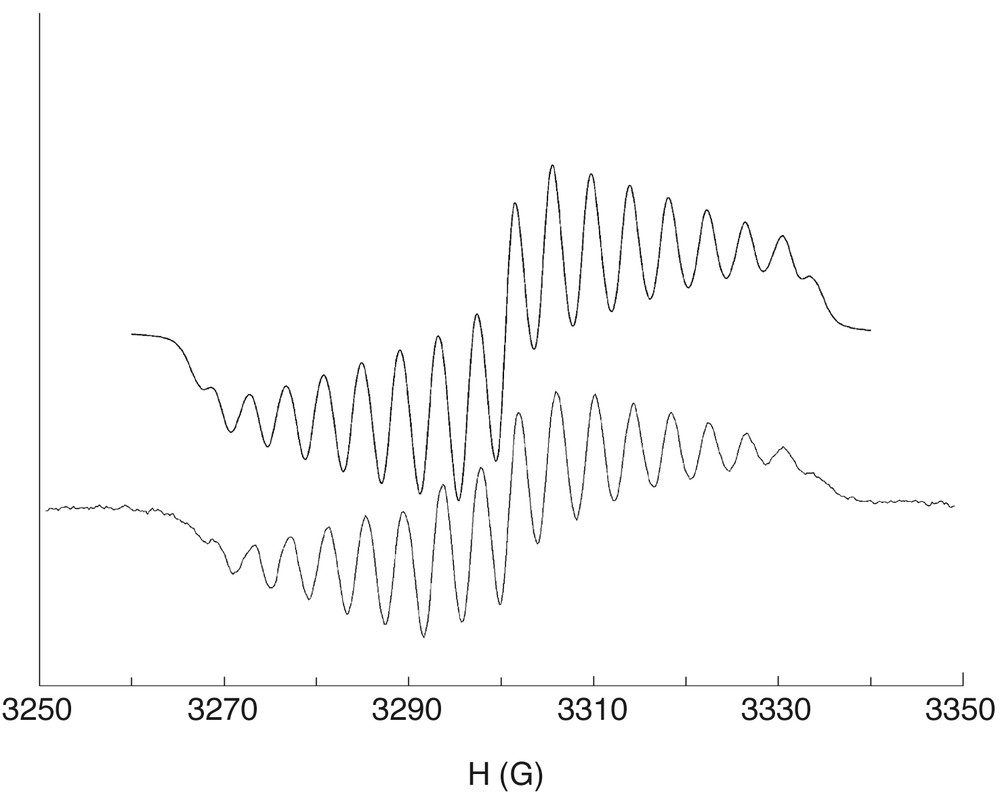
EPR spectrum of the Co2(CTH)2(Cat–SQ)3+ cation in 1,2-dichloroethane (lower curve experimental, upper simulation).
The temperature dependence of the magnetic susceptibility of the chromium derivative is shown in Fig. 4. The solid line represents the fitting of the magnetic data using the spin Hamiltonian:
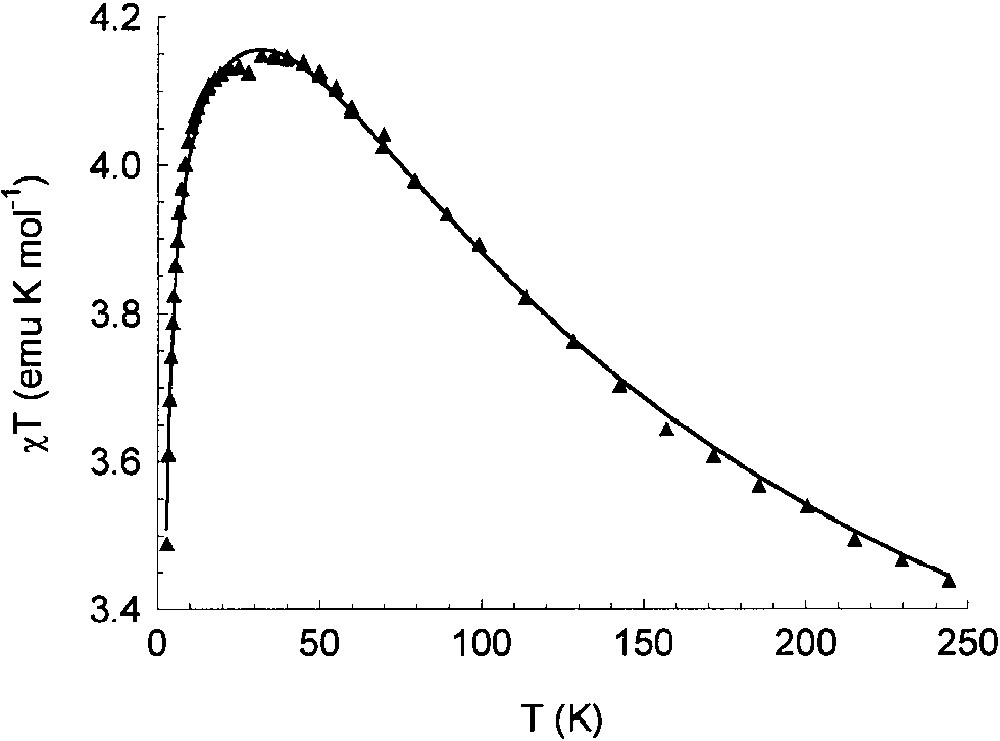
Temperature dependence of χT for the Cr2(CTH)2(Cat–SQ)(PF6)3 complex. Continuous line is the best-fit curve obtained with the parameters reported in the text.
In order to reach a better characterisation of these complexes, a DFT investigation was carried out. The calculated optimised geometry of a model radical SQ–Cat3– ligand showed that the two aromatic rings are not coplanar, their dihedral angle being 9°. However, when the same procedure was carried out for the model complex Co(NH3)4(SQ–Cat)Co(NH3)43+, some relevant geometrical differences were observed. The two dioxolene rings are significantly non-coplanar, the dihedral angle being 47°. The calculated Co–O and C–O bond lengths are intermediate between those expected for Co(III)-catecholato and Co(III)-semiquinonato complex, thus indicating a delocalised character of the unpaired electron. The SOMO orbital is close to the SOMO of the free ligand, with a small contribution from 3dπ orbitals of the metal ions. It should be stressed that ring-linking C–C bond was calculated to be shorter than expected for a single bond (1.46 vs. 1.49 Å), but considerably longer than expected for a double bond. Calculations show also that the delocalized character of the radical ligand can be removed when the dihedral angle between the dioxolene planes reaches the value of 90°. Both the ESR spectra and the magnetic properties of the chromium(III) complex were satisfactorily simulated by assuming the class III nature of the mixed valence ligand. The possibility of using this delocalized radical ligand as bridging linker between paramagnetic metal ions in order to assemble extended structures is under investigation.
As far as ferromagnetic coupling between radical moieties is needed, the most common approach is to attach the spin bearing units to a π system acting as an appropriate coupler [10]. The large amount of work developed by the organic chemists in the characterisation of the so-called non-Kekulè hydrocarbons provides the basis for the design of ferromagnetically-coupled bis- and tris-semiquinonate [43]. Indeed it has been shown that the non-Kekulè hydrocarbons 1,3-dimethylenebenzene and 1,3,5-trimethylenebenzene exhibit triplet and quartet electronic ground states, respectively. The corresponding dioxolene-substituted molecules 1,3-bis(3′,4′-dihydroxy-5′-tert-butylphenyl)-5-tert-butyl-benzene (m-Ph(CatH2) and 1,3,5-tris(3′,4′-dihydroxy-5′-tert-butylphenyl)benzene (Figs. 5 and 6) were prepared with the purpose of isolating the corresponding bis- and tris-semiquinonato derivatives of suitable paramagnetic acceptors. Our goal was to exploit the potential intramolecular ferromagnetic coupling of the semiquinonato ligands for enforcing the achievement of high-spin multiplicity in their metal derivatives.
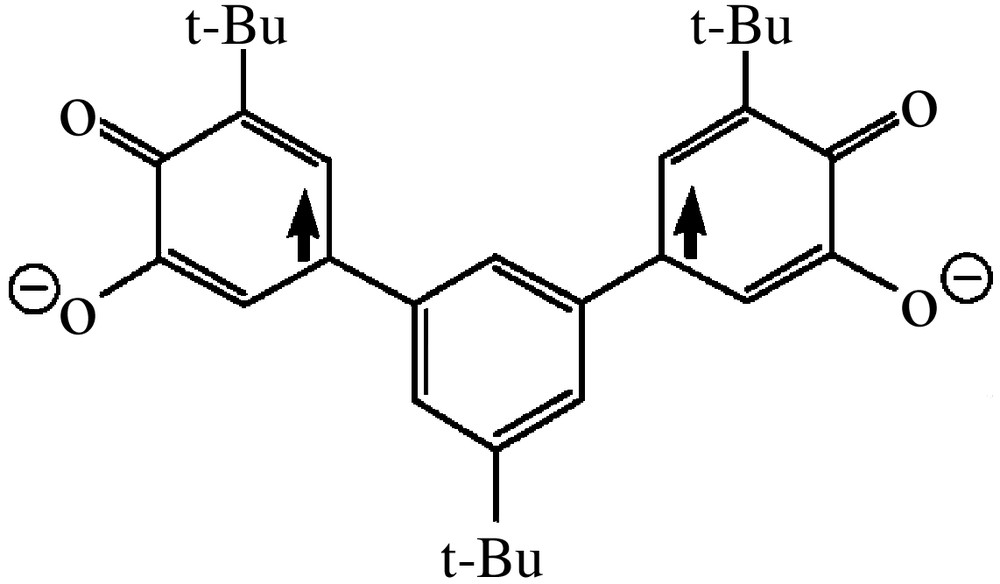
In the past, some of us have shown that the complexes Ni(CTH)(DBSQ)PF6 (see above for CTH and DBSQ) and Cu(Me3[12]N3)(DBSQ)ClO4 (Me3[12]N3 = triazamacrocycle) are characterised by quartet and triplet ground states respectively, arising from the ferromagnetic coupling of the metal ions with the radical ligand [44, 45]. In a similar fashion, the Cr(CTH)(DBSQ)(PF6)2 was shown to be a triplet ground state, arising from the antiferromagnetic coupling of the two magnetic centres [46]. On the basis of these results, the corresponding dinuclear complexes using the bis-dioxolene ligand above described were prepared as bis-semiquinonato derivatives [47].
The optical and electrochemistry properties of these complexes of general formula M2L2(mPh(SQ)2(PF6)2 (M = Cr, Ni, L = CTH; M = Cu, L = Me3[12]N3) were found to be strictly similar to those of the previously reported mononuclear complexes, but their magnetic properties showed very interesting differences. The temperature dependence of the magnetic susceptibilities of the three derivatives is shown in Fig. 7. According to the postulated dinuclear structure, we have fit the experimental data with the exchange Hamiltonian:
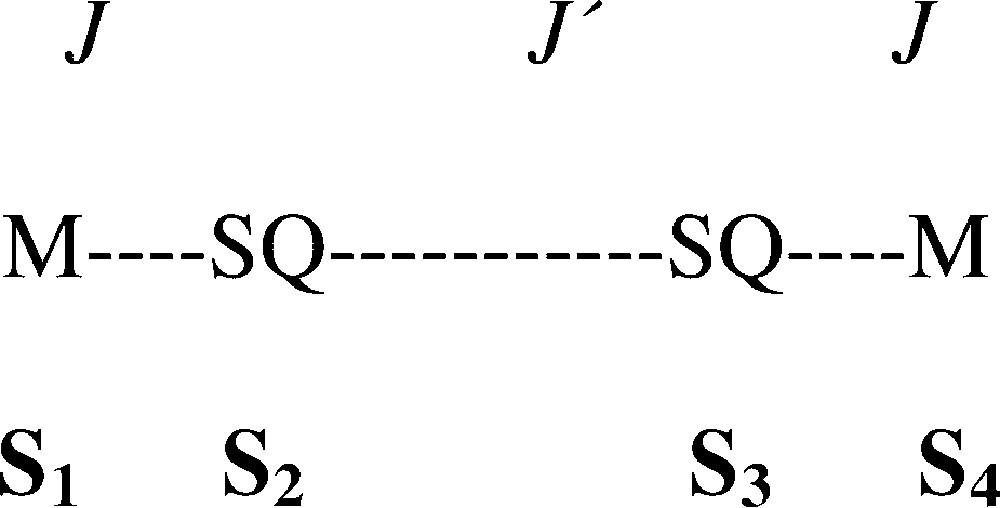
The magnetic behaviour of the nickel derivative is consistent with an incompletely populated septet electronic ground state arising from the ferromagnetic coupling of the four magnetic canters. As shown in Fig. 8, a value of 4.9 emu K mol–1 characterises this compound at room temperature, thus χT increases with decreasing temperature, reaching a value of 6.2 emu K mol–1 at 11 K (1 T). The fitting values obtained in the assumption of isotropic coupling and a weak intermolecular interaction were g = 2.22, J < –400 cm–1 and J′ = –27 cm–1. Therefore, in addition to the strong ferromagnetic coupling characterising the nickel–semiquinonato complexes, as observed in the mononuclear derivatives, the topology of the ligand induces as desired a further correlation between the two paramagnetic moieties, thus enforcing the high-multiplicity ground state of the system. It should be noted that with the observed parameters, a quintet state lies only 9 cm–1 above the ground state and further triplet and singlet states are lying above 18 cm–1. The low experimental value of χT can then attributed to the incomplete population of the electronic ground state. This suggestion is supported by magnetisation experiments which show a saturation value of 6.5 μB at 7 T and 2.1 K in full agreement with the expectations of an S = 3 ground state.
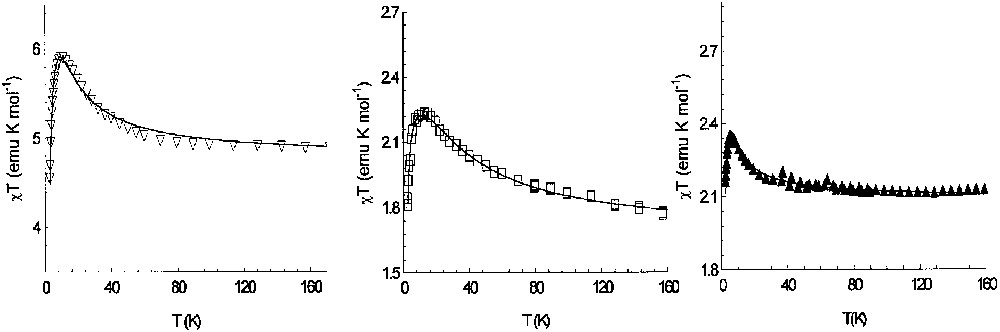
Temperature dependence of χT and best-fit curves for the M2(CTH)2(m-Ph(SQ)2)(PF6)n complexes (see text for details): M = Ni(II) left, Cu(II) centre, Cr(III) right.
The analysis of the magnetic properties of the copper and chromium derivatives yielded similar results. The best fit parameters for the copper compound were g = 2.106, J = –35 cm–1 and J′ = –6.3 cm–1, thus indicating a quintet ground state, whereas for the chromium one we found g = 1.99, J > 400 cm–1 and J′ = –32 cm–1, again in agreement with the expected quintet ground state.
These results therefore show that the intraligand exchange coupling in m-Ph(SQ)2 is ferromagnetic, in agreement with the connectivity of the spin coupler. However the observed exchange coupling values are smaller than expected. In agreement with the observed J-modulation due to bond torsion in organic diradicals, we proposed that the non-coplanarity of the semiquinonato and meta-phenylene planes is responsible for the small observed J′ values. This finding is in agreement with the conclusions of an investigation on dioxolene bridged dimolybdenum(V) complexes [48].
The strategy of topologically predetermining the high-spin multiplicity ground states of paramagnetic metal complexes by using a properly designed polyradical is supported by the results obtained with the above-mentioned tris-dioxolene ligand (Fig. 9). In order to facilitate the analysis of magnetic data, we have investigated tris-semiquinonato derivatives of two metal acceptors characterised by non-degenerate electronic ground states, i.e. high-spin pseudooctahedral nickel(II) and five-coordinate manganese(II) [49]. Indeed, the complexes [Ni3(CTH)3(TBSQ3)Ph](PF6)3 and Mn3(TpCum,Me)3(TBSQ3)Ph (TpCum,Me = hydridotris[3-(4'cumenyl)-5-methylpyrazolyl)borate) that we prepared were postulated to contain three six-coordinated nickel(II) and three five-coordinated manganese(II), bridged by the tris-bidentate dioxolene ligand. The features of the electronic spectra and electrochemical data well support the tris-semiquinonato formulation of these adducts.
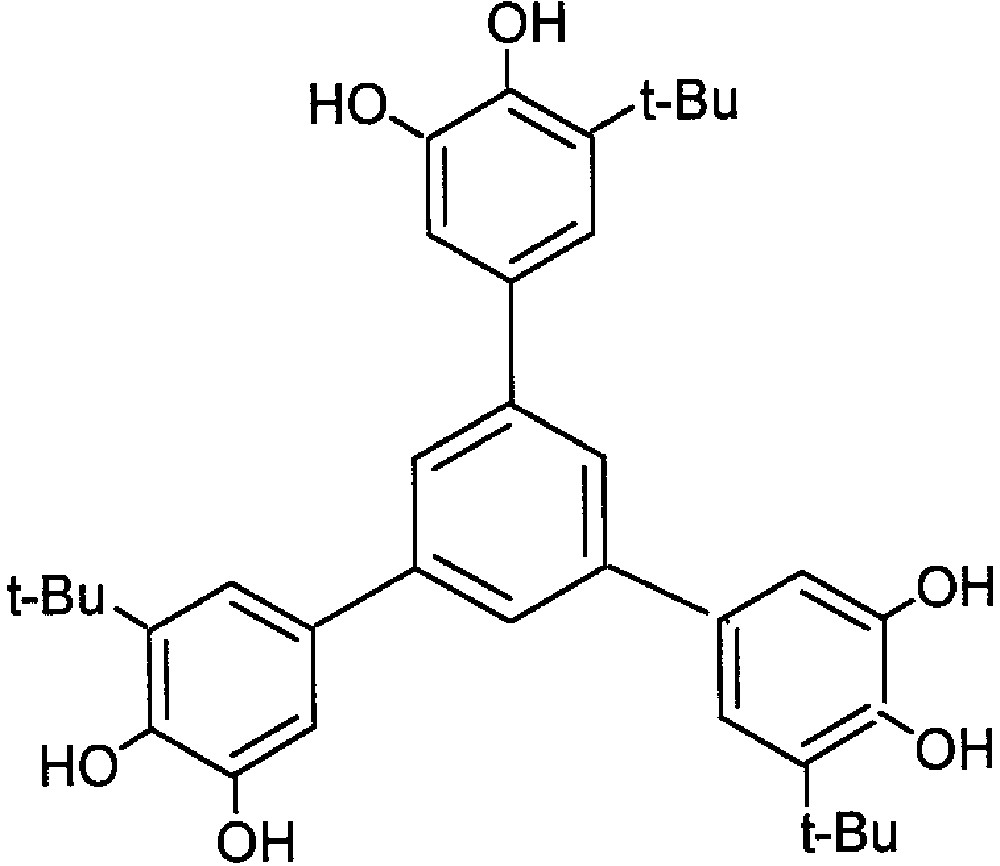
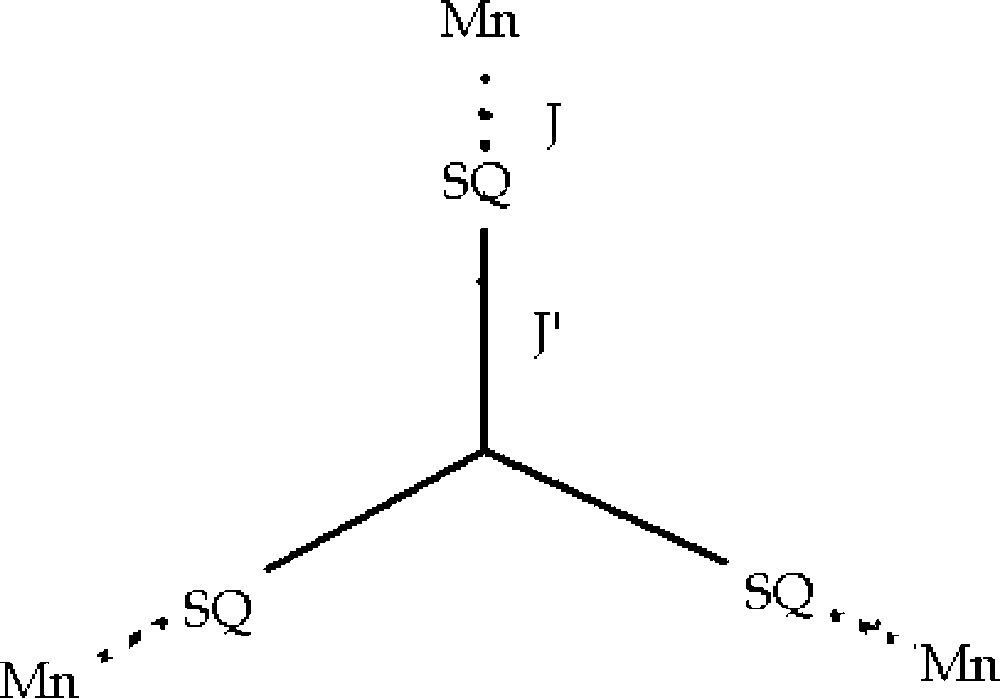
The χT vs T curve for the Mn3(TpCum,Me)3(TBSQ)Ph complex is shown in Fig. 10. At room temperature (300 K), the obtained χT value is 9.07 emu K mol–1. This value is much lower than the expected one for three S = 5/2 and three S = uncorrelated spins (χT = 14.25 emu K mol–1), while is in full agreement with the value expected for three S = 2 spins with g = 2 (9.00 emu K mol–1). On lowering temperature, χT increases, thus reaching a value of 19.7 emu K mol–1 at 2 K. This behaviour suggests the existence of a strong antiferromagnetic coupling between the radical ligand and the metal ions as well as a ferromagnetic coupling between the semiquinonato ligands. The observed low temperature χT value is consistent with an S = 6 ground state; the difference in χT observed vs the theoretical value (21 emu K mol–1) being again explained by assuming an incomplete population of the ground state. This interpretation is supported by magnetisation experiments (12 μB at 6 T) at 2.5 K. The fitting of magnetic data gave J = 350 cm–1 and J' = –40 cm–1 (g = 2.00 fixed) where the two exchange coupling constants are defined in Fig. 11.
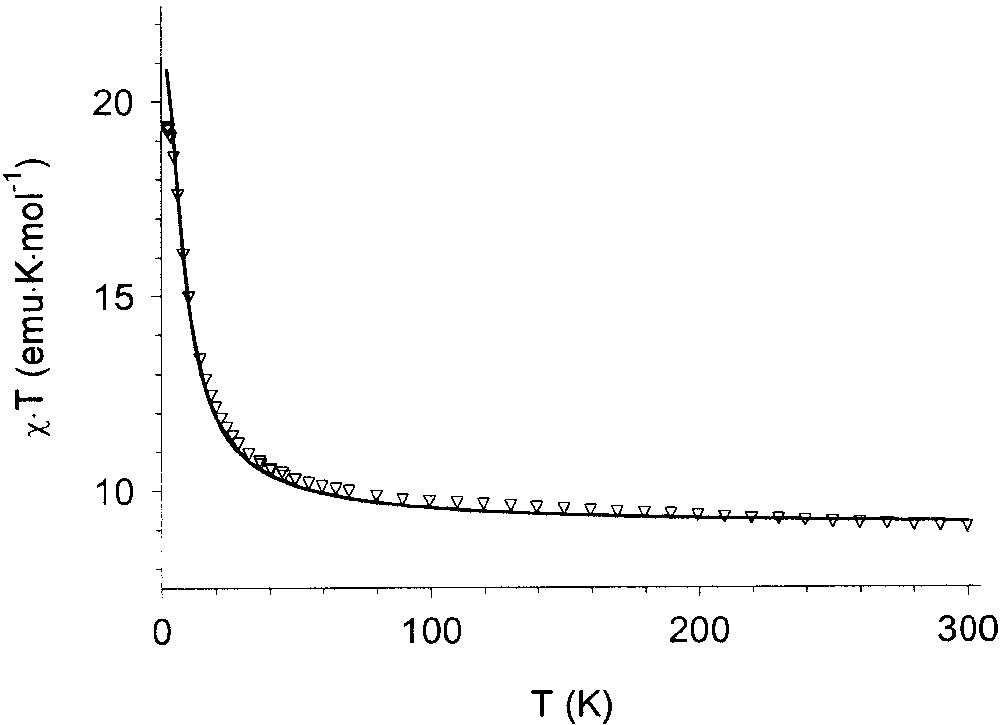
Temperature dependence of χT for the Mn3(CTH)3(TBSQ) complex. The continuous line is the result of the best fit obtained with the model described in the text.
It should be stressed however that a very good fit of the magnetic data can be obtained by assuming the existence of three ferromagnetically interacting S = 2 spins.
The interpretation of the magnetic properties of the nickel(II) complex can be made in a strikingly similar fashion. Fig. 12 shows the χT vs T curve for the nickel complex. The room-temperature value (6.25 emu K mol–1) is higher than expected for three S = 1 and three S = spins uncorrelated, but, taking into account that the mononuclear nickel(II)-semiquinonato derivatives experience ferromagnetic coupling thus showing χT values in the range 2.2–2.3 emu K mol–1, the observed value is close to that expected for the presence of three S = 3/2 uncorrelated spins. On decreasing temperature, the χT value increases, thus reaching a maximum of 10.53 emu K mol–1 at 10 K, and then decreases. The maximum value is lower that the 13.6 emu K mol–1 one expected for a S = 9/2 spin ground state. However, following the considerations above formulated for the Ni2(CTH)2(mPhSQ2) complex, it can be again explained by assuming population of spin states with lower multiplicity. Magnetisation experiments support this hypothesis. The analysis in this case is not straightforward like in the manganese complex because of the existence of non-significant zero-field splitting terms and magnetic anisotropy. Using Fig. 10 above, the following fitting parameters were found: g = 2.14, J = –173 cm–1, J′ = –26 cm–1. The observed g value is in agreement with the expected one related to a nickel(II)-semiquinonato couple according to the relationship gNisq = 2/3gNi – 1/3gsq which yields a gNi = 2.21, as well established for this metal ion in octahedral environment [50].
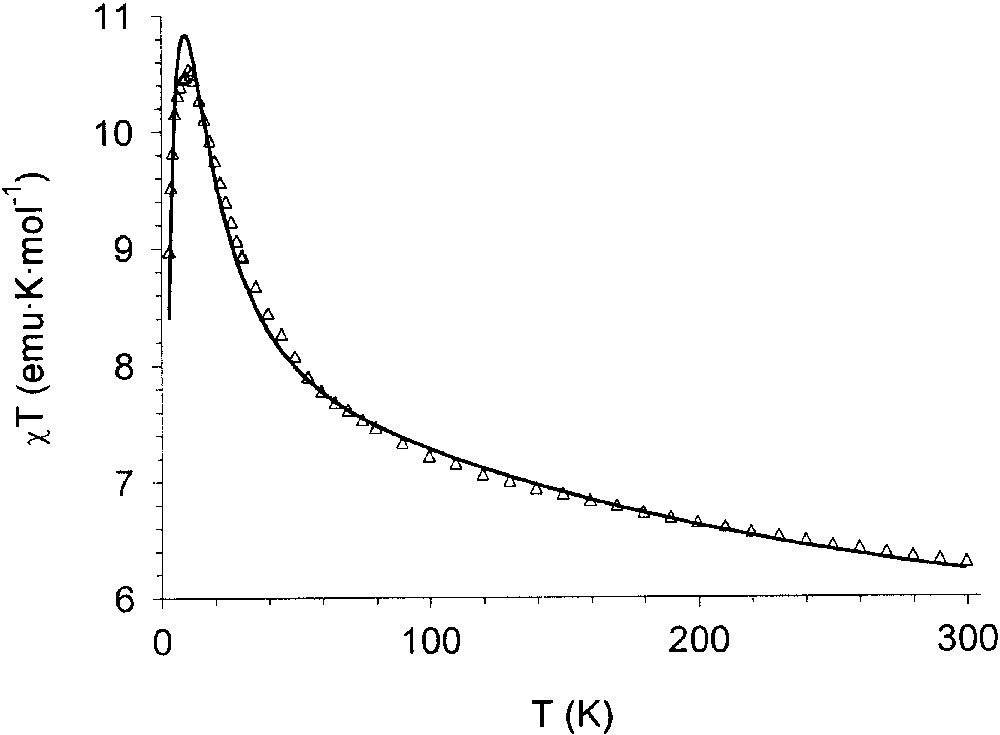
Temperature dependence of χT for the Ni3(CTH)3(TBSQ)(PF6)3 complex. The continuous line is the result of the best fit obtained with the model described in the text.
As observed for the bis-semiquinonato complexes, the low values of the exchange-coupling constant relating the three paramagnetic radicals are expected to be significantly determined by the dihedral angle between the semiquinonato and phenyl planes. This torsion angle is therefore a very important factor as far as the magnetic coupling of coordinated polyradicals is concerned. This point is better shown in the following example of an iminosemiquinonato polyradical system.
4 Polyiminosemiquinonato metal complexes
The non-Kekulè hydrocarbons approach led us to synthesise the ligand N,N′-bis(3,5-di-tert-butyl-2-hydroxyphenyl)-1, 3-phenylenediamine (m-PhCatH2) which once partially or fully deprotonated may act as bis-bidentate ligand towards two different metal ions (Fig. 13). Since the chemistry of this molecule was expected to be similar to that showed by catechols and o-phenylenediamines, it was also expected that this molecule might originate a five-member redox chain similar to the ones previously discussed. The third member of the above redox chain, i.e. the dinegative diradical SQ–SQ species, is expected to be characterised by a triplet ground state according to the non-disjoint character of its non-bonding molecular orbitals [51].
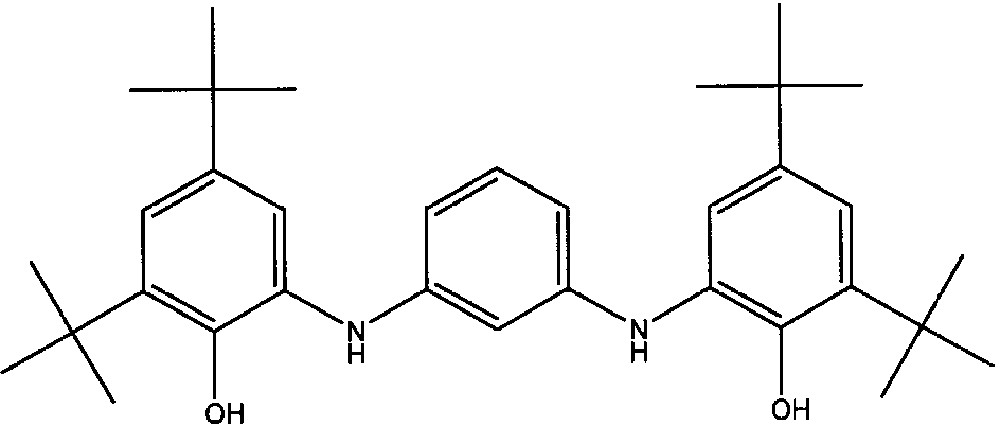
In principle, the possibility of isolating metal-complexes of the SQ–SQ ligand was believed rather stimulating since the coordination of three iminosemiquinonate fragments to one acceptor metal ion may afford two six-coordinated possible isomers, i.e. facial and meridional, as depicted in Fig. 14.
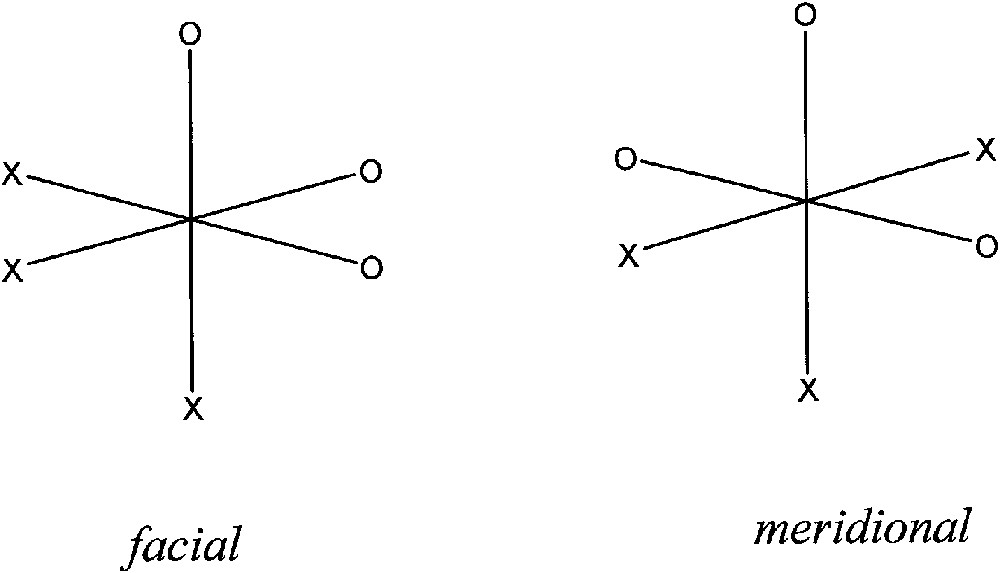
In a recent work, it has also been shown that the Co(SQ)3 complex (SQ = o-iminosemiquinonato) is six-coordinated with the N–O donors adopting a meridional configuration [33]. According to the diamagnetic nature of the low-spin cobalt(III) ion, the complex, as still observed for other tris-semiquinonato metal adducts, is characterised by a quartet ground state as a result of the ferromagnetic coupling between the three paramagnetic radical ligands. It is rather easy to realise that as far the same conformation would be adopted by metal complexes of the m-Ph(SQ)2, a polynuclear network of paramagnetic centres should be obtained.
Bearing this in mind, we have prepared the cobalt complex of analytical formula CoL1.5 [52]. The X-ray crystal structure of the compound is drawn in Fig. 15 and shows that the obtained complex is dinuclear, the three ligands acting as bis-bidentate towards two different cobalt ions. Both the metal ions are facially six-coordinated to deprotonated nitrogen and oxygen donor atoms. The structural parameters are fully consistent with a CoIII(SQ)3 charge distribution of this derivative. In addition it should be stressed out the different character of the two C–N bonds linking the nitrogen donor atom to the iminooxolene and meta-phenylene rings, the first one being 1.34(1) Å (C=N character), whereas the average value of the latter is 1.42(1) Å (C–N character).
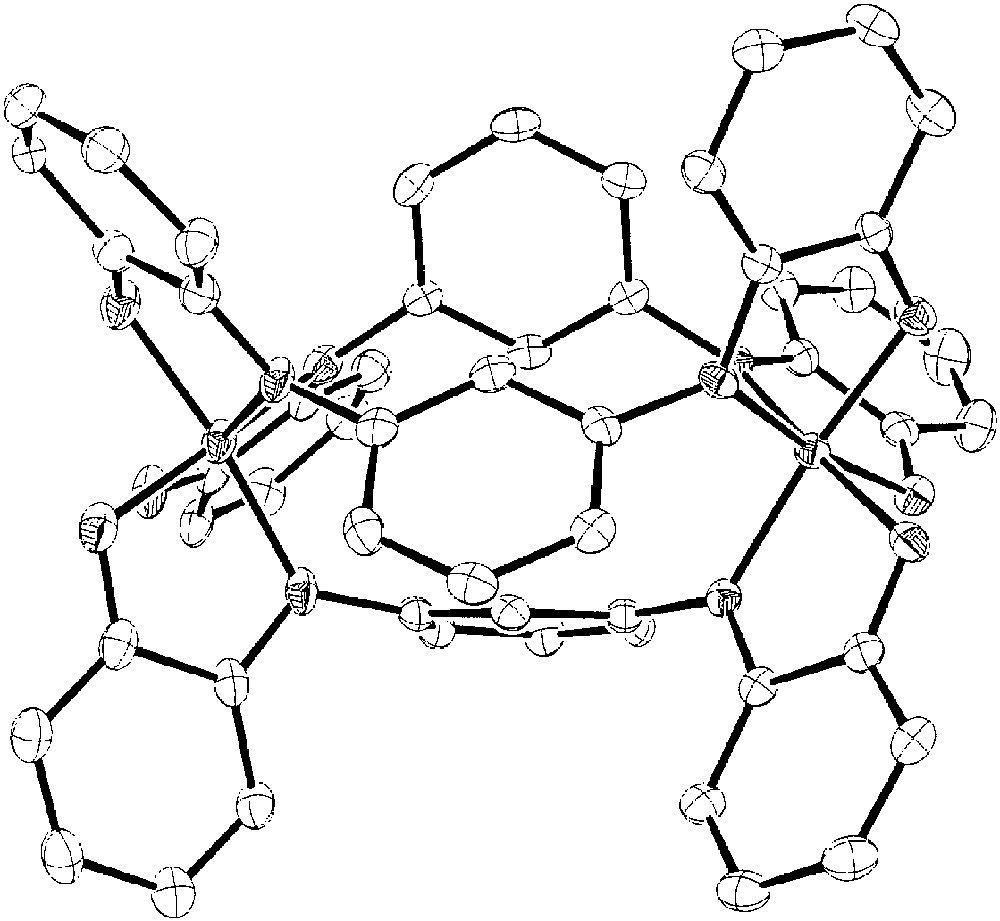
Crystal structure of the Co2(mPh(SQ)2)3 complex.
Another relevant point of this structure is the conformation of the iminosemiquinonato rings with respect to the linker meta-phenylene rings. The dihedral angles between the planes containing the next-neighbour rings are significantly different from those expected for the free ligand (~15–20°), reaching the values of 70–72° as a result of the six-coordinated nature of the metal centre. This is expected to deeply affect the magnetic properties of the bis(iminosemiquinonato) diradical ligand.
The magnetic behaviour of this complex is shown in Fig. 16 as χT vs. T plot. At room temperature (300 K) the χT value is 2.32 emu K mol–1, which is close to the expected one equal to 2.25 emu K mol–1 for six uncorrelated spins S = 1/2, and its tendency is to slowly increase on lowering temperature, thus approaching a maximum of 2.47 emu K mol–1 around 120 K. Below this temperature, there is a decrease of χT, which reaches a value of 0.2 emu K mol–1 at 4 K. Though the crystal structure shows that the iminosemiquinonato donors are not strictly equivalent, a satisfactory fit of the experimental data was obtained by assuming the simplest hamiltonian
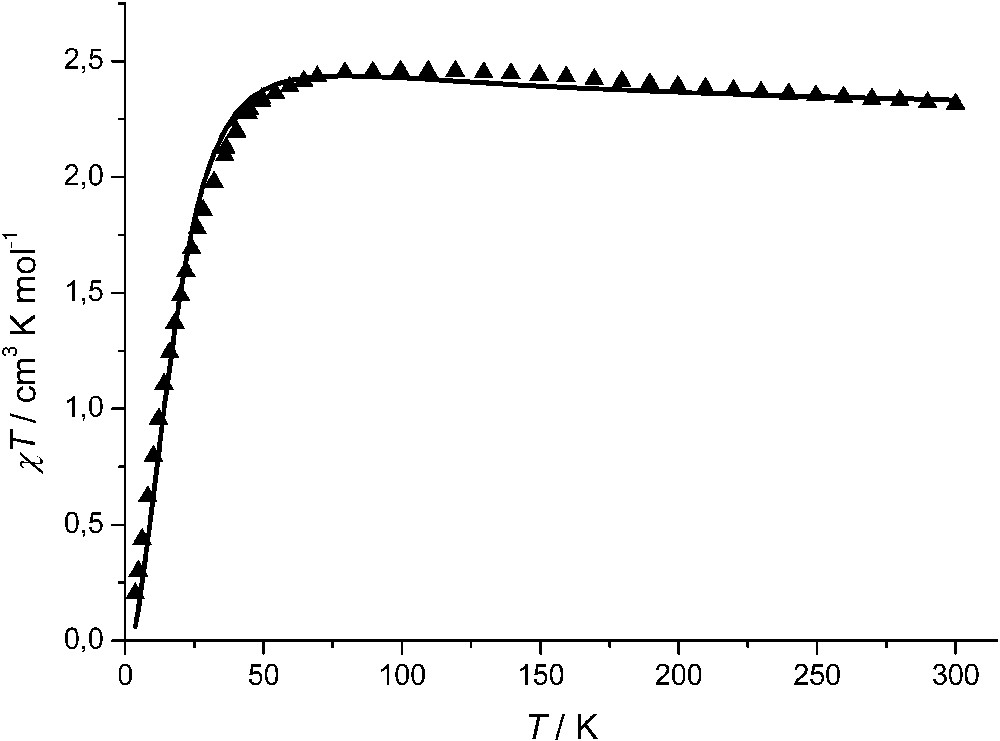
χT vs. T curve for the Co2(mPh(SQ)2)3 complex and best-fit curve (see text for details).
5 Valence tautomerism in cobalt–polydioxolene metal complex
The negligible mixing of metal and ligand orbitals in metal-dioxolene complexes must be considered an oversimplification and holds with sufficient approximation only for 3d and 4f metal complexes. However, within its limits, this approximation allows a simple rationalisation of the physical properties of these complexes, thus leading to the formulation of unusual simple relationships between the magnetic properties, the electronic spectra and the electrochemical properties of a given family of metal derivatives. In addition, the same approximation offered a rationale of a very intriguing phenomenon that has been termed valence tautomerism [16–18, 53, 54]. Following our approach, the concept of valence tautomerism describes an intramolecular electron transfer process between redox isomers under equilibrium conditions. Though the process is the same occurring in optical charge transfer transitions, the phenomenon is relatively rare, since it requires that the two redox isomers are in turn stabilised one with respect to the other depending on an external perturbation, like temperature, pressure or light. The cobalt–dioxolene complexes are the most attractive, since the intramolecular redox equilibrium cobalt(III)–catecholato/cobalt(II)–semiquinonato is associated with a change of the magnetic properties of the complex, the cobalt(III) ion being diamagnetic and the cobalt(II) ion adopting the d7 high-spin configuration (S = 3/2). This electronic lability is considered particularly important in the frame of potential technological application.
Though some recent work shed light on the detailed nature of the phenomenon, as the nature of the electronic ground state of the cobalt(II)-semiquinonato moiety [23], the mechanism of interconversion upon irradiation [55] and the proper molecular orbital description of valence tautomers [56], a necessary prerequisite for its application is the existence of cooperativity in condensed phase, which may induce hysteresis and then information storage.
Valence tautomers showing detectable hysteresis are scarce. A very small hysteresis effect (5 K) was found to characterise the tautomeric interconversion of the CoIII(Phen)(DBCat)(DBSQ)·C6H5CH3 complex (Phen = 1,10-phenanthroline) [57]. Therefore our attention was focused towards the design of molecular assemblies with metal centres mutually interacting through a polymeric structure. With this in mind, we have synthesised the cobalt-1,10-phenanthroline adducts of the tetraoxolene 3,5-bis(3′,4′-dihydroxy-5′-tert-butyl)-1-tert-butyl-benzene [58] (see above) and 3,3,3′,3′-tetramethyl-5,5′,6,6′-spiro-bis-indane. Both ligands may act as bis-bidentate ligands towards two different metal ions (Fig. 17). In addition, once coordinated they may originate by one electron oxidation the trinegative radical anions we indicate as SQ–Cat, which we suppose may act as Class-II mixed-valence radical. A further one electron oxidation yields in both cases the SQ–SQ ligands, the meta-phenylene being characterised by triplet ground state, whereas the latter one is expected to show singlet ground state, due to the weak antiferromagnetic coupling between the two semiquinonato halves. Two complexes of general formula Co(Phen)(tetrox)·n CH2Cl2 were obtained, which were found to be insoluble in all common organic solvents. They were postulated to contain a six-coordinated cobalt ion, like all the Co(N–N)(diox)2 previously described, the main difference being that each dioxolene is paramagnetic and coordinated to two different metal ions.
The temperature-dependent magnetic behaviours of the two complexes are shown in Figs. 18 and 19. The observed magnetic properties are consistent with the presence of a CoIII(SQ–Cat) dominant species at low temperatures, undergoing a thermally driven valence tautomeric transition to hs-CoII(SQ–SQ), according to the equilibrium:
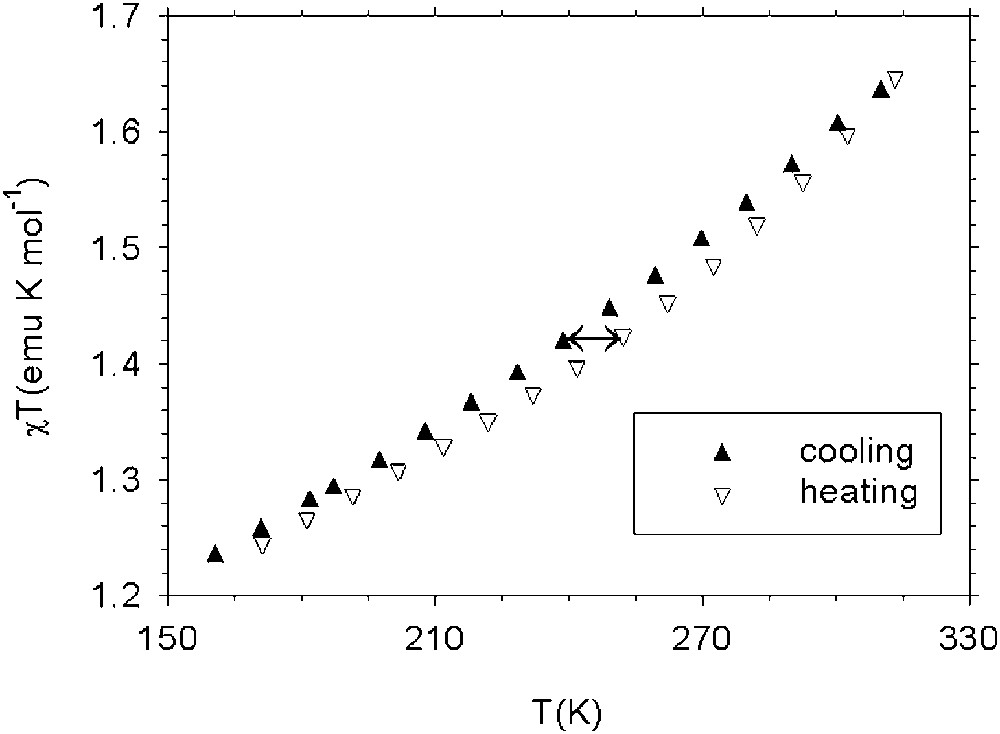
Temperature dependence of χT product for the Co(mPh(SQ)2(phen) complex when heating (empty triangles) and cooling (full triangles).
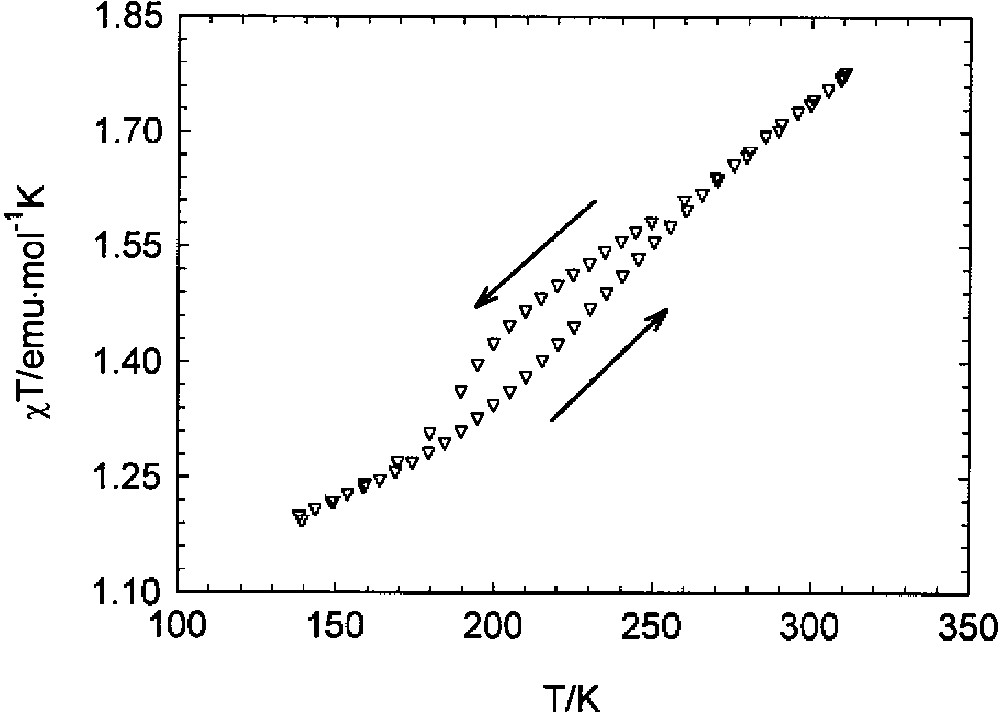
Temperature dependence of χT for the Co(spiro-Ph(SQ)2(phen) complex when heating and cooling (see the arrows).
Using the current nomenclature for spin crossover systems in both cases, the transitions can be classified as gradual and at 310 K, the highest temperature we have measured, both the observed transitions are far from being complete. Nevertheless, for the meta-phenylene derivative, a thermal hysteresis width of about 12 K is observed, though the optimum conditions for observing this phenomenon are not reached. For the spiro-bis-indane derivative, a transition with a thermal hysteresis of 22 K is observed, although the nature of the transition is unclear. The observed hysteresis loops are suggested to be a consequence of the strong cooperativity shown by these compounds, a property we were looking for in designing these molecular systems. The synthesis of similar systems using different poly-bidentate dioxolene ligands and diazine coligands are in progress.
6 Conclusions
The examples here reported show how an appropriate strategy in designing linked semiquinonate can be used to fix the magnetic properties of a collection of paramagnetic centres. The examples we have described indicate how the use of tetraoxolene radicals and bis- and tris-semiquinonato designed according to the non-Kekulè polyradical scheme may enforce the high-spin ground state of complexes formed by paramagnetic acceptors like 3d metal ions. Indeed the magnetic coupling occurring within the tris-semiquinonato ligand has been show to induce an S = 9/2 ground state when coordinated to three nickel(II) ions and an S = 6 ground state when coordinated to three manganese(II) ions, thus showing how an appropriate linker between the paramagnetic centres may propagate the predicted and desired magnetic interactions. On the other hand, the results we have obtained with the bis-iminosemiquinonato show how important the geometrical constraints can be as required by coordination. At this step therefore, there is the problem concerning the possibility of the utilisation of these systems as building blocks for a network coordination polymer. In this sense, a first result in this direction is the synthesis and characterisation of polymeric systems cobalt–dioxolene systems undergoing valence tautomerism. In this respect, the most significant property is the existence of strong cooperativity shown by the valence interconversion process, a property that we were looking for in designing these systems. We believe that this is induced by the existence of a polymeric structure, which in turn is due to the use of bis-bidentate character of the ligands we use. As a whole, these results should be considered as algorithms of a more complex design to be developed, in which it is possible to prepare families of polynuclear metal-polyoxolene complexes, whose magnetic properties can be predicted with a satisfying degree of approximation. Beyond any obtuse enthusiastic positivistic purpose, this feeling is supported by several results we have recently obtained on other systems, whose characterisation is in progress.
Acknowledgements
Financial support by MURST and Italian CNR, and by EC through TMR programs 3MD (No. ERB4061PL97-0197) and MONANOMAG (No. HPRN-CT-1999-00012) is gratefully acknowledged. D.A.S. thanks N.S.F. and the Petroleum Research Foundation for financial support. M.G.F. Vaz gratefully acknowledges the Brazilian Conselho Nacional de Desenvolvimento Cientifico e Tecnologico (CNPq).


