1 Introduction
C2 is a peculiar simple diatomic molecule [1]. Taken alone, it is not very stable although it can be generated in a carbon arc, is found in comets, or is responsible for the blue light we see in flames. It looks like a dumb-bell in which the two carbon atoms are separated from 1.24 Å in the ground state. Such a molecule can easily be stabilised by other atoms or group of atoms. In the realm of organic chemistry, it is contained in ethane, ethene, and acetylene, molecules which are the archetypical references for carbon–carbon single (1.54 Å), double (1.34 Å), and triple (1.20 Å) bonds, respectively. C2 units are also found in solid state chemistry [2], with different C–C separations depending on its formal electron count, leading to their interpretation as deprotonated ethyne, ethane or acetylene. For instance, a triple bond (1.19 Å) is assumed in CaC2 (Ca2+C22–). In Gd2Cl2C2 [(Gd3+)2(Cl–)2(C24–)2] [3], the C–C distance in the C2 units which reside in octahedral cavities is 1.36 Å, corresponding to a double bond. A C–C single bond (1.47 Å) is observed in Gd10Cl18C4 clusters, compatible with the presence of C26– fragments within octahedral metallic cages [(Gd3+)10(Cl–)18(C26–)2] [2b,4]. C2 can also be observed in numerous molecular organometallic compounds [5]. C2 can span two mononuclear metal fragments as in [ScCp*2]2(μ-C2) (Cp* = C5Me5) [6]. Five metallic atoms are caught in huddling around an exposed C2 fragment in the cluster Ru5(CO)11(μ-PPh2)2(μ-SMe)2(μ5-η4:η5-C2) [7]. C2 can also be fully encapsulated in a metallic cage as in [Co6Ni2(CO)16(μ8-η6:η6-C2)]2– [8].
As in organic or solid state chemistry, the C–C bond length largely varies in these organometallic systems, and different electronic structures can be assigned on the basis of the C–C distance, which can be related to those in acetylene, ethene or ethane or as well. A carbon–carbon separation corresponding to a triple bond is observed in [ScCp*2]2(μ-C2) [6] (1.22 Å) or [Ru(CO)2Cp]2(μ-C2) [9] (1.19 Å) complexes, whereas the C–C bond length of 1.37 Å measured in the binuclear species [Ta(t-Bu3SiO)3]2(μ-C2) [10] is more consistent with a C–C double bond. A C–C distance of 1.38 Å observed in [W(t-Bu3O)3]2(μ-C2) is rather assigned to a single bond [11]. C–C bond distances are generally more spread out when the number of metal atoms around the C2 unit increases as in Ru5(CO)11(μ-PPh2)2(μ-SMe)2(μ5-C2) (dC–C = 1.305 Å) or [Co6Ni2(CO)16(μ8-C2)]2– (dC–C = 1.48 Å) previously mentioned. The analogy between this type of compounds and purely organic or inorganic compounds is then less straightforward. Nevertheless, theoretical studies carried out on these high-nuclearity species by Halet and coworkers have shown that the bonding of C2 with its metallic host follows the Dewar–Chatt–Ducanson model, resulting from an important forward electronic donation from occupied orbitals of the C2 fragment toward acceptor metallic molecular orbitals (MO), but also from a back-donation from metallic orbitals into vacant C2 orbitals [12]. Such a bonding mode is in turn comparable to that previously established for acetylenic complexes [13] and absorbed acetylene on metallic surfaces [14].
Following these previous studies carried out on encapsulated and exposed C2-containing organometallic compounds [12], we have recently investigated the bonding and electronic structure of dinuclear (MLn)2(μ-C2) complexes in which the C2 entity is both end-capped by a metallic fragment. These compounds are of interest being thought as models for molecular-scale wires [5]. We report in this paper the main results obtained via extended Hückel theory (EHT) and density functional-theory (DFT) calculations on homometallic compounds containing metal fragments with π-acceptor ligands such as [Ru(CO)2Cp]2(μ-C2) [9] which have been little studied [15,16]. Dinuclear compounds with π-donor ligands such as [W(t-Bu3O)3]2(μ-C2) have not been considered, having been extensively studied previously [10b,11b,17].
2 Structural considerations and electron counts
Several homo- and hetero-dinuclear (MLn)2(μ-C2) complexes have been structurally characterised. They are reported in Table 1. In all those with π-acceptor ligands (top of Table 1), a nearly linear M–C–C–M backbone is found and a short carbon–carbon distance, ca. 1.20–1.25 Å, is measured. On the basis of such a C–C separation, the electronic structure of these compounds seems consistent with valence bond structure A rather than valence bond structures B or C (see Scheme 1) which feature compounds with π-donor ligands.
X-ray characterised acetylide-bridged organometallic binuclear complexes (MLn)2(μ-C2)
| Compound, structure typea | Metal d configuration | dC–C (Å) | References |
| Homo-dinuclear compounds with π-acceptor ligands | |||
| [ScCp*2]2(μ-C2), A | d0 | 1.224(9) | [6] |
| [SmCp*2(THF)]2(μ-C2), A | d0 | 1.213(10) | [18] |
| [TiCp2(PMe3)]2(μ-C2), A/Ba | d1 | 1.253(2) | [19] |
| [ZrCp2C(SiMe3)CH(SiMe3)]2(μ-C2), A | d0 | 1.212(12) | [20] |
| [ZrCp2NH(t-Bu)]2(μ-C2), A | d0 | 1.226(7) | [21] |
| [HfCp*2(CCH)]2(μ-C2), A | d0 | 1.24(3) | [22] |
| [W(CO)3Cp]2(μ-C2), A | d4 | 1.18(3) | [23] |
| [W(CO)3(η5-C5H4Me)]2(μ-C2), A | d4 | 1.216(9) | [24] |
| [Mn(CO)5]2(μ-C2), A | d6 | 1.201(2) | [25] |
| [Re(CO)5]2(μ-C2), A | d6 | 1.195(33) | [26] |
| [Fe(CO)2Cp*]2(μ-C2), A | d6 | 1.206(6)/1.211(6) | [27] |
| [Ru(CO)2Cp]2(μ-C2), A | d6 | 1.19(1) | [9] |
| [Ru(PPh3)2Cp]2(μ-C2), A | d6 | 1.230(7) | [28] |
| [Pt(PMe3)2I]2(μ-C2), A | d8 | 1.179(48) | [29] |
| [Pt(PPh3)2Cl]2(μ-C2), A | d8 | 1.221(9) | [30] |
| [(OC)(C6F5)2Pt][{C(Me)OEt}(PEt3)2Pt]μ-C2), A | d8 | 1.22(3) | [31] |
| {[Pt(t-Bu-tpy)]2(μ-C2)}2+, A | d8 | 1.118(11) | [32] |
| [Au(PMe3)]2(μ-C2), A | d10 | 1.21(2) | [33] |
| [Au(PEt3)]2(μ-C2), A | d10 | 1.21(2) | [33] |
| [Au(PPhMe2)]2(μ-C2), A | d10 | 1.216(7) | [33] |
| [Au(P(C6H5-3)3]2(μ-C2), A | d10 | 1.19(2) | [34] |
| [Au(P(C6H4Me-3)3]2(μ-C2), A | d10 | 1.19(2) | [34] |
| [Au(PCy3)]2(μ-C2), A | d10 | 1.19(1) | [35] |
| [AuPPh(naphthyl)2]2(μ-C2), A | d10 | 1.225(34) | [36,37] |
| [AuPPh2(naphthyl)]2(μ-C2), A | d10 | 1.222(16) | [36,37] |
| [AuPPhFc2]2(μ-C2), A | d10 | 1.196(12) | [37] |
| Homo-dinuclear compounds with π-donor ligands | |||
| [Ta(t-Bu3SiO)3]2(μ-C2), B | d0 | 1.37(4) | [10] |
| [W(t-BuO)3]2(μ-C2), C | d0 | 1.38(2)/1.34(3) | [11] |
| Hetero-dinuclear compounds | |||
| [RuCp(PMe3)][ZrClCp2] 2(μ-C2), A | d0/d6 | 1.251(20) | [38] |
| [ReCp*(NO)5PPh3][Pd(PEt3)2Cl](μ-C2), A | d6/d8 | 1.21(1) | [39] |
a See text.
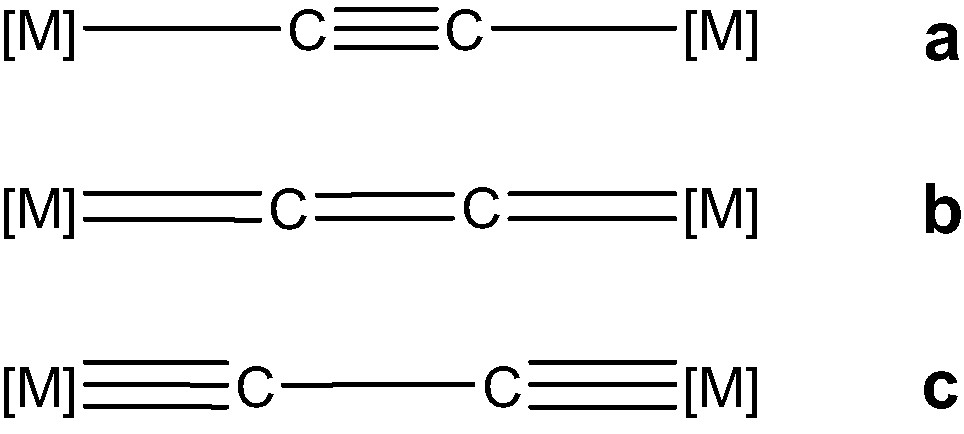
(MLn)2(μ-C2) complexes under investigation, i.e. those with π-acceptor ligands, can be divided in few groups depending on the nature of the metal, its electronic configuration and the number of surrounding ancillary ligands L. A partition according to the metal d configuration gives five groups. Note that this configuration is obtained assuming C22– ethynediide dianion. One group is made by early-transition metals (scandium and titanium triads) with a d0 or d1 configuration. Molecules in this group consist of Cp2M or Cp2ML fragments bonded to the C2 bridge. Interestingly, they do not conform to the 18-electron rule. Formal counts of 14 and 16 electrons are achieved for the scandium and samarium compounds, respectively. For the titanium triad compounds, a count of 16 electrons is also obtained for the Ti heavy congeners, Zr and Hf, whereas for titanium itself, a formal count of 17 electrons is reached assuming C22–. Compounds with mid-transition metal (chromium triad) contain d4 ML6 fragments framing the C2 dumb-bell. They conform to the 18-electron rule. This is also the case for compounds made by mid-to-late transition metals (manganese and iron triads), which are built from pseudo-octahedral d6 ML5 fragments. A 16-electron configuration for each metal is achieved for species containing T-shaped late transition metal (platinum) d8 ML3 fragments linked to C2. Finally, the last group is constituted of molecules with very-late transition metal (gold) d10 M–L fragments. In the latter species, each metal in linear L–M–L′ conformation bears 14 electrons.
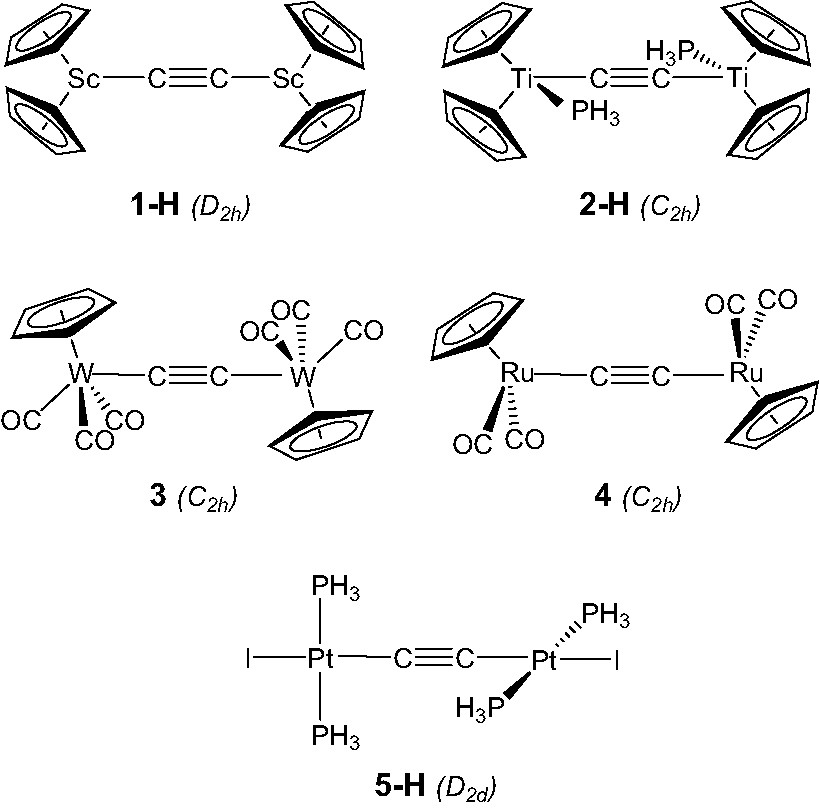
EHT and DFT calculations were carried out on complexes belonging to different groups (see the Appendix) in order to provide particular insight regarding various marked differences (if any) between this series of complexes. In order to reduce the computational effort, calculations were conducted on complex models [ScCp2]2(μ-C2) (1-H), [TiCp2(PH3)]2(μ-C2) (2-H), and [Pt(PH3)2I]2(μ-C2) (5-H) used to mimic [ScCp*2]2(μ-C2) [6] (1), [TiCp2(PMe3)]2(μ-C2) [19], (2), and [Pt(PMe3)2I]2(μ-C2) [29] (5), respectively, as well as on complexes [W(CO)3Cp]2(μ-C2) [23] (3) and [Ru(CO)2Cp]2(μ-C2) [9] (4). Calculations were made with symmetry constraints: D2h symmetry for 1-H, C2h symmetry for 2-H, 3 and 4, and D2d symmetry for 5-H (see Scheme 2).
3 Qualitative MO analysis
Before discussing DFT results concerning the bonding in these complexes, we think that a qualitative analysis based upon EHT offers an instructive general perspective. Indeed, the bonding between the C2 dumb-bell and metallic termini can qualitatively be understood using the frontier molecular orbitals (FMO) of the C22– dianion and two cationic organometallic fragments. Let us remind first that the former fragment is rather versatile throughout the energy and nodal properties of its FMOs and able to act as a formal donor of different numbers of electrons, depending on the electronic demands of the metallic fragments which it interacts with. The orbitals that may be involved in interaction with the metallic end-groups are the σs and σp non-bonding and π bonding occupied FMOs, and the π* bonding vacant FMOs [13].
3.1 d0–d0 and d1–d1 (MLn)2(μ-C2) complexes
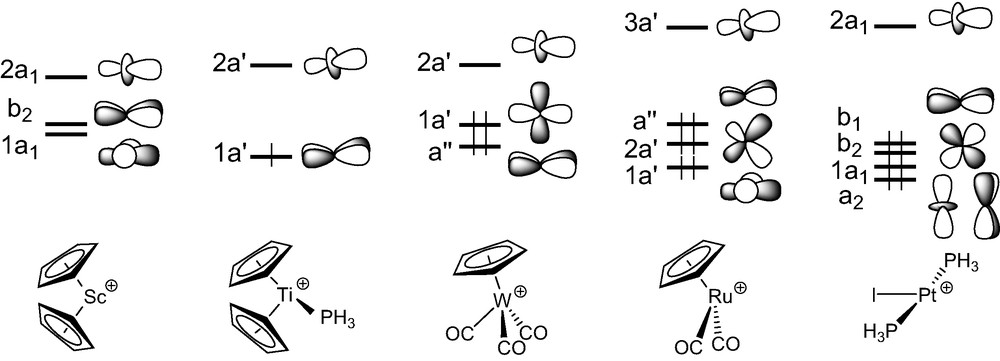
We commence with an analysis of the d0–d0 (MLn)2(μ-C2) complexes. In ScCp2]2(μ-C2), 1-H, the C2 entity is framed by two ScCp2 fragments. The three FMOs of each metal fragment can be derived from the t2g-like set of normal MCp2 complexes such as ferrocene. Fig. 1 illustrates the nodal properties of these three FMOs (two of σ type, 1a1 and 2a1, and one of π type, b2), split apart in energy and somewhat hybridised in the direction of an in-coming ligand, due to the bending of the Cp rings back from the parallel geometry [40]. Consequently, the dinuclear scandium fragment exhibits a set of six FMOs (out-of-phase 1b1u, 1b3g, and 2b1u, and in-phase 2ag, 1b2u, and 3ag combinations under D2h symmetry (see the left hand-side of Fig. 2), some of which might play a prime role in coordinating the C2 unit.
EHT FMOs of different MLn fragments.
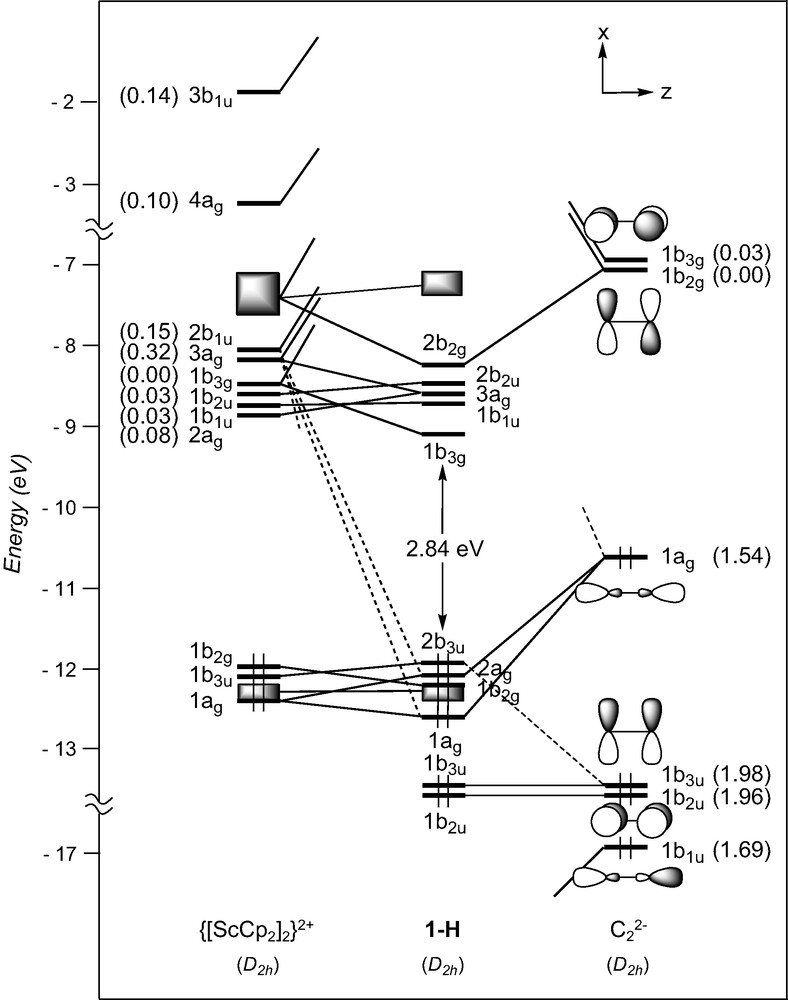
EHT orbital diagram for the model complex [ScCp2]2(μ-C2) (1-H). FMO occupations after interaction are given in brackets.
The bonding between the metallic and the carbon fragments is essentially governed by strong σ-type interactions involving the low-lying C2 orbitals 1b1u and 1ag with the metallic FMOs 3ag and 4ag, and 2b1u and 3b1u, respectively. Digits given in brackets in Fig. 2 which indicate the electron occupation of FMOs after interaction between the component fragments, illustrate numerically the degree of electron donation from the C22– spacer toward the metallic fragment. With metals formally d0, the σ-type Sc–C bonding cannot be complemented by π-type back-donation from the metallic fragment into the acceptor C2 π* orbitals. Some π-type Sc–C bonding could be expected resulting from stabilising interactions between the low-lying occupied π orbitals of C2 and the high-lying vacant metallic FMOs. It turns out that the large energy difference between them prevents significant interactions to occur. This is reflected in the electron occupation of the π orbitals of C2 close to two after interaction (see Fig. 2). It can then be considered that only σ-type Sc–C bonding is present in complex 1-H. This situation is reminiscent of ethyne.
The geometry of the d1–d1 complex [TiCp2(PMe3)]2(μ-C2), 2, can formally be derived from that of compound 1, by adding a σ bonding ligand on metal centres cis to the C2 entity. A fragment analysis of 2-H, used to mimic compound 2, with the ethyniide anion on one hand and the metal fragment {[TiCp2(PH3)]2}2+ on the other, leads us to first consider the bonding properties of the unsymmetrical [TiCp2(PH3)]+ fragment. Isolobal to [CH2]+, it has two FMOs, 1a′ and 2a′ under Cs symmetry which extent in the yz plane between the Cp rings (see Fig. 1) [40]. They intermix a little being of the same symmetry. Bringing two non-interacting [TiCp2(PH3)]+ fragments together gives rise to a set of four FMOs which span 2bu, 3ag, 1bu, and 2ag under C2h symmetry (Fig. 3). Only the 2ag FMO is occupied for the metal d1 configuration. Important σ donation occurs through strong interactions between the C2 σ-donor orbitals (1ag and 2ag) with metallic orbitals of the same symmetry. Conversely to compound 1, the σ-bonded framework is complemented by Ti–C π bonding due to attractive interactions between one component, 1bu, of the occupied π C2 orbitals and acceptor metallic FMOs, 2bu and 1bu, on one hand, and between one component, 3ag, of the π* C2 orbitals and the metallic 2ag FMO on the other hand. The out-of-phase combination of the former and the in-phase of the latter are the LUMO and HOMO, respectively, of compound 2-H. These rather strong interactions are reflected in the electron occupations after interaction of the involved FMOs (see Fig. 3). Partial depopulation of one π component and partial population of one π* component of C2 after interaction with the metallic fragment contribute to weaken the C–C bond and to strengthen the Ti–C bonds. This is consistent with dominant cumulenic valence structure B′ with three bonding π doublets (Scheme 3), often proposed in the literature to describe the electronic structure of 2 [19]. Nevertheless, population of the π* C2 orbital involved in Ti–C bonding being far from complete, participation of the limiting valence structure pattern A′ with two bonding and one non-bonding π doublets (Scheme 3) cannot be excluded.
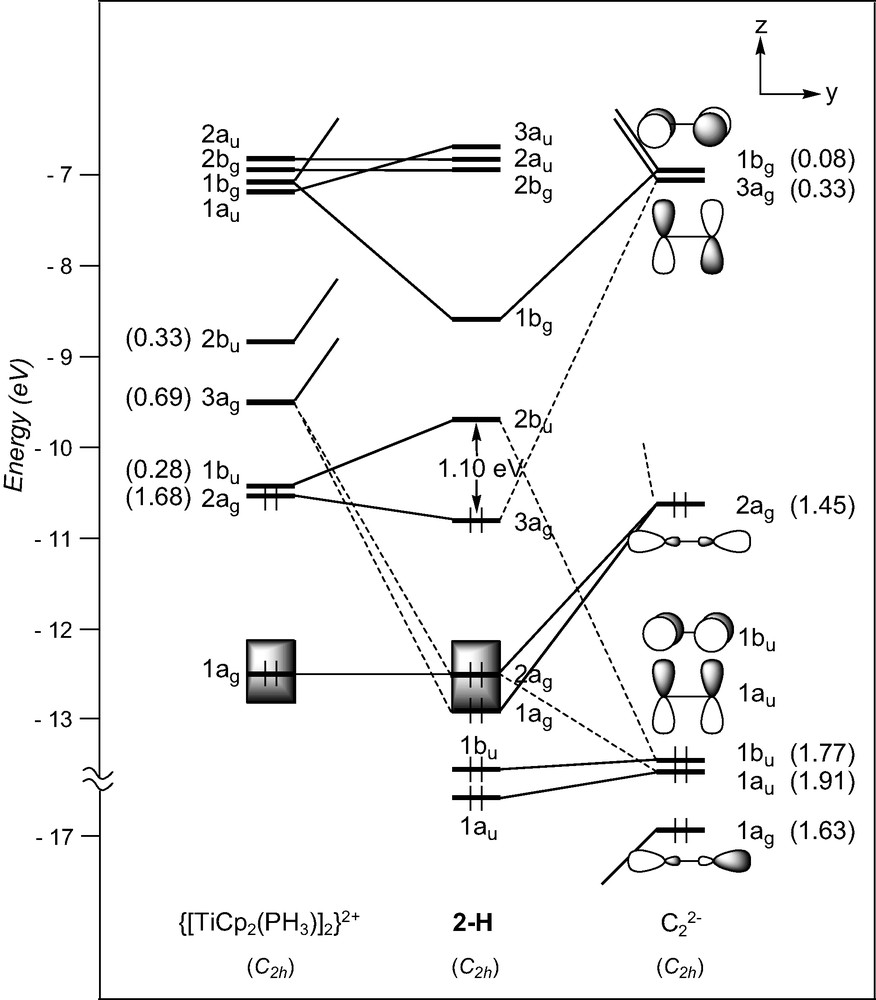
EHT orbital diagram for the model complex [TiCp2(PH3)]2(μ-C2) (2-H). FMO occupations after interaction are given in brackets.

3.2 d4–d4 (MLn)2(μ-C2) complexes
Only two d4–d4 (MLn)2(μ-C2) complexes have been characterised with metal fragments containing acceptor ligands, [W(CO)3Cp]2(μ-C2), 3 [23], and his derivative [W(CO)3(η5-C5H4Me)]2(μ-C2) [24]. In these complexes, the metal centres adopt a ‘four-legged piano-stool’ geometry [41], a high seven-coordination which allows them to achieve the 18-electron configuration. A fragment analysis of 3 can be done considering the molecule made of a C2 entity spanning two distorted octahedral d4 ML6 end-groups. The frontier orbitals of such a scarce metal fragment can be derived from those of a pseudo-octahedral MCpL3 arrangement upon tilting of the Cp ring [41]. They are illustrated in Fig. 1. They consist of three low-lying FMOs, a″ (π-type), 1a′ and 2a′ (σ-type), which descend from the ‘t2g’ set. In- and out-of-phase combinations of the FMOs of two non-interacting [W(CO)3Cp]+ fragments give rise to six FMOs which span 2bu (σ-type), 2ag (σ-type), 1ag (δ-type), 1bu (π-type), 1bg (δ-type), and 1au (π-type), under C2h symmetry. The two higher are vacant for d4 configuration (see Fig. 4).
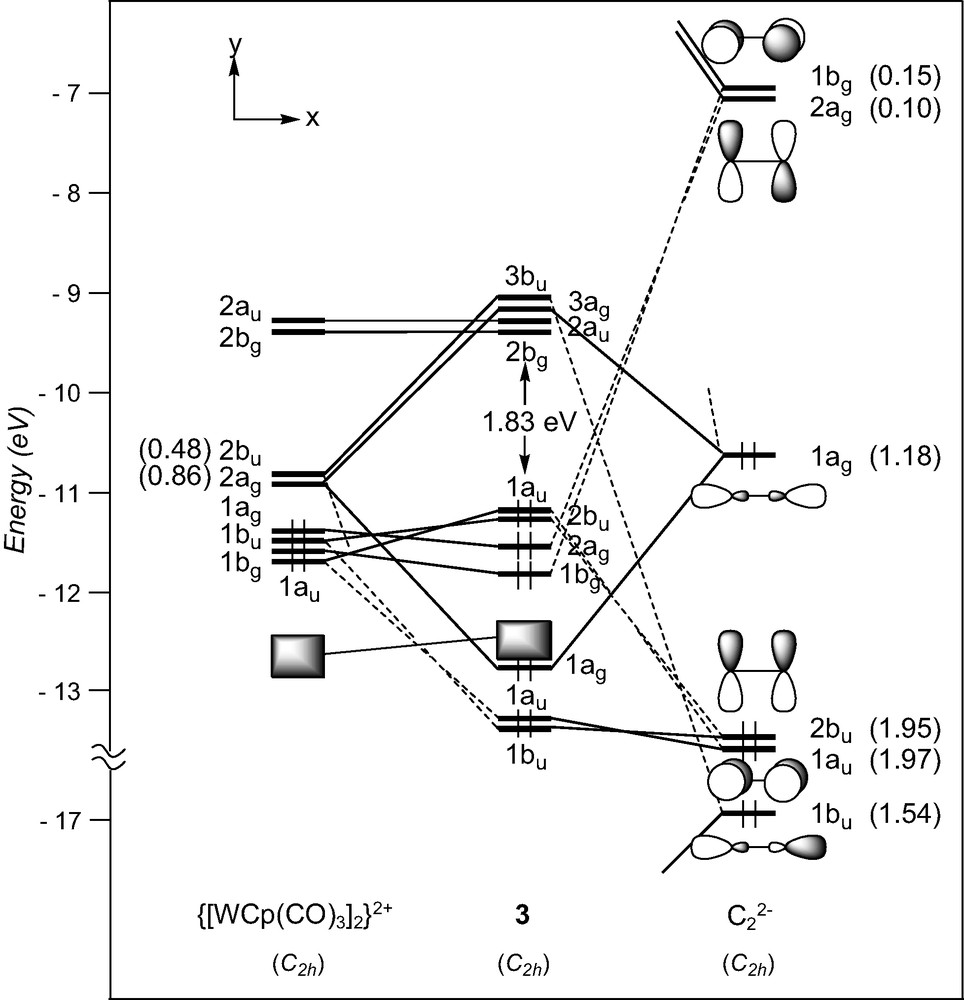
EHT orbital diagram for the complex [W(CO)3Cp]2(μ-C2) (3). FMO occupations after interaction are given in brackets.
A detective analysis of the interaction diagram of 3 shown in Fig. 4, reveals that the dominant interactions are again of σ-type, involving the acceptor metallic 2bu and 2ag FMOs and the σ-donor orbitals 1bu and 1ag of the dicarbon moiety. Small electron occupations following interaction of the π-acceptor C2 orbitals with the metal fragment, 0.10 and 0.15, indicate that the W–C σ-bonding is hardly complemented by back-donation from the occupied metallic FMOs toward C2. The HOMOs result from four-electron repulsive interactions between metal FMOs, 1au and 1bu, and π-type C2 orbitals and are consequently W–C antibonding and C–C bonding.
3.3 d6–d6 (MLn)2(μ-C2) complexes
In the d6–d6 (MLn)2(μ-C2) complex series, the C2 unit spans ML5 fragments with different metals and surrounding ligands (see Table 1). The bonding in [M(CO)5]2(μ-C2) (M = Mn, Re) has been studied previously with the aid of DFT calculations and therefore will not be discussed [16,26]. We rather devote our attention here to [Ru(CO)2Cp]2(μ-C2) [9], 4, the diphosphine relative of which, namely [Ru(PPh3)2Cp]2(μ-C2), undergoes facile reversible oxidations [28]. Each Ru(CO)2Cp fragment presents a ‘t2g’ set of d-type orbitals (2a′ and a″ of π-type, 1a′ of σ-type) situated below a radial hybrid orbital (3a′) (see Fig. 1) [42]. Out-of-phase and in-phase combinations of the orbitals of two non-interacting metal fragments give rise to a set of eight FMOs, four of σ-type, 1ag and 1bu (descending from 1a′) and 3ag and 3bu (descending from 3a′), and four of π-type, 1bg and 1au (descending from a”) and 2ag and 2bu (descending from 2a′) (see Fig. 5).
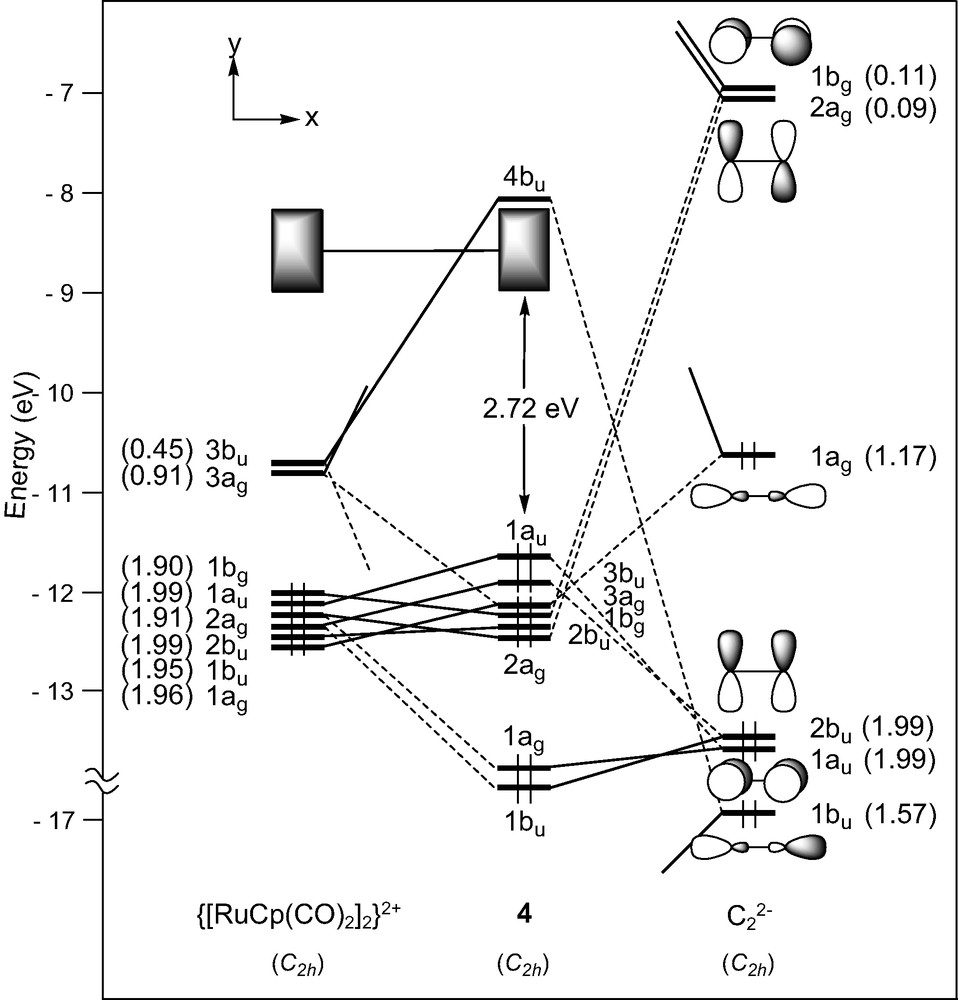
EHT orbital diagram for the complex [Ru(CO)2Cp]2(μ-C2) (4). FMO occupations after interaction are given in brackets.
Here again, strong σ-type interactions which occur between the 3bu and 3ag metallic FMOs and the σ-donor C2 orbitals, are mainly responsible for the M–C bonding in 4 (see electron occupation numbers after interaction in Fig. 5). This bonding is complemented by a rather weak π-type back-donation from occupied metallic FMOs into the π* acceptor orbitals of C2 1bg and 2ag. Indeed, the predominant Ru–C π-type interactions are actually filled–filled interactions involving occupied metal π MOs and occupied π MOs of C2, 2bu and 1au. Interestingly, the out-of-phase combination becomes the HOMO of the system, highly delocalised over the entire M–C2–M backbone. As expected, analogous results are observed for the compound [Fe(CO)2Cp*]2(μ-C2) which contains similar ML5 end-groups.
3.4 d8–d8 (MLn)2(μ-C2) complexes
Few ethynediyl platinum complexes have been reported. There is a current interest for these compounds, some of which have recently been shown to display luminescence behaviour [32]. They all contain d8 ML3 T-shaped fragments (see Table 1). The model [Pt(PH3)2I]2(μ-C2), 5-H, of D2d symmetry, was taken as a representative of this series1. The FMOs of a d8 [Pt(PH3)2I]+ fragment [43], drawn in Fig. 1, consist of one hybrid σ-type FMO, 2a1, above a set of four d orbitals, two of π-type (b1 and b2), one of σ-type (1a1), and one of δ-type (a2). The FMOs of the [I(PH3)2Pt…Pt(PH3)2I]2+ fragment of D2d symmetry are essentially the in- and out-of-phase combinations of the orbitals shown in Fig. 6: two vacant high-lying σ-type orbitals, 2a1 and 2b2, and a set of eight occupied low-lying d-type orbitals. The former interact strongly with the σ-type donor C2 orbitals, 1b2 and 1a1. As in the case of 4, back-donation from the occupied metallic FMOs into the vacant π* C2 orbitals is rather weak. Therefore, σ-type interactions mainly account for the Pt–C bonding in these species. Interestingly, some participation of the π C2 orbitals is noted in the HOMO, 5e, of the complex, which mainly derived from the π-type 3e metallic FMO.
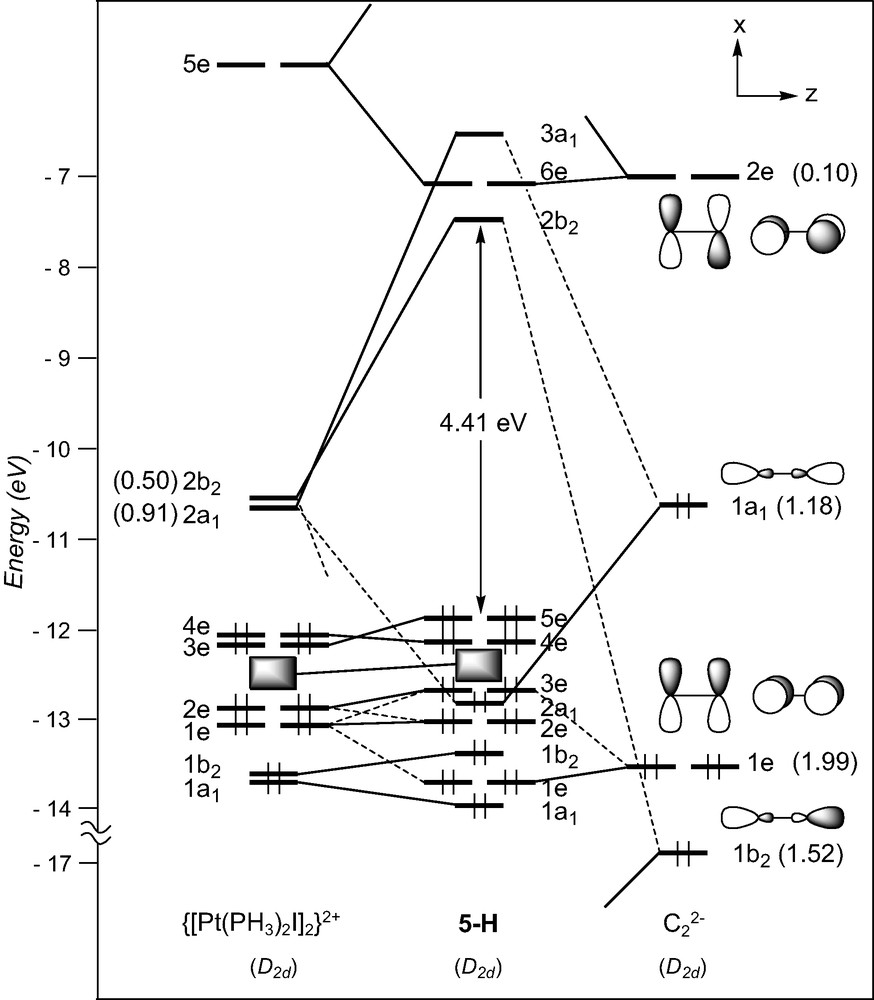
EHT orbital diagram for the model complex and [Pt(PMe3)2I]2(μ-C2) (5-H). FMO occupations after interaction are given in brackets.
3.5 d10–d10 (MLn)2(μ-C2) complexes
The last series is made of the d10–d10 gold complexes (AuPR3)2(μ-C2). With AuPR3 isolobal to H [44], the bonding in these complexes, not discussed here, is really comparable to that encountered in ethyne, with strong σ-type Au–C bonding.
4 Carbon–carbon bond strength
From Table 2 it is apparent that the EHT computed C–C overlap populations are quite similar in all studied complexes, ca. 1.90, except for the titanium compound 2-H where the C–C overlap population is markedly smaller (1.78). Surprisingly, the net charges of the C2 dum-bell somewhat differ with carbon atoms more negatively charged in early-transition metal complexes (see Table 2). Indeed, the electron loss from the C22– donor orbitals is more important in compounds 3, 4, and 5-H than in compound 1-H. This should lead to a weaker C–C bond in the former.
EHT computed characteristics for different models complexes (MLn)2(μ-C2)
| Complex | 1-H | 2-H | 3 | 4 | 5-H |
| Metal d configuration | d0 | d1 | d4 | d6 | d8 |
| C2 FMO occupations | |||||
| σu/σg | 1.54/1.69 | 1.45/1.63 | 1.18/1.54 | 1.17/1.57 | 1.18/1.52 |
| π* | 0.00/0.03 | 0.08/0.33 | 0.10/0.15 | 0.11/0.09 | 0.10/0.10 |
| Overlap population | |||||
| C–C | 1.95 | 1.78 | 1.88 | 1.89 | 1.89 |
| Atomic net charge | |||||
| C | –0.59 | –0.57 | –0.43 | –0.46 | –0.43 |
It is noteworthy that, despite similar net charges on the C2 entity, –1.18 vs. –1.14, the M–C and C–C bonding differ in the scandium and the titanium complexes. In the former, Sc–C bonding results only from some electron donation from C22– to the metal fragments, whereas Ti–C bonding is due to more important donation from C22– toward the titanium fragments and some back-donation from the metals into vacant C22– orbitals. Although both donation and back-donation compensate each other in the titanium complex to lead to C2 charge comparable to that of 1-H, they both contribute to a weakening of the carbon–carbon bond with respect to that in the scandium species.
5 DFT analysis
DFT calculations were performed on model compounds 1-H, 2-H, 3, 4, and 5-H in order to give support to the qualitative analysis and to bring additional results on their electronic properties.
5.1 Molecular geometries
The pertinent distances of the DFT optimised geometries for the different studied complexes are collected in Table 3 with few experimental estimates for comparison. The agreement is good overall. The computed carbon–carbon bond length in the ethynyl spacer is slightly overestimated by 2–5%. This is fully acceptable considering that the corresponding experimental values were measured with rather large uncertainties. Interestingly, except for the titanium compound where it is slightly longer, the C–C separation is nearly constant, ca. 1.24 Å, regardless of the metal bonded. This gives support to the comparable C–C overlap populations computed for complexes 1-H, 3, 4, and 5-H (see above). The calculated M–C bond lengths are underestimated by only 2–3% and fall in the range of M–C single bond distances generally measured experimentally for this kind of complex.
Selected DFT optimised distances (Å) for different models complexes (MLn)2(μ-C2)a
| Complex | 1-H | 2-H | 3 | 4 | 5-H |
| C–C | 1.254 1.224(9) | 1.276 1.253(2) | 1.240 1.18(3) | 1.235 1.19(1) | 1.238 1.179(48) |
| M–Cb | 2.186 2.194(7) | 2.018 2.051(2) | 2.141 2.172(22) 2.148(20) | 2.053 2.04(1) 2.05(1) | 1.968 1.973(30) 1.980(38) |
| M–Cp b | 2.192 2.171 | 2.113 2.080(2) 2.079(2) | 2.046 | 2.049 | |
| M–P | 2.599 2.549(1) | 2.293 2.302(11)c | |||
| M–C(O) | 1.995 | 1.848 1.87(1)c | |||
| Pt–I | 2.721 2.649(3)c |
a Corresponding experimental distances are given in italics when available.
b Cp centroid.
c Average distance.
5.2 MOs
The DFT MO diagrams of the studied models complexes are shown in Fig. 7. They are qualitatively similar to the EHMO diagrams given earlier. Except for the titanium compound 2-H, large HOMO–LUMO gaps, ca. 2 eV, are computed, regardless of the electron count around the metal atoms, 14 for Sc in 1-H, 18 for W in 3, 18 for Ru in 4, and 16 for Pt in 5-H. Some ethynediyl complexes undergo one-electron oxidation processes [28]. Therefore, it is informative to look at the energy and composition of the HOMOs to better discuss of the structural changes which may occur upon oxidation. To this end, a Mulliken atomic orbital population analysis and plots of the HOMO and HOMO-1 are given in Table 4 and Fig. 8, respectively. In 1-H, the HOMO and HOMO-1 lie at rather low energy and are largely separated. They are heavily weighed on C2 (64% and 84%). They derive from the C2 π orbitals, somewhat mixed with Sc–Cp orbitals.
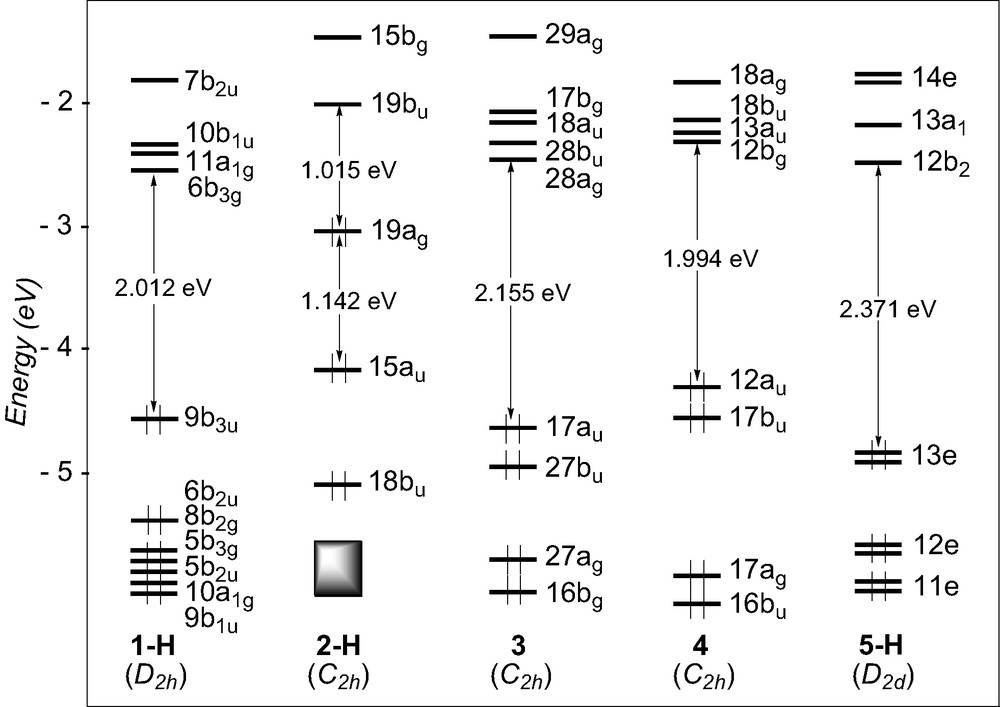
DFT diagrams for the model complexes 1-H, 2-H, 3, 4, and 5-H.
Energies (ε, eV) and percentage compositions of selected orbitals (MO) in the HOMO–LUMO region of different models complexes (MLn)2(μ-C2)
| 1-H | ||||||
| MO | 11a1g | 6b3g | 9b3u | 6b2u | 8b2g | 5b3g |
| ɛ | –2.368 | –2.548 | –4.560 | –5.394 | –5.724 | –5.826 |
| occ | 0 | 0 | 2 | 2 | 2 | 2 |
| Sc | 87 | 70 | 0 | 11 | 14 | 8 |
| C2 | 0 | 10 | 64 | 84 | 0 | 0 |
| C(Cp) | 12 | 17 | 35 | 1 | 79 | 87 |
| 2-H | ||||||
| MO | 15bg | 19bu | 19ag | 15au | 18bu | 14bg |
| ɛ | –1.465 | –2.007 | –3.022 | –4.165 | –5.066 | –5.584 |
| occ | 0 | 0 | 2 | 2 | 2 | 2 |
| Ti | 56 | 61 | 67 | 0 | 13 | 19 |
| C2 | 7 | 15 | 9 | 58 | 67 | 1 |
| P | 0 | 0 | 5 | 0 | 2 | 0 |
| C(Cp) | 24 | 13 | 10 | 41 | 6 | 69 |
| 3 | ||||||
| MO | 28bu | 28ag | 17au | 27bu | 27ag | 16bg |
| ɛ | –2.271 | –2.409 | –4.565 | –4.866 | –5.645 | –5.896 |
| occ | 0 | 0 | 2 | 2 | 2 | 2 |
| W | 22 | 15 | 27 | 31 | 55 | 54 |
| C2 | 14 | 16 | 47 | 34 | 2 | 3 |
| C(Cp) | 14 | 12 | 4 | 7 | 0 | 3 |
| CO | 50 | 56 | 15 | 24 | 37 | 35 |
| 4 | ||||||
| MO | 13au | 12bg | 12au | 17bu | 17ag | 16bu |
| ɛ | –2.212 | –2.268 | –4.262 | –4.519 | –5.804 | –6.046 |
| occ | 0 | 0 | 2 | 2 | 2 | 2 |
| Ru | 39 | 42 | 23 | 21 | 31 | 31 |
| C2 | 1 | 0 | 62 | 71 | 8 | 11 |
| C(Cp) | 20 | 22 | 9 | 1 | 39 | 33 |
| CO | 37 | 34 | 2 | 3 | 16 | 16 |
| 5-H | ||||||
| MO | 13a1 | 12b2 | 13e | 12e | 11e | 12a1 |
| ɛ | –2.179 | –2.486 | –4.857 | –5.582 | –5.874 | –6.164 |
| occ | 0 | 0 | 4 | 4 | 4 | 2 |
| Pt | 32 | 30 | 30 | 6 | 4 | 88 |
| C2 | 9 | 13 | 43 | 0 | 26 | 4 |
| I | 11 | 17 | 26 | 89 | 66 | 2 |
| P | 26 | 30 | 0 | 0 | 1 | 3 |

DFT contour plots of the HOMO (left) and HOMO-1 (right) for the model complexes 1-H (a), 2-H (b), 3 (c), 4 (d), and 5-H (e). Contour values are ± 0.035 (e/bohr3)1/2.
DFT MO diagrams of the tungsten and ruthenium complexes, 3 and 4, are quite similar with comparable HOMO–LUMO gaps, ca. 2eV, and nearly degenerated HOMO and HOMO-1 lying at relatively high energy. Examination of their composition confirms their delocalisation over the entire M–C2–M chain and features an appreciable component from the C2 unit (47% and 34% in 3, 62 and 71% in 4 for the HOMO and HOMO-1, respectively). The contour plots of these orbitals, illustrated in Fig. 8, confirm the EHT results, i.e. these MOs are π-type in character, antibonding between the metal centres and the C2 linkage and bonding between the carbon atoms. No electrochemical study has been carried out on compounds 3 and 4. On the other hand, studies performed on the parent molecule of 4, [Ru(PPh3)2Cp]2(μ-C2), which contains more electron-donating groups, indicate that it can undergo several one-electron oxidations [28]. Interestingly, X-ray measurements on the dicationic species reveal a shortening of the Ru–C bond and some lengthening of the C–C bond [28]. This change in Ru–C and C–C bond lengths upon oxidation can in turn be rationalised by the nodal properties of the two nearly degenerate HOMOs which are partially depopulated. Whereas [Ru(PPh3)2Cp]2(μ-C2) features the ethyne valence structure A, the dication {[Ru(PPh3)2Cp]2(μ-C2)}2+ is best described by the fully double-bonded cumulenic valence structure B (see Scheme 1).
A somewhat larger HOMO–LUMO gap, 2.371 eV, is computed for the platinum model complex 5-H. This is due to the degenerate HOMOs 3e which lies at lower energy. Analogously to compounds 3 and 4, they are delocalised over the metal–carbon chain (30% Pt and 30% C2), and exhibit the same nodal properties (see Fig. 8). Let us note that the iodine participation in these orbitals is quite important because of a strong π-interaction between the lone pairs of the halogen atoms and the Pt d-type orbitals.
The EHT MO diagram of the titanium complex 2-H, suggested that its electronic structure differs from that of the others. This is confirmed by DFT calculations: smaller HOMO–LUMO gap, 1.015 eV, and HOMO and HOMO-1 of different energy and nodal properties (see Fig. 8). The HOMO-1, derived from one component of the π C2 orbitals, is mainly carbon in character (58%) and, to a lesser extent, Cp in character. The HOMO, also of π-type is slightly more delocalised over the M–C2–M backbone (67% metal, 9% C2) and is Ti–C bonding and C–C antibonding, resulting from a bonding interaction between metallic orbitals and one component of the π* C2 orbitals. This strongly differs from the nodal properties of the HOMO in the other systems which generally are M–C antibonding and C–C bonding (vide supra).
Is 2-H a dimetalla–cumulene system that must be described with valence structure B′? The fact that the HOMO involves one component of the π* orbitals of the C2 unit gives support to such a structural pattern. Nevertheless, carbon participation in the MO is rather weak and the resonant ethyne valence structure A′ cannot be neglected in the description of the electronic structure of 2-H. Participation of structure patterns A′ and B′ in the electronic structure of the titanium species is supported by the optimised C–C bond distance, 1.276 Å (1.253 Å in 2) which is intermediate between a double and a triple bond. A HOMO rather high in energy and lying in the middle of a large energy gap suggests that oxidation of 2 should be possible. Indeed, preliminary DFT calculations on the dication model complex [2-H]2+ indicate some increasing of the Ti–C bond (from 2.018 to 2.104 Å) and some shortening of the C–C bond (from 1.276 to 1.256 Å), consistent with valence formula A. A significant HOMO–LUMO gap of 0.79 eV is computed. Such results suggest that electrochemical studies on 2 should be encouraged.
It is noteworthy that with the other metals of the Ti triad, Zr and Hf, ethynediyl complexes with two electrons less and shorter C–C bonds have been characterised (see Table 1). With formal d0 metal centres, the electronic structure of these zirconium and hafnium species is comparable to that of the scandium complex 1-H, i.e. best described by structure pattern A.
6 Conclusion
In summary, this study has highlighted the electronic structure of diverse acetylide-bridged organometallic binuclear complexes. Using EHT and DFT calculations, we have established that all the studied complexes feature the ethyne valence structure A regardless of the metal d configuration, except the titanium species 2 for which resonance forms of ethyne-type (structure A) and cumulenic-type (structure B) must be invoked to rationalise its structure. Results indicate that the σ-bonded framework is similar in all complexes and mainly governs the metal–carbon bonding in these species. In all cases but the titanium compound 2, the σ-type M–C is hardly complemented by π-back-donation from the metals into acceptor C2 orbitals. As noted previously [17], the C2 π* orbitals are well removed in energy from the donor metallic orbitals, and back bonding is therefore limited. The peculiar composition of the HOMOs, which are metal–carbon antibonding and carbon–carbon bonding in general for the metals at the right of the periodic table, can allow the observation of cumulenic structures B upon oxidation. This is nicely illustrated experimentally for the dicationic {[Ru(PPh3)2Cp]2(μ-C2)}2+ species [28].
Acknowledgements
We thank the ‘Pôle de calcul intentif de l’Ouest’ (PCIO) of the University of Rennes and the ‘Institut de développement et de ressources en informatique scientifique’ (IDRIS–CNRS) for computing facilities. N.O. is grateful to the French Ministry of Foreign Affairs for a travel grant (CMEP 02 MDU 552).
Appendix
Extended Hückel calculations [45] were carried out on models compounds derived from the experimental structures using the CACAO programme [46]. Standard Slater exponents and valence-shell ionisation potentials were used [46]. DFT calculations were carried out on model compounds using the Amsterdam Density Functional (ADF) program [47] developed by Baerends and coworkers [48]. Electron correlation was treated within the local density approximation (LDA) in the Vosko–Wilk–Nusair parameterisation [49]. The non-local corrections of Becke and Perdew were added to the exchange and correlation energies, respectively [50,51]. The atom electronic configurations were described by a triple-ζ Slater-type orbital (STO) basis set for H 1s, C 2s and 2p, O 2s and 2p, P 3s and 3p, and I 5s and 5p, augmented with a 3d single-ζ polarisation function for C, O, P atoms, with a 5d single-ζ polarisation function for I atom, and with a 2p single-ζ polarisation function for H atoms. The atom electronic configurations of the metal atoms were also described by a triple-ζ STO for the outer n d and (n + 1) s orbitals augmented with a single-ζ STO for the outer (n + 1) p orbitals (ADF basis set TZP) and with a frozen core approximation for the shells of lower energy. Geometry optimisations were carried out using the analytical gradient method implemented by Verluis and Ziegler [52]. For the tungsten and platinum molecules, relativistic corrections were added using the zeroth order regular approximation (ZORA) scalar Hamiltonian [53]. Representations of the molecular orbitals were done using MOLEKEL4.1 [54].
1 Experimentally, the coordination planes around the Pt atoms can be almost coplanar as in [(OC)(C6F5)2Pt][{C(Me)OEt}(PEt3)2Pt]µ-C2) (dihedral angle of 6.7°) [31], nearly staggered as in [Pt(PMe3)2I]2(µ-C2) (dihedral angle of 89.8°) [29] or [Pt(PPh3)2Cl]2(µ-C2) (dihedral angle of 82°) [30], or somewhat twisted as in {[Pt(tBu-tpy)]2(µ-C2)}2+ (dihedral angle of 35.83°) [32]. A twist of the metal moieties with respect to each other for some of them may help to relieve the steric strain arising from the bulky surrounding ligands.


