1 Introduction
Few branches of spectroscopy match in either breadth or depth the impact achieved by nuclear magnetic resonance (NMR) [1]. Originated as an unexpected by-product of the quantum mechanics revolution [2], NMR remained mostly a curiosity of the molecular beam community until Bloch, Purcell and their coworkers demonstrated the possibility of observing its manifestation in bulk [3]. This in turn triggered the use of nuclear spins as tiny ‘spies’ capable of characterizing the structure of organic molecules [4], a feature that transformed NMR into one of the cornerstones of modern chemical and pharmaceutical research. Over the years NMR undertook many other unforeseen applications: it became a common research tool in solid state chemistry and condensed matter physics; it afforded one of the few methods available for determining the structures of proteins and nucleic acids in their native solution state; and it expanded into medicine both as an imaging as well as a spectroscopy tool to study metabolism, diagnose malignancy, angiograph non-invasively, and reveal brain function [1,5–9]. A feature that distinguishes modern NMR from the few other techniques that might claim comparably wide impact areas of applicability is the fact that, broadly speaking, one common protocol underlies most of its very different applications. This protocol is multidimensional Fourier transform NMR, nD FT NMR, initially carried out along two axes [10,11] but eventually extended to the correlation of multiple spectral — and in the case of imaging, to the correlation of multiple spatial [9,12] — domains. nD NMR seeks to measure, spread and correlate NMR evolution frequencies. This is not generally carried out by exciting spectral lines but rather by manipulations in their Fourier conjugate space ; i.e. in the time-domain. For instance the basic scheme that started the 2D NMR revolution [10,11,13]
| (1) |
| (2) |
| (3) |
This expression may appear as a simple extension of 1D time-domain NMR to two dimensions, yet this similarity is deceiving and belies the insight involved in the transition from one- to multi-dimensional spectroscopy. Indeed the extraction variable against which data are transformed in 1D pulsed NMR is the physical acquisition time, of which Nature has given us only one [13,14]. Such acquisition time becomes t2 in 2D NMR spectroscopy, leaving the problem of how to sample points in the remaining time-domain axis. The answer to this riddle was provided by Jeener, who proposed acquiring complete 2D NMR frequency correlation sets by relying on a parametric incrementation of t1 in N1 steps of duration (Fig. 1 A). Although in appearance a very simple solution it is actually hard to emphasize the scientific insight of this contribution, whereby a 2D correlation between evolving coherences is extracted from a series of statistically independent experiments. In its stead, perhaps more indicative and meaningful is it to note the ca. 27 000 references arising from a contemporary data base search on the topic of multidimensional magnetic resonance, or the fact that in a very brief survey of its first 100 years the Nobel Foundation devoted a central spot to describing the impact of 2D NMR [15].
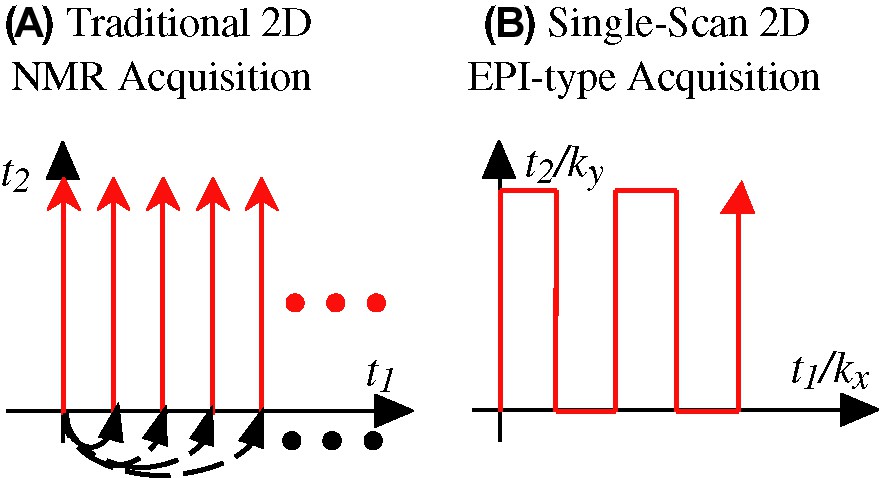
(A) Traditional Jeener/Ernst approach to the acquisition of 2D NMR spectra, based on the acquisition of numerous independent S(t2) signals as a function of an incremented t1 time parameter (dashed arrows). (B) Mansfield's approach to ultrafast MRI based on the continuous scanning of a 2D time-domain data within a single acquisition, using multiple manipulations of the interactions being correlated. In either case, the resulting temporal evolution obtained from the spins needs to be Fourier analyzed in order to extract the spectral correlations being sought.
In spite of the unambiguous gains resulting from upgrading NMR from one spectral dimension to two, a fundamental drawback also became associated to this transition. As each of the t1 points to be sampled along the indirect time-domain constitutes an independent acquisition, 2D NMR will demand tens or hundreds of transients in order to adequately sample the t1 domain — even if the signal-to-noise ratio (S/N) is acceptable within a single scan. Such complication is built-in into the scheme illustrated in eq. (1), and gets exponentially compounded when porting the 2D NMR principle to higher dimensions. The slow nature of multidimensional spectroscopy was found particularly confining in what eventually became the most widespread of all forms of bidimensional NMR, 2D FT MRI, an experiment where the spins' positions along orthogonal orientations become correlated by the action of external magnetic field gradients [16–18]. Yet in this case the availability of intense signals combined with the unparalleled flexibility with which MRI interactions could be manipulated enabled the eventual development of so-called ultrafast acquisitions techniques, capable of yielding complete 2D MRI data sets within a 0.1–1-s timescale (Fig. 1B). Principal among these methods stands echo planar imaging, EPI [12,19], and its daughter techniques [20]. This proposition was originally judged as ‘ahead of its time’ [21] yet eventually it became a cornerstone of magnetic resonance, contributing with the advent of functional MRI to what has arguably become the most exciting area in contemporary science.
Given the benefits that could be reaped from EPI, the question naturally arises of whether it is possible to extend its underlying principles to other, non-MRI types of NMR experiments. And yet except for a few rare cases where the interactions to be correlated can be controlled independently and with nearly ideal efficiency [22–24], one is forced to conclude that the spin physics underlying EPI techniques could not be directly exported into conventional high-resolution spectroscopy. Indeed EPI extends the principle in eq. (1) by coupling into it the possibility of ‘walking’ through the time domain [19,25,26]; that is, by introducing numerous periodical switchings and/or reversals of the interactions being correlated so as to sample a large region of the 2D time-domain space within a single continuous scan (Fig. 1 B). And although of a reliability beyond arguments it clear that such ‘walk in space’ approach is simply beyond the realm of the practical when relying on stochastic mixing processes like those involved in 2D Overhauser spectroscopy [13], or repeatable only very few times when dealing with J-mediated coherence transfers like those involved in homo- or hetero-nuclear 2D correlation sequences.
Still, challenged and inspired by these MRI-derived acquisition concepts, we sought for over a decade for a principle capable of reinstating the multiplexing advantages of 1D FT spectroscopy to multidimensional NMR — as well as potentially onto other forms of MR and non-MR time-domain spectroscopies. Very recently one such principle finally crystallized [27,28], which in analogy to the ultrafast MRI term proposed for imaging techniques capable of concluding their data acquisitions within sub-second timescales we have coined ‘ultrafast NMR’. This principle provides a general scheme for completing the acquisition of nearly arbitrary high-resolution multidimensional experiments within a single scan — regardless of whether their dimensions are 2, 3 or higher; regardless of whether they involve internal spin interactions, gradient-driven ones, or a combination of thereof. The goal of the present description is to present a brief summary of this new principle, and overview some of its potential applications.
2 Spatial encoding and the acquisition of 2D NMR spectra within a single scan
2.1 The principle
The main aspect distinguishing ultrafast from both traditional 2D NMR as well as from EPI-type acquisitions is a departure from the homogeneous encoding of the spin interactions. Instead, indirect-domain evolution frequencies are imparted in a heterogeneous fashion whereby spins positioned at different coordinates within the sample2 are allowed to evolve over different extents of time prior to the mixing period. A suitable read-out of the heterogeneous evolution thus encoded can then provide the full 2D NMR information being sought, within a single continuous data acquisition. Given present-day NMR hardware it appears that the simplest way to achieve this partitioning of the sample is by activating a magnetic field gradient G = ∂B0/∂r, discriminating spins according to their spatial coordinate r. A scheme such as the one illustrated in Fig. 2 can then be used to collect the indirect-domain spectral correlations. Such generic sequence assumes that the initial spin evolution is triggered by a frequency-incremented RF pulse, superimposed on top of an excitation gradient Ge. An important demand placed on this excitation module is that at its conclusion, the evolution phase of the excited spin packets should end up reflecting the effects of internal Ω1 couplings, but not those of the ancillary Ge gradient. Numerous strategies have already been devised for imparting such internal kind of spatial encoding [27–32], and it is likely that further optimizations will arise in the near future. In broad terms all these spatial encoding strategies involve the application of either discrete or continuous frequency-shifted selective RF pulses, in combination with alternating gradients designed so that their effects are eventually ‘echoed away’ at the conclusion of the irradiation. The common, important point of all these encoding alternatives is that at their conclusion, the combined use of frequency-shifted RF pulses and of spatially dependent resonance frequencies end up imparting on the spins an r-dependent purely internal evolution phase of the kind
| (4) |
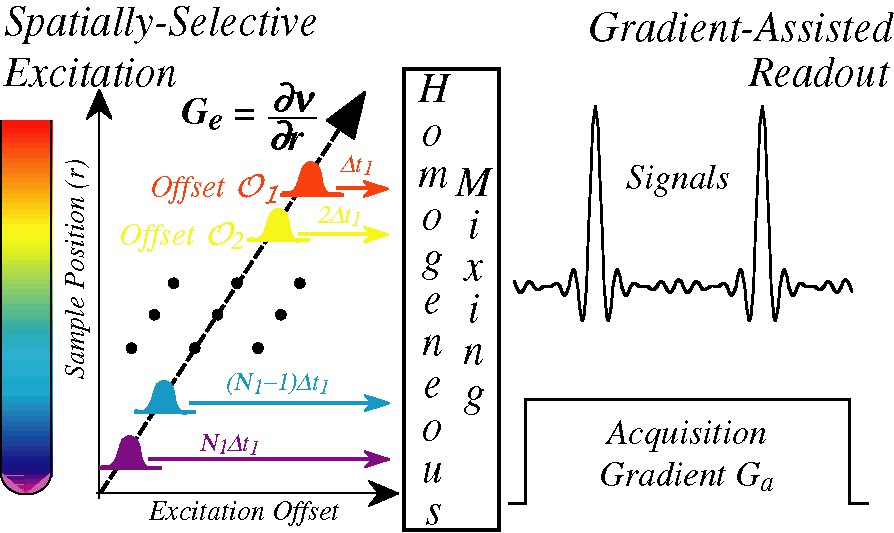
Starting point of the single-scan 2D NMR protocol: a time- and frequency-incremented RF irradiation applied in combination with a suitable gradient imposes an r-dependent evolution of the Ω1 spin interactions to be measured (left). Following a homogeneous mixing process this spatial encoding is preserved as either a phase- or an amplitude-modulation (Center), to be subsequently decoded by the application of a second acquisition gradient that reads out the Ω1 frequencies as site-specific echo signals (right).
Here C is a spatio-temporal ratio under the experimentalist's control relating a spin's displacement r – ro against the extent of its evolution time t1, and Ω1 is the rotating-frame internal frequency we are attempting to measure. Eq. (4) amounts to a ‘winding’ of the spin coherences, a pattern analogous to the one that would arise if a gradient along the direction were applied following a hard π/2 pulse. Analogous but not identical, since unlike what happens when applying a gradient, the pitch of the resulting winding will now be site-dependent. In fact, it will be governed by the indirect-domain interaction Ω1 conforming the observable that we are attempting to measure.
When inserted at the beginning of a generic 2D NMR experiment such winding will be preserved by the homogeneous mixing process (Fig. 2), and will consequently lead to no observable macroscopic signals when considering the sample as a whole. If, however, the signal detection is now implemented while subjecting the sample to an acquisition field gradient Ga possessing the same geometry as Ge, this spiral of magnetizations imparted by the Ω1 will eventually be unwound. The moment at which this Ω1-dependent unwinding occurs is easily observable, as only at its juncture will spin-packets located at different positions throughout the sample cease interfering and lead to a macroscopic overall signal. This in turn implies that the spatial encoding of the spins interactions and this subsequent gradient-assisted readout provides a way to monitor the indirect domain Ω1 evolution frequencies that affected the spins; not via the Fourier analysis of an evolving coherence as in usual time-domain spectroscopy, but via the displacement observed in the position of a site-specific echo created by interfering spins located at different positions throughout the sample. A graphical depiction of this unusual feature — whereby the time-domain signal becomes equivalent to its indirect domain frequency spectrum — is illustrated in Fig. 3 A, which analyzes the fate of magnetizations throughout a portion of an ultrafast acquisition assuming a simplified ‘five-slice’ sample.
(A) Simplified representation of how the combination of a spatial encoding before the mixing process and of a gradient-assisted decoding thereafter (as shown in Fig. 2) allows one to read out the indirect-domain spectral information. Notice that the mixing process is assumed here to preserve the phases of the t1-evolved coherences; analogous arguments could be derived in the case of amplitude modulations. (B) Extension of the single gradient-driven refocusing illustrated in (A), to a multiple gradient echo recording capable of yielding a mixed-domain S(k/ν1,t2) interferogram within a single scan.
Although this new approach may be capable of reading out an indirect-domain NMR spectrum, it may not be a priori clear of where would its eccentricity pay off in terms of facilitating the acquisition of multidimensional NMR spectra. What brings this about is the realization that unlike what happens with a conventional time-domain encoding, which is a unidirectional process that needs to proceed monotonically and over a relatively long period of time in order to properly characterize the spin evolution frequencies, the gradient-driven readout depicted in Fig. 3A can be concluded very quickly. Moreover, this is a process that can be done and undone numerous times over the course of the data acquisition, simply by reversing back and forth the currents generating the Ga gradient while collecting the data. This in turn enables the repetitive monitoring of the indirect-domain spectrum numerous times as a function of an acquisition time t2, leading to a mixed frequency/time-domain interferogram from which the 2D NMR spectrum can be retrieved by 1D FT. All of this, from an experiment that can effectively be concluded within a single scan (Fig. 3B).
2.2 2D NMR examples
Having surveyed the principles underlying single-scan 2D NMR, we dwell in this Paragraph onto some of its potential applications. The first question usually arising in this regard concerns whether the strategy just described can find potential uses in biomolecular NMR. The answer to this is “yes”; Fig. 4 for instance compares a conventional 2D HSQC spectrum collected on an 15N-labeled ubiquitin sample, with an ultrafast counterpart collected within four scans (the extra scans needed in part for the sake of phase cycling away the otherwise intense solvent signal remaining). As can be appreciated both sets convey similar information and at comparable qualities — at least at this level of sample concentration. This in turn opens interesting vistas regarding the possibility of employing real-time 2D NMR as a new tool to follow dynamic biomolecular processes. A second area where the short acquisition times involved in ultrafast 2D NMR could find interesting applications is that of in vivo spectroscopy; both because of the possibilities that this would open regarding the tracking of metabolic processes, as well as due to the opportunities that would arise if experiments where 2D spectroscopy and 3D imaging scans could be combined while acquisition times remain within patient-compatible levels. Fig. 5 illustrates that also in these areas there is a potential for ultrafast 2D NMR, at least judging by the comparisons made on phantom and/or model systems [33].
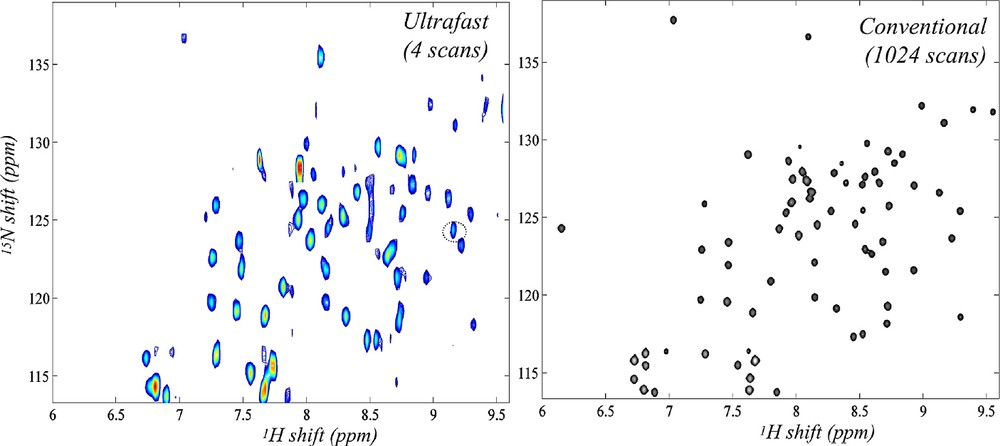
Comparison between ultrafast and conventional 2D HSQC NMR spectra recorded at 18.8 T on a 3.25 mM 15N-enriched ubiquitin sample dissolved in 93/7% H2O/D2O (courtesy of Boaz Shapira, unpublished).
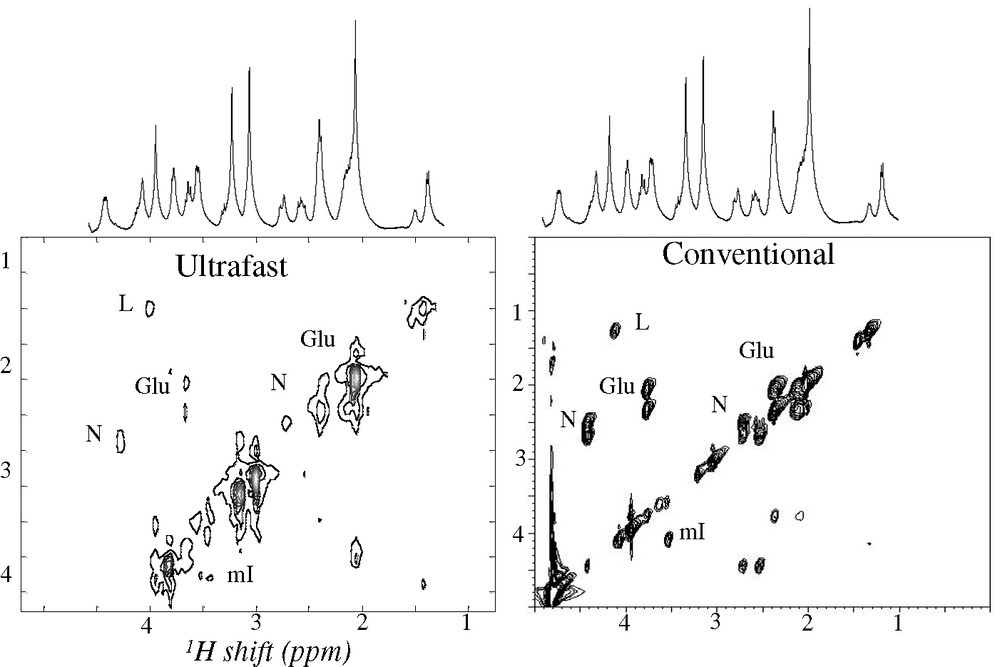
Comparison between ultrafast and conventional 2D TOCSY NMR spectra recorded on a 9.4-T microimaging system on a brain phantom [33]. Shown are principal cross-peaks assigned to lactate (L), N-acetyl aspartate (N), glutamate (Glu), myo-inositol (mI).
In addition to speeding up known applications of 2D spectroscopy, ultrafast 2D NMR could help support certain new technologies that are beyond the realm of the hitherto possible. One such option involves implementing 2D analyses of samples subject to a continuous flow through the NMR sample coil — a flow which could originate from either continuous sample separation requirements as in the case of liquid chromatography, or simply as a result of the desire to impart the highest possible rate of throughput to a chemical/physiological characterization. Under suitable sample sensitivity conditions the ultrafast protocol could make such a continuous flow scenario compatible with real-time 2D NMR acquisitions; Fig. 6 illustrates this with a series of 2D TOCSY NMR spectra collected using a home-built prototype on a chemical mixture, subject to a continuous chromatographic separation of its constituent components [34]. Another instance where new possibilities could be unlocked arises when considering the merger between 2D NMR and nuclear hyperpolarization methods. The latter include a number of specialized spin physics methodologies [35–37] capable of building up nuclear magnetizations that exceed their thermal equilibrium counterparts by several orders of magnitude. While the relatively long pre-polarizing periods and less-than-perfect reproducibility characterizing these methods do not make them suitable starting points for conventional 2D NMR experiments, they could constitute ideal counterparts to the single-scan acquisitions introduced in the preceding Paragraph. Fig. 7 shows a preliminary step in that direction, with a single-scan 2D TOCSY spectrum acquired following a brief period of CIDNP polarization enhancement [38]. The sub-mM concentration then required for implementing such study serves to exemplify the promises held by this new kind of NMR applications.
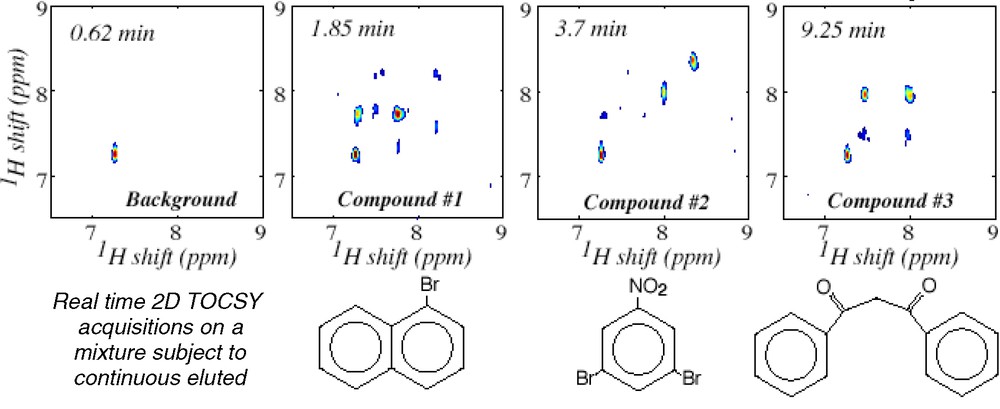
Real-time identification via 2D ultrafast TOCSY 1H NMR of a mixture of three compounds being continuously separated under standard on-flow LC conditions. In the actual experiment, 2D NMR spectra were constantly acquired 32 s apart over a 15-min elution period [34]; the figure concentrates on spectra corresponding to the drawn compounds appearing at the indicated elution times.
Example of the potential benefits resulting from the combination of pre-polarization and ultrafast 2D NMR methods. Both traces correspond to single-scan 2D TOCSY 1H NMR spectra recorded on a tyrosine-containing cyclic octapeptide dissolved in D2O at a 0.5 mM concentration. Shown on the left are the results observed under standard conditions; shown on the right are the results observed after pre-irradiating the sample for 0.5 s using a 480-nm light sources (2W) capable of inducing a CIDNP enhancement [38].
2.3 Spatial encoding as a new approach to ultrafast 2D MRI
The encoding principles described in the preceding paragraph could also find applications in MRI-oriented investigations. Here the goals sought usually go beyond a purely chemical or structural characterization, and include finding information about the spatial placing of the spins. There are at least two immediate ways by which ultrafast 2D NMR could help retrieve this information. One of these involves adapting the spatial encoding principle so as to transform it from a 2D spectroscopy protocol into a 2D imaging one. A simple route to achieving this is by spoiling the gradient echoing procedure deliberately inserted along ultrafast's indirect domain, imparting an evolution that instead of being purely spectroscopic encodes a position-related information [39]. Fig. 8 illustrates such a transition from a spectroscopic into an imaging scenario, where as usual in imaging instances we are assuming that the spin evolution is solely dictated by the offsets introduced by gradients, and that local interactions are negligible. By doing this modification one ends up with an alternative that although based on different physical principles than EPI, also enables the acquisition of multidimensional MR images within a single scan. An intriguing issue is whether this new protocol offers any competitive advantage over any of the existing ultrafast 2D MRI scanning options; at this point, this remains to be seen.
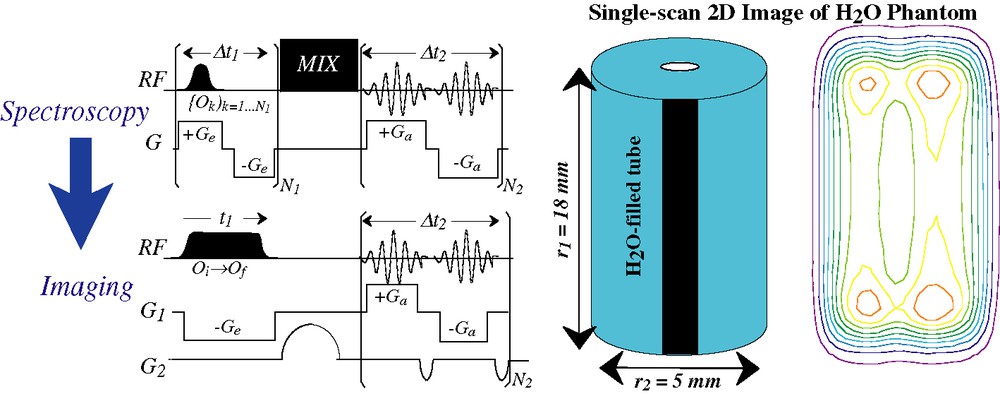
(Left) Translating the spatial encoding idea from a purely spectroscopic setting, to one where single-scan 2D imaging of positions is the goal [39]. In the illustrated imaging sequence, only G1 is assumed to be spatially encoded by the application of a frequency sweep; gradient evolution along the second dimension is conventional. (Right) Application of the sequence shown on the bottom left to a single-scan imaging experiment carried out on a water phantom at 11.7 T.
In addition to the approach just described ultrafast 2D NMR offers an alternative, somewhat less evident route to the retrieval of spatial information. As explained earlier 2D NMR spectra arise from these experiments by taking 2D data sets acquired as a function of k and t2, and subjecting them to FT solely along t2 — peaks along the indirect domain appearing simply as a result of echo phenomena upon the continued application of Ga. A question that then arises is: what would happen if one were to subject the resulting data to a second FT along the yet unprocessed domain? Since the corresponding peaks stem from an acquisition that took place while under the action of a gradient, one could assume that they will contain some imaging information. And indeed under ideal conditions, the point spread function characterizing each diagonal and/or cross peak along the indirect dimension of ultrafast spectra contains the signature of the spatial distribution originating a particular 2D NMR peak. All that is needed to retrieve such distribution is to extract this complex signal and subject it to a Fourier analysis along the k/ν1 domain: no additional imaging ingredient is necessary, beyond what had already been included in the original ultrafast 2D NMR pulse sequence. This in turn opens a very attractive route to spatial localization, as it means that the same protocol originating the 2D NMR spectrum within a single scan can also be exploited to retrieve the spatial origin of the spins at no additional expense in either acquisition time or sequence complexity. Fig. 9 presents an example of this procedure [40], which demonstrates the possibility of collecting spatially-resolved information from 2D NMR spectra while remaining in a sub-second timescale. Retrieving such spatially-localized information may be quite valuable, particularly when dealing with in vivo systems where the anatomical distribution associated to a particular NMR peak is of essence.
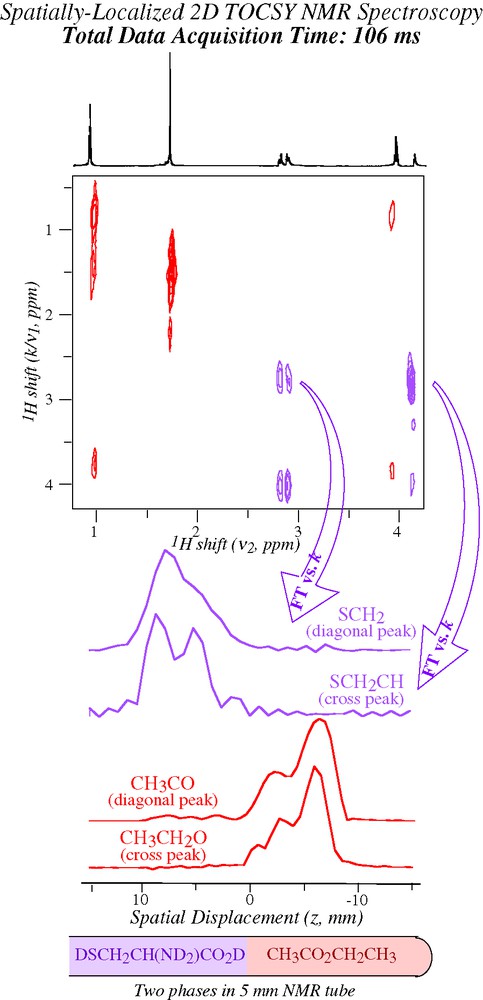
Illustration of how the post-processing of ultrafast 2D NMR spectroscopic data can afford additional information on spatial positions [40]. A single-scan 2D TOCSY 1H NMR spectrum was recorded on the indicated analytes, which were dissolved in separate organic (CCl4, pink) and aqueous (D2O, purple) phases. The spatial profiles indicated on the bottom resulted from extracting ca. 20 points in the neighborhood of the indicated 2D NMR peaks, and subjecting the resulting data to FT against their k/ν1 variable.
3 Perspectives
Few scientists need nowadays be reminded of the importance played by multidimensional magnetic resonance. Whether because of the need to characterize a new material, to elucidate a protein structure, to synthesize a new drug or to evaluate the possibility of disease, scientists involved in a wide variety of endeavors have already had the chance (or perhaps the forced duty) to become acquainted with those peculiar map-like plots first conceived by Jeener and Ernst. The possibilities that could open by speeding up the acquisition of such multidimensional NMR data — speeding up in some instances by several orders of magnitude — are definitely alluring. Yet instead of summarizing the various opportunities that could thus be opened it is perhaps more adequate to conclude the present account with a word of caution. Indeed it should be kept in mind that in spite of all the exciting potential that ultrafast nD NMR acquisition schemes may bring, they will not perform ‘magic’. Accelerated acquisition schemes may be capable of affording nD NMR spectra within a single scan, but will only do so if sufficient S/N is available to monitor the desired features within that single scan. This in turn highlights the importance of sensitivity as another major goal to focus upon — even if all these efforts are invested and then used up within a fraction of a second [41].
Acknowledgments
My thanks go to all the talented coworkers I had the luck to collaborate with over the course of this project, and in particularly to past and present members of my group: A. Lupulescu, B. Shapira, Y. Shrot, N. Sela, E. Morris, M. Mishkovsky, A. Tal, M. Gal, and F. Kramer. Financial support from the Ilse Katz Magnetic Resonance Center (Weizmann Institute), the Israel Science Foundation (grant 296/01), the Minerva Foundation (Munich), and the US National Institute of Health (GM72565) is also gratefully acknowledged.
1 Throughout the present work Ω1, Ω2 denote the actual values of the Bohr evolution frequencies experienced by the spins, while ν1 and ν2 represent the frequency-axis variables of a spectrum being plotted.
2 Or perhaps in the case of anisotropic media, spins oriented at inequivalent angles with respect to the magnetic field.