Multiple-quantum NMR on structure, orientation, morphology and dynamics of polymers, biomolecules and ordered tissues

Alina Adams Buda; Dan Eugen Demco; Marko Bertmer; Bernhard Blümich

doi:10.1016/j.crci.2005.06.020

Multiple-quantum NMR on structure, orientation, morphology and dynamics of polymers, biomolecules and ordered tissues

Alina Adams Buda ¹; Dan Eugen Demco ¹ ; Marko Bertmer ¹; Bernhard Blümich ¹

¹ Institut für technische Chemie und makromolekulare Chemie, Rheinisch-Westfälische Technische Hochschule, Worringerweg 1, 52074 Aachen, Germany

Comptes Rendus. Chimie, Volume 9 (2006) no. 3-4, pp. 346-356.

Abstracts

English
French

A survey of recent homo- (¹H) and heteronuclear (¹³C–¹H) multiple-quantum (MQ) NMR experiments performed in our group at RWTH-Aachen on soft solids is given. MQ build-up curves are used for measurement of residual van Vleck moments and as dipolar filters in spin-diffusion experiments. The orientation studies were made with the help of MQ edited spectra that show Pake doublets. Proton homonuclear as well as ¹³C–¹H heteronuclear residual dipolar couplings were measured site-selectively and for the overall polymer chains and correlated with the cross-link density and network deformation in elastomers and thermoplastic elastomers. The heterogeneity of the segmental dynamics of poly(dimethylsiloxane) chains grafted onto hydrophilic silica was studied by bimodal double- (DQ) and triple-quantum (TQ) build-up curves. The complex morphology of Nylon-6 fibers was characterized with the help of spin-diffusion experiments using a new dipolar filter based on the excitation of DQ coherences. The same procedure was employed for the investigation of the distribution of the residual dipolar couplings of lecithin molecules grafted on the walls of submicrone cylindrical pores. The distribution of the orientation of collagen fibrils in Achilles tendons was estimated from ¹H DQ filtered spectra. .

Nous présentons ici les expériences récentes en RMN multi-quanta (MQ) homo- (¹H) et hétéronucléaire (¹³C–¹H) réalisées sur des solides mous dans notre groupe à l’université d’Aix-la-Chapelle. Des courbes de montée MQ ont été utilisées pour mesurer les moments résiduels de van Vleck et comme filtres dipolaires dans les expériences de diffusion de spin. L’édition des spectres MQ montrant des doublets Pake a également permis d’étudier les systèmes orientés. Les couplages dipolaires résiduels homo ¹H–¹H et hétéronucléaires ¹³C–¹H ont été mesurés sélectivement sur certains sites ainsi que pour l’ensemble des chaînes polymères et corrélés avec la densité de réticulation et la déformation du réseau dans les élastomères et les polymères thermoplastiques. L’hétérogénéité dynamique des segments dans les poly(diméthylsiloxanes) greffées sur la silice hydrophile a été visualisée au travers d’une distribution bimodale des courbes de montée à deux et à trois quanta. La morphologie complexe de fibres de nylon-6 a été caractérisée à l’aide d’expériences de diffusion de spin utilisant un nouveau filtre dipolaire basé sur l’excitation de cohérences à deux quanta. La même procédure a été utilisée pour étudier la distribution des couplages dipolaires résiduels de molécules de lécithine greffées sur les parois de pores cylindriques. La distribution de l’orientation des fibres de collagène dans les tendons d’Achille a été estimée à partir de spectres filtrés à deux quanta. .

Metadata

Received: 2005-04-24
Accepted: 2005-06-06
Published online: 2005-08-24

DOI: 10.1016/j.crci.2005.06.020

Keywords: Multiple-quantum NMR, Spin-diffusion, Heterogeneity of segmental dynamics, Elastomers, Grafted polymers, Lipid films, Achilles tendon
Keywords: RMN multi-quanta, Diffusion de spin, Hétérogénéité structurale et dynamique, Élastomères, Polymères greffés, Films lipidiques, Tendon d’Achille

Author's affiliations:

Alina Adams Buda ¹; Dan Eugen Demco ¹; Marko Bertmer ¹; Bernhard Blümich ¹

¹ Institut für technische Chemie und makromolekulare Chemie, Rheinisch-Westfälische Technische Hochschule, Worringerweg 1, 52074 Aachen, Germany

@article{CRCHIM_2006__9_3-4_346_0,
     author = {Alina Adams Buda and Dan Eugen Demco and Marko Bertmer and Bernhard Bl\"umich},
     title = {Multiple-quantum {NMR} on structure, orientation, morphology and dynamics of polymers, biomolecules and ordered tissues},
     journal = {Comptes Rendus. Chimie},
     pages = {346--356},
     publisher = {Elsevier},
     volume = {9},
     number = {3-4},
     year = {2006},
     doi = {10.1016/j.crci.2005.06.020},
     language = {en},
}

TY  - JOUR
AU  - Alina Adams Buda
AU  - Dan Eugen Demco
AU  - Marko Bertmer
AU  - Bernhard Blümich
TI  - Multiple-quantum NMR on structure, orientation, morphology and dynamics of polymers, biomolecules and ordered tissues
JO  - Comptes Rendus. Chimie
PY  - 2006
SP  - 346
EP  - 356
VL  - 9
IS  - 3-4
PB  - Elsevier
DO  - 10.1016/j.crci.2005.06.020
LA  - en
ID  - CRCHIM_2006__9_3-4_346_0
ER  -

%0 Journal Article
%A Alina Adams Buda
%A Dan Eugen Demco
%A Marko Bertmer
%A Bernhard Blümich
%T Multiple-quantum NMR on structure, orientation, morphology and dynamics of polymers, biomolecules and ordered tissues
%J Comptes Rendus. Chimie
%D 2006
%P 346-356
%V 9
%N 3-4
%I Elsevier
%R 10.1016/j.crci.2005.06.020
%G en
%F CRCHIM_2006__9_3-4_346_0

Alina Adams Buda; Dan Eugen Demco; Marko Bertmer; Bernhard Blümich. Multiple-quantum NMR on structure, orientation, morphology and dynamics of polymers, biomolecules and ordered tissues. Comptes Rendus. Chimie, Volume 9 (2006) no. 3-4, pp. 346-356. doi : 10.1016/j.crci.2005.06.020. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2005.06.020/

Version originale du texte intégral

1 Introduction

Multiple-quantum (MQ) NMR experiments are designed to probe nominally forbidden degrees of freedom of a collection of coupled nuclear spins [1,2]. The spin modes of interest are coherent superpositions of Zeeman states for which the expectation value of the nuclear magnetic dipole moment is zero. This NMR method was applied in the past for simplification of highly complex single-quantum spectra [1,2], spin counting [2], enhancing the gradient effective strength in imaging and diffusion experiments (see Refs. [2,3] and references therein), and correlated fluctuations in transverse magnetization relaxation [2]. The description of the use of these collective spin modes for the characterization of many classes of soft solids and the complex morphology of semicrystalline polymers is the main goal to be addressed here.

Residual dipolar or quadrupolar interactions measured by NMR methods represent an important source of information about the structure and molecular dynamics in soft solids [4–7] (and references therein). Using these quantities structure–function relationships were investigated in elastomers that constitute an important class of soft-matter materials. The measurement of residual dipolar couplings in elastomer system is desirable because they reflect the hindrance to molecular motions by cross-linking, topological constraints and external forces like mechanical stress. The difficulties related to these measurements are due to the small values of the residual dipolar couplings, the many-body character of the dipolar couplings and the presence of molecular motions, which produce a supplementary encoding of the spin system response.

One-dimensional NMR methods based on the dipolar correlation effect in combination with Hahn and solid echoes, stimulated echo, magic echo, magnetization-exchange, and cross-polarization dynamics provide access only to the second van Vleck moment via a model which takes into account the solid-like and liquid-like contributions to the spin system response [6,7]. Model free access is given by the analysis of MQ excitation curves in the initial regime of the excitation/reconversion periods. Chemically site-selective residual dipolar couplings can be elucidated by two-dimensional NMR spectroscopy using NOESY MAS, DQ MAS, REDOR and ¹³C–¹H heteronuclear residual dipolar-encoded spinning sideband patterns [8].

2 Residual dipolar couplings in elastomers

MQ filtered NMR signal intensities can be used for the measurement of ¹H residual dipolar couplings and the associated dynamic order parameter especially in the short excitation regime. The measurements performed on 1,4-cis-polyisoprene show that ¹H residual dipolar couplings correlate linearly with cross-link densities [9]. Moreover, it was shown that the dipolar couplings measured from MQ coherences are more sensitive to the cross-link density as compared to transverse magnetization relaxation rates.

The microphase composition of poly(butylene terephthalate)-block-poly(tetramethylene oxide) (PBT-block-PTMO) thermoplastic elastomers with varying content of PTMO soft block and varying PTMO block length was studied by ¹H NMR transverse magnetization relaxation [10], ¹H 2D DQ MAS [10] and ¹H DQ build-up curves [11]. The ¹H 2D DQ BABA spectrum shows directly a close proximity of the aromatic protons from PBT and OCH₂ protons from PTMO suggesting molecular scale mixing of PBT and PTMO blocks [10]. The dynamic order parameter was measured for this thermoplastic elastomer using a combination of homo- and heteronuclear dipolar filters, e.g. ¹³C editing of ¹H DQ build-up curves [11]. From these measurements the average dynamic order parameter of mobile PTMO blocks was deduced. The segmental mobility of the soft blocks is responsible for the viscoelastic properties of thermoplastic elastomers. A strong correlation exists between this quantity and the sample composition.

Site-selective information about local segmental motions of individual CH_n fragments can be obtained by the determination of ¹³C–¹H heteronuclear dipolar couplings [12]. A systematic study was performed, by measuring heteronuclear residual dipolar couplings of natural rubber samples with different cross-link densities using heteronuclear DQ (HeDQ) build-up curves, solid-echo double resonance (SEDOR) and rotational-echo double resonance (REDOR) experiments. Even under static conditions, all five CH_n fragments of the monomer unit can be separated (Fig. 1). ¹³C–¹H heteronuclear dipolar couplings extracted from different experiments show a linear correlation with the cross-link density (Fig. 2). However, the residual dipolar couplings are also dependent on the individual functional group. In other words, the local motions of the functional groups are superimposed on the segmental motions of the chain-segment and have to be taken into account in the prediction of the dynamic order parameters.

Fig. 1
¹³C spectra of cross-linked natural rubber with 5 phr sulfur/accelerator [12]. The assignment of the signals is given in the inset. (a) Static spectra with ¹H decoupling; (b) 5-kHz MAS spectrum with ¹H decoupling, and (c) 5-kHz MAS spectrum without ¹H decoupling showing heteronuclear J-couplings.

Fig. 2
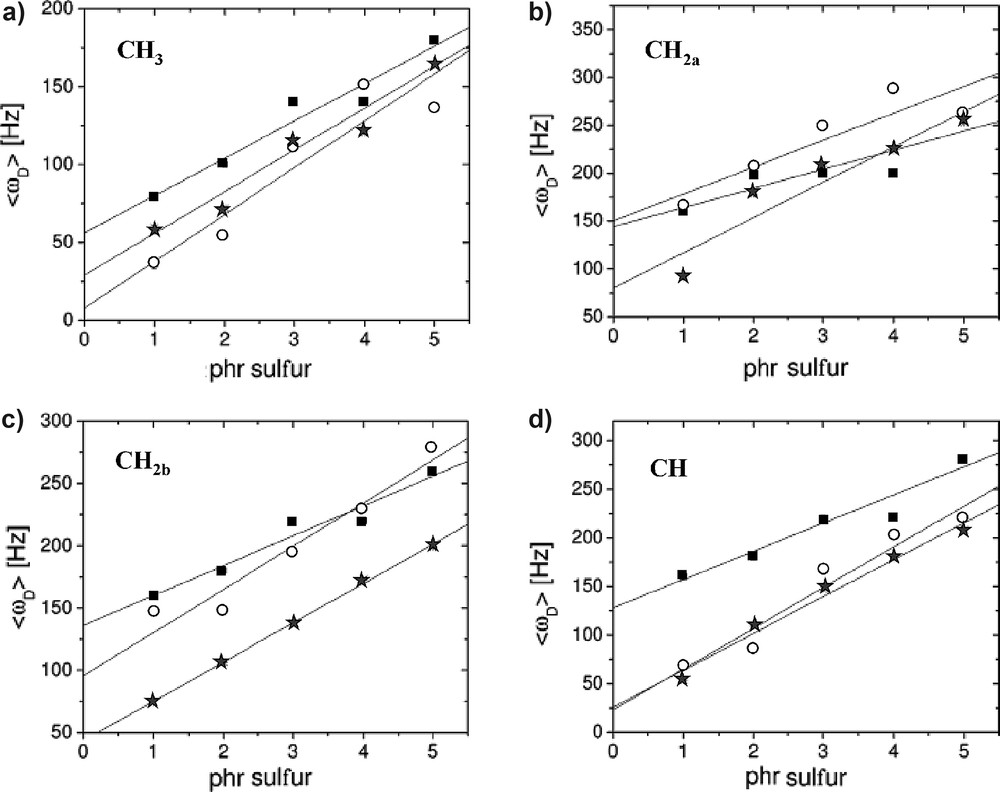
Measured ¹³C–¹H residual dipolar couplings using HeDQ (solid squares), SEDOR (open circles), and REDOR (stars) on a cross-linked series of natural rubber. The linear correlation is indicated by solid lines [12].

In the initial time regime of the excitation/reconversion periods only DQ build-up curves give a residual dipolar quantity, which can be correlated with the second van Vleck moment [13]. This enables one to compare these moments with the van Vleck moments measured by other NMR techniques. Recently, it was shown that higher-order MQ build-up curves edit moments different from the standard van Vleck moments [14]. Nevertheless, these higher-order edited moments are more sensitive to the changes in the polymer network properties than the residual second van Vleck moment [14].

Proton DQ solid-state NMR spectroscopy under fast magic-angle spinning (MAS) was introduced as a new spectroscopic tool for the investigation of the structure and local chain dynamics of elastomers [15]. Dipolar connectivities between the proton of the various functional groups can be directly established from the highly resolved DQ solid-state NMR spectra as is shown for a series of cross-linked poly(styrene-co-butadiene). More quantitatively, residual dipolar couplings within and between the functional groups are evaluated selectively from the build-up curves of the DQ signals. In particular, the CH–CH and the CH–CH₂ couplings of butadiene, which both act predominantly along the chain-segment direction, have been measured relative to the CH₂ coupling.

A two-dimensional DQ experiment under rotational resonance (R²) conditions was introduced for evaluating dipolar couplings in rotating solids [16]. The contributions from the R²-recoupled dipolar interaction and the J coupling can be conveniently separated in the resulting 2D R²-DQ spectrum, so that the unknown dipolar coupling can readily be extracted, provided that the values of the involved J coupling constants are known. The application of this technique to cross-link natural rubber demonstrates, that the rotational resonance phenomenon is not confined to rare isotopes in rigid biomolecules, but can be also used for determining small proton–proton residual dipolar couplings between different functional groups in polymer networks.

The possibility of exciting and detecting ¹H NMR DQ coherences in inhomogeneous static and radio frequency magnetic fields were shown using the NMR-MOUSE [17,18]. Even in such adverse conditions the DQ build-up and decay curves give access to quantitative values of the ratio of proton residual dipolar couplings, which are in good agreement with those measured in homogeneous fields.

3 Grafted polymers

The properties of polymers at interfaces are of growing technological importance due to extended use of surfaces modified by polymer films and polymer grafting and also due to the fundamental interest of surface effects on both polymer conformation and chain dynamics [19,20]. The preferred model polymer for such studies has been poly(dimethylsiloxane) (PDMS). The surface-induced orientational order of a monolayer thin film of this very flexible polymer, spin-coated on a polystyrene layer grafted on a silicon wafer [21] and deposited onto the walls of cylindrical pores [22] was investigated by ²H NMR spectroscopy. Recently, it was shown that the ¹H transverse relaxation is highly sensitive to the heterogeneous mobility of PDMS chains grafted onto a silica surface [23].

A bimodal distribution of the segmental-chain orientation corresponding to the interface and the mobile regions of PDMS chains grafted onto silica was detected by ¹H DQ and TQ NMR spectroscopy on static samples [24]. Normalized DQ build-up curves are shown in Fig. 3 for two different temperatures. The samples PDMS1-3 have an average number of siloxane bonds per grafted site of 7.7, 6.2, and 4.5, respectively. The same behavior was detected for TQ build-up curves [24]. These curves display two maxima. The first maximum corresponds to the most immobilized fraction of the grafted chains at the interface. The second maximum corresponds to a distribution of proton residual dipolar couplings of the mobile segments.

Fig. 3
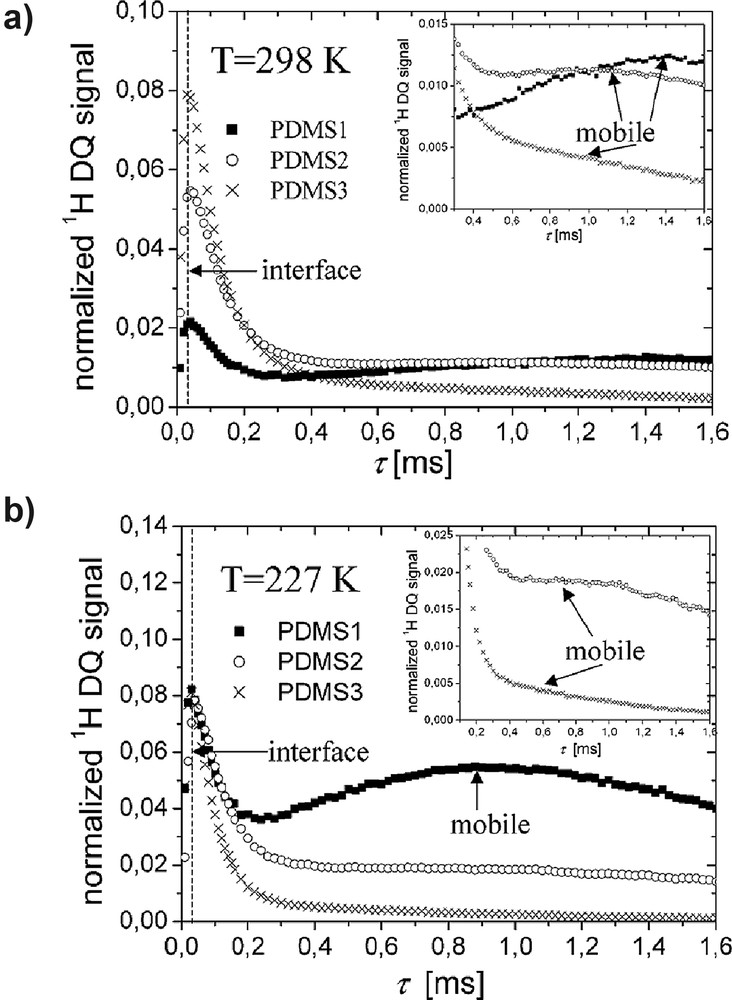
Proton DQ build-up curves of grafted PDMS samples recorded at T = 298 K (a) and T = 227 K (b) [24]. The region of the DQ build-up curves after the first maximum is enlarged in the insets.

The size of the interface was found to be independent of the total length of the PDMS chains. A broad distribution of segmental orientation prevails in the mobile region, and the segmental mobility is proportional to its fraction, and therefore, to the chain length. The results obtained by ¹H MQ NMR were corroborated by the measurements of the residual dipolar couplings using SEDOR and REDOR experiments [25].

Proton DQ and TQ NMR techniques have been also applied to study surface-induced order and anisotropic dynamics in ultra thin films (up to about four layers thick) of a flexible polymer, PDMS [26]. The residual dipolar couplings, and dynamic order parameter of the surface bound layer are estimated at different PDMS coverages. Results show that the thin PDMS films exhibit discrete dynamic layers with step-wise increase in their motional freedom with increasing film thickness. Dynamic heterogeneity is more pronounced at a film thickness of one monomer layer, which is absent for sub-monomer coverage.

4 Anisotropy of collagen fiber orientation in tendon

Most biological tissues possess some degree of order. In ordered tissues, where the molecular motion is anisotropic, dipolar and quadrupolar interactions are not averaged to zero. In such cases homo- and heteronuclear MQ coherences can be formed [27]. In collagen-containing tissues such as tendons, ligaments, cartilage skin, blood vessels and nerves, DQ coherences are formed as a result of the interaction of water molecules with the collagen fibers. Therefore, the orientation of the macromolecules induces an anisotropy in the residual dipolar couplings.

The anisotropy of the angular distribution of collagen fibrils in a sheep tendon was investigated by ¹H DQ build-up curves, DQ filtered NMR signals, and dipolar-encoded longitudinal magnetization (DELM) [28,29]. All these NMR quantities were measured with a five-pulse sequence for different angles between the direction of the static magnetic field and the axis of the tendon plug.

Proton DQ filtered spectra measured at an excitation/reconversion time of $τ = 80 μ s$ show a well resolved splitting (Fig. 4). These spectra prove that for sheep tendon at room temperature the approximation of spin-1/2 pairs is valid and that the residual dipolar interaction is not much smaller than the proton exchange rate [28]. The normalized quantities $〈 ϖ_{d}^{2} (θ) 〉 / 〈 ϖ_{d}^{2} (0) 〉$ , where $〈 ϖ_{d}^{2} (θ) 〉$ is related to the residual dipolar coupling measured from the slopes of the DQ build-up curves and the line splitting are shown in Fig. 5 as a function of the orientation angle $θ$ . The experimental data of Fig. 5 show that the minimum value of $〈 ϖ_{d}^{2} (θ) 〉$ is not zero, and the angular contrast in residual dipolar couplings is $| {〈 ϖ_{d}^{2} (0) 〉}^{1 / 2} / {〈 ϖ_{d}^{2} (90 °) 〉}^{1 / 2} | \approx 2.7 \pm 0.2$ . Both these facts can be explained by a distribution of the tendon fibril orientation described by the equations given below.

Fig. 4
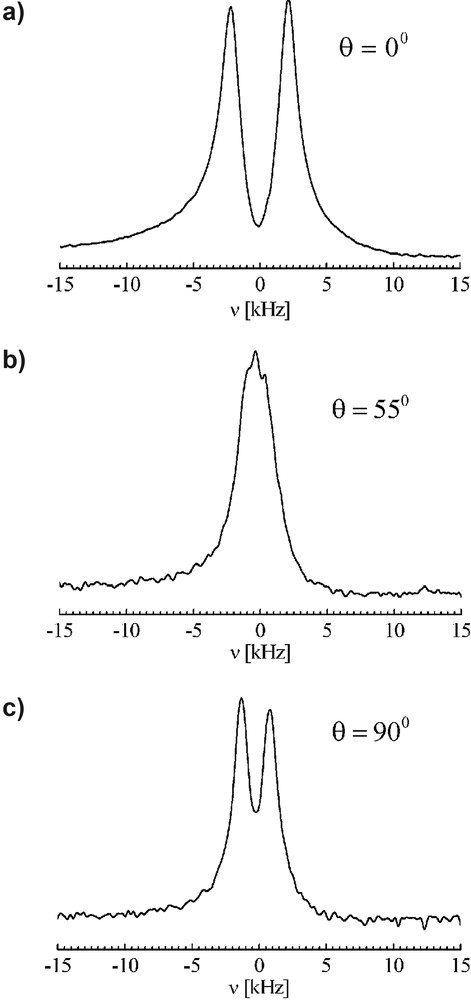
Proton DQ edited NMR spectra for the orientations $θ° = 0 °$ , $θ° = 55 °$ , and $θ = 90 °$ of the sheep tendon plug relative to the direction of the static magnetic field [29].

Fig. 5
Anisotropy of the normalized square of the residual dipolar couplings $〈 ϖ_{d}^{2} (θ) / ϖ_{d}^{2} (0) 〉$ measured from DELM (a), DQ (b), and DQ edited spectra (c) [29]. The continuous lines represent the best fits using Eqs. (5)–(7).

The normalized anisotropy of the square of the residual dipolar coupling can be written as:

\frac{〈 ϖ_{d}^{2} (θ) 〉}{〈 ϖ_{d}^{2} (0) 〉} = \frac{\int_{0}^{π / 2} | R (\tilde{β}; {\tilde{β}}_{0}) | f (\tilde{β}, θ) \sin \tilde{β} d \tilde{β}}{\int_{0}^{π / 2} | R (\tilde{β}; {\tilde{β}}_{0}) | f (\tilde{β},0) \sin \tilde{β} d \tilde{β}}

(1)

where the angular function

f (\tilde{β}, θ)

depends on the azimuthal angles

\tilde{β}, θ

[28].

R (\tilde{β}; {\tilde{β}}_{0})

is the uniaxial orientation distribution function of the collagen fibrils around the tendon plug axis. The center of the distribution function corresponds to the angle

{\tilde{β}}_{0}

. The normalized distribution of angle

\tilde{β}

can be described in the most general way by the Legendre polynomials expansion, i.e.:

R (\tilde{β}; {\tilde{β}}_{0}) = \frac{1}{8 π^{2}} \sum_{L = 0}^{\infty} (2 L + 1) 〈 P_{L} 〉 P_{L} (\cos (\tilde{β} - {\tilde{β}}_{0}))

(2)

where

〈 P_{L} 〉

are the moments or order parameters of the distribution.

The best fit of the data shown in Fig. 5 with Eqs. (1) and (2) lead to the evaluation of the center value and order parameters of the angular distribution function. These values are presented in Table 1 up to the order L = 6. In addition, the anisotropy of the residual dipolar couplings was evaluated in terms of a Gaussian angular distribution function with a standard deviation of $19 ° \pm 1 °$ and with the center of the distribution at $2 ° \pm 1 °$ [28].

Experiment	${\tilde{β}}_{0} {[°]}^{a}$	${〈 P_{2} 〉}^{a}$	${〈 P_{4} 〉}^{a}$	${〈 P_{6} 〉}^{a}$
DELM	1.79	0.99	0.91	0.82
DQ	1.79	0.86	0.84	0.28
line splitting	1.80	0.92	0.90	0.66

5 Complex polymer morphology based on spin-diffusion NMR using a double-quantum (DQ) filter

One established NMR method to investigate domain sizes and morphology of heterogeneous polymers is based on the magnetization exchange after production of a z magnetization gradient by a dipolar filter [30,31]. These spin-diffusion experiments are suitable to investigate different aspects of structural heterogeneities in a broad range of spatial dimensions from 0.1 nm to about 200 nm.

The majority of spin-diffusion experiments performed in the past used chemical or dipolar filters that select mainly the signal from the domains with high molecular mobility. MQ coherences of dipolar coupled spin-1/2 nuclei have also been exploited as a filter to separate different magnetization components in a spatially heterogeneous system. The first investigation of this type was reported in Ref. [32], where it was shown that by appropriate selection of excitation/reconversion periods of the MQ coherences the magnetization of the domains with stronger dipolar couplings in a heterogeneous sample would pass through the filter whereas that of the weaker dipolar couplings will be filtered out.

Recently, a DQ dipolar filter was implemented (Fig. 6) in conjunction with a MAPE (MAgic and Polarization Echo) filter [33], which selects the magnetization from the mobile regions in order to characterize the morphology of various heterogeneous polymeric systems [34]. This new approach makes also use of general analytical solutions developed for the case of a lamellar system composed of three domains with different sizes, diffusivities, and proton densities [34–36]. The advantage of a DQ filter is due to the fact that it is much easier to detect the narrow NMR signal which corresponds to the mobile domains since its integral intensity can be evaluated more accurately compared to the case of traditional spin-diffusion experiments in which the increase in the intensity of the broad NMR signal is measured. Nevertheless, the dipolar filter based on the selection of MQ coherences produces weak initial NMR signals because of the low efficiency in excitation of such coherences. Additionally, it was shown that information about the lamellar morphology of systems could be obtained independent of other techniques using such a combination of dipolar filters and analytical solutions of the spin-diffusion equation [34].

Fig. 6
Dipolar filter efficiency for a PEO-b-PS diblock copolymer [34]. Proton spectrum after (a) a 90° pulse;(b) using a DQ filter with an excitation time of 18 μs; (c) using a MAPE filter with a free evolution period of 110 μs. For both filters very short diffusion times were employed.

Furthermore, the above approach was successfully applied for the characterization of the morphology of Nylon-6 fibres [35,36]. Nylon-6 (PA6) is one of the most important synthetic fiber-forming materials used for high-speed melt spinning covering a broad range of applications. These fibres have a morphology consisting of a complex distribution of mobile amorphous, less-mobile amorphous and crystalline regions which, is hard to characterize by techniques such as X-ray diffraction.

A DQ filter was used in order to select the rigid domains in Nylon-6 fibers. In this way information about the dimensions of the crystalline and less-mobile amorphous domains is obtained along the fibril direction as well as perpendicular to it. As a first approximation the three-dimensional solutions of the spin-diffusion equation were used in terms of a product of one-dimensional solutions describing a lamellar morphology [36].

The morphology derived from this particular NMR experiment can be combined with that obtained by employing dipolar filters to select the signal from mobile domains [35,36] (Fig. 7). This latter spin-diffusion experiment reveals only the spatial distribution of the mobile amorphous domains and the aggregates of fibrils as a whole. These spin-diffusion data were interpreted in terms of a model in which z magnetization transfer takes place towards sinks of crystalline and less-mobile amorphous domains which are connected in series and in parallel and which form aggregates. These crystalline/amorphous aggregates separated by mobile amorphous domains involve about 4–10 fibrils. The mobile amorphous phase is located at the surface of these aggregates and its presence is due to the fact that from point to point there are voids where the chain mobility is higher. Hence, a more detailed picture of the Nylon-6 fiber morphology is obtained by these spin-diffusion experiments using tuned dipolar filters compared with the X-ray methods. The latter methods do not discriminate between semi-rigid and soft mobile phases. Moreover, the domain sizes of the Nylon-6 fibers along and perpendicular to the direction of fibrils as well as the changes produced by the variation of the winding speed and draw ratio are in agreement with the data from WAXD and SAXS [35,36].

Fig. 7
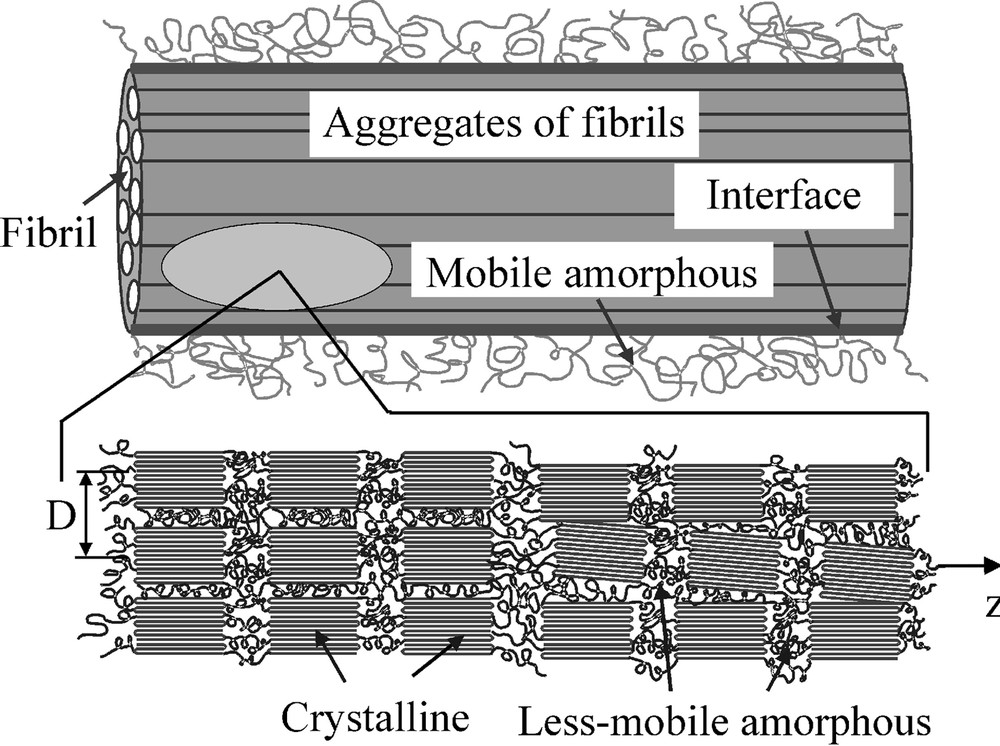
Model morphology of Nylon-6 fibres [35,36]. The distance between the fibrils is D. The fibrils are separated within the aggregate by a less-mobile amorphous domain. The axes of the fibrils are supposed to be oriented approximately parallel to the largest dimension of the interface and the mobile amorphous regions. Along the fibrils the lamellar stack of crystalline/less-mobile amorphous domains is present.

6 Molecular dynamic heterogeneities of confined thin lipid films

Molecular films of self-assembled single bilayer lipid membranes on solid planar supports and more recently lipid monolayers on silica beads, have attracted considerable attention due to their potential applications in biosensing and bioseparation as well as due to their interesting physical properties [37]. Knowledge of the role that the solid substrate plays with regard to the lipid molecular ordering and dynamics may serve as important information in the manufacture of biosensors. Hence the study of the dynamics of lipid molecules at various surface coverages ranging from bulk-like thick films to submonolayer effective thickness is essential for understanding the properties of lipid films at a molecular level.

Our study was focused on thin lipid films (egg-yolk lecithin, 99% pure) of submonolayer to one layer thickness confined in cylindrical Anopores of various diameters [38,39]. The Anopore membranes have uniform diameters of d = 200 nm and d = 20 nm. On the smooth surfaces of the membrane the molecular deposition is expected to be uniform and the thickness of the deposition depends on the concentration of lecithin in the solvent.

Magnetization-exchange experiments were performed in order to characterize the effect of the confinement on the heterogeneity of the chain dynamics [38]. The gradient of magnetization in this experiment was generated with the help of a DQ filter, which selects the magnetization from the most rigid part of the molecule. The magnetization-exchange decay and build-up curves were interpreted in terms of a theoretical model based on the approximation of one-dimensional spin-diffusion process in a three-domain morphology. The dynamic heterogeneities of the fatty acid chains and the effects of the surface area per molecule, the diameter of the pores, and the temperature were characterized with the help of spin-diffusion coefficients. The estimated values indicate that the surface induces the orientation of the confined molecules and, depending on the concentration and/or pore sizes, the lecithin chains will adopt different directions with regard to the pore wall (Fig. 8). For low concentrations the most favorable conformation is flat on the surface while for higher concentrations, the molecules will orient perpendicular to the surface. Moreover, a Gaussian distribution function of the ¹H residual dipolar couplings was introduced to quantify the effect of various parameters on the molecular dynamics of the mobile region of the fatty acid chains (Fig. 9). The results indicate that the effect of the surface is extended over the whole chain, and therefore, each part of the chain can independently reflect the effect of the interaction with the wall. Moreover, the heterogeneity of the chain dynamics is higher at higher concentrations and temperatures.

Fig. 8
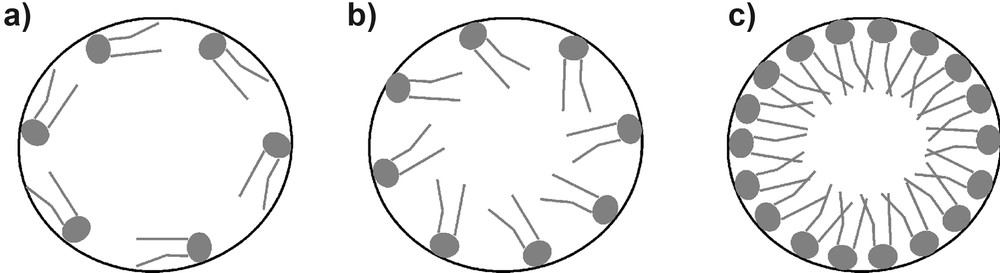
Possible anchoring directions that the lecithin molecules may adopt under confinement conditions: (a) flat on the surface, (b) tilted, and (c) axial.

Fig. 9
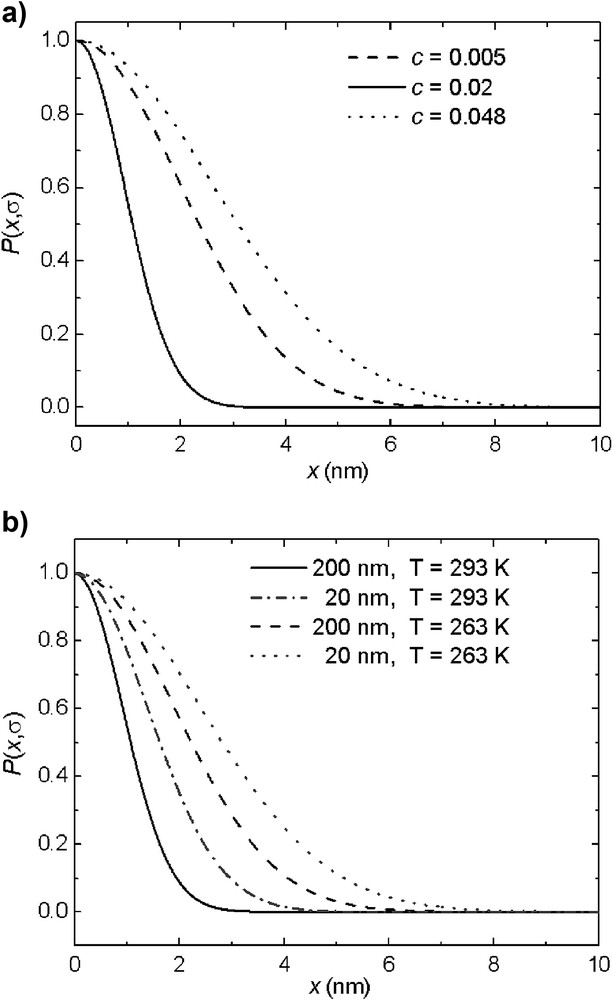
Dependence of the Gaussian distribution function on (a) surface coverage in pores with a diameter of 200 nm at T = 293 K, and (b) the pore size and temperature for a concentration of c = 0.02 [38].

Further on, MQ build-up curves and DQ edited spectra were used to compare the chain dynamics of the confined molecules with that in the free state [39]. The advantage of these methods is that they are model free and easy to be performed. The slopes of the DQ and TQ build-up curves (hence the respective values of the residual dipolar couplings) and the splitting of the DQ edited spectra (Fig. 10) are remarkably lower for the films compared to those in the bulk (at room temperature), indicating faster dynamics in the films. This is due to the fact that in the bulk state, lipid molecules are tightly packed and the dynamics of the fatty acid chains experience steric hindrances, which lead to a stronger dipolar interaction.

Fig. 10
DQ edited spectra of bulk lecithin and lecithin films of various concentrations confined in pores with a diameter of 200 nm [39]. The measurements were performed at room temperature.

7 Conclusions

Homonuclear and heteronuclear MQ NMR provides useful information related to the structure, orientation, complex morphology and segmental dynamic heterogeneities of elastomers, semicrystalline polymers, confined biomolecules and ordered tissues. This information is revealed by the measurements of the residual dipolar couplings and MQ edited spectra. MQ build-up curves in the initial excitation/reconversion regime allow us to measure residual dipolar couplings model free, i.e. without any knowledge of correlation time distribution as in the transverse magnetization measurements. Moreover, for orientation measurements in ordered tissues the MQ coherences filter out the free water being sensitive only to the collagen bound water. The possibility to used dipolar filters for editing of rigid or mobile phases in spin-diffusion experiments allow us to reveal more information in the case of complex morphologies of semicrystalline polymers.

In some favorable cases site-selective information can be obtained for non-rotating samples. This NMR method can be correlated with NMR parameters like transverse magnetization relaxation and self-diffusion for the characterization of dynamics and deformation of polymer networks.

References

[1] R.R. Ernst; G. Bodenhausen; A. Wokaun Principles of Nuclear Magnetic Resonance in One and Two Dimensions, Oxford, Clarendon, 1987

[2] M. Munowitz; A. Pines Adv. Chem. Phys., 66 (1987), p. 1

[3] B. Blümich NMR Imaging of Materials, Clarendon Press, Oxford, UK, 2000

[4] J.-P. Cohen Addad Prog. NMR Spectrosc., 25 (1993), p. 1

[5] G. Navon; H. Shinar; U. Eliav; Y. Seo NMR Biomed., 14 (2001), p. 112

[6] D.E. Demco; S. Hafner; H.W. Spiess Handbook of Spectroscopy of Rubbery Materials, Repra Technology Ltd., Shawbury, UK (V.M. Litvinov; P.P. De, eds.), 2002

[7] D.E. Demco; B. Blümich in: Encyclopedia of Polymer Science and Technology, 10 (2004), p. 637

[8] C. Malveau; P. Tekely; D. Canet Solid-State Nucl. Magn. Reson., 7 (1997), p. 271

[9] M. Schneider; L. Gasper; D.E. Demco; B. Blümich J. Chem. Phys., 111 (1999), p. 402

[10] V.M. Litvinov; M. Bertmer; L. Gasper; D.E. Demco; B. Blümich Macromolecules, 36 (2003), p. 7598

[11] M. Bertmer; L. Gasper; D.E. Demco; B. Blümich; V.M. Litvinov Macrom. Chem. Phys., 205 (2004), p. 83

[12] M. Wang; M. Bertmer; D.E. Demco; B. Blümich J. Phys. Chem. B, 108 (2004), p. 10911

[13] M. Voda; D.E. Demco; J. Perlo; R.A. Orza; B. Blümich J. Magn. Reson., 172 (2004), p. 98

[14] R. Fechete; D.E. Demco; B. Blümich J. Magn. Reson., 169 (2004), p. 19

[15] R. Graf; D.E. Demco; S. Hafner; H.W. Spiess Solid-State Nucl. Magn. Reson., 12 (1998), p. 139

[16] C. Filip; X. Filip; M. Bertmer; D.E. Demco; B. Blümich J. Magn. Reson., 150 (2001), p. 184

[17] A. Wiesmath; C. Filip; D.E. Demco; B. Blümich J. Magn. Reson., 149 (2001), p. 258

[18] A. Wiesmath; C. Filip; D.E. Demco; B. Blümich J. Magn. Reson., 154 (2002), p. 60

[19] H. Höcker, J. Kahovec (Eds.), Macromol. Symp. 139 (1999), and references therein.

[20] B. Zhao; W.J. Brittain Prog. Polym. Sci., 25 (2000), p. 677

[21] S. Rivillon; P. Auroy; B. Deloche Phys. Rev. Lett., 84 (2000), p. 499

[22] S.V. Primak; T. Jin; A.C. Daager; D. Finottello; E.K. Mann Phys. Rev. E., 65 (2002) (031804)

[23] V.M. Litvinov; H. Barthel; J. Weis Macromolecules, 35 (2002), p. 4356

[24] M. Wang; M. Bertmer; D.E. Demco; B. Blümich; V.M. Litvinov; H. Barthel Macromolecules, 36 (2003), p. 4411

[25] M. Wang, M. Bertmer, D.E. Demco, B. Blümich (to be published).

[26] B. Jagadeesh; D.E. Demco; B. Blümich Chem. Phys. Lett., 393 (2004), p. 416

[27] U. Eliav; G. Navon J. Am. Chem. Soc., 124 (2002), p. 3125

[28] R. Fechete; D.E. Demco; B. Blümich; U. Eliav; G. Navon J. Magn. Reson. (2003), pp. 16-166

[29] R. Fechete; D.E. Demco; B. Blümich NMR Biomed., 16 (2003), p. 479

[30] K. Schmidt-Rohr; H.W. Spiess Multidimensional Solid-State NMR and Polymers, Academic Press, London, 1994

[31] V.J. McBrierty; K.J. Packer Nuclear Magnetic resonance in Solid Polymers, Cambridge University Press, Cambridge, 1993

[32] R. Graf; D.E. Demco; J. Gottwald; S. Hafner; H.W. Spiess J. Chem. Phys., 106 (1997), p. 885

[33] D.E. Demco; A. Johansson; J. Tegenfeldt Solid-State Nucl. Magn. Reson., 4 (1995), p. 13

[34] A. Buda; D.E. Demco; M. Bertmer; B. Blümich; B. Reining; H. Keul; H. Höcker Solid-State Nucl,. Magn. Reson., 24 (2003), p. 39

[35] A. Buda; D.E. Demco; M. Bertmer; B. Blümich; V.M. Litvinov; J.P. Penning J. Phys. Chem., B 107 (2003), p. 5357

[36] A. Buda; D.E. Demco; B. Blümich; V.M. Litvinov; J.P. Penning ChemPhysChem, 5 (2004), p. 876

[37] J.T. Groves; N. Ulman; S.G. Boxer Science, 275 (1997), p. 651

[38] A. Buda; J. Bharatam; D.E. Demco; B. Blümich J. Chem. Phys., 122 (2005) (034701)

[39] B. Jagadeesh; A. Prabhakar; A. Buda; D.E. Demco; B. Blümich Chem. Phys. Lett., 404 (2005), p. 177

Comments - Policy