Classical and ab initio preparation of reliable structures for polymeric coordination compounds

Harald O. Jeschke; L. Andrea Salguero; Roser Valentí; Christian Buchsbaum; Martin U. Schmidt; Matthias Wagner

doi:10.1016/j.crci.2006.06.007

Classical and ab initio preparation of reliable structures for polymeric coordination compounds

Harald O. Jeschke ¹ ; L. Andrea Salguero ¹ ; Roser Valentí ¹ ; Christian Buchsbaum ² ; Martin U. Schmidt ² ; Matthias Wagner ²

¹ Institut für Theoretische Physik, Johann Wolfgang Goethe-Universität, Max-von-Laue-Str. 1, 60438 Frankfurt/Main, Germany
² Institut für Anorganische und Analytische Chemie, Johann Wolfgang Goethe-Universität, Max-von-Laue-Str. 7, 60438 Frankfurt/Main, Germany

Comptes Rendus. Chimie, Volume 10 (2007) no. 1-2, pp. 82-88.

Résumé

The detailed investigation of electronic and magnetic properties of polymeric coordination materials with accurate ab initio quantum mechanical methods is often computationally extremely demanding because of the large number of atoms in the unit cell. Moreover, usually the available structural data are insufficient or poorly determined, especially when the structure contains hydrogen atoms. In order to be able to perform controlled ab initio calculations on reliable structures, we use a two-step approach to systematically prepare model structures for polymeric coordination compound systems and to relax them to their equilibrium configuration. First, a structure is constructed on the basis of a crystallographic database and optimized by force field methods; in the second step, the structure is relaxed by ab initio quantum mechanical molecular dynamics. With this structure, we perform accurate electronic structure calculations. We will apply this procedure to a Fe(II) triazole compound and to a coordination polymer of Cu(II) ions with 2,5-bis(pyrazol-1-yl)-1,4-dihydroxybenzene.

Métadonnées

Reçu le : 2006-03-10
Accepté le : 2006-06-14
Publié le : 2006-12-18

DOI : 10.1016/j.crci.2006.06.007

Mots clés : Coordination polymer, Density functional theory, Structure optimization

Affiliations des auteurs :

Harald O. Jeschke ¹ ; L. Andrea Salguero ¹ ; Roser Valentí ¹ ; Christian Buchsbaum ² ; Martin U. Schmidt ² ; Matthias Wagner ²

¹ Institut für Theoretische Physik, Johann Wolfgang Goethe-Universität, Max-von-Laue-Str. 1, 60438 Frankfurt/Main, Germany
² Institut für Anorganische und Analytische Chemie, Johann Wolfgang Goethe-Universität, Max-von-Laue-Str. 7, 60438 Frankfurt/Main, Germany

@article{CRCHIM_2007__10_1-2_82_0,
     author = {Harald O. Jeschke and L. Andrea Salguero and Roser Valent{\'\i} and Christian Buchsbaum and Martin U. Schmidt and Matthias Wagner},
     title = {Classical and ab initio preparation of reliable structures for polymeric coordination compounds},
     journal = {Comptes Rendus. Chimie},
     pages = {82--88},
     publisher = {Elsevier},
     volume = {10},
     number = {1-2},
     year = {2007},
     doi = {10.1016/j.crci.2006.06.007},
     language = {en},
}

TY  - JOUR
AU  - Harald O. Jeschke
AU  - L. Andrea Salguero
AU  - Roser Valentí
AU  - Christian Buchsbaum
AU  - Martin U. Schmidt
AU  - Matthias Wagner
TI  - Classical and ab initio preparation of reliable structures for polymeric coordination compounds
JO  - Comptes Rendus. Chimie
PY  - 2007
SP  - 82
EP  - 88
VL  - 10
IS  - 1-2
PB  - Elsevier
DO  - 10.1016/j.crci.2006.06.007
LA  - en
ID  - CRCHIM_2007__10_1-2_82_0
ER  -

%0 Journal Article
%A Harald O. Jeschke
%A L. Andrea Salguero
%A Roser Valentí
%A Christian Buchsbaum
%A Martin U. Schmidt
%A Matthias Wagner
%T Classical and ab initio preparation of reliable structures for polymeric coordination compounds
%J Comptes Rendus. Chimie
%D 2007
%P 82-88
%V 10
%N 1-2
%I Elsevier
%R 10.1016/j.crci.2006.06.007
%G en
%F CRCHIM_2007__10_1-2_82_0

Harald O. Jeschke; L. Andrea Salguero; Roser Valentí; Christian Buchsbaum; Martin U. Schmidt; Matthias Wagner. Classical and ab initio preparation of reliable structures for polymeric coordination compounds. Comptes Rendus. Chimie, Volume 10 (2007) no. 1-2, pp. 82-88. doi : 10.1016/j.crci.2006.06.007. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2006.06.007/

Version originale du texte intégral

1 Introduction

Polymeric complexes form a class of materials that attract interest from chemists and physicists. The possibility to apply organic synthesis methods to produce families of compounds with similar structures, but subtly differing physical behavior, offers an opportunity to design materials with planned properties.

Materials showing temperature or pressure induced high-spin–low-spin transitions are currently being discussed for applications in data storage or spintronics. Such magnetic transitions can be optically triggered, raising hopes for technological applications. The cooperativity of such light-induced phase transitions also raises questions concerning the underlying microscopic processes [1–4]. Another important class of polymeric coordination compounds is, in general, low-dimensional magnetic materials where the coupling strengths between the metal ions can be tuned by chemically modifying the ligands and the transition metal ion coordination. Effects of, for instance, dimensional crossover can be studied in this way.

Most of these compounds generally contain a large number of atoms in the unit cell and a very low symmetry (in 80% of the cases triclinic or monoclinic), making the first principles study of the electronic and magnetic properties of these systems under different conditions (pressure, temperature, light irradiation) computationally very demanding. Moreover, since an accurate determination of hydrogen positions with X-ray diffractometry is very difficult, usually the available structure data are poorly determined, implying unstable quantum mechanical calculations. For some cases, the crystal structures are not even known, due to the absence of single crystals suitable for an X-ray structure analysis. In order to overcome these shortcomings, we use in this communication a two-step approach which allows us to perform accurate ab initio density functional theory (DFT) calculations on reliable model structures for coordination polymers. It should be noted that the expression ‘ab initio prediction of crystal structures’ is also used in the sense of ‘a priori prediction’, i.e. predictions without reference to diffraction data. Possible crystal structures of organic compounds with 20–60 atoms can be predicted within some days or weeks using force field methods [5]. This works also for organometallic compounds, e.g. pentamethylferrocene Fe(C₅H₅) [(C₅CH₃)₅] [6]. Quantum mechanical methods are much more time-consuming; hence their use is limited to local optimizations starting from a given structural model. Thus, quantum mechanical and force field methods can be combined by making first a global optimization using force field methods, followed by a local optimization with quantum mechanical methods. This was done for many inorganic systems, e.g. NaCl or MgF₂ [7], and a few simple organic compounds, e.g. glycole C₂H₄(OH)₂ and glycerol C₃H₅(OH)₃ [8]. In most other cases of crystal structure predictions, quantum mechanical calculations were only used for secondary calculations, e.g. to calculate molecular geometries and electrostatic charges, or to derive intramolecular or intermolecular potential curves for subsequent force field optimizations [9].

If experimental data are known, e.g. from crystal data of analogous structures, this knowledge should of course be used as far as possible in order to generate reliable model structures and to calculate solid-state properties. Here, we apply ab initio DFT methods to understand the relationships between the structures and the electronic and magnetic properties of both (i) spin crossover materials and (ii) low-dimensional spin systems. We will consider two representatives from this large class of compounds: (i) a Fe(II) triazole compound [10,11] which is thought to have a polymer structure and (ii) a coordination polymer of Cu(II) ions with 2,5-bis(pyrazol-1-yl)-1,4-dihydroxybenzene [12] (we shall denote it as [Cu(bpydhb)]_n; alternative names given in the literature are CuCCP [13]).

For the Fe(II) triazole system [10,11], there is no direct accurate determination of the crystal structure of the complex as it cannot be crystallized sufficiently well. A chain-like structure for such compounds of formula [Fe(Rtrz)₃]A₂·S, where A denotes the anion, was predicted from EXAFS spectroscopy [14]. For analogous Cu(II) compounds, this chain structure was confirmed by single crystal X-ray analysis (see e.g. Refs. [15,16]). Polymeric iron triazole compounds always show a poor crystallinity, and single crystals cannot be grown. Hence the X-ray structure analyses are limited to molecular compounds, e.g. trimers containing three Fe(II) ions connected by six triazole ligands and six terminal water molecules [17]. Polymeric iron triazole complexes have been studied by powder diffraction; but apart from a preliminary indexing of [Fe(Htrz)₃](ClO₄)₂·1.85 H₂O [18], no structural data have been published so far. On the other hand, these polymeric compounds show interesting high-spin–low-spin transitions in the solid state (see e.g. Ref. [19]), and quantum mechanical calculations could help to understand the mechanism of this spin crossover. Since all calculations of electronic and magnetic properties require a reliable and reasonable model of the crystal structure, we constructed the structures of a hypothetical polymer crystal. All available information of molecular iron triazole systems, and of analogous Cu(II) polymers were included. In order to make the ab initio DFT calculations feasible, we constructed at first some models containing small triazoles (e.g. methyl-triazole) and simple anions (e.g. F⁻). Our rationale is that the model compound still has the same coordination and immediate environment of the Fe(II) ion as the real material which should thus allow us to study the mechanisms of the high-spin–low-spin transition. Structures with more complex anions will be considered later.

The second system that we study, the coordination polymer of Cu(II) ions with 2,5-bis(pyrazol-1-yl)-1,4-dihydroxybenzene, [Cu(bpydhb)]_n, has been recently synthesized by Wagner et al. [12]. The Cu²⁺ ions in this compound form spin 1/2 antiferromagnetic Heisenberg chains running along the z-axis. We will analyze the influence on the electronic properties of slight structural modifications, like substitutions of small organic groups on the dihydroxybenzene or introduction of water ligands which change the coordination of Cu from square to octahedral. The structure of Cu(II) with 2,5-bis(pyrazol-1-yl)-1,4-dihydroxybenzene has been obtained by X-ray powder diffraction [12] and we will apply our two-step approach for the modified structures based on these data.

2 Methods

We derive and investigate model polymeric coordination compound structures in two steps. First, we create a rough structure on the basis of crystallographic databases [21]. If no crystal structures of similar compounds are known – like in the case of Fe triazoles –, we construct a hypothetical crystal structure having the highest possible symmetry, a small number of atoms per unit cell and a sensible arrangement of the individual fragments. The crystal structure is optimized by force field methods including the optimization of the unit cell parameters, but maintaining the crystallographic symmetry. We used the Cerius² program package [22] with a modified Dreiding [23] force field; atomic charges were calculated by the Gasteiger and Marsili method [24]. Afterwards we proceed to improve the structure by relaxing it again, but now with an ab initio quantum mechanical molecular dynamics method [25]. Note that we employ an all-electron method already at this step in order to obtain the best possible equilibrium structure even for demanding transition metal complexes. Finally, we analyze the properties of the relaxed model structure with an all electron ab initio DFT method of the highest precision [26].

Our Car Parrinello (CP) ab initio molecular dynamics (AIMD) calculations [25] are performed with a projector augmented wave (PAW) basis set [27]. This is an all-electron calculation based on the frozen core approximation. The exchange–correlation potential is evaluated in the generalized gradient approximation (GGA) as parameterized in Ref. [28]. After a first analysis of the electronic properties for the classically prepared model in order to determine the structural stability, we employ an AIMD with friction to refine the structure. We impose constraints on the atomic coordinates in order to preserve the space group symmetry of the compound.

For the final analysis step we employ the full potential linearized augmented plane wave (LAPW, APW + lo) method as implemented in the WIEN2k code [26].

3 Results

3.1 Fe(II) triazole

The Fe(II) spin crossover molecular systems have been intensively studied in the past [19] and various theories have been developed about the mechanism of the high-spin–low-spin transition. A few years ago, Kahn and Jay Martinez [10] proposed that the cooperativity of this transition may be enhanced by replacing molecular crystals by polymers, since in the latter the metallic sites are bridged by chemical linkers through which one may get efficient intersite coupling. A first-principle DFT study of such systems would bring some light into the properties of these materials. Unfortunately, to date it has not been possible to get an accurate X-ray structure determination of Fe(II) spin crossover polymer systems, as discussed above, which is an indispensable input for ab initio DFT calculations and therefore, to our knowledge, no reliable ab initio studies were performed. With the two-step method, we have obtained – based on known data for molecular Fe(II) spin crossover systems – optimized model polymer structures which can be used as input for ab initio DFT calculations. In Fig. 1 we present the structure of the polymer Fe(II) compound with 4-methyl-1,2,4-triazole moieties as bridging ligands between the Fe(II) cations. As anions we chose simple F⁻ ions in order not to complicate the DFT calculations. The structure has P2₁/m symmetry; a higher symmetry was not possible with this chemical composition. As an initial structure with low-spin character, the distances between the Fe(II) centers and the neighboring N atoms of the triazole rings were chosen to be d_Fe–N = 1.97 Å, close to the Fe–N distance of d_Fe–N = 2.0 Å, which is known to be typical for the low-spin variants of Fe triazole complexes [20], while for the structure with high-spin character we chose d_Fe–N = 2.2 Å. In Fig. 2 we present the spin-polarized density of states (DOS) obtained [26] for this system after structural optimization for the low-spin (Fig. 2(a)) and the high-spin (Fig. 2(b)) states. Shown is the total Fe d DOS for majority (upper panel) and minority (lower panel) spin states. Since Fe is in an octahedral environment of N, the 3 d states split into lower t_2g (d_xy, d_xz, d_yz) and higher e_g $(d_{x^{2} - y^{2}}, d_{z^{2}})$ states. In Fig. 2(a), the six electrons of Fe(II) 3d⁶ occupy fully the t_2g states (see DOS manifold between −2 and −0.2 eV) for both spins, thus corresponding to a low-spin S = 0 state. The e_g states are completely empty and lie above the Fermi level. In Fig. 2(b), the majority (spin up) t_2g and e_g states are occupied (upper panel DOS in the range between −3.8 and −0.6 eV), while the minority (spin down, lower panel) t_2g states are about one-third occupied and two-thirds empty. The minority e_g states are completely empty (states in the range of energies between 1 and 3 eV, lower panel). These results indicate that the system is in a high-spin S = 2 state. A detailed investigation of the magnetic properties of this polymer system for both spin states will be presented elsewhere [29].

Fig. 1
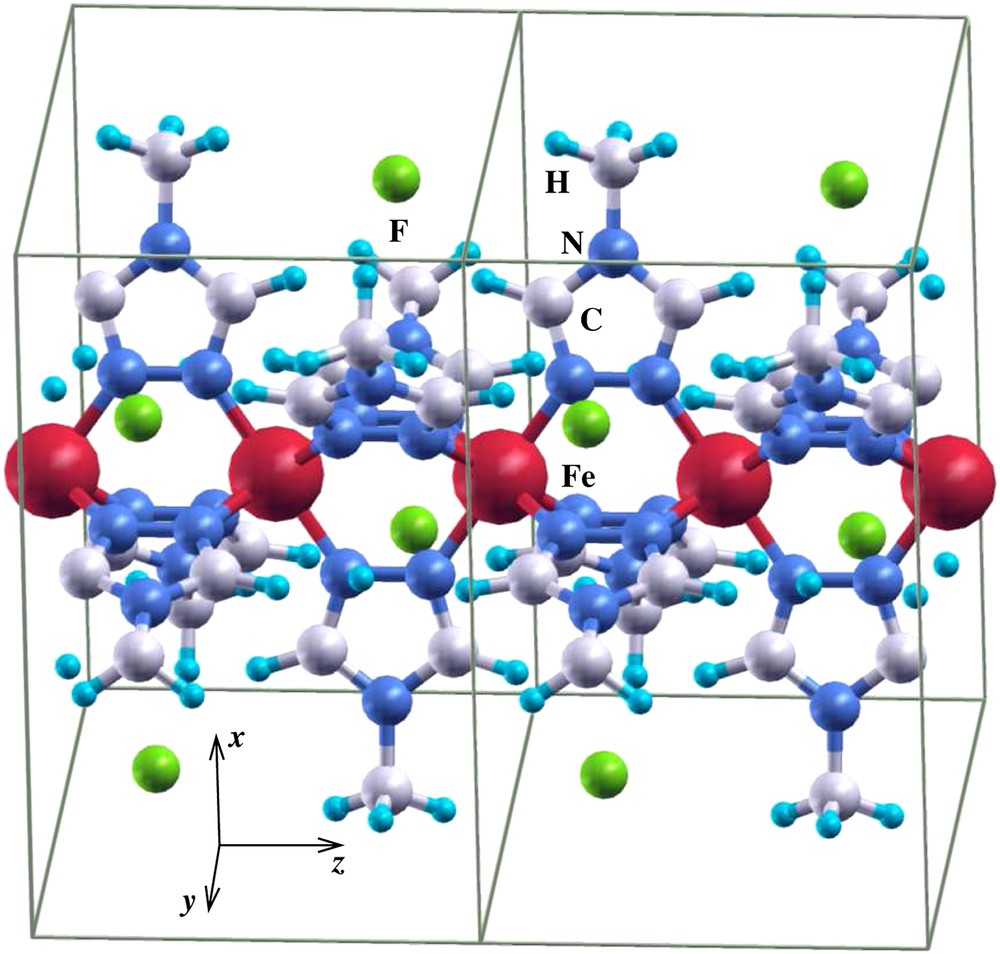
Two unit cells of the triazole model polymer. The usually complicated anions have been replaced by single atom F⁻ anions.

Fig. 2
Spin-polarized Fe d density of states of the Fe triazole structure in Fig. 1 in units of states/electronvolt/atom/spin. (a) For the S = 0 state of Fe; (b) for the S = 2 state of Fe. The upper and lower panels of the figure show, respectively, the density of states for the majority and minority spin states. The Fermi energy is indicated by a dotted line.

3.2 Cu(II)–polymer

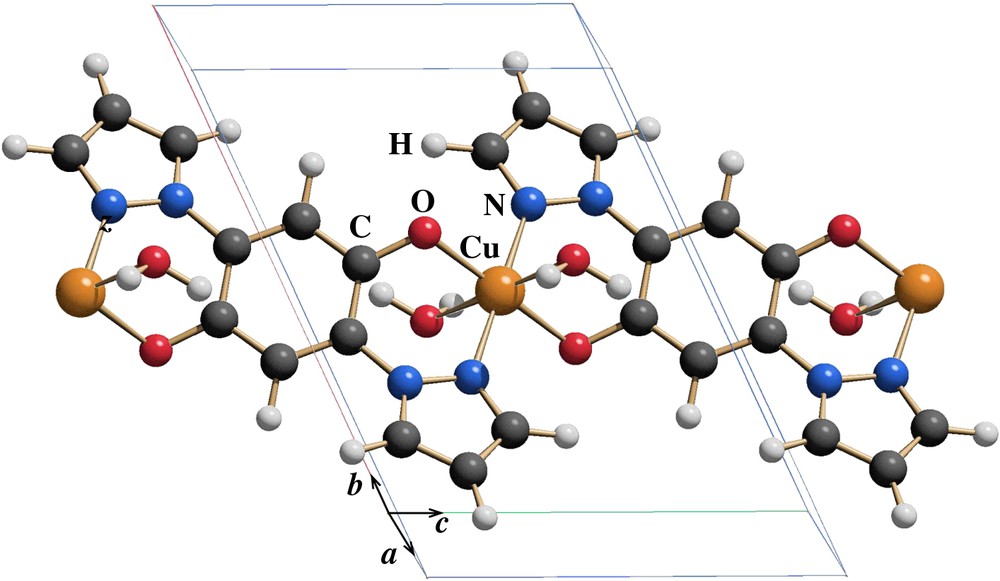
The Cu(II) coordination polymer [Cu(bpydhb)]_n synthesized by Wagner et al. [12] crystallizes in the triclinic space group $P \bar{1}$ (no. 2) and consists of stacks of chains of deprotonated 2,5-bis(pyrazol-1-yl)-1,4-dihydroxybenzene molecules connected by Cu²⁺ ions. This system behaves as a homogeneous antiferromagnetic spin 1/2 Heisenberg chain, with an exchange coupling constant J = 21.5 K/k_B estimated from magnetic susceptibility measurements [13]. The modular nature of this polymer makes it an adequate candidate to study chemically feasible structural modifications which may change the electronic and magnetic properties. Of special interest is the effect of dimensionality, i.e. tuning the crossover from one dimension to higher dimensions with the inclusion of adequately modified ligands. Since in this communication we want to stress the procedure we follow to design these structures and how we calculate the electronic properties, we will concentrate here on one substitution, namely two hydrogen atoms in the hydroquinone ring by two amino groups and show the efficiency of the two-step process. A second issue in this context that requires some attention is the study of the effect of two additional ligands at the Cu(II) ion, since such an octahedral coordination of copper is also frequently observed. We will here present the relaxation process on [Cu(bpydhb)]_n with two additional water molecules in the environment of copper.

In Fig. 3 we present the relaxed structure of [Cu(bpydhb)]_n where two hydrogen atoms in the hydroquinone rings have been substituted by two amino groups. This structure was obtained first by applying the force field method, which already has the correct information of the chemical distances and angles from databases. A quantum mechanical evaluation of the forces on the atoms (see Table 1) for this structure performed with the full potential LAPW method [26] (FPLAPW) still shows an unstable structure. Our aim is to relax this structure showing forces in the hundreds of mRyd/a_B with quantum mechanical molecular dynamics calculations, AIMD, until we find forces smaller than 25 mRyd/a_B which we set as upper bound for the force values. In order to get structures with forces smaller than 1 mRyd/a_B within the FPLAPW method, a fine tuning between the various first principles DFT methods we employ has to be considered. For our purposes here, a benchmark of 25 mRyd/a_B is reasonable.

Fig. 3
Four unit cells of [Cu(bpydhb)]_n (see text for the detailed formula) where two hydrogen atoms in the hydroquinone rings have been substituted by two amino groups. We find that the relaxed structure shows some tilting of the amino groups out of the plane defined by the benzene ring.

Atom	F_x	F_y	F_z
Cu	0	0	0
O	−47.4	−62.7	51.3
N1	89.1	32.8	−42.6
N2	22.4	27.2	−95.8
N3	−94.2	−66.8	33.5
C1	35.0	22.9	1.8
C2	−92.7	−29.2	111.1
C3	−39.2	−41.7	294.8
C4	−239.7	−104.1	16.5
C5	−26.6	−12.8	−304.2
C6	106.7	88.9	46.0
H1	128.6	−28.7	215.0
H2	255.3	106.1	−34.2
H3	23.8	25.6	−279.0
H4	4.8	10.8	−18.3
H5	−16.2	64.5	56.3

In Table 2 the forces after the AIMD relaxation are shown and we observe that the structure is relaxed to our required precision. The fractional coordinates of this structure are given in Table 3 where the symmetry and cell parameters were kept unchanged with respect to the unsubstituted Cu polymer system [Cu(bpydhb)]_n [12] a = 5.1723 Å, b = 7.9587 Å, c = 8.2298 Å, and angles α = 118.221°, β = 91.520°, γ = 100.148°.

Atom	F_x	F_y	F_z
Cu	0	0	0
O	12.7	16.9	21.7
N1	3.9	0.7	−17.2
N2	12.5	−2.3	8.4
N3	−21.0	−9.4	−5.5
C1	−1.0	−9.3	−19.4
C2	10.3	3.6	−2.1
C3	−7.1	−7.0	14.6
C4	−10.6	−12.7	−3.1
C5	−12.0	−6.0	−19.5
C6	12.0	3.4	−0.7
H1	1.4	−0.7	3.5
H2	3.1	−1.7	−1.4
H3	−0.4	−0.3	−4.1
H4	0.08	−5.5	−0.4
H5	1.1	−0.9	0.5

Atom	x	y	z
Cu	0.5	0.5	0.5
O	0.45952338	0.34384463	0.62047714
N1	0.87129861	0.67649196	0.85703667
N2	0.81592808	0.67403219	0.69273582
N3	0.89342131	0.81953377	0.25313235
C1	0.48379900	0.42607948	0.80332348
C2	0.68236558	0.58873536	0.92870320
C3	0.03998649	0.76736537	0.66677421
C4	0.23751744	0.83563448	0.81694695
C5	0.12514376	0.77281287	0.93447831
C6	0.70113966	0.66249861	0.12137891
H1	0.20669437	0.78002257	0.06146726
H2	0.43843580	0.91660682	0.83522646
H3	0.04936408	0.77481595	0.53807198
H4	0.82019516	0.86915420	0.37967013
H5	0.94873662	0.93065156	0.22239484

In a different modification of the Cu(II) polymer structure, we want to investigate the influence of a change of the Cu coordination from four to six on the electronic properties of the Cu(II) polymer. We added two water molecules bound to the Cu center and proceeded as outlined for the case of the NH₂ substitution: a first structure was obtained from the force field method, yielding high forces when we controlled it with an FPLAPW calculation. Further relaxation with AIMD yields forces around 20 mRyd/a_B. The corresponding structure is shown in Fig. 4, and the fractional coordinates are given in Table 4. The new unit cell is triclinic with space group $P \bar{1}$ (No. 2) as in the original Cu(II) polymer. The cell parameters are a = 5.2341 Å, b = 11.2493 Å, c = 8.0721 Å and the angles are α = 117.6108°, β = 68.8218°, γ = 127.1551°. Note the variation of these parameters with respect to those of [Cu(bpydhb)]_n [12], since in the relaxation process of the new structure the unit cell was allowed to relax properly in order to accommodate the water molecules.

Fig. 4
One unit cell of the [Cu(bpydhb)]_n polymer with water molecules bonding to the Cu(II) ion. The unit cell has been relaxed by the force field method but kept fixed in the AIMD relaxation. It differs considerably from the original [Cu(bpydhb)]_n polymer unit cell. The equilibrium positions of the water molecule lead to a nearly octahedrally coordinated Cu(II) ion.

Atom	x	y	z
Cu	0.5	0.5	0.5
O1	0.54548630	0.39146013	0.61449576
O2	0.11104809	0.50997119	0.71612732
C1	0.50846703	0.44754970	0.80067207
C2	0.68032852	0.61183880	0.90724635
C3	0.05894527	0.84496851	0.61704992
C4	0.26950758	0.95163087	0.75697623
C5	0.15279255	0.87395244	0.88376263
C6	0.32801067	0.33993413	0.89980571
N1	0.88662263	0.72926141	0.81944391
N2	0.82847386	0.71119262	0.65595860
H1	0.23644016	0.90962503	0.01364916
H2	0.47761970	0.07047826	0.76570604
H3	0.05611367	0.85699006	0.49132676
H4	0.20991897	0.21421176	0.81558567
H5	0.02924495	0.44665601	0.79637256
H6	0.92725690	0.45505960	0.64249638

We investigate now the electronic properties of the two model Cu(II) polymers with a precise FPLAPW calculation. A detailed account of the electronic and magnetic properties of both systems is presented elsewhere [30]. Here we would like to stress the effect of a planar Cu environment (for the Cu–NH₂ case) in comparison of an octahedral environment (for the Cu–H₂O case) on the Cu d density of states. In Fig. 5 (a) and (b) the Cu d density of states for both modifications is presented. While for both cases Cu is in an oxidation 2 + with the $d_{x^{2} - y^{2}}$ orbital half filled, the effect of the octahedral crystal field shows a splitting into t_2g (d_xy, d_xz, d_yz) for energies below −1.5 eV and e_g $(d_{z^{2}}, d_{x^{2} - y^{2}})$ states above −1.5 eV (see Fig. 5 (b)), while in the planar environment all d states are split and the states contributing to the bonding at the Fermi surface are mainly of $d_{x^{2} - y^{2}}$ character in the local coordinate frame of Cu which is defined with the local z direction pointing from the Cu to the O of the H₂O molecule and the y direction pointing from the Cu to the in-plane O atom.

Fig. 5
(a) Cu d density of states of the Cu polymer [Cu(bpydhb)]_n with two NH₂ groups, and (b) of the Cu polymer [Cu(bpydhb)]_n with two water ligands.

4 Conclusions

We have investigated the structural properties and its effects on the electronic properties of the quasi-one-dimensional polymer [Cu(bpydhb)]_n with small structural modifications and a model Fe(II) triazole polymer using classical and ab initio DFT methods. We demonstrate that the use of a stepwise approach to the study of complicated coordination polymer materials is an effective procedure to obtain reliable structures for accurate quantum mechanical analysis. We note that an exclusive use of ab initio molecular dynamics is very time-consuming, while the combination of the classical and quantum approaches speeds up the relaxation process considerably. We first employ a classical force field to create and relax plausible initial structures. In a second step, we proceed with ab initio molecular dynamics to relax these structures to a stable configuration. Finally we extract the electronic properties of the transition metal compounds with precise FPLAPW calculations.

Acknowledgments

H.O.J. gratefully acknowledges support from the DFG through the Emmy Noether Program. This work was financially supported by the Deutsche Forschungsgemeinschaft under the auspices of the Forschergruppe 412 “Spin and charge correlations in low-dimensional metalorganic solids”. We thank A. Kokalj for providing the visualization code XcrySDen [31]. We gratefully acknowledge support by the Frankfurt Center for Scientific Computing.

Bibliographie

[1] T. Tayagaki; K. Tanaka Phys. Rev. Lett., 86 (2001), p. 2886

[2] Y. Ogawa; S. Koshihara; K. Koshino; T. Ogawa; C. Urano; H. Takagi Phys. Rev. Lett., 84 (2000), p. 3181

[3] S. Koshihara; Y. Tokura; K. Takeda; T. Koda Phys. Rev. Lett., 68 (1992), p. 1148

[4] K. Miyano; T. Tanaka; Y. Tomioka; Y. Tokura Phys. Rev. Lett., 78 (1997), p. 4257

[5] P. Verwer; F.J.J. Leusen; W.T.M. Mooij; B.P. van Eijck; S.L. Price; P. Verwer; J. Kroon; J.P.M. Lommerse; W.D.S. Motherwell; H.L. Ammon; J.D. Dunitz; A. Gavezzotti; D.W.M. Hofmann; F.J.J. Leusen; W.T.M. Mooij; S.L. Price; B. Schweizer; M.U. Schmidt; B.P. van Eijck; P. Verwer; D.E. Williams; W.D.S. Motherwell; H.L. Ammon; J.D. Dunitz; A. Dzyabchenko; P. Erk; A. Gavezzotti; D.W.M. Hofmann; F.J.J. Leusen; J.P.M. Lommerse; W.T.M. Mooij; S.L. Price; H. Scheraga; B. Schweizer; M.U. Schmidt; B.P. van Eijck; P. Verwer; D.E. Williams; G.M. Day; W.D.S. Motherwell; H.L. Ammon; S.X.M. Boerrigter; R.G. Della Valle; E. Venuti; A. Dzyabchenko; J.D. Dunitz; B. Schweizer; B.P. van Eijck; P. Erk; J.C. Facelli; V.E. Bazterra; M.B. Ferraro; D.W.M. Hofmann; F.J.J. Leusen; C. Liang; C.C. Pantelides; P.G. Karamertzanis; S.L. Price; T.C. Lewis; H. Nowell; A. Torrisi; H.A. Scheraga; Y.A. Arnautova; M.U. Schmidt; P. Verwer Acta Crystallogr., Sect. B, 12 (1998), p. 327 (See e.g.)

[6] M.U. Schmidt; U. Englert J. Chem. Soc., Dalton Trans., 1996 (1996), p. 2077

[7] J.C. Schön; M. Jansen; J.C. Schön; M. Jansen Z. Kristallogr., 216 (2001), p. 307

[8] B.P. van Eijck; W.T.M. Mooij; J. Kroon J. Comput. Chem., 22 (2001), p. 805

[9] W.T.M. Mooij; F.B. van Duijnefeldt; J.G.C.M. van Duijnefeldt – van de Rijdt; B.P. van Eijck; W.T.M. Mooij; B.P. van Eijck; J. Kroon J. Phys. Chem. A, 103 (1999), p. 9872

[10] O. Kahn; C. Jay Martinez Science, 279 (1998), p. 44

[11] Y. Garcia; V. Ksenofontov; P. Gütlich Hyperfine Interact., 139/140 (2002), p. 543

[12] R. Dinnebier; H.W. Lerner; L. Ding; K. Shankland; W.I.F. David; P.W. Stephens; M. Wagner Z. Anorg. Allg. Chem., 628 (2002), p. 310

[13] B. Wolf; S. Zherlitsyn; B. Lüthi; N. Harrison; U. Löw; V. Pashchenko; M. Lang; G. Margraf; H.-W. Lerner; E. Dahlmann; F. Ritter; W. Assmus; M. Wagner Phys. Rev. B, 69 (2004), p. 092403

[14] A. Michalowicz; J. Moscovici; O. Kahn J. Phys. IV, 7 (1997), p. 633 (See and references therein)

[15] K. Drabent; Z. Ciunik Chem. Commun., 14 (2001), p. 1254

[16] Y. Garcia; P.J. van Koningsbruggen; G. Bravic; P. Guionneau; D. Chasseau; G.L. Cascarano; J. Moscovici; K. Lambert; A. Michalowicz; O. Kahn Inorg. Chem., 36 (1997), p. 6357

[17] Y. Garcia; P. Guionneau; G. Bravic; D. Chasseau; J.A.K. Howard; O. Kahn; V. Ksenofontov; S. Reiman; P. Gütlich Eur. J. Inorg. Chem. (2000), p. 1531

[18] E. Smit; B. Manoun; S.M.C. Verryn; D. de Waal Powder Diffr., 16 (2001), p. 37

[19] P. Gütlich; Y. Garcia; H.A. Goodwin Chem. Phys. Soc. Rev., 29 (2000), p. 419 (See and references therein)

[20] G. Vos; R.A. le Febre; R.A.G. de Graaff; J.G. Haasnoot; J. Reedijk J. Am. Chem. Soc., 105 (1983), p. 1682

[21] Cambridge Structural Database, Cambridge Crystallographic Data Centre, Cambridge, England, 2005

[22] Cerius², Version 4.9, Accelrys Inc., Cambridge/England, 2003.

[23] L. Mayo; B.D. Olafson; W.A. Goddard J. Phys. Chem., 94 (1990), p. 8897

[24] J. Gasteiger; M. Marsili Tetrahedron, 36 (1980), p. 3219

[25] R. Car; M. Parrinello Phys. Rev. Lett., 55 (1985), p. 2471

[26] P. Blaha; K. Schwartz; G.K.H. Madsen; D. Kvasnicka; J. Luitz WIEN2K, an Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties (K. Schwarz, ed.), Techn. University Wien, Austria, 2001 (ISBN: 3-9501031-1-2)

[27] P.E. Blöchl Phys. Rev. B, 50 (1994), p. 17953

[28] J.P. Perdew; K. Burke; M. Ernzerhof Phys. Rev. Lett., 77 (1996), p. 3865

[29] L.A. Salguero, H.O. Jeschke, R. Valentí, B. Rahaman, T. Saha-Dasgupta, C. Buchsbaum, M.U. Schmidt (in preparation).

[30] L.A. Salguero, H.O. Jeschke, R. Valentí, B. Rahaman, T. Saha-Dasgupta, C. Buchsbaum, M.U. Schmidt, cond-mat/0602633.

[31] A. Kokalj Comput. Mater. Sci., 28 (2003), p. 155 http://www.xcrysden.org/ (Code available from)

Commentaires - Politique