1 Introduction and structural aspects
The synthesis of new magnetic clusters with unprecedented spin topologies is a central topic in the field of molecular magnetism. Among the various strategies that have been developed, the design of molecules containing quantum rings with different values of the spin S and numbers N of magnetic sites represents an interesting approach [1].
In the previously reported ring-shaped molecular complex Cu6[(PhSiO2)6]2·6EtOH [1], it was demonstrated that the six copper ions within the ring are ferromagnetically coupled [2J/kB = −60 K, cf. Eq. (1)] with a total spin Stot = 3 ground state. In order to study in more detail the mechanisms leading to the formation of a high-spin ground state and the influence of the various radicals R or ligand groups of the molecule on the magnetic behaviour of the quantum ring, we have attempted to expand the existing class of molecular magnets by synthesizing new isostructural molecular complexes.
Recently, a large series of copper-containing siloxanolate complexes {CuN[(RSiO2)N]2}·N(ligand) (N = 6, 8, 10; R = Et, Ph, Me,…; ligand = EtOH, DMF,…) having a sandwich-like molecular structure has been obtained [1,2]. Here we report on the structural and magnetic properties of three representatives of the methyl family: oxygen-bridged polynuclear (N = 6, 8, 10) Cu(II) cyclomethylsiloxanolate complexes, Cu6[(MeSiO2)6]2·6DMF (1), {Cu8[(MeSiO2)8]2·8DMF}·EtOH (2) and {Cu10[(MeSiO2)10]2·10DMF}·6DMF (3). Compound 1 crystallizes in the monoclinic system, space group P1 21/n1 (No. 14), empirical formula [C30H78Cu6N6O30Si12], with a = 13.3683(14) Å, b = 15.388(2) Å, c = 17.4383(14) Å, β = 98.88(7)°, and Z = 2; compound 2 – monoclinic system, space group P21/c (No. 14), empirical formula [C42H110Cu8N8O41Si16], with a = 18.710(5) Å, b = 19.936(5) Å, c = 28.837(7) Å, β = 90.2(6)°, and Z = 4; compound 3 – monoclinic system, space group P1 21/n1 (No. 14), empirical formula [C68H172Cu10N16O56Si20], with a = 18.028(2) Å, b = 18.856(3) Å, c = 21.249(3) Å, β = 103.54(5)°, and Z = 2. All details of the synthesis and the single-crystal X-ray analysis will be published elsewhere [2]. These cluster compounds are distinct in that all three of them exhibit a very similar molecular structure consisting of rings of N = 6, 8 or 10 Cu(II) atoms sandwiched by two N-membered cyclomethylsiloxanolate ligands (see Figs. 1 and 2). The methyl group, attached to each of the 2N Si atoms, points away from the molecule. Within the rings, adjacent Cu2+ ions are linked by pairs of siloxanolate oxygen atoms which provide the magnetic exchange path for the Cu(II) S = 1/2 spins. These equatorial Cu–O bonds in 1, 2 and 3 vary in the range of 1.928–1.985 Å (av. 1.957 Å for 1; av. 1.951 Å for 2; av. 1.960 Å for 3), which is close to the expected values for copper atoms with a square-pyramidal coordination environment. The Cu–O–Cu angles, which mainly determine the magnetochemical behaviour of the polynuclear clusters, in 1, 2 and 3 vary in the range 91.2–97.7°, which is typical for other copper-containing organosiloxanes. The average value of the Cu–O–Cu angle is about 93.02° for 1, 95.26° for 2 and 96.50° for 3. The coordination environment of the copper atoms is a slightly distorted oxygen square-pyramidal configuration. The apical positions of all copper polyhedra in 1, 2 and 3 are occupied by DMF oxygen atoms and the Cu–OA bonds are always significantly longer than the equatorial Cu–O distances. The Cu–OA bonds vary in the range of 2.231–2.372 Å (av. 2.273 Å for 1; av. 2.303 Å for 2; av. 2.362 Å for 3). Thus, the methyl family offers the possibility to study the evolution of the static and dynamic magnetic properties of molecular quantum rings upon increasing the number of magnetic sites from N = 6 to 8 and to 10. It should be noted that there is only one structural difference observed for the present methyl family: one additional molecule of the EtOH solvent is present inside the molecular skeleton for complex 2; and two additional DMF solvent molecules are located inside the molecule for complex 3, cf. Fig. 1.
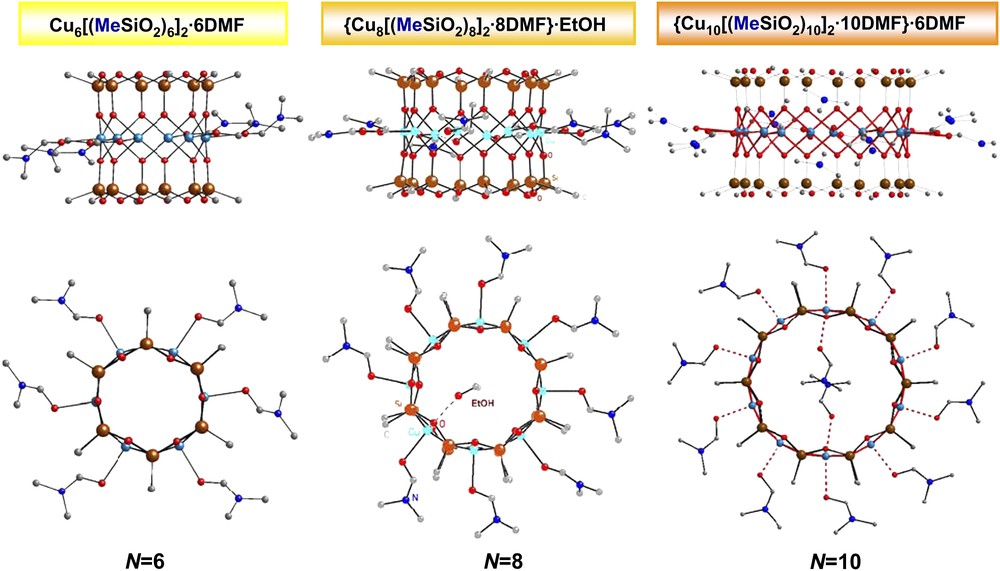
Side view (upper row) and top view (lower row) of the molecular structure of three ring-shaped polynuclear Cu(II) cyclomethylsiloxanolate complexes. Hydrogen atoms are omitted for clarity.
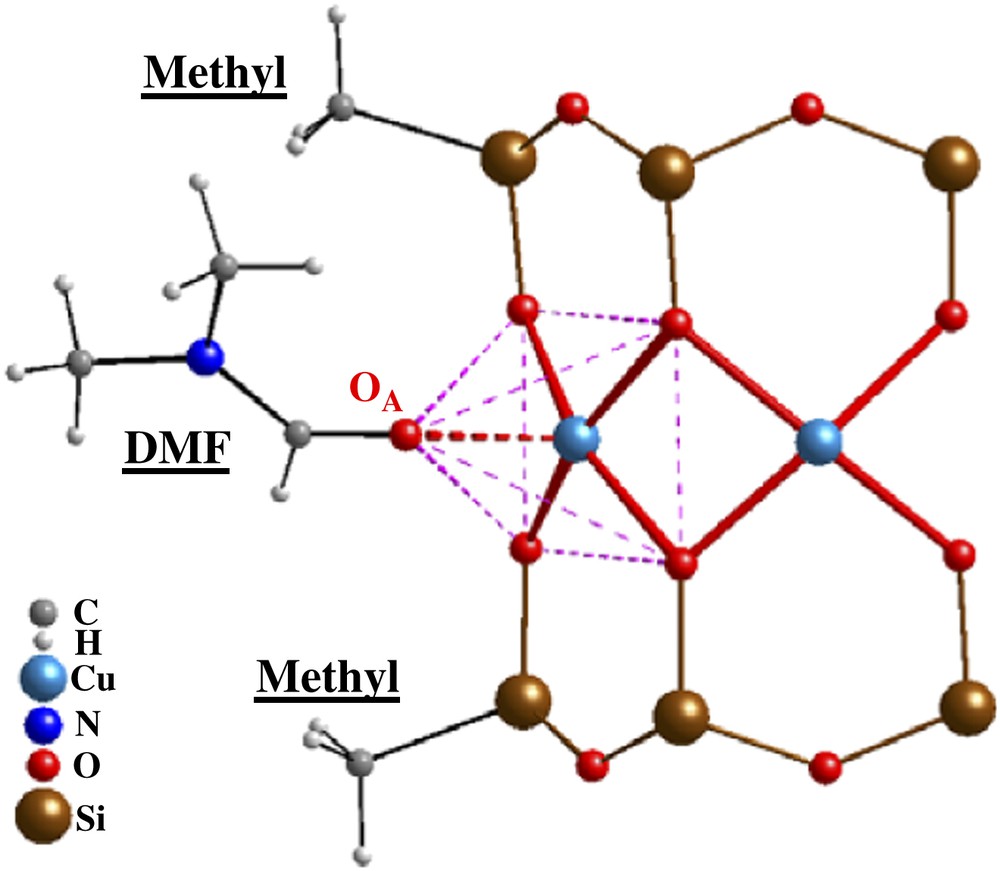
A fragment representing the main building blocks of the molecular ring structure, typical for all three complexes. Only two methyl groups and one DMF molecule are shown for clarity. The square-pyramidal configuration of Cu(II) atoms arises from the apical bonding (OA) with solvent.
A detailed analysis of the magnetic properties, in particular at high temperatures, reveals a strong ferromagnetic Cu–Cu exchange interaction (2J/kB = −50.4 K) for the N = 6 compound with an S = 3 high-spin ground state, a moderately strong ferromagnetic interaction (2J/kB = −27.6 K) for N = 8, and an antiferromagnetic interaction (2J/kB = +17.2 K) with a non-magnetic S = 0 ground state for N = 10. These results, together with structural data enabled us to correlate structural parameters, such as the average Cu–Cu distance, the average Cu–O–Cu bridging angle and the average diameter of the molecular rings, with the sign and strength of the magnetic exchange coupling J, cf. Table 1.
Comparison of the structural and magnetic parameters of polynuclear Cu(II) complexes
| 〈Cu–Cu〉 distances, Å | 〈Cu–O–Cu〉 angle | 〈Diameter〉, Å | 〈2J/kB〉, K | |
| {Cu6[(PhSiO2)6]2·6EtOH} | 2.807 | 92.25° | 5.614 | −60 (FM) |
| {Cu6[(MeSiO2)6]2·6DMF} | 2.839 | 93.02° | 5.677 | −50.4 (FM) |
| {Cu8[(MeSiO2)8]2·8DMF}·EtOH | 2.882 | 95.26° | 7.575 | −27.6 (FM) |
| {Cu10[(MeSiO2)10]2·10DMF}·6DMF | 2.911 | 96.50° | 9.410 | +17.2 (AFM) |
2 Experiment
The X-ray diffraction measurements were performed employing a Smart CCD diffractometer (Mo Kα-radiation, graphite-monochromator, ω-scan technique). The structure was solved by direct methods and refined by full-matrix least-squares against F2 in the anisotropic (H-atoms isotropic) approximation, using the SHELXTL-97 package [3]. Variable-temperature magnetic susceptibility measurements in the temperature range 2–350 K and magnetic fields up to 5 T were carried out using a Quantum Design SQUID magnetometer MPMS-XL. These measurements were complemented by isothermal magnetization runs at temperatures between 2 and 250 K for fields up to 5 T. All magnetic measurements were performed on polycrystalline samples of 1, 2 and 3.
3 Energy spectrum
Heisenberg rings with S = 1/2 have been investigated extensively in the past [4–8]. For an isotropic nearest neighbour exchange interaction, the model is exactly soluble, and the energy spectrum as well as the thermodynamics can, in principle, be calculated using Bethe ansatz techniques [4]. For small rings up to N = 7, the complete set of eigenstates can also be obtained from more elementary symmetry considerations [7]. Yet, a more realistic model of the materials under investigation would include perturbations away from this soluble limit. In particular, anisotropies in the exchange couplings and the local g-tensors could be important. Furthermore, inhomogeneous local environments of the magnetic centers might lead to a deformation of the exchange bridges and thus to site-dependent exchange couplings. Possibly, there also exist exchange paths for next nearest neighbour interactions. For an understanding of the influence of these perturbations on the energy spectrum, a complete numerical diagonalization and a comparison with detailed thermodynamic and spectroscopic measurements would be desirable.
In the search for a minimal model, one can try for the present to ignore these complications. Assuming only nearest neighbour interactions, the simplest exchange Hamiltonian of a ring of N spin S = 1/2 objects with a cyclic boundary condition SN+1 = S1, takes the form
| (1) |
This way of writing the exchange interaction is convenient for spin S = 1/2, since Pij = 2(Si·Sj + 1/4) then acts as a permutation operator of the spin states on sites i and j. The states with full ferromagnetic alignment and a total spin of Stot = Smax = N/2 have the energy EFM = JN and delimit the spectrum on one side, whereas the other boundary of the spectrum is given by the energy EAFM of the antiferromagnetic state with Stot = 0. The total width of the spectrum is equal to |(EFM − EAFM)/J| = 8.60555 for N = 6, and |(EFM − EAFM)/J| = 11.3022 for N = 8 [5]. For a ferromagnetic exchange interaction J < 0, the first low-lying states are single-magnon excitations with a finite energy gap of Δ = 2|J|·[1 − cos(2π/N)] above the high-spin ground state with Stot = Smax. For N = 6 and N = 8, this yields Δ/|J| = 1 and respectively. For temperatures below Δ, higher energy levels are frozen out and the magnetic system behaves as a large single spin with S = Stot. Consequently, the temperature dependence of χT should exhibit a characteristic plateau of width Δ/2 at χT|T→0 = (NAμB2g2)/kB·Smax(Smax + 1)/3. For high temperatures T the effective moment decreases, and for T much larger than the total width of the spectrum, the individual spins are independent leading to an asymptotic value of χT|T→∞ = (NAμB2g2)/kB·N/4. For an antiferromagnetic exchange interaction, the high-temperature asymptotic value of χT is identical to the ferromagnetic case, whereas χT decreases at lower temperature and shows a plateau at χT|T→0 = 0, the width of which is also determined by a finite-size gap.
Fig. 3 shows the experimental susceptibility data for the three different complexes. Complexes 1 and 2 exhibit a pronounced ferromagnetic behaviour at high temperatures with an increase of the effective magnetic moment upon cooling. This contrasts with the magnetic behaviour of complex 3, where the effective magnetic moment decreases all the way below room temperature indicating an antiferromagnetic exchange interaction. For compounds 1 and 3, we thus conclude that the molecular ground state is a high-spin state with Stot = 3 for N = 6 and a non-magnetic state with Stot = 0 for N = 10. On the contrary, the magnetic behaviour of compound 2 appears to be more complex showing an unusual behaviour below 20 K: while the high-temperature analysis of the data clearly reveals a ferromagnetic character of the magnetic interactions, the decrease of χT below 20 K seems to indicate the presence of significant antiferromagnetic correlations. Apparently, the energy spectrum for compound 2 is markedly different from that of a simple idealized homogeneous quantum ring. Thus, our data do not provide experimental evidence of a high-spin S = 4 ground state for compound 2 with N = 8.
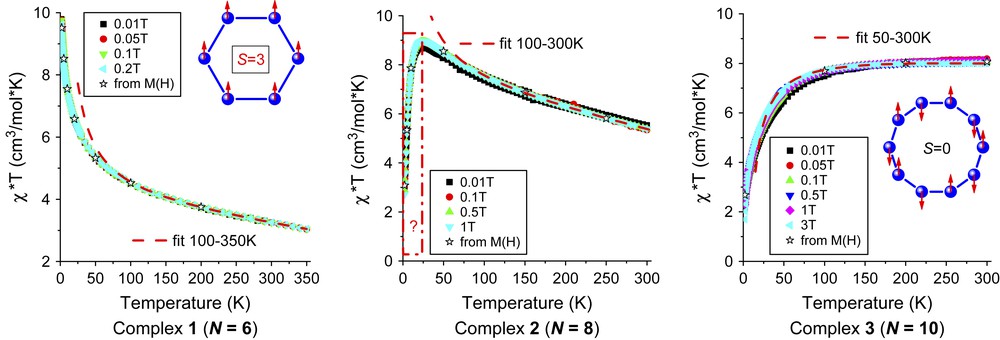
Effective magnetic moment χT as a function of temperature T for three polynuclear Cu(II) cyclomethylsiloxanolate complexes. Symbols correspond to the raw magnetic data collected at various applied magnetic fields in the range 0.01–3T. Star symbols denote the susceptibility data extracted from isothermal magnetization measurements. The dashed lines are fits to the high-temperature approximation in Eq. (3) with the parameter J given in the text.
Furthermore, a closer look at the susceptibility data in Fig. 3 reveals that χT does not show a low-temperature plateau for the six-membered ring either, although the low-temperature magnetization M(H) is satisfactorily described by a Brillouin function with S = 3. Because of the large distances between the molecules in the crystal, we believe that the absence of a plateau in χT cannot be explained by intermolecular interactions. More likely causes of this unusual behaviour are either an effective crystal zero-field splitting of the ground-state spin Smax multiplet or significant site-dependent variations of the exchange interactions due to deformations of the ring geometry. Such inhomogeneities can lead to a reduction of the magnon gap, but do not affect the value of the effective moment χT for T → 0, since the ground state is still given by the fully ferromagnetically polarized states with Stot = Smax. On the contrary, an effective zero-field splitting reduces the degeneracy of the ground state and can also lead to an increase of χT|T→0.
In order to obtain information on the splitting of the low-lying states, we have recorded ESR spectra for the methyl family compounds at a temperature of T = 1.5 K. In the frequency range 26–134 GHz, the frequency-field dependences of the resonance absorptions exhibit a gap at zero field suggesting that two levels are separated by 25–30 GHz for all three compounds. This would correspond to a zero-field splitting parameter D of the order of 1K. This value is not surprising insofar as similar axial magnetic anisotropies for effective high-spin ground states have also been reported for other compounds [1,5]. On the level of the microscopic Hamiltonian in Eq. (1), anisotropies would need to be included as anisotropic exchange terms and g-tensors, since a single-ion anisotropy term is not possible for spins with S = 1/2. The coordination of the copper ions in the rings suggests that the main axes of the local g-tensors point outwards in the radial direction. How such local anisotropies can lead to an effective zero-field splitting D is an interesting open question. In principle, one might hope to extract information on the local g-tensors from ESR measurements at higher temperatures. Yet, the ESR spectra at room temperature are still strongly exchange- and angular-averaged and the g-tensor is related more to the lattice as a whole than to the individual magnetic centers. At high temperatures T ≫ |J/kB|, ESR measurements for all members of the present methyl family reveal the same average g-factor for copper Cu2+ of g = 2.09. It should be noted that the knowledge of the molecular g-tensor could provide, in principle, interesting information on the nature of the N-coupled ring state, especially if it is possible to correlate this molecular tensor obtained at low temperatures with the N individual local g-tensors.
The structural data of the present methyl family also provide some indications in favor of inhomogeneities of the exchange couplings. The copper atoms in the rings have a strictly planar configuration with an average square-root deviation from the plane of the order of δ = 0.0002 Å (for N = 6); δ = 0.0006 Å (for N = 8) and δ = 0.0013 Å (for N = 10). This makes it easy to find out small structural deformations of the symmetry of the ring as a whole by comparing the distances between the nearest neighbour copper positions within the plane. For the ring-shaped complexes 1 and 3 with N = 6 and N = 10, respectively, we have found three and five pairs with identical distances between the copper atoms in the range 2.8113–2.8613 Å (an average value of about 2.839 Å) and 2.8696–2.9301 Å (av. 2.911 Å), respectively. In the case of compound 2 (N = 8) all Cu–Cu distances are non-equivalent and lie in the range 2.8371–2.9116 Å, yielding an average value of about 2.882 Å. The marked variations for compound 2 could be important in explaining the unexpected feature of χT below 20 K. For relatively weak average exchange interactions within the molecule, slight changes in the copper–copper distances might have a significant effect on the strength of the exchange couplings and one might also speculate about variations of the distances as a function of temperature by a dynamical coupling of the spin system to lattice distortions [9]. On the basis of the comparison of the experimental data for the three complexes at low temperatures, we note that, probably, the ferromagnetically coupled ring with N = 8 with a rather weak amplitude of the exchange interaction is most sensitive to inhomogeneities in the exchange interaction.
4 High-temperature approximation
From the discussion of the magnetic properties in Section 3, we expect that a composite analysis is useful for treating “low-” and “high-temperature” regions separately. For low temperatures, the details of the energy spectrum are important and for the optimization of the magnetic model it would be very useful to obtain direct experimental information about the splitting of the low-lying energy levels. This can be obtained, for example, from spectroscopic investigations on single crystals. We are currently trying to solve this problem by restoring the level structure experimentally. At high temperatures, the level splitting is not visible any longer and the effects of a crystal field (a magnetic anisotropy of the molecule as a whole) or of inhomogeneities of the exchange couplings within the ring can be neglected. The magnetic properties are then only sensitive to average values of the microscopic parameters. This fact can be explored to estimate the order of magnitude of the average exchange coupling J.
To obtain an estimate of J, we can use an expansion of the magnetic quantities in powers of J/T, where from now on, J denotes the average exchange interaction within the ring. To this end, we start from the partition function
| (2) |
| (3) |
We have compared this high-temperature approximation with results of a complete numerical diagonalization for spin S = 1/2 rings with N = 6, 8, 10 and conclude that Eq. (3) is in satisfactory agreement with the exact solution for temperatures above 3J.
Fig. 3 shows fits of the high-temperature approximation in Eq. (3) to the experimental susceptibility data in the high-temperature region. The range of the temperature interval for the fit is chosen as wide as possible, but compatible with the requirement T ≥ 3J mentioned above. Since the magnetic data presented in Fig. 3 are not yet corrected for a temperature-independent contribution χTIP resulting from a diamagnetic core contribution from the sample and a signal from the sample holder, these contributions have been accounted for by including an additional fitting parameter together with the parameter J. As the nearest oxygen environment of the copper atoms has a similar square-pyramidal configuration for all three complexes, we have assumed that the average spectroscopic g-factor for the local Cu2+ centers is fixed and equal to g = 2.09. It should be noted that the presence of a χTIP comparable with the magnitude of the susceptibility of the spin system may significantly affect the total temperature dependence of χT in the high-temperature region. The estimates for the exchange coupling J obtained from the fits are shown in Table 1 together with important structural parameters of the rings.
There is a well-known relationship between the singlet–triplet splitting (or the magnitude and sign of the exchange integral 2J) and the Cu–O–Cu bridging angle for the simple case of dihydroxo-bridged copper(II) dimers. According to the empirical works by Hatfield and Hodgson, there is a linear relation between the Cu–O–Cu bridging angle (as the Cu–Cu distance) within the Cu–O2–Cu group and the value of exchange parameter 2J for this class of materials [11]. Two critical structural parameters, such as a critical Cu–O–Cu bridging angle of 97.5° and a critical Cu–Cu distance of 2.888 Å, can be defined, which characterize the change of sign in the magnetic interaction. Given a fixed Cu–O bond length, these critical parameters are strictly connected to each other by geometry.
In analogy to the above-mentioned dimer system, we attempt to correlate the structural and magnetic properties (cf. Table 1) of the present methyl family, containing similar Cu–O2–Cu block as the main exchange path between the magnetic centers. For this purpose we have chosen the following three structural parameters: the average Cu–Cu distance, the average Cu–O–Cu bridging angle and the average diameter of the molecule (defined as the diameter of a circle going through all N copper sites). It should be noted that the average diameter of the molecule is determined by the average Cu–Cu distance and the number N of Cu sites forming the ring. In a first approach, using the average values of distances and angles, we have neglected the existing distortions of the Cu–O2–Cu groups producing the anisotropy of the exchange couplings within the ring and the distortions from planar geometry at the metal center, which also influence the magnitude of J. We have also assumed that the possible influence from the methyl groups and the DMF solvents on the magnetic coupling strength is identical (or negligible) for all three complexes 1, 2 and 3. Finally, it is necessary to notice that the parameter of exchange interaction, obtained from the high-temperature approximation, does not contain any information about the local site-dependent configuration of the magnetic interactions and simply reflects only an average value of these magnetic interactions within the ring.
The structural and magnetic parameters of the polynuclear Cu(II) cyclosiloxanolate complexes listed in Table 1 clearly demonstrate a systematic change of the exchange coupling J with the structural changes of the molecule. For a crude estimate of the critical structural parameters for the methyl rings a linear approximation is used yielding: a critical Cu–Cu distance about of 2.903 Å, a critical Cu–O–Cu bridging angle of 96.04° and a critical diameter of the molecule of 8.686 Å. We can consider the fair agreement of these critical parameters with those reported by Hatfield and Hodgson as an indication of the similarity of the methylsiloxanolate bridge for the N-membered rings to the dihydroxo bridge for the simplest dimers.
5 Conclusion
We have studied the structural and magnetic properties of three oxygen-bridged polynuclear Cu(II) (N = 6, 8, 10) cyclomethylsiloxanolate complexes: Cu6[(MeSiO2)6]2·6DMF (1), {Cu8[(MeSiO2)8]2·8DMF}·EtOH (2) and {Cu10[(MeSiO2)10]2·10DMF}·6DMF (3). All three complexes have a ring-shaped configuration of the copper S = 1/2 spins. For compounds 1 and 3, the molecular ground state has been identified as a high-spin S = 3 state and a non-magnetic S = 0 state, respectively. The analysis of the magnetic data, together with the structural information, has enabled us to correlate the evolution of the exchange coupling J between the magnetic S = 1/2 centers of the quantum ring as a function of the number N of magnetic sites to the structural changes of the molecular crystals (see Table 1). Our analysis reveals indications that structure-related inhomogeneities of the exchange couplings may have a significant influence on the low-temperature magnetic behaviour of the N = 8 compound 2 with a rather weak amplitude (compared with the effect of distortions) of ferromagnetic exchange interaction.


