1 Introduction
Ionic liquids (ILs), although known for a long time, have appeared only recently as potential “green” solvents in all fields of chemistry, in replacement of those traditional organic phases for which generation of volatile organic compounds is nowadays considered as a critical issue [1]. They display tunable properties, as a consequence of their variable chemical structure, and some ILs properties can be very different from those of usual organic solvents. In particular, ILs possess the almost unique advantage to dissolve both neutral and charged entities, allowing rather uncommon chemistry to occur. So far, the understanding of solvation mechanism in ILs is still in its infancy, which in turn limits their use. In the field of radiochemistry, ILs have already demonstrated their potential as An/Ln organic extracting phases [2–5] and as practical electrodeposition media [6–8]. Many papers have highlighted some of the very specific properties of ILs, which may open new routes for separation/partitioning of An/Ln, but very few works have focussed yet on the problems that can arise from the relatively high viscosity most of them display. Actually, large viscosity is usually associated with slow kinetics, which would hamper the development of ILs as solvents. In the present work, we take advantage of the keto-hydrate/enol equilibrium kinetics of thenoyltrifluoroacetone (TTA) dissolved in 1-butyl-3-methyl-imidazolium bistriflimide (BumimTf2N) to demonstrate that although viscous, BumimTf2N displays kinetics that is faster than can be observed in cyclohexane, a more common solvent. These experiments give some insights into the state of water in such media.
2 Experimental
1-Methyl-3-butyl-imidazolium bistriflimide (thereafter denoted as BumimTf2N, Tf2N− standing for (CF3SO2)2N−) is purchased from Solvionic (Verniolle, France). BumimTf2N was not fully dry and the amount of water in this solvent was measured both by IR and Karl–Fischer titration, leading to a value of 2.44 × 10−2 M (310 ppm). For all the solutions of this work, the water amount was adjusted by a rigorous degassing procedure, according to a previously published protocol [9], followed by addition of the required amount of ultra pure water, which was dissolved in the IL. The water amount in the BumimTf2N solutions of this work was measured taking advantage of the work of Tran and co-workers [10], extending the range up to 1 M of added H2O. We have established and used all throughout this work a linear calibration curve relating the water amount in BumimTf2N as determined by Karl–Fischer titration to the surface area in the range 5085–5385 cm−1 of the IR spectrum. A regression coefficient above 0.996 was obtained.
Cyclohexane was purchase from Aldrich (99.9%) and used as received. The water content was checked by means of Karl–Fischer titration (≈20 ppm).
TTA, purchased from ACROS Organics (99.5%), was contacted with deionized water in slight excess for about one week in the dark and at room temperature. The solid obtained, after drying, was recrystallized from diethylether, and the white powder, characteristic of the hydrated keto form of TTA [11], was stored at 8 °C in the dark. The presence of TTA, under the predominant keto-hydrate form, was confirmed by spectrophotometric measurements (strong adsorption between 275 and 300 nm) [11–13]. A kinetic study has shown that the product is stable over several months when stored in the above conditions.
The TTA concentration in BumimTf2N was in the range of 4 × 10−5 M and equal to 8 × 10−6 M in cyclohexane. All samples were protected from daylight, in order to avoid photodegradation.
The UV–vis spectra were recorded in the range 200–450 nm on a Cary 100. All measurements were performed at room temperature.
3 Results
TTA has been introduced in aliquots of BumimTf2N of known water contents. The TTA concentration ranged from 3.5 × 10−5 M to 4.25 × 10−5 M, so that the water amount added with the TTA was less than 6 ppm. UV–vis spectra were recorded as a function of time. Table 1 summarises the water amount in the various BumimTf2N solutions of this work, together with the values of the isobestic points observed for BumimTf2N and cyclohexane. Figs. 1 and 2 display some of the UV–vis spectra recorded as a function of time for [H2O] = 860 ppm and [H2O] = 8650 ppm as typical examples of the observed kinetics. Fig. 3 represents the absorbance variation obtained as a function of time at the two absorption maxima λ = 265 nm and 327 nm, for the same water amounts, while Fig. 4 displays the corresponding variations in cyclohexane ([H2O] ≈ 20 ppm), for which the maxima are located at λ = 260 nm and 317 nm.
Values of the water amount, TTA initial concentration (in its keto-hydrate form) and position of the isobestic points detected (see text)
| Solvent | [H2O] (ppm/M) | [TTA]0 (10−5 M) | Isobestic point (nm) |
| BumimTf2N | 50/3.9 × 10−3 | 3.5 | 293 |
| 860/6.8 × 10−2 | 4.25 | 293 | |
| 1600/1.3 × 10−1 | 3.8 | 294 | |
| 2150/1.7 × 10−1 | 4.1 | 294 | |
| 3000/2.4 × 10−1 | 3.8 | 294 | |
| 5900/4.6 × 10−1 | 3.95 | 294 | |
| 7100/5.6 × 10−1 | 4.25 | 296 | |
| 8650/6.8 × 10−1 | 4.25 | n.d. | |
| 11,900/9.4 × 10−1 | 4.25 | 301 | |
| Cyclohexane | ≈20 | 0.8 | 293 |
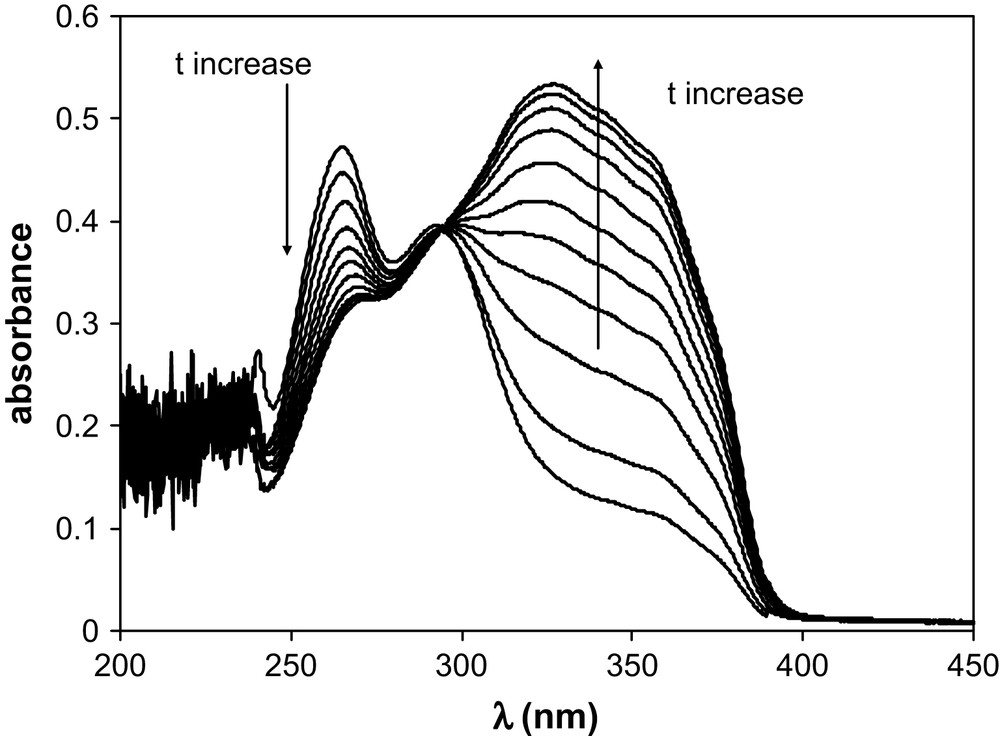
Absorption of TTA in BumimTf2N as a function of time in the range 15 min–1435 min; [H2O] = 860 ppm (see text).
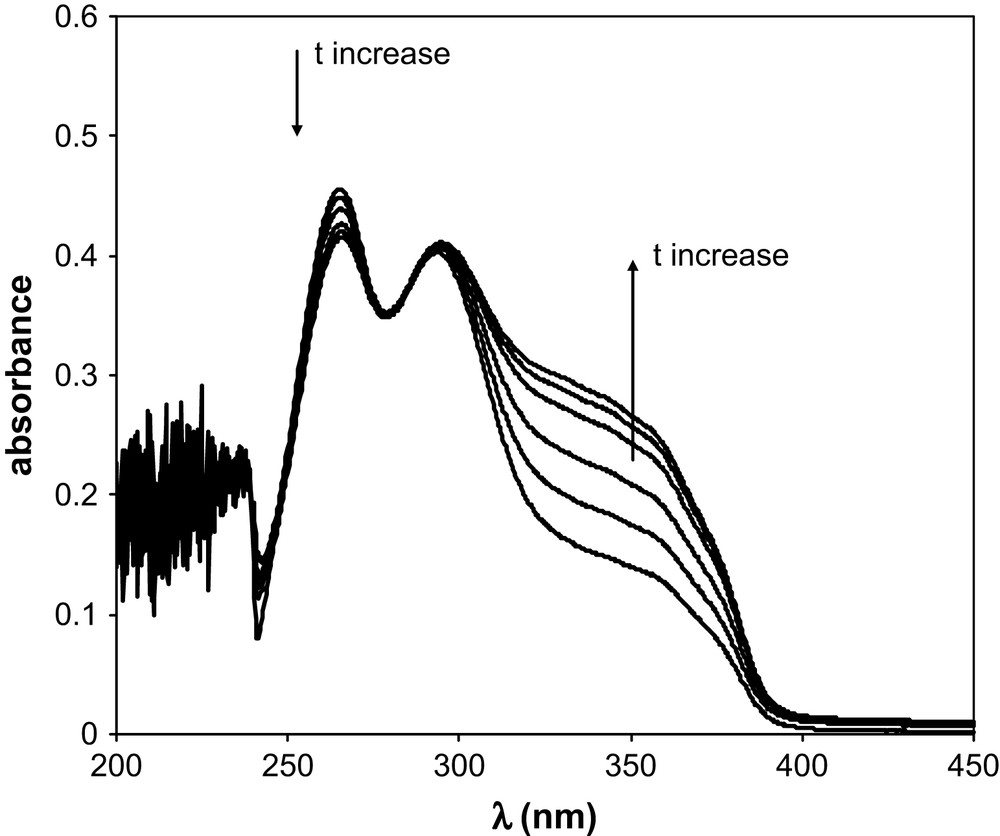
Absorption of TTA in BumimTf2N as a function of time in the range 15 min–1080 min; [H2O] = 8650 ppm (see text).
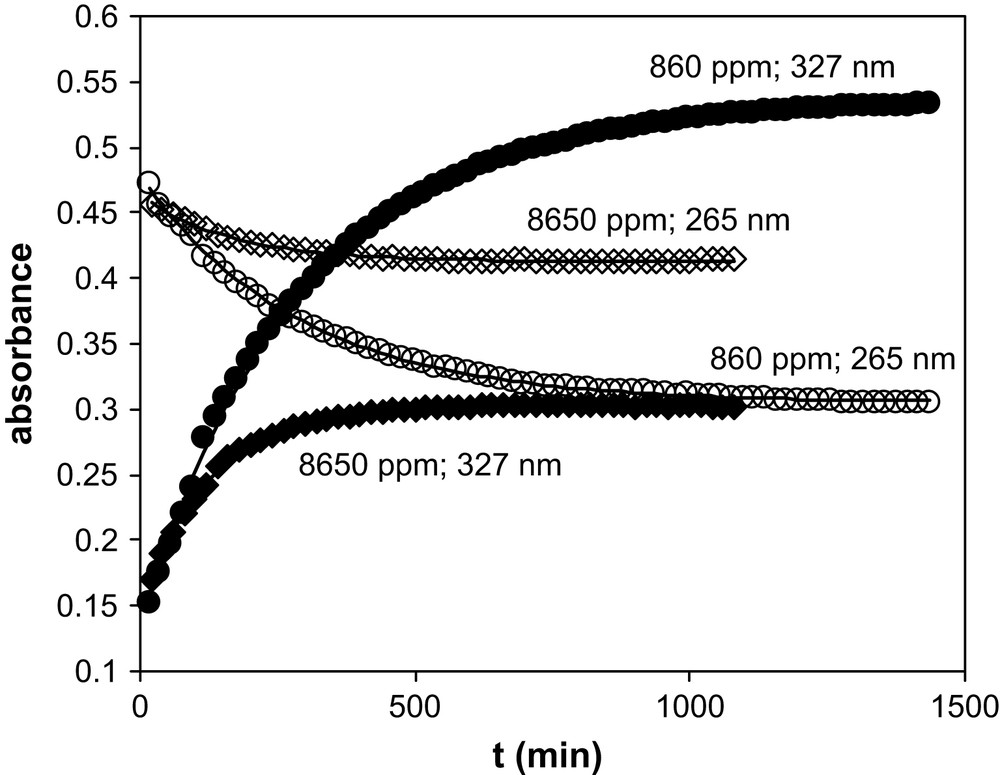
Variation of the absorbance of TTA in BumimTf2N recorded as a function of time for two H2O contents and at two wavelengths. Solid lines: fits of the individual series (see text).
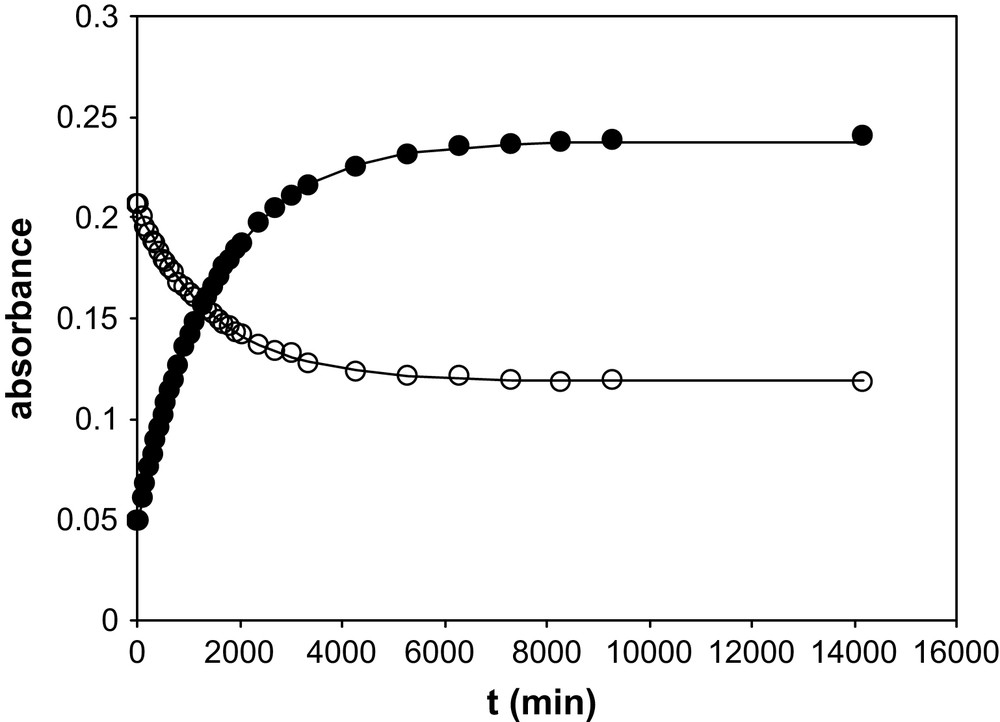
Variation of the absorbance of TTA in cyclohexane recorded as a function of time for [H2O] ≈ 20 ppm contents and at two wavelengths. Symbols: experimental values; solid lines: fits of the individual series (see text).
4 Discussion
The keto-hydrate TTA form (further denoted as TTA–H2O) can release one H2O entity to turn to the enol chemical structure, further denoted as TTA. Such a chemical equilibrium is illustrated by the presence of an isobestic point in Figs. 1 and 2. As already mentioned in the literature, one of the parameters driving the keto/enol equilibrium is the polarity of the solvent [14]. In addition, obviously, the enol/hydrate equilibrium depends on the total water amount in the solvent in which TTA is dissolved. Our data show that the higher the water amount in BumimTf2N, the faster the equilibrium is reached. The keto-hydrate/enol kinetics has been studied in C6H6 for example [11] by UV–vis, taking advantage of the two very distinct absorption spectra these two forms display. By comparison of the literature UV–vis spectra, the absorption spectrum obtained in the present work at short time is characteristic of the keto-hydrate observed in H2O, with an absorption maximum at λ = 265 nm, while the limiting spectrum obtained for [H2O] = 50 ppm and long time (t > 1000 min) corresponds closely to the enol form observed in benzene [11], with an absorption maximum located at λ = 327 nm and a shoulder around 360 nm. At equilibrium, the keto form is dominating the speciation for [H2O] = 11,900 ppm, while the enol is the major component for [H2O] = 50 ppm. It has been shown that the enol form predominates in water-saturated carbon tetrachloride [14], a phenomenon previously noticed for other non-polar organic solvents. In this respect, BumimTf2N behaves as a classical organic solvent, with the additional feature that the ratio enol/hydrate can be tuned by monitoring the water amount. In classical liquid/liquid extraction studies with ILs, owing to its hygroscopic properties, BumimTf2N is actually water-saturated, so that [H2O] is fixed at its maximum value, but in the case of the less-common supercritical CO2/LI extraction technique [15,16], such an aspect may have some interesting features. The keto-hydrate/enol equilibrium also occurs in cyclohexane, for which only one series at [H2O] ≈ 20 ppm has been measured. At equilibrium, the enol form dominates, with absorption spectra at short and long times very similar to those observed in BumimTf2N.
In a first attempt to fit the data, we adopted the following chemical model:
The initial conditions are
The mathematical treatment (performed using the Maple facilities) leads to:
| (1) |
In this expression, the unknown parameters are ɛ1, ɛ2, k1 and k2, the latter two being independent of the wavelength, while ɛ1 and ɛ2 depend on it. For each [H2O] value, Eq. (1) has been fitted (least-square fit) to the experimental data with the help of a Fortran procedure, for the two wavelengths λ = 265 nm and 327 nm independently. The quality of the fit is excellent in all cases, as illustrated in Fig. 3: at any given H2O content, Eq. (1) leads to a very good agreement between calculated and experimental values. This is also the case for the single series in cyclohexane (see Fig. 4). However, a close examination of the fitted parameter values for the nine experimental series in BumimTf2N shows that the k1 and k2 values are not consistent from one series to the other, while ɛ1 and ɛ2 appear to be reasonably constant. The progressive shift of the isobestic point (see Table 1) as a function of the water amount may be indicative of a change in the global solvent properties, as water is added to the solution up to the solubility limit. Actually, it has been shown in the literature that ILs' properties are heavily affected by water solubilisation [17–21] and so is the viscosity η [21], displaying a rough 30% decrease from dry to water-saturated BumimTf2N. In our model, this should have some impact on the k2 value, while k1 corresponds to a real mono-molecular reaction so that, in principle, its value should not be dependent on the viscosity. In an attempt to reconcile the fitted values for all the experimental series of this work, the nine series in BumimTf2N have thus been tentatively fitted together, imposing k2 to vary as a function of 1/η, keeping ɛ1, ɛ2 and k1 constant from one series to another, at a given wavelength. To this aim, the recent literature data of Widegren and co-workers on the η variation in BumimTf2N as a function of [H2O] have been used, for this work covers a range of variation in keeping with our experimental conditions [21]. Interpolation of the experimental η values has been made through a linear law (regression coefficient: 0.99). However, this does not improve significantly the quality of the global fit, which is poor. Furthermore, the kinetics is much longer in cyclohexane as in BumimTf2N (see Fig. 4). This is unexpected, because the higher viscosity in BumimTf2N as compared to cyclohexane (even for [H2O] = 11,900 ppm) would pledge for a slower kinetics in the former solvent, which is not experimentally verified. Clearly, although the mathematical form of Eq. (1) appears to be in agreement with the experimental variation observed, and although the chemical model itself makes sense, as a whole, the process leading to the enol/keto-hydrate equilibrium is complex and is not only governed by macro viscosity.
At present, we cannot propose a definitive explanation for the experiments, but we can suggest various possible tracks that would deserve further work in order to quantify their contribution to the observed trend. First, it is possible that, in cyclohexane, the activation energy of k2 is much higher than in BumimTf2N (possibly in the range of ca. 1 eV). Second, in cyclohexane, the rather low viscosity (as compared to BumimTf2N) most probably favors de-correlation of the H2O⋯TTA pairs formed through k1 readily after the keto-hydrate has dissociated, so that although viscosity is low, the overall equilibrium needs time to be reached in cyclohexane. Finally, it has been repeatedly mentioned by various authors that water may exist as clusters or nanodomains in ILs [10,17,22]. In such a case, the effective (i.e. efficient) H2O concentration would be decreased by a factor corresponding roughly to the aggregation number of such clusters. Depending on this value, homogeneous kinetics may not apply anymore in BumimTf2N, but the formation of clusters would have a rather negligible effect onto the overall kinetics, which would be mostly governed by the reaction of the correlated pairs instead, leading to a faster equilibrium to be reached in BumimTf2N as compared to cyclohexane.
5 Conclusion
We have investigated some of the features of TTA solvation and enolisation in BumimTf2N. The slow kinetics evidenced during the course of this work is most likely a general feature of ILs, providing another topic to be studied in those liquids. Insights into the state of water in BumimTf2N have been suggested, which would require additional experiments to be validated.
Acknowledgement
This work has been performed with the financial help of GDR PARIS, which is greatly acknowledged.


