1 Introduction
Les diaryléthènes (DA), synthétisés par Lehn et Irie à l'aube des années 1990 [1–3] occupent certainement une place privilégiée dans l'ensemble des molécules photochromes. En effet, les DA existent sous deux formes thermiquement stables (l'une ouverte et l'autre fermée), présentant des propriétés très différentes. C'est ainsi que la forme fermée est colorée et que la forme ouverte est transparente. Le passage d'une forme à l'autre s'opérant à des longueurs d'onde très distinctes et pouvant être réalisé à de nombreuses reprises, les DA sont les prototypes des interrupteurs moléculaires efficaces [4–9]. On peut classer les DA selon la nature chimique du pont moléculaire (soit le groupement qui lie les deux parties de la molécule ouverte) qu'ils possèdent. Les premiers DA synthétisés présentaient des ponts maléiques [1,10] ou cyano [1,10]. En 1992, Hanzawa et al. démontrèrent que les composés perfluorés présentent de nombreux avantages pratiques [11]; ceux-ci sont d'ailleurs toujours les plus répandus à ce jour. Plus récemment, des DA à pont cyclopentène [12], dihydrothiophène [13], dihydropyrrole [14], oxazole [15], thiazole et furanone [16] ont été isolés. Dans cette étude, nous nous concentrons sur les composés maléimides (voir Fig. 1), qui ont été synthétisés par plusieurs équipes depuis 1998 [17–23]. Notre objectif est d'établir une méthodologie rapide de prédiction de la couleur des DA fermés à l'aide d'une méthode ab initio. L'approche proposée doit ainsi permettre une sélection rapide des photochromes les plus prometteurs.
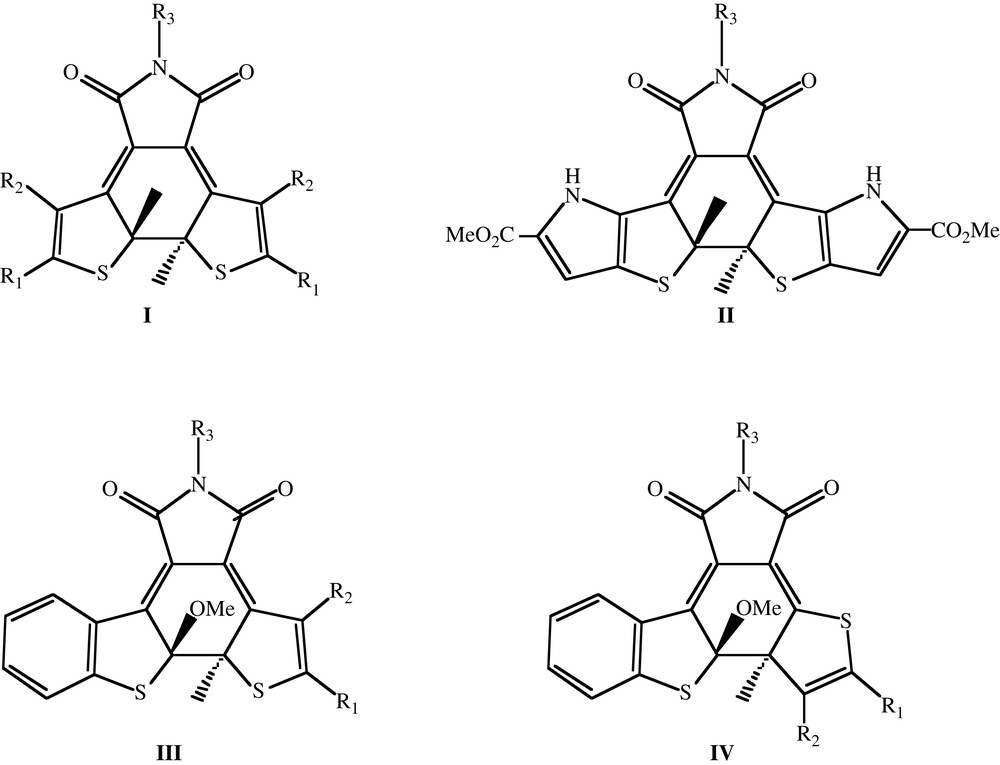
Structures développées planes des photochromes étudiés.
La détermination théorique des énergies de transition électronique dans les DA a été réalisée avec des méthodes semi-empiriques [10,24], qui, si elles peuvent fournir des conclusions qualitatives, ne peuvent sérieusement rivaliser avec la précision des calculs ab initio [25]. On relèvera également dans la littérature une étude SAC-CI [26], mais il n'est pas possible de recourir à ce type d'approche pour les composés repris dans la Fig. 1, si ce n'est qu'avec de très petites bases de fonctions atomiques ou en négligeant les effets d'environnement, combinaison pour le moins morganatique. C'est probablement pour cette raison que la plupart des études de spectre des DA ont été effectuées à l'aide de la théorie de la fonctionelle de la densité dépendante du temps (TD DFT) [25–36], qui sera également notre principal outil dans ce travail. On notera qu'aucune des références [25–36] ne porte sur les formes maléimides. De plus, à l'exception de nos travaux méthodologiques [25,35], tous les calculs TD–DFT pré-existants ont été effectués avec des bases de taille limitée [6-31G ou 6-31G(d)], et négligent de surcroît les effets de solvatation.
2 Méthodologie
Suivant le canevas récemment mis au point pour des photochromes du même groupe [25,35], nous avons établi une procédure calculatoire en trois étapes, à l'aide du logiciel Gaussian03 [37].
Tout d'abord, la géométrie de l'état fondamental singulet de chaque molécule a été déterminée de manière à réduire les forces exercées sur chaque atome. Pour mener à bien ces optimisations, une base triple-ζ polarisée 6-311G(d,p) a été selectionnée, car elle conduit à une description adéquate des paramètres structuraux de la plupart des molécules organiques [25,35,38–40].
Ensuite, les fréquences de vibration de chaque composé ont été évaluées avec la même base de fonctions atomiques, via le calcul analytique de la hessienne. Toutes les valeurs reprises dans ce travail relèvent de structures correspondant au minimum global de la surface d'énergie potentielle (absence de fréquence imaginaire).
Enfin, les trois premiers états électroniques de basse énergie sont obtenus avec la TD–DFT. Conformément aux données expérimentales, la couleur des DA résulte d'une excitation π → π∗ hautement probable. Au cours de cette ultime étape, la base 6-311 + G(2d,p) a été utilisée, car il a été montré qu'elle fournit des spectres d'absorption numériquement stables pour les chromophores possédant des cycles conjugués à cinq pièces [41]. Plus spécifiquement, l'ajout de fonctions supplémentaires de polarisation et/ou de diffusion n'engendre aucune fluctuation manifeste du λmax pour les DA [25,35].
Une simulation réaliste des conditions expérimentales exige la modélisation explicite des effets de l'environnement [42–46]. Nous avons dès lors retenu le modèle du continuum polarisable (PCM) de Tomasi [47] pour évaluer l'impact de la solvatation à chacune des trois étapes de notre schéma caclualtoire. Dans l'approche PCM, on scinde formellement le problème en deux sous-ensembles, avec d'une part le soluté (le photochrome) et d'autre part le solvant. Le premier se trouve au centre d'une cavité enveloppée par le second, celui-ci étant représenté comme un matériau sans structure, dont les caractéristiques physicochimiques découlent directement de ses propriétés macroscopiques. La méthode PCM procure d'excellents résultats pour peu qu'aucune interaction spécifique ne lie le soluté aux molécules de solvant. Pour construire la cavité, nous avons choisi les rayons UA0 (paramètre par défaut dans Gaussian), si ce n'est à l'occasion de quelques optimisations de structure, pour lesquelles les rayons UAKS ont permis une convergence plus rapide. Pour les calculs TD–DFT, l'approximation de non-équilibre, parfaitement adaptée à la simulation de spectres d'absorption, a été appliquée. Ainsi, on estime que seule la distribution électronique du solvant s'ajuste instantanément à l'état excité du soluté, alors que les noyaux sont trop patauds pour s'adapter brusquement à ce nouvel état.
Les publications décrivant la mise au point de point de nouvelle(s) fonctionnelle(s) soulignent souvent les qualités de celle-ci à l'aide d'exemples taillés sur mesure. En conséquence, le choix de la fonctionnelle de la densité utilisée pour des calculs (TD–)DFT sur une large gamme de molécules reste une gageure. On conviendra cependant que les fonctionnelles hybrides sont globalement reconnues comme étant les plus performantes pour évaluer les propriétés des molécules organiques. Ici, nous adoptons la fonctionnelle hybride PBE0 mise au point par Adamo et Barone en 1999 [48]. PBE0 se base sur la fonctionnelle pure PBE [49] et inclut 25% d'échange exact (Hatree–Fock). Par rapport à la plupart de ses concurrentes, PBE0 se singularise par une conception qui s'affranchit complètement des données expérimentales, puisque, en effet, seules des considérations purement théoriques sont invoquées lors de sa mise au point. PBE0 s'est ainsi montrée particulièrement satisfaisante pour les diaryléthènes [25,35], de même que pour de nombreuses autres familles de colorants organiques [42–44,50–52].
3 Résultats et analyses
Les valeurs théoriques et expérimentales des longueurs d'absorption maximale (λmax) sont reprises dans le Tableau 1 pour 26 composés à pont maléimide (voir Fig. 1). Soulignons que les mesures s'effectuent habituellement à l'état photostationnaire : les λmax expérimentaux correspondent au pic supplémentaire apparaissant, et non scrupuleusement à une solution de forme fermée « pure ». En effet, les solutions employées contiennent une fraction, parfois notable, de molécules sous leur forme ouverte.
λmax (en nm) pour les diaryléthènes de la Fig. 1
| Substitution | Solvant | λmax | Réf. | ||||
| R1 | R2 | R3 | Théo. | Exp. | |||
| I | Me | Me | o-OH–Ph | Cyclohexane | 529 | 533 | [17] |
| Ph | Me | o-OH–Ph | Cyclohexane | 570 | 563 | [17] | |
| Me | Me | o-COOMe–Ph | Cyclohexane | 529 | 524 | [17] | |
| Ph | Me | o-COOMe–Ph | Cyclohexane | 609 | 557 | [17] | |
| Me | H | H | CH3CN | 510 | 509 | [18] | |
| Me | H | Me | CH3CN | 508 | 500 | [18] | |
| Me | H | Bu | CH3CN | 508 | 500 | [18] | |
| Me | H | CH2Ph | CH3CN | 508 | 542 | [18] | |
| Me | H | C2H4OH | CH3CN | 513 | 509 | [18] | |
| II | – | – | Me | Toluène | 587 | 595 | [19] |
| – | – | OMe | CH3CN | 581 | 548 | [20] | |
| – | – | C2H4OH | CH3CN | 588 | 582 | [20] | |
| – | – | CH2CHCH2 | CH3CN | 584 | 583 | [20] | |
| – | – | o-Pyr | CH3CN | 597 | 588 | [20] | |
| – | – | Ph | CH3CN | 595 | 590 | [20] | |
| – | – | CH2Ph | Toluène | 589 | 595 | [19] | |
| – | – | CH2Ph | CH3CN | 585 | 584 | [20] | |
| – | – | CH2COPh | Toluène | 590 | 595 | [19] | |
| – | – | CH2COPh | CH3CN | 586 | 586 | [20] | |
| III | Ph | H | CN | Toluène | 576 | 547 | [21] |
| Ph | H | Ph | Toluène | 552 | 550 | [21] | |
| Ph | H | OMe | Toluène | 539 | 542 | [21] | |
| p-NO2–Ph | H | CN | Toluène | 612 | 570 | [21] | |
| Ph | Me | CH2CN | Hexane | 548 | 563 | [22] | |
| Me | Me | CH2CN | Hexane | 522 | 550 | [23] | |
| IV | Ph | Me | CH2CN | Hexane | 512 | 487 | [22] |
Pour les neuf molécules I, l'écart théorie/expérience est toujours en deçà des 10 nm, à l'exception de deux composés seulement. Dans la série II, on note un très bon accord théorie/experience, avec un pouvoir auxochromique relativement faible du substituant R3. Toutefois, l'effet du groupe méthoxy observé expérimentalement se détache nettement, effet que la TD–DFT ne parvient pas à restituer. Relevons néanmoins que les expérimentateurs s'étonnent également de la longueur d'onde mesurée pour ce DA [18]. Dans les séries III/IV, l'accord est uniquement qualitatif. Cette faiblesse est attendue pour des systèmes présentant des substituants fortement électroactifs (nitro, cyano…) entraînant des transferts de charge, car ceux-ci sont souvent mal décrits par la TD–DFT (cf. § Introduction). Pour deux photochromes de la série II (R3 = CH2Ph et R3 = CH2COPh), les longueurs d'onde ont été mesurées dans deux solvants (toluène et acétonitrile). Dans les deux cas, on remarque un solvatochromisme négatif, assez contre-intuitif pour une transition au caractère π → π∗, mais correctement reproduit par l'approximation du continuum, nonobstant des valeurs absolues de déplacement légèrement sous-estimées (–4 nm au lieu de –11 nm/–9 nm). Comme le modèle PCM néglige les interactions spécifiques entre le DA et son environnement, on a là une indication selon laquelle ce solvatochromisme négatif ne provient pas de liaisons de type pont hydrogène entre le photochrome et l'acétonitrile, mais bien d'une diminution du moment dipolaire de l'état excité.
Pour les 26 photochromes du Tableau 1, on calcule un écart moyen théorie/expérience (EM) de –5.2 nm (0,020 eV) et une erreur moyenne absolue (EMA) de 13,1 nm (0,053 eV). À titre de comparaison, nous avons récemment obtenu, en suivant une procédure identique, une EMA de 9,4 nm (0,036 eV) pour les photochromes maléiques [35] et de 26,2 nm (0,127 eV) pour les composés cyanos [25]. Malgré les quelques limites énumérées ci-dessus, l'approche mise au point paraît donc particulièrement efficace, puisque les longueurs d'onde d'absorption sont pronostiquées quasi quantitativement. Nous estimons qu'une précision de 13 nm n'est possible que grâce à la combinaison de deux facteurs fondamentaux, à savoir des bases de fonctions atomiques étendues et la modélisation du solvant. Il est vrai que, dans certains cas, seul un de ces paramètres importe, bien qu'effectuer un calcul en phase gazeuse avec une base étendue nous paraisse stérile. De plus, il s'agit d'une réelle performance si on compare à la précision moyenne attendue avec la TD–DFT [53]. En effet, en répertoriant les travaux concernant les états excités de valence de dérivés organiques conjugués, on remarque une EMA typique de l'ordre de 0,2 eV∼0,3 eV. Par exemple, Fabian et al. ont obtenu, au niveau B3LYP/6-31 + G(d), une EMA de (0,29 eV) 0,24 eV pour les transitions π → π∗ de composés (non) soufrés [54,55], alors que Guillaumont et Nakamura ont rapporté une EMA de 0,19 eV pour un ensemble hétérogène de colorants [56]. En fait, les publications concluant à de petites EMA se concentrent généralement sur des transitions localisées de type n → π∗ [54,55,57,58], ou incluent les effets du solvant [50,59–62]. Tous ces éléments mènent à la conclusion que la méthode PCM–TD–PBE0 se montre particulièrement performante pour les diaryléthènes étudiés ici.
Pour chacun des composés repris dans le Tableau 1, l'excitation responsable de la couleur est directement liée aux orbitales frontières, avec une transition de l'orbitale molculaire haute occupée (HO) à l'orbitale basse vacante (BV). Nous avons reproduit sur la Fig. 2 ces orbitales pour trois DA typiques. La HO des trois composés est principalement centrée sur les atomes de soufre ainsi que sur les doubles liaisons constitutives des cycles thiophènes et du lien mitoyen. Cette conclusion est en parfait accord avec les conclusions de Perrier, Maurel et Aubard [36]. Pour la famille II, on note cependant une densité électronique non négligeable sur les atomes de carbone vicinaux des groupements ester. Les BV sont plus diversifiées ; ainsi, pour la famille II, la BV est centrée sur la liaison mitoyenne, les deux carbones adjacents et les groupes ester. Elle est donc plus fortement délocalisée que celle repésentée dans la Réf. [36]. Ceci suggère clairement que le remplacement du groupe ester par des groupes fortement electroattracteurs ou électrodonneurs influence sensiblement la couleur de ces composés. À l'inverse, les orbitales frontières ne s'étendent pas sur le cycle aromatique placé en R3 : la conclusion quant au faible pouvoir auxochromique du groupe R3 en découle logiquement. Pour le composé de la famille III, on a une situation similaire à celle des photochromes cyano [25], avec néanmoins des participations plus modestes pour les phényles externes et le groupe cyano. Enfin, pour IV, la BV se situe davantage sur la gauche de la molécule (Fig. 2) : la couleur est liée à un transfert de charge du cycle de droite (HO) vers le pont et le cycle de gauche (BV).
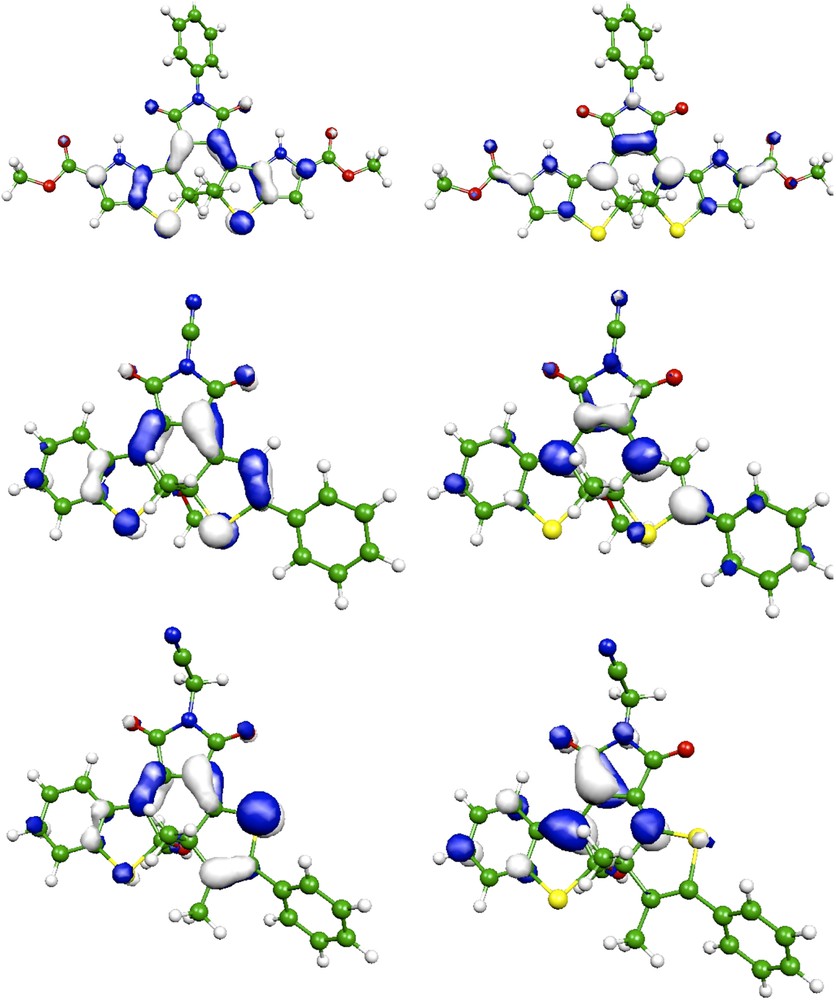
Orbitales frontières : HO (gauche) et BV (droite) pour II avec R3 = Ph (en haut), III avec R1 = Ph, R2 = H, R3 = CN (au milieu) et IV (en bas). Figure en couleur dans la version électronique de l'article.
4 Perspectives
Les λmax de DA à pont maléimide ont été calculés à l'aide d'une approche ab initio qui combine le modèle TD–PBE0 et l'approche du continuum polarisable. Pour les 26 composés considérés, la théorie reproduit parfaitement l'expérience, avec une erreur moyenne absolue de 13,1 nm seulement. Par ailleurs, les représentations des orbitales frontières ont permis d'identifier les positions auxquelles des substitants pourraient efficacement modifier la couleur de ces composés.
À le suite de ce succès, la méthode présentée dans ce travail est actuellement étendue aux DA perfluorés.
Remerciements
Les auteurs remercient le Fonds national de la recherche scientifique belge (FNRS) pour leur mandat de chercheur qualifié. Ils expriment toute leur gratitude au Pr. Jean-Marie André, dont le phénotype scientifique apparaît clairement en filigranne tout au long de ce travail, de même qu'à Mlle Adèle Laurent, pour son aide particulièrement efficace. Les calculs présentés dans ce travail ont été effectués au centre ISCF (Interuniversity Scientific Computing Facility), installé aux facultés universitaires Notre-Dame-de-la-Paix à Namur en Belgique, grâce à l'aide financière des FUNDP, du FNRS–FRFC et de la Loterie nationale via la convention 2.4578.02.


