1 Introduction
Eukaryotic chromosomes or sperm nuclei are highly condensed chromatin materials and they can sometimes present spectacular helical morphologies [1–4]. These helical shapes may originate from the chiral properties of DNA and other components of chromatin. Dense solutions of DNA and nucleosomes can be prepared in vitro to reproduce some of the characteristics of chromatin. They form multiple ordered phases, either mesophases or 3D crystals, that can be useful to analyze precisely how chiral structures can emerge, or not, from interactions between these constitutive elements.
DNA alone self-organizes to form a cholesteric liquid crystal under a moderate range of concentrations as described many years ago by Robinson [5]. A few years later, Yves Bouligand recognized that special chromosomes, from the Dinoflagellate algae, were organized in the same way, forming elongated cholesteric rods. He understood how their characteristic arched patterns seen on oblique sections arise from the chiral organization of DNA [6]. Their shape is not helical, although a double helical furrow can be seen sometimes at their surface, but they transform into a circular supercoiled double helical bundle when they are decondensed experimentally by spreading on the water surface [7]. Surface tension, and also probably removal of many chromosomal proteins, stretches and reorganizes the chromosome. The cholesteric twist between DNA is removed, but the chirality is still there and reappears as a true helical conformation. For higher DNA concentrations, DNA forms either 2D or 3D hexagonal phases [8,9]. This denser packing prevents the spontaneous twist between molecules and frustration arises. As a consequence, DNA, as other helical polymers, presents original textures that originate from the competition between two incompatible ordering constraints. The same frustration should arise in native systems, when DNA is hexagonally packed for example in the capsid of the bacteriophage [10] or in the sperm nuclei of certain species [11,12]. Constraints that arise in such conditions have been only marginally considered up to now.
In somatic eukaryotic cells, DNA is associated with histone proteins to form periodic structures called nucleosomes [13]. The chromatin fibre, whose organization is still a matter of debate, is confined in the small volume of a chromosomal territory [14]. To achieve its genetic activites, chromatin must present changes in its organization, both in space or time. Throughout the cell cycle, the nucleosome concentration can be roughly evaluated to range from 50 to 500 mg/ml. Geometrical constraints arising from this high local concentration of chromatin are not easy to explore in native systems at the molecular scale. An alternative approach to analyze such constraints under ranges of concentrations found in vivo is based on a simplified system made of the building blocks of chromatin, the nucleosome core particles (NCPs). Concentrated solutions of these NCPs can be prepared under well-defined conditions. Columns are spontaneously formed by the piling of isolated NCPs on top of one another, that self-organize to form multiple ordered phases whose nature depends on ionic conditions and NCP concentration. Among others, several types of columnar hexagonal phases have been described [15]. As for DNA, the anisotropy of the NCPs columns favours their dense hexagonal packing and, the columns being chiral, a competition also arises between chirality and dense hexagonal packing.
The question that we address here is to know how the hexagonal unidirectional packing may coexist with the spontaneous helical twist and whether the supramolecular macroscopic helicity could originate from this competition. We will first consider the DNA molecule, describe its characteristics, and present a few examples where cholesteric and hexagonal organizations coexist, either in pure DNA solutions in vitro or in sperm cells. We will also consider nucleosome core particles and present the structural details of the columnar hexagonal phases that they form under a variety of experimental conditions. Both systems present interesting patterns combining either helices or twist with the local hexagonal ordering. More generally, this competition between twist and hexagonal packing raises interesting theoretical questions [16–18] that will be discussed briefly here.
2 Material and methods
Short DNA fragments (146 bp, i.e. 50 nm) were prepared by enzymatic digestion of H1-depleted chromatin extracted from calf thymus nuclei. DNA was dissolved either in 10 mM Tris buffer added with 100 mM NaCl or 10 mM sodium cacodylate added with 250 mM ammonium acetate, and progressively concentrated to 300 < C < 450 mg/ml. Under these conditions the liquid crystalline phase is columnar hexagonal. The nature of the ordered phase was checked in polarizing microscopy.
Nucleosome core particles were also prepared from calf thymus chromatin. After removal of H1 histones, NCP were obtained by controlled digestion with micrococcal nuclease and purified by chromatography over a Sephacryl S300 HR column (Sephacryl S300, Pharmacia, Uppsala, Sweden). The mono-nucleosome fraction was dialysed against 10 mM TE buffer at a concentration of 1–3 mg/ml and further concentrated by ultrafiltration in a pressurised cell (Amicon 8010, Amicon Corp., Lexington, MA) through a hydroxypropylcellulose membrane (Amicon YM100) to a final concentration of 50–150 mg/ml. These stock solutions were stored at 0 °C. To prevent proteolysis, 0.5 mM PMSF was added to buffers at all steps of the preparation procedure. Higher concentrations (above 320 mg/ml) were reached by increase of the osmotic pressure, imposed by a neutral stressing polymer (polyethylene glycol, Fluka MW 20000, Fluka Chemical Corp., Milwaukee, WI). The solution was equilibrated by extensive dialysis (3 weeks) against the polymer dissolved in the same buffer at 35% (w:w).
Stallion sperm cells were washed in EBSS–Hepes buffer and centrifuged at 300 g for 10 min. The pellet was re-suspended in 20% Dextran solution (MW 42 kDa, Sigma, St. Louis, MO) dissolved in the same buffer and eventually added with 4 mM dithiotrehitol (DTT). After centrifugation (600 g, 10 min), the pellet was collected and vitrified as described below.
For optical microscopy observations, samples were deposited between slide and coverslip and the preparation was let to stabilize for hours, days or months. The coverslip was sealed to avoid any uncontrolled dehydration. Observations were recorded with a Nikon polarizing microscope. For electron microscopy analyses, DNA and NCP liquid crystalline samples were let to stabilize under humid atmosphere for a few hours before being frozen at liquid helium temperature with a slam-freezing device [19]. Spermatozoa were frozen in a high-pressure freezing machine (HPM 010, Balzers, Lichtenstein) [20]. Frozen specimens were stored in liquid nitrogen and later prepared for EM observations. Freeze-fracture was recorded in a Balzers BAF 400 T apparatus, under 2 × 10−7 Torr vacuum. Replicas were shadowed at 45° with Pt and carbon-coated, washed from the biological material and observed in an electron microscope (Philips CM12, Eindhoven, The Netherlands) at 80 or 100 kV. Cryosections were realised in a cryo-ultramicrotome (Leica, Vienna, Austria) and collected on 600 or 1500 mesh carbon-coated copper grids. Sections were transferred in a cryoholder (Gatan, Warrendale, PA) and observed under low-dose conditions in a CM12 electron microscope. Images were recorded on Kodak SO-163 films at 35,000 or 45,000 magnification and 600–1000 nm defocus.
3 Results
3.1 The helical structure of DNA and nucleosomes
DNA is a highly negatively charged polyelectrolyte, typically 10–50 μm long in the capsid of a bacteriophage and 1–10 cm long in a eukaryotic chromosome. The chain is semi-flexible, with a persistence length of about 50 nm. It is also a right-handed double helix with a pitch close to 3.4 nm and a diameter of 2.2 nm (Fig. 1a).

DNA (a) and nucleosome core particle (b top view, and b′ side view (from PDB 1aoi [13]), with their dimensions and geometrical properties.
Nucleosome core particles (NCP) are composed of a 146/147 bp DNA segment coiled around a central histone octamer. The atomic structure of the nucleosome core particle has been solved a few years ago [13] and further refined [21]. The NCP is a flat wedge cylinder 10.5 nm in diameter and 5.7 nm high. The right-handed DNA helix follows a left-handed helical path around the protein core, with a pitch of 2.8 nm (Fig. 1b and b′). Above a critical concentration, NCP spontaneously stack on top of each other to form columns that keep the helical character, despite the lack of continuity of the DNA chain from one NCP to the next.
The helical shape of DNA and NCPs provides them with properties that they share with many other biological polymers. We propose to briefly recall here a few geometrical considerations that may be useful before going into more detailed structural data. Under conditions of confinement, two helices usually prefer not to align perfectly in parallel, but to twist with an angle, as drawn in Fig. 2a. The formation of cholesteric and blue phases derives from this spontaneous twist. In the cholesteric phase (Fig. 2b), molecules are aligned in parallel and their orientation rotates continuously along an axis called the “cholesteric axis”, normal to the direction of the molecules. The pitch of the cholesteric phase corresponds to a rotation of 360° of the director. Frustration arises from this organization, since the twist occurs along only one direction. Two molecules coming close to each other may choose any direction of twist that is normal to the axis of the helix. This situation may be found in bundles of filaments, also called “double twist” bundles (drawn in Fig. 2c), which are the building blocks of the blue phases. To understand this structure, we may imagine a series of concentric cylinders of increasing diameters around a central helical chain (Fig. 2c). On the surface of these cylinders are drawn lines, representing helices. All helices of the first cylinder are twisted relative to the central one, with the same angle. They follow helical paths on the surface of the cylinder. The construction is the same for all successive cylinders. In this configuration, the twist occurs along all directions normal to the axis of the initial chain. The comparison of “single-twist” and “double-twist” configurations is clearly illustrated using the nail convention, as drawn in Fig. 2b′ and c′. The cholesteric organization may extend over large distances, whereas the double twist configuration is limited to small diameter bundles.
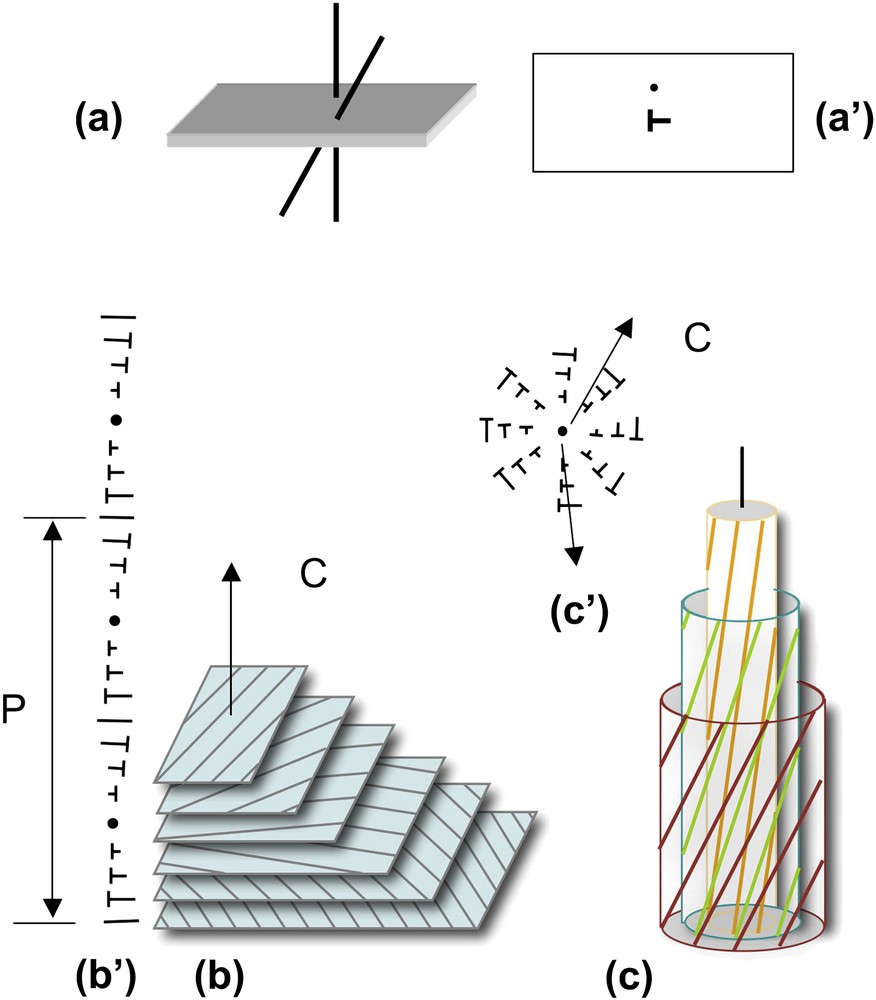
How helices twist and form supramolecular helical structures. Two molecules (helices) with a twist angle are seen in a perspective view (a) and in top view (a′). The nail convention is used to indicate the orientation of molecules in the plane of projection: dots for molecules normal to this plane and nails for oblique molecules. Lines would correspond to molecules lying in the plane. Twist between helices may lead to the formation of either “simple twist” or “double twist” configurations. In the cholesteric structure (b), molecules aligned in parallel planes rotate continuously along a direction C, the cholesteric axis, as seen in a perspective view (b) and using the nail convention in a plane parallel to the cholesteric axis (b′). The cholesteric pitch P corresponds to a rotation of 360° of molecular orientations. In the double twist configuration (c), twist occurs along all directions normal to the axis of the bundle, as seen in perspective view where molecules are drawn on concentric cylinders (c), and in projection on a plane parallel to the twist directions, using the nail convention (c′). Note that planes are used here to facilitate the drawing but they have no existence, the twist between molecules being usually continuous.
In the columnar hexagonal phase, one column corresponds to one DNA chain (or to DNA fragments stacking on top of one another) one column of solvent to one column of stacked NCPs’ (Fig. 3). In section planes normal to the direction of the columns (Fig. 3a and b), the three main directions of the hexagonal network can be seen, 60° apart. Each of these directions corresponds to a two-fold symmetry axis T2. Other symmetry axes L6, L3, L2 and θ2 are also indicated in Fig. 3c. The interhelix distance aH is equal to , d being the distance between reticular planes.

Parallel alignment of columns (a), forming a 2D periodic hexagonal lattice in projection onto a plane normal to their axis (b). The hexagonal network is sketched in (c) with its multiple axes of symmetry: the six-fold symmetry axis L6, the three-fold symmetry axis L3 and the two-fold symmetry axes L2, T2 and θ2. The distance between the reticular planes , with aH the inter-column distance. DNA and nucleosomes are sketched in d–f as elongated rods and flat cylinders, respectively. Columns that correspond to DNA chains or to piles of stacked nucleosomes may form simple hexagonal phases (d, e) or analogues of inverse hexagonal phases in the case of NCP (f).
3.2 Dense phases of DNA
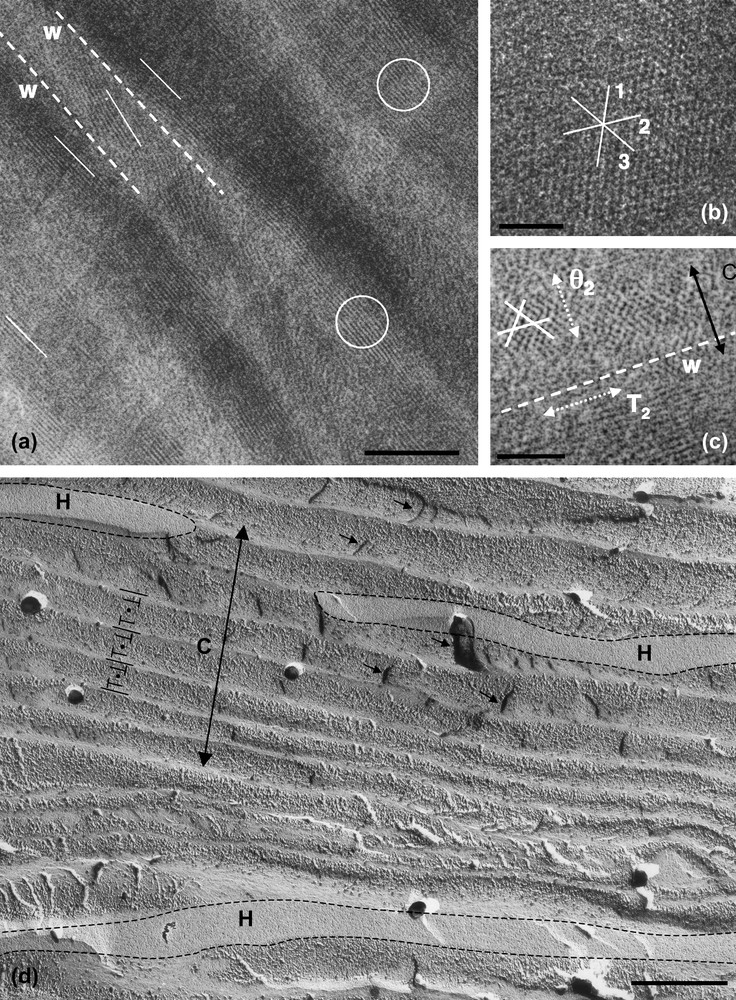
The rigidity of the DNA chain favours the self-assembly of the molecule into ordered phases. Using short DNA fragments and starting from an isotropic dilute solution, the concentration of the solutions can be increased progressively in the presence of monovalent ions, either by progressive dehydration of the sample (uncontrolled ionic conditions) or by applying osmotic pressure (controlled ionic conditions). Multiple ordered phases of DNA have been found. The first ordered phases are highly chiral mesophases with either double-twist (blue phases) or simple-twist (cholesteric phase) configurations. The 2D hexagonal [22] phases are also found for higher DNA concentrations, and also 3D crystals (review in Ref. [23]). A hexatic ordering has also been described with long DNA chains [24]. Using a sample prepared with short DNA fragments, it has been possible to measure the hexagonal parameter aH (also the distance between DNA chains) over a large concentration range. aH varies from 3.15 to 2.9 nm in the 2D phase and from 2.9 to 2.37 nm in the 3D phase [22]. The hexagonal lattice can be seen directly on cryosections of the vitrified material (Fig. 4b and c). Each dark spot corresponds to one DNA molecule seen from the top. Such observations are quite rare because the section must be perfectly normal to the direction of the columns. A slight obliquity is enough to transform the hexagonal pattern into a series of regular striations, with molecules aligned parallel to one series of reticular planes (usually one T2 direction of the lattice3). These striations are frequently observed (Fig. 4a (better seen in encircled domains) and in the lower part of Fig. 4c. In these samples, the measured lamellar periodicity, d = 2.3 ± 1 nm, provides us with the interhelix distance aH = 2.65 nm. We are thus dealing with the 3D hexagonal phase. Striated domains (with unidirectional orientation of the molecules) are separated by twist walls (w) on both sides of which the orientation of the striations changes abruptly, leading to the formation of “herring-bone” patterns. These patterns characterize twisted plywoods structures (see Y. Bouligand, this issue). Molecules are aligned in a series of parallel planes of a given thickness. Their orientation may change abruptly with formation of twist walls (w) (Fig. 5a′). Sections oblique to the C axis reveal the herring-bone patterns (Fig. 5a). A favourable situation to analyse the orientation of molecules on both sides of a twist wall is given in Fig. 4c. In the top domain, molecules are normal to the section plane, with one T2 direction parallel to the twist wall (w). In the lower part of the micrograph, one T2 direction (revealed by the striations) also lies parallel to the wall plane. The direction of the molecules has rotated along the twist axis (C). C being normal to the T2 directions, we can conclude that the C axis lies parallel to one θ2 direction of the hexagonal network. A schematic representation of this twist wall is given in Fig. 8a.
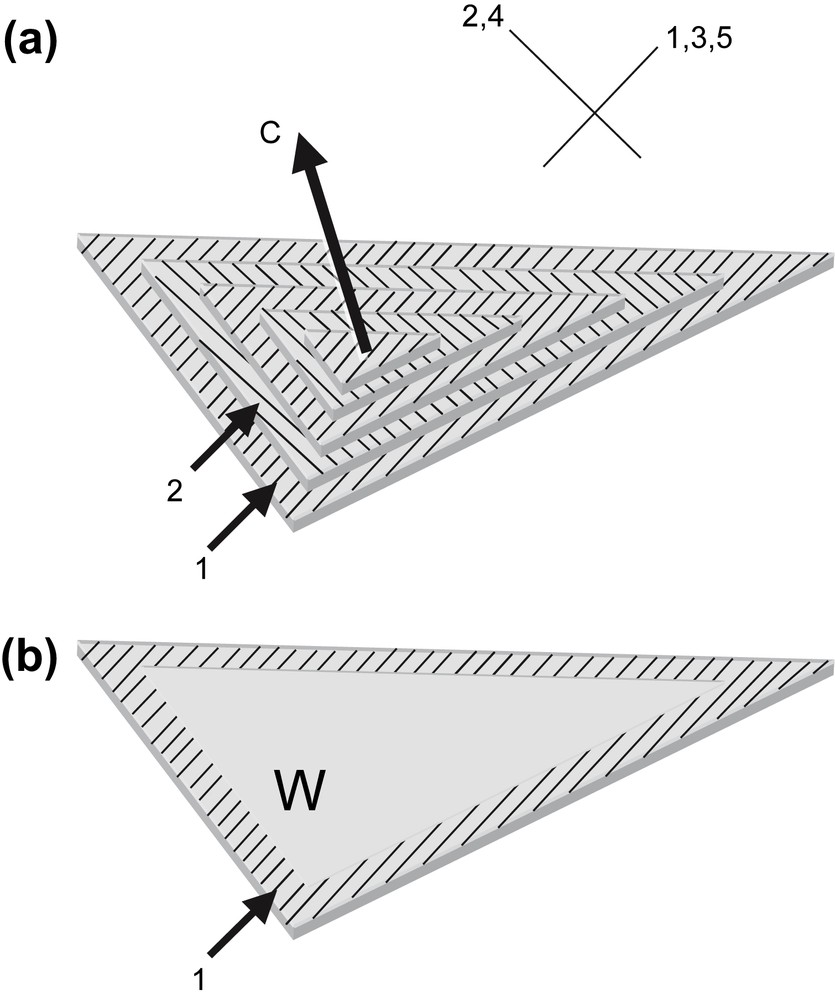
Drawing showing how herring-bone patterns are formed by introduction of twist walls (w) in a regular stacking of molecular planes. Parallel chains are indicated by lines drawn on stacked parallel planes. Their orientation changes from plane to plane along the twist axis C by an angle that is equal here to 90°. Orientations are identical in planes 1, 3, 5 and different from planes 2, and 4. Herring-bone patterns that appear on oblique sections (three are drawn here) may be symmetric or not depending on the orientation of the section planes with respect to the alignment of molecules. Twist walls correspond to surfaces where chains superimpose with different orientations. As an example, the wall separating planes 1 and 2 has been evidenced in (b).

Hexagonal phase of nucleosomes (inverse, low salt) observed in polarizing microscopy (a) and by freeze-fracture electron microscopy (c, c′). In (b) are sketched, in top views, the possible organizations of NCP columns in the hexagonal network. Each unit cell, either a regular or an irregular hexagon, is composed of 15, 12, 9 or 6 columns, to adjust decreasing sizes of the hexagonal parameter aH. The two triangular lattices, corresponding to the hexagonal network itself and to the local packing of the columns, are indicated. They are rotated by 30° in a15 and a9, and by an angle 30° ± α in a12 and a6. In (c, c′), the fracture plane is almost normal to the six-fold axis. Two out of the three main directions of the hexagonal network are underlined in (c′). These are not straight lines, as it would be expected in a perfect hexagonal lattice. A slight divergence of the lines is also seen, from top to bottom for the continuous lines, and from left to right for the dotted lines. Bar = 50 μm (a), 200 nm (c).
The coexistence of the cholesteric and hexagonal phases can be observed also in phase-transition domains. We analyzed two situations in order to understand (i) how the hexagonal order nucleates and propagates inside the cholesteric phase and (ii) how the twist establishes upon melting (dilution) of the hexagonal phase, using two different experimental models.
- (i) Starting from a DNA solution, the distance between helices was progressively decreased by raising the DNA concentration up to the phase-transition concentration. The two phases may be seen in coexistence over a given concentration range (Fig. 4d). The cholesteric-to-hexagonal phase transition generally occurs along with a slight untwisting of the cholesteric structure (the average twist angle between DNA molecules decreases from 0.8° to 0.3°), which favours the unidirectional alignment into the hexagonal lattice [17]. In some cases, another situation occurs, as seen in Fig. 4d, by freeze-fracture electron microscopy. Domains of the hexagonal phase (limited by dotted lines) are growing between the cholesteric layers. The orientation of the cholesteric axis (C, double arrow) is normal to the cholesteric layering, and the pitch (P) can be measured. It equals about 0.6 μm here (versus 2.5 μm in the pure DNA cholesteric phase). From their flattened shape, we deduce that the hexagonal domains grow easily in the plane of the molecules (normal to the cholesteric axis) and that their growth is strongly impeded in the direction of twist. The limits between the hexagonal and the cholesteric domains mostly correspond to twist walls. Unfortunately, the resolution obtained by freeze-fracture EM here is not good enough to determine the directions of the hexagonal lattice in each domain.
- (ii) The reverse transition (from hexagonal to cholesteric) was induced experimentally using sperm chromatin. The structure of chromatin is hexagonal in a few species [8,11]. It has been described as a twisted plywood, locally hexagonal, with twist and many defects in stallion and human sperm cells [25]. The structure is extremely dense as seen on EM cryosections of the intact vitrified cells (Fig. 6a). Basic proteins, called protamines, that have replaced histones during spermatogenesis, contain cysteine aminoacids. These residues form disulfide bonds and stabilize the ultimate states of chromatin condensation in mature sperm cells. Using DTT to reduce the disulfide bonds, it is possible to initiate the decondensation process. Upon extended decondensation, chromatin is transformed into a cholesteric phase, containing numerous defects (not shown). We focus here on intermediate states of decondensation (Fig. 6b–d). Small and almost circular double-twist bundles are formed sometimes (Fig. 6b), and were analyzed previously [25]). We also observed the coexistence of dense and partially striated elongated domains, well visible in Fig. 6c (asterisks), surrounded by a more dilute chromatin, with a fibrous appearance, better seen in Fig. 6d. The two images of two analogous regions enhance the signal coming either from the hexagonal phase (asterisks in (c)) or from the surrounding phase in (d), which is most likely cholesteric since we observe locally remnants of characteristic arched patterns. As described above, the striated domains correspond to a hexagonal packing of chromatin filaments. The periodicity is equal here to 2.7 nm as in the native sperm nucleus, which corresponds to an inter-filament distance of 3.1 nm. Dense domains without visible striations more likely correspond to unfavourable orientations of the lattice. The coexistence of the cholesteric and hexagonal orderings reveals that the decondensation process does not occur in a homogeneous way with a progressive increase of the average distance between the DNA fibres. Instead, we understand this process as a melting of the hexagonal domains into a more dilute cholesteric phase that would grow progressively at the expense of the initial phase. We may wonder whether this process results from the structural constraints of the initial structure that would be relaxed first along fragile lines or whether it could result from a inhomogeneous diffusion of DTT inside the condensed chromatin along facilitated diffusion lines. The initial structure was not a perfect hexagonal crystal, and it seems reasonable to assume that the defect lines of the initial structure may be involved in the fragmentation of the initial hexagonal structure into these isolated hexagonal domains. Unfortunately, the presence of numerous defects impedes here to check whether the cholesteric axis is also parallel to the θ2 direction of the hexagonal lattices.

EM cryosections of native (a) and decondensed chromatin (b, c, d) from stallion sperm nuclei. (a) Periodic layering of elongated domains with transverse 2.7-nm striations is marked by arrows (image filtered as described in Ref. [25]. (b) Isolated thread of partially decondensed chromatin, cut perpendicular to its elongation axis and showing its double-twist conformation. (c, d) Two sections of similar regions of inhomogeneously decondensed chromatin. Dense elongated domains (⋆) are immersed in a surrounding less concentrated fibrous phase showing arched patterns (underlined in d). According to the imaging conditions (choice of defocus), either the 2.7-nm striation (reticular planes of the hexagonal lattice) or the more distant DNA segments of the surrounding cholesteric phase are visualised. The periodic striations of the dense domains are well resolved in (c), whereas the arched patterns drawn by the more distant filaments in the surrounding phase are better seen in (d). Bar = 50 nm.
3.3 Nucleosome core particles
Nucleosome core particles spontaneously organize to form columns by stacking on top of each other [26]. For high enough nucleosome concentrations, these columns organize in multiple ways, depending on the ionic conditions [27]. We will focus here on hexagonal structures that may be of two different types: a direct hexagonal phase (Fig. 3e), or an inverse hexagonal phase (Fig. 3f). These two types of hexagonal phases of nucleosomes exhibit different textures in optical microscopy. Both show multiple illustrations of how hexagonal and chiral ordering may combine to produce complex patterns, that we detail below.
The compact direct hexagonal phase may be either 2D or 3D. From X-ray diffraction experiments, it was shown that nucleosomes are free to rotate in the columns in the 2D phase, whereas a correlation exists between the longitudinal and the lateral ordering in the 3D phase [28]. This nucleosome ordering was obtained under multiple ionic conditions: (i) in the presence of monovalent ions and under an applied osmotic pressure (Fig. 7a–f), (ii) in the presence of a trivalent ion, spermidine, in aqueous solution [29] (Fig. 7g–m) or in the presence of spermine in alcoholic solution ([30]; Fig. 7n–p). In the inverse hexagonal phase, each column corresponds to channels of solvent. The walls of the channels are made up of piles of nucleosomes arranged into bilayers (Figs. 3f and 9b). We lack information to determine precisely how nucleosomes are organized along the columns. This organization was obtained under low monovalent salt conditions and under applied osmotic pressure. We do not intend to focus here on the experimental conditions that determine the formation of one or another structure; we will instead consider the multiplicity of geometric situations that were encountered.
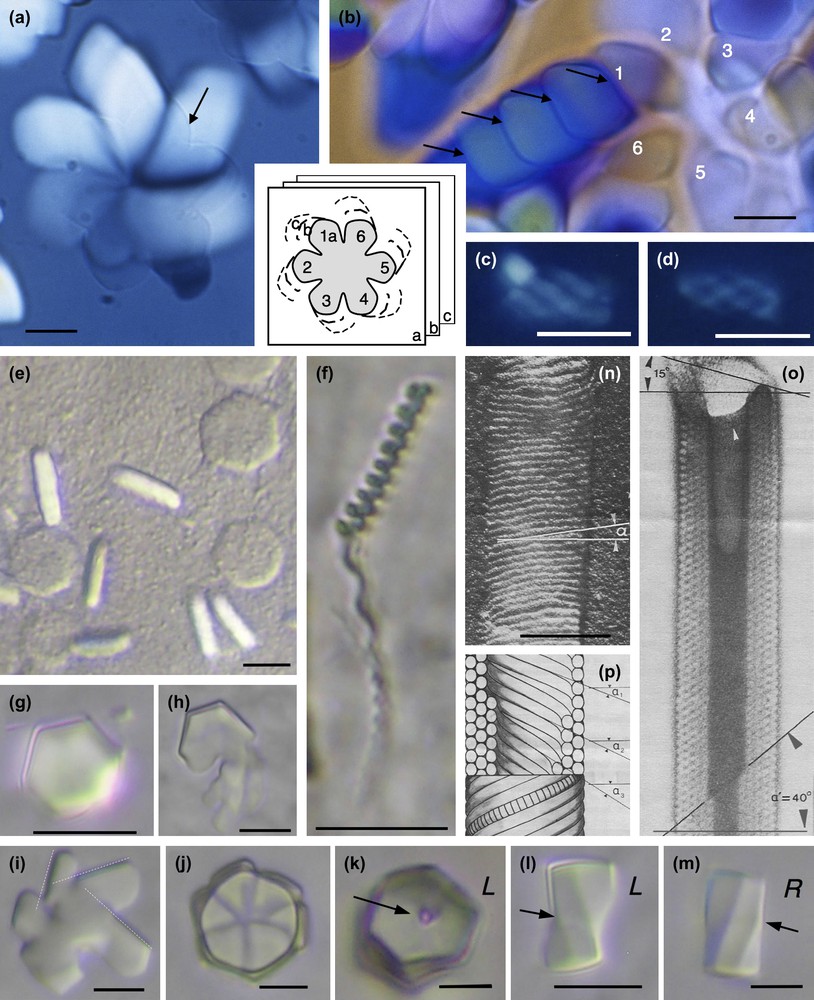
Examples of hexagonal crystals of nucleosome core particles showing macroscopic chirality. Samples are prepared in 10 mM Tris–Cl− buffer with added monovalent Na+ cations and under osmotic pressure (19% PEG MW 20,000, i.e. ∼5 atm) (a–f), in the presence of 3 mM spermidine (trivalent cation) from NCP solution at 14 mg/ml in 10 mM Tris–Cl− buffer (g–m), and in presence of 11 μM spermine (tetravalent cation), 9% isopropanol from NCP solution at 19.75 mg/ml in 10 mM sodium cacodylate buffer (n–p). (a) Hexagonal domains at the coverslip level (arrow) extends down in the thickness of the preparation as drawn in the inset, and enlarges to produce spiral patterns. (b) The growth from the initial part No. 1 of the hexagonal domain occurs with formation of twist walls (arrows). (c, d) Hexagonal domains may also keep a global cylindrical shape. (e, f) Under identical conditions are formed flat hexagonal platelets observed in top and side views, with no observable chirality (e) and long helical bundles (f). (g–m) Hexagonal domains in top (g–k) and side views (l–m) that may be either left (L) or right (R) handed, showing twist walls underlined by the arrows. The dislocation line (arrow) is well visible in (k). (n–p) Cylinders of nucleosomes (reprinted from Ref. [30]). Observations in polarizing microscopy, between circular crossed polars (a–d), in Nomarski interferential contrast (e–m), and in electron microscopy after shadowing (n) or staining (o). Bar = 100 nm (n–p).
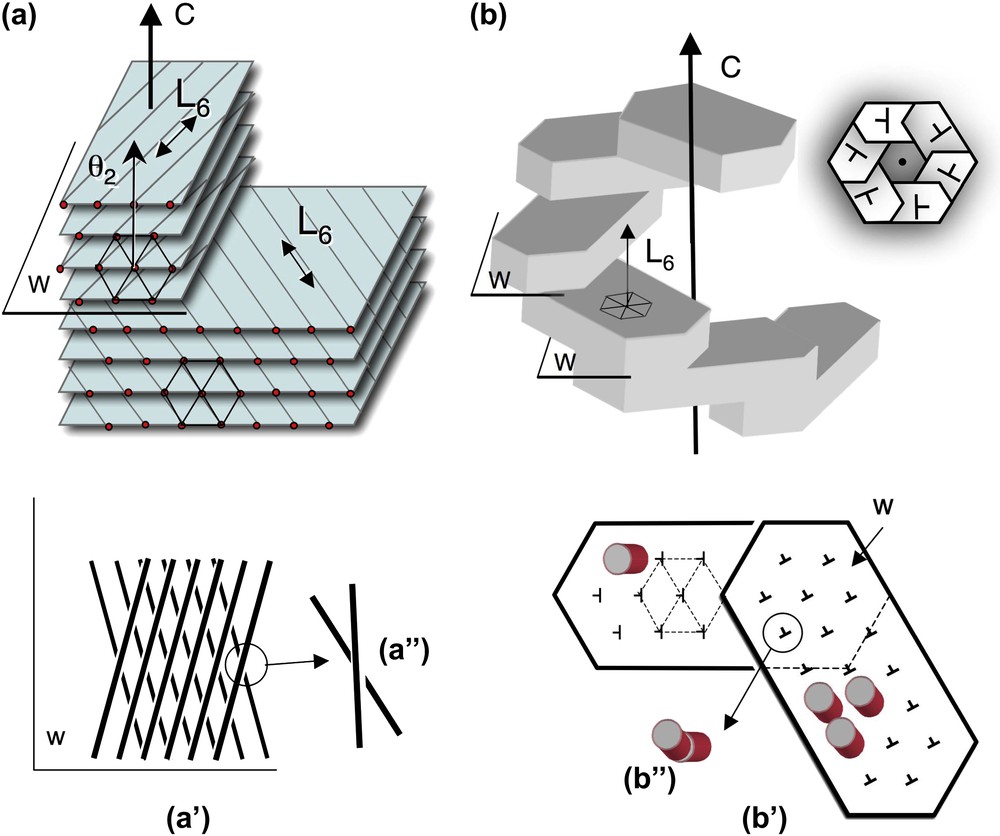
Twist walls in hexagonal columnar phases, either parallel (a) or normal (b) to the direction of the columns. (a) Twist walls (w) separating two domains of hexagonally packed columns. The wall lies parallel to the direction of the columns (and to the L6 axis of the hexagonal lattice) and normal to the twist axis C. The orientation of columns changes on both sides of the twist wall, as seen on the projection onto this plane (a′, a″). The twist is left-handed here. The θ2 direction of the lattice network lies parallel to the C axis (as explained in the text from the analysis of Fig. 4a and c). (b) Twist walls (w) separating domains of hexagonally packed columns. The walls lie almost normal to the direction of the columns (not drawn in the perspective view) (and to the L6 axis) and normal to the twist axis C. In top view the stacking of hexagonal domains form hexagonal shapes (see Fig. 7i–k) with a double-twist configuration. The direction of the columns is slightly tilted on both sides of the wall (notice that the orientation of the nails has changed (b′). Seen from the top, columns from below and above this plane are not aligned in parallel (b″). Their piling would draw here a left-handed helix along the C direction.
Let us first consider the compact hexagonal structure with a selection of examples presented in Fig. 7. Two types of hexagonal domains were described previously [31]: large six-fold symmetry “flower” domains (Fig. 7a and b) and small cylindrical helical bundles (Fig. 7c and d). The small cylindrical bundles are formed by six left-handed helical threads coiled around each other. Because of their small size, we were not able to determine whether and how they were connected together. We proceeded further in the analysis of the larger domains and showed how a flat, hexagonal “flower” domain (Fig. 7a) grows both in the direction of the columns (in the thickness of the preparation), and also laterally to form spiral patterns. In the initial six-fold symmetry domain (pointed by the arrow in Fig. 7a) that is almost extinguished between crossed polars, columns (parallel to the L6 axes) are normal to the surface of the preparation. The radial growth of the crystal occurs first with rotation of the columns in a typical double-twist configuration [31]. A continuous twist coexists with a local hexagonal order. At the microscopic level, freeze-fracture analyses reveal that the continuous double twist coexists with double splay between columns (not illustrated here) [31]. The lateral extension of the double-twist configuration, however, is limited. At a later stage of the crystal growth, the excess of twist is relaxed by steps, with formation of twist walls. To help the observer understand the process, a drawing summarizing the successive steps of the growth is given as an inset of Fig. 7a and b. A series of superimposed planes (a, b, c) represent the successive steps of the growth, deeper and deeper in the preparation plane. For each of the six initial domains of the crystal, a series of secondary domains can be seen (1a–c; 2a–c; etc…). This is well visible in Fig. 7b, starting from the domain No. 1. Each domain is separated from the next one by a twist wall (arrows). In addition to being regularly distributed in the double twist configuration, the twist is now also localized along these wall surfaces. The direction of the columns changes suddenly from one domain to the next. As analyzed below, the twist walls are here slightly oblique with respect to the direction of the columns.
Under related conditions, monodispersed flat hexagonal platelets were formed (Fig. 7e). They are isotropic in top view and birefringent in side views, revealing that columns of NCP are normal to the plane of the platelet, as expected. These domains do not present any apparent chirality. Considering the dimensions of the crystals, each platelet would contain about 1800 NCP columns, each about 800 NCPs long. Close by in the same preparations are found very long and helical threads length (Fig. 7f). These are about 500 nm wide (i.e. only 45 NCPs columns) and infinite in length. Their pitch varies here from 2 to 4 μm. We assume that the packing of the columns is also hexagonal in these helical bundles, but we cannot precise whether it is a 2D or a 3D ordering. From the observation of these two coexisting germs, we understand that the helicity of the bundles becomes apparent when the L/D ratio is increased.
Another interesting situation was observed in NCP aggregates formed by addition of spermidine, a trivalent cation. Conditions of precipitation are detailed elsewhere [29]. The hexagonal domains of the dense phase of nucleosomes are in equilibrium with a dilute solution of nucleosomes (Fig. 7g–m). They present well-defined hexagonal limits (Fig. 7g) due to the faceting. They may correspond either to monodomains or be made of six parts (Fig. 7j). These latter crystals grow around a vertical disclination line parallel to the elongation axis of the germ, well visible in Fig. 7k, since there is an empty hole along this line. The role of such defect lines in crystal growth is well established. These germs are usually left-handed (Fig. 7k and l), and only exceptionally right-handed (Fig. 7m), as can be unambiguously determined from lateral views. These facetted helical germs remind us of the crystals seen in Fig. 7a, with differences in the interfacial conditions since we observe hexagonal instead of flower-like six-fold symmetry patterns. One interesting point is raised by the observation of initial steps of the formation of these crystals (see Fig. 7h and i). In many cases, they are formed by the piling (or juxtaposition) of several sub-domains with well-defined limits, 60° apart, that reveal the three main directions of the hexagonal lattice (Fig. 7i). All sub-domains present identical directions. Therefore, each domain interacts (and often superimposes) with the next one with the constraint that the reticular planes must be superimposed. These domains are apparently slightly oblique with respect to the preparation plane. The superimposition of facetted platelets leads to the formation of a six-blade propeller structure (Figs. 7j and 9b). This suggests that on opposite sides of the hexagonal domain, the NCP columns are slightly tilted on opposite directions (Fig. 9b), as in classical double-twist configurations. The difference here comes from the presence of defect walls separating the faceted planes while they pile on top of each other. These surfaces would be close to be normal to the direction of the columns. They are schematically represented in top view in Fig. 9b and b′).
Other original nucleosome crystals were also obtained many years ago in the presence of micromolar concentrations of spermine (4+) and 9% isopropanol or 20% dioxan [30]. These are regular hollow cylinders of nucleosome core particles adsorbed to a positively charged carbon film, freeze-dried and shadow-cast (Fig. 7n) or negatively stained (Fig. 7o) before observation in the electron microscope. From the stained image, we see that the walls of the cylinder are made up of several layers (four in the upper part, five in the lower part of Fig. 7o). The external layer of the cylinder is seen in Fig. 7n. The schematic drawing of the cylinder (Fig. 7p) offers in its lower part a view of the external layer of a cylinder (see Fig. 7n), with individual nucleosome core particles drawn in one of the helices. In the upper part, a longitudinal section of the cylinder reveals its interior (see Fig. 7o). Helices of stacked nucleosomes are closely packed into a pseudo-hexagonal lattice. The columns from the successive layers have different pitch angles noted α1, α2 and α3 in Fig. 7p. Their obliquity varies from one layer to the next, revealing the presence of twist between these columns.
The inverse hexagonal phase of nucleosome core particles presents textures, such as the twisted threads seen in Fig. 8a, which unambiguously reveal the chirality of the phase, although we did not analyze them in detail. Freeze-fracture electron microscopy provides an interesting approach to investigate the hexagonal/chiral interplay. The hexagonal network is recognized at a first glance (Fig. 8c). A careful examination of the lattice reveals that the three main directions of the hexagonal network are not straight, as expected in a perfect hexagonal crystal (two of them are underlined in Fig. 8c′). Their curvature reveals that the reticular planes themselves are curved. A slight divergence is observed between these lines; their interdistance is smaller in the right part. The precise analysis of such patterns (described in detail in the case of the high salt columnar hexagonal phase in Ref. [31]) reveals the presence of curvature and splay in this phase. We are dealing here with double-twist bundles of limited size (typically 600–1200 nm in diameter). Two other domains can be seen in the lower part of the micrograph and are indicated by asterisks.
The inverse hexagonal phase is found above 320 mg/ml. To account for the decrease of solvent that occurs upon increase of the nucleosome concentration, columns reorganize to adjust the NCP/solvent ratio. The number of columns per hexagonal cell varies by steps of 3, leading to discrete changes of concentration correlated with discrete variations of the hexagonal parameter aH. Four different honeycomb-like arrays are expected to account for the relevant concentrations, displayed in Fig. 8b. The corresponding hexagonal parameter is, respectively, noted a15, a12, a9 and a6, the subscript number referring to the number n of columns involved in each hexagonal unit cell. We observed the first three lattices (a15 = 55 nm, a12 = 46 nm and a9 = 38 nm), as determined from the measurements of aH parameters on freeze-fracture micrographs. The respective concentrations can be calculated as 335, 380 and 450 mg/ml. It is likely that the last lattice (a6 = 28 nm) also exists at higher concentration (calculated as 520 mg/ml). Note that the hexagonal cell is not necessarily a regular hexagon (a15 and a9). We are dealing here with two superimposed triangular lattices, the lattice of the hexagonal network itself and the lattice of the columns that is restricted to the double layers forming the walls of the polygons. Interestingly, these two triangular lattices never superimpose. They are rotated by 30° in a15 and a9. In a12 and a6, they are rotated by 30° + α or 30° − α, with α = 1/((n/3) + 1)√3. This means that in a15 and a9, the T2 axis of one network is superimposed to the θ2 axis of the other. These are achiral configurations. On the contrary, in a12 and a6, there is no fit between the two networks and the structures are chiral. This chirality is not related to the chirality of the nucleosome, but to the matching of two lattices, as in certain lamellar systems [33]. As a consequence, the two configurations should in principle occur with equal probability. However, in our system, the chirality of the nucleosome may somehow play a role in the chirality of the super-lattice, and favour one or the other configuration. We did not control the concentration of our samples with enough precision to determine to what extent the chirality of the lattice is of importance in the macroscopic helicity illustrated in Fig. 8a. An extensive analysis of several controlled specimens would be necessary to answer the question. Likewise, more analyses would be necessary to understand the relationship between the longitudinal ordering of NCP along the columns and the type of lattice.
4 Discussion
How does chirality express in hexagonal phases made of chiral objects such as DNA or NCPs? We presented a few examples showing a diversity of situations:
- – the twist can be homogeneously diluted in the phase (continuous, at the scale of observation), and/or expelled from the phase and localized along twist walls;
- – hexagonal domains may be facetted with either flower-shapes of simple hexagonal limits;
- – they are either filled with material when their growth is limited in the direction of the columns (Fig. 7a and e) or grow around a central disclination line, thus creating an axial empty core (Fig. 7k);
- – when they are long enough compared to their diameter, the hexagonal domains turn usually helical with a helical pitch that may vary significantly with respect to the diameter of the bundle (Fig. 7c,d,f, for NCPs). Such situations impose that columns follow helical paths. A very clear example of such helical columns is given in Fig. 7n–p;
- – we observed single and double-twist situations.
In DNA hexagonal phases analyzed so far, twist occurs in one direction and is localized along twist walls parallel to the columns (Fig. 9a). Double-twist configurations are locally observed at the level of defect cores (sperm cells) and upon partial decondensation. In NCPs, twist occurs in all directions normal to the columns (double twist), and may be continuous and/or expelled along twist walls nearly perpendicular to the columns (Fig. 9b). On account of the diversity of the situations, it is likely that different combinations are possible in each system, and would be evidenced upon exploration of other physico-chemical conditions.
It is well established that a cholesteric and a hexagonal order can coexist as long as the distance between the chains is large enough [34]. Upon increase of the polymer concentration, chirality competes with the hexagonal packing of molecules. Theoretical approaches [17,35] predicted two types of phases: Twist Grain Boundaries (TGB) and “moiré” phases based on the presence and distribution of defects. They defined two types of chirality: (i) the usual cholesteric-like twist of the local director around the pitch and (ii) the rotation of the local bond orientational order. The examples presented above illustrate how twist may occur either normal to the direction of the columns (as drawn in Fig. 9a) and/or along the direction of the columns (as drawn in Fig. 9b).
- (i) Robinson already raised the question of the direction of twist with respect to the directions of the hexagonal lattice in the case of a polypeptide, the PolyBenzyl-l-Gluramate (PBLG) [34]. We have been able to answer this question, at least for DNA solutions, and to show that the twist axis lies parallel to the θ2 direction (Figs. 4c and 9a). This observation was made possible by the use of high-resolution EM observation of cryosections and facilitated by the presence of twist walls. We assume that the co-alignment of C and θ2 directions is also preferred when the twist is equally distributed in the bulk. The question remains as to know why C superimposes to one θ2 direction of the hexagonal lattice (instead of T2) and whether this situation is the rule for other helical macromolecules that are hexagonally packed. We have shown that the growth of the hexagonal lattice occurs more easily in the direction normal to the cholesteric layers, to form thin and flat domains limited by twist walls. Such defects lead to the formation of TGB phases as described long ago with DNA [9].
- (ii) The twist occurring in the direction of the columns that was predicted theoretically has been clearly observed in spermidine-NCPs crystals (Fig. 7i–m). This twist was already present in samples shown in Fig. 7a, but not described as such in Ref. [31]. We propose a schematic interpretation of these twist walls in Fig. 9b. Since the limits of the facets of the hexagonal superimposed domains follow three identical directions, this reveals that the three main directions of the hexagonal lattice are superimposed in the different domains. There are anyway slight distortions between these different domains, since they do not merge at least at the first stages of formation of the structures (Fig. 7i and j). One interpretation is that the direction of the NCP columns is not exactly parallel to the C direction. The tilt direction of NCPs would be rotated by 60° from one hexagonal domain to the next, as illustrated in Fig. 9b′. These walls would relax the constraint between NCP from neighbouring columns closely packed in the hexagonal domains. Columns remain almost straight, but their orientation rotates at each wall step. These walls are usually not resolved in optical microscopy. Nevertheless, side views of these helical crystals reveal the presence of some of these walls, where the inclination of the columns changes abruptly (arrows in (Fig. 7l and m).
Two double-twist configurations are expected, either cylindrical with flexible columns (Fig. 10a) or toroidal with rigid chains (Fig. 10b). DNA is a semi-flexible polymer with a persistence length of 50 nm that can be bent strongly under favourable ionic conditions. The conformation of cylindrical bundles is therefore possible, and found in the decondensed thread of Fig. 6b, and in the double-twist configurations of blue phases [36] and precholesteric stages [37]. Toroidal DNA structures [38] (that we do not consider in this article since they deserve a complete study) are particular cases of these cylindrical double-twist bundles. With nucleosome core particles, both situations were observed. The cylindrical configuration is seen in Fig. 7e and d, where the six strands of the germ follow true helical paths although the resolution of optical microscopy does not provide us with enough details to understand very precisely the structure. The toroidal structure is observed in large flower-shaped domains (Figs. 7a and 13 in Ref. [31]). We lack direct evidence but we suspect that flexible columns belong to the 2D-ordered phase and rigid columns to the 3D crystalline phase. An interesting particularity of NCPs columns is that they can be interrupted since they are formed by the piling of NCP on top of each other. This character would permit to relax the longitudinal twist and to create either punctual defects or twist walls normal to the direction of the columns. Such defects are usually prevented with infinite columns such as DNA chains. The cylindrical crystalline tubes of NCPs (Fig. 7n–p) represent an interesting situation. NCPs are piled into columns packed in a pseudo-hexagonal lattice, but the twist occurring in the direction of the columns is not relaxed with formation of defects walls between top and bottom surfaces of NCPs. Instead, NCPs columns follow helical paths. Because of particular solvent conditions (alcohol was present in these samples), interactions between top and bottom surfaces of the NCPs favour a regular curvature of the columns that is prevented otherwise. Indeed, under identical experimental conditions, columns were shown to form arcs instead of linear objects, due to the wedge shape of the particles [30]. Only a pseudo-hexagonal ordering can be obtained since columns are helices and a compromised structure is formed, leading to this particular type of cylindrical structure in which we can observe the longitudinal twist mentioned above, and the transverse twist between columns of the successive layers.
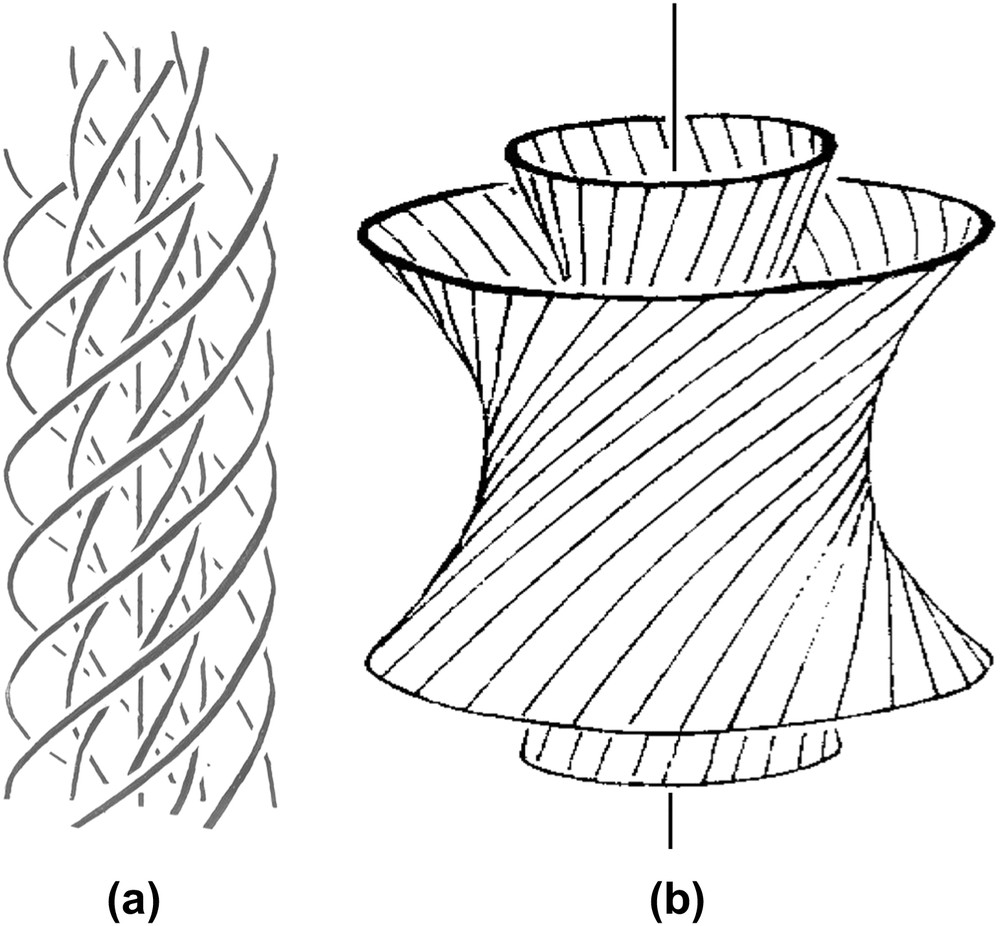
Double-twist configurations (b is redrawn from Ref. [42]). Each line has to be considered here as the L6 axis of the hexagonal network (not drawn) (parallel to the direction of the columns). In (a), twist is associated with curvature while in (b), twist is associated with splay. The (a) situation is more likely with flexible columns, while the (b) case is expected with rigid columns.
The collection of structural observations presented here illustrates how structures made of closely packed helices may find multiple solutions to account for the competition that arises between close packing and chirality. The DNA molecule being a polyelectrolyte, the interaction potential is actually influenced by the amount and type of counterions present in the solution. Other structural data have not been considered here: among them, the distortions of the hexagonal network that arise when the interhelical distances between helices is decreased or the decrease of the helical pitch of DNA chains observed with short DNA fragments in extremely dense samples [22]. Such effects more likely rely on lateral correlations that arise between aligned columns. The physics of such systems raises fascinating questions that are far from being understood yet [16,39–41]. More high-resolution data probably need to be collected to go deeper into the understanding of these questions.
Acknowledgements and remarks
Françoise Livolant wrote the article with the assistance of Amélie Leforestier. Micrographs are from Amélie Leforestier (2d; 4a–d; 5), Aurélie Bertin (4e–m), Nathalie Sartori (3a–d), Karsten Richter (2a–c), Jacques Dubochet (4n–p). J.D. also supervised the cryosection works of A.L., K.R. and N.S. in his laboratory. This work was partly supported by ANR-06-BLAN-0195-01.
3 We never observed striations with a period that would underline one θ2 direction.