1 Introduction
Le nom de clathrate – du latin clatratus et du grec klathron, évoquant un espace clos, fermé par une barrière à claire voie, a été proposé par Powell [1] et accepté depuis pour désigner une catégorie de composés atypiques dont la structure pouvait être décrite comme constituée d'un réseau d'accueil tridimensionnel comportant de vastes lacunes en forme de cages d'une première espèce chimique majoritaire, au centre desquelles étaient insérées des molécules d'une seconde espèce minoritaire formant un sous réseau hôte. Outre leur architecture particulière, les structures de type clathrate, qui font partie de la famille des composés d'inclusion, possèdent les caractéristiques suivantes:
- (i) les mailles élémentaires sont le plus souvent hautement symétriques avec de grands paramètres variant peu avec la nature de l'espèce chimique constituant le sous réseau hôte,
- (ii) le réseau d'accueil considéré comme seul correspond à une variété allotropique métastable de l'espèce chimique majoritaire, qui s'accommode de la présence des espèces hôtes,
- (iii) il n'existe en général que de faibles interactions – ou du moins relativement faibles – entre les atomes du réseau d'accueil et du réseau hôte, impliquant une sorte d'association entre les deux composants plutôt qu'une véritable combinaison au sens chimique du terme [1].
De nombreuses familles de clathrates sont connues, dont les réseaux d'accueil et les sous réseaux hôtes sont de nature organique ou inorganique: les structures et les propriétés correspondantes sont maintenant largement décrites dans les ouvrages de référence de chimie structurale et de chimie du solide [2]. La plus représentative de ces familles est sans conteste celle relative aux hydrates des gaz et des liquides, à laquelle se rattachent du point de vue structural les clathrates à base de silice (ou clathrasils) et les clathrates des éléments de la colonne 14: Si, Ge et Sn.
Le présent article concerne précisément les clathrates du silicium et des éléments apparentés, avec pour objectif de présenter une rétrospective de l'essor de ce thème de recherche depuis la découverte des premières structures de type clathrate du silicium en 1965 jusqu'aux plus récents développements. Pour mieux appréhender le cheminement parcouru à la fois du point de vue structural, des méthodes de synthèse et de caractérisation, ainsi que des propriétés physiques de ces clathrates, quelques brefs rappels ont été faits sur des sujets de recherche apparentés : hydrates des gaz et des liquides, clathrasils, fullerènes.
Historiquement, les recherches sur les composés de type clathrates concernées se sont développées selon trois périodes. La première correspond aux années 1965–1973, pendant lesquelles les recherches ont été essentiellement menées au Laboratoire de chimie minérale de la faculté des sciences de Bordeaux en France, où les structures clathrates du silicium ont été découvertes, et en Allemagne dans le groupe du Professeur Klemm à l'Université de Munster en particulier, où quelques études préliminaires sur ce sujet avaient été réalisées. Au cours de la période intermédiaire comprise entre 1973 et 1990, les recherches ont été interrompues à l'Université de Bordeaux et se sont poursuivies essentiellement en Allemagne dans le groupe du Professeur von Schnering à l'Institut Max-Planck de Stuttgart, avec une contribution limitée dans le temps de la part d'un groupe de physiciens de l'Université de Londres au Royaume Uni. La période récente, de 1990 à nos jours, a été la plus féconde, car elle a été très fortement impulsée par la découverte des formes fullerène du carbone qui a attiré l'attention de nombreux laboratoires dans le monde entier sur les structures à cages du silicium et suscité l'intérêt de nombreux chercheurs, chimistes, physiciens et théoriciens pour les propriétés physiques et les applications potentielles de ces dernières. Compte tenu du regain d'intérêt qui se manifestait alors pour ces clathrates, les recherches dans ce domaine ont été reprises dès 1994 à l'Institut de chimie de la matière condensée du CNRS à l'Université de Bordeaux 1, en étroite collaboration dans un premier temps avec le Laboratoire de physique de l'état solide de l'Université de Lyon 1 (Dr. Perez et ses collaborateurs) et ont fait peu de temps après l'objet d'un Projet de recherche internationale, CNRS-JSPS, impliquant plusieurs laboratoires japonais, en particulier celui du Professeur Yamanaka à l'Université de Hiroshima.
2 Première période: 1965–1973
2.1 Les siliciures de sodium de type clathrate Na8Si46 et NaxSi136 (0 ≤ x ≤ 24)
Les structures de type clathrate du silicium ont été identifiées et isolées pour la première fois dans les résidus de dégradation thermique ménagée du siliciure de sodium NaSi.
Après plusieurs tentatives de synthèse infructueuses ou ayant donné des résultats contestables par des auteurs antérieurs, c'est Hohmann [3] qui a obtenu les premiers siliciures et germaniures alcalins de formules générales MSi et MGe (M = Na, K, Rb, Cs) par synthèse directe entre les éléments en opérant dans un réacteur en acier à joint de cuivre et sous atmosphère d'argon, à une température voisine de 700 °C. Extrêmement hygroscopiques et réagissant vivement avec l'eau, la manipulation de ces composés nécessitait l'utilisation d'une boîte à gants sous atmosphère rigoureusement sèche. Thermiquement peu stables, ils se décomposaient sous vide en leurs éléments dès 500 °C environ, mais en opérant à plus basse température, les spectres de rayons X des résidus obtenus dans le cas des combinaisons comportant des alcalins lourds (K, Rb, Cs) faisaient apparaître des raies de diffraction nouvelles. Ces phases correspondantes répondaient du point de vue chimique à la formulation MSi8 et MGe4, respectivement. Seules les combinaisons NaSi et NaGe se décomposaient sans formation de phases intermédiaires. Les travaux de Hohmann furent repris quelques années plus tard par Schäfer et Klemm [4], qui attribuèrent aux phases intermédiaires de symétrie cubique les formules KSi6, RbSi6 et CsSi8 avec a ∼ 1340 pm, d'une part, et KGe4, RbGe4 et CsGe4 avec a ∼ 1400 pm, d'autre part. Pas plus que Hohmann, ces auteurs ne mirent en évidence des phases intermédiaires pauvres en sodium. La structure des phases KSi, RbSi et CsSi, ainsi que KGe, RbGe, et CsGe furent déterminées par Bushman [5] et celles de NaSi et NaGe par Witte et von Schnering [6]. Elles correspondaient toutes à des phases dites de Zintl caractérisées par la présence d'entités tétraédriques (Si4)4− et (Ge4)4−, analogues aux molécules (P4)0 et (As4)0, entourées par quatre ions M+ qui assuraient la neutralité électrique.
Au début de la décennie 1960–1970, des travaux de recherche avaient été entrepris au Laboratoire de chimie minérale de la faculté des sciences de Bordeaux sur les dérivés du silicium faisant intervenir l'action du silane, SiH4. Ce gaz n'étant pas encore disponible auprès des fournisseurs de produits chimiques, sa préparation par hydrolyse ménagée du siliciure de sodium, NaSi, avait été envisagée, mais à cause de la très grande réactivité de ce dernier, cette voie de synthèse fut rapidement abandonnée. Ayant acquis une certaine expérience dans la manipulation des métaux alcalins et maîtrisant bien la synthèse d'échantillons très purs de NaSi, il fut alors décidé de reprendre les travaux de Hohmann et de Schäfer et Klemm pour essayer de lever les doutes et les ambiguïtés qui subsistaient quant à l'existence ou non d'une phase intermédiaire dans le cas du sodium, et de préciser les données cristallographiques et la composition exacte des phases obtenues avec les autres métaux alcalins : K, Rb et Cs.
A la différence des expériences réalisées par les auteurs antérieurs qui opéraient sous vide, les premiers essais de thermolyse ménagée de NaSi furent conduits sous très faible courant d'argon sec, à diverses températures comprises entre 410 et 520 °C et pendant une dizaine de jours. Les spectres de diffraction des rayons X (méthode de Debye-Scherrer) des résidus obtenus montrèrent la présence de très nombreuses raies nouvelles indiquant la formation d'une phase intermédiaire. En fait, une étude systématique permit rapidement de constater que l'intensité de certaines raies de diffraction se modifiait en fonction de la température, laissant supposer l'existence de deux phases intermédiaires qui furent désignées par A et B. A 420 °C, seules les raies de diffraction de la phase A étaient observées avec le plus souvent quelques traces de celles de la phase B. Entre 420 et 450 °C, les spectres de rayons X montraient la présence d'un mélange des deux phases A et B. Au-dessus de 455 °C, les raies du silicium commençaient à être visibles et leur intensité augmentait avec la température, au détriment de celles de A et de B. Au-dessus de 520 °C, seules les raies du silicium étaient visibles dans le spectre indiquant une décomposition totale. L'hypothèse de l'existence de deux phases intermédiaires fut rapidement corroborée par les résultats obtenus par décomposition sous vide qui nous permirent d'obtenir, entre 320 et 450 °C et pendant des temps de réaction de l'ordre de 60 heures seulement, des résidus de pyrolyse dans lesquels les raies de diffraction de la seule phase B étaient observés, avec le plus souvent quelques faibles traces de celles de la phase A. De plus, il apparaissait nettement que l'intensité des raies observées se modifiait avec la température de pyrolyse, ce qui semblait indiquer que le taux de sodium inclus dans la phase B diminuait avec la température. Entre 450 et 500 °C, les raies du silicium coexistaient avec celle de B et la variation d'intensité observée continuait à être perceptible, indiquant que l'appauvrissement en sodium se poursuivait jusqu'à 500 °C.
Contrairement au siliciure de départ, NaSi, les résidus obtenus s'avéraient peu réactifs vis-à-vis de l'eau et même des solutions acides concentrées, comme c'est le cas pour le silicium. Leur insensibilité à l'air nous permit de les manipuler plus facilement et d'utiliser la technique du diffractogramme pour les études aux rayons X, qui permettait un suivi plus précis des variations d'intensités observées. L'analyse chimique avait donné pour la phase A un rapport Na/Si constant aux incertitudes près de 0,158, correspondant à la formule NaSi6. Pour la phase B le rapport Na/Si était nettement plus faible et diminuait avec la température de pyrolyse: 0,076 pour 340 °C, 0,064 pour 380 °C et 0,02 pour 445 °C, et la formulation NaxSi avec x = 0,08, 0,06 et 0,02, respectivement, fut retenue indiquant qu'il s'agissait d'une sorte de solution solide faiblement concentrée de sodium dans une matrice de silicium. Dans les résidus obtenus entre 450 et 500 °C, compte tenu des variations d'intensités des raies observées, la valeur de x semblait même devenir inférieure à 0,02, mais n'était pas accessible à l'analyse en raison de la présence de quantités croissantes de silicium.
Une tentative d'indexation des raies de diffraction X des phases de types A, qui comportait un grand nombre de raies fines, conduisit rapidement à attribuer à cette phase une maille de symétrie cubique avec un paramètre a = 1019 ± 2 pm. Aucune règle d'extinction systématique n'ayant pu être observée un mode primitif P fut retenu. La détermination de la masse volumique expérimentale, d = 2,27 g/cm3, était compatible avec 8 motifs NaSi6 par maille (dcalc. = 2,38 g/cm3). Les raies de la phase de type B furent quant à elles indexées dans une maille de symétrie cubique à faces centrées avec a = 1462 ± 2 pm et l'existence des seules raies d'indices 00l avec l = 4n nous conduisit à proposer pour cette phase le groupe d'espace Fd-3 m. La masse volumique expérimentale, comprise entre 2,03 et 2,12 gr/cm3 pour 0,02 < x < 0,08, impliquait un nombre de motifs NaxSi par maille voisin de 132. A partir de ces données, des essais d'identification de ces structures par isotypie avec d'autres phases connues furent tentés, mais sans succès dans un premier temps [7,8]. Ces résultats originaux furent bien évidemment publiés aux Comptes rendus de l'Académie des sciences.
La solution du problème fut rapidement apportée par la contribution du cristallographe J. S. Kasper, qui ayant assisté aux USA à une conférence de P. Hagenmuller sur ces nouvelles phases du silicium, s'est souvenu de l'existence de deux phases de symétrie cubique avec de grands paramètres, ayant respectivement 46 (∼8 × 6) et 136 (∼132) motifs par maille, qui correspondaient aux deux types les plus connus d'hydrates de type clathrate: les hydrates des gaz et les hydrates des liquides. Sur la base des données expérimentales que nous avions obtenues, les calculs confirmèrent rapidement l'isotypie entre les phases de type A et B des siliciures de sodium avec celles des hydrates concernés: le réseau d'accueil de silicium était identique à celui de la glace dans les hydrates (le silicium y occupe les mêmes positions atomiques que l'oxygène) et le sous réseau hôte de sodium est le même que celui de l'espèce gazeuse ou liquide insérée dans les cages des deux types de structures [9].
Avant de décrire les structures des phases clathrates du silicium, il nous a semblé opportun de rappeler brièvement l'historique des hydrates correspondants et de la longue quête qui a conduit à en appréhender les étonnantes architectures cristallines.
2.2 Rappels sur les structures clathrate des hydrates des gaz et des hydrates des liquides
Les hydrates des gaz et hydrates des liquides sont connus depuis longtemps [10,11]. Leurs compositions et conditions de formation ont fait l'objet de nombreuses études au cours du XIXe et au début du XXe siècle, notamment en France à la suite des travaux de Villard et de Forcrand au laboratoire de chimie de l'Ecole nationale supérieure [12,13]. Dans un article de revue exhaustif daté de 1927, Schroeder [14] signale déjà près de trois cents références sur ce sujet.
Avec des molécules de petite taille, qui correspondaient le plus souvent à des gaz dans les conditions ambiantes de température et de pression -d'où le nom d'hydrates des gaz- les phases obtenues correspondaient à un rapport H2O/M voisin de 6 (M = Xe, Cl2, SO2, H2S, CO2, CH4, CH3Cl), ou 8 (M = C2H6, CH3Br, CH3SH). Avec des molécules de plus grande taille, correspondant le plus souvent à des liquides – d'où le nom d'hydrates des liquides – l'analyse chimique faisait apparaître un rapport H2O/M' voisin de 15 (M' = C6H6, CH3I, CCl4, CHCl3, CH2Cl2, C2H5Cl,…). Il existait également des hydrates doubles MM' dans lesquels les molécules M' étaient associées à des molécules gazeuses M telles que H2S ou H2Se. L'étude des diagrammes de phases de ces hydrates avait montré que la température de décomposition de ces hydrates était d'autant plus élevée que les molécules gazeuses ou liquides concernées étaient plus volumineuses, variant de ∼−40 °C pour les plus petites à ∼20 °C pour les plus grosses.
Les structures de ces hydrates sont demeurées longtemps ignorées, bien que les divers auteurs qui s'étaient essayés à leur détermination aient eu l'intuition qu'elles devaient correspondre à des assemblages particuliers de tétraèdres, comme ceux qui existent dans la variété classique de la glace (Ih). A partir des spectres de diffraction des rayons X, obtenus dans des conditions expérimentales difficiles, von Stackelberg était arrivé à la conclusion que les hydrates des gaz cristallisaient dans un système cubique de symétrie Oh3 (Pm-3n) avec un paramètre de maille voisin de 1200 pm et qu'il en était de même pour les hydrates doubles M'/H2S, mais avec un groupe d'espace différent. Le réseau d'accueil de la structure proposée était constitué de 48 molécules d'eau et de 8 lacunes en forme de cages (H2O)24, dont 2 plus petites que les autres, avec un diamètre libre de 580 pm et 660 pm, respectivement [15] (le diamètre libre correspond à la distance entre deux atomes opposés d'une cage diminuée du diamètre de l'atome concerné). La validité de cette structure fut rapidement contestée par Claussen [16] en raison de la présence d'angles de liaisons de 60°, très différents des 109,47° attendus pour une structure à base de tétraèdres. A partir de modèles constitués de boules et de tiges de bois, Claussen étudia toutes les possibilités d'arrangement de tétraèdres permettant de remplir l'espace et laissant entre eux des lacunes de taille suffisante pour accueillir les molécules des espèces chimiques hôtes. Un tel raisonnement le conduisit à envisager l'existence d'un polyèdre en forme de dodécaèdre pentagonal comportant 12 faces pentagonales et 20 sommets, dans lequel les angles de liaison entre les molécules H2O est de 108°, c'est-à-dire très proches de 109,47° (Fig. 1a). Toutefois, il n'était pas possible de concevoir une structure uniquement constituée de tels dodécaèdres, qui ne remplissaient pas entièrement l'espace en raison de leur symétrie d'ordre cinq. Claussen découvrit alors que ces dodécaèdres pouvaient être associés de telle sorte que les deux atomes diamétralement opposés d'un dodécaèdre soient superposés aux deux atomes de carbone d'une liaison C–C dans une structure de type diamant, ce qui revenait à remplacer chaque liaison par un dodécaèdre centré sur le milieu de la liaison concernée. Il obtint ainsi une volumineuse structure cubique à faces centrées comportant de vastes lacunes qui s'avéraient correspondre à un nouveau type de polyèdre en forme d'hexacaïdécaèdre (16 faces) ayant 12 faces pentagonales et 4 faces hexagonales pour un total de 28 sommets (Fig. 1b). Ces nouveaux polyèdres pouvaient accueillir en leurs centres des molécules hôtes de plus grande taille que celles susceptibles d'entrer dans les dodécaèdres pentagonaux. La maille élémentaire d'une telle structure faisait apparaitre la présence de 16 dodécaèdres pentagonaux pouvant être occupés par des molécules d'un gaz M et 8 hexakaïdécaèdres disponibles pour des molécules d'un liquide M'. Le réseau d'accueil ainsi constitué comporterait 136 molécules d'eau, le rapport M/H2O étant de 2/17 et le rapport M'/H2O de 1/17, cette dernière valeur étant parfaitement compatible avec la composition des hydrates des liquides. La validité du modèle proposé par Claussen fut confirmée par von Stackelberg sur la base des données cristallographiques: la structure des hydrates des liquides et des hydrates doubles est caractérisée par un paramètre de maille voisin de 1720 pm, le groupe d'espace est Oh7 (Fd-3m) et elle est différente de celle des hydrates de gaz [17].
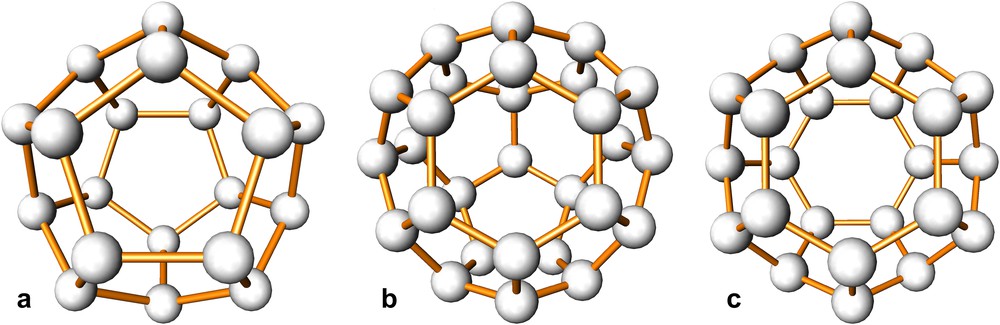
Les polyèdres caractéristiques des structures des hydrates de types I et II: (a) dodécaèdre pentagonal (H2O)20, (b) hexacaïdécaèdre (H2O)28 et (c) tétracaïdécaèdre (H2O)24. Seuls les atomes d'oxygène sont représentés.
Peu de temps après, Claussen [18] proposa une possible structure pour les hydrates des gaz, basée sur l'arrangement de 2 dodécaèdres pentagonaux occupant les sommets et le centre d'une maille cubique simple, associés à 6 polyèdres en forme de tétracaïdécaèdres (14 faces) ayant 12 faces pentagonales et 2 faces hexagonales pour un total de 24 sommets (Fig. 1c). Les faces hexagonales caractéristiques de chacun de ces nouveaux polyèdres résulteraient de l'addition de 6 molécules d'eau judicieusement placées entre les dodécaèdres, qui fourniraient les liaisons complémentaires permettant d'engendrer les six tétracaïdécaèdres. La maille cubique de ∼1200 pm comporterait un total de 46 molécules d'eau et offrirait deux types de sites pour les molécules de gaz: 2 au centre des dodécaèdres et 6 autres, un peu plus volumineux, au centre des polyèdres à 14 faces. Selon que les deux types de sites ou seulement les plus volumineux d'entre eux seraient occupés, la formule chimique correspondante serait M8(H2O)46 (rapport M/H2O = 1/5,75) ou M6(H2O)46 (rapport M/H2O = 1/7,67). La validité de ce modèle fut confirmée par Pauling et March suite à une étude sur monocristal de l'hydrate de chlore (Cl2)6H2O)46, ainsi que par Müller et von Stackelberg sur les hydrates de chlore ((Cl2)6(H2O)46) et de brome ((Br2)6(H2O)46), ce dernier possédant en fait une structure clathrate de type III qui sera décrite ultérieurement [19,20].
Il existe d'autres hydrates de type clathrate dont les structures sont différentes de celles décrites ci-dessus, mais qui comportent également des dodécaèdres pentagonaux comme polyèdres de base, ces derniers étant associées à d'autres sortes de polyèdres, comme par exemple le polyèdre à 15 faces (12 pentagonales et 3 hexagonales), qui existe par exemple dans les hydrates de types III et IV ou le polyèdre à 20 faces (12 pentagonales et 8 hexagonales), (H2O)36, plus récemment découvert dans une structure de symétrie hexagonale appelée clathrate de type H [2,21,22].
Certains de ces hydrates existent à l'état naturel sur Terre et très probablement dans les pôles de Mars, le sous-sol de Titan et les glaces cométaires [23,24], en fait partout où des molécules telles que CO2, CH4, NH3, SO2 se trouvent en contact avec de l'eau dans des conditions appropriées de température et de pression. Il semble par ailleurs qu'ils interviennent dans certains processus biologiques comme la narcose, mais cette hypothèse longtemps sujette à controverse n'est actuellement plus considérée comme plausible [25]. Parmi ces clathrates, l'hydrate de méthane, (CH4)8(H2O)46, fait à l'heure actuelle l'objet d'un intérêt particulier en tant que source d'énergie potentielle pour le futur, mais constitue également une grave menace pour l'avenir du climat sur Terre. D'énormes gisements de cet hydrate, évalués à deux fois l'équivalent des réserves prouvées de charbon, de pétrole et de gaz naturel – soit ∼3000 Gt d'équivalent carbone – ont été découverts sur les talus continentaux de nombreux pays ainsi que dans les zones de pergélisol [26,27]. L'exploitation de ces gisements, si elle est un jour possible à l'échelle industrielle, compte tenu des difficultés rencontrées, permettrait de subvenir aux besoins énergétiques mondiaux pendant plusieurs siècles. D'un autre côté, la fragile stabilité thermique de ces hydrates fait redouter des dégazages intempestifs et catastrophiques de méthane- gaz beaucoup plus néfaste que le dioxyde de carbone pour ce qui est de l'effet de serre-, qui résulteraient d'une élévation trop importante de la température des océans et des terres [28]. Autre hydrate de type clathrate qui présente un grand intérêt, (CO2)8(H2O)46, dont l'utilisation a été envisagée pour la séquestration du dioxyde de carbone atmosphérique.
2.3 Les structures des siliciures de sodium Na8Si46 et NaxSi136
La structure du siliciure Na8Si46, isotype de celle d'un hydrate de type I, est représentée à la Fig. 2. Les données cristallographiques et les positions atomiques occupées par les atomes de silicium et de sodium dans la maille élémentaire sont reportées dans le Tableau 1.
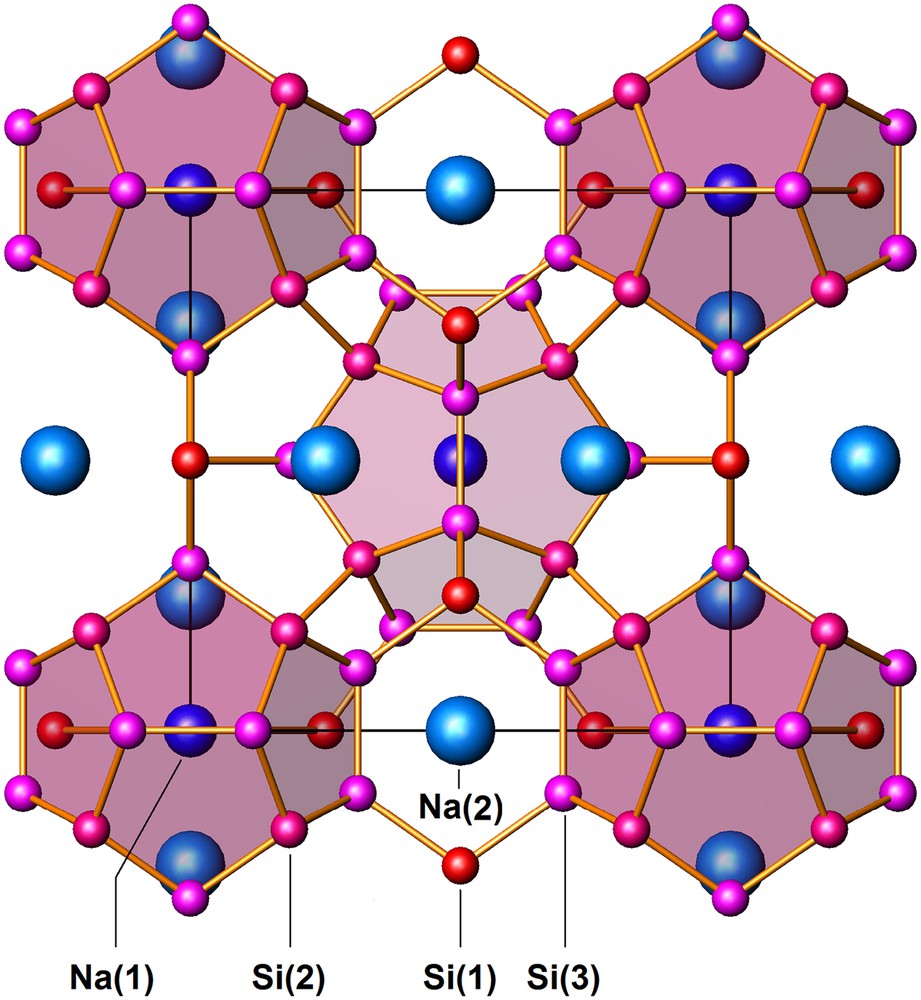
Structure de Na8Si46 (type I) vue selon la direction [100]. Les atomes Si(2) et Si(3) occupent les sommets des dodécaèdres pentagonaux Si20 ombrés en rose. Les atomes Si(1) complètent les faces pentagonales des polyèdres complémentaires Si24 qui n'ont pas été représentés par soucis de clarté.
Données cristallographiques pour les structures de Na8Si46 et NaxSi136.
| Phase | Na8Si46 | NaxSi136 |
| Système | Cubique | Cubique |
| Paramètre | a = 1019 ± 2 pm | a = 1462 ± 2 pm |
| Groupe d'espace | Pm-3n (N° 223) | Fd-3m (N° 227) |
| Positions atomiques | Si(1) en 6(c) | Si(1) en 8(a) |
| Si(2) en 16(i) x = 0,183 | Si(2) en 32(e) x = −0,094 | |
| Si(3) en 24(k) y = 0,310, z = 0,116 | Si(3) en 96(g) x = −0,058, z = −0,246 | |
| Na(1) en 2(a) | αNa(1) en (16c) | |
| Na(2) en 6(d) | βNa(2) en (8b) | |
| α = 0,19; β = 0,79 pour x = 9,5 | ||
| Masse volumique calculée (g/cm3) | 2,316 | 2,16 pour x = 10,9 |
| 2,06 pour x = 2,7 | ||
| Masse volumique exp. (g/cm3) | 2,27 | 2,115 pour x = 10,9 |
| 2,036 pour x = 2,7 |
Deux dodécaèdres pentagonaux occupent les sommets et le centre de la maille et apportent ainsi 40 des 46 atomes de silicium (positions atomiques Si(2) et Si(3)). Ces deux dodécaèdres n'ont pas de sommet commun et il suffit d'ajouter six atomes de silicium supplémentaires (position atomique Si(1) dans le Tableau 1) pour induire la formation de six polyèdres à 14 faces qui remplissent complètement l'espace résiduel (Fig. 2). En raison de leur géométrie (Fig. 1c), ces polyèdres à 14 faces sont associés par l'intermédiaire de leurs faces hexagonales communes formant ainsi des files dirigées parallèlement aux axes principaux de la maille. Une autre manière de décrire l'architecture du réseau de silicium est de considérer qu'il est formé de files de polyèdres à 14 faces orientées selon les trois directions Ox, Oy et Oz de la maille, dont l'intersection engendre la formation d'espaces vides en forme de dodécaèdres pentagonaux.
Les atomes de sodium Na(1) occupent le centre des deux dodécaèdres pentagonaux et les atomes Na(2) le centre des six polyèdres à 14 faces. Le sous réseau hôte de sodium ainsi constitué est identique à la distribution des atomes dans la structure des phases intermétalliques de type A15 (notation Strukturbericht), dont Cr3Si et W3O β sont les prototypes et qui constituent la structure des supraconducteurs classiques tels que Nb3Ge ou Nb3Sn. Cette étonnante similitude avait été antérieurement soulignée par Franck et Kasper [29]: « It is a fascinating matter that there exists a strict correspondence between the structures of such chemically different substances as the gas hydrates and the intermetallic compounds of the class we have considered here ».
Dans une telle structure, chaque atome de silicium est au centre d'un tétraèdre légèrement distordu formé par quatre homologues. La distance interatomique Si-Si moyenne (237 pm) est légèrement supérieure à celle qui existe dans le silicium élémentaire de type diamant (235 pm) et l'angle moyen proche de la valeur 109,47° qui caractérise l'hybridation sp3 du silicium. Ce sous réseau de silicium correspond à une sorte de variété allotropique métastable du silicium moins compacte que la variété diamant (volume atomique: 23 × 106 au lieu de 20 × 106 pm3/atome). Les distances Na1–Si varient entre 323 et 337 pm et les distances Na2–Si entre 341 et 379 pm. A partir de ces valeurs le rayon libre de chacune des deux sortes de lacunes peut être calculé: r1(I) ∼ 204 pm pour les lacunes dodécaédriques et r2(I) ∼ 223 pm pour les lacunes tétracaïdécaédriques.
La structure du siliciure Na8Si46 s'est également avérée isotype de celle d'une variété naturelle et peu connue de silice, la mélanophlogite, dont la structure de type clathrate I avait été publiée peu de temps auparavant par Kamb, après être restée longtemps inconnue [30]. Dans la structure de ce minéral le réseau d'accueil (a ∼ 1337 pm) est constitué de tétraèdres de silice SiO4 liés entre eux par des liaisons Si–O–Si formant un angle compris entre 150 et 180°, de sorte que les atomes de silicium occupent des positions identiques à celles décrites ci-dessus pour le clathrate Na8Si46. Le sous réseau hôte est constitué de molécules organiques ou minérales telles que N2, H2S, CO2, CH4, …, occupant partiellement ou totalement les deux types de sites disponibles (la teneur en silice varie de 88 à 92%). La formule chimique correspondante pour une phase stœchiométrique est M8 (SiO2)46. Des études plus récentes ont montré que la mélanophlogite est en fait pseudo cubique à température ambiante (a = b–2c) et qu'elle peut être obtenue par synthèse hydrothermale [31]. Elle fait maintenant partie de la famille des « clathrasils » voisine de celle des zéolites, dont elle se distingue par des réseaux d'accueil uniquement constitués de silice comportant des lacunes en forme de cages plutôt que de tunnels [32,33].
La structure du siliciure NaxSi136, isotype de celle d'un hydrate de type II, est représentée à la Fig. 3. Les données cristallographiques et les positions atomiques occupées sont reportées au Tableau 1. La maille élémentaire comporte 16 dodécaèdres pentagonaux groupés en quatre blocs de quatre, formant des tétraèdres. Les atomes de silicium situés au centre de chacun des blocs (Si(1)) coïncident avec les positions occupées par le silicium dans une structure de type diamant. L'ensemble des seize dodécaèdres ainsi disposés ne remplit pas l'espace et laisse apparaître les 8 volumineuses lacunes en forme d'hexacaïdécaèdre, qui s'enchaînent par l'intermédiaire de faces hexagonales communes pour former également un réseau de type diamant identique au précédent, mais décalé de 1/2 1/2 1/2.

Structure de Na24Si136 (type II) vue selon [110]. Le réseau d'accueil de silicium est formé de 16 dodécaèdres Si20 ombrés en rose, laissant entre eux 8 lacunes Si28 en forme d'hexcaïdécaèdres.
Le réseau de silicium ainsi constitué de 136 atomes peut comporter au total 24 atomes de sodium, dont 16 Na(1) situés au centre des dodécaèdres pentagonaux et 8 Na(2) localisés au centre des hexacaïdécaèdres. La distribution des atomes alcalins dans la maille élémentaire est de manière étonnante identique à celle qui caractérise les structures intermétalliques de type C15, dont le prototype est la phase de Laves Cu2Mg [29]. Au contraire de la structure de Na8Si46 pour laquelle aucune non-stœchiométrie prononcée de ses espèces hôtes n'a jamais été mise en évidence, le taux d'occupation global des sites disponibles dans la structure du clathrate NaxSi136 est variable avec la température de décomposition et, on sait depuis, avec la durée du traitement. De plus, le taux d'occupation de chacun des deux sites Na(1) et Na(2) s'est avéré différent et les premières études structurales avaient montré que les sites les plus volumineux étaient préférentiellement occupés (Tableau 1). Ce résultat qui paraissait paradoxal dans la mesure où les petits atomes de sodium auraient dû occuper les plus petits sites a été depuis confirmé par plusieurs études structurales plus récentes. Les premiers résultats expérimentaux avaient donné 3 ≤ x ≤ 11, mais il avait été observé que la valeur de x pouvait devenir inférieure à 3 dans les échantillons obtenus aux plus hautes températures, où la présence de silicium de type diamant était observée. La question qui se posait alors était: peut-on obtenir ce clathrate exempt de sodium ou est-il nécessaire qu'il subsiste quelques uns de ces atomes qui joueraient le rôle de clés de voûte pour stabiliser la structure? La réponse à cette question est maintenant connue : on sait que x peut non seulement être diminué jusqu'à une valeur quasi nulle (x(Na) = 0,0058, i.e. 35 ppm Na), mais aussi devenir très supérieur à 11 et atteindre pratiquement la plus haute valeur possible, x = 24 [34–40]. En raison de ce comportement particulier la phase NaxSi136, apparaît extrêmement originale et n'a pas d'équivalent parmi les autres structures de type clathrate.
Dans la structure de NaxSi136, chaque atome de silicium est entouré par quatre homologues formant un tétraèdre légèrement déformé. Les distances Si–Si sont très légèrement supérieures (237 pm) à celle qui existe dans le cas du silicium de type diamant (235 pm) et les angles de liaison qui varient entre 108 et 120° sont en moyenne très proches de 109,47°. Ce réseau d'accueil peut donc être considéré comme une variété métastable du silicium élémentaire moins compacte que la variété diamant, en raison de la présence de vastes lacunes pouvant être occupées ou non par des atomes de sodium. Le volume atomique, 23 × 106 pm3/atome, est identique à celui calculé pour la phase de type I, Na8Si46, et supérieur de 15% à celui du silicium dans la variété diamant, 20 × 106 pm3/atome. Les distances Na1–Si varient entre 317 et 332 pm et les distances Na2–Si sont toutes proches de 398 pm. De la même façon que pour la structure de type I, on peut calculer le rayon libre de chacun des sites polyédriques de cette structure de type II: r1(II) ∼ 200 pm pour les sites dodécaédriques et r2(II) ∼ 275 pm pour les sites hexacaïdécaédriques. Si on compare ces rayons libres avec ceux déterminés pour le clathrate de type I, on arrive à la séquence suivante: r1(II) < r1(I) < r2(I) < r2(II), qui montre que les lacunes dodécaédriques dans le clathrate de type II sont légèrement plus petites que dans le type I.
Depuis les travaux de Gies [41], on sait qu'il existe une structure clathrate comportant un réseau d'accueil constitué de silice dans lequel les atomes de silicium occupent les mêmes positions que dans le siliciure NaxSi136. Il s'agit d'un autre clathrasil appelé dodecasil 3C, ou MTN, de formule M16M'8(SiO2)136, obtenu par synthèse hydrothermale, dans laquelle le sous réseau hôte est constitué de grosses molécules M' telles que la triméthylamine ou la pyridine qui occupent les lacunes hexacaïdécaédriques et de plus petites autres (M = N2, CH4, CO2) incluses dans les lacunes dodécaédriques.
2.4 Structures clathrates obtenues avec les autres métaux alcalins (K, Rb, Cs); structures clathrates du germanium et de l'étain
Les résultats ci-dessus concernant le système silicium–sodium étant connus, l'étude des résidus de thermolyse des siliciures KSi, RbSi et CsSi fut entreprise et étendue au cas des germaniures [42–44].
Les résultats obtenus sont rassemblés dans le Tableau 2 dans lequel les données concernant NaSi ont été ajoutées pour comparaison. L'interprétation de l'ensemble de ces résultats sur la base du principe établi pour les hydrates selon lequel le clathrate formé est celui qui correspond au meilleur accord possible entre le volume libre des lacunes disponibles et le volume de l'atome qui les occupe, nous a permis de formuler un certain nombre de conclusions qui ont été étayées par des études structurales. Dans le cas des clathrates de silicium avec le sodium comme atome hôte, les deux phases de types I et II apparaissent de manière concurrente selon les conditions expérimentales, ce qui implique que la taille du sodium est compatible avec les deux structures possibles et les deux types de lacunes polyédriques de l'une et de l'autre. Avec le potassium, quelles que soient les conditions de traitement, la seule phase de type I est observée avec x ∼ 7 en accord avec l'occupation des lacunes polyédriques à 12 et 14 faces. Le même type structural est observé avec le rubidium, mais la valeur x = 5 implique la seule occupation des lacunes polyédriques à 14 faces. Avec le césium, le plus gros des alcalins, la seule phase formée est de type II, avec x = 7, valeur compatible avec l'occupation des seules lacunes polyédriques à 16 faces.
Résultats obtenus lors de la thermolyse des siliciures et germaniures alcalins.
| Siliciure ou germaniure | Conditions expérimentales | Phase obtenue | x | Paramètre a (pm) | Remarques |
| NaSi | 420–450 °C / 10 jours Courant d'argon sec | NaxSi46 | 8 | 1019 |
|
| 320–450 °C/60 h Sous vide | NaxSi136 | 3 ≤ x ≤ 11 | 1462 | Présence très fréquente de traces de NaxSi46 | |
| KSi | 420–480 °C/10 jours Courant d'argon sec | KxSi46 | 7 | 1026 | Pas de trace d'un clathrate de type II, quelles que soient les conditions |
| 320–480 °C/60 h Sous vide | KxSi46 | 7 | 1026 | ||
| RbSi | 320–470 °C/60 h Sous vide | RbxSi46 | 5 | 1027 | Pas de trace d'un clathrate de type II |
| CsSi | 320–470 °C/60 h Sous vide | CsxSi136 | 7 | 1464 | Spectres de diffraction X flous: faible granulométrie |
| NaGe | 320–400 °C/60 h Sous vide | NaxGe136 | ? | 1540 | Présence d'une seconde phase, NaGe4, de structure inconnue. NaxGe136 minoritaire; x indéterminé |
| KGe | 320–380 °C/60 h Sous vide | KxGe46 | 8 | 1066 | |
| RbGe | 320–370 °C/60 h Sous vide | RbxGe46 | ? | 1070 | Spectre de diffraction X très mal résolu; x indéterminé |
| CsGe | 320–460 °C/60 h Sous vide | ? | ? |
|
Dans la série des clathrates de germanium qui comportent des lacunes polyédriques de dimensions très légèrement supérieures à leurs équivalents dans les clathrates de silicium (d(Ge–Ge) ∼ 247 pm contre d(Si–Si) ∼ 237 pm), on retrouve avec le sodium le seul clathrate de type II, sans aucune trace du clathrate de type I, mais mélangée à une autre phase de composition NaGe4 dont la structure n'a pu être établie. Le potassium conduit à la formation du seul clathrate de type I avec x = 8, indiquant une totale occupation des deux sortes de lacunes polyédriques à 12 et 14 faces. Le rubidium donne également naissance à un clathrate de type I pour lequel la valeur de x n'a pu être déterminée. Avec le césium, la mauvaise qualité du spectre de diffraction obtenu, qui comportait des raies très diffuses, ne nous avait pas permis de trancher entre une structure de type I ou de type II.
D'une manière générale, le comportement structural des clathrates à réseaux de silicium ou de germanium était donc analogue à celui des hydrates des gaz et des liquides, mais une importante différence était apparue, qui concernait le cas du sodium. Alors que dans les hydrates il avait été systématiquement observé que les molécules de petite taille induisaient la formation du seul clathrate de type I, mais que certaines d'entre elles désignées par le terme de « gaz d'appoint » (H2S, H2Se) pouvaient également s'insérer dans les petites lacunes vides d'un hydrate de type II pour former un hydrate double, comme (H2S)16(CCl4)8(H2O)136 par exemple, aucune structure de type II n'avait été identifiée comportant uniquement des molécules de gaz de petite taille. L'existence et le comportement bien particulier du clathrate NaxSi136, ainsi que de son homologue NaxGe136, n'avaient pas d'équivalent dans la série des hydrates. Cette donnée nouvelle n'était pas en désaccord avec le principe de formation des clathrates; bien au contraire elle le confortait, et son importance était d'autant plus grande que l'on sait maintenant que les hydrates des plus petites espèces gazeuses (O2 Ar, N2 et même H2) induisent effectivement la formation d'une structure de type II prévue par Holder et Manganiello [45], identifiée par Davidson et al. en 1984 [46] et confirmé plus récemment [47].
A partir des valeurs des rayons libres des lacunes polyédriques présentes dans les deux structures et des résultats reportés dans le Tableau 2, il nous avait été possible de proposer un diagramme de corrélation entre la nature et la stœchiométrie du clathrate obtenu et le « rayon effectif » de l'atome alcalin inséré dans les lacunes correspondantes, comme cela avait été fait dans le cas des hydrates par Schroeder [14] et von Stackelberg et Müller [48] et confirmé depuis [23] (Fig. 4). Les tables disponibles fournissaient trois sortes de données pour les alcalins : les rayons ioniques, les rayons covalents et les rayons métalliques [49]. Les rayons ioniques qui varient entre 97 et 167 pm ne permettaient pas – comme on pouvait s'y attendre compte tenu du fait que le réseau d'accueil est essentiellement neutre – d'expliquer les résultats obtenus, puisque tous nettement inférieurs au rayon libre des plus petites lacunes disponibles r1(I) ∼ 200 pm. D'un autre côté, les rayons métalliques, compris entre 190 et 267 pm, apparaissaient trop élevés et ne permettaient pas d'expliquer la formation du clathrate de type I avec le potassium avec la stœchiométrie K8Si46, de surcroît. La prise en considération des rayons covalents, compris entre les rayons ioniques et métalliques, conduisait par contre à une interprétation satisfaisante des résultats. Des caractérisations spectroscopiques ultérieures montreront qu'une telle hypothèse était pleinement justifiée.
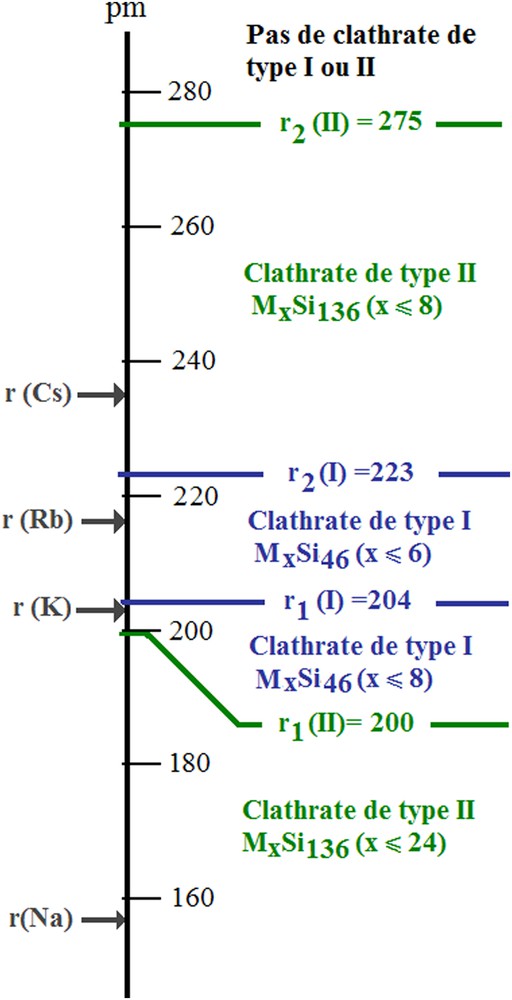
Diagramme comparatif entre le « rayon libre » des deux sortes de cages 1 et 2 des deux structures I et II et le rayon covalent des atomes de métal alcalin.
Le sodium (rcov. = 157 pm) peut occuper en raison de sa petite taille toutes les lacunes disponibles des deux structures, ces deux dernières apparaissant comme concurrentes. Le potassium (rcov. = 203 pm) forme uniquement le clathrate de type I avec x ∼ 8, ce qui implique que son rayon effectif soit situé dans l'étroit domaine 200–204 pm, qui correspond au rayon libre des lacunes dodécaériques du clathrate de type I. Le rubidium (rcov. = 216 pm) forme également le clathrate de type I, mais avec x ≤ 6, ce qui indique que son rayon effectif est seulement compatible avec le rayon libre des lacunes r2(I). Le césium (rcov. = 235 pm), quant à lui, induit la formation du seul type II avec x ≤ 8 et son rayon effectif n'est donc compatible qu'avec le rayon libre des 8 lacunes hexacaïdécaédriques (r2(II) ∼ 275 pm).
Un raisonnement analogue avait été conduit dans le cas des clathrates de germanium, pour lesquels les rayons libres des lacunes disponibles sont un peu plus grands (∼4%). Les résultats obtenus pour le système potassium silicium et potassium germanium furent confirmés par une étude structurale menée par Galmeier et al. sur des monocristaux de clathrates obtenus par synthèse directe à haute température, K8Si46 et K8Ge46, ainsi que K8Sn46, premier clathrate connu comportant un réseau d'accueil constitué d'atomes d'étain, autre élément de la colonne 14 [50].
2.5 Les formes clathrates en tant que structures alternatives des composés à motifs tétraédriques
Les structures de types I et II telles qu'elles sont décrites ci-dessus font apparaître des polyèdres complexes résultant d'arrangements particuliers de tétraèdres, qui constituent en fait les plus petites entités unitaires. Les structures à motifs tétraédriques les plus connues sont les types diamant et lonsdaleite (diamant hexagonal) qui correspondent le plus souvent aux deux formes alternatives des éléments de la colonne 14 et des composés tels que SiC, BN, AlN, ZnS, H2O, SiO2, … La variété normale du silicium, la variété Ic de la glace et la forme cristobalite β de la silice appartiennent au premier type, la forme londsdaleite du silicium, la structure Ih de la glace et la variété tridymite β de la silice au second.
Dans les structures de type diamant, les tétraèdres élémentaires sont tous en position dite « décalée », c'est-à-dire que la figure constituée de deux tétraèdres consécutifs possède un centre de symétrie situé au milieu de la liaison commune (Fig. 5a). La structure peut être décrite comme formée de chaînes en zigzag qui se croisent à angle droit et se développent parallèlement aux diagonales des faces du cube.

Arrangement de trois tétraèdres consécutifs dans la structure (a) du diamant, (b) de la londsdaléite et (c) d'un clathrate.
Dans les structures hexagonales de type lonsdaleite, les tétraèdres élémentaires consécutifs dans la direction de l'axe c sont alternativement en position décalée et « éclipsée » (la figure formée par deux tétraèdres consécutifs en position éclipsée possède un plan de symétrie passant par le milieu de la liaison commune). La structure peut être décrite comme constituée le long de l'axe c de files d'atomes en forme de vilebrequin (Fig. 5b). Intermédiaires entre ces deux types structuraux il existe un grand nombre de polytypes dans lesquels le taux de tétraèdres en position éclipsée le long de l'axe c est inférieur à 50%, comme c'est le cas pour les composés binaires tels que SiC ou ZnS [51].
Dans les structures de type clathrate les tétraèdres unitaires sont tous en position éclipsée (Fig. 5c) [29,43,44]. En fait, il suffit que trois tétraèdres consécutifs occupent une telle position pour former une première face plane qu'une très légère déformation permet de transformer en une face pentagonale régulière ayant un angle au sommet de 108 au lieu de 109,47°. Compte tenu de la direction des autres liaisons dans l'espace, une telle disposition conduit à engendrer la formation d'un premier dodécaèdre pentagonal, qui peut se combiner avec lui-même, mais pas à l'infini car ne remplissant pas totalement l'espace, soit à d'autres types de polyèdres un peu différents possédant un nombre limité de faces hexagonales, dont la présence est nécessaire pour obtenir une structure reproductible à longue distance. Ces faces hexagonales résultent d'une déformation plus importante de l'angle au sommet d'une face pentagonale de 108 à 120°, avec ajout d'un atome supplémentaire. Dans les phases de types I et II, le taux de faces hexagonales est de 14,28%, soit une pour six faces pentagonales. La Fig. 6 représente l'arrangement des tétraèdres autour des atomes Si(1) et Si(2) dans la structure clathrate de type I.
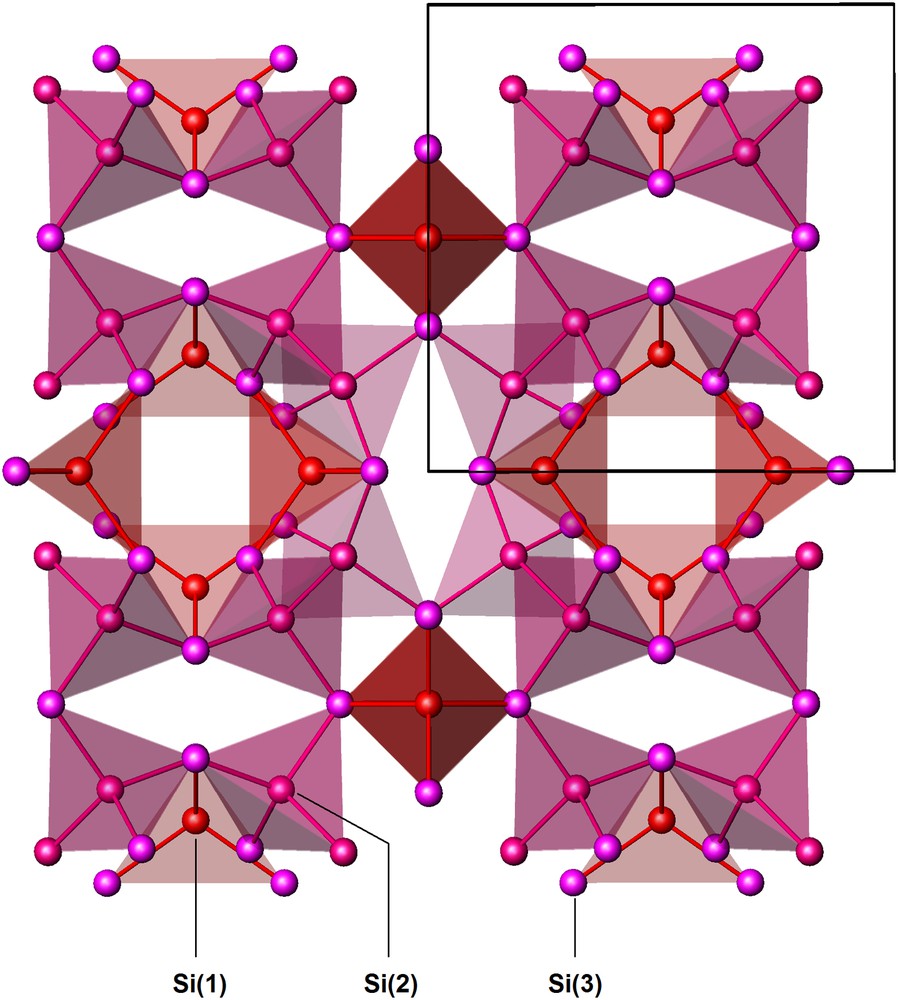
Arrangement des tétraèdres centrés sur les atomes de silicium Si(1) et Si(2) dans la structure de Na8Si46. Pour plus de clarté, les tétraèdres complémentaires entourant les atomes de silicium Si(3) ne sont pas représentés.
La position éclipsée des tétraèdres élémentaires, qui est à l'origine de la formation des faces pentagonales majoritaires complétées par une minorité de faces hexagonales constitue la caractéristique essentielle des structures clathrates de types I et II, mais aussi des autres types structuraux apparentés. Il n'est donc pas étonnant de constater que des espèces chimiquement aussi différentes que l'eau à l'état solide, la silice et les éléments tels que le silicium, mais toutes constituées du point de vue structural d'entités tétraédriques, donnent naissance à des réseaux d'accueil identiques dans lesquels les sous réseaux hôtes, eux aussi de nature très différente, interviennent essentiellement par leur taille. Sur la base de ces considérations, il semble donc possible que d'autres composés à motifs tétraédriques appartenant aux familles ci-dessus indiquées puissent également former des structures clathrates de types I et II.
D'un autre côté, la similitude entre les structures des clathrates et celles des composés intermétalliques A15 et C15 n'est pas fortuite et se conçoit facilement dans la mesure où ces dernières comportent des lacunes tétraédriques dont le nombre et la disposition dans l'espace sont parfaitement compatibles avec l'arrangement des tétraèdres unitaires existant dans les réseaux d'accueil des clathrates concernés [29]. Il est à noter qu'en plus des types structuraux I et II, le clathrate de type H, qui existe dans le cas des hydrates (M3M'2M″(H2O)34) et des clathrasils (1H ou DOH de formule M″3M'2M(SiO2)34), mais pas pour les éléments de la colonne 14 considérés, la structure formée est isotype des composés intermétalliques D2h dont le prototype est CaCu5 (M + M' = 5; M″ = 1) [22,23,33,52]. Des structures hypothétiques de clathrates, analogues à celles d'autres composés intermétalliques, ont même été envisagées [29]. Par ailleurs, il est intéressant de constater que des architectures géantes de certains matériaux mixtes métalliques-organiques – ou MOFs pour metal-organic frameworks – ont été récemment synthétisés à l'Institut Lavoisier de l'Université de Versailles, dont les structures sont très étroitement apparentées à celle d'un clathrate de type II. Les deux sortes de cages sont formées par l'arrangement de « super-tétraèdres » constitués par des trimères de clusters octaédriques de chrome liés entre eux soit par des molécules de tricarboxylate 1,3,5 ou de dicarboxylate 1,4 de benzène dans les matériaux appelés MIL-100 et ML-101, respectivement [53]. Les dimensions exceptionnelles des pores dans ces structures géantes (a ≈ 7290 pm, V ≈ 388×109 pm3 pour MIL-100 et a ≈ 8900 pm, V ≈ 702×109 pm3 pour MIL-101) induisent des capacités d'absorption inégalées pour les gaz (H2, CO2, CH4, …). L'arrangement des super-tétraèdres selon une structure analogue à celle d'un clathrate de type I n'a pas été vérifié expérimentalement, mais apparait comme possible d'après les calculs d'énergie de stabilisation.
2.6 Premières études des propriétés physiques des phases de type clathrate du silicium et du germanium: conductivité électrique, pouvoir thermoélectrique et susceptibilité, comportement sous haute pression
Les premières études de la conductivité électrique des phases de type clathrate du silicium et du germanium ont été réalisées à la faculté des sciences de l'Université de Bordeaux sur des échantillons de poudre compactée et très faiblement frittés, compte tenu de la faible stabilité thermique des matériaux concernés. Bien que sujets à caution en raison de l'influence des joints de grains, les résultats obtenus ont donné des informations cohérentes qui ont été confirmées depuis par des études effectuées sur des échantillons de meilleure qualité ainsi que par des calculs théoriques [42,43].
Pour les échantillons de Na8Si46 et K7Si46, dans lesquels la totalité ou du moins la quasi-totalité des lacunes est occupée par des atomes alcalins, un comportement de type métallique a été observé dans tout l'intervalle de température compris entre 77 et 600 K. Pour les échantillons de NaxSi136 avec x = 3, 7 et 11, la variation de la conductivité en fonction de la température était conforme à celui d'un semi conducteur fortement dopé, caractérisé par un domaine de conductivité extrinsèque à basse température avec une énergie d'activation décroissante avec x (0,04, 0,018 et 0,013 eV pour x = 3, 7 et 11, respectivement) et un domaine de conductivité intrinsèque à haute température. Une étude complémentaire réalisée un peu plus tard sur la phase quasi stœchiométrique Na22Si136, obtenue par action de la vapeur de sodium sur une phase pauvre en alcalin, montrait également un comportement quasi métallique, indiquant qu'avec des valeurs croissantes de x la conductivité électrique de NaxSi136 évoluait graduellement d'un régime semi conducteur à métallique. L'interprétation qui avait été donnée était la suivante: la présence dans le réseau du silicium de quantités croissantes de métal alcalin induisait la formation dans la bande interdite d'une bande d'impuretés qui se remplissait progressivement avec x et dont le sommet se rapprochait progressivement du bas de la bande de conduction du silicium et finissait par la recouvrir pour les valeurs les plus élevées de x. Pour le clathrate K8Ge46, l'évolution de la conductivité en fonction de la température était de type semi conducteur, mais avec une très faible énergie d'activation de 0,01 eV.
Les mesures des coefficients de Seebeck de K7Si46 et NaxSi136 avec x = 3, 7 et 11, ainsi que de K8Ge46, se sont avérées en accord avec les données de conductivité électrique. Pour la phase métallique K7Si46, une valeur faiblement négative de α (coefficient de Seebeck) était observée qui variait linéairement de −2 à −8 μV K−1 entre 77 et 300 K. Pour les phases semi conductrices NaxSi136 les valeurs de α conservaient des valeurs négatives mais nettement plus fortes que pour la phase conductrice et diminuaient fortement pour des valeurs croissantes de x. Une évolution similaire était observée pour K8Ge46 (α ∼ −100 μV K−1 à 300 K).
L'évolution thermique de la susceptibilité magnétique de ces mêmes clathrates entre 100 et 300 K avait montré un comportement faiblement diamagnétique variant peu avec la température, à l'exception de K7Si46 pour lequel un faible paramagnétisme était observé.
Peu après leur publication, les résultats ci-dessus firent l'objet d'une interprétation par Mott [54], qui considérait ce système comme un exemple de dopage du silicium par des électrons provenant d'atomes étrangers en position interstitielle et non plus en position substitutionnelle, comme c'est le cas dans le dopage classique par le phosphore. Selon Mott, la variation de conductivité pour des valeurs décroissantes de x illustrait de manière satisfaisante une transition métal isolant en passant par les quatre étapes successives classiques: conductivité de type métallique correspondant à un gaz d'électrons dégénérés pour les valeurs les plus élevées de x, puis gaz d'électrons hautement corrélés, métal antiferromagnétique pour x ∼ 11 et finalement isolant antiferromagnétique au travers d'une transition de Mott. En conclusion, ce dernier suggérait d'étendre les mesures à plus basse température et d'envisager des méthodes d'étude complémentaires telles que la RMN.
2.7 Première étude du comportement sous haute pression des clathrates Na3Si136 et Na11Si136
La première étude du comportement sous haute pression des clathrates de silicium NaxSi136 avec x = 3 et 11 a été réalisée par Bundy et Kasper sur des échantillons préparés à l'Université de Bordeaux [55]. L'appareillage utilisé était une presse de type belt pouvant engendrer des pressions jusqu'à 20 GPa. Les changements de structure induits étaient suivis par mesure des variations de résistance de l'échantillon étudié, à température ambiante, et comparés à ceux observés sur des échantillons témoins de silicium et de germanium. Les résultats obtenus ont montré qu'à pression croissante la résistance des échantillons de Na3Si136 et Na11Si136, qui ne variait d'abord que très faiblement avec la pression, diminuait brusquement de quatre ordres de grandeur pour le premier dans l'intervalle 9,5–10,5 GPa, et de deux ordres de grandeur pour le second entre 16 et 18 GPa, impliquant la formation d'une phase à caractère métallique (cf. paragraphe 4.10 et Fig. 15). A pression décroissante la résistance des échantillons augmentait de manière beaucoup plus progressive pour atteindre une valeur sensiblement inférieure à celles observées en début de cycle. L'interprétation de ces résultats semblait indiquer que la phase métallique obtenue à haute pression correspondait à un alliage de sodium et de la variété étain β du silicium. L'analyse par diffraction des rayons X des échantillons en fin du cycle de pression montrait que la transformation structurale était irréversible mais ne permettait pas d'identifier la nature de la phase ou des phases–résiduelle(s). En raison de l'amplitude et du très étroit domaine de pression correspondant à la transition de résistivité observée pour Na3Si136, l'utilisation de ce composé en tant qu'étalon de pression à 10 GPa avait été suggérée.
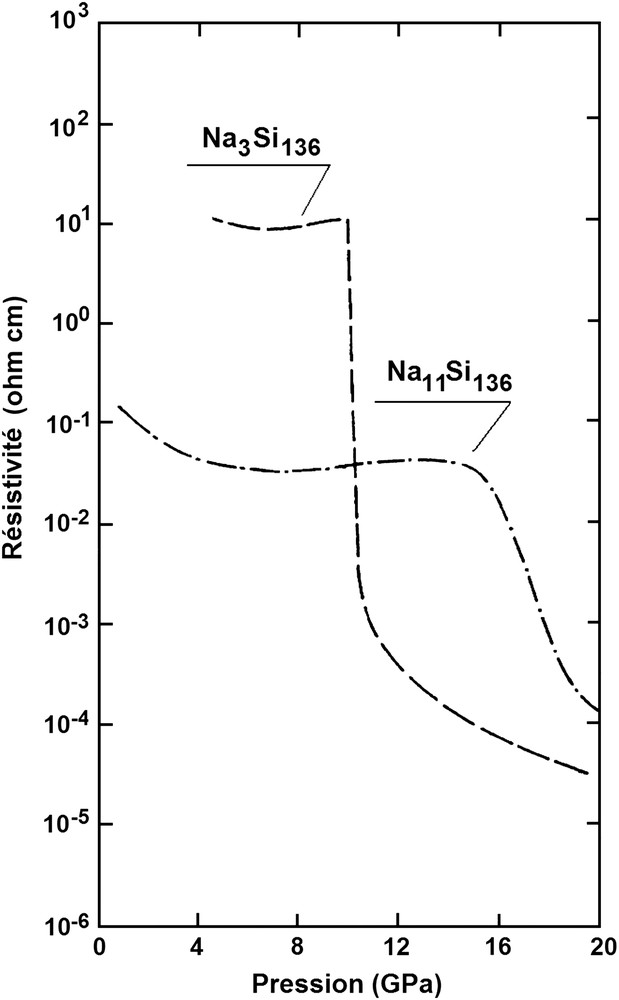
Variation de la résistivité de Na3Si136 et Na11Si136 en fonction de la pression selon Bundy et Kasper [54]. La transition structurale se manifeste par la formation d'une phase conductrice à ∼10 GPa pour x = 3 et ∼15 GPa pour x = 11.
3 Période intermédiaire: 1974–1990
3.1 Substitutions dans les réseaux d'accueil et sous réseaux hôtes des clathrates de types I et II
La structure des clathrates de type I s'est révélée particulièrement adaptable à de nombreuses substitutions portant à la fois sur le sous réseau hôte avec la possibilité d'inclure des halogènes (Cl, Br, I) et des alcalino-terreux (Sr, Ba), mais aussi et surtout sur le réseau d'accueil lui-même, pour former des réseaux mixtes comportant des éléments étrangers aussi divers que ceux des colonnes 13 (Al, Ga, In) et 15 (P, As, Sb) ou des éléments de transition de droite (3d, 4d, 5d, 5f). Les recherches sur les structures dérivées du type I ont débuté vers les années 1970 et se poursuivent encore à l'heure actuelle. Elles ont conduit à l'élaboration d'un grand nombre de phases nouvelles dont les propriétés physiques sont modulables en fonction de la nature et du nombre des espèces chimiques substituées, avec en particulier la possibilité d'obtenir un réseau d'accueil chargé positivement ou négativement.
Au cours d'expériences de cristallogénèse de composés du système germanium/phosphore utilisant l'iode comme vecteur gazeux, Menke et von Schnering [56] avaient obtenu des cristaux de symétrie cubique, dont la structure s'est avérée analogue à celle des clathrates de type I, répondant à la formule I8Ge38P8. La mise en œuvre d'autres atomes d'halogènes et d'autres éléments de la colonne 15 leur avait permis d'obtenir toute une série de composés isotypes, X8Ge38A8 (X = Cl, Br, I; A = P, As, Sb), qui constituaient les premiers exemples de clathrates à sous réseau hôte anionique et à réseau d'accueil mixte et cationique. La formation de telles phases impliquait que les huit électrons excédentaires apportés par les atomes A soient transférés sur les atomes d'halogène, conduisant ainsi à la formulation suivante: X−8(Ge038A+8). L'étude radiocristallographique avait montré que le paramètre cristallin était compris entre 1035 et 1087 pm, soit en moyenne très proche de celui de la phase K8Ge46 (1071 pm). Les huit atomes A sont ordonnés dans le réseau d'accueil, ce qui induit un abaissement de symétrie de la maille se traduisant par le dédoublement du site cristallographique 16i du groupe d'espace Pm-3n (cf. Tableau 1) en deux sites d'appellation 8e du sous groupe P-43n (xxx avec x = ∼0,185 pour Ge(2) et ∼0,815 pour A). Les mesures de conductivité indiquaient que ces clathrates anioniques à réseaux mixtes étaient des semi conducteurs ayant une largeur de bande interdite de 0,9 eV par exemple pour I8Ge38Sb8. Ces mêmes auteurs avaient également synthétisé des clathrates à sous réseau anionique mixte de formule Br8−nInGe38P8 (n = 2, 4, 6) ainsi que d'autres phases telles que I8Ge38−2xGaxAsxAs8 et I8Ge38−2xGaxSbxSb8, dans lesquelles 2x atomes de germanium dans les structures précédentes étaient remplacés par x couples iso électroniques Ga/As et Ga/Sb, comme par exemple dans I8Ge14(GaSb)12Sb8 [57]. De plus, au cours d'essais de synthèse du clathrate vide Ge46, Nesper et al. [58] avaient obtenu de manière inattendue une phase de composition voisine de Ge4I, qui s'est avérée correspondre à I8Ge46−xIx avec x = 8/3, dans lequel les atomes d'iode du sous réseau hôte portent des charges négatives et ceux du réseau d'accueil, occupant partiellement et statistiquement les sites d'appellation 6c, trois charges positives, soit (I−)8(Ge043,33 I3+2,67).
Sur la base du concept de Zintl–Klemm, selon lequel les électrons 3s du potassium sont transférés sur le réseau qui comporte alors 8 charges négatives en excès, von Schnering [59,60] et Llanos [61] avaient repris l'étude structurale du clathrate K8Ge46 et mis en évidence que le réseau de germanium ne comportait en fait que 44 atomes, soit K8Ge44X2, et qu'en raison des deux atomes manquants, l'équilibre des charges était ainsi assuré. Une telle stœchiométrie était en accord avec les résultats de notre étude de conductivité sur le clathrate concerné, pour lequel un comportement semi-conducteur avait été observé, à la différence de K7Si46, conducteur métallique [42,43]. Les phases isotypes rubidium/étain et césium/étain avaient pour formules respectives Rb8Sn44,6 [62] et Cs8Sn44 [63,64]. Une série de clathrates de composition A8BxB'46−x avec A = Na, K, Rb, Cs; B = Al, Ga, In; B' = Si, Ge, Sn avaient été obtenue par Llanos [61]. Dans de telles structures, le réseau d'accueil est parfaitement stœchiométrique et les électrons provenant des atomes alcalins induisent la formation d'atomes B− iso électroniques de B'. Parmi les éléments de la colonne 12, le zinc avait été substitué à l'étain dans les clathrates A8Zn4Sn42 (soit: (A+)8(Zn2−4Sn042)) avec A = Rb et Cs [65].
Avec les métaux alcalino-terreux, des phases de composition générale A8B16B'30 avec A = Sr, Ba, B = Al, Ga et B' = Ge, Sn avaient également été synthétisées, dans lesquelles les atomes alcalino-terreux fournissaient les seize électrons manquants au réseau mixte BB' [66]. Toutes ces combinaisons adoptaient une structure clathrate de type I, dans laquelle les 16 atomes B se distribuaient de manière différente selon les éléments concernés dans les trois sites 6c, 16i et 24 k de la structure. Seul, le composé Ba8Ga16Sn30 se différenciait de ses homologues par un groupe d'espace différent, I-43 m, et un autre type de structure.
Plus récemment, Cordier et Woll [67] avaient préparé des phases de formule générale Ba8(TSi)6Si40 et Ba6(TGe)6Ge40, avec T = Ni, Pd, Pt, Cu, Ag, Au, dans lesquelles les atomes T se substituaient partiellement ou totalement au silicium et au germanium sur les seuls sites 6c de la structure. Selon ces mêmes auteurs, le clathrate Ba8Ge46−x dans lequel x devrait être égal à 4, n'existe pas. Herrmann et al. [68] ont confirmé l'existence des composés à caractère métallique Ba8Au6Si40, Ba8Au6Ge40 et Ba8Au6Si20Ge20. En revanche, ils ont obtenu une phase semi conductrice de composition Ba8Ge43 dont la maille élémentaire correspond à une sur-structure (a' = 2a) de celle du type I, dans laquelle les atomes de baryum cédaient en moyenne 1,5 électron de leur couche périphérique au réseau de germanium. Une étude détaillée de cette phase par Okamoto et al. [69] avait permis de préciser que le groupe d'espace correspondant était Ia-3d et que les lacunes étaient localisées dans les sites d'appellation 24c (1/8,0,1/4). Avec le baryum également, Kröner et al. [70] et Kröner [71] avaient obtenu une phase de composition Ba6In4Ge21, premier membre connu d'une nouvelle famille de clathrate, dont le prototype est Ba6Ge25 ou Ba24Ge100. Cette structure sera décrite au paragraphe 4.3.
A la différence du clathrate de type I, les substitutions possibles dans la structure du clathrate de type II sont nettement plus limitées et n'ont été étudiées pour la plupart que récemment. Les substitutions dans le réseau d'accueil sont à notre connaissance limitées au cas du gallium dans les clathrates Rb8Ga8Si128 et Cs8Ga8Si128 [72]. D'un autre côté, sans qu'il s'agisse en fait de substitutions, des clathrates de silicium et de germanium à réseaux hôtes mixtes Na + Rb, Na + Cs, Na + Ba, K + Rb ont été obtenus soit de manière directe soit indirecte, dans lesquelles les atomes de sodium ou de potassium occupent toutes les lacunes dodécaédriques et les atomes de rubidium, de césium ou de baryum les huit lacunes hexacaïdécaédriques [73–76]. En particulier, les clathrates Na16Rb6Ge136 et Na16Cs8Ge136, préparés par synthèse directe par Bobev et Sevov, sont caractérisées comme leurs homologues Na16Rb8Si136, Na16Cs8Si136 par un comportement métallique n'impliquant pas une structure déficitaire de type Zintl comme c'est le cas pour les phases du germanium de type I ci-dessus évoquées [73b].
3.2 Magnétisme et spectroscopie de RPE des clathrates Na8Si46 et NaxSi136
Suite aux suggestions de Mott dans son article sur les propriétés physiques des clathrates de silicium [54], Sim [77] et Roy et al. [40] avaient entrepris au début des années 1980 des études complémentaires sur les propriétés magnétiques du clathrate NaxSi136 (0 ≤ x ≤ 24), en particulier dans le domaine des basses températures qui n'avait pas été exploré jusqu'alors. La détermination préalable par analyse des spectres de diffraction X des sites cristallographiques occupés pour les diverses compositions des échantillons synthétisés avait confirmé les études antérieures. Pour x < 8, les atomes de sodium étaient localisés préférentiellement dans les sites 8b de la structure et pour des valeurs supérieures de x les sites 16c se remplissaient progressivement. L'évolution entre 1,5 et 20 K de la susceptibilité magnétique montrait un comportement de type Curie–Weiss avec une faible valeur du moment effectif, diminuant rapidement avec x dans le domaine de composition x < 10 et impliquant de faibles interactions antiferromagnétiques (0 ≤ θ ≤ 3 K). Un tel comportement montrait que pour les plus faibles valeurs de x une très faible partie seulement des atomes de sodium correspond à des espèces isolées. La forte diminution observée du moment effectif pour x > 10 était en accord avec la formation d'une phase conductrice et un paramagnétisme de type Pauli.
Une étude par spectroscopie de résonance paramagnétique électronique avait confirmé les résultats de l'étude magnétique. Les spectres obtenus à 9 K sur les échantillons correspondant aux plus faibles valeurs de x montraient la présence d'un quadruplet hyperfin centré sur g = 2,021, d'une raie intense et assez fine centrée sur g = 1,994 et d'une raie très large également centrée sur g = 2,021. Le spectre hyperfin était attribué à la présence d'atomes de sodium isolés et les deux raies larges à des clusters. L'interprétation plus détaillée de ces spectres sera discutée au paragraphe 4.10 faisant état de résultats plus récents.
4 Période récente: de 1990 à nos jours
Quelques années après la découverte des fullerènes en 1985 [78], les recherches sur les clathrates du silicium et des éléments apparentés ont fait l'objet d'un regain considérable d'intérêt. Les phases concernées se sont trouvées impliquées dans plusieurs des thématiques émergeantes du moment:
- (i) les structures à cages de type fullerène;
- (ii) les composés supraconducteurs à haute température critique (C60 dopé par des métaux alcalins);
- (iii) les nouveaux matériaux semi-conducteurs à large bande interdite;
- (iv) les matériaux ultra-lectriques;
De plus, les importantes avancées réalisées dans les domaines de la synthèse (hautes pressions), des caractérisations fines (microscopie électronique, spectroscopies RMN, RPE, Raman, etc.) et des méthodes de calculs ab initio et semi empiriques ont été mises en œuvre pour réaliser des études plus précises des clathrates connus et prévoir l'existence de phases encore hypothétiques pouvant avoir des propriétés particulièrement intéressantes.
4.1 Les clathrates et les fullerènes: similitudes et différences
Les fullerènes, de formule générale CN avec 20 ≤ N ≤ ∞ et pair, correspondent à des clusters creux d'atomes de carbone. Leur forme quasi sphérique résulte de la juxtaposition de faces pentagonales et hexagonales conformément à la règle d'Euler qui stipule qu'un tel polyèdre comporte nécessairement 12 faces pentagonales associées à un nombre quelconque n de faces hexagonales (0 ≤ n ≤ ∞). Sous sa forme générale, la règle concernée s'écrit: N + F − A = 2, où N est le nombre de sommets du polyèdre, F le nombre de faces et A le nombre d'arêtes. Pour le plus connu des fullerènes, C60, (Fig. 7) le nombre de faces hexagonales n est égal à 20, le nombre d'arêtes à 90 et N est relié à n par la relation N = 20 + 2n, qui implique que chaque face hexagonale ajoutée augmente N de deux unités. Le plus petit possible des fullerènes, C20, est caractérisé par n = 0, F = 12, A = 30 et correspond à un dodécaèdre pentagonal, qui possède la même symétrie icosaédrique, Ih, que C60 (Figs. 1-a et 7). Pour des valeurs croissantes de n, le rayon de courbure du cluster augmente progressivement et le plus extrême d'entre eux (N = ∞) se résume à un feuillet plan de graphène ayant un rayon de courbure infini.
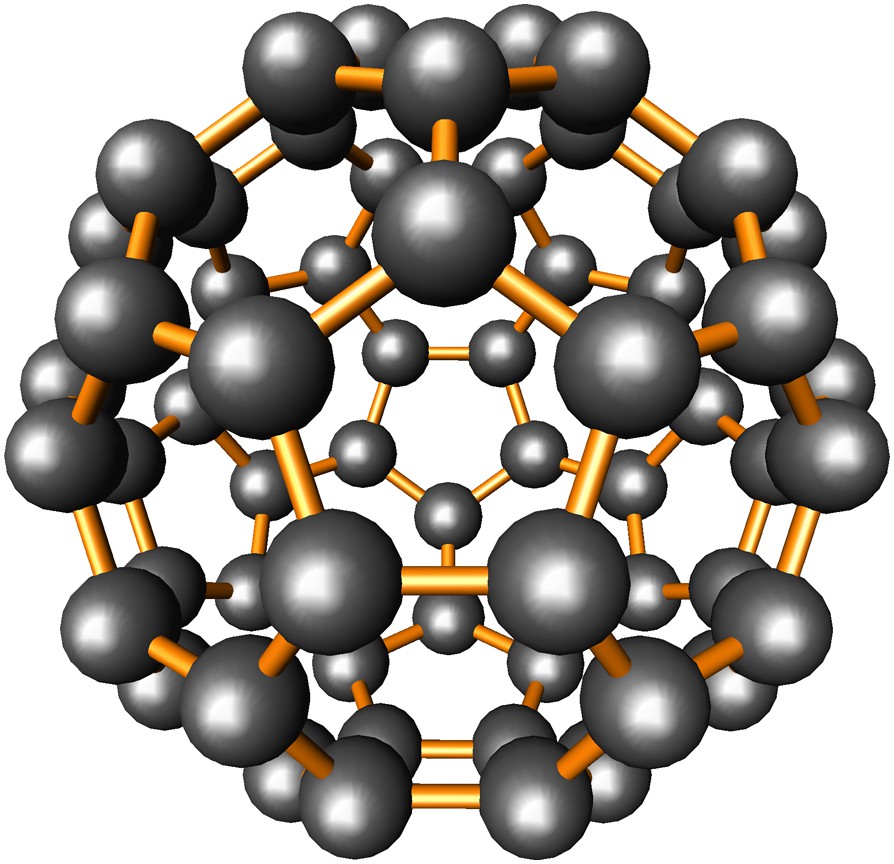
La molécule de fullerène C60. La symétrie icosaédrique Ih est la même que celle de Si20 représenté à la Fig. 1-a. Les faces pentagonales sont isolées les unes des autres par une couronne de cinq faces hexagonales.
La plus grande stabilité du fullerène C60 et dans une moindre mesure du C70 a été interprétée par Kroto comme résultant de la présence de faces pentagonales isolées (Fig. 7) [79]. Cette règle empirique, qui n'est plus satisfaite pour N < 60, expliquerait la diminution des quantités obtenues lors des synthèses de fullerènes pour de telles valeurs de N, sauf pour quelques nombres particuliers: N = 50, 36 et 32. Au-dessous de N = 32, les fullerènes sont très instables en raison de fortes contraintes locales dues à la présence d'un grand nombre de faces pentagonales ayant des arêtes communes. Ces contraintes sont maximales pour le cluster C20, qui n'a jamais été observé dans les spectres obtenus par irradiation laser, mais synthétisé depuis par déshydrogénation du dodécaédrane, C20H20 [80].
La stabilité du cluster C60 résulte aussi du fait qu'il est le plus petit des fullerènes dans lequel tous les électrons de valence du carbone sont engagés dans des liaisons simples ou doubles, ces dernières, au nombre de 60, étant localisées le long des arêtes des 20 faces hexagonales. Pour les valeurs de N inférieures à 60, les clusters concernés comportent des liaisons pendantes qui les rendent réactifs et par conséquent de plus en plus instables à mesure que N tend vers sa valeur minimale. L'état d'hybridation du carbone dans les fullerènes est intermédiaire entre sp2 pour les valeurs les plus élevées de N et sp3 pour les valeurs inférieures. Selon Haddon, l'hybridation du carbone dans C60 est sp2,28 [81].
Les réseaux d'accueil des structures de type clathrate du silicium, du germanium et de l'étain apparaissent comme constitués de cages analogues à celles des plus petits clusters de type fullerènes, avec N = 20, 24 et 28, ainsi que N = 26 dans les nouveaux clathrates de type III qui seront décrits au paragraphe 4.12. Ces réseaux peuvent être considérés comme résultant de la coalescence de deux ou trois sortes de ces petits clusters arrangés de façon à remplir complètement l'espace. Dans de tels arrangements, le problème posé par les liaisons pendantes présentes dans les petits clusters isolés est résolu de manière satisfaisante, puisque chaque atome concerné se trouve ainsi engagé dans un réseau 3D en coordinence tétraédrique sensiblement sp3. Dans le cristal de C60, au contraire, les clusters unitaires ne sont reliés les uns aux autres que par de faibles liaisons de type van der Waals. Alors que le carbone adopte préférentiellement l'état d'hybridation sp2, il n'en est pas de même pour le silicium, et l'existence de clusters isolés de cet élément semble peu probable pour les valeurs de N supérieures à celles indiquées ci-dessus, sauf dans le cas bien particulier des clusters à cœur plein avec N = 33, 36, 39 et 45 [82]. Des calculs effectués par divers auteurs sur un hypothétique cluster Si60 de symétrie icosaédrique ont montré qu'il serait instable et se relaxerait en une forme distordue de moindre symétrie [83]. En revanche, rien ne semble aller à l'encontre de l'existence de structures de type clathrate à réseaux de carbone. La réponse à cette question sera abordée au paragraphe 4.5.
4.2 Supraconductivité dans les clathrates de types I et II
Dès que fut connue la possibilité d'obtenir le fullerène C60 en quantité macroscopique, de très nombreuses études sur leurs propriétés physiques et chimiques furent entreprises [84]. C'est ainsi qu'un groupe de chercheurs de la compagnie AT&T Bell Laboratories mit en évidence la formation de composés d'intercalation des métaux alcalins K, Rb et Cs dans les sites tétraédriques et octaédriques vacants localisés entre les volumineuses molécules C60 de la structure (cubique; a = 1419,8 pm; groupe d'espace Fm-3m). Les composés obtenus, de formule générale MxC60, étaient caractérisés pour la plupart par une conductivité électrique élevée, avec un maximum pour x = 3 et M = K [85]. Pour les phases de composition M3C60 avec M = K, K + Rb, Rb, et Rb + Cs, un comportement supraconducteur était observé avec des températures critiques variant de 19 K (K3C60) à 32 K (Rb2CsC60), les plus élevées observées pour des supraconducteurs « moléculaires » [86,87]. Un mécanisme de supraconductivité classique de type BCS avait été proposé, et l'évolution quasi-linéaire de la température critique avec le paramètre de maille interprétée comme résultant d'une augmentation de la densité d'états au niveau de Fermi, mais aussi et surtout de l'influence des modes de vibration intramoléculaires des clusters C60, facilitant la formation des paires de Cooper [88].
Les nombreuses similitudes existant entre les structures des clathrates de silicium M8Si46 et MxSi136 et les composés d'intercalation des métaux alcalins dans C60, combinées aux avantages qu'auraient les composés du silicium, parfaitement insensibles à l'humidité atmosphérique (endo-fullerènes) par rapport à ceux du carbone hautement réactifs (exo-fullerènes), incitèrent Roy et al. [40] à réaliser les premiers tests de supraconductivité sur les phases Na8Si46 et NaxSi136 (1,5 ≤ x ≤ 22), qui s'avérèrent négatifs pour T ≥ 2 K. Peu de temps après, Kawaji et al. observèrent par contre un comportement supraconducteur de type II pour le clathrate (Na,Ba)8Si46 (TC ∼ 4 K pour la composition Na2,9Ba4,5Si46), dans lequel les sites 2a étaient entièrement occupés par du sodium (cf. Tableau 1) [89]. Ce composé, isotype de Na8Si46, obtenu de manière indirecte par décomposition thermique de Na2BaSi4, résultant de la réaction entre NaSi et BaSi2, correspondait au premier supraconducteur connu comportant un réseau de silicium à l'état d'hybridation sp3. La supraconductivité observée résultait de la forte hybridation des états du baryum et du silicium induisant une forte densité d'états au niveau de Fermi. Ces mêmes auteurs étudièrent ensuite les propriétés supraconductrices de la solution solide NaxBa6Si46 avec 0,2 < x < 1,5. La température critique observée diminuait avec la fraction molaire de sodium de 4,8 à 2,6 K. Herrmann et al. [90] étendirent ces résultats aux phases Ba8TxSi46−x (T = Cu, Ag, Au; 0 ≤ x ≤ 6) sur des échantillons assez impurs (présence de BaSi2 et/ou Si) et observèrent un comportement supraconducteur avec des températures critiques comprises entre 5 et 6 K pour des valeurs de x proches de 1. L'augmentation de la température critique par rapport à celle des clathrates NaxBa6Si46 était attribuée à la présence d'une teneur supérieure en baryum. L'ensemble de ces résultats fut complété par une étude réalisée sur la phase Ba8Si46 obtenue par réaction sous pression (1–5 GPa) à 800 °C d'un mélange de silicium et de BaSi2 [91]. La température critique observée de 8 K confirmait le rôle de l'hybridation des états 5d du baryum avec ceux de la bande anti-liante du silicium dans le mécanisme de supraconductivité, résultat qui sera corroboré par des calculs théoriques et des études expérimentales complémentaires.
Un comportement supraconducteur a également été observé pour la phase à réseau d'accueil mixte Ba8Ga16Ge30 (TC = 7,5 K) par Bryan et al. [92], mais qui n'a pas été confirmé par une étude plus récente de Sales et al. [93]. Dans cette phase, le réseau d'accueil est déficitaire en électrons, ce qui implique que les seize électrons des huit atomes de baryum soient transférés dans la bande de valence plutôt que dans la bande de conduction du silicium. Dans la mesure où une conductivité métallique est observée, il semble par conséquent que cette bande de valence ne soit que partiellement remplie. Dans la série des clathrates supraconducteurs Ba8GaxSi46−x, la température critique diminue de 8 K pour x = 0 à 5,5 K pour x = 6 et devient inférieure à 1,8 K pour x ≥ 10 [94]. Le clathrate de type II, Na16Ba8Si136 obtenu par Rachi et al. [73], dans lequel les atomes de baryum occupent les sites 8b de la structure, n'est quant à lui pas supraconducteur pour T ≥ 2 K, sans doute en raison d'une plus faible densité d'états au niveau de Fermi que pour le clathrate Na2Ba6Si46.
4.3 Structure et propriétés supraconductrices des clathrates K8Sn25, K6Sn25, Ba8In4Sn21, Ba24Si100 et Ba24Ge100
Comme nous l'avons signalé au paragraphe 3.1, le premier représentant de cette nouvelle famille de clathrates, Ba6In4Sn21, a été obtenu par Kröner et al. [70], qui en ont déterminé la structure, assez proche de celle d'un clathrate de type I. Lors de l'étude du système K/Sb, Zhao et Corbett [62] ont observé la formation d'une phase de composition KxSn25 avec 4,35 ≤ x ≤ 12,5 et étudié la structure correspondante sur un monocristal de composition K7,4Sn25. Sur la base des données obtenues pour Ba6In4Sn21 et compte tenu du fait que certaines distances K–K déterminées par Zhao et Corbett semblaient anormalement courtes (292 pm), Fässler et al. [95] ont réexaminé la structure concernée et lui ont attribué la composition K6Sn25. Peu de temps après, une structure isotype, Ba6Ge25 (soit Ba24Ge100), était obtenue dans le système Ba-Ge et étudiée par Carrillo-Cabrera et al. [96] et Fukuoka et al. [97]. La phase Ba4Na2Ge25 possède la même structure que Ba24Ge100 [98] et il en est de même pour Ba24Si100 synthétisée sous haute pression par Fukuoka et al. [99]. Ces nouveaux clathrates ont été parfois désignés sous le nom de type III, nomenclature que nous n'avons pas retenue dans cet article dans la mesure où on sait maintenant qu'il existe des structures du silicium et de l'étain isotypes des hydrates de type III déjà connus depuis longtemps.
La structure du clathrate Ba24Ge100, par exemple, possède une symétrie cubique (a = 1456,35 pm) avec le groupe d'espace P4132 (no. 213). Les atomes de germanium occupent six sortes de sites: Ge(1) en 8c, Ge(2) en 24e, Ge(3) en 12d, Ge(4) en 24e, Ge(5) en 24e et Ge(6) en 8c. Les atomes de baryum Ba(1), Ba(2) et Ba(3) sont localisés dans des sites 8c, 12d et 4b, respectivement, auxquels correspondent trois sortes de polyèdres de coordination. Les premiers, centrés sur les atomes de baryum Ba(1), correspondent à des dodécaèdres Ge20 analogues à ceux qui existent dans les clathrates de type I et II. Ces dodécaèdres sont connectés par trois de leurs faces pentagonales au lieu de quatre, comme dans le type II, et forment des chaînes hélicoïdales qui se développent dans la direction des trois axes 41 (Fig. 8), conférant à la structure un caractère chiral. En plus de ces trois connections par faces communes, chaque dodécaèdre est relié à un quatrième homologue par l'intermédiaire d'une liaison inter cluster isolée Ge(6)–Ge(6). Les polyèdres du second type, centrés sur les atomes de baryum Ba(2), contribuent au remplissage de l'espace laissé entre les dodécaèdres et correspondent également à des entités Ge20, dont la forme correspond à un tétracaïdécaèdre ouvert ayant perdu 4 de ses 24 sommets, transformant ainsi les deux faces hexagonales en deux faces pseudo-carrées. Les polyèdres du troisième type, centrés sur les atomes de baryum Ba(3) sont des pseudo-cubes dont les sommets correspondent aux atomes de germanium Ge(1) et Ge(5) formant les faces carrées des polyèdres Ge20 ouverts. Les relations existant entre la structure de Ba24Ge100 et celle d'un clathrate de type I ont été décrites par Fukuoka et al. [97].

Vue partielle de la structure du clathrate Ba25Ge100 approximativement selon [111] (reproduite à partir des données de Fukuoka [97]). Le réseau hélicoïdal de dodécaèdres est représenté en rouge et les polyèdres pseudo-cubiques en bleu clair. Les atomes de baryum Ba(1) occupent le centre des dodécaèdres et les atomes Ba(3) le centre des pseudo-cubes. Les douze polyèdres ouverts Si20 entourant les atomes Ba(2) ne sont pas représentés pour plus de clarté.
La structure des clathrates de type Ba24Ge100 possède une caractéristique bien particulière. La présence de polyèdres ouverts Ge20X4 implique que les atomes Ge(1) et Ge(5) – soit 32 sur un total de 100 – n'échangent que trois liaisons σ au lieu de quatre avec leurs homologues, ce qui implique selon le concept de Zintl-Klemm que les atomes concernés soient négativement chargés. Dans ces conditions l'équilibre des charges dans un tel clathrate est le suivant: (Mn+)24[(Ge−)32(Ge0)68], impliquant soit un excès de 16 ou 4 électrons par unité formulaire quand M = Ba ou Na + Ba dans le rapport 1/1, soit un déficit de 8 électrons quand M = K.
Les phases Ba24Si100 et Ba24Ge100 se sont avérées supraconductrices avec des températures critiques à pression ambiante de ∼1,4 et ∼0,27 K, respectivement, qui évoluent de manière différente sous l'effet de la pression. Un accroissement de TC jusqu'à ∼3,2 K est observé pour la phase au germanium sous l'effet d'une pression de 1,5 GPa, qui inhibe une transition structurale observée vers 180 K à pression ambiante. La phase isotype du silicium ne subit quant à elle aucune transition de phases et la valeur de TC diminue sensiblement avec la pression pour atteindre 1 K sous 1,15 GPa [100–102].
4.4 Apport des méthodes de calculs théoriques à la connaissance des structures de type clathrate
A la suite des études théoriques réalisées dans le cadre des fullerènes et de leurs divers composés d'intercalation, de nombreux théoriciens se sont intéressés aux structures à cages de type clathrate avec deux objectifs en vue. Le premier avait pour but de contribuer à une meilleure connaissance du mécanisme de supraconductivité mis en jeu dans les phases telles que Na2Ba6Si46, dans lesquelles les atomes de baryum jouaient un rôle prépondérant par rapport à ceux de sodium. Le second objectif concernait les réseaux de silicium exempts d'atomes hôtes, Si34 (dans la mesure où Si136 est une structure cubique à faces centrées, les physiciens utilisent par commodité Si34, soit 1/4 (Si136) pour désigner le clathrate de type II; dans ce qui suit nous parlerons indifféremment de Si34 et Si136) et Si46, qui constituaient deux nouvelles variétés de silicium pouvant avoir des propriétés semi conductrices particulièrement intéressantes, susceptibles de permettre l'accès de cet élément à la classe des semi conducteurs à large bande interdite et si possible à transition directe. Le silicium diamant, Sid, le plus utilisé des semi conducteurs, présente en effet l'inconvénient d'avoir une faible largeur de bande interdite (1,17 eV) et une transition indirecte, caractéristique incompatible avec une utilisation en optoélectronique, domaine réservé à des matériaux de type III–V ou II–VI. Un certain nombre de méthodes avaient été envisagées pour modifier la structure de bandes du silicium Sid, mais aucune d'entre-elles n'avait conduit à des progrès décisifs. Le meilleur résultat avait été obtenu avec le silicium amorphe, mais le mécanisme de luminescence mis en jeu restait assez mal compris. La présence dans les phases de type clathrate de nombreuses faces pentagonales et de longueurs et angles de liaisons présentant une certaine dispersion au lieu de valeurs fixes comme dans Sid, semblait pouvoir induire une modification importante de la structure de bandes.
Adams et al. [103] ont effectué les premiers calculs sur Si46 et Si34 conduisant à des énergies de cohésion presque aussi élevée en valeur absolue que celle de la variété diamant. La différence entre les énergies de cohésion de Si34 et Si46 et celle du silicium Sid n'est que de l'ordre de 0,07 eV/atome, ce qui est étonnamment faible si on considère qu'elle est égale à 0,27 eV/atome entre les formes diamant et étain β. Le résultat le plus intéressant de cette étude concernait la structure de bandes de ces formes clathrates, qui apparaissent nettement différentes de celle du silicium diamant. Les valeurs calculées de la largeur de bande interdite pour les formes clathrate et diamant à partir de méthodes dérivées des théories de la différentielle de la fonctionnelle de la densité (DFT) et des ondes planes (FLAPW) sont de l'ordre de 2,4 et 1,7 eV, respectivement, ce qui implique un élargissement de ∼0,7 eV de la largeur de bande des clathrates par rapport à la forme diamant. La valeur effective de ΔE pour ce dernier étant de 1,17 eV, la largeur de bande interdite pour les formes clathrates serait ainsi voisine de 1,8 eV, c'est-à-dire du même ordre de grandeur que pour le silicium amorphe. Comme pour le silicium diamant, la transition serait indirecte pour les deux clathrates.
Au cours de la même année, Saito et Oshiyama [104] ont effectué des calculs sur Si46 et Na2Ba6Si46 par la méthode DFT–LDA (local density approximation), qui ont donné des résultats similaires et complémentaires à ceux des auteurs précédant. La différence entre les énergies de cohésion de Si46 et Sid est évaluée à 0,09 eV/atome. La structure de bandes et la densité d'états correspondante font apparaître d'importantes différences entre Si46 et Sid :
- - la largeur totale de la bande de valence de Si46 est plus étroite (11 au lieu de 11,9 eV) et comporte une étroite bande interdite intermédiaire;
- - la largeur calculée de la bande interdite fondamentale est égale à 1,26 eV alors qu'elle est de 0,54 eV au-lieu de 1,17 eV pour Sid. Ceci implique une sous estimation de 0,72 eV de la largeur de bande par le calcul et une largeur effective de la bande interdite pour le clathrate de ≈1,9 eV (1,17 + 0,72);
- - le haut de la bande de valence et le bas de la bande de conduction se situent tous deux sur la ligne Γ–X de la zone de Brillouin et correspondent à des vecteurs k très proches;
- - les différences entre Si46 et Sid résulteraient essentiellement de la présence dans la forme clathtrate de faces pentagonales ayant un nombre impair de sommets, conclusion qui sera corroboré expérimentalement et par des calculs complémentaires de Mélinon et al. [105].
Selon Saito et Oshiyama [104], la bande de valence de Na2Ba6Si46 est similaire à celle de Si46, mais la bande de conduction est différente et comporte une densité d'états élevée au niveau de Fermi, qui est la conséquence d'une forte hybridation entre les états électroniques du silicium et ceux des atomes de sodium et de baryum. Selon ces mêmes auteurs, le clathrate Na2Ba6C46 serait métallique et pourrait être supraconducteur. Par ailleurs, il pourrait aussi avoir une dureté comparable à celle du diamant (ultra dur métallique).
L'ensemble de ces importants résultats a été confirmé par de nombreuses autres études portant sur les clathrates à cages vides ou occupées du silicium, mais aussi du germanium et de l'étain [106–112]. Des calculs dans le cadre de la théorie DFT sur la structure électronique de la phase Na8Si46, métallique et non supraconductrice ont été repris par Morigushi et al. [112] et étendus à la phase Ba8Si46, supraconductrice avec TC = 8 K. Ces auteurs ont montré, comme c'était le cas pour la phase Na2Ba6Si46, que les atomes de baryum induisent une importante modification du bas de la bande de conduction par rapport à celle de Si46, qui se traduit par une densité d'états élevée au niveau de Fermi, résultant d'une forte hybridation des états du baryum avec les électrons de conduction du silicium. Dans le cas du sodium, l'hybridation est nettement moins importante et se traduit par une plus faible densité d'états, expliquant ainsi l'absence de supraconductivité. Les diagrammes représentant les contours de densité des électrons de valence pour les deux clathrates montrent très clairement une délocalisation moins importante des électrons périphériques dans le cas du sodium que dans le cas du baryum. Pour confirmer ces études théoriques, les contributions individuelles des électrons des orbitales 6s et 5d du baryum et s et p du silicium à la densité des états ont été évaluées à partir de la comparaison entre les profils de diffusion Compton expérimentaux et théoriques de Ba8−xSi46 par Itou et al. [113]. Les orbitales 6s se sont avérées pratiquement vides, ce qui implique un transfert des électrons 6s dans les orbitales 5d qui sont hybridées avec les orbitales 3p du silicium, formant ainsi un pic de densité au voisinage du niveau de Fermi.
Des calculs de structure de bandes de NaxSi136 (0 ≤ x ≤ 24) – soit Nax/4Si34 – ont été réalisés par Demkov et al. [114], Smielansky et Tse [115] Brunet et al. [116] et Tournus et al. [117]. Comme Si46, le clathtrate vide Si34 correspond à un semi conducteur, mais à transition directe dont la largeur de bande interdite est là encore proche de 1,9 eV (0,7 eV plus élevé que pour Sid). Selon Demkov et al., les résultats obtenus pour le clathrate NaxSi136 ne confirment pas entièrement l'hypothèse selon laquelle les états du sodium constitueraient une bande d'impuretés dans la bande interdite du silicium, comme envisagée antérieurement, mais les états du sodium formeraient au contraire une bande étroite au bas de la bande de conduction de Si136, qui serait à moitié remplie pour x = 4 et pleine pour x = 8. La plus haute bande occupée est triplement dégénérée au point Γ de la zone de Brillouin. Selon ces auteurs, le clathrate Na4Si136 serait un conducteur métallique à bande étroite avec une faible conductivité et Na8Si136 un isolant à basse température, mais ceci n'a jamais été vérifié expérimentalement. Smelyansky et Tse interprètent leurs propres résultats de manière différente. Pour 0 < x ≤ 8, les interactions entre le réseau d'accueil et les atomes de sodium situés dans les cages hexacaïdécaédriques sont faibles et les densités de charges sont essentiellement localisées sur les atomes de métal. A basse température, de tels clathrates sont des isolants de Mott, mais une faible conductivité thermiquement activée peut se manifester à plus haute température. Pour 8 < x ≤ 24 les cages dodécaédriques se remplissent progressivement et les interactions de transfert de charges sont plus fortes, induisant ainsi une conductivité de type métallique. Ces résultats sont en accord avec les données expérimentales [43]. Brunet et al. [116] ont caractérisé par spectroscopies XPS, XANES et EXAFS l'état électronique du silicium et du sodium dans le clathrate NaxSi136 (x = 1 et 8) et effectué des calculs sur le déplacement induit par la distorsion Jahn–Teller des atomes de sodium par rapport au centre des cages Si28. Pour le clathrate Na8Si136 le niveau de cœur de Na1s (1778,2 et 1778,8 eV par XPS et XAS, respectivement) se situe entre les valeurs caractéristiques d'un état métallique et d'un état atomique et s'avère incompatible avec un état ionique. Le déplacement observé des atomes de sodium par rapport au centre des cages s'élève à 100 pm et se traduit par la formation de paires Na–Na engendrant des chaînes qui se développent dans les trois directions de l'espace. Cette dimérisation est assimilable à une distorsion de Peierls combinée à un effet Jahn–Teller. Tournus et al. ont effectué des calculs complémentaires sur ce point et souligné la nécessité d'études structurales fines sur les clathrates concernés. Les études sur les réseaux de silicium dopés ont été étendues aux cas de l'iode et du xénon [118,119]. Le clathrate Xe8Si46, s'il était synthétisé, serait un semi conducteur ayant une bande interdite de 2,25 eV et à transition directe pouvant être utilisé comme diode émettrice dans le vert.
Des calculs ont également été effectués sur les clathrates vides et dopés du germanium et de l'étain. Par la méthode DFT–LDA, Dong et Sankey [120] ont calculé que l'énergie de cohésion des clathrates vides Ge34 et Ge46 (−5,128 et −5,112 eV/atome, respectivement) n'était, comme dans le cas du silicium, que très légèrement supérieure à celle de la variété diamant (−5,172 eV/atome) et nettement inférieure à celle de la variété étain β (−4,986 eV/atome). Dans les deux cas, le volume atomique est de 14% supérieur à celui de la variété diamant et le module de compression de 61,9 et 61,3 GPa au lieu de 70,2 GPa. La structure de bandes électroniques fait apparaître, comme dans le cas du silicium, un élargissement de la bande interdite de 0,75 et 1,21 eV par rapport à celle de la variété diamant (0,7 eV), soit une largeur totale de 1,45 eV pour Ge34 et 1,91 eV pour Ge46; la transition est respectivement directe au point L et quasi directe au point X de la zone de Brillouin. Le diagramme de densité d'états montre, comme dans le cas du silicium, un rétrécissement de ∼1 eV de la largeur totale de la bande de valence et la formation d'une bande interdite secondaire entre les contributions des états sp et p. Zhao et al. ont réalisé une étude comparative de Ge46 et K8Ge46 qui a conduit à des résultats très proches des précédents [106]. La présence d'atomes de potassium dans les cages ne modifie pas de manière significative la bande de valence de Ge46, mais induit quelques différences au bas de la bande de conduction. Le diagramme des contours de densité électronique sur le plan (100) montre qu'il y a un transfert total de l'électron 4s du potassium sur le réseau de germanium, ce qui est en accord avec la formulation: (K+)8(Ge44X2)8− dans laquelle les huit électrons donnés par le potassium compensent le déficit de charges du réseau.
Les calculs d'équation d'état et d'énergie de cohésion effectués par Myles et al. sur Sn34 et Sn46 ont montré que par rapport à la forme diamant de l'étain, ces clathrates sont caractérisés par des énergies de cohésion inférieures de seulement ∼0,04 eV/atome, des volumes atomiques supérieurs de ∼13% et des modules de compression ∼13% inférieurs [108]. Les structures de bandes sont conformes à celle d'un semi conducteur ayant une largeur de bande interdite de 0,458 eV, avec une transition directe au point L pour Sn34 et 0,855 eV avec une transition quasi directe entre les points Γ et X pour Sn46. Par insertion d'atomes de césium, la formation d'une phase déficitaire de symétrie quadratique, Cs8Sn44X2, est favorisée par rapport à la phase stœchiométrique cubique Cs8Sn46, ce qui modifie sensiblement la structure de bandes, qui est alors caractéristique d'un semi conducteur à très faible largeur de bande, à la différence de Cs8Sn46 qui est métallique. La substitution d'atomes de gallium ou de zinc à des atomes d'étain pour obtenir un réseau compensé dans les composés Cs8Ga8Sn38 et Cs8Zn4Sn4é se traduit par un abaissement de symétrie (Oh → Td et Oh → C2v, respectivement) et la structure de bandes des composés formés implique un comportement semi conducteur avec une largeur de bande interdite de 0,619 et 0,574 eV. D'autres phases clathrates de l'étain ont été étudiées [108].
4.5 Etudes théoriques et expérimentales sur les phases clathrate du carbone
Les premières études théoriques sur les clathrates hypothétiques de carbone C34 et C46 ont été effectuées par Nesper et al. [121], suivie peu après par celle d'Adams et al. [103], puis de Saito et Oshiyama [104]. Les très intéressants résultats obtenus ont incité de nombreux autres auteurs à effectuer des calculs très complets sur les caractéristiques physiques de ces nouvelles formes hypothétiques du carbone [110,118,119,122–130]. Ces résultats, qui sont rassemblés pour la plupart dans le Tableau 3, ont confirmé que les structures concernées, si elles existaient, auraient des caractéristiques assez proches de celles de la forme diamant, mais avec des différences qui les rendent particulièrement attractives, compte tenu des possibilités de dopage qu'elles offrent. Avec quelques variations dues aux méthodes de calculs utilisées, toutes les études montrent que les clathrates C34 et C46 seraient presque aussi stables que le diamant, avec des différences d'énergie de cohésion supérieures de seulement 0,1 à 0,18 eV/atome à celle du diamant. Les valeurs du module de compression, B0, sont assez proches, mais plus faibles que celle du diamant de ∼15%, ce qui implique une faible compressibilité. Les structures de bandes font apparaître que les deux clathrates seraient des semi conducteurs ayant une bande interdite à transition quasi directe, plus étroite de ∼15% environ par rapport à celle de la variété diamant, à la différence de ce qui est observé pour les autres éléments de la colonne 14. Selon Perottoni et Da Jordana, C46 aurait une dureté inférieure de 24% à celle du diamant, mais plus élevée que celle du nitrure de bore cubique (cf. Tableau 3) [110]. Selon Blase et al. [128], ce même clathrate serait caractérisé par des propriétés mécaniques exceptionnelles malgré des valeurs plus faibles de ses constantes élastiques et de son module de compression par rapport au diamant. En raison de sa structure à cages, le clathrate C46 ne comporterait pas de plans de clivage {111} aussi faciles que dans le diamant et ne présenterait aucune instabilité vis-à-vis de la forme graphitique sous contrainte.
Résultats des calculs sur les structures clathrates hypothétiques du carbone.
| Diamant/clathrate | Cdiamant | C34 | C46 | C40a | Réf. |
| Paramètre cristallin | 668 | [103] | |||
| 664 | [123] | ||||
| [118] | |||||
| a (pm) | 669,6 | [124] | |||
| 6,70 | [110] | ||||
| 665,8 | [122] | ||||
| 679,6 | 671,6 | [125] | |||
| c (pm) | 681 | [125] | |||
| Différence de volume atomique par rapport au diamant ΔV (%) | ∼15 | ∼15 | [121] | ||
| 18,6 | 14 | [103] | |||
| 14,5 | [124] | ||||
| 13,6 | 13,6 | [122] | |||
| Différence d'énergie de cohésion par rapport au diamant (eV/atome) | 0,113 | 0,144 | [103] | ||
| 0,07 | 0,09 | [121] | |||
| 0,10 | [118] | ||||
| 0,113 | 0,152 | [122] | |||
| Module de compression B0 (GPa) | 376 | [123] | |||
| 462 | 398 | [118] | |||
| 371 | [124] | ||||
| 454 | 409 | [110] | |||
| 427,3 | 302,8 | [122] | |||
| 356 | 361 | 351 | [125] | ||
| 4,21 | 3,26 | 3,96 | [121] | |
| 6,18 | 5,00 | 5,16 | [103] | ||
| 3,75 | [123] | ||||
| 5,60 | 5,15 | 5,25 | [118] | ||
| Pression de transition | |||||
| Diam → C46 (GPa) | −37,3 | [110] | |||
| −7,2 | [122] | ||||
| Diam → C34 (GPa) | −7,8 | [122] | |||
| Dureté calculée H (GPa) | 95 (exp:80) | 73 | [110] | ||
| 61b | [110] |
a Structure de symétrie quadratique apparentée aux hydrates de type IV et comportant des cages C20, C24 et C26.
b Valeur corrigée tenant compte de la différence entre la valeur calculée et expérimentale pour le diamant : 73 × (80/95).
L'influence du dopage des clathrates C34 et C46 par diverses espèces chimiques hôtes a également été envisagée: Li [123, 124], Na et Na + Ba [110], Na + Ca, Ar, Xe [104], Be, Mg [126], F, I [125], et des calculs détaillés ont été effectués pour Li8C46, Na8C46, Na2Ba6C46 et FC46. Selon Timoshevskii et al. et Rey et al. l'insertion de lithium dans le réseau de C46 induirait un comportement métallique. Elle augmenterait sensiblement le paramètre de maille (683,3 au lieu de 669,6 pm) et rendrait la structure plus compressible (B0 = 356 au lieu 371 GPa), à la différence de ce qui est évalué dans le cas de Si46 pour lequel la compressibilité diminue par dopage. La différence d'énergie de cohésion par rapport au diamant serait nettement plus élevée pour le clathrate dopé que pour le clathrate vide (1,48 au lieu de 0,092 eV/atome). Les calculs d'enthalpie montrent que le clathrate Li8C46 ne devient stable vis-à-vis du diamant que pour des pressions très fortement négatives (−187 GPa), beaucoup plus négatives que pour C46 (−19 GPa) [124]. Selon Perottoni et da Jornada, l'insertion de sodium provoquerait un important accroissement du paramètre de maille (697,82 au lieu de 670,29 pm pour la structure vide) et se traduirait par une plus grande compressibilité (358 au lieu de 409 GPa) ainsi qu'une plus grande différence d'énergie de cohésion avec celle du diamant (1,077 eV/atome) [110]. Ces mêmes auteurs ont calculé que ces effets seraient encore plus importants pour le clathrate Na2Ba6C46, conduisant à de fortes contraintes structurales dans le réseau C46 (distances C–C anormalement élevées), énergétiquement défavorables. Les calculs d'enthalpie confirment que les clathrates C46 et Na8C46 ne sont stables vis à vis du diamant qu'à des pressions très fortement négatives (−37,3 GPa pour C46 et −77,1 GPa pour Na8C46), ce qui explique les difficultés rencontrées pour leur synthèse. Selon Zipoli et al. [125], l'insertion d'un atome de fluor au centre d'une cage hexacaïdécaédrique de C34 induirait une conductivité de type métallique résultant de la formation de trous en haut de la bande de valence par transfert électronique sur l'espèce dopante, ainsi qu'un comportement supraconducteur avec une température critique qui serait comprise entre 35 et 77 K. Ces mêmes auteurs ont effectué des calculs sur une autre structure hypothétique, C40, dont le réseau d'accueil, apparenté à celui des hydrates de type IV comporte des cages C20, C24 et C26. Ce clathrate pourrait être dopé n par insertion de lithium et p par substitution de bore au carbone dans le réseau d'accueil [129]. De même, il a été calculé que le fullerène C28, dont le rayon de courbure est nettement plus faible que celui du fullerène C60, serait caractérisé par une valeur du potentiel de couplage électron phonon, λ/N(EF) – où λ est la constante de couplage et N(EF) la densité d'états au niveau de Fermi – 3,4 fois plus élevée que pour le fullerène C60, et qui permettrait d'envisager pour des clathrates supraconducteurs formés de clusters C28 des températures critiques huit fois plus élevées que dans les composés M3C60 [130]. Le cas du fullerène C36, étudié par Côté et al., a conduit à des résultats similaires (TC(C36) ≈ 6 TC(C60) [131]. Dans leur interprétation des propriétés supraconductrices de Ba8Si46, Connétable et al. ont montré que la supraconductivité est une propriété intrinsèque des réseaux sp3 et que les clathrates de carbone constitués de clusters à faibles rayons de courbure sont susceptibles de conduire après dopage approprié à des températures critiques plus élevées que pour les composés d'intercalation du fullerène C60 [132].
A la différence de leurs homologues du silicium, du germanium et de l'étain, tous ces calculs théoriques ne sont jusqu'à présent étayés par aucun résultat expérimental, bien que de nombreuses tentatives aient été entreprises en ce sens. Certaines avancées ont toutefois été obtenues pour des phases apparentées. Par traitement thermique à 600 °C sous une pression de 15 GPa d'un polymère 2D du C60, Yamanaka et al. [133] ont obtenu un polymère 3D de symétrie orthorhombique centré, dans lequel les molécules C60 sont déformées. Ce nouveau polymère est caractérisé par une conductivité métallique et une micro dureté Vickers comparable à celle du nitrure de bore cubique. Wang et al. [134] ont obtenu, par irradiation ionique d'un échantillon de polyéthylène à très haute masse molaire, un solide cristallisé de symétrie hexagonale formé de clusters C20 identifiés par spectrométrie de masse, diffraction électronique et diffusion Raman. Dans un récent brevet, Lueking et Naryanan revendiquent la synthèse d'un matériau correspondant à un clathrate de carbone et d'hydrogène [135].
4.6 Etudes expérimentales et théoriques des propriétés vibrationnelles des clathrates
Les propriétés vibrationnelles des clathrates ont fait l'objet de nombreuses études en vue d'une meilleure interprétation des mécanismes régissant leurs propriétés supraconductrices (interactions électron phonon) et de leurs propriétés de transport thermique qui interviennent de manière prépondérante dans leur aptitude à constituer des matériaux thermoélectriques. Ces études ont le plus souvent été menées de pair avec des calculs de stabilité et de structures électroniques; elles complètent de ce fait les articles cités au paragraphe 4.4.
Dans le cadre d'une étude générale sur les propriétés de vibration des variétés polymorphes du silicium et du germanium, Alben et al. ont effectué en 1975 la première étude théorique portant sur la densité d'états de vibration et les spectres Raman et infra rouge des clathrates Si34 et Si46 sur la base d'un modèle semi empirique de liaison forte [136]. Plus récemment, en 1997, Menon et al. [137] et Kahn et Lu [138] ont réalisé de nouveaux calculs à l'aide de méthodes plus élaborées. Les résultats de ces divers auteurs sur le décompte des modes actifs en Raman (A1g, Eg et T2g) et en infra rouge (T1u) s'accordent parfaitement pour le clathrate Si46 qui comporte 18 modes actifs en Raman (3A1g + 7Eg + 8T2g) et 9 en infra rouge, une légère différence apparait cependant pour le clathrate Si34. Alors qu'Alben et al. et Kahn et Lu ont dénombré 15 modes actifs en Raman, mais avec une distribution un peu différente (3A1g + 5Eg + 7T2g et 3A1g + 4Eg + 8 T2g, respectivement), Menon et al. ne décomptent que 14 modes actifs en Raman (3A1g + 4Eg + 7T2g). Les fréquences calculées pour les modes actifs en Raman diffèrent sensiblement selon la méthode de calcul utilisée. Elles se situent pour les deux clathrates dans l'intervalle 110–600 cm−1 et les plus hautes de ces fréquences calculées sont proches (Kahn et Liu) de celle du silicium de type diamant déterminée par les mêmes méthodes (605 cm−1) ou même supérieures (Alben et al.). Dans la mesure où la fréquence maximale expérimentale pour le silicium de type diamant se situe à 519 cm−1 et que la valeur calculée est de 605 cm−1, Kahn et Lu considèrent que les valeurs déterminées pour les clathrates nécessitent d'être corrigées par un facteur d'échelle de 0,85. Alben et al. et Menon et al. ont procédé de la même manière.
Les premières données expérimentales concernant les spectres Raman des clathrates ont été publiées en 1997 par Fang et al. [139] sur Na8Si46, K7Si46, Na0,2Ba5,6Si46 et K2,9Ba4,9Si46 et Guyot et al. [140] sur K8Si46 et NaxSi136 avec x = 1, 6 et 10. Par déconvolution des raies multiples observées, Fang et al. ont obtenu une quinzaine de modes sur les vingt prévus (soit 18 pour le réseau vide et 2 raies dues au sous réseau hôte) dont l'intensité et la largeur varient avec la nature et la composition du réseau hôte. Ces données expérimentales sont comparées aux valeurs calculées de Alben et al., qui ne conduisent pas à un accord satisfaisant surtout pour les fréquences les plus élevées. Aucune différence notable de la largeur des raies observées entre les spectres des phases métalliques Na8Si46 et K7Si46 et supraconductrices Na0,2Ba5,6Si46 et K2,9Ba4,9Si46 (Tc ∼ 3,5 K) n'a toutefois été mise en évidence permettant d'illustrer l'influence d'interactions électron phonon plus fortes dans les phases supraconductrices. Les résultats de Guyot et al. sont en bon accord avec ceux des auteurs précédents. Pour le clathrate de type I, K8Si46, six raies ont été identifiées dans l'intervalle 175–450 cm−1, dont une isolée et très intense à 175 cm−1. Pour les clathrates de type II, NaxSi136, quatre raies intenses sont observables dans le spectre Raman obtenu avec une longueur d'onde excitatrice de 514,5 nm et cinq avec une longueur d'onde de 647,1 nm, soit 122, 135, 275, 325 et 460 cm−1. D'une manière générale aucune différence notable n'existe entre les spectres enregistrés en polarisation parallèle (VV) et croisée (HV). La fréquence maximale observée pour NaxSi136 (490–500 cm−1) est inférieure à celle qui caractérise le silicium diamant (520 cm−1). La comparaison des données expérimentales et théoriques montre que les valeurs calculées, même en tenant compte des facteurs d'échelle ci-dessus mentionnés, ne permettent pas une interprétation satisfaisante des spectres, surtout dans le domaine des hautes fréquences, ce qui implique la nécessité de modèles plus élaborés tenant compte de la présence d'une majorité de faces pentagonales dans les structures concernées. A partir des résultats d'une étude expérimentale par diffusion inélastique des neutrons, Mélinon et al. ont établi les diagrammes complets de densité d'états de phonons pour les clathrates NaxSi34, (x = 0,15, 2 et 6), Na8Si46 et K8Si46, qu'ils ont comparés à celui de la variété diamant du silicium [141]. Pour les valeurs croissantes de l'énergie, ces diagrammes comportent trois domaines distincts de vibrations correspondant successivement aux modes acoustiques (AM) seuls, aux modes mixtes (AM + OM) et aux modes optiques seuls (OM). Pour le clathrate quasi vide, Na0,15Si34, un décalage sensible des modes acoustiques vers les hautes énergies et des modes optiques vers les basses énergies est observé par rapport au silicium diamant. Ceci se traduit par un resserrement de l'ensemble de la densité des états de phonons, sans doute attribuable à la présence de cycles ayant un nombre impair d'atomes de silicium (un comportement similaire a été observé dans les diagrammes de densité des états électroniques). Pour les clathrates de type I, Na8Si46 et K8Si46, les densités d'états de phonons sont assez différentes en raison d'un décalage vers les hautes énergies des modes acoustiques et vers les bases énergies des modes optiques du clathrate K8Si46 par rapport à Na8Si46, qui semble résulter d'interactions M–Si (M = métal) plus faibles dans le cas du potassium. Les modes de vibration des métaux alcalins apparaissent à 83 cm−1 pour le sodium et 100 cm−1 pour le potassium sous forme de raies fines et intenses. L'influence du nombre d'atomes de sodium sur la densité des états de phonon de NaxSi34 avec x = 0,15, 2 et 5 montre un décalage assez important avec x des modes optiques vers les basses énergies. Les spectres des phases pleines ou quasi pleines Na8Si46 et Na6Si34 (Na24Si136) sont très proches et il doit en être de même pour Si34 et Si46. Ces résultats ont été complétés par Reny et al. dans une étude comparative des clathrates Na8Si46, K8Si46 (conducteurs métalliques), Ba8Si46 (supraconducteur) et I8Si46 (isolant ou faible conducteur électronique) par diffusion inélastique des neutrons et spectroscopie EXAFS [142]. L'interprétation des résultats expérimentaux montre que d'une manière générale les atomes hôtes localisés dans les cages Si20 sont fortement couplés au réseau, mais qu'il n'en est pas de même pour ceux situés au centre des cages Si24. Un couplage plus important observé dans le cas du baryum par rapport au sodium et au potassium apparaît comme le facteur principal favorisant un comportement supraconducteur pour Ba8Si46, qui possède par ailleurs une forte densité d'états au niveau de Fermi. Ce couplage résulte d'interactions entre les phonons acoustiques du réseau et les modes acoustiques du baryum. Le plus fort couplage au sein des cages Si24 est observé dans le cas de l'iode, mais la valeur nulle ou faiblement élevée de la densité d'états au niveau de Fermi inhibe l'apparition d'un comportement supraconducteur pour ce clathrate.
A la suite des résultats expérimentaux de Guyot et al., Dong et al. ont effectués des nouveaux calculs sur la structure électronique et le spectre de vibrations du clathrate Si34, ainsi que sur l'évolution de ce dernier sous l'effet de la pression [143]. Le diagramme représentant la densité d'états de phonons fait apparaître que la plus haute fréquence calculée se situe à 487 cm−1, soit 30 cm−1 au-dessous de celle du silicium (521 cm−1) et qu'il existe une bande vide entre 190 et 270 cm−1. Les fréquences des quinze modes calculés actifs en Raman s'avèrent sensiblement différentes des données des auteurs antérieurs, surtout dans le domaine des hautes fréquences. Parmi ces quinze fréquences possibles, cinq d'entre elles correspondent de manière satisfaisante aux valeurs expérimentales de Guyot et al. L'influence de la pression se traduit par un décalage des modes d'énergies les plus faibles vers les faibles énergies et un décalage des autres modes d'énergies intermédiaires et supérieures vers les fortes énergies. L'évolution observée indique une possible transition de phase vers 27,8 GPa. Dans un autre calcul des propriétés énergétiques et thermodynamiques des clathrates Si34 et Si46 par la méthode du potentiel de Terzoff, Morigushi et al. ont également déterminé les courbes de dispersion et les densités d'états de phonons des clathrates concernés [144]. Les fréquences actives en Raman calculées sont proches de celles des auteurs antérieurs, avec un maximum situé à 515 cm−1. L'évolution des spectres de diffusion Raman de Ba8Si46 et Ba6,6Si46 entre la pression ambiante et 20 GPa ont été étudiés par Kume et al. [145]. A pression ambiante les fréquences caractéristiques du baryum dans les cages se situent à 49, 60 et 89 cm−1. Sur la base des intensités observées pour les deux compositions, les deux premières valeurs correspondent essentiellement aux vibrations des atomes de baryum dans les sites Si24 et la dernière essentiellement à celle des atomes hôtes dans les cages Si20. A pression croissante, une première transition de phases est observée à 7 GPa, qui se traduit par la quasi disparition des modes de vibration dues aux atomes de baryum dans les sites Si24, ainsi qu'une seconde à 15 GPa, au cours de laquelle la raie située à ∼100 cm−1 et attribuée aux atomes de baryum dans les petites cages Si20 disparait à son tour. A pression décroissante, un comportement réversible est observé pour les deux transitions à 15 et 7 GPa. Ces mêmes auteurs ont ensuite étendu leur étude au cas d'I8Si44I2 ainsi que K8Si46 [146,147].
Des informations supplémentaires sur le mécanisme de supraconductivité dans les clathrates comportant un sous réseau hôte de baryum ont été apportées par Tanigaki et al. suite à une étude comparative des spectres Raman de Ba8Si46 (TC = 8 K) et Ba8Au6Si40 (non supraconducteur) dont les réseaux d'accueil ont été substitués ou non par l'isotope 30Si [148]. Les décalages observés des seules fréquences du réseau de silicium ont permis d'identifier parmi les cinq modes majeurs un nouveau mode attribuable aux atomes de baryum, localisé à 252 cm−1 pour le réseau Si46 et 256 cm−1 pour le réseau Au6Si40. Pour ce dernier, un décalage vers les basses fréquences (415 cm−1) de la bande située à 437 cm−1 pour le réseau Si46 montre qu'une valeur élevée de cette fréquence semble favoriser la formation de paires de Cooper. Des mesures de température critique par susceptibilité magnétique sur Ba828Si46 (TC = 8,07 K) et Ba830Si46 (TC = 8,02 K) ont permis à ces mêmes auteurs de calculer que le coefficient isotopique α (TC ∼ M−α où M est la masse correspondant à Si46) était compris entre 0,12 et 0,23. A partir de l'équation de McMillan TC = [<ωlog>/1,20] exp{−[1,04(1 + λ)]/[λ − μ*(1 + 0,62λ)]} dans laquelle <ωlog> est la fréquence moyenne des phonons, λ = V/N(EF) la constante de couplage électron phonon et μ* le pseudo potentiel de répulsion de Coulomb, des valeurs de λ comprises entre 0,79 et 1,2 et de μ* comprises entre 0,23 et 0,31 ont été calculées, qui sont proches de celles qui caractérisent les supraconducteurs conventionnels, mais à la limite supérieure pour μ*. A partir des mesures de chaleur spécifique sur Ba8Si46 ayant une teneur naturelle en isotope 28Si, une densité d'états au niveau de Fermi de ∼30 états/eV/Si46 a été déterminée, qui est supérieure à celle qui caractérise les composés M3C60 (10–20 états/eV/C60). Ces divers paramètres sont du même ordre de grandeur que ceux qui caractérisent ce type de supraconducteur tel que MgB2, dont la plus haute valeur de TC (∼40) par rapport au clathrate concerné résulte essentiellement de la présence dans sa structure d'atomes plus légers. Le clathrate Ba8Si46 apparaît comme un supraconducteur classique de type BCS (electron–phonon mediated supraconductor) à couplage moyen. Récemment, Fukushima et al. ont réalisé une étude comparative de Ba8Si46 et Ba8Ge43X3, ce dernier comportant dans son réseau d'accueil des lacunes ordonnées (paragraphe 3.1) impliquant la présence d'atomes de germanium triplement liés seulement [149]. Les spectres de diffusion Raman des deux clathrates sont très proches pour les fréquences inférieures à 200 cm−1, mais diffèrent nettement pour les plus hautes fréquences en raison de la quasi-disparition dans le spectre du clathrate lacunaire de modes de vibrations nettement visibles pour le clathrate stœchiométrique. L'évolution du spectre de Ba8Ge43X3 avec la pression montre qu'un nouveau mode apparaît entre 150 et 200 cm−1 à 8 GPa, qui ne résulte pas d'une transformation structurale observable par diffraction des rayons X, et à plus haute pression (22 GPa) la formation d'une phase amorphe. Le comportement particulier de Ba8Ge43X3 sous pression est similaire à celui observé pour les clathrates Ba24Si100 et Ba24Ge100 qui possèdent eux aussi des atomes triplement liés dans leurs réseaux.
D'autres études sur les propriétés vibrationnelles des clathrates ont été réalisées dans le but de mieux appréhender l'influence des interactions entre les modes de vibration des atomes hôtes et ceux du réseau d'accueil sur la conductivité thermique étonnamment faible de la plupart des clathrates et de prévoir ainsi les combinaisons réseau d'accueil-sous réseau hôte les plus appropriées. Une comparaison détaillé des propriétés vibrationnelles des clathrates Na8Si46 et Cs8Sn44X2, dont l'évolution thermique de la conductivité est respectivement de type amorphe – ou glasslike selon le terme anglo-saxon – (conductivité pratiquement indépendante de T à haute température) et normale (variation en 1/T à haute température), a été effectuée par Tse et al. [150]. Pour le clathrate Na8Si46, la structure de bandes de phonons fait apparaître qu'il existe effectivement un couplage entre les modes de vibration à caractère localisé des atomes de sodium et les modes acoustiques longitudinaux et transverses du réseau, qui se situent dans le domaine de fréquences 50–150 cm−1. Ces modes de vibration apparaissent à 72 et 98 cm−1 pour les atomes Na(2) situés dans les cages Si24 et à 135 cm−1 pour les atomes Na(1) inclus dans les cages Si20. Il résulte de ce couplage que l'énergie thermique transportée par les phonons acoustique est dissipée par les modes de vibration des atomes hôtes, réduisant ainsi la contribution du réseau à la conductivité thermique. La structure de bandes de phonons du clathrate Cs8Sn46 apparaît notablement différente de celle de Na8Si46 et montre que les vibrations des atomes de césium sont davantage impliquées dans les vibrations du réseau de sorte qu'ils ne peuvent plus être considérés comme des entités indépendantes, ce qui inhibe le mécanisme de diffusion des phonons acoustiques. Il en est de même pour le clathrate lacunaire Cs8Sn44X2. La différence de comportement entre les clathrates à réseau de silicium et d'étain est liée au fait que les liaisons Si-Si dans le réseau du premier sont plus fortes que les liaisons Sn–Sn du second. Les propriétés vibrationnelles des clathrates Sn46, Sn136 et Cs8Ga8Sn38 ont fait l'objet d'une étude théorique par Myles et al., dont les résultats ont été comparés aux valeurs expérimentales pour Cs8Ga8Sn38 [151]. Les structures de bandes de phonons de Si46 et Si136 montrent la présence de deux domaines de fréquences à forte densité d'états, l'un situé entre 40 et 65 cm−1, juste au-dessus des modes acoustiques, et l'autre entre 175 et 190 cm−1. Les valeurs des fréquences actives en Raman et infra rouge ont été calculées, parmi lesquelles 9 et 8 raies Raman majeures, respectivement. La structure de bandes de phonons de Cs8Ga8Sn38 s'avère assez voisine de celle de Si46, mais avec deux différences. Deux étroits domaines de fréquences à forte densité d'états sont observés à ∼195 et ∼210 cm−1, attribuables aux modes de vibrations des atomes de gallium et de nouvelles bandes apparaissent entre 25 et 40 cm−1 correspondant aux modes de vibration des atomes de césium dans les deux types de cages, qui induisent un rétrécissement de 25% environ de la zone de fréquences des modes acoustiques du réseau. Une telle situation est favorable à une atténuation de la conductivité thermique du réseau. Les spectres Raman calculés pour une polarisation verticale (VV) et horizontale (HV) comportent une vingtaine de raies, dont trois attribuables aux modes localisés du césium et sont en bon accord avec les spectres expérimentaux. Une autre étude par Nolas et al. [152] porte sur les clathrates de type II, Si136, Cs8Na16Si136 et Cs8Na16Ge136. Les spectres Raman expérimentaux et calculés sont là aussi en bon accord. Les modes de vibration du césium sont identifiés à 57 et 18 cm−1 pour Cs8Na16Si136 et Cs8Na16Ge136, respectivement. Une analyse détaillée de la dynamique des atomes hôtes dans les deux types de cages des clathrate Sr8Ga16Ge30, Ba8Ga16Ge30 et Eu8Ga16Ge30 a été réalisée par Hermann et al. [153,154] par diffusion inélastique des neutrons pour les deux premiers et diffusion inélastique nucléaire pour le dernier. Les énergies de vibration associées aux atomes Sr et Ba dans les cages tétracaïdécaédriques sont identifiés à 4,4 et 4,9 meV (soit 35,48 et 39,52 cm−1), respectivement, et ceux attribuables à ces mêmes atomes dans les cages dodécaédriques n'apparaissent pas, car masqués par la large et intense bande correspondant aux phonons optiques. Les énergies de vibrations dues aux atomes d'europium dans les cages du réseau Ga16Ge30 sont difficiles à déterminer à partir des données expérimentales sur les densité d'états de phonons en raison de la possible présence de trois raies attribuables à l'europium dans les cages tétracaïdécaédriques résultant d'un décalage de l'atome hôte par rapport au centre de la cage (ce point sera précisé dans le paragraphe 4.13). Les valeurs obtenues dans cette hypothèse sont de 3,0, 4,9 et 7,5 meV (soit 24,19, 39,52 et 60,48 cm−1) pour l'europium dans les plus grandes cages et 6,7 meV (54,02 cm−1) pour les plus petites et les plus symétriques. Dong et al. [155] ont étudié par la méthode de la DFT l'influence de la nature et du nombre des atomes hôtes K, Rb, Cs, Sr et Ba sur les interactions réseau hôte-réseau d'accueil pour GaxGe46−x avec x = 14 et 16. Les modes de vibrations attribuables aux atomes alcalino-terreux sont localisés à plus basse fréquences que ceux des métaux alcalins qui interagissent plus faiblement avec les modes acoustiques du réseau.
4.7 Caractérisation des clathrates par résonance magnétique nucléaire
La résonance magnétique nucléaire a été utilisée pour caractériser l'environnement électronique des atomes hôtes dans les cages, ainsi que celui des atomes constituant les réseaux d'accueil dans les clathrates de types I et II. Dans une première étude par RMN du 23Na dans (Na,Ba)xSi46 et NaxSi136 (x = 4 et 9), Gryko et al. ont été les premiers à observer un déplacement de Knight δ de 1213 ppm de la raie de résonance du sodium dans les cages Si20 de la phase supraconductrice (Na,Ba)xSi46, déplacement qui est légèrement supérieur à celui caractérisant le sodium métallique (δ = 1123 ppm) [156]. Pour les phases isolantes ou très faiblement conductrices NaxSi136, les raies du sodium dans les deux types de cages apparaissaient encore plus déplacées avec des valeurs de 1756 et 2012 ppm pour x = 4 et 1595 et 1796 ppm pour x = 9. Les auteurs concernés ont attribué ces décalages à une localisation partielle des électrons 3s au niveau du noyau de l'atome de sodium, avec un déplacement plus important pour les atomes situés dans les plus grandes cages. La raie de résonance du 23Na pour la phase NaSi, apparaît à 45 ppm en accord avec sa structure ionique de type Zintl. Shimizu et al. ont étudié le spectre de RMN des atomes 29Si, 23Na, 137Ba et 135Ba dans le clathrate NaxBaySi46 au dessus de sa température critique [157]. Trois pics distincts correspondant aux trois sites non équivalents du silicium dans la structure ont été observés, avec des déplacements de Knight de 2036 ppm (Si(2) en 16i), 862 ppm (Si(1) en 6c) et 720 ppm (Si(3) en 24k) à 90 K et une intensité des raies variant selon la distribution 16:6:24. A 4,2 K la raie de résonance du 137Ba est située à 5930 ppm (4030 ppm pour le baryum métallique) et celle du 23Na à ∼ 900 ppm, par rapport à 137Ba et 23Na dans une solution aqueuse de BaCl2 et NaCl, respectivement. La variation thermique du temps de relaxation spin réseau T1 pour les divers atomes de la structure est conforme à la relation de Korringa (T1T = constante) et en accord avec le caractère métallique de la structure. Les résultats montrent que les atomes de sodium et de baryum ne sont que partiellement ionisés à la différence du cas des fullerènes dopés avec des alcalins pour lesquels l'ionisation est pratiquement totale. Les spectres de RMN en mode statique de 23Na dans Na8Si46 et NaxSi136 avec diverses valeurs de x ont été étudiés par Reny et al. à partir d'échantillons comportant ou non de faibles quantités d'impuretés (NaxSi136 dans Na8Si46 et Na8Si46 dans NaxSi136) [158]. Deux raies de résonance fines et fortement décalées sont observées pour les phases à caractère métallique comme Na8Si46 (1767 et 2019 ppm) et Na23Si136 (1608 et 1812 ppm), alors qu'une seule raie large et diffuse centrée à 1700 ppm apparait pour les phases faiblement conductrices NaxSi136 (x ≤ 16) ne comportant pas ou peu de Na8Si46. Le spectre (a) de la Fig. 9 correspond à un échantillon de Na8Si46 comportant une quantité assez élevée de NaxSi136 avec x ∼ 24 et le spectre (b) à un échantillon de NaxSi136 (x ∼ 24) pratiquement exempt de Na8Si46. Sur la base de l'intensité relative des deux raies caractéristiques de Na8Si46, la plus décalée et la plus intense a été attribuée au sodium dans les cages Si24 (raie A dans Fig. 9-a) et l'autre au sodium situé dans les plus petites cages Si20 trois fois moins nombreuses (raie B). Pour la même raison, la plus intense des raies de NaxSi136 (x ∼ 24) a été interprétée comme due au sodium dans les plus petites cages Si20 (raie C), deux fois plus nombreuses que les cages Si28 (raie D). Ces résultats ont été confirmés par Gryko et al. [159] lors d'une étude du déplacement des raies de résonance en fonction de la température et de l'influence de la délocalisation électronique sur la densité d'états au voisinage du niveau de Fermi. La raie de résonance du sodium dans les petites cages de la structure de (Na,Ba)xSi46 est observée à 1205 ppm. Le spectre de résonance RMN de 29Si dans Na8Si46 a été étudié par Ramachandran et al. [160]. Outre des raies de faible intensité dues aux bandes de rotation qui leur sont associées, trois raies principales fines et intense sont identifiées à 617, 653 et 842 ppm, qui correspondent respectivement aux atomes de silicium dans les trois sites non équivalents de la structure, Si(2) en 16i, Si(1) en 6c et Si(3) en 24 k, avec des intensités sensiblement proportionnelles au nombre d'atomes concernés. Le plus important déplacement de Knight de la raie attribuable au silicium en site 24 k par rapport à ceux des deux autres sites est en bon accord avec les résultats des calculs de la contribution de la densité d'états des orbitales s des atomes concernés à la densité totale d'états au niveau de Fermi. Ces mêmes auteurs ont ensuite étendu leur investigation au cas du clathrate Na16Cs8Si136 [161]. La raie de résonance du 23Na dans les sites Si20 est identifiée à 1738 ppm et celles du 29Si dans les trois sites non équivalents de la structure à 210 ppm (Si(1) en 8a), 426 ppm (Si(2) en 32e) et 713 ppm (Si(3) en 96 g). Les valeurs calculées de la contribution des états s du silicium relatifs aux trois sites 8a, 32e et 96 g à la densité totale d'états sont dans les rapports 1:1,5:3,5 et conformes aux intensités observées (1:2,03:3,4). Des valeurs de déplacement de Knight très voisines ont été observées sur le même clathrate par Pouchard et al. [162], ainsi que par Latturner et al. [163] pour Na16Rb8Si136. Pour ce dernier, la raie du 23Na dans les cages Si20 se situe à ∼ 1770 ppm, la raie du 87Rb dans les cages Si28 à ∼ 3700 ppm et les raies du silicium à 275 ppm (Si(1) en 8a), 420 ppm (Si(2) en 32e) et 735 ppm (Si(3) en 96 g); les intensités correspondantes sont dans les rapports 1:3,9:12,1. He et al. ont repris de manière détaillée l'interprétation des spectres de NaSi, Na8Si46 et NaxSi136 avec 0 ≤ x ≤ 24, qu'ils ont complétée par des études de spectroscopies XPS et XANES [164]. Pour NaSi, la raie de résonance du 23Na est observée à 48,6 ppm et celle du 29Si à –364 ppm, sous forme d'une raie large à deux composantes non résolues provenant de la présence de deux sortes de sites cristallographiques pour le silicium [6]. L'important déplacement négatif de −364 ppm par rapport à la valeur observée pour le silicium de type diamant (−81,3 ppm) résulte de l'effet d'écran des électrons portés par les entités ioniques (Si4)4−. Pour les clathrates Na8Si46 et NaxSi136 avec x proche de 24, les déplacements observés des raies de résonance RMN du 23Na sont en accord avec les résultats de Reny et al., mais sur la base de la forme des raies et de la symétrie du site correspondant, les auteurs concernés attribuent les raies les plus décalées et isotropes aux atomes de sodium dans les sites les plus symétriques, i. e. 2019 et 1768 ppm pour les cages Si20 et Si24 de la structure de Na8Si46, respectivement, et 1810 et 1601 ppm pour les cages Si28 et Si20 de la structure de NaxSi136 (x ∼ 24), respectivement. La plus faible intensité des raies anisotropes, bien que le nombre d'atomes concernés soit plus élevé (3 et 2 fois, respectivement), résulte d'un effet quadripolaire qui se traduit par la présence de nombreux satellites de rotation de part et d'autre de la raie centrale, qui conduit à une diminution importante de l'intensité de cette dernière. Pour des valeurs décroissantes de x dans le clathrate lacunaire NaxSi136, les raies caractéristiques de l'atome de sodium deviennent de plus en plus larges et diffuses en raison des modifications induites dans leurs environnements et finissent par disparaitre. Un élargissement des raies du 29Si est également observé sans diminution notable de l'intensité et avec une évolution du centre de gravité du spectre vers de plus faibles valeurs du décalage. Pour les plus faibles valeurs de x, les déplacements observés restent toutefois très supérieurs à celui qui caractérise le silicium de type diamant semi conducteur, ce qui indique qu'il subsiste dans la structure des échantillons étudiés suffisamment d'atomes de sodium pour engendrer la présence d'électrons de conduction.
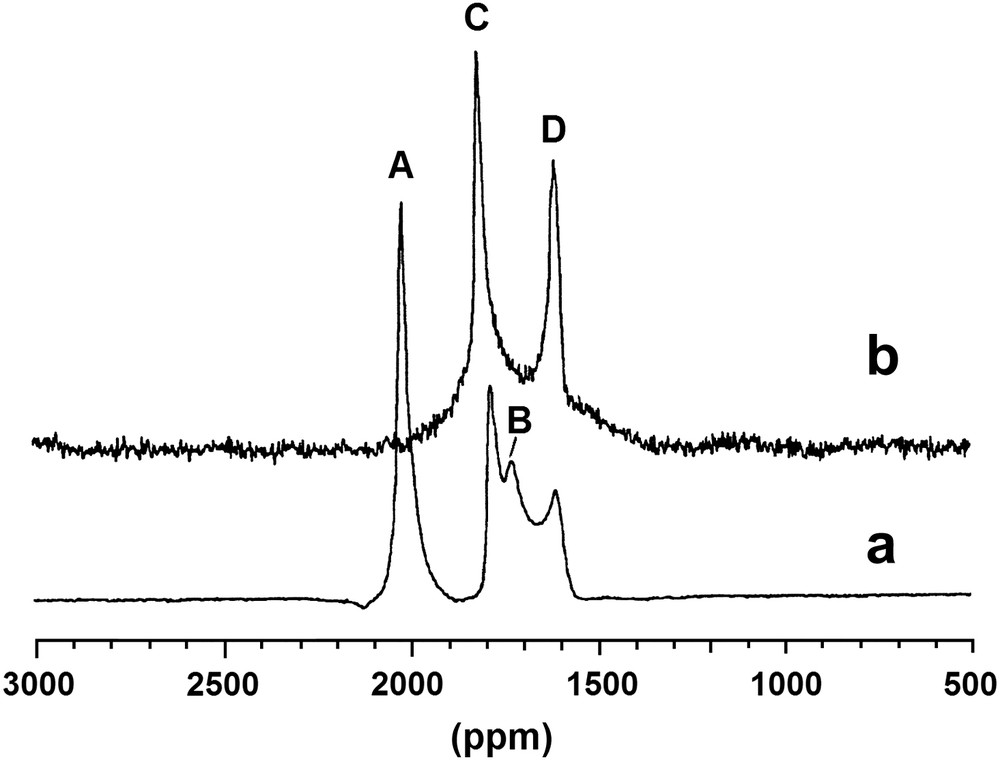
Spectre RMN en mode statique du 23Na obtenu dans (a) un mélange de Na8Si46 et NaxSi136 (x ∼ 24) montrant des raies fines fortement déplacées et (b) NaxSi136 avec x ∼ 24. Les raies A et B et C et D correspondent aux atomes de sodium dans les clathrates Na8Si46 et NaxSi136 (x ∼ 24), respectivement.
Une étude comparative des spectres de RMN MAS (magic angle spinning) du 23Na dans les clathrates NaxSi136 (x ∼ 24) et Na16Cs8Si136 a été effectuée par Pouchard [162] et Jaussaud [165], qui a confirmé l'interprétation de He et al. [164]. Pour la phase NaxSi136, deux raies principales sont observées à 1800 – la plus intense – et 1600 ppm, ainsi que de nombreuses bandes de rotation de satellites quadripolaires de part et d'autre de la raie située à 1600 ppm, qui correspond par conséquent aux atomes de sodium situés dans les cages Si20 les plus nombreuses mais les moins symétriques (Fig. 10-a). Le spectre de Na16Cs8Si136 comporte quant à lui une seule raie à 1700 ppm centrée sur une série de bandes de rotation satellites quadripolaires, correspondant aux atomes de sodium localisés dans les seules cages accessibles Si20 (Fig. 10-b). La raie la plus intense et la plus décalée de NaxSi136 correspond donc bien aux atomes de sodium dans les cages Si28 (sites 8b).
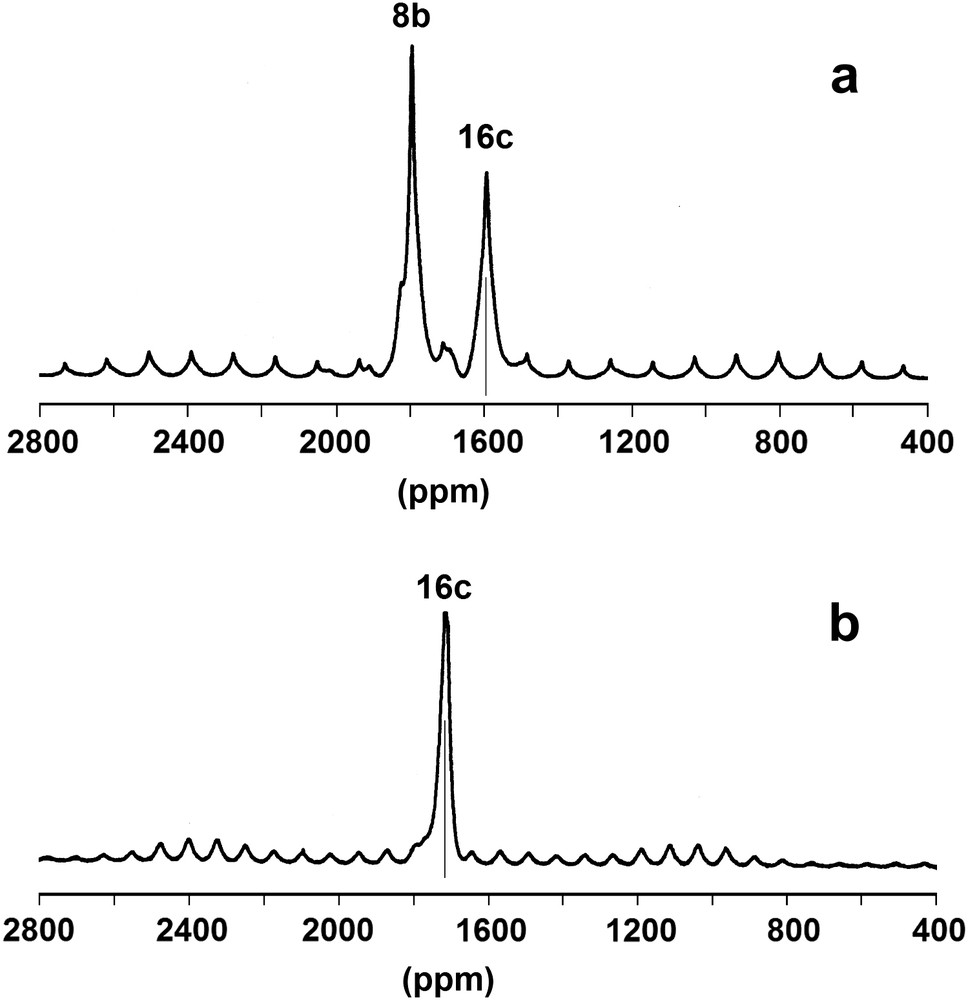
Spectre de RMN MAS du 23Na pour (a) NaxSi136 (x ∼ 24) montrant la présence de raies de rotation des satellites quadripolaires centrées sur la raie à 1600 ppm et (b) Na16Cs8Si136.
Le spectre de résonance RMN du 29Si dans le clathrate vide Si136, obtenu par une série de traitements thermiques sous vide poussé d'une phase NaxSi136, a été étudié par Gryko et al. [35]. Alors que le spectre correspondant à une phase quasi vide Na0,5Si136 comporte des raies très larges, celui de Si136 dans lequel la teneur en sodium est d'environ 600 ppm est caractérisé au contraire par des raies fines qui se situent pour les trois principales à 0,3 ppm (Si(3) en 96g), 50,4 ppm (Si(1) en 8a) et 98,0 ppm (Si(2) en 32e); les autres raies de faible intensité correspondent aux bandes de rotation associées. Les intensités sont dans les rapports 12:1:4. La raie caractéristique du 29Si dans le silicium de type diamant est observée à −79 ppm. Des valeurs tout à fait comparables ont été obtenues par Pouchard et al. [162] et Jaussaud [165] sur un échantillon ne contenant plus que ∼35 ppm de sodium, obtenu par la combinaison de traitements thermiques sous vide et de traitements chimiques d'une phase NaxSi136 plus riche en métal alcalin (Fig. 11a et b).

Spectre RMN MAS du 29Si obtenu pour (a) le clathrate Na16Cs8Si136 montrant des raies fines assez fortement décalées par rapport à celle du silicium et (b) le clathrate vide X24Si136 comportant des raies très fines et peu décalées.
4.8 Caractérisation du clathrate NaxSi136 par résonance paramagnétique électronique
La spectroscopie de résonance paramagnétique électronique (RPE) a été utilisée pour caractériser l'état électronique de l'atome de sodium dans le clathrate NaxSi136 pour les plus faibles valeurs de x. Les résultats de la première étude réalisée par Sim [77] et Roy et al. [40] ont été décrits au paragraphe 3.2. Plus récemment, Yahiro et al. [166] ont enregistré le spectre de RPE de Na3Si136 à 4 K qui présente les mêmes caractéristiques que ceux des auteurs précédents. Outre la présence d'une raie intense centrée à g = 2,0019, un spectre hyperfin à quatre raies est observé correspondant à des atomes de sodium isolés (I = 3/2), pour lesquels la densité de spin dans l'orbitale 3s est égale à 42% de celle d'un spin unitaire. Deux raies de très faible intensité localisées entre les raies MI = −3/2 et −1/2 et 1/2 et 3/2 du spectre hyperfin sont interprétées comme faisant partie d'un spectre hyperfin à sept raies, dont les cinq autres sont superposées à celles du quadruplet, résultant de la présence de dimères Na2+. L'intensité des raies du spectre hyperfin diminue avec la température et s'annule au-dessus de 200 K. La raie centrale intense de forme asymétrique est attribuée à la présence de clusters d'atomes de sodium.
Une étude plus récente du spectre RPE du clathrate NaxSi136 très faiblement dopé en sodium a été réalisée par Ammar et al. [34] et Jaussaud [165] sur des échantillons ayant subi une série de traitements sous vide poussé, complétée par des traitements par l'iode permettant de diminuer autant que faire se peut la valeur résiduelle de x. Le spectre à 4,2 K d'un échantillon de composition voisine de x = 1 après quatre traitements sous vide et un traitement par l'iode comporte les mêmes caractéristiques que ceux des auteurs antérieurs (Fig. 12-a). Les quatre raies du spectre hyperfin sont centrées sur g = 2,0363 et espacées de 13,3 mT (133 Gauss). La raie large et diffuse attribuée à la présence de clusters de sodium dont les électrons 3s interagissent entre eux est centrée sur g = 2,0043 et la raie fine et intense dont l'origine n'a pu être clairement établie apparait à g = 2,0089. L'évolution du spectre RPE avec le nombre de traitements par l'iode montre que l'intensité de la raie fine et étroite diminue nettement et finit par s'annuler, que la raie large et diffuse due à la présence de clusters de sodium diminue également d'intensité, mais dans une bien moindre mesure, et que celle des raies du spectre hyperfin augmente par contre très sensiblement (Fig. 12-b, c et d). Le spectre RPE (d) correspond à un échantillon ayant subi cinq traitements sous vide et sept traitements par l'iode, dans lequel il ne subsiste plus que les quatre raies du spectre hyperfin, la raie large et diffuse qui se confond pratiquement avec la ligne de base, ainsi que trois raies très faibles localisées entre les quatre raies du spectre hyperfin, résultant de la présence de dimères Na2+ [166].
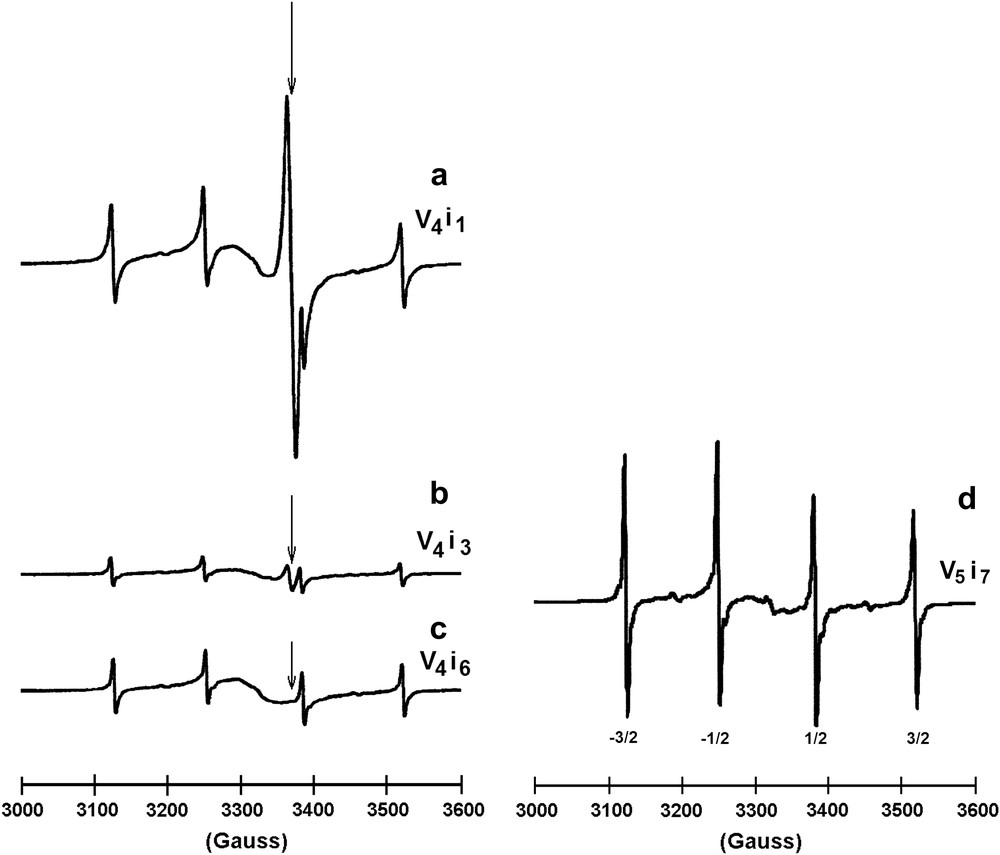
Spectre de RPE d'un échantillon V4in de NaxSi136 (a) après une série de 4 traitements (V4) sous vide et n = 1 (a), 3 (b) et 6 (c) traitements par l'iode, montrant la diminution de l'intensité de la raie fine qui finit par disparaitre et (d) d'un autre échantillon V5i7 dans lequel la teneur résiduelle en sodium n'est plus que de l'ordre de 35 ppm (x ∼ 0,006).
La détermination du taux de sodium résiduel par les méthodes classiques dans un échantillon tel que V5i7 (Fig. 12-d) conduirait à des résultats très imprécis en raison de la présence de quelques traces (2 à 3%) de Na8Si46. En effet, bien que n'influençant nullement le spectre RPE, de telles impuretés contiennent une quantité de sodium très supérieure à celle que l'on veut mesurer dans les échantillons de NaxSi136 concernés. La teneur résiduelle de sodium a donc été déterminée quantitativement par comparaison de l'intensité des signaux de RPE enregistrés avec ceux d'étalons paramagnétiques (aluns dopés au Cr3+). Le taux de sodium dans l'échantillon V5i7 a été ainsi évalué à 35 ppm, ce qui correspond à une valeur x dans NaxSi136 aussi faible que 0,006. Il s'agit donc d'une véritable variété allotropique nouvelle du silicium cristallin (paragraphe 4.11).
4.9 Apport des hautes pressions à la synthèse de nouveaux clathrates
L'utilisation des techniques de hautes pressions à permis de synthétiser de nouveaux clathrates qui ne peuvent être obtenus dans des conditions de pression ambiante. L'intérêt de réaliser des synthèses sous l'action de hautes pressions combinée à de hautes températures est de pouvoir tirer profit du déplacement d'équilibre d'une réaction dans le sens conduisant à une diminution de volume, conformément au principe de Le Chatelier. Les réactions sont effectuées dans des appareillages spécifiques de type multi enclumes ou « belt », capables d'engendrer des pressions jusqu'à ∼20 GPa et comportant un dispositif de chauffage interne jusqu'à ∼1700 °C.
Le premier clathrate synthétisé sous haute pression a été Ba8Si46 [91] (3 GPa/800 °C), dont les propriétés supraconductrices ont été reportées en détails dans les paragraphes précédents. Peu de temps après, le clathrate Ba24Si100, dont la structure est décrite au paragraphe 4.3, a été obtenu sous une pression de 1,5 GPa à 800 °C [99]. Par traitement thermique à 1000 °C et sous une pression de 15 GPa de Ba8Si46 ou d'un mélange de BaSi2 et de silicium, Yamanaka et Maekawa [167] ont obtenu une nouvelle phase, BaSi6, pouvant être considérée comme un pseudo-clathrate dont la structure est isotype de celle d'EuGa2Ge4 (Fig. 13). Les atomes de baryum sont au centre de cages polyédriques Si18 à faces communes et arrangées selon un réseau formé de tunnels parallèles orientés selon la direction [100] de la maille orthorhombique (a = 448,5 pm, b = 1037,5 pm, c = 1196; groupe d'espace Cmcm). Les mesures électriques indiquent un comportement faiblement métallique. Des structures analogues ont été obtenues sous haute pression (5 GPa/1200 °C) par Fukuoka et al. [168,169] pour LaGe5 et SrGe6−δ (δ = 0,5). De même, le clathrate isotype SrSi6 a été synthétisé par Wosylus et al. sous une pression de 10 GPa à 1520 °C [170]. Les contributions à la densité d'états électronique des états Si(p), Si(s), Sr(d) et Sr(s) ont été déterminées, ainsi que la distribution des charges sur les atomes Sr et Si, qui s'est avérée ne pas correspondre à une phase de Zintl idéale [Sr2+][Si6]2−, mais à la distribution des charges suivante: [Sr1,86+][Si6]1,86−.
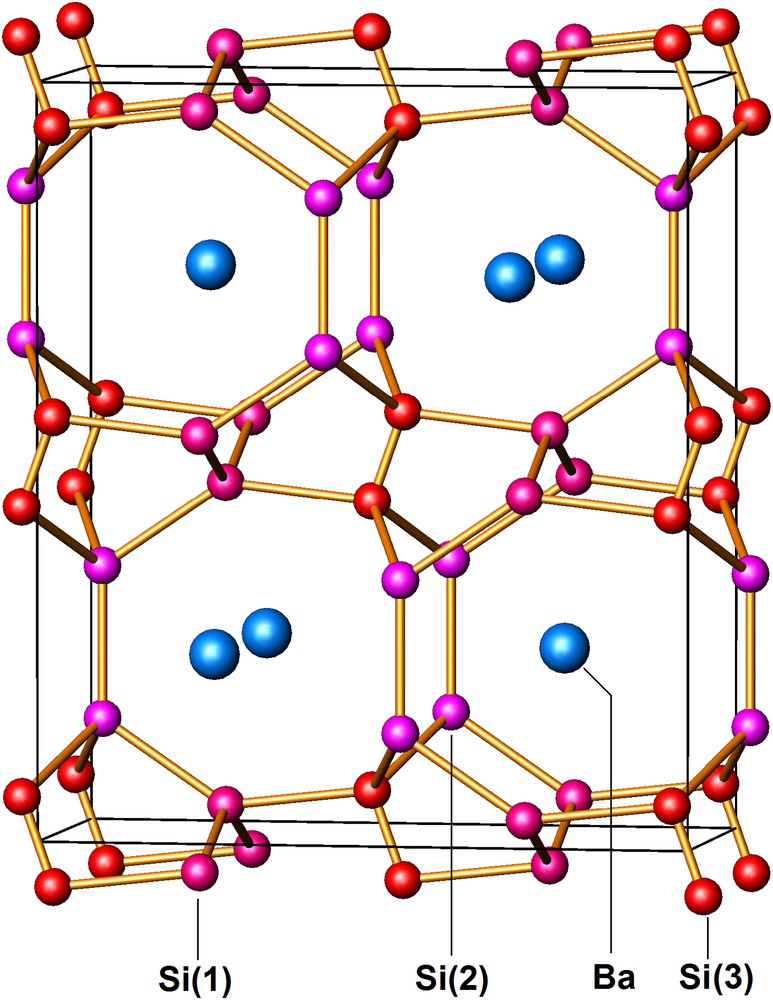
Structure de BaSi6 vue approximativement selon [010] et reproduite à partir des données de Yamanaka et Maekawa [167]. Les atomes de silicium occupent les positions cristallographiques 8f (0,y,z) du groupe Cmcm, avec trois valeurs différentes de y et z. Les atomes de baryum sont localisés dans les sites 4c.
Sous une pression de 3 GPa à 800 °C, Toulemonde et al. [171] et San Miguel et Toulemonde [172] sont parvenus à substituer partiellement le calcium et le strontium au baryum dans la phase Ba8Si46 pour former CaxBa8−xSi46 (0 ≤ x ≤ 4) et SrxBa8−xSi46, (0 ≤ x ≤ 6). La température critique supraconductrice diminue fortement avec x en raison d'une plus faible densité d'états au niveau de Fermi résultant d'une hybridation moins importante des orbitales d du calcium et du strontium avec les états anti-liants du réseau de silicium par rapport au baryum.
Par action de l'iode sur le silicium, le composé I8Si46−xIx (x ∼ 2), isotype de I8Ge46−xIx (x = 8/3) obtenu par décomposition thermique de GeI2 à pression ambiante, a été synthétisé sous une pression de 5 GPa à une température de 750 °C pendant un temps de réaction d'une heure par Reny et al. [173]. Les deux atomes d'iode en position de substitution dans le réseau d'accueil (a = 1041,94 pm) occupent 11% des sites Si(2), à la différence de la phase au germanium dans laquelle les atomes d'iode substitutionnels sont localisés dans les sites Si(1) du réseau d'accueil.
Alors qu'aucune phase de type clathrate n'a été obtenue par réaction du tellure sur le silicium dans des conditions ambiantes, l'utilisation de hautes pressions dans un équipement de type belt a permis à Jaussaud et al. [165,174,175] d'isoler deux nouveaux clathrates. Le premier a été obtenu dans des conditions de pression voisines de 5 GPa, une température de 800 °C, un temps de réaction de 30 minutes et pour un rapport Te/Si de ∼0,5, nettement supérieur à 0,174 (8/46). Le spectre de diffraction X de la nouvelle phase ainsi obtenue présente de nombreuses similitudes avec celui d'un clathrate de type I avec a0 = 1052 pm, mais la présence d'autres raies de faible intensité indique une structure plus compliquée ou l'existence d'une seconde phase. Une étude par diffraction électronique à permis de déterminer que le paramètre cristallin a est en fait de 2123,62 pm (soit ∼2 × a0) et le groupe d'espace Fd-3c au lieu de Pm-3n. La structure de ce nouveau clathrate, résolue par la méthode de Rietveld (Fig. 14) est nettement différente de celle d'un type I et fait apparaitre une sorte de « double clathration ». Une partie des atomes de tellure (Te(1) en 16a) se situe au centre de dodécaèdres isolés de silicium qui se trouvent eux-mêmes enfermés dans un réseau de cages connectées de type sodalite en forme d'octaèdres tronqués constitué des atomes de tellure Te(2) en 96 g. A une telle architecture cristalline correspond la formule idéale (Te7Si20)16 avec un rapport Te/Si de 0,35, soit presque exactement le double que dans une structure de type I (0,174). En fait, malgré les différences de structure de ce nouveau clathrate avec celle d'un type I, il existe entre elles une filiation structurale indiquée dans le Tableau 4 (1ère et 2ème colonnes). L'analyse chimique et structurale fine montrent en fait qu'il y a un excès d'atomes de tellure, conduisant à la formulation (Te7+xSi20−x)16 avec x ∼ 2,5 et un rapport Te/Si de 0,54, en accord avec les proportions optimales de réactifs observées lors des synthèses.

Structure du clathrate Te7Si20 obtenu sous haute pression, vue selon [100], montrant la double « clathration » des atomes de tellure Te(1) au centre des dodécaèdres pentagonaux (en rouge) eux-mêmes enfermés dans le réseau de type sodalite des atomes de tellure Te(2).
Positions atomiques occupées dans un clathrate de type I et dans les clathrates (Te7Si20)16 et Te8(Si38Te8) de haute et basse températures.
| Na8Si46 Type I | (Te7Si20)16 | Te8(Si38Te8) h.t. | Te8(Si38Te8) b.t. R3c (161)° |
| Pm-3n (223) | Fd-3c (228) | P-43n (218) | a = b = c = 1046,5 pm |
| a0 = 1019 pm | a = 2113,8 pm | a = 1045,7 pm | α = β = γ = 89,88 |
| Na(1) en 2a | Te(1) en 16a | Te(1) en 2a | Te(1) en 6a |
| Na(2) en 6d | Te(2) en 96 g | Te(2) en 6c | Te(2)en 18b |
| Si(1) en 6c | Si(1) en 6d | Si(1) en 18b | |
| Si(2) en 16i | Si(21) en 64e | Te(3) en 8e | Te(31) en 6a |
| Te(32) en 18b | |||
| Si(22) en 64e | Si(2) en 8e | Si(21) en 6a | |
| Si(22) en 18b | |||
| Si(3) en 24 k | Si(1) en 192 h | 2/3 × Si(31) en 24i | Si(31) en 18b |
| Si(32) en 18b | |||
| 1/3 × Si(32) en 24i | Si(33) en 18b | ||
| Si(34) en 18b |
Le second clathrate de silicium dopé au tellure a été synthétisé sous une pression de 5 GPa à 1200 °C avec un temps de réaction de 60 mn. Sa structure déterminée par diffraction des rayons X sur monocristal dérive également du type I et comporte une variété de haute température cubique (groupe d'espace P-43n) faiblement distordue par rapport au type I idéal et une variété de basse température rhomboédrique (groupe d'espace R3c) plus déformée. La formulation correspondante, Te16Si38 (soit Te8(Si38Te8)), implique un rapport Te/Si de 0,42. Huit atomes de tellure se substituent au silicium dans les seize sites dérivant de Si(2) dans la structure idéale, qui se subdivisent alors dans la structure cubique et rhomboédrique en deux et quatre sites, respectivement (Tableau 4 – 1ère, 3ème et 4ème colonnes). L'équilibre des charges implique la distribution suivante: (Te2−)16[(Si−1)32 (Si06)]. A la petite différence près de la division des sites Si(3) en Si(31) et Si(32), la structure de la variété cubique de Te16Si38Te8 est identique à celle de la série des clathrates A8Ge38X8 (A = Cl, Br, I; X = P, As, Sb) étudiée par Menke et von Schnering [56].
Sans qu'il soit nécessaire de recourir à des hautes pressions, des clathrates mixtes de types I comportant du tellure en position d'insertion dans les cages ou de substitution dans le réseau d'accueil ont été récemment synthétisés. Il s'agit de Te8Si46−xPx avec 11 < x < 17, semi conducteur avec ΔE = 0,8 eV et I8Ge40Te5,3, semi conducteur de type p avec ΔE = 1,24 eV, illustrant les deux possibilités pour le tellure de se comporter soit comme un atome hôte, soit comme un élément de substitution dans le réseau d'accueil [176,177].
4.10 Comportement des clathrates sous hautes pressions
L'évolution de la structure des clathrates en fonction de la pression a été largement utilisée pour mieux interpréter leurs propriétés, évaluer leur stabilité et mettre en évidence les possibles transitions de phases. Ces travaux impliquent en particulier des études structurales, mais aussi d'autres méthodes de caractérisation telles que la diffusion Raman qui a été précédemment évoquée au paragraphe 4.6. Des cellules à enclumes de diamant, capables d'atteindre des pressions de plusieurs dizaines de GPa, à basse et haute température, constituent les équipements les plus appropriés dans ce but.
La première étude antérieurement réalisée par Bundy et Kasper [55] à l'aide d'une presse de type belt (paragraphe 2.6) avait montré que malgré son apparente fragilité, le clathrate NaxSi136 (x = 3 et 11) était étonnamment stable vis-à-vis de la pression jusqu'à ∼10 et 15 GPa, respectivement, c'est-à-dire à une pression proche de celle correspondant à la transition du silicium de type diamant en la forme étain β plus compacte (Fig. 15). Beaucoup plus récemment, San Miguel et al. [178] ont repris l'étude de l'influence de la pression sur la structure des clathrates NaxSi136 avec x ∼ 1 par diffraction des rayons X in situ à l'aide d'une cellule à enclume de diamant en utilisant le rayonnement synchrotron comme source de rayons X. En accord avec les résultats de Bundy et Kasper, aucune transition structurale n'est observée pour le clathrate Na1Si136 jusqu'à 11 GPa, pression à laquelle il se transforme directement en une phase de type étain β, sans passer par la formation intermédiaire d'une structure de type diamant, probablement en raison de la barrière d'énergie résultant du passage de deux tétraèdres consécutifs d'une configuration éclipsée à une configuration décalée (la transition diamant → étain β du silicium se situe à 11,5 GPa). La variation de volume consécutive à la transition structurale du clathtrate est de 33%, ce qui est une valeur exceptionnellement élevée (Fig. 16). Entre la pression ambiante et 11 GPa, la compressibilité du clathrate s'avère pratiquement équivalente à celle du silicium diamant. A partir de l'évolution du volume atomique et sur la base d'une équation d'état de Murnaghan, une valeur du module de compression B0 de 90 ± 5 GPa a été obtenue en fixant la dérivée B'0 à 3,6. La valeur obtenue pour le silicium diamant étant B0 = 97,688 GPa avec B'0 = 4,24, le module de compression du clathrate n'est inférieur que de 8% environ à celui du silicium de type diamant. Des résultats très comparables ont été obtenus par Ramachandran et al. [179] pour le clathrate vide Si136. La valeur de B0 déterminée à partir des données expérimentales sur la base d'une équation d'état de Birch-Murnaghan en attribuant à B'0 la valeur 4 est de 90,3 GPa, en bon accord avec les valeurs calculées par la méthode DFT–LDA, sauf pour la pression de transition qui est prévue à 3,5 GPa mais expérimentalement observée dans l'intervalle compris entre 8 et 12 GPa.
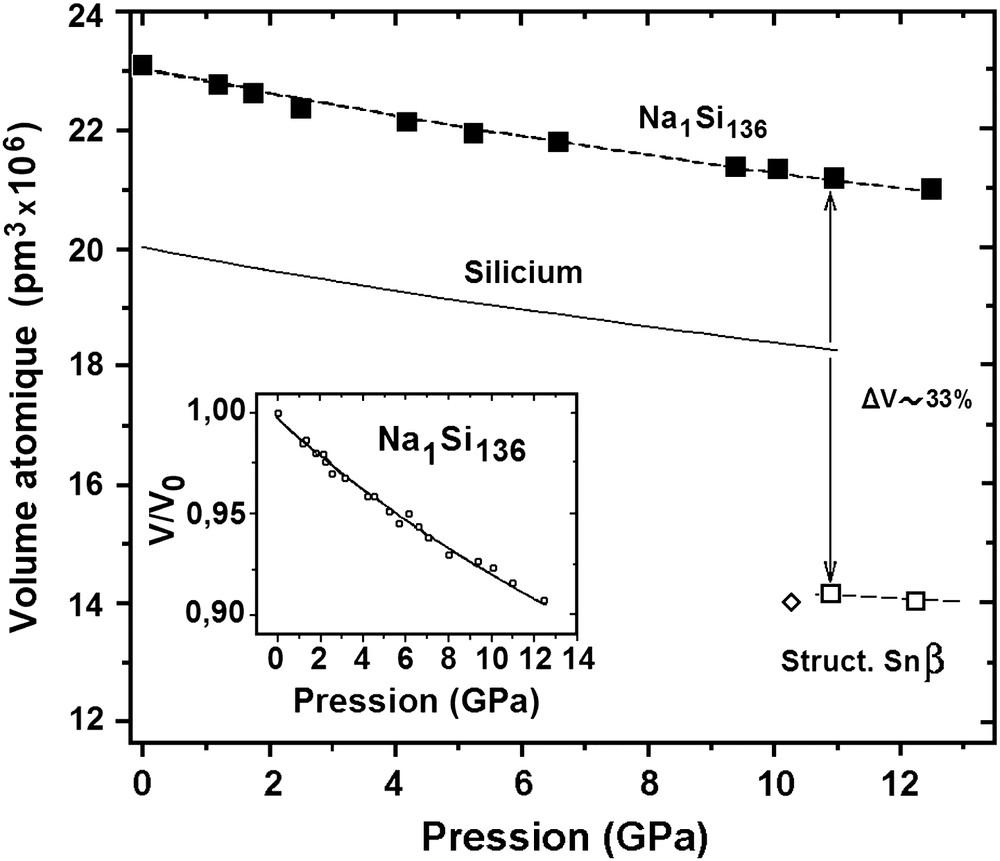
Evolution en fonction de la pression du volume atomique de Na1Si136 selon San Miguel et al. [178]. Les carrés pleins représentent les points expérimentaux et la courbe en pointillés les valeurs calculés à partir d'une équation d'état de type Murnaghan avec B0 = 90 et B0′ = 3,6. Les carrés vides correspondent à la structure de type étain β obtenue après la transition structurale consécutive à une variation de volume ΔV de 33%. La courbe en trait plein est relative au silicium de type diamant (B0 = 97,88 et B0′ = 4,24), dont le volume atomique de la forme étain β est indiqué par un losange vide. L'évolution du volume réduit V/V0 en fonction de la pression de Na1Si136 est représentée en encart.
Pour le clathrate de type I, Na8Si46, une transition du premier ordre est observée à 13 ± 2 GPa avec formation d'une structure de symétrie hexagonale simple correspondant à la seconde variété haute pression du silicium diamant [172]. Les autres clathrates de type I, K8Si46 [180], Ba8Si46 [181,182], I8Si46−xIx [182] et Rb6Si46 [183], qui comportent tous des atomes hôtes plus volumineux que le sodium, ont conduit à des comportements différents du précédent, qui ont été analysés en détail par San Miguel et Toulemonde [172]. Les structures concernées se compriment normalement jusqu'à une pression comprise entre 13 (Ba8Si46) et 35 GPa (I8Si46−xIx), où une transition du second ordre, sans changement de structure, est observée. Au-delà de cette pression, les structures s'avèrent plus compressibles et deviennent finalement irréversiblement amorphes à des pressions plus élevées, variables entre 32 (K8Si46) et 47 GPa (I8Si46−xIx). L'étude de l'évolution avec la pression de la distance interatomique moyenne Si–Si montre que la transition du second ordre se produit lorsque la distance concernée devient inférieure à une valeur critique de 230 pm. Ces résultats, obtenus par diffraction des rayons X, ont été corroborés par ceux issus des spectres de diffusion Raman sous haute pression évoqués au paragraphe 4.6 [146].
Les modules de compression B0 déterminés à partir des données expérimentales pour les clathrates concernés sont tous proches de celui du silicium de type diamant et même très proches pour les phases dopés au baryum et à l'iode (respectivement 93 ± 5 et 95 ± 5 GPa, au-lieu de 97,88 GPa) [182,184]. D'une manière générale, il apparait que l'insertion d'atomes hôtes de taille optimale dans les cages disponibles d'un clathrate vide ne diminue que faiblement sa compressibilité, mais sans la rendre cependant comparable à celle du silicium diamant. Par contre cette insertion permet d'accroitre considérablement le domaine de stabilité du clathrate sous pression (par un facteur 3 dans le cas de l'iode).
L'extrapolation au cas du carbone des conclusions ci-dessus, selon lesquelles une structure de type clathrate convenablement dopée est aussi peu compressible qu'une structure de type diamant, revêt une importance considérable. Ces structures à cages de carbone pourraient ainsi se classer parmi les matériaux ultra-durs, avec une dureté intermédiaire entre celles du nitrure de bore et du diamant (cf. paragraphe 4.5).
4.11 Sur l'existence et la synthèse de clathrates vides
Alors que de très nombreux clathrates dopés par divers atomes hôtes ont été synthétisés, seuls deux clathrates vides, Si136 et Ge136, ont été jusqu'ici obtenus. La possibilité d'obtenir la phase X24Si136 par traitement thermique sous vide de NaxSi136 a été envisagée depuis nos premiers travaux, mais l'extraction des ultimes traces de sodium semblait difficile en raison de la formation concurrentielle de silicium de type diamant. Cette méthode de synthèse a été a nouveau considérée et menée à son terme.
Par une série de traitements thermiques entre 350 et 375 °C sous vide (10−5 Torr) et purification par centrifugation dans un mélange de dibromométhane et de méthanol, Gryko et al. [35] ont obtenu un clathrate Si136 avec une teneur en sodium résiduel inférieure à 600 ppm et un faible pourcentage de silicium de type diamant. Le spectre de résonance magnétique nucléaire du 29Si, évoqué au paragraphe 4.8, comporte des raies fines et faiblement déplacées. La variation thermique de la conductivité fait apparaitre un comportement semi conducteur avec deux régimes de conductivité sur poudres compactées, l'un à basse température au dessous de 454 K avec une énergie d'activation de ∼1,2 eV et l'autre à haute température avec une énergie d'activation de ∼2 eV. Cette dernière valeur, conforme aux prévisions des calculs pour un semi conducteur à large bande (cf. paragraphe 4.4), est corroborée par des mesures optiques (1,9 eV). La conductivité thermique a été étudiée par Nolas et al. [185] ainsi que par Tang et al. [186] qui ont également réexaminé théoriquement et expérimentalement le spectre de diffusion Raman et les propriétés thermodynamiques de ce clathrate pratiquement exempt d'atomes hôtes. Ammar et al. [34] ont utilisé une méthode de préparation un peu différente, combinant des traitements sous vide (10−5 Pa) et l'action de faibles quantités d'iode pour extraire le maximum d'atomes de sodium. La teneur résiduelle finale en alcalin déterminée quantitativement à partir des spectres de RPE (cf. paragraphe 4.8) est de 35 ppm seulement -soit sensiblement vingt fois plus faible que dans les échantillons de Gryko et al. – et le silicium diamant n'est qu'en très faibles traces. Cette méthode permet d'obtenir des échantillons ayant un degré de pureté satisfaisant mais le nombre élevé de traitements rend la préparation très longue et occasionne des pertes de matière conduisant à des quantités finales de l'ordre de 100 mg. Par ailleurs, une étude par microscopie électronique à haute résolution de NaxSi136 traité sous vide montre la présence de nombreuses macles et défauts d'empilement qui ne sont pas observés dans le cas du clathrate Na8Si46 dont l'écart à la stœchiométrie n'a jamais été mis en évidence, même après un long traitement sous vide [187]. Dans ces conditions, l'utilisation en tant que matériau électronique ou optoélectronique du clathrate vide Si136 - ou de Si46 - ou implique la mise en œuvre de méthodes de synthèse directe, soit sous forme de couches minces ou de monocristaux.
Des essais ont été réalisés en ce sens, basées ou non sur des études théoriques ou des simulations. Sans chercher en fait à élaborer une structure de type clathrate, Kamalakaram et al. [188] ont obtenu par évaporation thermique du silicium sous une pression de 100 Torr d'hélium des nanoparticules en forme de fils et de tubules, ainsi que quelques microcristaux d'une nouvelle phase cubique à faces centrées ayant un paramètre de maille de 1425 pm et une structure constituée de clusters Si28. Cette étonnante coïncidence avec le clathrate Si136, dont ils semblent ignorer l'existence, n'a pas été relevée par les auteurs concernés qui n'ont pas donné suite à cette intéressante expérience. En combinant les données expérimentales connues avec les calculs théoriques qui prévoient que la phase Si136 devient plus stable que la variété diamant au-dessous de −3 GPa, McMillan [189] a proposé un diagramme de phases hypothétique faisant intervenir des pressions positives et négatives. Ce diagramme fait apparaitre que la phase Si136 pourrait être en équilibre avec la vapeur à des pressions fortement négatives, le problème étant alors de trouver une méthode permettant d'obtenir un dépôt de la phase concernée à l'état métastable. Cette étude a été complétée par des calculs de simulation par dynamique moléculaire pour des pressions comprises entre −3 et −12 GPa par Wilson et McMillan [190] Dans leur étude théorique sur les semi conducteurs Si34−xGex, Morigushi et al. [191] ont envisagé une méthode possible de synthèse des clathrates vides par croissance épitaxiale en présence d'un germe qui pourrait être un clathrate dopé comme Ba8Si46, dans la mesure où le paramètre de maille n'est que très peu affecté par la présence d'atomes hôtes. A l'aide de simulations de dynamique moléculaire, Munetoh et al. [192] ont modélisé le processus de croissance épitaxiale des clathrates Si46 et Si136 à partir de germes cristallisés et de silicium amorphe. Dans le cas de Si46, une transformation en Si136 est observée dans la direction [001] où les deux structures présentent une grande similitude, indiquant une plus grande stabilité de cette dernière phase. Les auteurs concluent que la méthode de croissance par épitaxie en phase solide dérivée de celle utilisée pour le silicium amorphe devrait permettre d'obtenir Si136 sous forme de couche mince. Miranda et Antonelli [193] ont récemment réétudié les propriétés thermodynamiques des clathrates vides Si34 et Si46 par la méthode Monte Carlo et les ont comparées à celles du silicium de type diamant, du silicium amorphe et du silicium à l'état liquide. Les calculs d'enthalpie libre en fonction de la température montrent que le clathrate de type II est plus stable que le clathrate de type I et qu'ils sont tous deux plus stables que la variété amorphe du silicium, quelle que soit la température. Leur point de fusion respectif est de 1522 ± 25 K et 1482 ± 25 K. En accord avec les auteurs précédents, il apparait que les clathrates vides devraient pouvoir être obtenus par épitaxie en phase liquide à partir d'un germe dopé ou par épitaxie en phase solide à partir du silicium amorphe. La transformation de Si46 en Si136 lors de sa croissance pourrait être évitée en abaissant la température.
Récemment, une méthode prometteuse et entièrement nouvelle de synthèse a été mise à profit par Guloy et al. [194] pour préparer le clathrate Ge136, qui consiste en une oxydation contrôlée de l'anion Ge94− en Ge0 suivie d'une polymérisation par un liquide ionique tel qu'un mélange eutectique de chlorure de dodécyltriméthylammonium (DTAC) et de trichlorure d'aluminium à 300 °C. Le produit obtenu sous forme de poudre est caractérisé par un paramètre de maille de 1521,15 pm. Il contient un faible taux de germanium de type diamant et d'une phase amorphe dont la présence se manifeste par un fond continu significatif. L'analyse du spectre de diffraction des rayons X par la méthode de Rietveld indique que les deux sortes de cages sont vides d'atomes hôtes. La susceptibilité magnétique est pratiquement indépendante de la température et la résistivité électrique compatible avec un comportement semi conducteur, sans qu'il soit possible de déterminer de manière précise l'énergie d'activation correspondante. A partir de mesures optiques, un gap direct de 0,6 eV a été déterminé. Le clathrate vide Ge136 constitue une nouvelle variété allotropique du germanium pouvant être préparée en quantité importante dans des conditions expérimentales relativement aisées [195]. La transposition de cette méthode au cas du silicium apparait comme particulièrement intéressante.
Le comportement sous pression jusqu'à 21,5 GPa de X24Ge136 a été récemment étudié par Schwarz et al. [196]. Entre l'ambiante et 12,7 GPa, pression au dessus de laquelle il ne subsiste plus qu'une phase de type étain β, des transitions sont observées à pression montante et descendante. Une phase nouvelle, Ge(hR8), a été identifiée et étudiée, dont la structure rhomboédrique est isotype de celle de Si(hR8). La formation de germanium de structure diamant n'a jamais été observée.
4.12 Sur l'existence de clathrates de type III pour les éléments de la colonne 14
La structure d'un clathrate de type III a été brièvement évoquée au paragraphe 2.2 [21]. Elle est très caractéristique d'une série d'hydrates à réseaux hôtes complexes constitués de sels d'ammonium quaternaire comme n-(C4H9)4N+, iso-(C5H11)4N+, etc., combinés à des anions tels que F−, OH−, CrO42−, WO42−, etc., qui participent partiellement au réseau d'accueil. Elle a été attribuée à l'hydrate de brome (Br2)20X10(H2O)172 ou d'oxyde de diméthyle (CH3)2O par Allen et Geffrey et Bonamico et al. [197] et jusqu'à un récent passé n'avait jamais été observée parmi les clathrates des éléments de la colonne 14. L'existence d'une telle structure a été prouvée en 2001 par Bobev et Sevov [198] dans une phase à très étroit domaine d'existence de formule M30(Na(1,33x−10)Sn172−x), où M est le césium ou un mélange Rb + Cs et x une valeur proche de 9,6. De plus, dans un très récent article, Zaikina et al. ont reporté l'existence d'un clathrate de type III à réseau de silicium de formule Tey(PxSi172−x) avec x = 2y et y > 20 [199].
La maille élémentaire d'un clathrate de type III est de symétrie quadratique (c/a ∼ 1,52) et le groupe d'espace correspondant P42 /mnm (no. 136). Le réseau d'accueil est formé par la juxtaposition de trois sortes de polyèdres au lieu de deux comme dans les clathrates de types I et II: dix dodécaèdres pentagonaux, seize polyèdres à 14 faces et quatre polyèdres à 15 faces – où pentacaïdécaèdres – possédant 3 faces hexagonales et un rayon libre intermédiaire entre ceux d'un polyèdre à 14 et 16 faces (Fig. 17). Le nombre de sites disponibles pour les atomes hôtes est de 30 et celui du total des atomes du réseau d'accueil de 172, répartis en 17 sites cristallographiques, ce qui correspond à un rapport 30/172 = 1/5,73 qui est du même ordre de grandeur que pour les clathrates de type I (46/8 = 1/5,75) et II (136/24 = 1/5,67). Dans les structures à réseau d'étain de Bobev et Sevov, les 30 sites disponibles du réseau hôte sont occupées par les volumineux atomes de césium et de rubidium et quelques atomes de sodium (∼3) sont en position de substitution dans le réseau d'étain faiblement lacunaire, soit Cs30(Na3Sn162). Selon les auteurs, ces lacunes sont dues à l'absence de paires Sn-Sn qui induisent la formation de charges négatives (six par paire manquante) compensées par l'apport des charges positives provenant des atomes alcalins ionisés. La structure concernée correspond ainsi à une phase de Zintl diamagnétique. La présence des quelques atomes de sodium en position de substitution semble être une condition nécessaire pour stabiliser cette structure. Dans le clathrate Tey(PxSi172−x), le réseau d'accueil est stœchiométrique et c'est au contraire le réseau hôte qui est lacunaire. Cette situation découle du fait que le clathrate concerné correspond également à une phase de Zintl: les atomes de phosphore apportent au réseau d'accueil x charges positives qui sont compensées par x/2 = y charges négatives provenant des atomes de tellure ionisés Te2− du réseau hôte lacunaire (30-y): (Te2−)y(P+xSi0172−x). La valeur déterminée par analyse des données cristallographiques, y = 21, implique la présence de 9 lacunes qui sont toutes localisées dans les 10 dodécaèdres pentagonaux. Une telle distribution est pratiquement analogue à celle qui existe pour l'hydrate de brome, (Br2)20(H2O)172, dans lequel les lacunes dodécaédriques sont totalement vides. Le clathrate Tey(PxSi172−x) est un semi conducteur à très faible énergie d'activation (0,02 eV) qui se caractérise par une haute température de décomposition pour un clathrate: 1510 K.

Le polyèdre à 15 faces caractéristique des clathrates de type III (a) et (b) structure d'un clathrate M10M′16M″4X172 où M, M′ et M″ représentent les espèces hôtes et X les atomes du réseau d'accueil, vue selon [001]. Huit des seize tétracaïdécaèdres accolés par leurs faces hexagonales et centrés sur les atomes M′(1) forment des files qui se développent selon [001]. Chacun des huit autres tétracaïdécaèdres, centré sur un atome M′(2), a ses deux faces hexagonales parallèles à [001] et met en commun une de ces faces avec un homologue et l'autre avec un pentacaïdécaèdre. Les quatre pentacaïdécaèdres, centrés sur les atomes M″, ont leurs trois faces pentagonales également orientées parallèlement à [001], dont une est commune à un homologue et les deux autres avec un tétracaïdécaèdre. L'espace résiduel est complété par les dix dodécaèdres, centrés sur les 2 atomes M(1) et les 8 atomes M(2), groupés en deux blocs de cinq. Pour plus de clarté, les pentacaïdécaèdres sont ombrés en rose.
4.13 Les clathtrates en tant que matériaux thermoélectriques
L'étude et la mise au point de matériaux thermoélectriques capables de transformer l'énergie thermique en énergie électrique (générateur électrique) et vice versa (dispositifs de chauffage et de réfrigération) constituent une activité de recherche récurrente depuis de nombreuses décennies [200,201]. L'enjeu est d'autant plus important à l'heure actuelle que leur principe de fonctionnement présente beaucoup d'avantages:
- - ils produisent une énergie électrique – ou une chaleur – « propre » car non polluante et ne nécessitant pas de pièces mécaniques mobiles engendrant des frottements et des vibrations (moteurs et compresseurs);
- - ils sont autonomes et parfaitement adaptés à l'alimentation et au chauffage – ou au refroidissement – de petits équipements ou unités de faible puissance comme les ordinateurs, les composants électroniques ou optoélectroniques (détecteurs infra rouge, diodes lasers, processeurs CMOS, etc.).
Les performances d'un matériau thermoélectrique s'expriment essentiellement par la valeur de sa « figure de mérite », ZT = α2σT/κ, expression sans unité dans laquelle α est le coefficient de Seebeck, σ la conductivité électrique et κ la conductivité thermique qui est la somme de deux contributions, celle du réseau κL et des électrons κE. Un matériau sera d'autant plus performant que la valeur de ZT sera plus élevée, ce qui implique d'optimiser le produit α2σT et de minimiser κ au travers de la diminution de la contribution du réseau à la conductivité thermique. Les meilleurs compromis entre ces trois variables, qui ne sont pas indépendantes (κE est relié à σ par la relation de Wiedemann–Franz, κE = L0σT, où L0 est le nombre de Lorentz ((π2/3)×(kB/e)2 = 2,45 × 10−8 V2 K−2) sont obtenus avec des semi conducteurs ou des semi métaux pour lesquels des valeurs ZT sont voisines de 1. Ces performances ne sont actuellement pas suffisantes pour que les systèmes basés sur de tels matériaux puissent supplanter les générateurs et réfrigérateurs classiques sauf pour des applications bien spécifiques ci-dessus évoquées, mais toute amélioration de ZT les rendrait plus compétitifs et étendrait considérablement leurs domaines d'applications.
En 1995, Slack [202] avait développé le concept de PGEC (phonon-glass and electron crystal) pour déterminer les critères requis pour sélectionner les meilleurs matériaux thermoélectriques. Ces derniers doivent combiner le comportement électronique d'un conducteur à l'état cristallin et d'une phase amorphe ou vitreuse du point de vue de la contribution du réseau à la conductivité thermique. Ces matériaux doivent correspondre à des semi conducteurs à bande étroite (ΔE ∼ 0,25 eV) avec une importante mobilité des porteurs (μ ∼ 2000 cm2 (V s)−1), favorisée par la présence dans la structure d'atomes lourds tels que Ge, Sn, Se, Te, Bi. La contribution de la conductivité thermique du réseau, κL ≈ vsCLph (vs = vitesse du son, C = chaleur spécifique et Lph = libre parcours moyen des phonons), est minimale lorsque Lph est égal à la distance entre les atomes du réseau. L'expression de la conductivité thermique κE combinée à la définition de ZT conduit à la relation ZT = α2/L0 impliquant une valeur minimale α = L01/2 = 157 μV K−1 pour ZT = 1 et 222 μV K−1 pour ZT = 2 [200]. De leur côté, Dong et Rowe [203] ont établi une relation permettant de calculer la valeur maximale de ZT en fonction de T dans l'hypothèse où κL = 0,25 W/mK pour les thermoélectriques conventionnels BiSb, Bi2Te3, PbTe, SiGe: ZT ∼ 2 à 300 K et ∼3 à 600 K.
Selon Slack, un matériau thermoélectrique idéal doit être constitué d'au moins trois élements, dont deux forment un réseau bien cristallisé, alors que le troisième occupe des sites au sein desquels il se comporte comme un atome « vibrateur » (rattling atom en anglo-saxon) créant un désordre local qui inhibe la propagation des vibrations du réseau. Un tel raisonnement a été appliqué avec succès au cas des structures de type skutterudite AB3, soit X2A8B24, dont les lacunes sont occupées par des ions lourds de petite taille comme Ln3+ (Ln = La, Ce, Nd, Sm) [200].
Depuis une dizaine d'années, les structures de type clathrate sont venues s'ajouter aux quelques familles de matériaux thermoélectriques les plus performants, car elles comportent également des réseaux à cages renfermant des atomes faiblement liés au réseau et vibrant à faibles fréquences. Selon Nolas et Slack [200], Nolas et al. [204,205], la caractéristique la plus marquante des clathrates, comme par exemple Sr8Ga16Ge30, est que la conductivité thermique κ et sa variation avec T sont comparables à celles de matériaux tels que la silice vitreuse ou le germanium amorphe. La conductivité thermique et les performances en tant que matériaux thermoélectriques de type n ou p de nombreux clathrates ont été étudiées [93,206–208]. Les valeurs de ZT observées sont dans la majorité des cas encore inférieures à 1, mais les structures concernées se prêtent à des modifications de composition et de propriétés qui n'ont pas toutes été explorées jusqu'ici et qui permettent d'espérer de notables améliorations. Nolas et al. [204] ont obtenu ZT ≈ 0,25 à 300 K et l'extrapolation de leurs résultats permet d'envisager que ZT dépasse 1 au-dessus de 700 K pour Sr8Ga16Ge30. Une étude théorique de Blake et al. [206] a permis de mettre en évidence dans ce même clathrate un faible transfert de charges entre les atomes de strontium et le réseau, à la différence de ce qui est observé pour Ba8Ga16Ge30. Les performances respectives des clathrates Sr8Ga16Ge30, et Eu8Ga16Ge30 ont été analysées par Sales et al. [93]. A partir des spectres de diffraction des neutrons, les densités de charges nucléaires ont été déterminées au voisinage du centre des cages tétracaïdécaédriques (positions atomiques 6d); elles font apparaitre des atomes de baryum parfaitement localisés au centre de leur cage, alors que ceux de strontium ont tendance à se décentrer avec une augmentation sensible des paramètres d'agitation thermique. Les atomes d'europium sont par contre nettement délocalisés sur quatre sites cristallographiques distants de 30 à 50 pm du centre de la cage. La variation en température de la conductivité thermique du réseau κL des clathrates de strontium et d'europium est analogue à celle d'un matériau amorphe et celle du clathrate de baryum est au contraire analogue à celle d'un solide à l'état cristallin, bien que possédant une faible conductivité (1,3 W/mK). Latturner et al. [207] ont déterminé la structure du clathrate de composition Ba8,05Ga17,31Sb2,15Ge25,9, dans lequel les atomes d'antimoine sont substitués au germanium dans les seuls sites 24 k et effectué des mesures de coefficient de Seebeck et de conductivité électrique. La valeur positive de α (100 μV K−1 à 40 K) implique un comportement de type p et la variation thermique de σ (224 S cm−1 à 273 k et 88 S cm−1 à 323 K) celui d'un semi métal. Kuznetsov et al. [208] ont effectué une étude comparative des propriétés de transport et des performances thermoélectriques des clathrates Ba8Ga16Si30, Ba8Ga16Ge30, Ba8Ga16Sn30 et Sr8Ga16Ge30 Les valeurs maximales estimées de ZT sont de 0,7 à 700 K pour Ba8Ga16Ge30 et 0,87 à 870 K pour Ba8Ga16Si30, respectivement.
Plusieurs articles de revue récents sur les clathrates en tant que matériaux thermoélectroniques ont été publiés par des spécialistes du sujet concerné, que le lecteur est invité à consulter pour de plus amples informations [209].
5 Conclusions et perspectives
Cet article montre que les structures clathrates du silicium et des autres éléments de la colonne 14, qui ne constituaient à l'origine qu'une simple curiosité cristallographique, sont devenues au cours des quinze dernières années un sujet de recherche majeur en raison de leurs diverses et intéressantes propriétés physiques. Leurs étonnantes structures cristallines formées de tétraèdres arrangés en polyèdres plus complexes se comparent de manière satisfaisante à celles des hydrates de gaz, des clathrasils et des plus petites formes fullerènes du carbone, en raison de la présence de liaisons à caractère sp3. Leurs propriétés physiques qui varient depuis un comportement de type semi conducteur à large bande interdite à un conducteur métallique et même supraconducteur par la modification du nombre et de la nature des espèces chimiques occupant les cages, permettent d'envisager pour ces phases des applications comme nouveaux semi conducteurs à base de silicium utilisable en optoélectronique et comme nouveaux matériaux thermoélectriques. Si de nombreux objectifs restent encore à atteindre, comme l'obtention de Si46 ou Si136 sous forme de films ou de monocristaux, l'amélioration des performances des matériaux thermoélectriques et la découverte de matériaux ultra durs à base de clathrates de carbone, le sujet concerné continue à mobiliser l'activité de très nombreux expérimentateurs (synthèses, caractérisations) et théoriciens. La liste non exhaustive ci-jointe des références bibliographiques donne un aperçu de l'ampleur du travail réalisé depuis leur découverte il y a quarante trois ans [7–9].
Comme beaucoup d'autres, l'exemple des clathrates montre que l'avancement des connaissances scientifiques dans un domaine donné ne progresse pas de manière linéaire, voire régulière et conçue ou programmée à l'avance, mais procède le plus souvent par étapes successives en tirant souvent profit des progrès et découvertes effectués dans des thématiques apparemment différentes. Sans la découverte des structures à cages des fullerènes du carbone et des propriétés supraconductrices de ses composés d'intercalation avec les métaux alcalins, les clathrates n'auraient pas attiré autant l'attention des chercheurs par leurs intéressantes propriétés structurales et physiques. De même, si des objectifs prévus d'un programme de recherche ne sont pas toujours atteints, il arrive souvent que des résultats expérimentaux inattendus conduisent à d'importantes avancées.
L'exemple des clathrates illustre parfaitement la nécessité d'une mise en commun de compétences et de points de vue de spécialistes issus de disciplines diverses pour parvenir à une meilleure compréhension de leurs propriétés de base et au delà de celles des matériaux qui en seront issus. A l'heure actuelle, il apparait que les prévisions basées sur des calculs et des modélisations commencent à précéder les découvertes expérimentales elles mêmes, et fédèrent l'essor des activités de recherche actuelles et futures.
Enfin, n'oublions pas les propos prémonitoires de John Kasper, récemment disparu, qui mettaient l'accent sur cette surprenante analogie entre clathrates moléculaires et phases d'alliages métalliques. Demain verra peut-être, comme nous l'avons évoqué au début de cette revue, une puissante industrie basée sur l'exploitation des hydrates de méthane si les contraintes techniques et de sécurité inhérentes à leur extraction off shore peuvent être maitrisées. D'ores et déjà des entreprises avancées ont envisagé et réalisé la production sur terre de tels hydrates pour le transport du méthane à moindre coût dans des conditions de température et de pression plus aisées qu'actuellement [23,210].
Remerciements
Les auteurs remercient vivement Paul Hagenmuller, Professeur honoraire à l'Université de Bordeaux 1 et Directeur honoraire du Laboratoire du CNRS, pour sa participation initiale au sujet concerné, l'aide qu'il leur a apportée et les conseils et encouragements qu'il leur a prodigués. Ils remercient également les chercheurs, enseignants chercheurs, ingénieurs et techniciens du laboratoire de physique de la matière condensée et nanostructures (LPMCN) et du laboratoire de physico-chimie des matériaux luminescents (LPCML) de l'Université de Lyon 1, ainsi que les équipes japonaises des Professeurs Yamanaka (Université d'Hiroshima), Tanigaki (Université de Tohoku), Nozue (Université d'Osaka) et Shimizu (Université de Gifu) pour leur très importante contribution au sujet concerné et leur fructueuse et amicale collaboration. Ils remercient enfin leurs élèves, stagiaires et collègues pour leur active participation aux recherches menées à l'Institut de chimie de la matière condensée de Bordeaux et dans les laboratoires qui l'ont précédé.


