1 Introduction
The light alkanes, C1C4, are present in the natural gas and are also formed during the oil processing. One of the major objectives of the future chemistry consists in the finding of suitable active and selective catalysts for oxidative dehydrogenation (ODH) of the light alkanes into the highly valuable olefins such as ethylene, propene and butenes. At present, the most studied catalysts concern the ODH of ethane [1] and propane [2,3] and are different oxides of
- – alkaline and alkaline earth (AE) elements: Li/X/MgO (X=Co, Sn, Cu Ti, Zr, Nb, Ce, B);
- – transitional metals: V2O5, V2O5/SiO2, V2O5/Al2O3, VMgO, V/α-Ti phosphate, MoVNbSb(Ca)O;
- – rare-earth elements: La2O3, CeO2, Sm2O3, Pr6O11 and so on;
- – perovskite type: La1–xSrxB1–yMyO3–δ (B=Co, Cr, Fe, Cu, Mn, Y) (M = Nb, Ti); and
- – supported noble metals: Pt/Al2O3.
From the literature data, it appears that the catalysts should contain redox elements to activate the alkanes and other elements to control the acid–base character of the surface for facilitating the fast desorption of the intermediate species.
In the 1980s, VMgO oxide was found to be rather active for ODH of propane. The basic character of the catalyst was suggested to favour the rapid desorption of the adsorbed olefin formed as intermediate from propane and, therefore, to avoid its further oxidation to oxygenates or COx. Unfortunately, the selectivity to propene was too low at high conversion to lead to commercialisation. The usual process of direct dehydrogenation of propane to propene on Pt-M/Al2O3 (M = Sn, Re, so on) or on chromium oxide–type catalysts remains the major industrial process at present, although it is quite endothermal and leads to coke formation and rapid deactivation of the catalyst, regenerated by burning off the coke to CO2.
It clearly appears that the most active and selective metal mixed oxide catalysts in heterogeneous catalysis are in fact mixtures of several oxide phases. In this connection, a series of samples of mixed rare-earth oxides, as neodymium oxides, with alkaline earth oxides (AEOs) was studied to elucidate the complex relationship among the composition, catalyst structure and defects and the catalytic performance. The catalyst samples (5 mol % AEO) were prepared by the coprecipitation procedure from an aqueous solution of neodymium nitrate and an acidic solution (1 M oxalic acid) of the nitrate of AE element [4,5]. Doping of neodymium oxide with AEO improves its selectivity in the reaction of oxidative coupling of methane (OCM). Among them, strontium-doped Nd2O3 sample has the best selectivity towards higher hydrocarbons [4].
Burrows et al. [6] studied structure/function relationships in Nd2O3-doped MgO catalysts for the OCM reaction. Compared with pure MgO, the Nd2O3/MgO catalyst exhibits significant improvements in methane conversion efficiency and selectivity to C2 hydrocarbons. The level of catalytic improvement was shown to be dependent on the Nd2O3 concentration and on the catalyst preparation method. The impregnation and coprecipitation routes (from nitrate, hydroxide and carbonate) have been used. The results strongly suggest that there is a certain neodymia morphology (or combination of morphologies) of the MgO, which is responsible for the increased catalytic activity and selectivity. The presence of a disordered and impure “glassy” neodymia phase is most effective in enhancing the OCM performance. The Nd2O3/MgO catalyst exhibiting the highest C2 selectivity of 71.5% so far was the ex-carbonate coprecipitated sample.
The equimolecular mixture MO–Nd2O3 (M = Be, Mg, Ca, Sr) prepared starting from the tartrate complexes of the metals has been investigated in the OCM reaction [7]. The authors established a quantitative relationship between the basic character of these catalysts and the active site in the OCM reaction. The order of catalytic activity for hydrocarbon production at 775 °C was the following: Ca > Mg ≈ Sr > Be.
Recently, new solid base mixed catalysts of CaONiO and CaONd2O3 obtained by the coprecipitation process showed remarkable activity in the synthesis of fatty acid methyl esters from crude Jatropha Curcas oil [8]. These catalysts have the highest basic character as compared with the pure oxides, mainly associated with Ca2+–O2− pairs on the surface, that favour transesterification reaction.
The demand for new catalytic materials has imposed the study of their preparation by non-traditional methods to obtain the features required for each process in which they are used. The sol–gel technique represents the ideal non-traditional method for the preparation of catalytic materials with very homogeneous compositions and special textures [9,10]. Because homogeneous mixing can be made at the molecular scale, the chemical reactivity of the oxide surface can be greatly enhanced; thus powders with high surface area and optimized pore size distribution can be obtained. However, many parameters are involved along the process: chemistry during hydrolysis and condensation of the precursors, physical chemistry of aggregation, gelation, drying and finally thermal processes to account the properties of the materials. Each step has to be optimized depending on the required application. Therefore, a real mastery of the sol–gel process would require an emphasis that relates chemical reactivity to gel formation and powder morphology.
The present study reports the obtaining and characterisation of sol–gel MO–Nd2O3 catalysts (M = Mg, Ca, Sr with a molar ratio MO/Nd2O3 = 95/5). A systematic study versus the type of precursor used for the determination of the most propitious synthesis conditions has been done. One had in view the structural evaluation and crystallization behaviour with thermal treatment by differential thermal analysis/thermogravimetric analysis (DTA/TGA), infrared (IR) spectroscopy and X-ray diffraction (XRD), correlating the obtained results. A detailed XRD analysis, based on a proper calculus program, has established the mixtures of crystalline polyphases and showed the presence of solid solutions with formation of Nd3+ agglomerates on the surface and the existence of the dispersed cation vacancies. The lattice constants, the average size of the crystallites, the average lattice strains and the mass of unit cell variation have been calculated. The program also allowed the calculus of the anisotropy factor, which can give the image of the structural disorder. Some catalytic activity measurements have established the potential of the prepared sol–gel mixed oxides to be used in the ODH process of light alkanes.
2 Experimental section
2.1 MO–Nd2O3 synthesis
The chemical compositions and experimental conditions for the preparation of oxide catalysts in the binary system MO–Nd2O3 (M = Mg, Ca, Sr) are presented in Table 1.
The chemical compositions and experimental conditions for preparation of samples in the binary systems MO–Nd2O3 (M = Mg, Ca, Sr).
| Sample | Reactants | Molar ratios of reactants | Reaction conditions | Time | Drying conditions | Thermal treatment | ||||||
| Precursors | Solvents | Catalyst (C) | MIIO/Nd2O3/S1∗/H2O/C | T [°C] | pH | Gelling [h] | T [°C] | t [days] | 3 h plateau [°C] | |||
| for MIIO (P1) | for Nd2O3 (P2) | for P1 (S1) | for P2 (S2) | |||||||||
| 1MgNd | Mg acetylacetonate (Mg(Acac)2) | Nd(NO3)3 6H2O | C2H5OH | H2O | NH3 | 1/0.05/296/59/19 | 40 | 7.5 | 72 | 80 | 3 | 650 |
| 2MgNd | Mg ethoxide (Mg(OEt)2) | Nd(NO3)3 6H2O | C2H5OH | H2O | NH3 | 1/0.05/29.6/14.7/2.2 | 80 + rt | 7.0 | 96 | 80 | 1 | 650 |
| 1CaNd | Ca acetate (Ca(CH3COO)2) | Nd(NO3)3 6H2O | CH3COOH + H2O | H2O | NH3 | 1/0.05/18/38/3.6 | 40 | 4.5 | 24 | 80 | 4 | 750 |
| 2CaNd | Ca acetate (Ca(CH3COO)2) | Nd(NO3)3 6H2O | Citric acid + H2O | H2O | NH3 | 1/0.05/0.10/90/1.6 | rt | 9.0 | 1.5 | 80 | 2 | 750 |
| 3CaNd | Ca methoxide (Ca(CH3O)2) | Nd(NO3)3 6H2O | C2H5OH | H2O | NH3 | 1/0.05/29.6/14.7/2.2 | 80 + rt | 7.5 | 72 | 80 | 1 | 750 |
| 4CaNd | Ca acetylacetonate (Ca(Acac)2) | Nd(NO3)3 6H2O | C2H5OH | H2O | NH3 | 1/0.05/296/18.4/4.8 | rt | 9.0 | 96 | 80 | 3 | 750 |
| 1SrNd | Sr acetate (Sr(CH3COO)2 | Nd(NO3)3 6H2O | CH3COOH + H2O | H2O | NH3 | 1/0.05/9.2/37.1/3.6 | 40 | 3.5 | 552 | 80 | 5 | 850 |
| 2SrNd | Sr acetate (Sr(CH3COO)2) | Nd(NO3)3 6H2O | Citric acid + H2O | H2O | NH3 | 1/0.05/0.10/86.6/0.80 | rt | 9.0 | 24 | 80 | 6 | 850 |
| 3SrNd | Sr acetylacetonate (Sr(Acac)2) | Nd(NO3)3 6H2O | C2H5OH | H2O | NH3 | 1/0.05/287/12.6/2.8 | rt | 9.0 | 72 | 80 | 3 | 850 |
A total of nine samples belonging to the MgONd2O3, CaONd2O3 and SrONd2O3 systems, respectively, have been prepared. Different precursors as AE metal oxide source (MO), various starting solution compositions expressed in various molar ratios between reactants and different synthesis parameters (pH, temperature and time of reaction) have been used.
Mg acetylacetonate (Mg(acac)2, 98%, Merck) for sample 1MgNd and Mg ethoxide (Mg(OEt)2, Fluka) for sample 2MgNd were used as magnesium precursors. Ca acetate (Ca(CH3COO)2) for samples 1CaNd and 2CaNd, Ca methoxide (Ca(CH3O)2, 97%, Aldrich) for sample 3CaNd and Ca acetylacetonate (Ca (Acac)2, >95%, Fluka) for sample 4CaNd were used as calcium precursors. Sr acetate (Sr(CH3COO)2) for samples 1SrNd and 2SrNd and Sr acetylacetonate (Sr(Acac)2, 97%, Aldrich) for sample 3SrNd were used as strontium precursors.
Neodymium (III) nitrate, Nd(NO3)3⋅6H2O (99.9% Alfa Aesar), as Nd2O3 source has been used for all samples. The solvents used were ethanol absolute (Merck) for the AE acetylacetonates and for Ca and Mg alkoxides. The acetic and citric acids were the solvents used for Ca and Sr acetate and the distilled water for the neodymium nitrate salt. The gelation process was accomplished under reflux in the temperature range between room temperature and 80 °C depending on the type of sample, the gelation time being 1.5 h–23 days. All of the obtained samples were dried at 80 °C and then were thermally treated according to the DTA/TGA results with a 3 h plateau at 650 °C for MgNd samples, at 750 °C for CaNd samples and at 850 °C for SrNd samples.
2.2 Characterization
2.2.1 Thermal analysis
The thermal behaviour was analysed by DTA/TGA with a Mettler Toledo Star System TGA/SDTA 851/LF 1600 °C DTA/TGA apparatus in air at a heating rate of 10 °C/min, for temperatures up to 1000 °C.
2.2.2 IR spectroscopy
It has been performed on a Carl Zeiss Jena Specord M−80 IR spectrophotometer with the KBr pellet technique.
2.2.3 XRD analysis
The analyses were performed using a conventional Shimadzu XRD 6000 diffractometer with Ni filter and Cu Kα radiation. For the identification of the crystalline phases, the following powder diffraction files were used: 45-0946 for MgO; 48-1467 for CaO; 48-1477 for SrO and 41-1089 for Nd2O3.
Estimated calculations of the mass density occupying the unit cell volume (UCV) were undertaken for all oxide phases MO (M = Mg, Ca, Sr) and Nd2O3 to give some qualitative considerations regarding the nature of defects, which represent some of the possible sources of lattice strains. The calculation formula used in this work was ρ[g cm−3] = N × M/V, in which N is the number of molecules in UCV (N = 4 for MO, M = Mg, Ca, Sr and N = 1 for Nd2O3), M is the atomic mass of the oxide phase and V is the volume of the unit cell determined from the lattice constant values calculated from XRD patterns.
As reference, the densities of the standard oxide phases (in Powder Diffraction File) were used, which are considered as control in the phase analysis. Their values were the following: ρ0 [g cm−3] = 3.585 (MgO), 3.346 (CaO), 5.010 (SrO) and 7.333 (Nd2O3).
To calculate the loss or gain in mass of the unit cell, the values of V0 volumes of the same crystalline oxide phases used in identification were taken into consideration. The used formula was ΔΜ = (ρ − ρ0) × (V − V0), in which V0 = 74.68 Å3 (MgO), 111.33 Å3 (CaO), 137.39 Å3 (SrO) and 76.19 Å3 (Nd2O3).
The calculation of the microstructural factors, the mean crystallite size <D> and the internal strain <S> was based on obtaining the value of the integral width of each profile (the ratio between the area and the maximum of the profile) from XRD patterns. The <D> and <S> values were determined using the classic Williamson-Hall graphical method [11] modified for “double-Voigt” model.
The profiles were simulated by Pearson-VII functions and their integral widths were calculated considering a known model and under the name of double-Voigt. The convolution with double-Voigt functions between all of the factors that compete to the deformation of profiles because of either instrumental causes or other internal causes, such as different defects in the local structure, leads to simultaneously crossed contributions of Cauchy and Gauss type for the crystallite dimension and the tensions. The consequence is that Williamson–Hall graphical method has two equations: one in which Cauchy-type integral widths contributions are summed and another in which the square of the Gauss components are summed [12–14]. Some details on the calculation mode are presented in our previous article [15].
2.2.4 Catalytic activity measurements
The equipment and working conditions to study the propane ODH reaction are presented in detail in our previous article [16].
3 Results and discussion
3.1 DTA/TGA
Fig. 1 presents the thermal analysis curves for the powdered precursors derived from the acetylacetonate of AE metal (M(Acac)2) and neodymium(III) nitrate hexahydrate (Nd(NO3)3·6H2O).
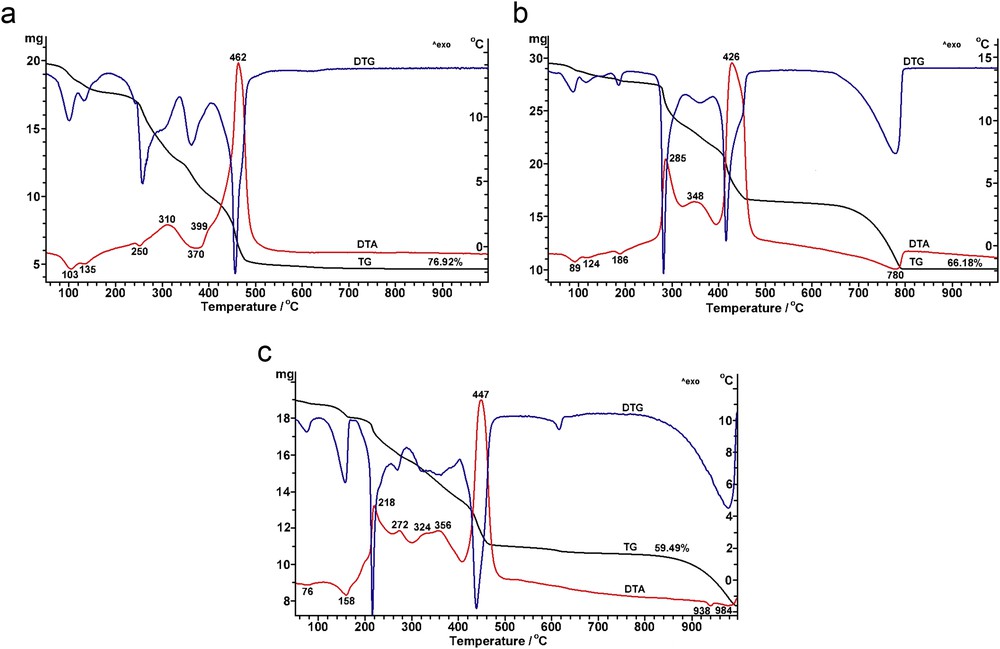
Thermal behaviour of the powdered precursors derived from neodymium(III) nitrate hexahydrate and alkaline earth metal acetylacetonate (M(Acac)2): (a) Mg(Acac)2; (b) Ca(Acac)2 and (c) Sr(Acac)2.
In the case of the precursor derived from Mg(Acac)2, the DTA curve reveals two low temperature endothermic effects centred at 103 and 135 °C, corresponding to the early stages of dehydration process of Nd(NO3)3·6H2O and also to the release of the adsorbed water [17] (Fig. 1a).
In the temperature range of 240–480 °C, a sequence of several endothermic and exothermic effects accompanied by mass loss was detected on the DTA and TGA curves. The endothermic processes centred at the temperatures of 250 and 370 °C can be assigned to (1) breakage of chemical bonds in Mg acetylacetonate, (2) solvent removal and (3) further release of crystallisation water and gradual removal of NO3− ions from the dopant reagent. The exothermic processes centred at 310, 399 and 462 °C are assigned to the multistep combustion of the organic matter. In the temperature range of 600–660 °C, a weak endothermic process, which is not visible on the DTA curve but is indicated by the small mass loss recorded on TGA curve, as well as by the flattened feature detected on the DTG curve, can be attributed to the decarbonation of the residual MgCO3, most likely formed as intermediate in the first stages of Mg(Acac)2 decomposition.
A quite similar thermal behaviour was noticed for the powdered precursor derived from Ca(Acac)2 (Fig. 1b). In this case, the endothermic effects centred at 89, 124 and 186 °C determined by the volatile release, as well as the exothermic processes centred at 285, 348 and 426 °C because of the oxidative decomposition of the organic groups, are shifted to lower temperature values relative to those observed for the precursor originated from Mg(Acac)2. The high temperature endothermic process, which takes place in the temperature range of 660–810 °C and is accompanied by a mass loss of ˜30%, corresponds to the decomposition of the carbonate-type intermediate, leading to the formation of the mixed oxide Ca1–3x/2NdxO.
In the case of the precursor derived from Sr(Acac)2, the decomposition process of the organic matter seems to be even more complicated, so that several exothermic effects centred at 218, 272, 324, 356 and 447 °C were recorded on the DTA curve (Fig. 1c). The high temperature decarbonation process occurs in two steps, at 938 and 984 °C, respectively.
One can conclude that the more pronounced the basic character of the AE metal ion is, the lower are the temperature values at which the exothermic effects corresponding to the decomposition of the organic matter occur and the higher are the temperatures at which the endothermic processes associated with the intermediates' decarbonation are shifted.
The thermal behaviours of the precursors derived from different calcium sources, calcium acetate (Ca(C₂H₃O₂)₂) and calcium methoxide (Ca(CH3O)2), are presented in Fig. 2 and will be discussed comparatively with the one corresponding to the precursor derived from calcium acetylacetonate Ca(C5H7O2)2 described above (Fig. 1b).
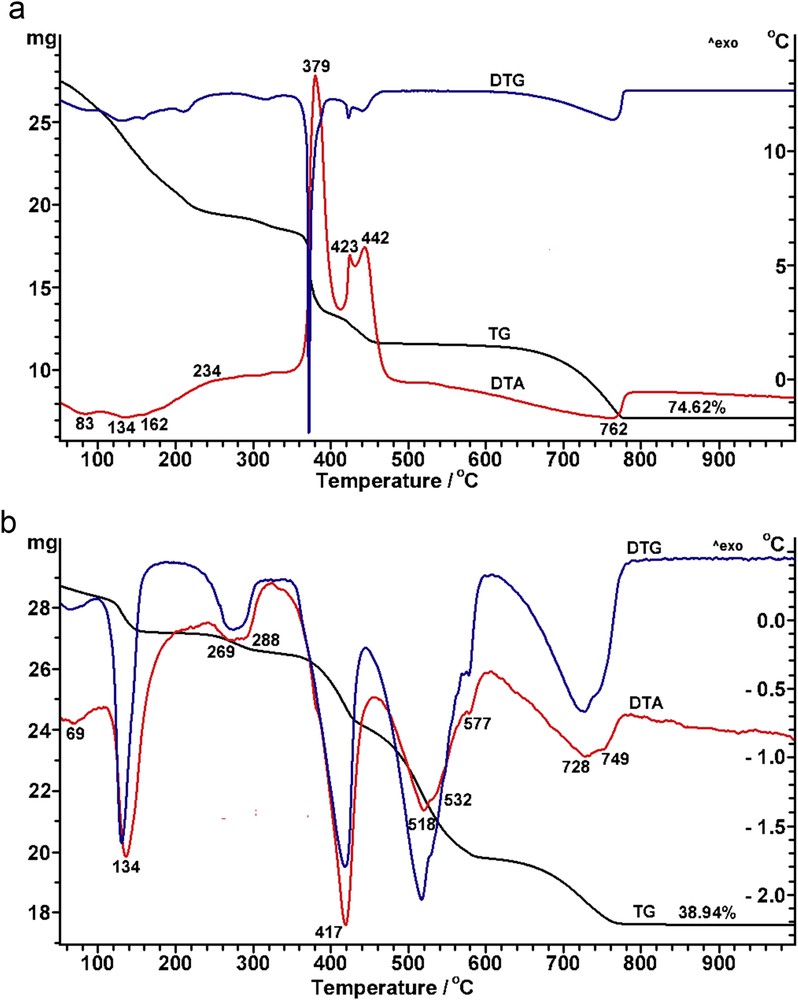
Thermal behaviour of the powdered precursors derived from neodymium(III) nitrate hexahydrate and different calcium sources: (a) Ca(CH3COO)2 and (b) Ca(CH3O)2.
Thus, the processes occurring during the thermal treatment of the precursor derived from calcium acetate are similar to those observed in the case of the precursor derived from calcium acetylacetonate, that is, endothermic effects because of the volatile releases at 83, 134 and 162 °C and the decomposition of (Ca,Nd)CO3 at 780 °C and exothermic effects determined by the combustion of the organic matter centred at 234, 379, 423 and 442 °C (Fig. 2a). A higher total mass loss of 74.62% was recorded on the TGA curve, most likely because of the additional oxidative decomposition of the acetic acid used as solvent, in comparison with a total mass loss of 66.18% in the case of the precursor derived from calcium acetylacetonate, when volatile ethanol was used as solvent.
For the powder derived from calcium methoxide, the thermal behaviour seems to be very different. Thus, in this case, the complex and stepwise decomposition process of the precursor is reflected only in endothermic effects, as the DTA curve reveals (Fig. 2b). The decomposition ends at 800 °C and a significantly lower total mass loss of only 38.94% was recorded on the TGA curve. This means that, in the temperature range of 250–650 °C, the endothermic effects assigned to the decomposition processes prevail over the exothermic combustion, most likely because of the lower carbon content in the organic matter determined by the short chain in the methoxy group of the calcium reagent.
3.2 IR spectroscopy
The determined vibration bands together with the corresponding assignments for the nine prepared sol–gel binary oxides MO–Nd2O3 are presented in Table 2.
IR results for the prepared sol–gel samples.
| Sample | Vibration band [cm−1] | Assignment |
| 200–600 | MgO bond | |
| 1440–1480 | m CH scissor vibration, CH2 | |
| 1MgNd | 1640 | HOH molecular water |
| 2850, 2960 | Carbonaceous contamination residues, RCH3, s-m CH stretching vibration | |
| 3440 | Structural OH− | |
| 2MgNd | idem 1MgNd | idem 1MgNd |
| 300–600 | CaO bond | |
| 680, 890, 1090, 1430 | Carbonate species | |
| 1CaNd | 1640 | HOH molecular water |
| 2860, 2920 | Carbonaceous contamination residues | |
| 3430 | Structural OH− | |
| 2CaNd | idem 1CaNd | idem 1CaNd |
| 3CaNd | idem 1CaNd | idem 1CaNd |
| 4CaNd | idem 1CaNd | idem 1CaNd |
| 300–500 | SrO bond | |
| 660–680, 850(860), 1040–1070, 1430–1460 | Carbonate species | |
| 1SrNd | 1640 | HOH molecular water |
| 1770 | RCOOH, vs CO stretching vibration | |
| 2880, 2960 | Carbonaceous contamination residues | |
| 3440 | Structural OH− | |
| 2SrNd | idem 1SrNd | idem 1SrNd |
| 3SrNd | idem 1SrNd | idem 1SrNd |
As it can be seen for each series of AE cation (Mg, Ca, Sr, respectively) the same vibration bands have been founded. From qualitative point of view, there are no differences between samples 1MgNd and 2MgNd, as between samples 1CaNd and 4CaNd and/or between 1SrNd and 3SrNd. Slight quantitative differences can be noted, referring to the intensities of the bands. Regarding the structural characterization accomplished by IR spectroscopy, slight differences can also be observed even between the three series of samples, which differ from one another by the AE element. Thus, for Mg, the MgO bond is signalised in the largest domain of 200–600 cm−1, for Ca, the CaO bond is signalised in the 300–600 cm−1 domain and for Sr, in the narrowest interval of 300–500 cm−1. Another difference between the three series of samples refers to the presence of carbonate species that are absent from the IR spectra of the Mg-containing samples but appear in the IR spectra of the Ca- and Sr-containing samples, which is normal, taking into account the increasing basicity of these cations, from Mg to Ca and from Ca to Sr, respectively.
3.3 XRD
3.3.1 Phase identification
In case of the nine samples discussed in this article, about 220 XRD profiles were digitally registered. Because of the structural complex situation, the observed profiles are strongly asymmetric suggesting that they are the result of a partial or total overlapping of more simple lines. Because of this fact their analytical separation was undertaken. For this purpose, the X-ray 5.0 program package was needed [18,19]. The registered profiles were separated and evaluated for about 550 elementary lines by simulation by fitting. Of these, about 340 evaluated lines could be attributed to some compounds, which are mentioned in Tables 3–5. The other non-attributed lines can belong to intermediary phases.
The calculated and reference (ASTM – American Society for Testing and Materials) values of the lattice constants for MgONd2O3 samples.
| Sample | Identified phases | Cryst. system | a [Å] | c [Å] | V [Å3] | Wt [%] |
| 1MgNd | MgO | Cubic | 4.2197(19) | – | 75.14(10) | 81 |
| (1) Nd2O3 | Hexagonal | 3.7808(97) | 5.9882(273) | 74.13(72) | 10 | |
| (2) Nd2O3 | Hexagonal | 3.8277(87) | 6.0026(203) | 76.16(60) | 9 | |
| 2MgNd | MgO | Cubic | 4.2167(8) | – | 74.97(4) | 81 |
| (1) Nd2O3 | Hexagonal | 3.7993(48) | 5.9715(125) | 74.65(35) | 13 | |
| (2) Nd2O3 | Hexagonal | 3.8186(319) | 5.9179(542) | 74.73(1.91) | 6 |
The calculated and reference (ASTM) values of the lattice constants for CaONd2O3 samples.
| Sample | Identified phases | Cryst. system | a [Å] | c [Å] | V [Å3] | Wt [%] |
| 1CaNd | CaO | Cubic | 4.7994(15) | – | 110.55(11) | 75 |
| Nd2O3 | Hexagonal | 3.8235(16) | 5.9860(57) | 75.79(14) | 19 | |
| CaCO3 | 4 | |||||
| Ca(OH)2 | 2 | |||||
| 2CaNd | (1) CaO | Cubic | 4.8039(11) | – | 110.86(8) | 75 |
| (2) CaO | Cubic | 4.7376(377) | – | 106.3(2.5) | 2 | |
| (1) Nd2O3 | Hexagonal | 3.8272(14) | 6.0091(42) | 76.22(11) | 14 | |
| (2) Nd2O3 | Hexagonal | 3.8234(21) | 5.9518(53) | 75.35(15) | 8 | |
| 3CaNd | (1) CaO | Cubic | 4.8070(10) | – | 111.08(7) | 67 |
| (2) CaO | Cubic | 4.7545(45) | – | 110.22(31) | 24 | |
| (1) Nd2O3 | Hexagonal | 3.8224(35) | 5.9716(95) | 75.56(26) | 5 | |
| (2) Nd2O3 | Hexagonal | 3.8323(116) | 6.0481(252) | 76.93(78) | 2 | |
| CaCO3 | 1 | |||||
| 4CaNd | CaO | Cubic | 4.8019(11) | – | 110.72(8) | 91 |
| Nd2O3 | Hexagonal | 3.8338(86) | 5.9846(181) | 76.18(57) | 4 | |
| CaCO3 | 2 | |||||
| Ca(OH)2 | 4 |
The calculated and reference (ASTM) values of the lattice constants for SrONd2O3 samples.
| Sample | Identified phases | Cryst. system | a [Å] | c [Å] | V [Å3] | Wt [%] |
| 1SrNd | (1) SrO | Cubic | 5.1005(61) | – | 132.69(48) | 9 |
| (2) SrO | Cubic | 5.1186(55) | – | 134.11(43) | 3 | |
| (1) Nd2O3 | Hexagonal | 3.7694(171) | 5.8410(35) | 71.87(1.08) | 9 | |
| (2) Nd2O3 | Hexagonal | 3.7666(222) | 5.9069(474) | 72.57(1.42) | 2 | |
| SrCO3 | 77 | |||||
| 2SrNd | (1) SrO | Cubic | 5.1069(66) | – | 133.19(52) | 9 |
| (2) SrO | Cubic | 5.1578(102) | – | 137.21(81) | 3 | |
| (1) Nd2O3 | Hexagonal | 3.8357(58) | 5.9513(120) | 75.83(38) | 24 | |
| (2) Nd2O3 | Hexagonal | 3.7755(191) | 5.8556(394) | 72.29(1.21) | 11 | |
| SrCO3 | 54 | |||||
| 3SrNd | (1) SrO | Cubic | 5.1037(36) | – | 132.94(28) | 11 |
| (2) SrO | Cubic | 5.1660(70) | – | 137.87(56) | 5 | |
| (1) Nd2O3 | Hexagonal | 3.8326(51) | 5.9676(134) | 75.91(37) | 13 | |
| (2) Nd2O3 | Hexagonal | 3.7677(147) | 5.8358(306) | 71.74(93) | 9 | |
| SrCO3 | 63 |
One of the first general conclusions obtained by phase analysis is that by sol–gel preparation method multiphase mixtures of the MO (M = Mg, Ca, Sr, cubic) and Nd2O3 (hexagonal) type were generated.
3.3.2 Volume of the unit cell, lattice constants and phase concentration (wt %)
The values of lattice constants, volumes of elementary cells and concentrations calculated from the diffraction spectra are presented in Tables 3–5. From the analysis of the relative value of UCVs compared with corresponding standards, one considered that the MO and Nd2O3 phases are solid solutions.
At the same time, solid solution formation depends on the following factors: (1) the difference between ionic radii of the host cell and those of the foreign ion; (2) diffusion difficulties, more pronounced because of the differences between crystallographic systems; and (3) the possibility of adjustment of the foreign ions to the new configuration (coordination incompatibility).
The concentration of each phase in the mixture, wt %, was calculated from ratios such as wt % = Ii (100%)/ΣIj (100%). Summing were accomplished for all identified phases in each sample, in which Ij is the 100% line amplitude for each XRD pattern corresponding to one phase in the multiphase mixture. To calculate the wt % factor without the corresponding standards, we assumed that the value of the volume fraction of the oxide component ‘i’ of the multiphase mixture is represented by the Ii (100%) diffraction line intensity corresponding to that phase.
From Tables 3–5, one can conclude that the concentration values wt % for MO (M = Mg, Ca, Sr) have the tendency to decrease in the following order: Mg > Ca > Sr. At the same time moderate increases were found (a few percents) in Nd2O3 concentrations in case of the samples from MgNd and CaNd series. The samples from the SrNd series contain higher percents of SrCO3, this phase concentration reaching about wt = 77% (1SrNd).
3.3.3 Lattice defects and <D> and <S> factors
The XPS analysis of the sol–gel samples obtained from acetylacetonate precursors (1MgNd, 4CaNd and 3SrNd) presented in Ref. [15] indicated that their surfaces contain elements of different oxides such as Ca, Mg, Sr, Nd, O and C elements, which can be found in the composition of the compounds determined by XRD.
To solve the mechanisms that make most elements in the precursor composition reach the surface, the mass changes, ΔΜ, from the elementary cell are graphically presented (Figs. 3–5) and the values are given in Table 6. It was found that ordinates at origin of the corresponding linear regressions have in order MgO, CaO, SrO the following values: 108 × ΔΜ [g] = −0.016 (MgNd); −0.219 (CaNd) and −0.816 (SrNd). The evolution clearly indicates the decrease in the mass of the unit cell of the mentioned oxide phases. This can be easily noticed on the graphic axes (Y1 in Figs. 3–5).
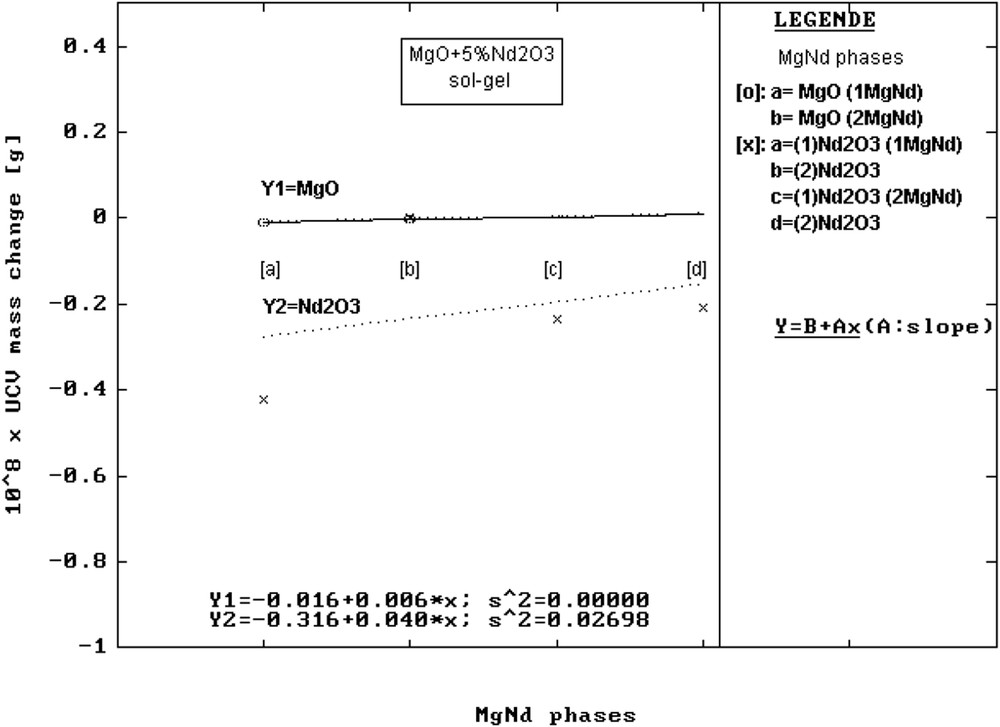
Change in the mass, ΔΜ, of the elementary cells vs precursors for MgNd series samples.
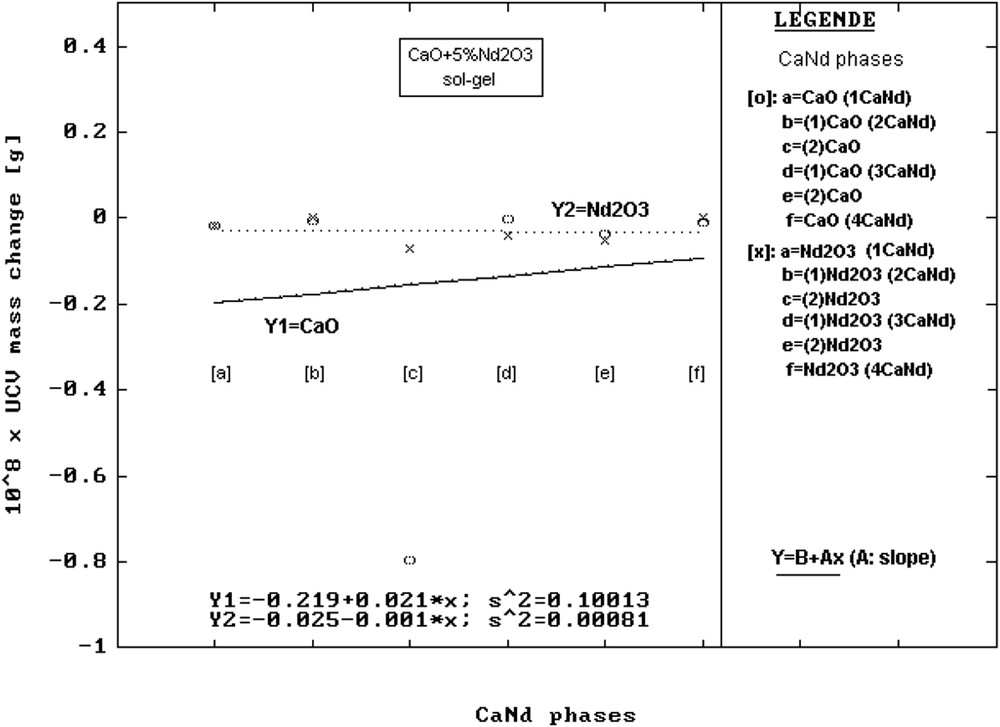
Change in the mass, ΔΜ, of the elementary cells vs precursors for CaNd series samples.
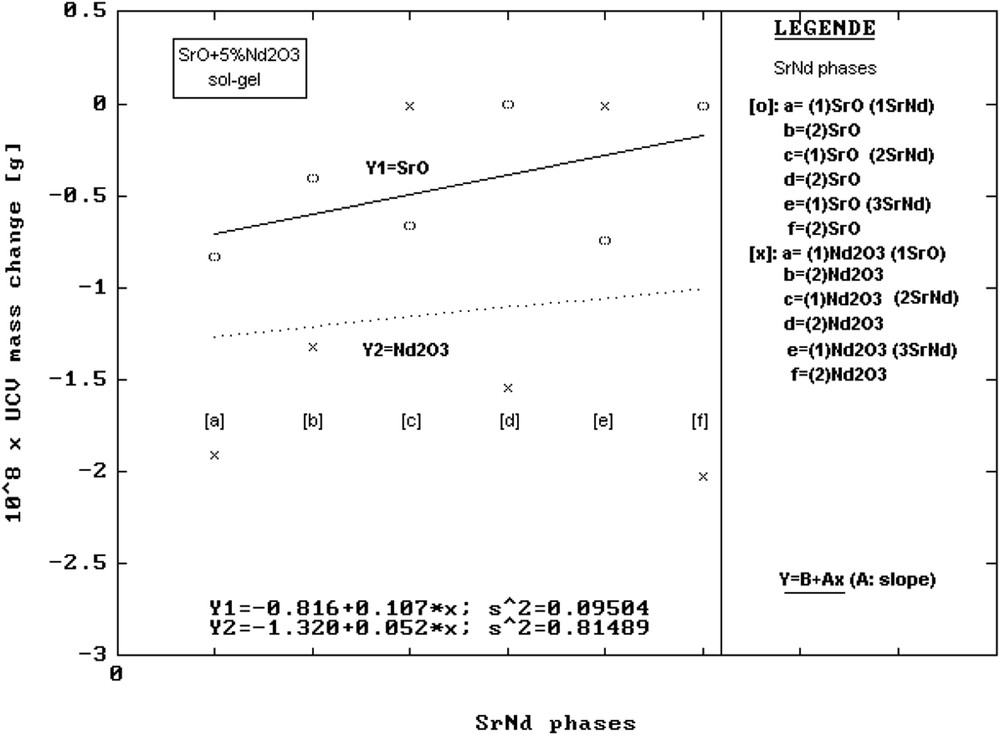
Change in the mass, ΔΜ, of the elementary cells vs precursors for SrNd series samples.
Mean crystallite size and mean lattice strain values; deviations of density calculated from XRD data, unit cell volume and mass of elementary cell vs standard cells of oxide phases.
| Sample | Phase | Double-Voigt integral width | (ρ−ρ0) [g cm−3] | (V− V0) [Å3] | 108 × ΔΜ [g] | |
| <D> [Å] | <S> × 103 | |||||
| 1MgNd | MgO | 285(84) | 0.7(5) | −0.022 | 0.46 | −0.010 |
| (1) Nd2O3 | 416(81) | 0.6(3) | 0.204 | −2.06 | −0.421 | |
| (2) Nd2O3 | 233(24) | 2.0(3) | 0.003 | −0.03 | −0.0001 | |
| 2MgNd | MgO | 259(80) | 1.7(7) | −0.013 | 0.29 | −0.004 |
| (1) Nd2O3 | 247(58) | 1.2(7) | 0.152 | −1.54 | −0.234 | |
| (2) Nd2O3 | 235(6) | 1.6(1) | 0.144 | −1.46 | −0.210 | |
| 1CaNd | CaO | 1117(74) | 0.7(1) | 0.024 | −0.78 | −0.018 |
| Nd2O3 | 255(37) | 2.1(5) | 0.039 | −0.40 | −0.016 | |
| 2CaNd | (1) CaO | 539(113) | 0.7(3) | 0.014 | −0.47 | −0.007 |
| (2) CaO | 571(44) | 1.2(1) | 0.158 | −5.03 | −0.795 | |
| (1) Nd2O3 | 481(60) | 0.1(2) | −0.002 | −0.03 | −0.0001 | |
| (2) Nd2O3 | 719(131) | 1.2(2) | 0.082 | −0.84 | −0.069 | |
| 3CaNd | (1) CaO | 442(25) | 0.72(8) | 0.007 | −0.25 | −0.002 |
| (2) CaO | 1508(469) | 0.6(2) | 0.034 | −1.11 | −0.037 | |
| (1) Nd2O3 | 371(14) | 1.2(1) | 0.062 | −0.63 | −0.039 | |
| (2) Nd2O3 | 484(43) | 0.7(1) | −0.070 | 0.74 | −0.052 | |
| 4CaNd | CaO | 461(62) | 0.6(2) | 0.018 | −0.61 | −0.011 |
| Nd2O3 | 394(38) | 1.1(2) | 0.001 | −0.01 | 0.0001 | |
| 1SrNd | (1) SrO | 483(143) | 0.9(4) | 0.177 | −4.70 | −0.832 |
| (2) SrO | 859(324) | 0.3(3) | 0.122 | −3.28 | −0.400 | |
| (1) Nd2O3 | 555(39) | 0.6(1) | 0.441 | −4.32 | −1.9064 | |
| (2) Nd2O3 | 578(38) | 0.5(1) | 0.366 | −3.62 | −1.326 | |
| 2SrNd | (1) SrO | 423(134) | 0.8(6) | 0.158 | −4.20 | −0.662 |
| (2) SrO | 562(113) | 0.7(3) | 0.006 | −0.18 | −0.001 | |
| (1) Nd2O3 | 650(94) | 0.7(2) | 0.035 | −0.36 | −0.013 | |
| (2) Nd2O3 | 591(44) | 0.6(1) | 0.396 | −3.90 | −1.545 | |
| 3SrNd | (1) SrO | 410(94) | 1.1(4) | 0.167 | −4.45 | −0.744 |
| (2) SrO | 577(158) | 0.7(3) | −0.018 | 0.48 | −0.009 | |
| (1) Nd2O3 | 535(83) | 0.5(2) | 0.028 | −0.28 | −0.008 | |
| (2) Nd2O3 | 612(6) | 0.5(1) | 0.455 | −4.45 | −2.026 |
For the ordinate at origin corresponding to Nd2O3 phases, the values found were 108 × ΔΜ [g] = −0.316 (MgNd); −0.025 (CaNd) and −1.320 (SrNd), indicating a similar behaviour of the MO phases (Y2 axes in Figs. 3–5).
Since the 1960s, one knew that when reactions with ionic changes take place, in the ideal case the number of atoms in the cell does not change but the mass of the host cell can change because of atomic mass differences of the elements involved in the ionic change. When vacancies appear in an ideal lattice, without defects, the theoretical number of atoms decreases, and as a consequence the mass and density will decrease [15,20]. This behaviour offers an explanation for mass variation of MO and Nd2O3 elementary cells.
At molecular level between precursors, the sol–gel reactions favour the apparition of point defects (voids and vacancies) even from the phase of early formation of MO and Nd2O3 crystalline germs. By thermal treatment and as the crystalline structures finalize, these tend to distribute homogeneously in the oxide mass. There is a possibility for the number of point defects (voids and vacancies) to multiply in the order MgNd > CaNd > SrNd in both phases, MO and Nd2O3, identified in all mixtures.
3.3.3.1 Samples from MgNd series
From Fig. 3, one can also notice that for MgO, the nature of precursors influences only at a very small extent the elementary cell mass, because the slope of the line has a small value (Y1 in Fig. 3). This means that there is almost no ionic exchange between MgO as a host and Nd2O3 as impurity, which can be explained by the too large difference between the ionic radius of Mg2+ = 0.72 Å and Nd3+ = 0.98 Å [21].
A previous study suggested that although Nd3+ ions cannot directly get into the MgO cubic lattice, a solid solution can be formed by the diffusion of some non-stoichiometric agglomerates of the Nd3+Ox type [15]. But when Nd2O3 becomes host, MgO diffusion in the host lattice with hexagonal symmetry seems to be more and more favoured, as a function of the nature of reagents (see Y2 in Fig. 3). So because of supplementary mass, the mass of the elementary cell has the tendency to slowly increase with the nature of precursors. The small increase in slope can be explained by the small concentrations of the Nd2O3 phases in the mixtures.
Although MgO forms solid solutions in the mentioned conditions, the average strain factor <S> has the tendency to significantly increase with the nature of reagents. Consequently, because the order was affected in the lattice, the <D> values tend to decrease (histograms in Fig. 6a). A similar behaviour could be observed in case of Nd2O3 phases (Fig. 6b) regarding <D> and <S> factors.
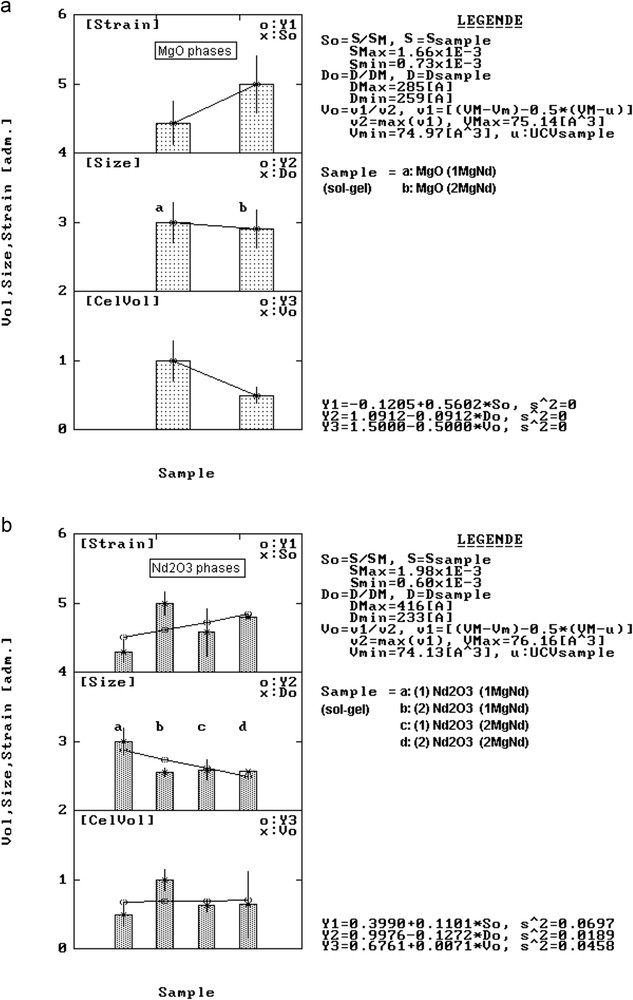
Structural variation in lattice strain, crystallite size and unit cell volume for MgO phases (a) and Nd2O3 phases (b) from MgNd series samples.
3.3.3.2 Samples from CaNd series
If CaO is host, the tendencies of the regressions representing the change in the mass of elementary cells of the oxide mixtures in CaNd samples change (Fig. 4). According to the graphical representation, the deviation of the CaO elementary cell compared to the ideal lattice starts from smaller values but has a positive moderate slope (see Y1 in Fig. 4). This aspect indicates a greater facility in the acceptance of ionic change with Nd3+. This facility can be easily explained by the small difference between the Ca2+ (1 Å) and Nd3+ (0.98 Å) ions.
When Nd2O3 becomes host, the regression line Y2 (Fig. 4) starts from a value little higher and decreases very slowly, the slope value being negative. The decrease in the mass of elementary cells of Nd2O3 phases is because of Nd3+ substitution by Ca2+.
As represented in Table 6, <D> and <S> values are greater for both CaO and Nd2O3 lattices compared with the samples in MgNd series, which indicates that these lattices are more relaxed. One can also notice a greater value of gravimetric concentrations of Nd2O3 compared with MgNd series.
From the corresponding histograms of <D> and <S> (Fig. 7), it results that <D> and <S> tend to decrease with the nature of reagents for the CaO phases, whereas for the Nd2O3 phases the <D> factor tends to increase and <S> tends to decrease. This behaviour is probably influenced by specific features of the sol–gel reaction connected with Ca participation.
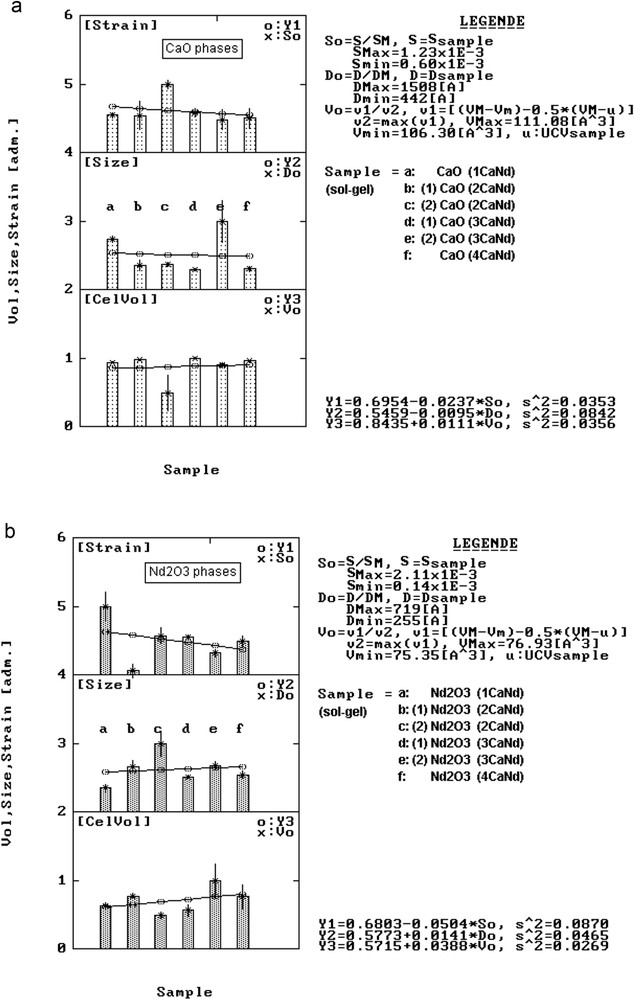
Structural variation in lattice strain, crystallite size and unit cell volume for CaO phases (a) and Nd2O3 phases (b) from CaNd series samples.
3.3.3.3 Samples from SrNd series
The results are presented in Figs. 5 and 8. In Fig. 5, one can notice that the ordinate at origin of the Y1 line has a smaller value than in case of CaNd series. This means that as a result of sol–gel reactions in the SrO crystalline lattice the number of point defects is greater than in case of the former series.
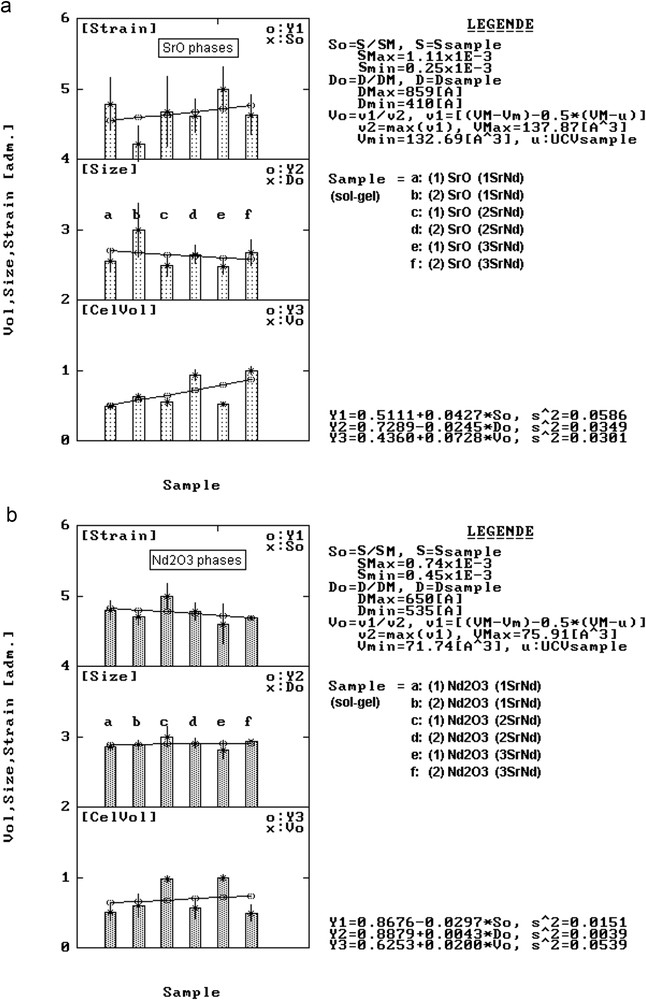
Structural variation in lattice strain, crystallite size and unit cell volume for SrO phases (a) and Nd2O3 phases (b) from SrNd series samples.
According to previous studies, SrO shows a great tendency to form solid solutions with non-stoichiometric composition [22]. According to Shannon [21], the ionic radii are as follows: Ca2+ = 1 Å (V0 = 111.33 Å3), Nd3+ = 0.98 Å (V0 = 74.68 Å3) and Sr2+ = 1.18 Å (V0 = 137.39 Å3).
The presence of a great number of point defects and the great value of the elementary cell volume enable SrO to form a solid solution because of an easy acceptance of Nd+3 ions. This is confirmed by an increase in the elementary cell mass of SrO solid solutions and by the pronounced positive slope of Y1 line in Fig. 5.
When SrO is the host lattice, the increase in the elementary cell mass with the nature of reagents suggests that the number of ionic exchange processes outnumbers the point defects. Thus, in the multiphase mixture, the main source of defects is more from ionic exchange processes than from the presence of voids.
Regarding Nd2O3 phases, Y2 regression indicates a great value (in absolute value) of the ordinate too, showing here also a great number of voids in the lattice, favoured by the great tendency of SrO to accept Nd+3. So the departure of Nd+3 generates supplementary point defects and electrostatic imbalances. In these favourable conditions, some Sr ions can undertake the role of Nd ions, which have already departed from the Nd2O3 lattice, trying to re-establish the balance in the Nd oxide lattice. The positive slope of Y2 line (Fig. 5) suggests that the nature of precursors enhances the number of Sr ions that replace Nd.
The <D> and <S> values presented in Table 6 show a slight tendency to increase in case of the samples in SrNd series compared to the samples in MgNd and CaNd series. At the same time, the nature of reagents determines the behaviour of <D> and <S> factors noticed in Fig. 8. Thus, in case of SrO, the <S> values tend to slightly increase and the <D> values tend to slowly decrease. In case of Nd2O3, the behaviour of the two microstructural factors is inverted, the <S> values slowly decrease and the <D> values tend to slightly increase. Their antagonistic behaviour suggests that although Sr easily accepts Nd on its positions, the nature of the precursors can somehow influence, simultaneously and in anti-phase, the extent of distortions in the two oxide lattices.
- • Although the compositions of elementary cells were not precisely known, we specify that in all samples the solid solutions are formed, an approximate calculation of the deviation of the mass of the elementary cell compared to an ideal lattice enabled a qualitative estimation of the nature of defects in the lattices.
- • In the samples from the MgNd series, MgO difficultly forms solid solutions with Nd2O3 and this does not happen directly, by ionic exchange with Nd+3. The contribution of the exchange reactions is small, the great number of voids (vacancies) being emphasised. CaO and especially SrO can form more easily solid solutions with Nd2O3. In case of the CaNd series samples, the variation in the mass the elementary cells suggests a certain equilibrium between the number of voids and the mutual ionic exchange. For SrNd series, solid solutions are formed most easily favoured by the close ionic radius of Sr2+ and Nd3+, as well as by the high basicity of Sr. The results suggest that the exchange reactions are the main disorder source in the lattice, coexisting with point defects (voids and vacancies).
3.4 Catalytic testing
Some catalytic activity measurements have established the potential of the prepared sol–gel mixed oxides to be used in the ODH process of light alkanes [16]. Catalytic data for propane ODH have already been published [16] (Table 1). The best sample was observed to be 3SrNd sample (1 m2 g−1) with 56 and 16% selectivities in propene and ethylene, respectively, at 5% conversion at 550 °C compared to 4CaNd (13 m2 g−1; 17% conversion and 31 and 22% selectivities to propene and ethylene at 550 °C) and 1 Mg-Nd (60 m2 g−1; 32% conversion and 33 and 25% selectivities at 550 °C). Such selectivity in olefins was also observed to increase with conversion at variance with usual behaviour for redox mechanism (Mars and van Krevelen type), typical of catalysts with metal oxide of variable oxidation state such as V or Mo cations. The selectivity to olefins was therefore observed to increase from Mg to Sr, that is, to follow the basicity strength of the catalyst surface, as shown by CO2-Temperature-Programmed Desorption (TPD) [16]. This phenomenon could be explained by a better incorporation of Nd into the AEO lattice, which created cationic vacancies for attaining electroneutrality and rendered nearby oxide anions coordinatively unsaturated and more basic. It was then suggested that the catalytic reactions most probably proceeded according to a complex heterogeneous–homogeneous scheme through the Eley–Rideal mechanism and the active centres were regenerated through gas-phase O2 participation without lattice oxygen removal. Thus created structural defects were agglomerated or dispersed, depending on the preparation procedure and the cation radii match. It could be concluded that the dispersed local defects (favoured by the sol–gel method) led to higher selectivity, whereas Nd3+ agglomerates led to higher conversion in agreement with the observation that Nd2O3 itself gave the highest propane conversion. In the present work, it has been clearly shown that the surface defects are a consequence of structural changes inside of the crystalline lattice of the solid solutions and are quite important for catalytic properties in the ODH reaction.
4 Conclusions
A structural study of MO–Nd2O3 system obtained by the sol–gel procedure was accomplished.
X-ray diffraction indicates that all compounds in the MgNd, CaNd and SrNd series obtained by the sol–gel method are crystalline oxide mixtures of the MO type (M = Mg, Ca, Sr) and Nd2O3. All MO and Nd2O3 crystalline phases are solid solutions with more or less distorted cells.
The analysis of microstructural factors of the crystalline lattices obtained from XRD patterns, lattice constants, UCV, <D> and <S>, suggest that two sources of defects could compete in the space of these oxide lattices, namely, formation of voids (vacancies) and ionic exchange reactions. In the frame of each series of samples, MgNd, CaNd or SrNd, the precursors used in the sol–gel synthesis favour one of the two sources of structural disorder: generation of voids and ionic exchange.
The surface defects are a consequence of structural changes inside of the crystalline lattice of the solid solutions. Thus, to compensate for the shortage of local charge and to establish the electroneutrality of the lattice, the defects are generally mobile. Distortions in the crystalline lattice determine a greater mobility of these defects; thus, they can reach the surface of the polycrystals where they will be found free or in different combinations. These defects (point or agglomerations) on the crystal surface become active catalytic centres and are quite important for catalytic properties in the ODH reaction. In case of SrNd series, solid solutions are formed most easily and favoured by the close ionic radius of Sr2+ and Nd3+, as well as by the high basicity of Sr and the presence of a great number of point defects. The results suggest that the exchange reactions are the main disorder source in the lattice, coexisting with point defects (voids and vacancies). This may explain higher catalytic activity and selectivity to olefins of the 3SrNd sample compared with 1MgNd and 4CaNd samples.
Acknowledgements
The financial support by the French Ministries of Foreign Affairs and of National High Education and Research via EGIDE and by the Ministries of Education and Science of Bulgaria and Romania through the National Science Funds within the programmes Rila and Brâncuşi is gratefully acknowledged.


