Structural, electrical and optical properties of Lin@C20 (n = 1–6) nanoclusters

Zohreh Khajehali; Hamid R. Shamlouei

doi:10.1016/j.crci.2018.02.005

Structural, electrical and optical properties of Li_n@C₂₀ (n = 1–6) nanoclusters

Zohreh Khajehali ¹; Hamid R. Shamlouei ¹

¹ Department of Basic Sciences, Lorestan University, Khorramabad, Iran

Comptes Rendus. Chimie, Volume 21 (2018) no. 5, pp. 541-546.

Abstract

The current research was undertaken to investigate the structural, electrical, and optical properties of C₂₀ fullerene decorated with different numbers of lithium (Li) atoms on its surface. The stability of the structure increased as the number of lithium atoms increased. Increasing the number of lithium atoms around C₂₀ from one to four slightly increased the E_g (energy gap between the highest occupied molecular orbital and the lowest unoccupied molecular orbital). Increasing the number to five or six narrowed the E_g. The electrical properties such as ionization potential (I), electron affinity (A), chemical potential (μ), global hardness (η), global softness (γ), global electrophilicity (ω), and electronegativity (χ) were also calculated. The polarizability (α) and first hyperpolarizability (β₀), which correspond to the linear optical and nonlinear optical properties, respectively, were also calculated. An intense increase in β₀ was recorded as the effect of five Li atoms adsorbed onto the C₂₀ surface. The results of this study can be used to design and fabricate nanomaterials with adjustable electro-optical properties.

Metadata

Received: 2017-11-24
Accepted: 2018-02-12
Published online: 2018-03-16

DOI: 10.1016/j.crci.2018.02.005

Keywords: HOMO–LUMO gap, Li_n@C₂₀ (n = 1–6) nanostructure, NLO properties, First hyperpolarizability

Author's affiliations:

Zohreh Khajehali ¹; Hamid R. Shamlouei ¹

¹ Department of Basic Sciences, Lorestan University, Khorramabad, Iran

@article{CRCHIM_2018__21_5_541_0,
     author = {Zohreh Khajehali and Hamid R. Shamlouei},
     title = {Structural, electrical and optical properties of {Li\protect\textsubscript{\protect\emph{n}}@C\protect\textsubscript{20}} (\protect\emph{n}~=~1{\textendash}6) nanoclusters},
     journal = {Comptes Rendus. Chimie},
     pages = {541--546},
     publisher = {Elsevier},
     volume = {21},
     number = {5},
     year = {2018},
     doi = {10.1016/j.crci.2018.02.005},
     language = {en},
}

TY  - JOUR
AU  - Zohreh Khajehali
AU  - Hamid R. Shamlouei
TI  - Structural, electrical and optical properties of Lin@C20 (n = 1–6) nanoclusters
JO  - Comptes Rendus. Chimie
PY  - 2018
SP  - 541
EP  - 546
VL  - 21
IS  - 5
PB  - Elsevier
DO  - 10.1016/j.crci.2018.02.005
LA  - en
ID  - CRCHIM_2018__21_5_541_0
ER  -

%0 Journal Article
%A Zohreh Khajehali
%A Hamid R. Shamlouei
%T Structural, electrical and optical properties of Lin@C20 (n = 1–6) nanoclusters
%J Comptes Rendus. Chimie
%D 2018
%P 541-546
%V 21
%N 5
%I Elsevier
%R 10.1016/j.crci.2018.02.005
%G en
%F CRCHIM_2018__21_5_541_0

Zohreh Khajehali; Hamid R. Shamlouei. Structural, electrical and optical properties of Li_n@C₂₀ (n = 1–6) nanoclusters. Comptes Rendus. Chimie, Volume 21 (2018) no. 5, pp. 541-546. doi : 10.1016/j.crci.2018.02.005. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2018.02.005/

Version originale du texte intégral

1 Introduction

Nanoscience and nanotechnology are the latest revolutionary developments in science and engineering, which are rapidly moving forward. To measure the new and improved properties of nanomaterials requires a close connection among the physical, chemical, biological, and engineering sciences. One of the most widely used nanomaterials is fullerene. A fullerene is a molecule of carbon in the form of a hollow sphere, an ellipsoid, tube, or other shape. Harry Kroto, Richard Smalley, and Robert Curl discovered fullerenes in 1985 and won the 1996 Nobel Prize in chemistry [1,2]. Much experimental and theoretical work has been done to discover and provide fullerenes, in particular C₆₀. A fullerene is a deceptive molecule; it is a nonlinear optical (NLO) nanocluster and has a large number of conjugated double bonds. These characteristics suggest large nonlinear hyperpolarizabilities. Many studies on the NLO properties of fullerenes are either experimental or theoretical [3–12]. Because of the widespread use of optical materials in information storage, optical communication, and computing and optical switching devices, the design of high-performance NLO materials is an important area of physical chemistry research [13–28]. The presence of CH bonds usually has a harmful effect on NLO responses; therefore, pure carbon systems such as fullerenes are good candidates for exploitation of NLO properties. Because additional electrons play an important role in increasing the first hyperpolarizability (β₀), species that contain extra electrons can show a significant NLO response [29–38]. Recently, M₃O (M = Li, Na, and K) has been used to increase the NLO response [39]. The C₂₀ molecule, with a dodecahedral cage structure, is the smallest and truly unique member of the fullerene family [40]. It is thought that the smallest fullerene C₂₀ with positive electron affinity is a new organic nanoelectronic material. Its structure is very simple and highly symmetrical, consisting of 12 five-membered rings only [41]. In this work, we present a density functional theory (DFT) study on the exohedral interaction between lithium atoms and fullerene C₂₀.

2 Methods

The nanostructure of fullerene C₂₀ and Li_n@C₂₀ (n = 1–6) structures was completely optimized at the theoretical B3LYP/6-31+G(d) level [42,43]. All calculations were performed using the unrestricted spin method. Geometry optimization also was performed using the CAM-B3LYP [44] and WB97XD [45] methods in conjunction with the 6-31G(d), 6-31+G(d), and 6-311+G(d) basis sets for all complexes to examine the extent of difference in geometries optimized using long-range corrected calculation. B3LYP is a reliable method for the study of nanostructures [46–49]. Frequency calculations of all optimized structures were done at the B3LYP/6-31+G(d) level. The density of state was calculated in GaussSum.3.3.9 [50]. The HOMO–LUMO (highest occupied molecular orbital–lowest unoccupied molecular orbital) gap energy (E_g) of structures was determined from the difference between Ɛ_H (HOMO energy) and Ɛ_L (LUMO energy). Polarizability (α) and β₀ as linear optical and NLO properties, respectively, were examined at the theoretical CAM-B3LYP/6-31+G(d) level. The β₀ is a factor in the NLO response coefficient and can be calculated using the following equations:

β_{0} = {(β_{x}^{2} + β_{y}^{2} + β_{z}^{2})}^{1 / 2}

and

β_{i} = \frac{3}{5} (β_{i i i} + β_{i j j} + β_{i k k}), i, j, k = X, Y, Z

Because the S² values for the nanoclusters with one unpaired electron were in the range of 0.751–0.785, the computational methods were found to be reliable and spin contamination negligible. All calculations were done in Gaussian 09 package [51]. Natural bond orbital (NBO) analysis [52] was also performed.

3 Results and discussion

Fig. 1 shows the optimized structures of all nanostructures studied.

Fig. 1
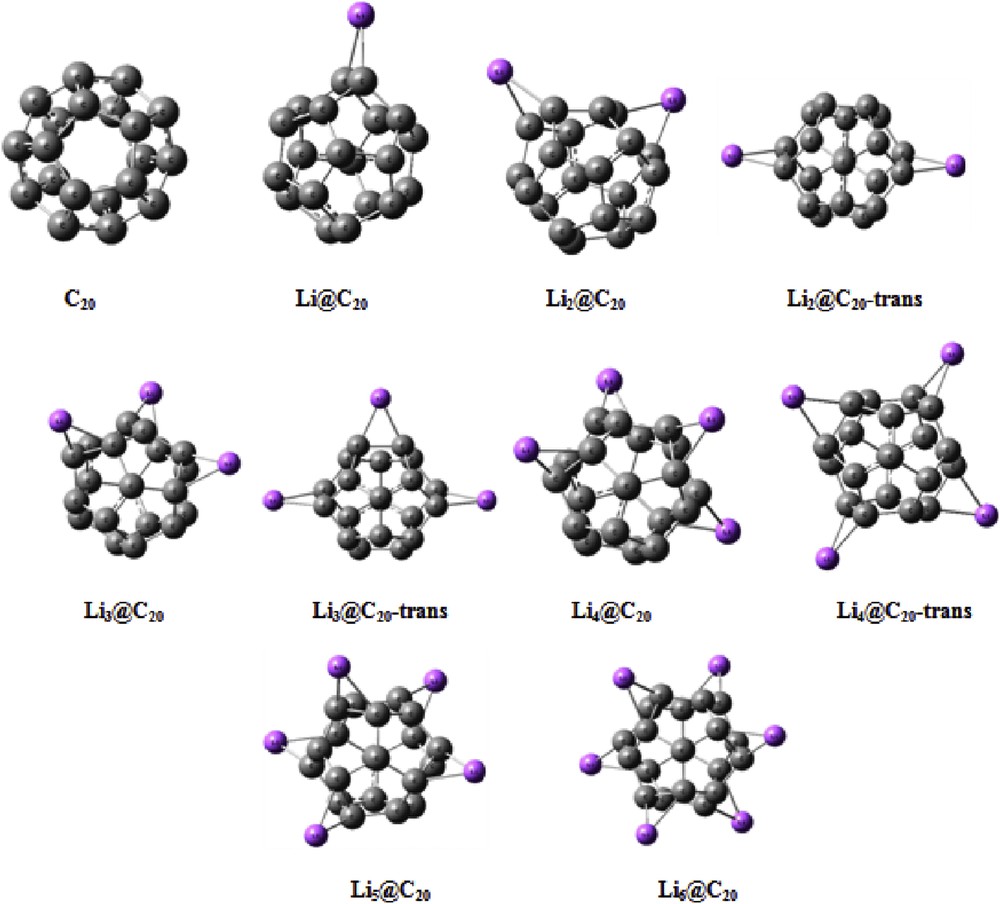
Optimized structures of C₂₀ and Li_n@C₂₀ nanoclusters.

After optimization and frequency calculations, the energetic properties of all nanoclusters were calculated, for example, the binding energy (E_int) was determined from the following equation:

E_{int} = E_{{Li}_{n} @ C_{20}} - [E_{C_{20}} + n E_{Li}]

where

E_{{Li}_{n} @ C_{20}}

corresponds to the energy of C₂₀ fullerene decorated with n lithium atoms,

E_{C_{20}}

corresponds to the energy of C₂₀ fullerene, and E_Li corresponds to the energy of an isolated lithium atom. Table 1 lists the binding energies as well as the change in enthalpy, free energy, and entropy of Li_n@C₂₀ formation.

Structure	E_int (kcal/mol)	ΔH (kcal/mol)	ΔG (kcal/mol)	ΔS (kcal/mol)
Li@C₂₀	−48.6200	−49.1642	−40.5604	−0.0288
Li₂@C₂₀	−91.3402	−91.2412	−73.6572	−0.0589
Li₂@C₂₀-trans	−99.1734	−98.5856	−81.0481	−0.0588
Li₃@C₂₀	−124.1404	−124.5445	−99.7328	−0.0832
Li₃@C₂₀-trans	−133.7791	−133.7569	−108.4452	−0.0849
Li₄@C₂₀	−172.3620	−171.7263	−137.7813	−0.1138
Li₄@C₂₀-trans	−175.8398	−175.1099	−141.2144	−0.1138
Li₅@C₂₀	−193.1880	−193.7764	−152.9408	−0.1369
Li₆@C₂₀	−203.2263	−204.3173	−155.9811	−0.1621

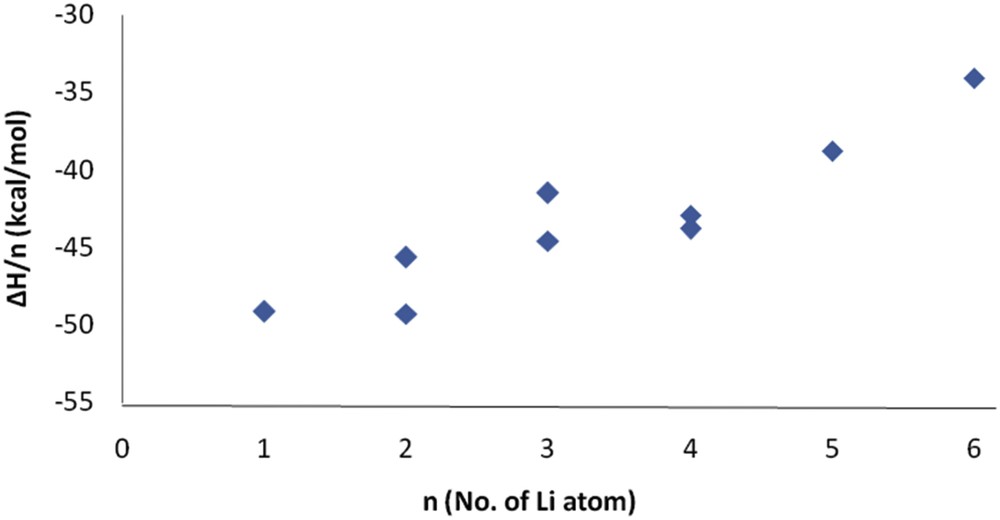
As seen in Table 1, the addition of lithium atoms to the surface of C₂₀ is highly exothermic. The binding energy, enthalpy, and free energy of the Li_n@C₂₀ formation increased as the number of lithium atoms increased. The enthalpy change per lithium atom was calculated as the fraction $Δ H / n$ , in which n corresponds to the number of lithium atoms adsorbed onto the C₂₀ surface. Fig. 2 plots the value of $Δ H / n$ as a function of the number of lithium atoms (n) adsorbed onto the C₂₀ surface.

Fig. 2
Changes in $Δ H / n$ relative to the number of Li atoms adsorbed onto the C₂₀ surface.

Fig. 2 shows that when the number of Li atoms increased, the enthalpy of the reaction per lithium atom decreased. Although this value for the sixth lithium atom is negative, the reaction remains exothermic. To confirm the results of the adsorption energy of Li onto the C₂₀ surface, the interaction energies were calculated using the WB97XD and CAM-B3LYP methods and 6-31G(d), 6-31+G(d), and 6-311+G(g) basis sets. The results are presented in Table 2. As seen, the interaction energies for all structures showed a similar trend for different methods and basis sets.

Compound	Method
Cam-B3LYP/6-31G(d)	Cam-B3LYP/6-31+G(d)	Cam-B3LYP/6-311+G(d)	WB97XD/6-31G(d)	WB97XD/6-31+G(d)	WB97XD/6-311+G(d)
Li@C₂₀	−51.17	−52.24	−52.87	−51.10	−52.35	−53.06
Li₂@C₂₀	−95.74	−97.77	−99.57	−96.39	−98.77	−100.59
Li₂@C₂₀-trans	−104.95	−106.60	−108.27	−105.67	−107.87	−109.56
Li₃@C₂₀	−133.03	−135.96	−138.42	−133.68	−137.29	−139.80
Li₃@C₂₀-trans	−143.55	−145.93	−148.35	−144.05	−147.22	−149.70
Li₄@C₂₀	−186.37	−188.84	−192.30	−186.85	−190.48	−193.99
Li₄@C₂₀-trans	−190.36	−192.36	−195.66	−190.80	−194.16	−197.49
Li₅@C₂₀	−199.56	−206.55	−203.08	−195.84	−207.39	−211.03
Li₆@C₂₀	−208.17	−206.69	−210.82	−202.83	−206.49	−208.68

The HOMO (Ɛ_H) and LUMO (Ɛ_L) orbital energies were obtained from the density of state spectrum of each nanocluster. The Ɛ_H, Ɛ_L, and E_g are reported in Table 3. The HOMO and LUMO energies and the gap energy for fullerene C₂₀ were −5.5, −3.62, and 1.88 eV, respectively. Other chemical parameters, which relate to the stability and reactivity of nanoclusters, such as the chemical potential (μ), global electrophilicity (ω), ionization potential (I), electron affinity (A), softness (γ), global hardness (η), and electronegativity (χ), were calculated and are reported in Table 3. The behavior of gap energy as a function of the number of lithium atoms (n) is shown in Fig. 3.

Structure	Ɛ_H (eV)	Ɛ_L (eV)	E_g (eV)	%ΔE_g	I (eV)	A (eV)	μ (eV)	η (eV)	γ (eV⁻¹)	ω (eV)	χ (eV)
C₂₀	−5.5	−3.62	1.88	–	5.5	3.62	−4.56	0.94	1.0638	11.0604	4.56
Li@C₂₀	−4.8	−2.95	1.85	−1.57	4.8	2.95	−3.875	0.925	1.0811	8.1165	3.875
Li₂@C₂₀	−4.51	−2.52	1.99	5.85	4.51	2.52	−3.515	0.995	1.0050	6.2086	3.515
Li₂@C₂₀-trans	−4.3	−2.23	2.07	10.10	4.3	2.23	−3.265	1.035	0.9662	5.1498	3.265
Li₃@C₂₀	−3.98	−1.6	2.38	26.59	3.98	1.6	−2.79	1.19	0.8403	3.2706	2.79
Li₃@C₂₀-trans	−3.56	−1.44	2.12	12.76	3.56	1.44	−2.5	1.06	0.9434	2.9481	2.5
Li₄@C₂₀	−3.49	−1.27	2.22	18.08	3.49	1.27	−2.38	1.11	0.9009	2.5515	2.38
Li₄@C₂₀-trans	−3.27	−1.11	2.16	14.89	3.27	1.11	−2.19	1.08	0.9259	2.2204	2.19
Li₅@C₂₀	−2.13	−1.57	0.56	−70.21	2.13	1.57	−1.85	0.28	3.5714	6.1116	1.85
Li₆@C₂₀	−1.93	−1.59	0.34	−81.91	1.93	1.59	−1.76	0.17	5.8823	9.1106	1.76

Fig. 3
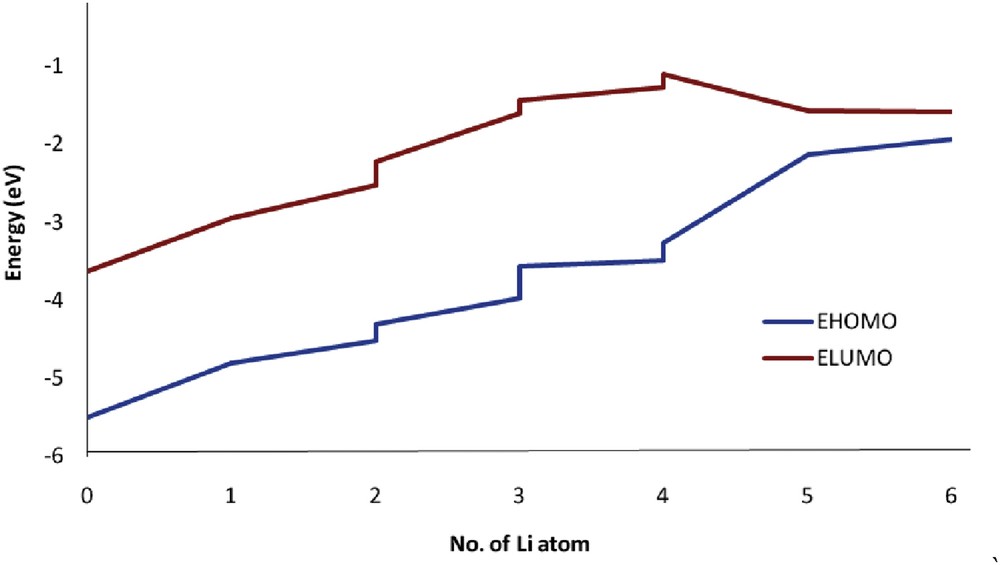
HOMO and LUMO energies as a function of the number of Li atoms adsorbed onto C₂₀ surface.

Fig. 3 shows that adding Li atoms to the fullerene surface increased the HOMO and LUMO energies. The gap energy values increased up to the Li₄@C₂₀ structure, but the Li₅@C₂₀ and Li₆@C₂₀ structures show a sharp decrease in the gap energy and the greatest deviation in the gap energy deviation (70.21% and 81.91%, respectively).

Chemical hardness relates to the stability and reactivity of a chemical system. It measures the resistance of a compound to a change in the electron density or electron transfer distribution. Chemical hardness is directly proportional to the energy gap between HOMO and LUMO. An increase in hardness is a sign of a more stable and less reactive combination. In a chemical process, electrophilicity measures the capacity of a species to accept electrons; therefore, the stability of the structure after the receipt of the additional electronic charge by the system is shown [53]. A good reactive nucleophile molecule is characterized by a smaller amount of μ, ω, and, conversely, high electrophilicity with high values of μ and ω. Fig. 4 shows the changes in μ and ω relative to the number of Li atoms added to the C₂₀ surface.

Fig. 4
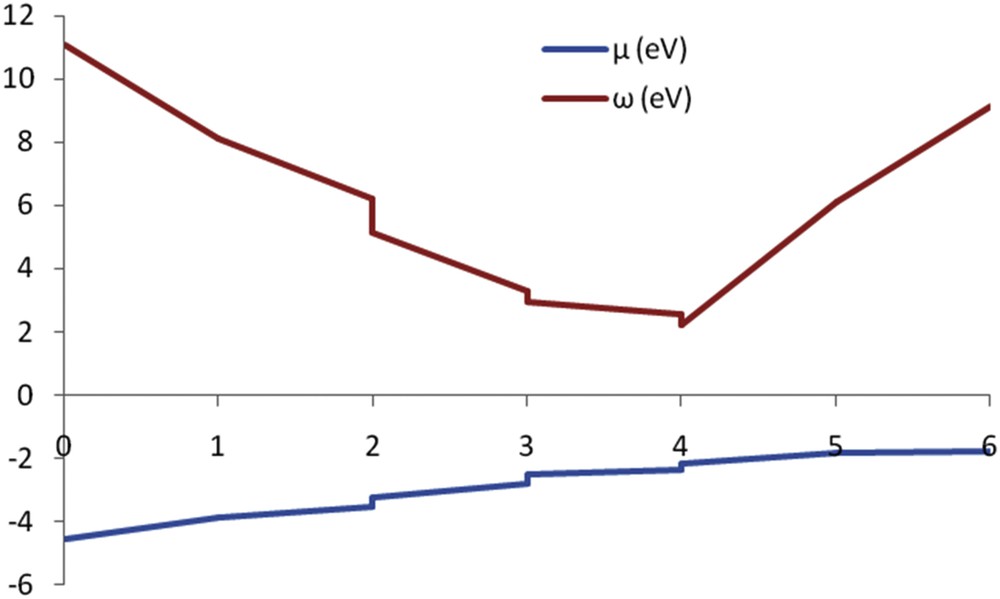
Changes in μ and ω relative to the number of Li atoms added to the C₂₀ surface.

Fig. 4 shows the minimum global electrophilicity was attributed to four Li atoms adsorbed onto the C₂₀ fullerene surface. Dipole moment (μ), α, and β₀ as optical properties for all nanostructures were calculated and listed in Table 4. A high value for β₀ is a prerequisite for the good behavior of NLO materials.

Structure	μ (a.u.)	α (a.u.)	β₀ (a.u.)
C₂₀	0.0000	188.17	0.40
Li@C₂₀	2.8120	211.80	1565.87
Li₂@C₂₀	4.1110	227.08	2840.01
Li₂@C₂₀-trans	0.0000	238.33	0.11
Li₃@C₂₀	5.0202	253.81	4347.71
Li₃@C₂₀-trans	2.5999	257.87	3395.08
Li₄@C₂₀	3.8429	274.07	3850.67
Li₄@C₂₀-trans	0.00016	285.19	0.30
Li₅@C₂₀	1.9739	2088.69	4,034,196.74
Li₆@C₂₀	0.00028	2804.79	302,865.14

It is evident that polarizability and hyperpolarizability depend on various factors. The degree of symmetry and extent of charge available in the molecules are two important factors. If the degree of symmetry increases, polarizability and hyperpolarizability must decrease. If the number of available electrons in the molecules increases, the probability of distortion as the result of external field increases and hyperpolarizability must increase. The s valence electron of the Li atom is pushed out and turns into a diffuse excess electron for the whole system and the extent of the existing electron increases as the result of Li atom adsorption onto its surface [54]. The higher polarizability and β₀ for Li₅@C₂₀ and Li₆@C₂₀ nanostructures (Table 4) could be the result of higher electron transfer from the Li atoms to a cluster. However, the lower value of β₀ for Li₆@C₂₀ can be explained by its higher degree of symmetry. NBO analysis was carried out in terms of the natural electron configuration and charge transfer. The value of the charge transfer (CT) from the Li atoms to the C₂₀ fullerene is shown in Table 5.

Structure	CT value	Structure	CT value	Structure	CT value
Li@C₂₀	0.85743	Li₃@C₂₀	2.53233	Li₄@C₂₀-trans	3.30459
Li₂@C₂₀	1.69844	Li₃@C₂₀-trans	2.52752	Li₅@C₂₀	3.43132
Li₂@C₂₀-trans	1.69458	Li₄@C₂₀	3.3199	Li₆@C₂₀	3.62532

As shown in Table 5, increasing the number of Li atoms increased the CT values. As shown previously, the enthalpy of the Li atom adsorption improved as the CT increased. Fig. 5 plots the enthalpies of Li adsorption onto the C₂₀ surface as a function of the CT value.

Fig. 5
Change in enthalpy of Li adsorption as a function of CT value.

Fig. 5 reveals that increasing the electron transfer from the Li atoms to the C₂₀ fullerene increases the exothermic reaction. As expected, the excess electrons transferred from the Li atoms to the C₂₀ changed its electronic properties. As mentioned above, the NLO of the system altered in the presence of the Li atoms. The natural electron configurations of the Li atoms in the structures are summarized in Table 6. The results indicates that, by the adsorption of the Li atoms onto the surface of the C₂₀, the p-character of the Li atoms in the Li⋯C interactions of the nanoclusters increased remarkably, particular in Li₅@C₂₀ and Li₆@C₂₀ nanostructures.

Compound	Spin multiplicity	Atom	Natural electron configuration
Li@C₂₀	2	Li	[He]2s(0.04)2p(0.10)
Li₂@C₂₀	1	Li	[He]2s(0.03)2p(0.10)3p(0.01)
Li	[He]2s(0.04)2p(0.11)3p(0.01)
Li₂@C₂₀-trans	1	Li	[He]2s(0.06)2p(0.07)3p(0.01)
Li	[He]2s(0.06)2p(0.07)3p(0.01)
Li₃@C₂₀	2	Li	[He]2s(0.04)2p(0.12)
Li	[He]2s(0.05)2p(0.12)
Li	[He]2s(0.04)2p(0.09)
Li₃@C₂₀-trans	2	Li	[He]2s(0.05)2p(0.11)
Li	[He]2s(0.06)2p(0.11)
Li	[He]2s(0.05)2p(0.11)
Li₄@C₂₀	1	Li	[He]2s(0.05)2p(0.12)
Li	[He]2s(0.04)2p(0.13)
Li	[He]2s(0.05)2p(0.13)
Li	[He]2s(0.05)2p(0.12)
Li₄@C₂₀-trans	1	Li	[He]2s(0.08)2p(0.10)
Li	[He]2s(0.04)2p(0.12)
Li	[He]2s(0.08)2p(0.10)
Li	[He]2s(0.04)2p(0.12)
Li₅@C₂₀	2	Li	[He]2s(0.13)2p(0.11)
Li	[He]2s(0.16)2p(0.13)
Li	[He]2s(0.12)2p(0.11)
Li	[He]2s(0.07)2p(0.12)
Li	[He]2s(0.46)2p(0.15)
Li₆@C₂₀	2	Li	[He]2s(0.26)2p(0.14)
Li	[He]2s(0.26)2p(0.14)
Li	[He]2s(0.26)2p(0.14)
Li	[He]2s(0.26)2p(0.14)
Li	[He]2s(0.26)2p(0.14)
Li	[He]2s(0.26)2p(0.14)

4 Conclusions

The present study calculated the structural, electronic, and optical properties of C₂₀ and Li_n@C₂₀ (n = 1–6) nanoclusters. It was shown that the interaction of Li atoms onto the C₂₀ surface is highly exothermic and the values of enthalpy per Li atom decreased slightly when the number of Li atoms increased. In addition, it can be seen that the adsorption of one to four Li atoms onto the C₂₀ surface increased its gap energy. The addition of five or six Li atoms onto its surface decreased the value of E_g. NBO analysis of the nanoclusters showed that an increase in the number of Li atoms increased the value of electron transfer. It was shown that the enthalpy of the adsorption reaction increased as the value of the charge transfer reaction increased. The effect of the Li atoms on the NLO properties of C₂₀ fullerene was explored. It was shown that the interaction of five or six Li atoms with C₂₀ fullerene greatly increased its first hyperpolarizability, making the value of β₀ for Li₅@C₂₀ very interesting.

References

[1] H.W. Kroto; J.R. Heath; S.C. O'Brien; R.F. Curl; R.E. Smalley Nature, 318 (1985), p. 162

[2] W.W. Adams; R.H. Baughman Science, 310 (2005), p. 1916

[3] W.J. Blau; H.J. Byrne; D.J. Cardin; T.J. Dennis; J.P. Hare; H.W. Kroto; R. Taylor; D.R.M. Walton Phys. Rev. Lett., 67 (1991), p. 1423

[4] Z.H. Kafafi; E.J. Bartoli; J.R. Lindle; R.G.S. Pong Phys. Rev. Lett., 68 (1992), p. 2705

[5] F. Kajzar; C. Taliani; R. Zamboni; S. Rosini; R. Danieli Synth. Met., 54 (1993), p. 21

[6] J.S. Meth; H. Vanherzeele; Y. Wang Chem. Phys. Lett., 197 (1992), p. 26

[7] H. Hoshi; N. Nakamura; Y. Maruyama; T. Nakagawa; S. Suzuki; H. Shiromaru; Y. Achiba Jpn. J. Appl. Phys., 30 (1991) (L1397)

[8] J.R. Lindle; R.G.S. Pong; E.J. Bartoli; Z.H. Kafafi Phys. Rev. B, 48 (1993), p. 9447

[9] S.R. Flom; R.G.S. Pong; F.J. Bartoli; Z.H. Kafafi Nonlinear Optics, 10 (1995), p. 183

[10] K. Harigaya; S. Abe Jpn. J. Appl. Phys., 31 (1992) (L887)

[11] Q. Gong; Y. Sun; Z. Xia; Y.H. Zou; Z. Gu; X. Zhou; D. Qiang J. Appl. Phys., 71 (1992), p. 3025

[12] F. Kajzar; C. Taliani; R. Zamboni; S. Rossini; R. Danieli Synth. Met., 77 (1996), p. 257

[13] D.F. Eaton The Great and Near Great, ACS Symposium Series, 455 (1991) no. 8, p. 128

[14] D.R. Kanis; M.A. Ratner; T.J. Marks Chem. Rev., 94 (1994), p. 195

[15] G. de la Torre; P. Vázquez; F. Agullo-Lopez; T. Torres Chem. Rev., 104 (2004), p. 3723

[16] O. Ostroverkhova; W.E. Moerner Chem. Rev., 104 (2004), p. 3267

[17] K.B. Eisenthal Chem. Rev., 106 (2006), p. 1462

[18] B.J. Coe Acc. Chem. Res., 39 (2006), p. 383

[19] K. Okuno; Y. Shigeta; R. Kishi; M. Nakano J. Phys. Chem. Lett., 4 (2013), p. 2418

[20] S. Muhammad; H.-L. Xu; R.-L. Zhong; Z.-M. Su; A.G. Al-Sehemi; A. Irfan J. Mater. Chem. C, 1 (2013), p. 5439

[21] R.-L. Zhong; H.-L. Xu; S. Muhammad; J. Zhang; Z.-M. Su J. Mater. Chem., 22 (2012), p. 2196

[22] C. Tu; G. Yu; G. Yang; X. Zhao; W. Chen; S. Li; X. Huang Phys. Chem. Chem. Phys., 16 (2014), p. 1597

[23] Y. Zhou; X. Cheng; D. Du; J. Yang; N. Zhao; S. Ma; T. Zhong; Y. Lin J. Mater. Chem. C, 2 (2014), p. 6850

[24] K. Hatua; P.K. Nandi J. Phys. Chem., A117 (2013), p. 12581

[25] S. Muhammad; H. Xu; Z. Su J. Phys. Chem., A115 (2011), p. 923

[26] Y.-Y. Hu; S.-L. Sun; S. Muhammad; H.-L. Xu; Z.-M. Su J. Phys. Chem. C, 114 (2010), p. 19792

[27] H.-Q. Wu; R.-L. Zhong; S.-L. Sun; H.-L. Xu; Z.-M. Su J. Phys. Chem. C, 118 (2014), p. 6952

[28] P. Karamanis; C. Pouchan J. Phys. Chem. C, 116 (2012), p. 11808

[29] R.-L. Zhong; H.-L. Xu; Z.-R. Li; Z.-M. Su J. Phys. Chem. Lett., 6 (2015), p. 612

[30] W. Chen; Z.-R. Li; D. Wu; Y. Li; C.-C. Sun; F.L. Gu J. Am. Chem. Soc., 127 (2005), p. 10977

[31] G. Yu; X. Huang; S. Li; W. Chen Int. J. Quantum Chem., 115 (2015), p. 671

[32] S. Muhammad; H. Xu; Y. Liao; Y. Kan; Z. Su J. Am. Chem. Soc., 131 (2009), p. 11833

[33] G. Yu; X.R. Huang; W. Chen; C.C. Sun J. Comput. Chem., 32 (2011), p. 2005

[34] L.-J. Wang; S.-L. Sun; R.-L. Zhong; Y. Liu; D.-L. Wang; H.-Q. Wu; H.-L. Xu; X.-M. Pan; Z.-M. Su RSC Adv., 3 (2013), p. 13348

[35] E. Shakerzadeh; E. Tahmasebi; H.R. Shamlouei Synth. Met., 204 (2015), p. 17

[36] S. Kamalinahad; M. Solimannejad; E. Shakerzadeh Bull. Chem. Soc. Jpn., 89 (2016), p. 692

[37] F. Ma; Z.J. Zhou; Y.T. Liu ChemPhysChem, 13 (2012), p. 1307

[38] E. Shakerzadeh; E. Tahmasebi; Z. Biglari J. Mol. Liq., 221 (2016), p. 443

[39] M. Noormohammadbeygi; H.R. Shamlouei J. Inorg. Organomet. Polym. Mater., 28 (2018) no. 1, p. 110

[40] F. Lin; E.S. Sørensen; C. Kallin; A.J. Berlinsky (2014), pp. 29-31

[41] H. Kawabata; H. Tachikawa J. Carbon Res. C, 3 (2017), p. 15

[42] A.D. Becke J. Chem. Phys., 98 (1993), p. 5648

[43] C. Lee; W. Yang; R.G. Parr Phys. Rev. B, 37 (1988), p. 785

[44] T. Yanai; D. Tew; N. Handy Chem. Phys. Lett., 393 (2004), p. 51

[45] J.-D. Chai; M. Head-Gordon Phys. Chem. Chem. Phys., 10 (2008), p. 6615

[46] A. Ahmadi; N.L. Hadipour; M. Kamfiroozi; Z. Bagheri Sens. Actuators, B., 161 (2012), p. 1025

[47] J. Beheshtian; A.A. Peyghan; Z. Bagheri Comp. Mater. Sci., 62 (2012), p. 71

[48] J. Beheshtian; M. Kamfiroozi; Z. Bagheri; A. Ahmadi Physica E, 44 (2011), p. 546

[49] J. Beheshtian; A.A. Peyghan; Z. Bagheri Sens. Actuators, B, 171–172 (2012), p. 846

[50] N.M. O'boyle; A.L. Tenderholt; K.M. Langner J. Comput. Chem., 29 (2008), p. 839

[51] M.J. Frisch; G.W. Trucks; H.B. Schlegel; G.E. Scuseria; M.A. Robb; J.R. Cheeseman; G. Scalmani; V. Barone; B. Mennucci; G.A. Petersson; H. Nakatsuji; M. Caricato; X. Li; H.P. Hratchian; A.F. Izmaylov; J. Bloino; G. Zheng; J.L. Sonnenberg; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; T. Vreven; J.A. Montgomery; J.E. Peralta; F. Ogliaro; M. Bearpark; J.J. Heyd; E. Brothers; K.N. Kudin; V.N. Staroverov; R. Kobayashi; J. Normand; K. Raghavachari; A. Rendell; J.C. Burant; S.S. Iyengar; J. Tomasi; M. Cossi; N. Rega; J.M. Millam; M. Klene; J.E. Knox; J.B. Cross; V. Bakken; C. Adamo; J. Jaramillo; R. Gomperts; R.E. Stratmann; O. Yazyev; A.J. Austin; R. Cammi; C. Pomelli; J.W. Ochterski; R.L. Martin; K. Morokuma; V.G. Zakrzewski; G.A. Voth; P. Salvador; J.J. Dannenberg; S. Dapprich; A.D. Daniels; Ö. Farkas; J.B. Foresman; J.V. Ortiz; J. Cioslowski; D.J. Fox Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2009

[52] A.E. Reed; R.B. Weinstock; F. Weinhold J. Chem. Phys., 83 (1985), p. 735

[53] A. Vektariene; G. Vektaris; J. Svoboda Arkivoc, 7 (2009), p. 311

[54] M. Solimannejad; S. Kamalinahad; E. Shakerzadeh J. Electron. Mater., 46 (2017), p. 4420

Comments - Policy