1 Introduction
Water pollution is recognized as one of the major problems in the world. It represents a serious threat to human health because of the uncontrolled industrial discharges, the intensive use of chemical fertilizers in agriculture, and the disorderly exploitation of water resources. Many minerals such as Ca2+, Mg2+, Na+, Cl−, and F− are essential to the body; however, the excessive intake of these substances can cause harmful effects to human health and the environment [1]. In addition to arsenic and nitrate, fluoride ions (F−) have been classified as one of the most dangerous groundwater contaminants that lead to large-scale health problems by the World Health Organization [2]. Different technologies such as adsorption [3,4], oxidation [5], ion exchange [6], precipitation [7], electrodialysis [6], and reverse osmosis have been used for fluoride removal from water. Adsorption is reported as one of the most effective and economical techniques for water defluorination. The adsorption process is known to be simple and efficient in pollutant treatment in concentrated form at a low cost. In addition, it is relatively considered as an environmentally friendly process [7]. Many low-cost adsorbents have been used for fluoride removal from water [8,9], including activated alumina [10], activated carbon [11], kaolinite, bentonite, and montmorillonite [12], and so forth. The frequent use of clays is mainly because of their abundance and large reactive surface. In addition, clays can be preferred to synthetic adsorbent materials because of their relatively low costs [13].
Clay and clay mineral application in fluoride removal from water is well supported in the literature. In fact, considerable quantities of montmorillonite, kaolinite, or pyrophyllite clay display a huge potential for fluoride adsorption [14–16]. The positively charged surface of clay minerals provides an explanation for the high affinity uptake of the negatively charged ions at near neutral pH. The fluoride removal capacity of clay and clay minerals is impacted by different factors, such as pH and the medium's strength, and thermodynamic conditions [17,18]. Raw clay and clay minerals are rarely used and they are often used after physicochemical modifications such as metal oxide amendment, acid treatment, and thermal activation. Such modifications enhance stability at the optimal operating pH, active sites accessibility, adsorption capacity, and surface area [17,19]. Effective defluoridation with acid-activated kaolinite compared with raw kaolinite, where maximum sorption capacity of acid-activated clay ranged between 0.0450 and 0.0557 mg g−1 at different temperatures, was reported in Ref. [20].
In the past decades, most articles on fluoride adsorption onto clay fields have interpreted the results with a pseudo-first-order or pseudo-second-order kinetic models [14,17,19,21,22]. Besides, Elovich kinetics model has been applied to chemisorption on the heterogeneous surface [4]. The traditional and routine fitting with pseudo-first-order and pseudo-second-order kinetic equations can sometimes give good fits with a coefficient of determination or correlation function (R2) values greater than 0.995 as this is the case here. However, we cannot be assured of an equation that does not give a correct time variation in the rate and veils the true evolution of the kinetics, whose rate is not necessarily uniform (pseudo-first-order), linear (pseudo-second-order). Nevertheless, it is well documented in the literature that the overall adsorption in a porous adsorbent must not only consider the adsorption rate on an active site but also the external mass transfer, surface diffusion, intraparticle diffusion, and pore volume diffusion [21].
The aims of this work were as follows: first, to study the fluoride adsorption kinetics onto activated clay; second, to assess the solution agitation speed, initial fluoride ion concentration, and adsorbent dosage effect on matter transfer rate, and eventually to find a simple mathematical model suitable for a better understanding of the physical phenomena involved in a more appropriate design, operation, optimization, and control of the industrial process separation. Simplified models of external diffusion are tested to describe the adsorption process. The external diffusion coefficient, kf, is determined using different models and then correlated with the experimental variables.
2 Experimental section
2.1 Materials
In this work, bentonite clay selected from an El-Hicha site in the south of Tunisia was used as a raw material. The material was purified by aqueous dispersion and decantation. After the purification process, the clay remained quartz free and the fraction with a particle size less than 40 μm was separated and subjected to activation. Sulfuric acid treatments were used to increase the clay mineral surface area and to obtain high porosity.
The activated sample was obtained according to the following procedure: 100 g of material clay micropowder was mixed with an aqueous H2SO4 solution (acid concentration of 13.8%) in a jacketed glass reactor regulated at a fixed temperature (75 °C) by a thermostated bath for 3.75 h under mechanical stirring at 200 rpm. Then, it was washed with distilled water many times until pH of 6 was reached. The obtained samples were dried at 60 °C for 24 h.
The physicochemical and textural characteristics using the Brunauer, Emmett and Teller method (BET), described in a previous work [24] are shown in Table 1.
Physicochemical properties of the studied clay samples.
| Chemical composition (% by weight) | Natural clay | Acid activated clay |
| SiO2 | 47.70 | 50.12 |
| Al2O3 | 18.71 | 18.26 |
| Fe2O3 | 12.37 | 9.12 |
| CaO | 3.67 | 1.93 |
| MgO | 2.59 | 1.89 |
| K2O | 1.05 | 0.87 |
| Na2O | 0.96 | 0.17 |
| P2O5 | 0.32 | 0.02 |
| SO3 | 0.96 | 4.91 |
| Li | 14 | 12 |
| Structural parameters | ||
| Specific surface of BET (m2 g−1) | 86 | 167 |
| Total pore volume (cm3 g−1) | 0.1394 | 0.1986 |
| Mean pore diameter (Å) | 40.53 | 49.03 |
2.2 Adsorption test experiments
A sodium fluoride stock solution was prepared by dissolving 2.21 g of sodium fluoride (analytic reagent grade) in 1000 mL of double glass distilled water, the stock solution of desired fluoride concentration. The residual fluoride concentration in each sample was determined using ion selective electrode, fluoride electrode, and “Orion ion analyzer” model 9409-SC.
2.3 Equilibrium isotherm studies
To determine the activated clay adsorption capacity of the fluoride ion, 1 g of activated clay was added into 100 mL of fluoride ion solutions with initial concentrations ranging between 50 and 500 mg L−1. The resulting suspensions were shaken at a constant stirring rate 400 rpm for 3 h to reach equilibrium. The experiments were carried out at 25 °C with a pH value adjusted to 5 [25].
The amount of fluoride adsorbed onto the activated clay at equilibrium, qe (mg g−1), was obtained as follows:
| (1) |
2.4 Batch kinetic studies
The study is carried out at the laboratory in a liquid phase in an agitated “adsorber” tank operating in batch mode. It is a 2 L volume jacketed reactor maintained at constant temperature and equipped with a paddle stirrer. We introduced 1 L of fluoride ion solution at concentrations ranging from 30 to 90 mg L−1, for different mass adsorbents varying from 0.5 to 1.5 g and different stirring speeds ranging between 150 and 300 rpm and at pH 5 and at a temperature of 25 °C. The samples taken intermittently made it possible to pursue the concentration of fluoride solution residual. Samples of 5 mL were taken and centrifuged for a minimum time at a speed of 2000 rpm [26]. The fluoride solution residual concentration was determined from a previous calibration curve. We follow for a dry activated clay mass of 1 g L−1 of solution, an initial fluoride ion concentration of 30 mg L−1, a variable stirring speed, and the evolution of the reduced concentration, Ct/C0, with function of time.
3 Theoretical model
The solute adsorption mechanism on the surface of a solid goes through several successive elementary stages. Each of these stages can control the global phenomenon under given conditions. Fluoride adsorption requires (1) sorbate transport from the bulk of the solution to the exterior film surrounding the adsorbent; (2) sorbate movement across the external liquid film boundary layer to external surface sites; and (3) sorption of sorbate at internal surface sites. The last step is much faster than the first two and consequently its contribution to the overall resistance to the adsorption process is often neglected. Accordingly, the limiting step of the process can be of external type, internal type, or both.
Two resistance models are very complex because the transfer equations are coupled and the resolution of the equation system requires numerical resolution methods.
It is difficult to predict if one or both resistances (external or internal) limit the overall process without adsorption experiments.
Several researchers have studied the problem of external transport to define the conditions under which the hypotheses of this type of transfer and consequently the calculating method of the coefficient in the outer film, kf, are valid [23,27]. In all these calculating methods kf the resistance in the outer film is the limiting step at the beginning of adsorption.
In the present work, we faced the problem of determining the method of choice for calculating kf and so retain the model that best describes the physical reality of the adsorption process. Therefore, four methods taken from the bibliography, namely, the following models of the initial slopes of Furusawa and Smith (Model I), Mathews and Weber (Model II) [23], Furusawa and Smith for a linear isotherm (Model III), and dimensional analysis of Harriott (Model IV) [23] were tested. Note that the first three methods are based on experimental adsorption data whereas the last is completely empirical.
3.1 Model of initial slopes
This model was initially used in the adsorption of benzene on activated carbon [27]. In a perfectly stirred adsorber, the solute concentration, Ct, at different times and the solid concentration, ms, were supposed to be uniform within the liquid phase. ms can be calculated by the following equation:
| (2) |
For average diameter spherical particles, dp, bulk density, ρp, and external exchange area can be obtained as follows:
| (3) |
The solute concentration variation in the liquid phase as a function of time is related to the external transfer coefficient, kf (m s−1), by the following relation:
| (4) |
| (5) |
Thus kf can simply be determined from the initial slope of the curve Ct/C0 as a function of time. Then, the values of kf are correlated with each variable (concentration, stirring speed, and adsorbent dosage), X, by a general equation of the type [23]
| (6) |
3.2 Model of Mathews and Weber
The integration of Eq. 4, when t and Cs tend to zero, leads to
| (7) |
3.3 Linear model of Furusawa and Smith (FS)
In the case where the equilibrium between the solute and the solid is of the linear type (qe = KLCe), the equation of the model will be [28]
| (8) |
From the ordinate at the origin, msKL/(1 + msKL), and the slope, −((1 + msKL)/msKL)kfAp, of the line ln(Ct/C0 − 1/(1 + ms + KL)) as a function of time, kf is deduced.
3.4 Dimensional analysis: Harriot method
According to Harriot, the material transfer coefficient between the liquid and the suspended particles in a stirred tank, kf, can be calculated from the Tien relation [28]:
| (9) |
| (10) |
The molecular diffusion coefficient of the solute in the liquid phase, Dm, is given by the Wilke–Chang relation [30]:
| (11) |
4 Results and discussion
4.1 Equilibrium studies
The equilibrium biosorption data are analyzed using the Langmuir model as shown by the following equation:
| (12) |
| (13) |
Fig. 1 shows the Langmuir isotherm plots of the experimental data for fluoride ion biosorption onto activated clay. The isotherm constants of the Langmuir model are shown in Table 2. The results indicate that the adsorption capacity of activated clay particles is high for the F− 75.757 mg g−1 at 25 °C. The RL values dictate favorable adsorption for 0 < RL < 1. On the basis of the R2 = 0.995, there is an overall agreement that Langmuir model is the most suitable for designing industrial adsorption processes. The comparison of maximum adsorption capacity of F− ions onto various adsorbents is presented in Table 3. It shows that the activated clay studied in this work has acceptable adsorption capacity.
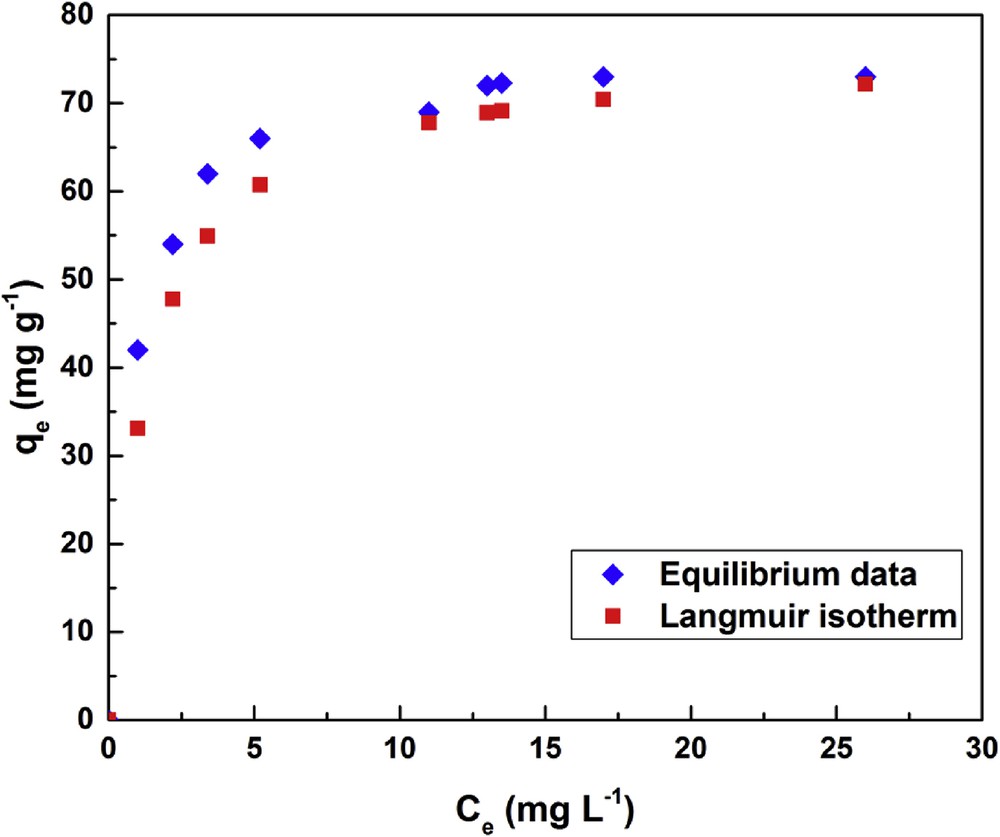
Adsorption of fluoride ions onto activated clay using the Langmuir isotherm.
Langmuir isotherm constants for fluoride ions onto activated clay.
| Constants | qm (mg g−1) | b (L mg−1) | KL = b×qm (L g−1) | RL | R2 |
| Fluoride | 75.757 | 0.776 | 58.787 | 0.36 | 0.995 |
4.2 Kinetic studies – external mass transfer
4.2.1 Stirring speed effect
Fig. 2 shows that adsorption rate depends on the stirring speed, N, and that it is fast for t < 20 min, then it slows down. This phenomenon can be due to the increase in the stirring speed, which affects the resistance to the material transfer outside the clay particle [34]. Hereafter, for the calculation of kf, we will detail the method of initial slopes for its simplicity. Fig. 3 shows the variation of ln kf as a function of ln N. Relying on this variation, we found the following correlation between kf and N: kf = 1.077 × 10−4 N0.639
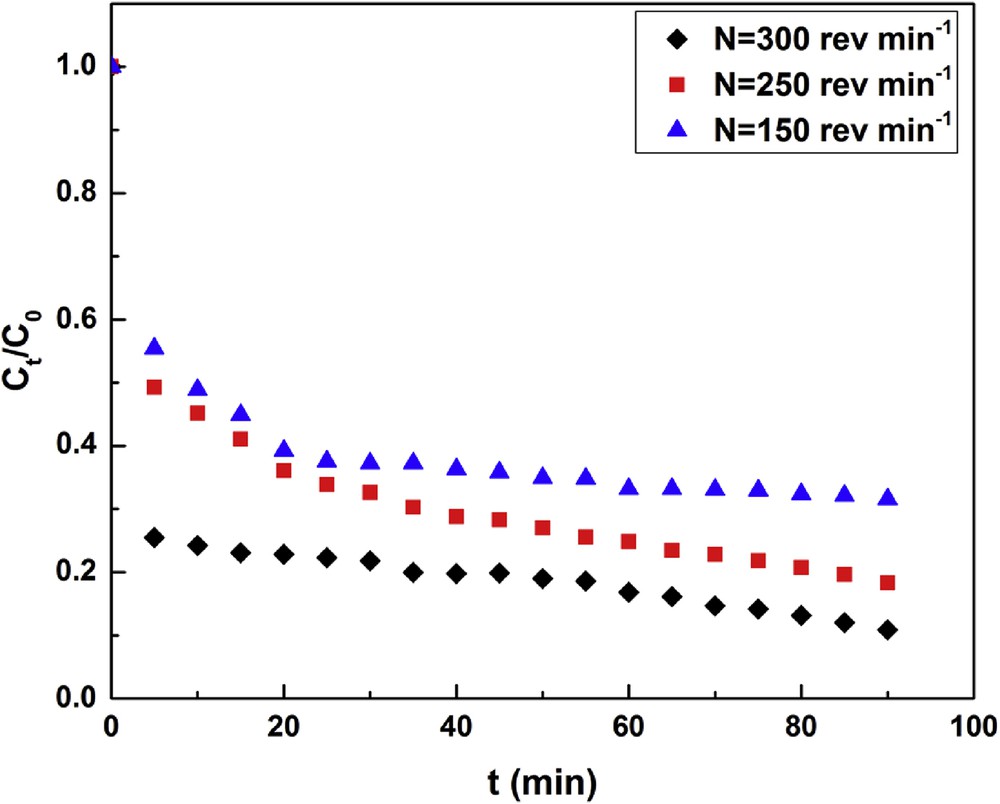
Effect of the stirring speed (pH = 5, T = 25 °C, m = 1 g, C0 = 30 mg L−1).

ln(104 kf) versus ln(N).
4.2.2 Adsorbent dosage effect
Fig. 4 illustrates that for a contact time of 20 min, the adsorption kinetics goes up by increasing the mass of clay to 1.5 g. It also displays beyond 90 min, the material transfer rate tends to zero. As shown in Fig. 5, the correlation between kf and m is
| kf = 22.965 × 10−4 m0.55 |
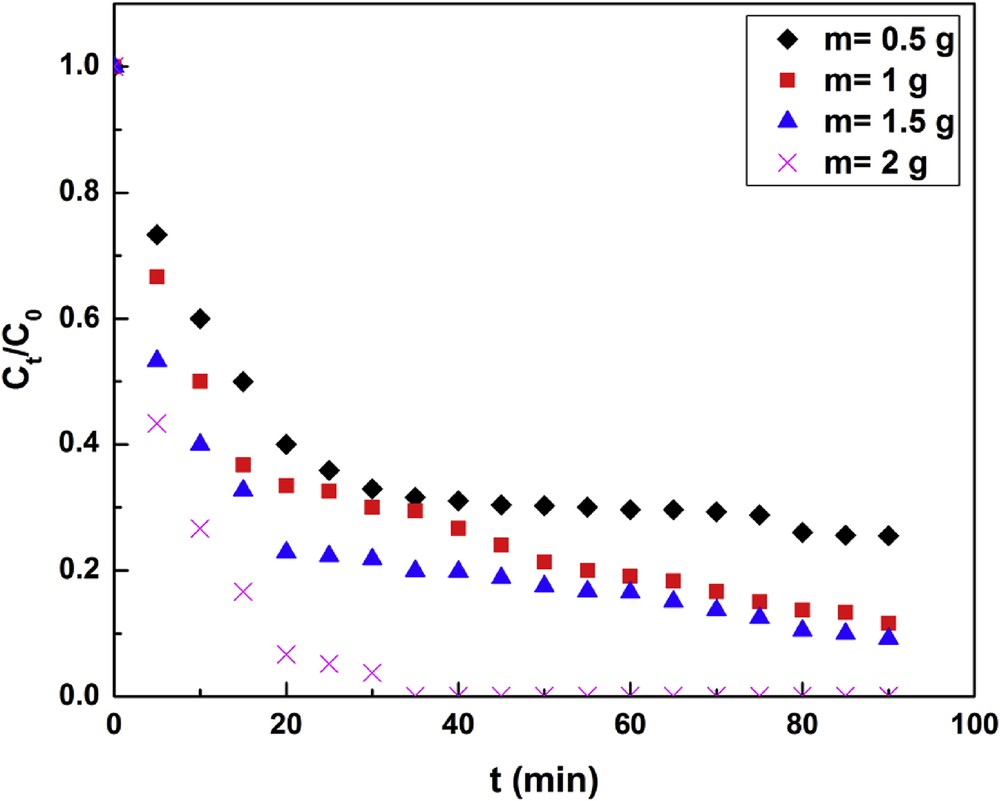
Adsorbent dosage effect (pH = 5, T = 25 °C, C0 = 30 mg L−1, N = 250 rpm).
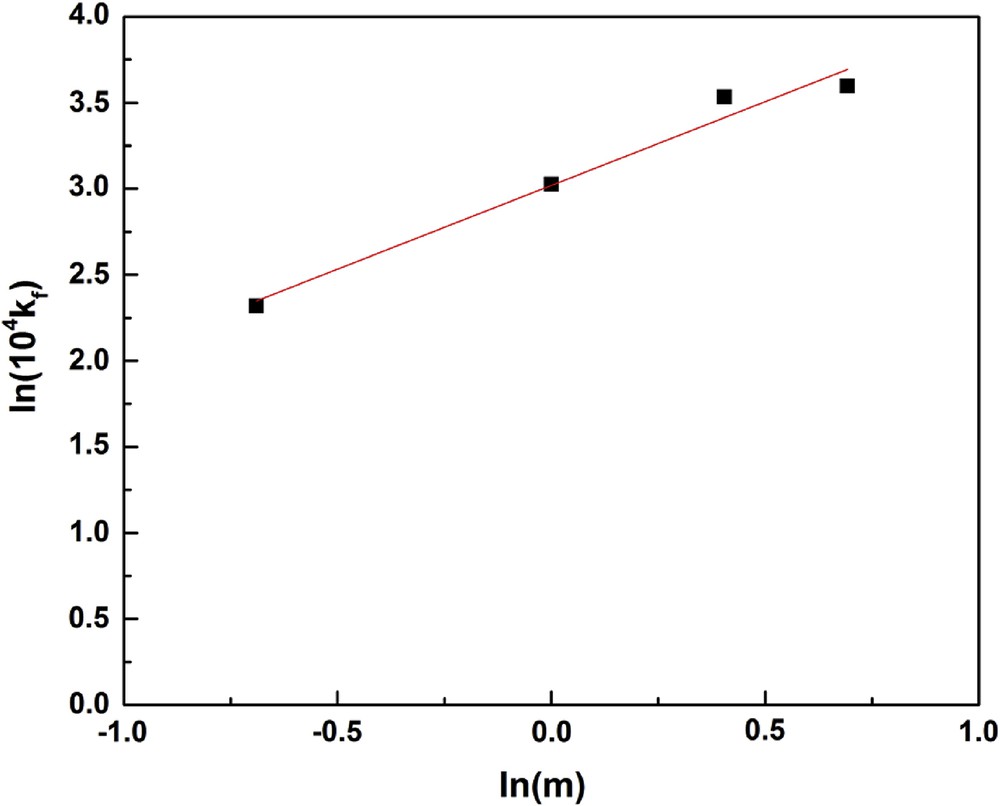
ln(104 kf) versus ln(m).
This result indicates that the fluoride solute transport in the outer film is also controlled by the clay mass in solution. Increasing the mass of clay in solution helps to augment the liquid film transfer coefficient. Literature in general indicates an increased removal efficiency (RE) with adsorbent dose. Kim et al. [35] observed that an increase in pyrophyllite dose (from 0.05 to 2.0 L−1) improves the RE (25–98.5%) at a fixed initial fluoride concentration. Similar observations have been reported by others [19,36] while carrying out fluoride removal studies with kaolinite and bentonite. It can be inferred from the literature that the increase in RE is mainly attributed to the enhancement number of active sites available for adsorption of fluoride ions.
4.2.3 Initial concentration effect
Fig. 6 shows that the adsorption is faster at its beginning than at its end. For instance, after 40 min, the adsorption slows down: this deceleration is probably because of the resistance to the material transfer inside clay particles. Toward high concentrations, the gap becomes tight and the adsorbed fraction is small. In addition, the time required to reach equilibrium varies with the initial fluoride concentration. As shown in Fig. 7, the correlation between kf and C0 is
| kf = 36.52 × 10−4 C0−0.132 |
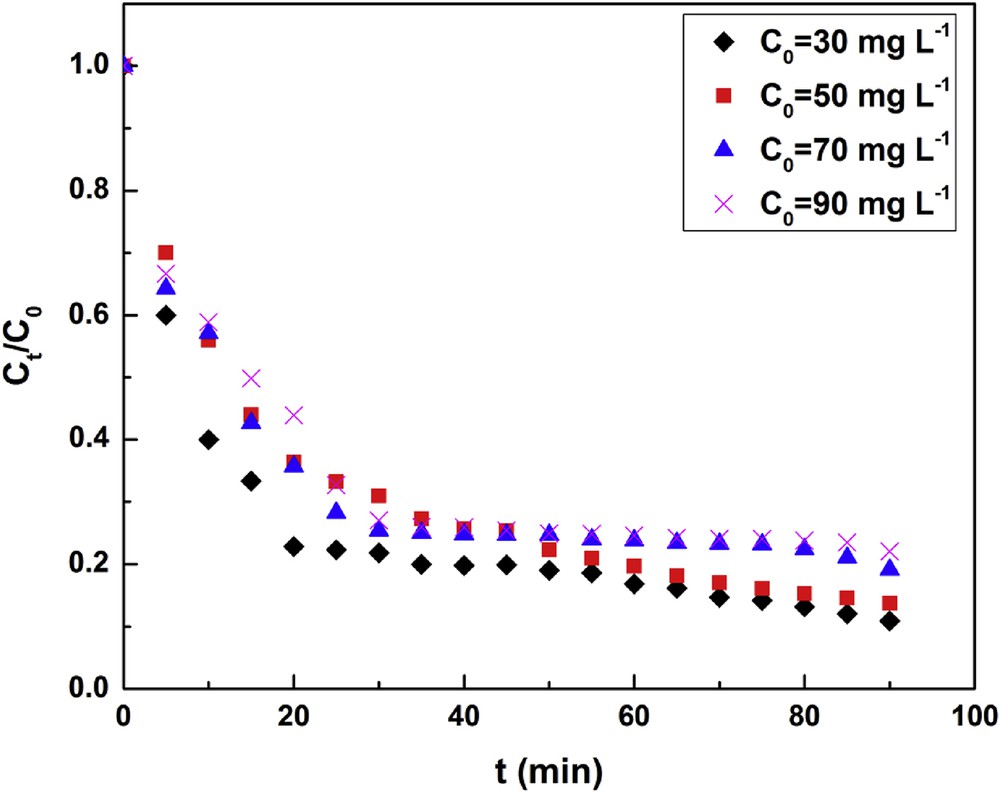
Effect of the initial concentration (pH = 5, T = 25 °C, m = 1 g, N = 250 rpm).
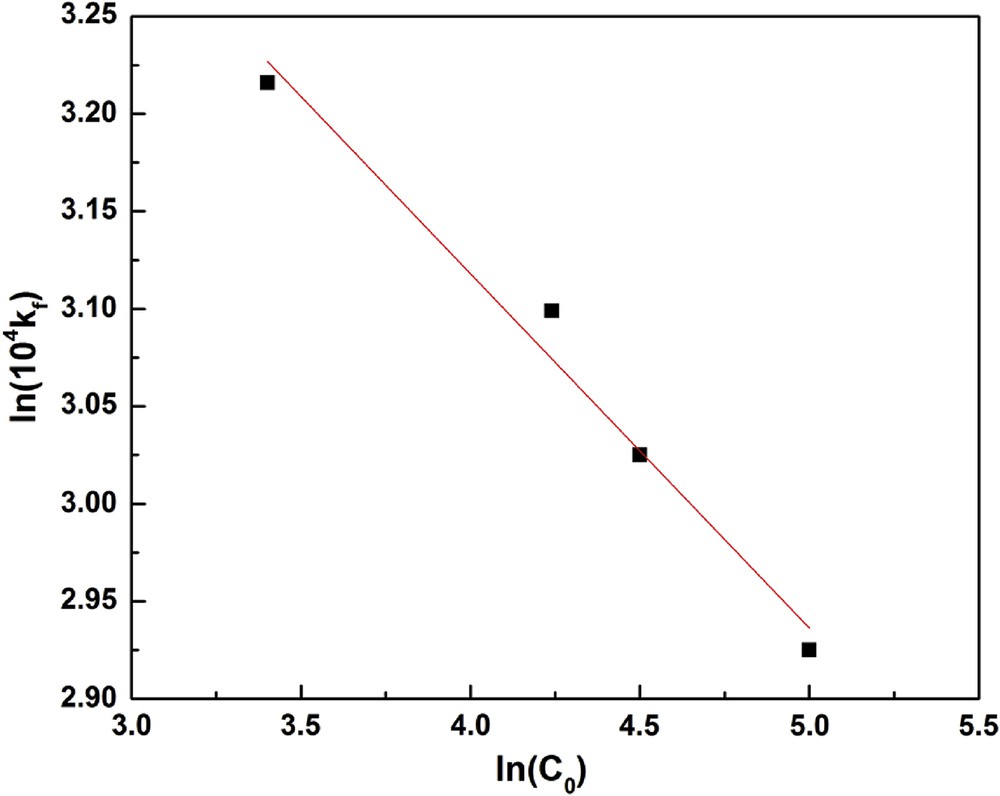
ln(104 kf) versus ln(C0).
The negative value of p indicates that, for the fluoride/clay pair studied, the transfer coefficient in the outer film decreases with the initial fluoride ion concentration, in agreement with the observations of Mckay et al. [37]. Using magnesium incorporated bentonite and pyrophyllite [15,19] showed that increase in initial fluoride concentration leads to a decrease in RE. The authors explained the behavior in terms of exhausted binding capacity of bentonite or increased competition for the active adsorption sites at higher fluoride concentration.
Table 4 regroups the final and complete result of kf values calculated by the different models. Table 5 involves a comparison between our results and those found in the bibliography. Thus, we remark the following:
- - Despite the diversity of studied pairs, the magnitude order of kf is in the range of 10−5–10−4 m s−1.
- - For all solute/adsorbent pairs, an increase in variation of kf with m.
- - The effect of the initial solute concentration is negative: an effect contrary to that of the stirring speed.
- - The calculation of kf by the adimensional analysis method does not provide the variation of this coefficient with the initial concentration and the mass of adsorbent in solution. Besides, the laws of the boundary layer theory state that kf is proportional to the solute diffusion coefficient of the solute in the surrounding medium and the flow conditions around the solid particles. We made this variation with C0 and m at the concentration gradient established at the beginning of the adsorption process. Despite this handicap by this method, the order of magnitude of kf is always in the margin mentioned.
- - The difference between the values of kf calculated by models II and III is very small. This result is attributed to the term ms×KL/(1 + ms×KL), which is almost equal to 1 in the case of the study couple. The use of Model I for the experimental determination of kf can be suggested because of its simplicity.
Results of the calculation of kf by the different models (×10−5 m s−1).
| Solute | Effect of model | I | II | III | IV | |
| F− | N (rpm) | 150 | 13.38 | 1.86 | 1.68 | 13.5 |
| 200 | 20.60 | 2.17 | 1.89 | 20.3 | ||
| 250 | 23.62 | 2.27 | 1.95 | 23.5 | ||
| 300 | 33.07 | 2.47 | 2.70 | 33.45 | ||
| C0 (mg L−1) | 10 | 10.89 | 3.10 | 2.52 | 33.45 | |
| 30 | 10.23 | 2.49 | 2.00 | 33.45 | ||
| 50 | 8.00 | 2.10 | 1.19 | 33.45 | ||
| 70 | 7.66 | 1.50 | 1.65 | 33.45 | ||
| m (g) | 0.5 | 10.23 | 1.44 | 1.65 | 33.45 | |
| 1 | 20.60 | 2.75 | 2.57 | 33.45 | ||
| 1.5 | 34.25 | 3.75 | 4.44 | 33.45 | ||
| 2 | 36.48 | 7.08 | 9.52 | 33.45 |
External transfer coefficient kf (m s−1); comparison with the bibliography.
| Adsorbent | Field of validity | Solute | Variables | Model | Reference | ||
| N (rpm) | C0 (g L−1) or T (°C) | m (g) | |||||
| Bone char | 2 ≤ C0 ≤ 5 mmol/L 6.5 ≤ m ≤ 10.5 g 250 ≤ dp ≤ 100 μm | Cd2+ | 4.36 × 10−6 ≤ kf ≤ 7.30 × 10−6 | 5.47 × 10−6 ≤ kf ≤ 6.23 × 10−6 | FS | [23] | |
| Cu2+ | 6.14 × 10−4 ≤ kf ≤ 1.0 × 10−3 | 8.01 × 10−6 ≤ kf ≤ 8.99 × 10−6 | |||||
| Zn2+ | 4.75 × 10−4 ≤ kf ≤ 7.39 × 10−4 | 5.34 × 10−6 ≤ kf ≤ 6.40 × 10−6 | |||||
| Natural clay | 207 ≤ N ≤ 684 rpm 0.05 ≤ m ≤ 0.25 g 5 ≤ C0 ≤ 30 mg L−1 0.45 ≤ dp ≤ 1.75 | BM | kf = 2.73 × 10−5 N0.28 | kf = 5440 × 10−5 C0−1.91 | kf = 190 × 10−5 m1.83 | FS | [32] |
| VM | kf =1.22 × 10−5 N0.19 | kf = 11.63 × 10−5 C01.4 | kf = 7.57 × 10−5 m0.28 | ||||
| RC | kf = 1.26 × 10−9 N1.81 | kf = 17.1 × 10−5 C0−0.66 | kf = 26 × 10−5 m0.88 | ||||
| China clay | 30 < T < 50 °C | F− | 2.716 < kf < 5.042 × 10−5 | FS | [33] | ||
| Activated clay | 150≤ N ≤ 300 rpm 0.5 ≤ m ≤ 1.5 g 30 ≤ C0 ≤ 90 mg L−1 | F− | kf = 1.077 × 10−4 N0.639 | kf = 36.52 × 10−4 C0−0.132 | kf = 22.965 × 10−4 m0.55 | FS | This study |
5 Conclusions
In the present work, we studied the adsorption kinetics of fluoride onto activated clay to design an industrial adsorber. It was demonstrated in the first part that the optimal adsorption time is 30 min for a solution clay concentration of 1.5 g L−1, at a minimum stirring speed of 300 rpm. Under these conditions, the pollutant elimination rate is greater than 90%. The transfer coefficient in the outer boundary layer was determined. This coefficient varied with the agitation speed, the initial fluoride ion concentration, and the adsorbent mass. Despite the diversity of the studied pairs, kf magnitude order was in the range of 10−5–10−4 m s−1.
Nomenclature
AP
surface area of sorbent (m−1)
Bequation constant
bLangmuir isotherm constant (g L−1)
Crliquid phase concentration at radius r (mg L−1)
C0initial liquid phase concentration (mg L−1)
Ceequilibrium liquid phase concentration (mg L−1)
Csliquid phase concentration at external sorbent surface (mg L−1)
Ctliquid phase concentration at time t (mg L−1)
Dmmolecular diffusion coefficient of fluoride ions (m2 s−1)
dp:diameter of sorbent (m)
KL:Langmuir constant (L g−1)
kfExternal mass transfer coefficient (m s−1)
Equilibrium external mass transfer coefficient (m s−1)
mmass of dry sorbent (g)
Mmolecular weight of the solvent (g mol−1)
msconcentration of sorbent (g L−1)
Nstirring speed (rpm)
Pequation constant
rradius of concentration front of metal ions penetrating adsorbent (m)
tcontact time (s)
utterminal velocity (m s−1)
Vliquid phase volume (L)
Vmmolar volume (m3 mol−1)
φsolvent-fluoride ion association factor (pour l'eau φ = 2.26)
μdynamic viscosity of fluid (kg m−1 s−1)
νkinematic viscosity (m2 s−1)
ρp:particle density (kg m−3)
ρsolution density (kg m−3)


