1 Introduction
The possibility to combine, in a single material, interesting physical properties [1] with thrilling architectures [2], makes extended coordination polymers (CPs) [1,3–5] very attractive compounds for scientists working in the multidisciplinary field of coordination chemistry. In particular, the myriad of intriguing magnetic properties that CPs can present are particularly appealing to design materials of interest in the field of molecular magnetism [6,7]. They can include varied properties such as slow magnetic relaxation effects [8], when single-ion magnets (SIMs) [9–14] constitute the nodes of the network and, more commonly, the appearance of a spontaneous magnetization below a critical temperature (TC) [15].
In connection with the last point, a careful choice of paramagnetic ions and organic ligands, capable of transmitting the magnetic coupling in the appropriate way, turns out to be crucial in designing CPs exhibiting a long-range magnetic ordering. In addition, an accurate control of the coordination network structure, which is not easy as a consequence of the many subtle factors that may affect the assembly process [16,17], should be achieved. For example, oxamato ligands [18] have already been shown to be effective in two ways: First, they efficiently transmit the magnetic coupling (ferromagnetic [19–21] or antiferromagnetic [22,23]) between neighboring metal atoms; second, they allow the rational synthesis of two-dimensional (2D) [24–26] and three-dimensional (3D) [27–34] magnets with first row transition metals through their free carbonyl groups (Scheme S1). Therefore, they seem to be a good choice for the design of new magnets. About paramagnetic metal ions, most examples with oxamato ligands reported so far involve only 3d metal ions [35]. In this context, the lack of examples of CPs with lanthanide(III) ions exhibiting a long-range magnetic ordering is rather paradoxical, taking into account that rare-earth garnets, alloys, and oxides usually exhibit magnetic order and they effectively find application in industry [36]. This is usually explained considering that lanthanide(III) ions (where unpaired electrons are in the inner 4f orbitals) exhibit very weak magnetic couplings [37]. The most common strategy to overcome this situation relies on the use of radicals [38–40] or ligands (such as CN−) [41–47] capable of allowing very strong magnetic couplings and thus long-range magnetic ordering. In any case, it is clear that novel examples of lanthanide-based compounds with organic ligands showing strong magnetic interactions are still interesting.
Overall, although many lanthanide-based SIMs [48], single-molecule magnets (SMMs) [49], and single-chain magnets (SCMs) [50] have been reported, as mentioned previously, examples of high-dimensional lanthanide-based magnets are still very scarce and much work remains to be done. Kahn et al. [51] explored the efficiency oxamato and oxamidato ligands to transmit the magnetic coupling between 3d and 4f metal ions. Therefore, Kahn et al. [51] published a few pioneering works on 3d-4f 1D and 2D Cu2+-Ln3+ CPs [51], showing infinite chains [52], ladder-like type [53,54], and honeycomb [55] architectures; these compounds, with the only exception of the very poorly diffracting Nd2[Cu(opba)0.5(ox)]3(DMF)9 [51], lacked X-ray characterization, and long-range ferromagnetic orderings could be observed only at a low temperature such as 1.78 K [55].
2 Results and discussion
In this work, we use the “complex-as-ligand” approach [56] for the rational synthesis of a novel 3d-4f CP. We have previously demonstrated [35] that a variety of oxamato-based copper(II) precursor complexes can be used as building blocks, through the free carbonyl oxygen atoms of their oxamate groups, for the rational synthesis of high-dimensional CPs. In particular, taking Kahn's work as a basis and our results with the anionic oxamato-based mononuclear copper(II) complex, [CuII(Me2pma)2]2– (Scheme S1) [Me2pma = N-2,6-dimethylphenyloxamate] [25,57], which already led to successful results with transition metal ions, herein we report and characterize, structurally, a new 2D CP of formula [LiI(OH2)4]2[DyIIICuII2(Me2pma)4ClH2O] (1), showing a ferromagnetic interaction through the oxamato bridges connecting the copper(II) and dysprosium(III) centers. The crystal structure could be resolved allowing a relationship between the structure and the magnetic properties of 1.
Cubic prisms of 1, suitable for X-ray diffraction, were obtained after some days of slow evaporation of a water/acetonitrile/methanol solution (1:10:10 volume ratio) containing stoichiometric amounts of Li2[CuII(Me2pma)2] . 2H2O and DyCl3 with an excess of LiCl (see Supporting Information). Interestingly, the excess of LiCl seems to play a key role in the crystallization process that leads to the formation of the final network. This behavior can be attributable to different parameters such as solubility, supramolecular interactions including hydrogen bonds (see section 2.1), ionic force, and/or equilibrium displacement.
2.1 Crystal structure
Compound 1 crystallizes in the I4/m space group of the tetragonal system (Table S1, Supporting Information). The structure of 1 consists of an anionic 2D network, {DyIII[Cu(Me2pma)2]2Cl(H2O)}2-, and Li(H2O)4+ countercations, which are intercalated within adjacent square-grid layers of (44·62) net topology growing in the ab plane (Fig. S1), together with disordered crystallization water molecules (Fig. 1).
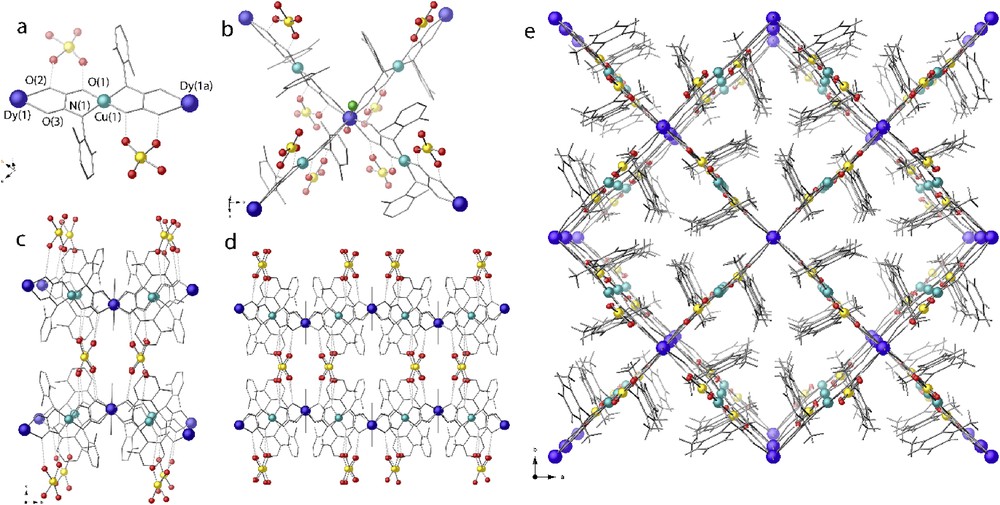
View of fragments of the anionic network of 1. [CuII(Me2pma)]2- entities acting as a bridge toward DyIII metal ions together with Li(H2O)4+ countercations H-bounded to oxamate moieties (a,b). Views along the a and c directions of {DyIII[Cu(Me2pma)2]2Cl(H2O)}2- square grids interconnected by Li(H2O)4+ ions (c–e). Cu, Dy, Li, and O atoms are depicted as green, blue, gold, and red spheres, respectively, whereas ligands are represented by sticks.
Within the anionic oxamato-bridged framework of 1, each CuII ion is surrounded by two DyIII ions, whereas each DyIII ion is surrounded by four CuII ions, thus accounting for the final 2:1 Cu:Dy stoichiometry (Fig. 1a–b). Thus, each square grid is defined by DyIII corners and CuII ions residing in the middle of the square side arranged pretty close to an ideal square grid with a Cu(1)–Dy(1)–Cu(1c) [(c) = y, −x, z] angle of 88.7°. Furthermore, squares are decorated and almost entirely filled by the aromatic rings of the oxamate ligands pointing inward the pores.
Overall, the connectivity of the CuII and DyIII ions in 1, acting as biconnectors and tetraconnectors (Fig. S2), respectively, yields a 2D net similar to those found when n-Bu4N salt of the copper(II) precursor [CuII(Me2pma)]2- is reacted with the nitrate salt of the SrII and BaII ions (Fig. 1c–b) [58]. Each CuII ion is tetra-coordinated by two bis(bidentate) oxamate bridging ligands in a square-planar CuN2O2 geometry [with average Cu–O and Cu–N bond distances of 1.86(2) and 1.85(5) Å, respectively]. In turn, the DyIII ions are ten-coordinated being surrounded by four oxamate bridges from different [CuII(Me2pma)]2- entities, a chlorine, and a water molecule in a distorted bicapped cubic geometry MnO9Cl (Fig. 2). The two crystallographically distinct Dy-Ooxamate bond lengths of 2.37(1) and 2.44(2) Å [for Dy-O2 and Dy-O3 and their symmetrical equivalents, respectively (Fig. 2a)] are shorter than those of the Dy-Ow [2.59(2) Å for Dy-O4] and Dy-Cl [2.62(3) Å] ones but in agreement with those found in literature for analogue environments [59,60].

Views of the DyIII coordination polyhedron of 1 showing the bicapped cubic geometry with the labeling of the metal coordination environment in the ab (a) and bc (b) planes, respectively. Dysprosium, water-oxygen, and chlorine atoms are represented by blue, red, and green spheres, respectively, whereas ligands are represented by sticks.
Eclipsed anionic heterobimetallic open frameworks of 1 (Figs. S3 and S4) interact with Li(H2O)4+ cations through multiple hydrogen-bonding O(oxamate)···H-Ow host–guest interactions [O(oxamate)···H-Ow of 3.02(4) Å] (Figs. 1 and 3, S2 and S4) describing a supramolecular motif reminiscent of Li-ion batteries where solvated alkali metal ions are intercalated within anionic graphite-like layers. As shown in Fig. 3, hydrophobic and hydrophilic regions alternate as a result of the disposition of the dimethyl-substituted phenylene spacers, pointing outward or inward of the voids, respectively. The terminal chlorine atoms are pretty confined in the hydrophilic sides, the aforementioned Li+ intercalation being further stabilized or likely driven by hydrogen bonds involving Li(H2O)4+ cations and the coordinated water molecules [Li-Ow···H–O1w of 2.9(4) Å].

Perspective views of the {DyIII[Cu(Me2pma)2]2Cl(H2O)}2- entities and tetraaqua species Li(H2O)4+ in the bc (b) planes, with details of dimethyl-substituted phenylene ligands orientation and resulting voids. Dysprosium, coordinated water–oxygen, and chlorine atoms are represented by blue, red, and green spheres, respectively, whereas ligands and Li+ water environment are represented by sticks.
Even if it was not possible to find a reasonable model for the disordered water molecules (see Supporting Information), the structural analysis revealed an estimated volume of accessible solvent voids of 1936.1 Å3 that represent up to 29.7% of the total unit cell volume [6190.5 Å3]. This feature would likely account for the embedding cocrystallized water molecules placed within the sheets, in good agreement with the elemental analyses for 1.
2.2 Thermogravimetric analysis and X-ray powder diffraction of 1
The solvent contents of compound 1 were determined by thermogravimetric analysis (TGA) under dry N2 (Fig. S5). It shows a very fast mass loss from room temperature to around 70 °C, followed by a plateau under further heating up to 200 °C, when decomposition starts. Overall, the mass loss of ca. 18.5% at 150 °C corresponds to ca. 13 molecules per formula unit, and, together with elemental analysis, the final chemical nature of the compound was determined (see Supporting Information).
The powder X-ray diffraction (PXRD) pattern of a polycrystalline sample of 1 (Fig. 4) confirms the isostructurality with the crystal selected for single-crystal X-ray diffraction and pureness of the bulk.

Calculated (bold line) and experimental (normal line) PXRD pattern profiles of 1.
2.3 Magnetic properties
Fig. 5a shows the temperature dependence of the direct current (dc) magnetic susceptibility of 1, in the form of the χMT versus T plot (χM being the dc molar magnetic susceptibility per Cu2Dy unit). At room temperature (R. T.), χMT value for 1 (14.76 cm3 K mol−1) is similar to that expected for the sum of two square-planar CuII ions (χMT = 0.80 cm3 mol−1 K with gCu = 2.1 and SCu = ½) and one DyIII ion [χMT = (Nβ2gDy2/3kB)J(J + 1) = 14.15 cm3 mol−1 K with J =15/2 and gDy = 4/3]. Upon cooling, χMT for 1 decreases, most likely as a consequence of the first-order angular momentum and crystal field effects of the DyIII ion [61] (6H15/2 term with S = 5/2 and L = 5), and it attains a minimum at ca. 14 K (inset of Fig. 5a). Below the minimum, χMT increases sharply to reach a χvalue of 19.32 cm3 K mol−1 at 2.0 K. Such a sharp increase below 14 K (Fig. 5a) can hardly be explained only through intralayer ferromagnetic interactions. Antiferromagnetic interactions between CuII and DyIII ions could turn 11 into a ferrimagnetic system with also a sharp increase of χMT at low temperatures. However, the observed minimum value of χMT is too high, exceeding that expected for two CuII ions magnetically uncoupled with the ground doublet of the DyIII ion.
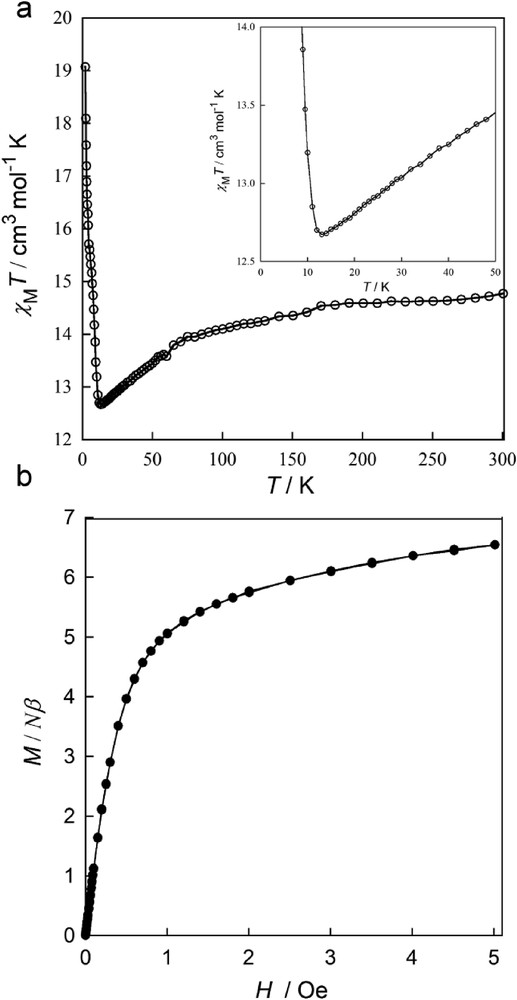
(a) Temperature dependence of χMT for 1 under an applied dc field of 100 Oe (T < 50 K) and 1 T (T ≥ 50 K). The inset shows the minimum of χMT in detail. (b) Field dependence of M at 2.0 K.
The M versus H plots (M being the molar magnetization per Cu2Dy unit and H the applied dc magnetic field) at 2.0 K (Fig. 5b) further confirm this ferromagnetic behavior. The isothermal magnetization curve of 1 exhibits a quite fast saturation with a maximum M value of 6.55 Nβ at 5.0 T, which is very similar to that expected, considering a parallel alignment of the spins of two CuII (SCu = 1/2) and one DyIII (SDy = 5/2) ions, thus suggesting a particularly strong ferromagnetic interaction between neighboring metal ions. However, no hysteresis was observed for this compound at 2.0 K because of its small value, requiring a lower temperature to allow its record. Moreover, within the 2D anionic CuII2DyIII and 1D neutral CuIIDyIII networks, the ferromagnetic nature of the magnetic coupling between the DyIII and the CuII ions through the oxamate bridge was already reported in the past [54,62]. Therefore, it seems obvious to expect that the observed magnetic behavior is a consequence of a ferromagnetic intralayer coupling. Thus, even if χMT decreases in the range 300–314 K for 1, owing to the depopulation of the excited Stark sublevels of DyIII ions, the ferromagnetic interaction within the plane can slightly mask this drop of χMT.
Unfortunately, there is no analytical expression capable of simulating the magnetic behavior of this regular 2D network, but it contains two different metal ions, and one of them possesses coupled spin and angular momenta. This last point makes the study of the magnetic properties particularly tricky, even more, when some effects are acting at the same time, that is, when the effect of the magnetic coupling is playing its role during the depopulation of the excited doublets caused by the spin-orbit coupling (SOC) on the DyIII ion. In other words, some methodologies based on effective unities could help in a relatively simple way when a phenomenon is dominant, but in 1, the magnetic coupling is strong enough so that its effect comes together with those from SOC shown by the DyIII ion. In such circumstances, the simulation of the magnetic behavior of 1 becomes an impossible task.
Therefore, the experimental data above 50 K, where the influence of the magnetic coupling is not significant yet, were analyzed. The spin Hamiltonian used and summarized in Eq. 1 embodies the SOC of the DyIII ion and the Zeeman effect of this ion and two uncoupled CuII ions. Structural distortions in the coordination sphere of the DyIII ion appear as an axial zfs parameter (Δ) on its angular momentum. The spin–orbit coupling constant was considered constant and equal to the value of the free ion (λ = −380 cm−1). The ideal spin momentum (S = 5/2) for the DyIII ion in this model has, therefore, a g-factor equal to 2.0, the value for the free electron (ge). The low delocalization of the f orbitals in the rare-earth complexes supports the assignation of the unity as value for κ. Having in mind these particularities, with a g-factor of 2.00 for the CuII ion (gCu), the Δ parameter for the best fit above 50 K takes a value of +66.5 cm−1, which is in agreement with values for other dysprosium(III) complexes reported previously [54]. The agreement factor between experimental and simulated data, defined as , with P being the measured physical property, is F = 1.6 x 10−5. A simulation with these values agrees reasonably well with the experimental curve; however, it is not perfect even if any restraint on the values of λ and κ is removed. Probably, a possible effect of the magnetic coupling occurs even above 50 K, which, if small or moderate, was also observed in a Dy2Cu3 network with oxamate as a bridging ligand [54].
| (1) |
CASSCF/NEVPT2 calculations on a DyCu4, or even on a DyCu model, could procure both the splitting of the ground term promoted of the ligand field on the DyIII ion and the magnetic coupling between DyIII and CuII ions. This study is prohibitively expensive because of the excessive size of the chosen active space to build the ground and excited states. Besides, the magnetic interactions between 4f and 3d ions involve the empty 5d orbitals of the lanthanoid ions, which requires an enormous increase of the active space [63–65]. Moreover, these factors make the convergence of this kind of calculations difficult. Because there can be no doubt about the ferromagnetic nature between DyIII and CuII ions, choosing a model that allows studying only the splitting of the f orbitals and the ground term promoted of the ligand field on the DyIII ion is a good option. In this case, from the experimental geometry of 1, the appropriate model (DyZn4) is built replacing paramagnetic CuII ions by diamagnetic ZnII ones in, keeping the electronic features of the chemical surrounding (Fig. 6). This splitting leads to a few low-lying excited sextets very near to the ground state (Fig. 7 and S6), as demonstrated for the CASSCF/NEVPT2 calculations. Specifically, 10 of these excited states are in the range of 1161 cm−1, and three of them place only 31, 258, and 266 cm−1 above the ground state. This fact agrees with a stronger influence of the SOC on the splitting of the states and the magnetic properties than the ligand-field effect. By the previous discussion about the analysis of the magnetic data, the presence of close low-lying excited states makes the analysis of the simulation of the magnetic behavior of 1 difficult, which becomes impossible when the magnetic couplings throughout the 2D network are included. Next sextet excited states are placed 7550 cm−1 above the ground state. Quartet excited states are placed beyond 24,000 cm−1.
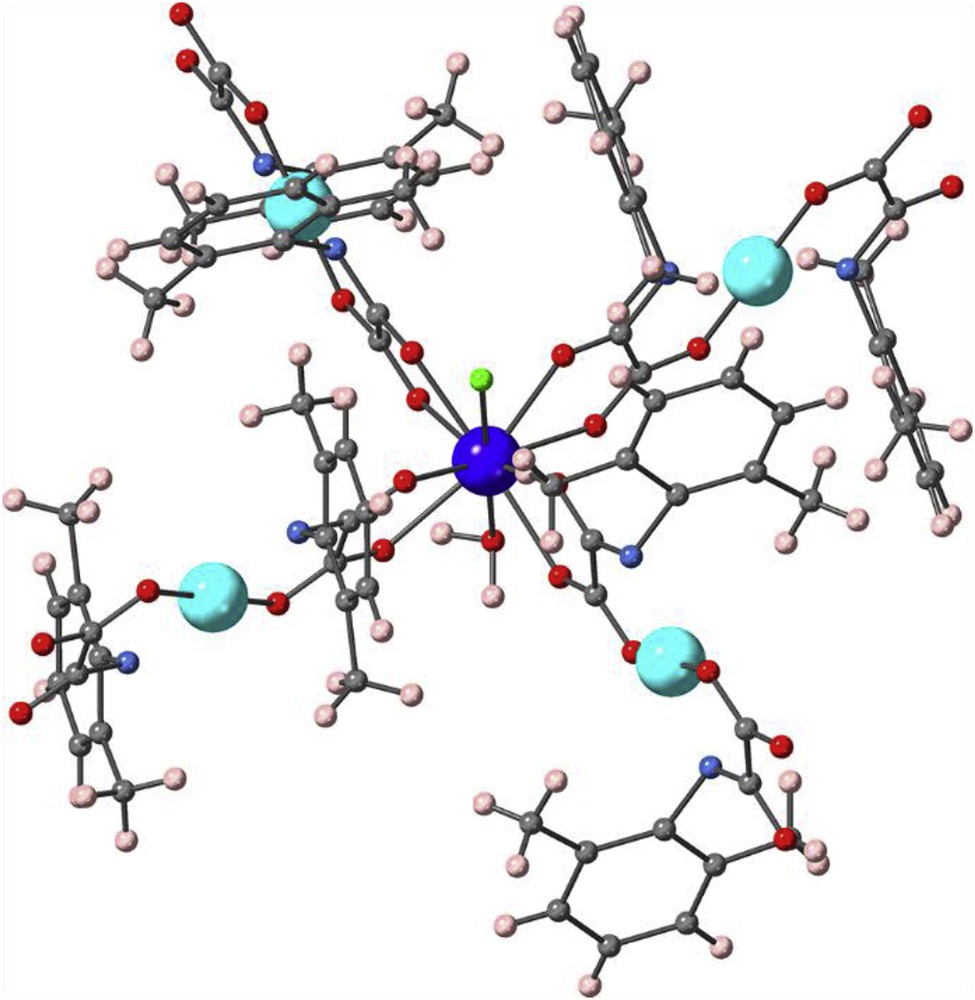
View of the DyZn4 molecular model used in CASSCF and CASSCF/NEVPT2 calculations and built from the experimental geometry of 1. For clarity, the hydrogen atoms are masked.

Splitting of the f orbitals by the crystal field obtained from a CASSCF calculation on a DyZn4 model built from the experimental geometry of 1. The isodensity surfaces of natural orbitals correspond to a cut-off value of 0.01 e bohr−3. The labels state the correspondence with the pure f orbitals. The values correspond to the energies in eV for the natural orbitals of which the contribution of f orbitals prevails. For clarity, only a cut on the molecular core composed of the DyIII ion and the coordination environment is visualized.
On the other hand, 10 donor atoms organized in a bicapped square prism constitute the coordination sphere of the DyIII ion. In this coordination polyhedron, four chelating oxamate ligands in “equatorial” positions occupy the eight vertices of the square prism. Considering each oxamate ligand with two coordinate donor atoms as the only coordination point, the coordination would look like an octahedron in a D4h symmetry and with four oxamate ligands in its equatorial plane, this being the cause of the use of “equatorial” term in the present discussion. Although the Dy-O(oxamate) bond lengths are longer than those in a previous system, the Dy-O(water) bond length is shorter than that of the majority of the reported dysprosium(III) compounds. The weaker ligand field of “axially” coordinated chloride and water ligands than the “equatorial” oxamate groups makes the dysprosium(III) compound exhibit an in-plane anisotropy [66–68], that is, an easy magnetization appears in the “equatorial” plane, which divides the coordination polyhedron into two separate square pyramids. This particular magnetic anisotropy could spread throughout the 2D DyCu2 network through intralayer ferromagnetic couplings.
Compound 1 shows a paramagnetic-to-ferromagnetic phase transition at TC = 7.5 K, which is confirmed by both (i) the presence of sharp non–frequency-dependent peaks at 7.5 K in the χ″M versus T plot (Fig. 8a) and (ii) the divergence of the field-cooled magnetization (FCM) and the zero-field-cooled magnetization (ZFCM) curves at the same temperature (Fig. 8b). In general, a 2D network cannot display a magnetic order, but 1 does. The non–frequency dependence of the χ″M peaks (Fig. 8) rules out a slow relaxation of the magnetization on the DyIII ion. On the other hand, the presence of moderate ferromagnetic intralayer interaction cannot explain this magnetic ordering without the inclusion of (i) ferromagnetic interlayer interaction between neighboring planes or (ii) a magnetic anisotropy that 1 behaves as a magnetic XY plane [69]. The first case is based on the most likely dipolar nature of the interactions, but they are often weak and antiferromagnetic. However, in 1, the first-order SOC in the DyIII ion with an in-plane anisotropy transfers a magnetic anisotropy to the DyCu2 layer, this being an XY plane where a long-range magnetic ordering is possible without the presence of the interlayer couplings, which seems reasonable from the crystal structure. Yet the behavior of this kind of 2D systems is not simple. They exhibit a particular phase transition of infinite order from a high-temperature disorder phase to a low-temperature quasi-ordered phase. However, they can explain the observed behavior for 1. Interestingly, although a good number of oxamato-based CPs merely with 3d metal ions exhibiting ferromagnetic ordering have been reported, ferromagnetic ordering in CPs involving 4f metals is very rare. Thus, with isolated exceptions, such as polymeric compounds involving interchain interactions [40,45] and a 2D compound reported by Evangelisti et al. [55], in which a ferromagnetic ordering was observed below 2.0 K by specific heat measurements, compound 1 is one of the very first 3d-4f magnets and indeed exhibits the largest TC reported so far for lanthanide-based CPs.

(a) Temperature dependence of the out-of-phase ac magnetic susceptibility χM″ for 1 in an oscillating 1.0 Oe field at frequencies of 100 (red) and 1000 (blue) Hz. (b) FCM (●) (measured upon cooling within a field of 50 Oe) and ZFCM (○) (measured after cooling in zero field and then warming within the field) for 1.
3 Conclusions
In conclusion, we report a novel 2D oxamato-based copper(II)-dysprosium(III) CP, which was obtained following a rational programmed strategy. The 2D CP shows a square [DyIIICuII2] layered structure of (44.62) net topology. Interestingly, the combination of two factors, the well-known efficiency of oxamato ligands to transmit strong magnetic couplings between neighboring atoms and the mentioned structural topology, is responsible for the observation of ferromagnetic interactions between copper(II) and dysprosium(III) cations, allowing the presence of a ferromagnetic ordering, very uncommon in lanthanide-based CPs. Current efforts are devoted to study the influence of the hydration/dehydration processes in the magnetic properties.
4 Experimental section
4.1 Materials
All chemicals were of reagent-grade quality. They were purchased from commercial sources and used as received. The proligand HEt–Me2pma and the mononuclear copper(II) complex (n-Bu4N)2[Cu(Me2pma)2] · 2H2O were prepared as previously reported [25,57]. Preparation of Li2[Cu(Me2pma)2] · 2H2O is given in detail in the Supporting Information.
4.2 Preparation of [LiI(OH2)4]2[DyIIICuII2(Me2pma)4ClH2O] . 4H2O (1)
Well-formed dark green prisms of 1, which were suitable for X-ray diffraction, were obtained by slow evaporation of 10 mL of a water/acetonitrile/methanol solution (1:10:10 volume ratio) containing stoichiometric amounts of Li2[CuII(Me2pma)2] . 2H2O (0.10 g, 0.20 mmol) and DyCl3 (0.027 g, 0.10 mmol) with an excess of LiCl (0.5 mmol). After several days standing on air, green crystals of 1 appeared. They were filtered off and air-dried. Yield: 59%; elemental analysis calcd. (%) for C40H62Cu2DyLi2N4O25Cl (1337.9): C 35.91, H 4.67, N 4.18; found: C 35.78, H 4.59, N 4.21; IR (KBr): ν = 1601 (C]O).
4.3 Single-crystal X-ray diffraction
Crystal data for 1: C40H652Cu2DyLi2N4O21Cl, Mr = 1236.76, tetragonal, space group I4/m, a = 15.9307(5), c = 24.3926(9) Å, V = 6190.5(5) Å3, T = 90(2) K, λ = 0.71073 Å, Z = 4, ρcalc = 1.356 g cm−3, μ = 1.983 mm−1, 2188 unique reflections [35,182 measured (Rint = 0.0270)] and 1898 observed with I > 2σ(I), 1.53° ≤ θ ≤ 25.24°, R = 0.1319 (0.1380 for all data), wR = 0.3715 (0.3806 for all data) with 114 parameters and 18 restraints, the final Fourier-difference map showed maximum and minimum height peaks of 4.144 and −3.600 e Å−3. Crystal structure deposited at Cambridge Crystallographic Database with CCDC 1891550.
Single-crystal of 1 was mounted on glass fibers in a grease drop and very quickly placed on a liquid nitrogen stream cooled at 100 K to avoid the degradation upon dehydration. Diffraction data were collected on a Bruker-Nonius X8APEXII CCD area detector diffractometer using graphite-monochromated Mo Kα radiation (λ = 0.71073 Å). The data were processed through the SAINT [70] reduction and SADABS [71] multi-scan absorption software. Despite the high quality of the full set of data, a quite low θmax of diffraction (θ = 27°) was obtained (detected as Alerts A in the checkCIF), even if many efforts have been made to extract the best diffraction data from the sample. Furthermore, high residual electron density, which is less than 1 Å from the metal atom, is due to the effect of the dysprosium and even copper ripples. However, the solution and refinement parameters are suitable, compared with analogue MOF structures previously reported; thus, we are convinced that the structure found is consistent [72–75].
The structure was solved by the Patterson method and subsequently completed by Fourier recycling using the SHELXL-2013 software package [76,77]. All nonhydrogen atoms were refined anisotropically except Li+ alkali metal and some disordered carbon or oxygen atoms from ligands and water molecules. The hydrogen atoms were set in calculated positions and refined as riding atoms. The high thermal vibration parameters (Alerts A and B in the checkCIFs) displayed for some atoms in the organic ligand are consequence of contributions from different factors, including (a) the flexibility of the framework and consequential disorder, (b) the high residual electron density produced by the methyl groups that are dynamic components of the walls, and (c) the use of some bond length and angle restrains during the refinements or fixed positions of some highly disordered atoms. Furthermore, and as expected for such systems, the lattice water molecules were highly disordered and cannot be satisfactory modeled (at the origin of the first levels Alerts A). Those found from the ΔF map were the coordinated ones refined with restraints and their hydrogen atoms were neither found nor calculated. As a consequence, the contribution to the diffraction pattern from the highly disordered water molecules of crystallization (6 molecules of H2O located in the voids of the lattice that amount to ca. 30% percentage void volume of the unit cell) was subtracted from the observed data through the SQUEEZE method, implemented in PLATON [78]. The final formulation for each compound is consistent with the residual electron density and volume. The final full-matrix least-squares refinements on F2, minimizing the function ∑w(|Fo|-|Fc|)2, reached convergence with the values of the discrepancy indices given in Table S1. High R values (levels Alert A in checkCIFs) are, most likely, mainly affected by the ripples and contribution of the highly disordered solvent to the intensities of the low angle reflections. The final geometrical calculations and all the graphical aspects were carried out with CRYSTAL MAKER and WinGX [79–81].
4.4 X-ray powder diffraction
A polycrystalline sample of 1 was introduced into a 0.5 mm borosilicate capillary and then it was mounted and aligned on an Empyrean PANalytical powder diffractometer, equipped with Cu Kα radiation (λ = 1.54056 Å). For each sample, five measurements were collected at room temperature (2θ = 2–40°) and merged in a single diffractogram.
4.5 Magnetic measurements
Variable-temperature direct current (dc) and alternating current (ac) magnetic susceptibility measurements were carried out with a Quantum Design SQUID magnetometer. The susceptibility data were corrected for the diamagnetism of both the constituent atoms and the sample holder.
4.6 Theoretical calculations
To evaluate the splitting of the states promoted by crystal field on the DyIII ion in 1, the relative energies of the ground and low-lying excited states were computed by calculations based on the second order N–electron valence state perturbation theory (NEVPT2) applied on the wave function, which was previously obtained from complete active space (CAS) calculation. These calculations were performed with the version 4.0 of the ORCA program on a DyZn4 molecular model built from the experimental geometry of 1 and by replacing paramagnetic CuII ions by diamagnetic ZnII ones, to keep to the utmost, the electronic features of the system [82]. The TZVP basis set proposed by Ahlrichs and the auxiliary TVZ/C Coulomb fitting basis sets were used for all atoms [83,84]. Electronic relativistic effects introduced by the dysprosium atom were considered through the ZORA Hamiltonian [85] and the SARC (segmented all-electron relativistically contracted) version of the TZVP basis set (SARC-ZORA-TZVP) [86–90]. The energies of 21 sextet and 12 quartet states generated from an active space with nine electrons in seven f orbitals were calculated. See Supporting Information for further details.
Acknowledgements
This work was supported by the MINECO (Spain) (Projects CTQ2016-75671-P and CTQ2016-75068-P) and the Ministero dell'Istruzione, dell'Università e della Ricerca (Italy). A. P.-A. thanks the MINECO for a predoctoral contract. Thanks are also extended to the “Subprograma Atracció de Talent-Contractes Post-doctorals de la Universitat de Valencia” and the “2018 Leonardo Grant for Researchers and Cultural Creators, BBVA Foundation” (J.F.S.). E.P. acknowledges the financial support of the European Research Council under the European Union's Horizon 2020 research and innovation programme/ERC Grant Agreement No 814804, MOF-reactors.


