1 Introduction
Conceived and explored in 1945 in physics laboratories [1–5], Nuclear Magnetic Resonance (NMR) spectroscopy is arguably nowadays one of the most essential tools for analyzing the structure of mineral, organic, or biological molecular systems. This fantastic achievement was possible with the development of Fourier-Transform NMR (FT-NMR) proposed by R.R. Ernst [6], that in turn opened the door to first NMR experiments based on sophisticated multipulse sequences [7,8]. Concomitantly, the application of NMR principles/concepts has also offered fundamental opportunities for medical imaging for robust diagnostic purposes. Behind the vast practical aspects of analysis of matter, NMR basics underlie varied and sophisticated theoretical concepts in physics (data sampling), mathematics (Fourier Transform (FT) principle), electronics (resonating circuit), or quantum mechanics (Hamiltonian, operator density…), as nicely described in many theoretical/practical books that are references for any NMR spectroscopists or experienced users [9–16].
As a brief reminder, Table 1 provides a chronological summary of the main technological/methodological advances from the 1950s to the present days, in conjunction with the magnetic field strength for a continuous enhanced spectral resolution and sensitivity.
Historical overview of main instrumental/methodological achievements.
Unfortunately, the increasing "race of Tesla" has a significant financial cost (purchase) and periodic maintenance (cryofluids), and hence the need for cryofluid-free, FT-NMR spectrometers is becoming acute again. In addition, nowadays, the availability of rather small permanent magnets (soft iron) with a good magnetic homogeneity (up to 10−4) and stability and the significant improvement in electronic performance make it possible to offer very compact, versatile benchtop FT-NMR spectrometers at a reduced cost, making again this new generation of instrument very attractive for various applications in chemistry [17].
In this article, we propose to revisit the development and assembly of a very low-cost (∼10 Keuros), portable (benchtop) FT-NMR spectrometer by integrating magnetic and electronic classical elements. For this, the essential units required will be described, detailing their respective role in the excitation/detection process of signal, for instance. In a memorial approach, in particular, toward chemists who have generally forgotten the NMR principles, we will start from some (important) basic physical principles of NMR to organize and choose the key block elements necessary for the realization of this "artisanal" or home-made (as anglicists would say) spectrometer. Interestingly, such a project is possible with laboratory instrumentation (function generator, oscilloscope…) accessible at a lower cost. All requested, specific electronic components/devices with their current nomenclature are listed in Appendix and are commercially available.
Proposing an inexpensive, home-made FT-NMR instrument is above all an exciting task of engineering integrated into an educational project, for instance. It obviously cannot be considered as a competition with the new generation of benchtop FT-NMR spectrometers available in the market today from different manufacturers (Magritek, Oxford, Thermofisher, Nanalysis…), which integrates many optional modules (locking, sample spinning…) [17]. Moreover, although the overall cost (material/electronic supplies) of the instrument seems attractive at first sight, it does not include the actual human costs (total cost), in particular in view of its pedagogical dimensions in Academic Education. This home-built NMR spectrometer can be seen as an “alive” support instrument for teaching NMR. Finally, this type of mobile NMR apparatus is well suited for scientific research by coupling NMR and another instrument (such as a microscope).
To have an idea, the time needed by a single engineer to build a one-channel mobile NMR may be estimated as two months, including the tests (and assuming that all electronic hardware components have been already purchased).
2 Contribution of modern electronics
Electronics has developed considerably in recent decades, making it possible to build high-performance systems with high functional integration. To illustrate the evolution of the power of electronic component, we have included the number of transistors integrated on the same chip over the years in Table 1. For example in 1965, a microprocessor integrated nearly 2000 transistors on the semiconductor chip. The density of the components has increased by a factor of 106 in 45 years (1965–2010), thereby reducing the size of the electronic circuits. Currently, a simple integrated circuit is capable of performing signal acquisition, processing, and control functions. The modern smartphone is a blatant illustration of the high-tech concentrate contained in such a small volume. As the density of the components increases, the operating frequency of the hardware circuits has also increased considerably. Hardware can now operate at frequencies of several gigahertz compared to a few hundred kilohertz in the 1970s. These high working frequencies allow complex processes to be carried out with extremely short times.
Another huge leap in the field of electronic equipment is the memory capacity of components. It is now possible to store and manipulate memory spaces of more than 64 gigabytes. Data storage is no longer a real limitation and it is possible not only to acquire large amounts of data, but also to store the ever more sophisticated programs to control and process these data.
The frequency synthesis is now digitally based on DDS (Direct Digital Synthesis) cards over a very wide range of frequencies with very high accuracy. In Table A1 (nomenclature of components) presented in Appendix, we list the references of a synthesis unit capable of generating frequencies from a few kHz to more than 300 MHz. Analogically, the sizes and costs of low-noise preamplifier components, mixers, and other hardware have been reduced. For example, the low-noise preamplifiers in the acquisition chain can be made with a few circuits for a hundred euros.
Finally, an important point to keep in mind is the reduction of the energy consumption of modern components, allowing complete battery-powered systems to be powered, making them autonomous and therefore portable. This aspect was unthinkable in the 1980s. In summary, the performance of electronic components has increased while sizes and costs have been reduced, so the realization of complex units such as a small NMR spectrometer is possible in research laboratories.
3 Some specificities of a benchtop FT-NMR spectrometer
Classical or benchtop/mobile FT-NMR spectrometer is a complex instrument, but it can be easily divided into distinct and clearly identified functional blocks [18]. In practice, this instrumentation involves many domains of electronics such as radiofrequency (RF), audio chain, power electronics, low-noise preamplification, and transmission lines. In this first decade of the 21st century, FT-NMR spectrometers are fully digital and multi-nucleus. Gradually, they are connected by internet, and therefore they can be remotely controlled and (unfortunately for experimenters) fully automated. The two operating modes of FT-NMR spectrometers (excitation and detection steps) are performed by fast microprocessors and executed by suitable softwares.
As a matter of principle, the channels (1H, 13C, X…) of spectrometers are similar but independent of each other, all of them are synchronized by a master clock; a dedicated pulse sequencer controlling the complex multi-channel pulse sequences of the spectrometer. This sequencer takes into account the different transmission delays and hardware dead times (such as the pre-scan delay) to produce a reliable and precise pulse timing controlled by the software. The duration of the (hard or soft) electromagnetic pulses (μs to ms) and the delays between events (μs to s) are those actually achieved by the electronics, without the need to add small compensation delays in the pulse programs. These specificities are made possible, thanks to the very high speed and stability of modern electronics.
The assembly of mobile NMR consists of three distinct parts: the magnet, probe, and data acquisition and processing spectrometer. The magnet and probe depend on the chosen application: low field or high field. We discuss these aspects later in this article.
The electronics of our mobile NMR spectrometer is designed to acquire very low value signals (less than μV) over a high dynamic range (the noise factor of the detection chain is less than 2 dB), and the sampling is adapted to the required dynamics (8, 12, 16, or 24 bits). The same applies to frequency synthesis and quadratic demodulation, which can be adapted to a very wide range of frequencies. Note that all the electronic hardware components (RF power amplifier, mixer, preamplifier…) have been chosen to work in a wide frequency range (from 1 to 400 MHz). This allows the portable FT-NMR spectrometer to work at low field (with a static permanent magnet) or at high frequency (with a superconducting magnet).
4 Sensitivity and resolution
The homogeneity and strength of the magnetic field of a permanent magnet define the sensitivity and spectral resolution of any NMR experiment. The temporal magnetic stability of a magnet obviously limits the duration of the measurements. Homogeneity and magnetic stability must allow a coherent accumulation of signals in phase.
NMR is often defined as rather insensitive and high-field magnets are needed to achieve robust sensitivity and resolution to analyze complex molecules. In high-resolution NMR, chemical shifts must be measured with a resolution of about 0.01 ppm to solve the J couplings of a few Hertz. Magnetic fields are of the order of several Tesla and are generated by superconducting magnets cooled by helium and liquid nitrogen. A system of compensation for inhomogeneity (shims) is essential to obtain the required resolution.
Permanent magnets with low field (<0.94 T or 40 MHz for 1H) are called low resolutions due to their low sensitivity and homogeneity. In an inhomogeneous field, the magnetic strength varies in relation of the spatial position in the magnet. Such effect leads to significant broadening or/and overlapping of resonance peaks on spectra, thus preventing exploitable spectral resolution. Nevertheless, the measurement of distribution of relaxation times or diffusion coefficients of molecules is accessible at low fields. Quantitative analysises are also possible. The characterization of materials (liquid, powder) can be carried out at low resolution with a home-made spectrometer that is much less cumbersome, less expensive in cryogenic maintenance, and accessible because it is close to the synthetic bench of molecules. The latter reduces the cost and workflow of any research activity. The mobile NMR spectrometer we are describing is part of this approach: it is compact and can be used with a low-field magnet at Larmor frequencies ranging from 1 to 15 MHz in the set presented.
Although intended for low-field, low-frequency applications, as mentioned above, the design and electronic components of our mobile NMR spectrometer can operate at frequencies up to 300 MHz (see the Table in the Appendix). As a result, this mobile NMR spectrometer can also be used, without major modifications, at high field using the magnet and the probe part of the industrial spectrometer. In this type of application, the interest is methodological: development of a specific auxiliary channel, magnetization manipulation to control radiation damping, and development of new strategies (multiple acquisitions).
5 Back to the principles of NMR and practical consequences
The nucleus of atoms (1H, 13C, 15N, 19F, 31P…) is characterized by a quantum quantity, the spin, which is specific to each nucleus and determines its magnetic properties. The magnetic moment, μ, of a nucleus is directly related to I by its gyromagnetic ratio, γ, which is a constant depending on the nature of the nucleus. The magnetic moment being quantified, the energy states are degenerated.
When this nucleus is immersed inside the static magnetic field, B0, the degeneration of energy level is lifted, leading to several energy levels according to the spin value (Zeeman effect). If the nucleus is then subjected to a radiofrequency wave at a specific frequency (Larmor frequency), the atomic nucleus will absorb the energy of this radiation and release it during relaxation mechanisms. This process at the origin of the NMR phenomenon depends on the magnetic field and the properties of the molecules. The study and measurement of an isolated atom is not possible due to a lack of sensitivity of NMR; the result is that we are still dealing with a very large set of nuclear spins, the macroscopic result of which we will measure: magnetization. In the presence of a magnetic field B0, the resultant of macroscopic magnetization is collinear to B0 at equilibrium and proportional to the spin populations (number of nuclei).
Under the action of B0, the magnetic moment, μ, of any magnetically active nucleus (I ≠ 0) is subjected to a force,
| (1) |
| νLarmor = ν0 = −γ B0/2π | (2) |

Pulse-acquisition 1D NMR experiment. The macroscopic magnetization is aligned along the B0 axis (Oz) at equilibrium state, ideally at the end of the relaxation delay. After an RF excitation pulse, M0 is flipped in the Oxy plane. The precession of this magnetization gives the impulse response (or FID) which is detected.
At equilibrium, all nuclei of a sample are subjected to B0. The resulting macroscopic magnetization (M0) is oriented along the Oz axis. The first step of any FT-NMR experiment is to excite the spin system with a (generally short) RF pulse to remove it from its equilibrium state by tilting the M0 magnetization in the xy plane (see Fig. 1). The return of M0 to equilibrium (denoted Free Induction Decay (FID)) is then detected and processed by FT to obtain a frequency spectrum in Hertz or expressed in parts per million (ppm). The magnetization, M0, observable for a set of nuclei of spin I, is given by the following law:
| (3) |
In practice, the magnetization, and therefore the sensitivity of a NMR experiment, is directly dependent on the value of B0. The exact magnetic-field dependence of the NMR sensitivity (considering the detection coil) can be written as the energy (E in Joule) detected in a coil of volume, V, namely:
| E = M0·B0·V | (4) |
A priori, it is therefore preferable to work with high magnetic fields, which are also at the origin of high-resolution NMR in liquids. For instance, at room temperature (300 K) and for a B0 field of 11.7 T (500 MHz), the detectable magnetization is about 3 × 10−6 (in SI unit), or an energy of about 10−4 μJ for a sample volume V of 1 cm3 (E = M0·B0·V). This corresponds to a reception power of about 1 μW for an acquisition time of 0.1 ms. As seen, the strength of detected signal is therefore very low. De facto, using a so-called low-field NMR, where the B0 strength varies between 0.15 and 1.5 T, makes the experimental NMR detection much more critical.
From an electronic viewpoint, the voltage of detected signal (before its amplification) is of low amplitude, with an order of microvolt (μv). In practice, the experimental conditions as well as the instrumentation electronics must therefore be optimized to reach acceptable signal-to-noise ratios (SNR). This challenge can be met, thanks to the performance of modern electronic components. In addition, the transmission power required to energize a frequency band of about 10 kHz (for the 1H nucleus) for a 1 cm3 volume sample is about 11 W (@500 MHz or 11.7 T). For a low-field spectrometer, an excitation power of about 5 W for a pulse duration of about 20 μs is sufficient to generate an instantaneous tilting of 90° of M0, i.e. in the xy plane.
6 NMR instrumentation
6.1 The magnet
In the applications of this study, we use a permanent magnet that is sufficiently homogeneous and stable to provide consistent NMR measurements. Considering the analytical purposes of low-field NMR and its transportability, the weight of the permanent magnet to be used must be reasonable (< 80 kg), and generate at least a field of 0.15 T (1500 Gauss), leading to a resonant frequency for protons around 6.4 MHz. The axis of the magnet is horizontal and perpendicular to the probe (coil), which consists of a vertical solenoid, and in which the sample is positioned (5-mm tube) (see Fig. 2).

Permanent horizontal magnet and its probe placed at the center of the magnet gap with a sample tube of 5 mm, inside.
The NMR probe (the antenna) is carefully placed at the magnetic center of the magnet to both excite (with a perpendicular field, B1) and detect the signal along one of the four axes perpendicular to B0 (x, −x, y, −y). The probe includes its frequency and impedance system (tuning and matching) that is connected to the electronic chain of the equipment. Note that it is easy to add two external coils on either side of the magnet to produce a field gradient that can potentially be used for possible monodimensional imaging applications. As the static magnetic field is not homogeneous over all the surface of the magnet, it is therefore necessary to accurately measure the value of B0 for determining the Larmor frequency (ν0). To this aim, a field map can be made within the permanent magnet to determine the exact value using a gaussmeter (Teslameter) that is slowly moved into the air gap of the magnet. In our case, the value measured at the center of the air gap is 1492 Gauss, which corresponds to a resonance frequency, ν0, of 6.28 MHz for 1H.
6.2 Excitation vs detection
To perform FT-NMR experiments, three steps are necessary: i) create a homogeneous magnetic field, B0; ii) excite the spin system to tilt it from its equilibrium state by means of an excitation coil generating a B1 field perpendicular to B0; and iii) detect the FID signal by means of a receiver coil (which is also the same generating the B1 field excitation), the whole satisfying the Larmor's resonance condition, νexc = νdéc ≈ ν0.
The "block" diagram setting up the main parts of an NMR spectrometer is shown in Fig. 3, which shows the permanent magnet and the NMR probe inside the magnet, an electronic "transmitter" block responsible for exciting the spin system with RF powers of several dozen watts, and a second "receiver/detection" block that amplifies the FID signal of very low power (μW) and demodulates the signal in two components of low frequency (separate operations). These two steps can be controlled by a "programmable sequencer" that generates the multiple RF pulses trains and controls the delays during the experiment. For very simple experiments (pulse-acquisition), a laboratory pulse generator is sufficient. Finally, data processing and visualization can be performed using a simple oscilloscope, but in a more modern way using a computer (PC) with its software interface. It should be noted that the probe is connected to the excitation and reception blocks via a unit called duplexer. This element can be seen as a signal "switcher" that aims to protect the preamplifiers of the detection channel from high RF excitation power. The duplexer directs all RF power to the probe during the excitation step (by closing access to the receiving channel) first, and then redirects the detected NMR signal to the preamplification/demodulation chain.

Simplified "block" diagram of an NMR spectrometer.
For a spectrometer operating at frequencies of the order of 15 MHz and with relatively low powers, a simple structure based on a π quarter-wave filter can be used to perform this function. It is a design strategy for a very low-cost mobile NMR. First, the π filter requires only a few electronic components at a very low cost (self and capacities), capable of withstanding high powers (several Watts). In addition, it works automatically and there is no need to control it during acquisition, simplifying any pulse programs. The realization of the circuit is simple and fast. We will describe how to make a quarter-wave duplexer in Section 8.4 for a frequency around 6.4 MHz. Because the π filter (or quarter-wave filter) is a circuit tuned to the Larmor frequency of the nucleus under consideration, its use is limited to a small frequency band.
For wide band applications (i.e. frequencies from MHz to a few hundred MHz), a duplexer based on fast RF electronic switches with fast diodes is mandatory. This type of duplexer is much more complex to implement because a pulse program within a microprocessor must control it. The description of such a circuit is out of scope for the version of the mobile NMR spectrometer we present in this article. We are targeting here a low-cost mobile NMR, with laboratory instrumentation, a duplexer π filter, and a low-field magnet operating at 0.15 T (or 6.4 MHz for 1H).
6.3 The lock system
An electronic locking system may be easily added to make the mobile NMR device capable to continously control the stability of the magnet, to avoid a slow shift of the magnetic field over time [see for instance, pp. 44 to 50 of ref. 19]. The lack of lock control can be particularly troublesome when working at high magnetic fields, and/or when recording long-term acquisition NMR experiments. Considering the aims (pedagogical aspects), application domains (1D NMR, detection of abundant nuclei), and the cost of this home-made instrument, no locking system has been integrated into the instrument.
7 NMR device synoptic
For clarity, the general electronic diagram of a NMR spectrometer is schematically proposed in Fig. 4. As seen, the attenuators and tuning/matching circuits are present at the input and output of the power amplifier to avoid excess power that can be harmful to the detection chain. The excitation step generates one or more RF pulses at the Larmor frequency. These pulses are directed via the duplexer to the NMR probe to tilt M0 perpendicularly to the z axis. The high-frequency resonance free induction decay signal (HFFID) is then routed via the duplexer to the detection circuit. The detection circuit includes at least two very low-noise RF preamplifiers to amplify this HFFID signal. The signal is then demodulated with an intermediate frequency, in quadrature (quadratic detection leading to a 90° phase shift of the signal), to generate a real (R) and an imaginary (I) component accordingly to Eq. 5,
| S (t) = A × {cos(2πνit + ϕ) + i sin(2πνit + ϕ)} | (5) |

Schematic description of the NMR spectrometer blocks along with the visualization of some of key signals obtained. Note the presence of the duplexer.
Although the spectrometer is optimized to work around the 6.4 MHz frequency, it can easily operate efficiently over a wider band. All the electronic components required for the construction of a low-cost NMR spectrometer are listed in Table A1, with the adequate associated nomenclature. The choice of the bandwidths of the various elements present in the nomenclature makes it possible to work up to frequencies around 500 MHz. The assembly of the various blocks can be made entirely on a printed circuit board or more simply by connexion components (BNC or SMA outputs).
8 Key electronic elements of the spectrometer
Let us now review the key elements of the equipment (probe, switch, RF preamplifier…) in the order of the synoptic block diagram presented in Fig. 4.
8.1 RF pulse generator
The first important function of an NMR spectrometer is the generation of the basic frequencies (BF) necessary for excitation/reception of signal. The RF excitation pulse is realized by means of a switch connected to a frequency synthesizer and a pulse generator. However, to perform a synchronous detection (resonance), part of this frequency must be directed to the detection circuit.
The generation of RF pulses can be performed in different ways. The first one consists of using a standard frequency and pulse generator present in any physicist laboratory. To ensure sufficient stability and accuracy for NMR, the resolution of the function generator must be at least 10−6. Typically, an arbitrary function generator of type HP33120A or Agilent 33220A operating up to 15 and 20 MHz, respectively, with a power of 10 dBm is perfectly suited for a low-field NMR spectrometer. For pulses, the pulse generator can also be used to produce square-shaped pulses. For pulses of the order of 10 μs, a pulse generator with a resolution of less than 100 ns is sufficient (e.g., Keysight 33220A). The time and frequency parameters are adjusted from the control panels of these laboratory instruments. In this case, only very simple single-pulse sequences are possible: 90° pulse - acquisition; 180° inversion pulse - acquisition, etc. The primary advantage of laboratory equipment is their availability at a lower cost, their speed, and simplicity of implementation (no software development for pulse programs). The second way to generate pulse sequences is to use a board based on an Advanced Reduced instruction set computing Machines (ARM) microcontroller, a Field Programmable Gate Area (FPGA) unit, and a Direct Digital Synthesis AD9959 (DDS), which allow digital frequencies up to 300 MHz to be synthesized. The advantage in this case is to have a very compact and powerful unit to generate the basic pulses and frequencies. It can be developed, for example, from an NXPLPC1768 ARM, an Altera Cyclone II FPGA [20, 21], and a DDS. This board is capable of sequencing four fully independent channels. The FPGA allows the most complex pulse sequences to be performed, and the ARM component then manages both the system and data processing. This option allows stand-alone battery operation for outdoor (off-laboratory) use.
8.2 The switch
The role of this circuit is to switch the RF signal for a controlled pulse duration. This element can be realized by means of four fast diodes (type 1N4148) mounted in head to tail or with a PS1211 mini-circuit component (switch), which offers fast switching times (< 500 ns) and very low channel imbalance (see Fig. 5).
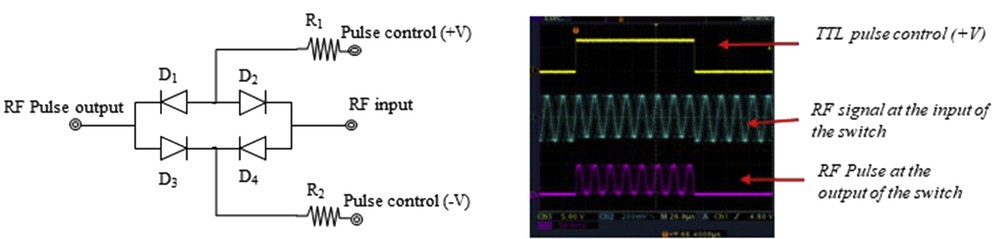
(On Left) Structure of an RF switch based on fast diodes. (On Right) Example of input and output signals from an RF switch. Here, the RF pulse has a length of 80 μs.
8.3 The RF power amplifier
As our mobile NMR is aimed to work from low to high field, it is necessary to have a broadband RF excitation pulse. The excitation provided to the spin system must be sufficiently high, with relatively short RF pulses (10–100 μs) to excite a bandwidth covering the spectral width of an observed nucleus. The selected power amplifier must be able to operate in pulse mode but also in continuous wave (CW), if nuclear decoupling or any other type of low power excitation needs to be achieved. It is imperative that the amplifier has a good linearity to adjust the RF pulse accurately. A power amplifier generates a high noise level at the output even at rest. It is therefore necessarily not activated. We used for our prototype a ZHL-5W-1 unit operating in a frequency range from 1 to 500 MHz.
8.4 The duplexer
As already mentioned above, the duplexer has a very important role, in particular, to protect, during reception, the low-noise preamplifier chain from the high RF power emitted during excitation. It is a three-port system A, B, and C (see Fig. 6), where the first port (A) is connected to the power amplifier, the port (B) is connected to the probe, and the output (C) is directed to the low-noise detection preamplifier chain. For broadband systems, it is preferable to use a switch network electronically controlled by the pulse sequencer. In low-frequency (low-field) NMR applications, a structure based on diode arrays and a quarter-wave filter can be used; the diagram is shown in Fig. 6. A first network of four head-to-tail diodes (noise gate 1) acts as an automatic switch: these diodes are blocked (open circuit) for small amplitudes, thus preventing any return of the signal from the probe to the power amplifier. The quarter-wave system, referred to as the π filter, has an input (B)/output (C) phase shift of 90°. It is called a quarter wave because it has a phase shift optimized at 90° around a given frequency, in our case, around 6.28 MHz. This filter consists of a choke and two capacitors. The filter input is connected to the probe (port B) and the output (port C) to the low-noise preamplifier chain. For a specific frequency, a quarter-wave filter has a minimum amplitude at its output (C) when its input (B) is maximum. To reinforce the protection of the preamplifiers, a second network of head-to-tail diodes can be incorporated to protect the detection circuit by short-circuiting (at the threshold of the diodes) any residual voltages. The filter setting must combine input and output impedance matching, as well as phase shift and attenuation at the resonance frequency. The characteristics of the quarter-wave filter were adjusted to the network analyzer with the Smith diagrams of the input (S11) and output (S22) impedances as a function of frequency. The input (S11) and output (S22) impedances have been adjusted to have an actual value as close as possible to 50 Ω (in practice 44.5 Ω at the resonance frequency of 6.28 MHz), while maintaining a 90° phase shift between the input and output.

Electrical diagram of the duplexer, including two diode arrays and the π filter. The π filter has a minimum RF signal at the receiver (port C) when there is a maximum on the probe (port B). The "noise gate 1″ isolates any signal feedback from the probe to the power amplifier to minimize losses during detection. The "noise gate 2″ protects the detection chain from residual voltages eliminated by the π filter.
8.5 The NMR probe
Different probe body shapes (solenoid, saddle coil) can be produced and used depending on the adaptability to the magnet. The most simple detection antenna consists of a solenoid coil. A probe body made entirely of glass (borosilicate) can be used (see Fig. 7a). For a 10-mm probe, the solenoid is wound on the glass tube with an inner diameter of 10 mm, thus allowing the detection of a large amount of analyte, but small diameter (5 mm) could be used. The capacitive network is integrated into the probe. The solenoid is made of rigid copper wire with a diameter of 1–1.5 mm and includes about 20 turns with a diameter of 10 mm over a length of 20 mm; the better the quality of the winding, the smaller the artefacts will be. The elementary structure of the frequency tuning and impedance matching system is described in Fig. 7b. A network of capacitors adjustable from 5 to 500 pF allows frequency tuning (Ct) and impedance matching (Cm) for a coil of the order of 2.2 μH. The tuning allows the probe to be adjusted to the resonance frequency (ν0 ≈ ν1 = 1/2π√LC). Impedance matching is performed at this frequency to adjust the probe circuit to 50 Ω and minimize the energy losses.

(a) Example of a probe made of glass with its integrated capacitive devices Cm and Ct. (b) NMR probe wiring diagram: Cm and Ct are adjustable capacitances from 5 pF to 500 pF, inductance coil, L = 2–3 μH.
Frequency tuning and impedance matching are performed using a network analyzer to accurately position the probe's attenuation peak at the desired resonance frequency while observing the impedance evolution on the Smith chart (see Fig. 8). Impedance matching consists of refining and lowering the resonance peak as low as possible to absorb all the energy in the coil. In our case, the resonance is adjusted with the network analyzer at 6.284 MHz, the attenuation obtained is −50.816 dB with a very good impedance matching (49.72 Ω), and consequently a good detection sensitivity is obtained for a low-field spectrometer. The half-height width obtained at this frequency is 35 kHz, giving a quality coefficient Q of 179, a very acceptable value.
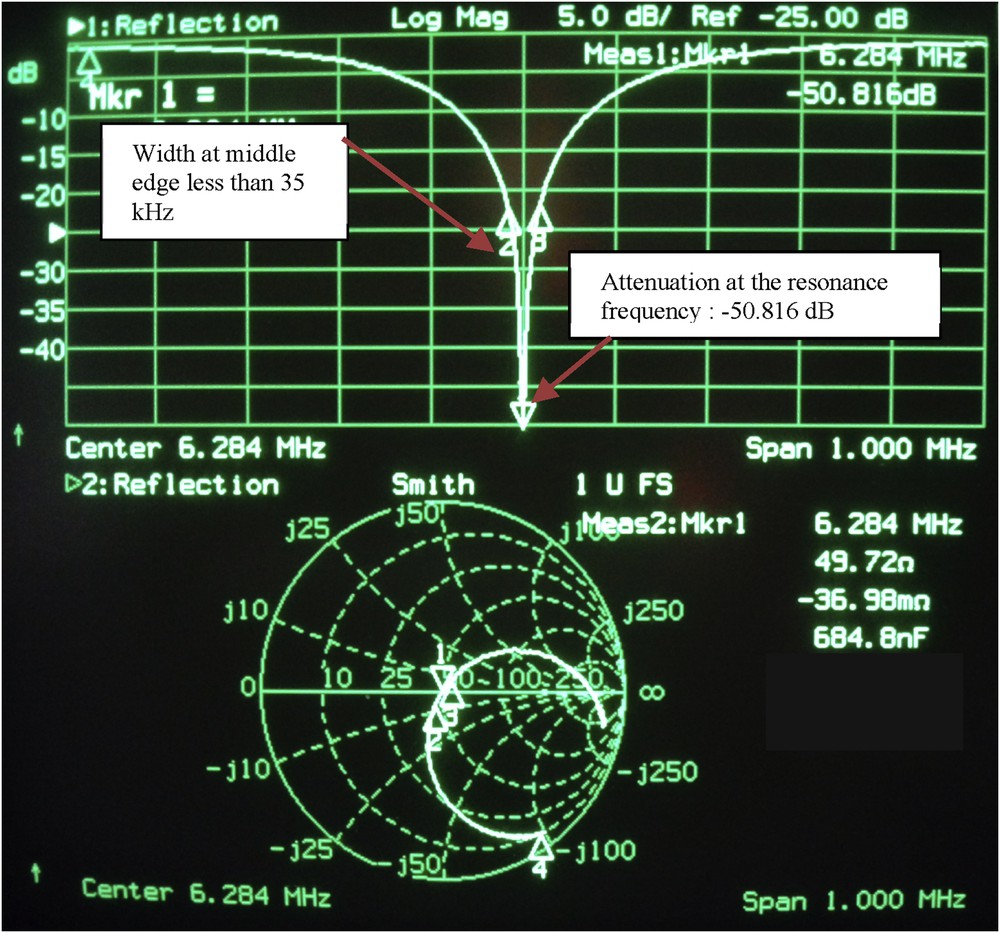
Picture showing the measurement of the frequency tuning and impedance matching curve (top) and on the Smith chart (bottom) on a network analyzer.
Once the frequency tuning has been achieved, the second important parameter to be estimated is the dead time (or response time) of the probe (see Fig. 9). The dead time is the time required for the probe to dissipate the energy stored during excitation. Some of the excitation energy is sent to the probe via the duplexer, but once the RF pulse has disappeared, significant energy remains in the probe. The higher the quality factor Q of the probe, the higher the dead time is. This is a disadvantage for detection, because it will be necessary to delay the measurement of this time: i) not to destroy the low-noise preamplifiers and ii) not to superimpose the low detection signal on the high amplitude due to the probe signal.
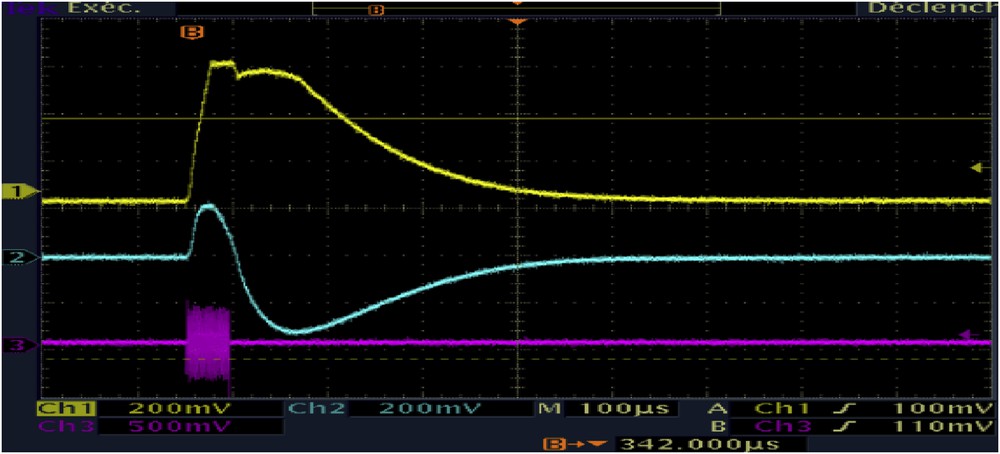
Observation of the probe's dead time: about 250 μs. At the top and in the middle are displayed the two quadrature detection channels (yellow and blue). At the bottom is displayed the rectangular (purple) RF excitation pulse (50 μs of length).
In the model presented in this article, the dead time is about 250 μs before the two quadrature detection channels return to zero (see Fig. 9). The detection of the useful signal needs to be delayed by this delay and the detection circuit is reinforced, by a network of diodes, to support the peak amplitudes of several volts for a few hundred microseconds.
8.6 The receiving chain: radio frequency preamplifier
The signal from the probe is too weak and cannot be used directly, and so it must be amplified. The amplification chain consists of two stages with radiofrequency preamplifiers in series. The noise factor of a preamplifier cascade is almost equal to that of the first stage. A "BA01500" preamplifier with the lowest factor is placed first, followed by a RF2046 home-made broadband preamp unit. The low-noise amplifier LN BA01500-35 has a frequency range varying from 0.1 to 500 MHz with a gain of 35 dB. The intermodulation product power at the output is +12 dBm (output IP3), and the undistorted input power is −35 dBm (1 dB compression point). Thus, the maximum permissible input power is therefore −35 dBm.
Our home-made preamplifier is made with three RF2046 components in series: the overall gain of the channel measured at the network analyzer (without distortion) is 35 dB at 6 MHz and 31 dB at 1 MHz and the operating frequency range is from DC continuous to 1 GHz. The output intermodulation product (IP3) is +23 dBm and the noise factor (NF) is equal to 3.8 dB. This configuration of the elements as well as their performances allows us to ensure the detection of signals on a large dynamic range without distortion: typically from some 100 μV to 14 mV.
8.7 Quadrature demodulation
Quadratic demodulation is based on the principle of synchronous detection to obtain real and imaginary components of the NMR signal. Its structure is based on a Quadrature Intermediate Frequency Mixer (QIFM) demodulator whose schema is given (see Fig. 10). It consists of a 90° hybrid splitter, two mixers, and a 0° combiner (summing). Each of these elements is listed in the table of components (see Table A1).

Structure of a Quadrature Intermediate Frequency Mixer demodulator (QIFM). Mixers: X2L-06–414 from Pulsar Microwave.
At the input of the 90° hybrid divider, we have the base frequency of the Local Oscillator (LO) input spectrometer; this is actually the Larmor frequency of the spectrometer. At the input of the 0° divider, we have the FID: this is the high-frequency response RF. At the output of the quadratic demodulator on channels I (imaginary) and Q (quadratic), the signals are of the form: i) cos [2π(νrf + ν0)t)] + cos [2π(νrf − ν0)t)]; ii) sin [2π(νrf + ν0)t)] − sin [2π(νrf − ν0)t). We therefore obtain two quadrature components with all the "sum" and "difference" frequencies of the demodulated signals: 2π(νrf + ν0) and 2π(νrf − ν0), plus harmonics. Only low-frequency signals in the 10-kHz range are interesting, and the signal must be filtered to retain only the lowest frequencies using a low-pass filter.
8.8 Double active audio low-pass filter
An active double low-pass filter is required to keep only the low frequencies of the demodulated signals (see Fig. 11). Each filter is designed to charge the demodulators on 50 Ω and consists of two stages allowing an overall gain of about 30 dB in voltage. As around the resonance, the measured frequency differences are about ten kilohertz, the filter bandwidths are adjustable over a range from 100 Hz to 500 KHz.

1H signal (one component) of a water sample (5 mm) obtained (one SCAN: NS = 1) after the demodulation stage and low pass filtering, observed on a digital oscilloscope with FFT. Top: FID component. Bottom: spectrum: presence of the peak at 4.92 KHz. Note the linewidth of 423 Hz. The Larmor frequency was ν0 = 6.4 MHz. The RF excitation pulse length is 50 μs. See Appendix for the details of the experimental setup.
The two filter channels must be adjusted to have the same frequency and phase responses throughout the useful bandwidth. This is to avoid unbalancing between the real and imaginary components of the signal, which would degrade the spectrum in frequency (quadrature artifact, zero frequency…). Precise gain and phase adjustments in the bandwidth are made with a network analyzer, the only true and effective way to visualize the response of both channels as a function of frequency.
9 Setting of spectrometer
9.1 Probe control
The tuning of the probe to the resonance frequency has been described above.
9.2 Cancellation of the DC offsets
Any DC voltage offset in the detection circuit generates a zero frequency component that will affect the quality of the spectra. To reduce this unwanted effect, it is important to carefully cancel the offset voltages of the active double low-pass audio filter to have a signal close to zero when the input signal is nul.
9.3 Signals at the output of the audio amplifier without sample
At first, we work without putting a sample in the magnet to minimize the imperfections of the assembly: adjustment of the LO level (10 dBm) and cancellation of continuous offsets. In the absence of a sample, the voltage offsets are less than 1 mV. In addition, note that the deadtime of the probe after the RF pulse is 400 μs (see Fig. 12a).
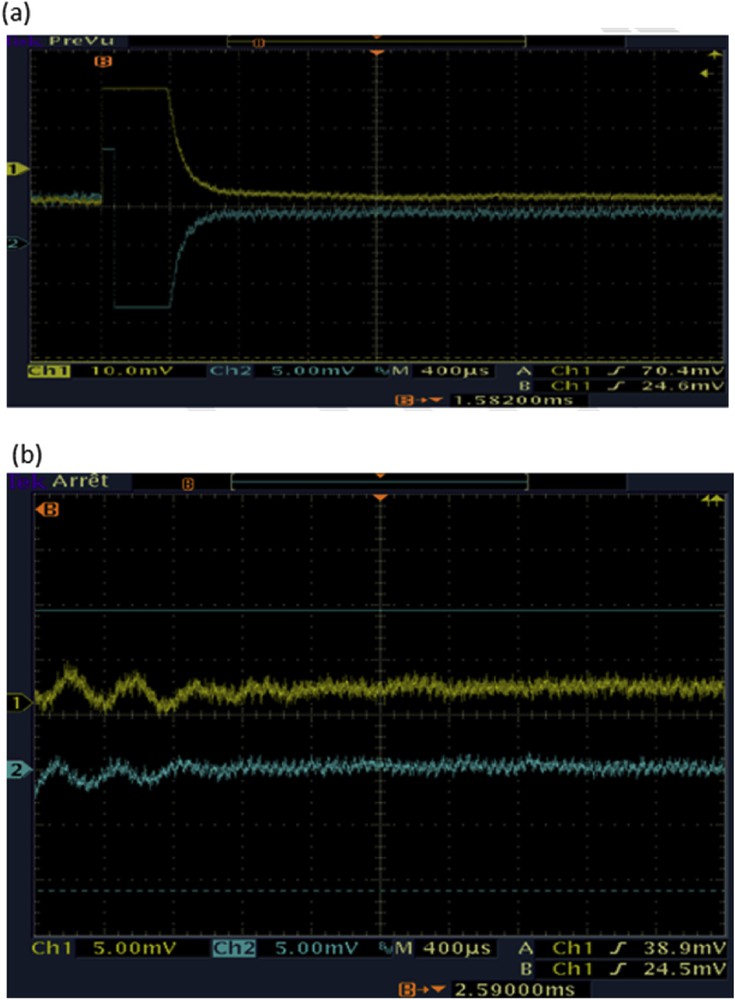
(a) No NMR tube: real (high, channel 1) and imaginary (low, channel 2) components at the output of the audio frequency amplifier after an RF excitation pulse length of 50 μs. (b) Example of one-scan quadrature detection of a low-magnitude 1H signal (5-mm water tube). See Appendix for the experimental setup.
9.4 Signals at the output of an audio amplifier with sample
The imperfections of the assembly having been minimized, we introduce our sample (a 5-mm tube of water), and we visualize the precession signals in quadrature mode (see Fig. 12b). Note the very low magnitude of the signals.
9.5 Optimization of the 90° flip angle
The NMR signal obtained at this step, although observable, is relatively small in amplitude. To maximize the amplitude of the FID, it is now necessary to adjust the strength excitation pulse for a tilting of M0 equal to 90°. For this reason, the duration of the pulse is varied until a magnetization is obtained whose intensity in the xy plane is maximum (see Fig. 13). The amplitude variation of the magnetization vector is observed as a function of the excitation pulse duration. In our case, the pulse duration is between 13 and 14 μs. Another approach is to determine the pulse duration corresponding to an angle of 180°, for which the macroscopic magnetization is then null (tilted to the −Oz axis).
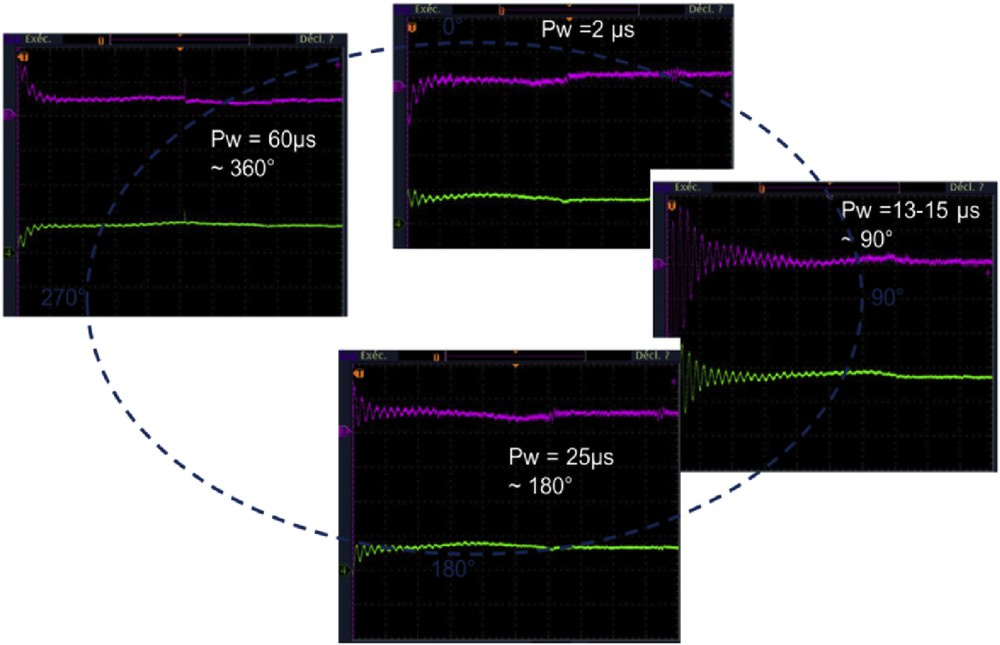
Adjustment of the RF excitation pulse duration to obtain a maximized signal corresponding to a 90° pulse.
9.6 Increase in the S/N ratio
The signal-to-noise ratio of an NMR experiment involves numerous factors such as: i) the magnetization M0, ii) the filling factor and the quality factor of the probe, iii) the noise factor of the preamplifier, and so on [22]. After optimization of all the electronic hardware and parameters, we can also increase the SNR during the acquisition. The SNR can be improved by averaging the FID signals over a large number of acquisitions (NS scans). Indeed, on an average of NS acquisitions, the noise will be averaged toward zero due to its random origin, whereas the useful signal will increase on average. Thus, the SNR is improved at the root of NS as displayed in Fig. 14.
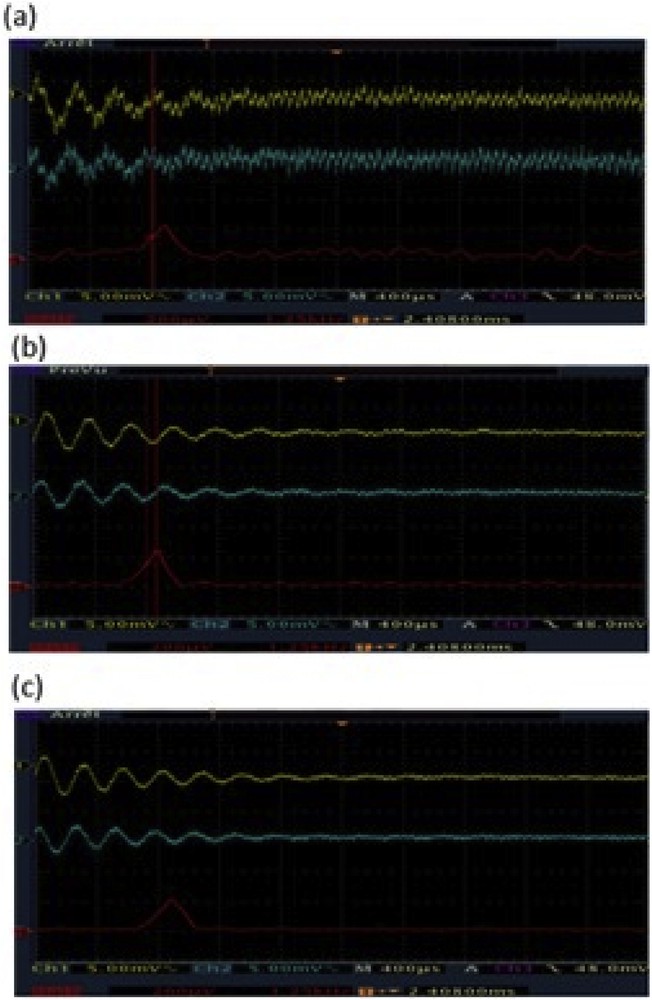
Effect of averaging on the SNR. Comparison of the FIDs obtained by adding successively: (a) 2, (b) 32, and (c) 64 scans (5-mm water tube). On (c), note the vertical line setting at 3.45 kHz. See Appendix for the experimental set up.
10 Possible applications
Benchtop FT-NMR allows many applications in chemistry, such as the analysis or characterization of small molecules, or the monitoring of chemical reactions. The teaching of NMR methodologies (effects of excitation/inversion pulses, pulse calibration, optimization of acquisition parameters, as well as the description of some experiments as the measurement of relaxation parameters, spin echoes…) is also another aspect of their use. The portable low-field NMR is particularly suitable for nuclei with high natural sensitivity, such as 1H, 19F, 31P, and 29Si. However, other « exotic » nuclei with high gyromagnetic ratios such as 7Li, 11B, and 23Na can also be detected [27,28].
A (home-built) mobile NMR spectrometer can also be used to develop projects that aim to couple NMR and optical microscopy in a semiconductor [23] to locally polarize nuclear spins (dynamic polarization) and measure the spatial profile of nuclear magnetization using an optically detected NMR, with good spatial resolution. This fundamental study of nuclear spin diffusion does not require a high magnetic field (less than 0.15 T). For this kind of experiment, NMR functionalities are reduced to signal excitation and detection for parameter optimization, without the need for frequency resolution.
11 Conclusion
The low-field FT-NMR spectrometer presented in this article is fully operational. This revisited instrument can be exploited to carry out simple NMR measurements such as the determination of chemical shifts (δ), spin echoes, measurement of T2(1H) or T1(1H) relaxation times, etc. On the other hand, it provides a pedagogical approach to the teaching of NMR to students at all levels, from the physical concept to the electronic realization through the many possible analysis applications [24, 25, 26]. It is also an excellent demonstration element at scientific events for a more general public. Finally, it can be inserted in real experiments of physics requiring NMR to be coupled with another measurement technique such as optics, for example.
Noteworthy technical developments of the instrument are possible. Thus if the permanent magnet is equipped with an additional pair of coils with currents in the range of 1–3 A, it can then be injected to create additional field gradients to B0. The spectrometer is then able to perform some simple 1D imaging experiments or to experimentally measure molecular diffusion coefficients.
Although sensitivity is reduced at low-field strength, quantification and measurement of relaxation and diffusion parameters of neat samples or solutions are possible [27, 28]. This kind of portable NMR spectrometer could then appear the ideal tool for outdoor NMR analysis of ecosystems.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
A.L-J. thanks the physics department of the "École polytechnique" and its Polytechnician students, as well as the LPMC (UMR CNRS 7643) for their contributions to the development of mobile NMR. P.L. thanks CNRS for its support to fundamental research and the divulgation of fundamental sciences.
Appendix
Definitions of acronyms and notations used
ARM: Advanced Reduced instruction set computing Machines
ADC: Analog-to-Digital Converter
BNC: Bayonet Neill–Concelman (connector)
B0: Static magnetic field
BF: Basic Frequency
B1: RF coil.The term B1 is used to characterize the field, in the plane, orthogonal to the static B0 field. In the terminology frequently encountered in the fields of NMR, the B1 coil is a resonant LCR circuit tuned to the Larmor frequency. This coil is used for the detection and the excitation of the nuclei in FT-NMR experiments. L is inductance, C is capacitance, and R is resistance.
CW: Continuous Wave
dB: Decibel
dBm: Power in decibel: 0 dBm = 1 mW/50 Ω
DDS: Direct Digital Synthesis
FFT: Fast Fourier Transformation
FID: Free Induction Decay
FT: Fourier Transformation
FPGA: Field Programmable Gate Area
HFFID: High-Frequency Free Induction Decay
LO: Local Oscillator
M0: Magnetization at equilibrium
NF: Noise Factor
NMR: Nuclear Magnetic Resonance
Q: Quality factor
QIFM: Quadrature Intermediate Frequency Mixer
RF: RadioFrequency
SMA: SubMiniature version A (connector)
SNR: Signal-to-Noise Ratio
TROSY: Transverse Relaxation Optimal SpectroscopY
TTL: Transistors Transistors Logics
T2: Spin–spin relaxation time
T1: Spin–lattice relaxation time
ν0: Larmor frequency (MHz)
Experimental setup (except otherwise in the text)
All NMR and test experiments have been made with the electronic setup outlined in Fig. 4. A permanent magnet with a field of 1500 G (6.4 MHz) is used for the static magnetic B0 field (see Fig. 2). A home-made solenoid-type probe device and a 5-mm water sample tube were used for the tests. The frequency and the RF pulse duration have been set with the frequency generator and the pulse generator mentioned in the text. Data have been acquired and processed using some digital oscilloscopes with sensitivities of 1 or 2 mV/div.
Characteristics and nomenclature of the electronic components
Table A1 provides the characteristics and nomenclature of the electronic components used.
Characteristics and nomenclature of electronic components.
| Characteristics | Designation | Number of devices | Frequency range (MHz) |
| 1500 G permanent magnet, 40-mm air gap, NMR homogeneity on a useful diameter of 20 mm, divergent polar pieces on a diameter of 200 mm, height 400 mm | TE2M C4-1367 1500 G | 1 | 6.2–6.8 |
| Directional coupler 30 dB, 3W, SMA (Pulsar) | C5-08-411 | 2 | 5–1000 |
| SMA connector (pulsar) | 20 | 0.1–1000 | |
| Mixer level 7 dBm SMA (Pulsar) | X2L-06-414 | 2 | (LO/RF) 1–1000: (IF) DC-1000 |
| Power divider/combiner, 2 way (0°), phase balance: 2°, amplitude balance: 0.3 dB Insertion loss 0.8 dB, SMA (Pulsar) | P2-09-411 | 3 | 5–1000 |
| 90° hybrid power divider Phase balance 2°, amplitude balance 0.4 dB, insertion loss 0.5 dB, SMA (pulsar) | QE-01-412 | 1 | 2–10 |
| Low-noise RF preamplifier NF = 2, gain: 35 dB, RF output power: 5 dBm Absolute maximum rating input RF power: −35 dBm (Elhyte) | BA01500-35 | 1 | 0.1–500 |
| Low-noise RF preamplifier NF = 2.9, gain: 25 dB, output RF power: 5 dBm (mini circuit) | ZFL1000LN+ | 1 | 0.1–1000 |
| Low-noise RF preamplifier RF; NF = 3.8, gain: 23 dB, RF output power: 5 dBm (home made) | RF2046 | 3 | DC -1000 |
| Power amplifier | ZHL 5W−1 | 1 | |
| Operational amplifier | OP27 | 1 | DC - 8 |
| Operational amplifier | OP37 | 1 | DC - 60 |
| Resistor | 1 kΩ, 10 kΩ | 10 | |
| Variable capacitor | 5 pF–500 pF | 4 | |
| Probe (home made) | 1 | 6.1–6.8 | |
| Sequencer board with ARM + DDS (home made) Or frequency generator and laboratory pulse generator (see text). | NXPLPC1767+ DDS 9959 | 1 1 | 0.01–301 |
| Analog or digital oscilloscope with FFT | 1 | ||
| AC/DC adapter 24 V/6.4 A | AHM150PS24 | 1 | |
| Total estimated cost | ∼10 k€ |


