1. Introduction
The development of chemical, metallurgical and mining industries in the Congo Basin subregion and Gabon in particular, contributes to environmental pollution by heavy metals (Cu, Fe, Mn, Cr, …) [1, 2]. The huge exploitation of these materials is the main cause of the pollution of water resources and soil.
Copper (Cu) for example, in its ionic form, is toxic to species in aqueous media and can cause major health problems in humans. The presence of copper(II) ions (Cu2+) at high concentrations in waters, can cause, during repeated exposure or by ingestion, several health problems: anemia, weight loss, breathing difficulties, kidney and liver damages that can lead to death [3]. The World Health Organization (WHO) recommends a limit value for Cu2+ of 2 mg/L in drinking water due to its toxicity [4]. Thus, the treatment of industrial and drinking water is important before discharge into the environment and before distribution in the drinking water systems, respectively.
In fact, in industrial environments, wastewater treatment techniques exist. Thus, decantation, flocculation or chemical coagulation [5, 6], chemical precipitation [7] and reverse osmosis [8] are among the methods used. These water treatment methods are very expensive and very effective for the removal of organic matter but require additional treatments. In addition, they have limited effectiveness for ionic species, due mainly to the high water solubility and non-biodegradability of these ionic species [9].
On the other hand, adsorption techniques which use porous solids, such as activated carbons (AC), appear to be the least expensive and have fewer disadvantages [10]. These methods have been extensively studied to compensate the shortcomings of other methods used in the treatment of industrial or drinking water [10]. According to the literature, adsorption studies in static (batch) or dynamic conditions have shown that AC-type adsorbents prepared from agricultural waste or biomass with a high carbon content [3, 8, 11, 12, 13] can be used to trap metal ions in aqueous solution. In the case of copper(II) ions, studies under static conditions showed that pH and concentration of the initial solution, mass of adsorbent and contact time, influenced the adsorption capacities at saturation of ACs [3, 14, 15, 16, 17, 18, 19, 20, 21]. In addition, the kinetic studies have shown that the pseudo-second-order kinetic model appears most suitable to describe the adsorption kinetics of copper(II) ions on ACs in static adsorption mode [18, 20, 21, 22]. However, very few studies on the elimination and in particular on the adsorption kinetics of copper(II) ions, in dynamic conditions on fixed-bed columns, have been carried out.
Thus, the goal of this work was to valorize waste from coconuts (shells) of the Haut-Ogooué region (Franceville) in Gabon, in the preparation of AC-type adsorbents, thus to carry out dynamic Cu2+ adsorption studies in aqueous media on a fixed-bed column under different experimental conditions and subsequently, to study the Cu2+ adsorption kinetics on the prepared AC.
2. Experimental
2.1. Preparation of Cu2+ solution
A solution of 500 mg/L of Cu2+ was prepared by dissolving 1.965 g of copper sulphate pentahydrate salt (CuSO4⋅5H2O) from LABOSI in a 500 mL volumetric flask. The mixture was stirred for 20 min and thereafter water was added to obtain a solution of concentration 250 mg/L. The latter solution was then used as initial solution for all dynamic adsorption experiments.
2.2. Preparation of activated carbon
The AC preparation method from coconut shells is the same as that used in a recent study [23]. The coconut shells were cleaned, washed several times with distilled water, and then dried at room temperature for 7 days. The dried solids were then crushed, washed with distilled water, dried in an oven for 24 hours (h) at 110 °C and kept in a borosilicate glass crucible. Then, 50 g of the dry material were soaked in a solution of zinc chloride at 1 M (ZnCl2: dry material = 1:1 % by weight) for 72 h. The impregnated solid was dried in the oven for 24 h at 110 °C, then heated to 600 °C under air, in a NABERTHEN brand oven, for 1 h and 30 minutes (min) with a rise in temperature of 5 °C/min. The AC obtained was left to cool, rinsed with a solution of HCl (0.1 M), and washed with distilled water until pH of the residual water became neutral. The AC was then dried for 48 h at 110 °C and sieved using a TAMISAR sieve (Standard: AFNOR_NF-X11-501) to obtain different sizes of AC particles.
2.3. Characterizations
Measurements of surface areas and pore volumes were carried out with a Micromeritics TRISTAR 3000 instrument [24]. 100 mg of adsorbent were pretreated for 1 h at 90 °C and 10 h at 350 °C, successively. The nitrogen (N2) isotherm was acquired at −196 °C. The specific surface area of the AC prepared was determined by means of the Brunauer, Emmett and Teller (BET) theory [25]. Mesoporous and microporous volumes were obtained by the t-plot method of De Boer and Dubinin-Radushkevich equations, respectively [26, 27, 28].
The pH at the point of zero charge (pHpzc) of the adsorbent prepared was evaluated based on the acid–base titration method [29] and described in a recent study [2]. pHpzc was determined by the point of intersection between the experimental curve and the theoretical curve of pHf = f(pHi).
Assessments of surface functional groups of the adsorbent were performed using the modified Boehm method [30]. The concentrations (mmol/g) of acid or basic groups were calculated using the following equation:
2.4. Experiments of dynamic adsorption on column
For dynamic adsorption experiments of Cu2+ on the prepared AC, we used a Pyrex brand glass column of length 55 cm and diameter 1.4 cm. The protocol and scheme of the experimental set-up were reported in a recent study [2].
During the experiments, various parameters were kept constant: concentration (C0 = 250 mg/g), pH of the solution (pH = 6.5) and temperature (T = 25 ± 2 °C). In contrast, particle sizes, heights of adsorbent bed and flow rates were modified according to experiments.
The experiments were stopped when the residual concentrations (C) were equal to the concentrations at the inlet of the column (C ∕ C0 = 1).
The breakthrough curves were established by varying the ratio C ∕ C0 versus time (t). Exploitation of curve data (C ∕ C0 = f(t)) gives an area (A) in minutes obtained by integration according to the trapeze method [31, 32]:
The Cu2+ amounts (qads) and saturation adsorption capacities (Qsat) were calculated with the following relations [23]:
Removal percentages (E) of copper(II) ions on the prepared adsorbent were determined by the relation below [23]:
2.5. Adsorption kinetics studies
In order to describe the dynamic behavior and to evaluate the adsorption kinetics of copper(II) ions in adsorption experiments on a fixed-bed column, four mathematical models were applied to the experimental data: the Thomas model, the pseudo-first-order, pseudo-second-order, and intraparticle kinetic models.
2.5.1. Thomas model
The Thomas model [33], described by Sarkar et al. and in a recent work [23, 34], assumes the Langmuir kinetic model is valid with no mass transfer and axial dispersion during the fixed-bed column adsorption process. It is expressed as:
2.5.2. Pseudo-first-, pseudo-second-order, and intraparticle kinetic models
The pseudo-first-order model is described by the following relation [23, 35]:
The pseudo-second-order model is described by the following relation [23, 36]:
According to Webber and Morris [35], the kinetic expression of intraparticle diffusion is described by:
3. Results and discussion
3.1. AC chemical and textural properties
Textural and chemical properties of the prepared adsorbent were evaluated jointly by N2 physisorption, quantification of the surface functional groups and determination of pH at zero charge point (pHpzc).
Figure 1a presents the N2 physisorption isotherm. Textural and chemical properties are listed in Table 1. According to IUPAC classification [37], the isotherm obtained is of type I, indicating a microporous material with a hysteresis loop of type H4 which reveals the presence of slit-shaped pores. Results in Table 1 confirm these observations. In fact, the total pore volume (0.087 cm3/g) is very close to the microporous volume (0.082 cm3/g). The average pore size and specific surface area obtained are 1.68 nm and 208.2 m2/g, respectively.
N2 adsorption–desorption isotherm (a) and pore sizes distribution (b) of prepared activated carbon (AC).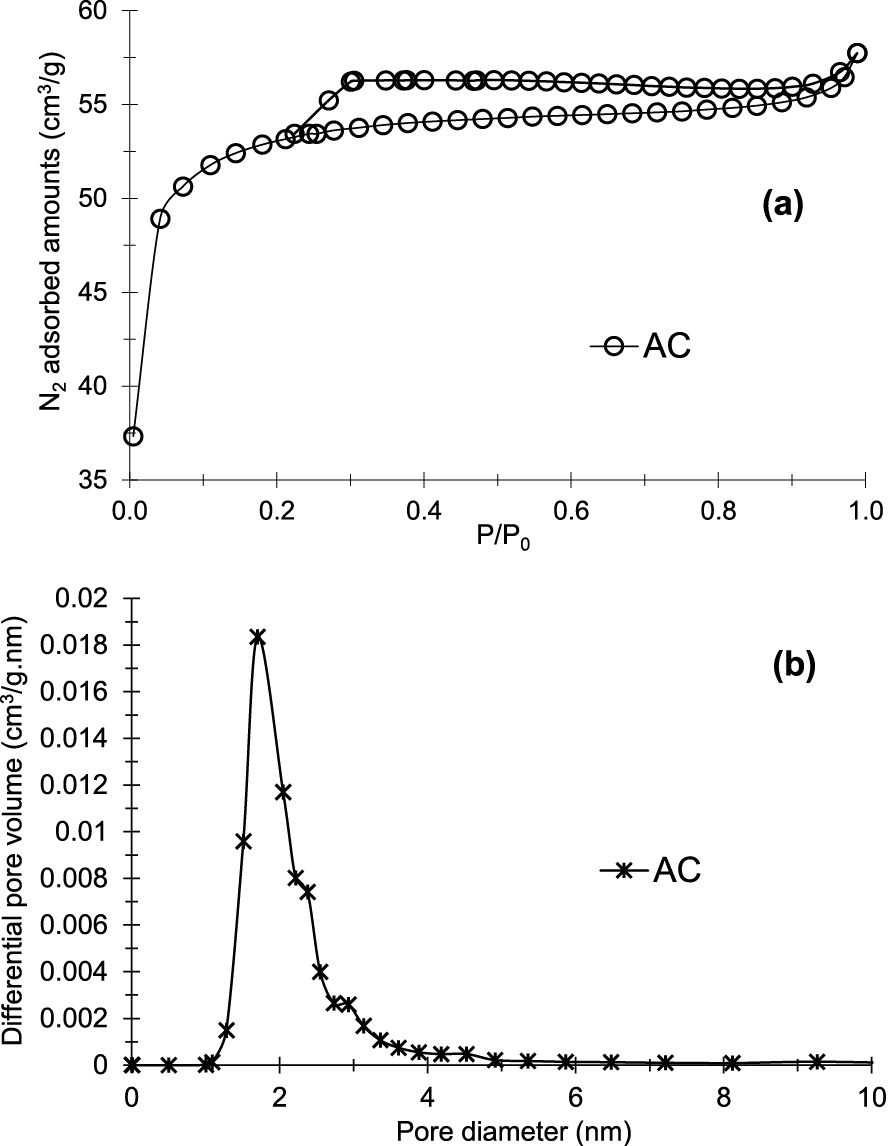
Structural and chemical characteristics of prepared activated carbon (AC)
| Sample | SBET (m2/g) | Vmicro. (cm3/g) | Vmeso. (cm3/g) | Average pore size (nm) | pHpzc | Basic functions (mmol/g) | Acidic functions (mmol/g) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Total | Carboxyl | Lactone | Phenol | |||||||
| AC | 208.2 | 0.082 | 0.003 | 1.68 | 6.3 | 0.12 | 3.39 | 1.45 | 1.08 | 0.86 |
SBET: specific surface area BET. Vmicro: microporous volume. Vmeso: mesoporous volume.
Based on the results of N2 physisorption, the prepared AC shows predominantly a microporous structure.
Results of the chemical properties study from the surface functional group quantification by the Boehm titration method [30] revealed the presence of basic functional groups and phenolic (–OH), lactonic (–COO–), and carboxylic acids (–COOH). Basic functional groups are less abundant than acidic functional groups (Table 1). Moreover, carboxylic acid functional groups (1.45 mmol/g) are more abundant than lactone (1.08 mmol/g) and phenol (0.85 mmol/g) functional groups. Benmahdi et al. [38] observed similar results in their work on the synthesis and characterization of microporous granular AC using ZnCl2 activation. It appears that the activating agent ZnCl2 promotes the formation of acidic functional groups and microporous structure in the AC preparation.
The evaluated pHpzc of the prepared AC is 6.3 (Figure 2). This acidic value confirms the results obtained on surface functional groups where the acidic functional groups are in majority. In addition, it reveals that the surface of the prepared adsorbent will be positively charged when pH < pHpzc, and vice versa [2, 38].
pHpzc determination of prepared activated carbon (AC) using Boehm titration method [30].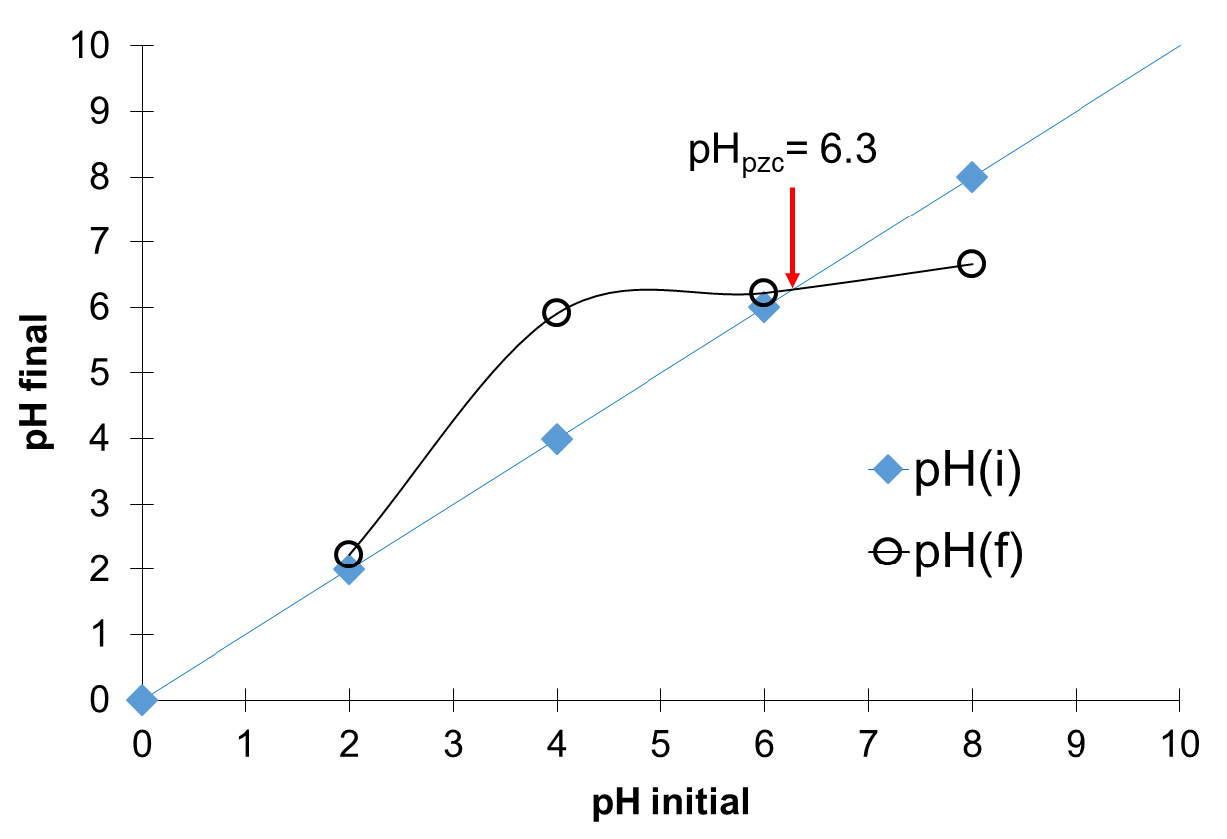
Therefore, to increase the number of adsorption sites on the surface of the prepared AC (–COO−, –O−, etc.) favorable to Cu2+–AC interactions, the pH of the solution must be greater than pHpzc.
3.2. Dynamic adsorption experiments
The adsorption capacities at saturation and removal percentage of Cu2+ were evaluated. Moreover, effects of various parameters on the bed efficiency were studied, including the size (x) of the particles composing the adsorbent bed of the column, flow rate (D), and bed height (h); and Cu2+ adsorption kinetics studies were performed.
3.2.1. Effect of particle size, flow rate and bed height
Two sizes were studied: 0.1 < x < 0.25 mm and 0.01 < x < 0.04 mm. Figure 3 shows breakthrough curves (Figure 3a) and the evolution of Cu2+ removal efficiency (Figure 3b) obtained.
Breakthrough curves (a) and evolution of Cu2+ removal efficiency (b) obtained at 25 °C on the prepared AC with various particle sizes (h = 1 cm, D = 2 mL/min, C0 = 250 mg/L and pH = 6.5).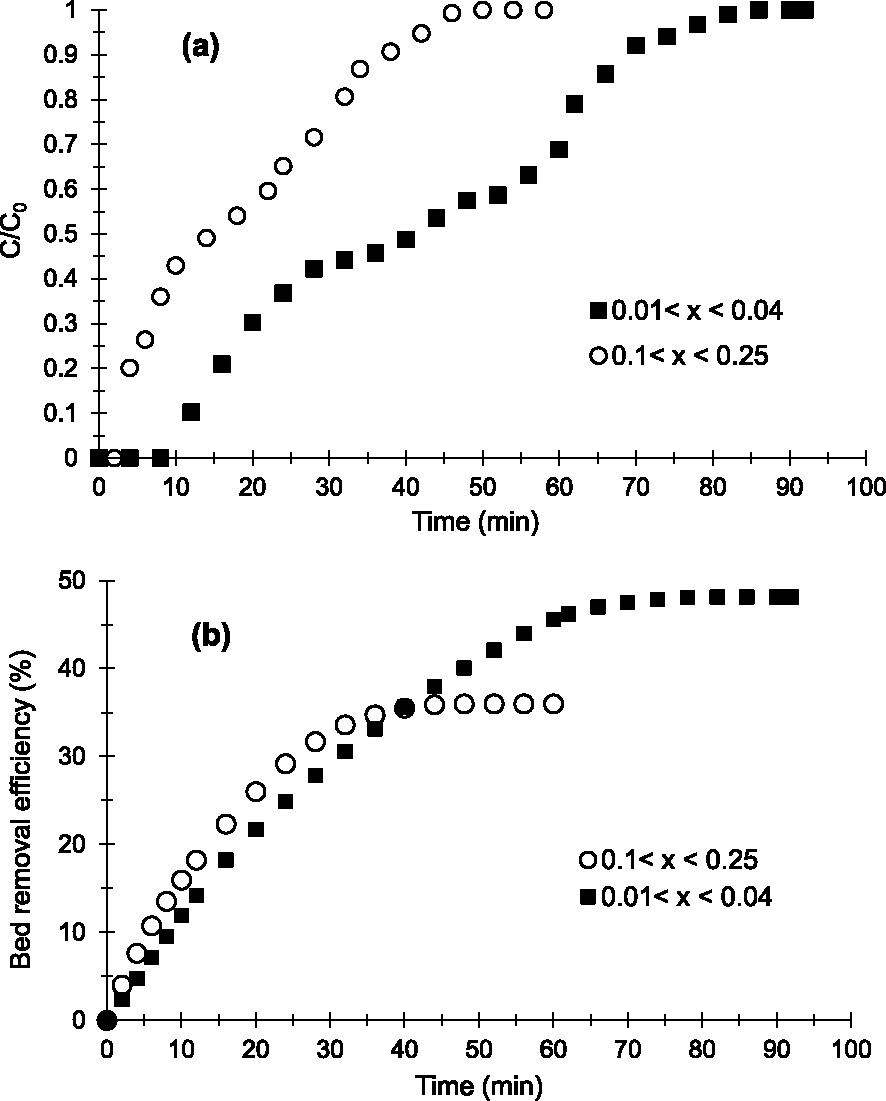
The breakthrough curves show a multistep adsorption kinetics of Cu2+ on the prepared AC according to the time intervals (adsorption zones). The profiles obtained seem to show comparable adsorption kinetics, diffusion and Cu2+–AC interaction energies on beds of 0.1 < x < 0.25 mm and 0.01 < x < 0.04 mm in the first adsorption domain (5–10 min and 10–30 min respectively) and the third zone (35–55 min and 65–95 min respectively). Indeed, the slopes obtained in these zones (Figure 3) are almost similar [39].
However in the second adsorption zone (10–30 min and 30–60 min, respectively), the adsorption kinetics, the diffusions and the adsorption sites strengths are different. The particle bed of 0.01 < x < 0.04 mm shows slower adsorption kinetics and diffusion of the aqueous phase between grains or in the microporosity with stronger Cu2+–AC interactions on the material surface or in the pores. The slope for 0.01 < x < 0.04 mm (Figures 3a and 3b) tends more towards the horizontal compared to that for 0.1 < x < 0.25 mm in the second adsorption zone [25].
In addition, Figures 3a and 3b reveal that the bed with 0.01 < x < 0.04 mm is more efficient in removing Cu2+. Indeed, the breakthrough (tp) and saturation (tsat) times obtained (Table 2) on the bed with 0.01 < x < 0.04 mm (12 and 84 min respectively) are higher than those obtained on the bed with 0.1 < x < 0.25 mm (4 and 50 min respectively). Also, the results shown in Table 2 indicate that the amounts of Cu2+ adsorbed (qads), the adsorption capacities at saturation (Qsat) and the elimination percentage (E) obtained on the finer particles bed (20 mg; 40.44 mg/g and 48.14%, respectively) are higher than those of the larger particles bed (8.99 mg; 12.85 mg/g and 35.97% respectively). Based on Weber’s work [35], this can be explained by the fact that smaller particles have greater flow resistance and a shorter diffusion path in pores or between grains, allowing Cu2+ to easily access the surface of AC particles and providing a larger accessible surface area or adsorption sites.
Experimental results of Cu2+ removal in aqueous media on the prepared AC at 25 °C and under different experimental conditions
| Parameters | Experimental conditions | tc (s) | tp∕tsat (min) | qads (mg) | Qsat (mg/g) | E (%) |
|---|---|---|---|---|---|---|
| Particle sizes (mm) | 0.01 < x < 0.04 | 46.18 | 12/84 | 20.22 | 40.44 | 48.14 |
| 0.1 < x < 0.25 | 4/50 | 8.99 | 12.85 | 35.97 | ||
| Bed heights h (cm) | 1 | 46.18 | 12/84 | 20.22 | 40.44 | 48.14 |
| 2 | 92.36 | 18/120 | 30.74 | 46.23 | 51.23 | |
| 3 | 135.54 | 24/134 | 36.87 | 52.52 | 55.02 | |
| Flow rates D (mL/min) | 2 | 46.18 | 12/84 | 20.22 | 40.44 | 48.14 |
| 4 | 23.09 | 8/68 | 24.44 | 30.55 | 47.92 | |
| 6 | 15.39 | 4/52 | 27.23 | 19.79 | 35.49 |
In general, breakthrough curves showed slow adsorption kinetics and diffusion of the aqueous phase between grains, with stronger Cu2+–adsorbent interactions as the adsorbent bed particle size decreases. This allows a better affinity (adsorption) between Cu2+ and the prepared AC. In our experimental conditions, the bed composed of the lowest particle sizes (0.01 < x < 0.04 mm) appears more efficient in the elimination of Cu2+.
In the study of bed height (h) influence, three bed heights (1; 2 and 3 cm) were studied. Figure 4a shows the breakthrough curves obtained. Regardless of bed height, the multistep adsorption process is always visible on the adsorption profiles obtained. The adsorption kinetics and diffusion of the Cu2+-containing aqueous phase on the surface of the materials or between the grains are comparable for heights 2 and 3 cm (Figures 4a and 4b). On the other hand, in the third adsorption zone for h = 1 cm (65–95 min), the Cu2+ adsorption kinetics and the diffusion of the aqueous phase are faster compared to those with h = 2 and 3 cm (80–105 min and 95–120 min, respectively). Indeed, the slope for h = 1 cm tends to be much more vertical compared to that for h = 2 and 3 cm (Figure 4a).
Breakthrough curves (a) and evolution of bed removal efficiency (b) of Cu2+ obtained at 25 °C on the prepared AC at various bed heights (D = 2 mL/min, C0 = 250 mg/L and pH = 6.5).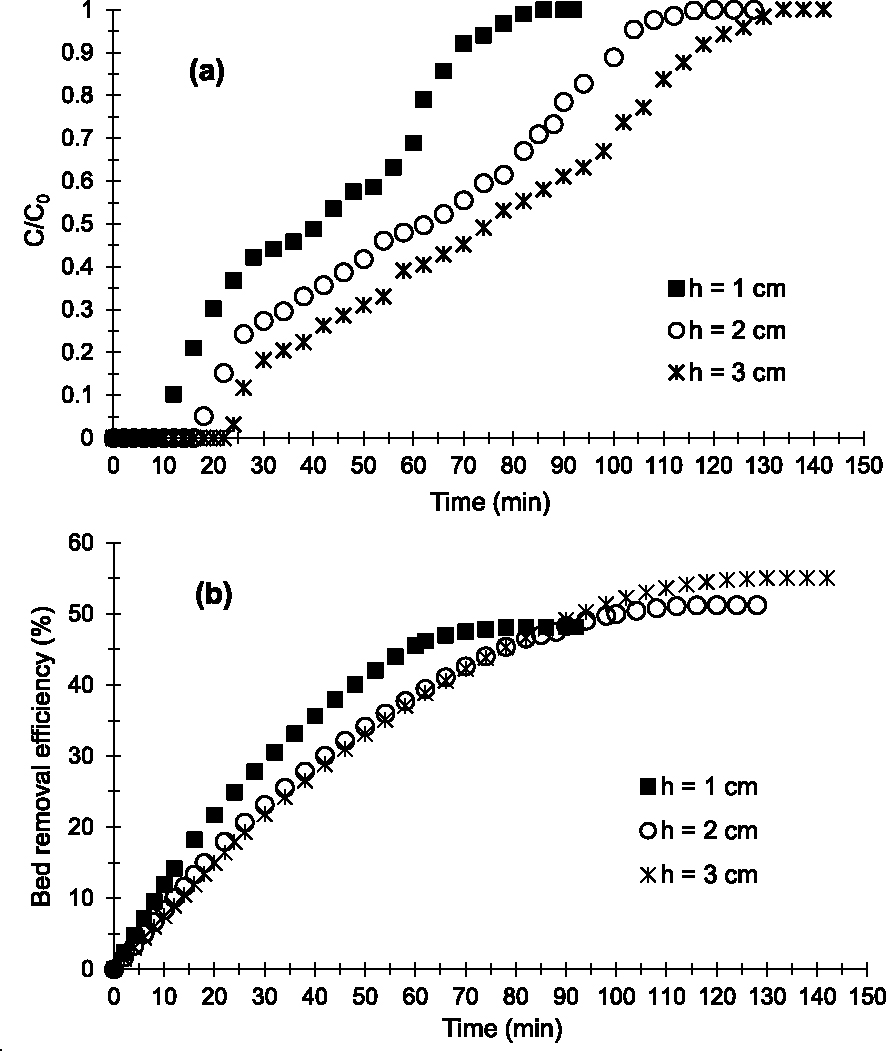
Figures 4a and 4b indicate that the bed h = 3 cm is more efficient in removing Cu2+. Indeed tp (24 min) and tsat (134 min) obtained are higher than those obtained with beds h = 2 and 1 cm (Table 2). In addition, qads, Qsat and E obtained with h = 3 cm (36.87 mg; 52.52 and 55.02%) are higher than those with h = 2 and 1 cm as summarized in Table 2. This could be explained by the fact that an increase in h leads to an increase in the accessible surface area of the adsorbent and a greater dispersion of adsorption sites favorable to Cu2+–AC interactions. Similar results were observed in the work of Hasfalina et al. [39] and Kavianinia et al. [40]. Thus, the higher the adsorbent bed, the more efficient the bed becomes in removing Cu2+ under our operating conditions.
Regarding the influence of flow rate (D), 2; 4 and 6 mL/min were flow rates studied. Based on Figure 5a, the multistep adsorption mode disappears when D increases. With 6 mL/min, a single-step adsorption is visible. It seems that the diffusion of the Cu2-containing aqueous phase is rapid between grains and therefore limits the Cu2+–AC interactions.
Breakthrough curves (a) and evolution of Cu2+ removal efficiency (b) obtained at 25 °C on the prepared AC at various flow rates (h = 1 cm, C0 = 250 mg/L and pH = 6.5).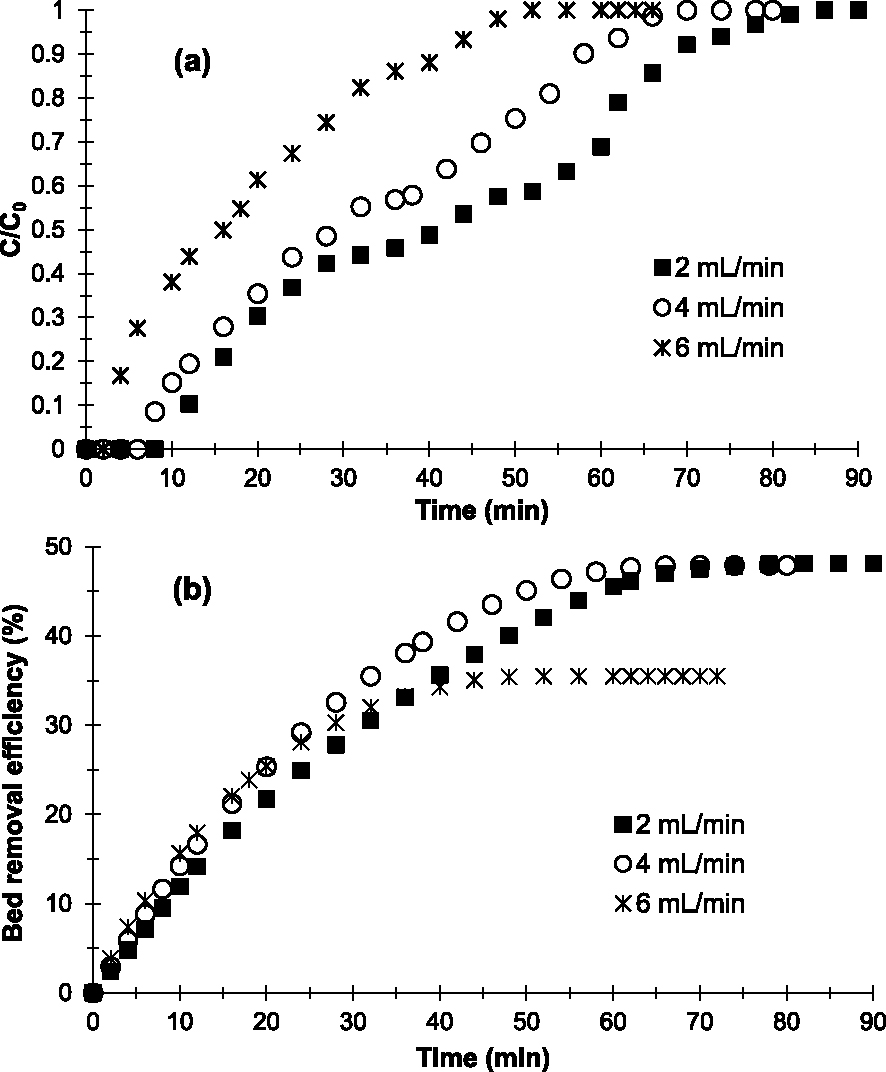
The results in Table 2 show that when D increases, qads, Qsat and E decrease. These results also indicate that the prepared AC is more effective in removing Cu2+ when the applied flow rate is 2 mL/min. Indeed, Qsat and E obtained with 2 mL/min (40.44 mg/g and 48.14%, respectively) are higher than those obtained with 4 mL/min (30.55 mg/g and 47.92%, respectively) and 6 mL/min (19.79 mg/g and 35.49%, respectively). The decrease in E at higher flow rates is due to the decrease in contact time (Table 2) between the Cu2+-containing aqueous phase and the adsorbent. This resulted in low diffusion of adsorbate into the surface or rapid diffusion between the grains of the adsorbent bed [41]. Chen et al. [21] observed similar results in their studies concerning the effect of contact time on the removal of copper ions in an aqueous solution on ACs.
Based on results of the influence of flow rates, it appears that increasing the flow rate decreases the efficiency of the prepared AC in Cu2+ removal. In our experimental conditions, 2 mL/min is the optimal flow rate.
3.2.2. Adsorption kinetics studies
Adsorption kinetics studies were carried out on experiments performed on the influence of flow rates. Several kinetics models (Thomas, pseudo-first-, pseudo-second-order and intraparticle) were applied to experimental data in this study.
Figure 6 shows the linear plots after application of the Thomas linear model. According to these profiles, the experimental points are in agreement with the model. Indeed, the linear regression coefficients R2 of each curve are very close to 1 (Table 3).
Parameters of the Thomas, pseudo-first-order, pseudo-second-order, and intraparticle kinetic models of Cu2+ adsorption ions on the prepared AC
| Experimental data | Thomas model | Pseudo-first-order | Pseudo-second-order | Intraparticle | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D (ml/min) | Qe exp (mg/g) | Qe cal (mg/g) | kTh ×10−3 mL/(mg⋅min) | R2 | Qe cal (mg/g) | k1 ×10−4 (1/min) | R2 | Qe cal (mg/g) | k2 ×10−6 (g/(mg⋅min)) | R2 | Kd (mg/(min1∕2⋅g)) | Cd | R2 | ||||
| 2 | 40.44 | 40.27 | 147 | 0.976 | 43.86 | 359 | 0.989 | 95.24 | 121 | 0.979 | 6.05 | 8.54 | 0.998 | ||||
| 4 | 30.55 | 31.76 | 257 | 0.989 | 40.50 | 467 | 0.986 | 78.74 | 200 | 0.986 | 5.93 | 7.32 | 0.997 | ||||
| 6 | 19.79 | 15.79 | 346 | 0.989 | 21.76 | 708 | 0.992 | 31.25 | 1364 | 0.992 | 3.67 | 2.83 | 0.992 | ||||
Linear plots of the Thomas kinetic model applied to experimental data of Cu2+ removal on the prepared AC at various flow rates.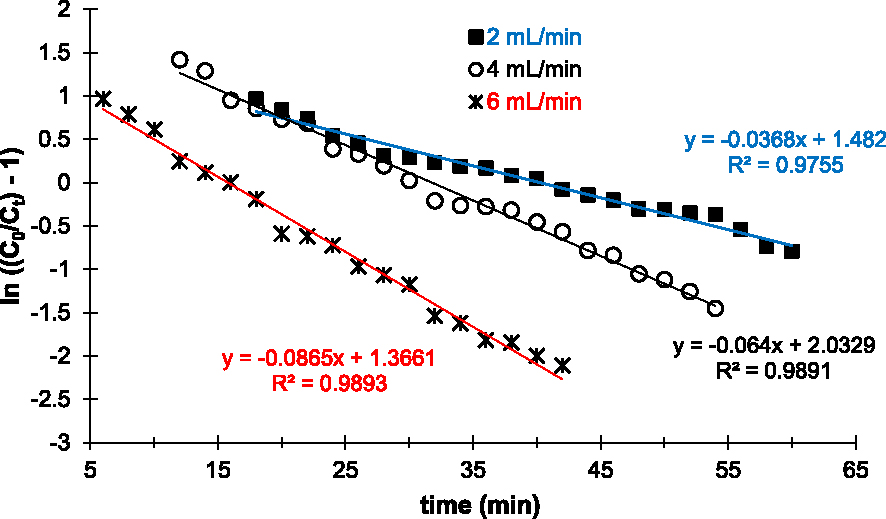
In addition, the calculated capacities at saturation (Qe,Cal) are close to the experimental capacities (Qe,exp) as summarized in Table 3. In particular for the linear plot obtained with 2 mL/min, Qe,exp and Qe,cal are 40.44 and 40.27 mg/g, respectively. Based on these results and according to the Thomas model, external and internal diffusion limitations are non-existent in the Cu2+ adsorption experiments performed, the driving force follows the Langmuir isotherm and the reaction kinetics is reversible. Thus, Cu2+ adsorption on the prepared AC is limited by physical interactions or physisorption, but it is controlled by mass transfer at the interface.
Figure 7 shows the linearization of the pseudo-first- (Figure 7a) and pseudo-second-order kinetic models (Figure 7b) applied to experimental data for Cu2+ adsorption. According to the results of linearization, both kinetic models are in good agreement with the experimental points. The linear regression coefficients R2 obtained in both cases are all close to 1 (Table 3). The results indicate that we have two types of interactions on the surface of the prepared AC: chemisorption and physisorption. These results differ from those of Chen et al. [21] obtained during their work on kinetic adsorption studies of copper(II) ions on ACs in an aqueous media by batch adsorption.
Linear plots of pseudo-first-order (a) and pseudo-second-order (b) kinetic models applied to experimental data of Cu2+ removal on the prepared AC at various flow rates.
However, the calculated capacities at saturation (Qe,cal) according to the pseudo-second-order kinetic model are very high compared to the experimental values (Qe,exp). In contrast, Qe,cal obtained with the pseudo-first-order kinetic model is close to the values of Qe,exp (Table 3).
It therefore seems that the pseudo-first-order kinetic model is the model that best describes the adsorption kinetics of copper(II) ions on the prepared AC in our experimental conditions. On the other hand, in addition to reversible interactions (physisorption), it seems that irreversible reactions (chemisorption) also take place on the surface of the adsorbent. Chemisorption, also known as chemical adsorption, involves the formation of chemical bonds. In other words, it is mainly based on interactions of a covalent nature, i.e., involving the formation of a bond between the adsorbate and the adsorbent, the effects of which are often irreversible [42]. In our experimental conditions (pH = 6.5), the products of chemical reactions at the surface of the adsorbent appear to be the CuO copper oxide [43, 44].
Figure 8 shows the linear plots obtained after application of the intraparticle model to the Cu2+ adsorption data on the prepared adsorbent. Results show that regardless of the flow rate applied, the linear plots do not pass through the origin (Cd≠0). According to this model [35, 45], in our experimental conditions, intraparticle diffusion is involved in the Cu2+ adsorption mechanism on the prepared AC. Thus, it is not the limiting step and the only process controlling Cu2+ adsorption.
Intraparticle kinetic model applied to experimental data of Cu2+ removal on the prepared AC at various flow rates.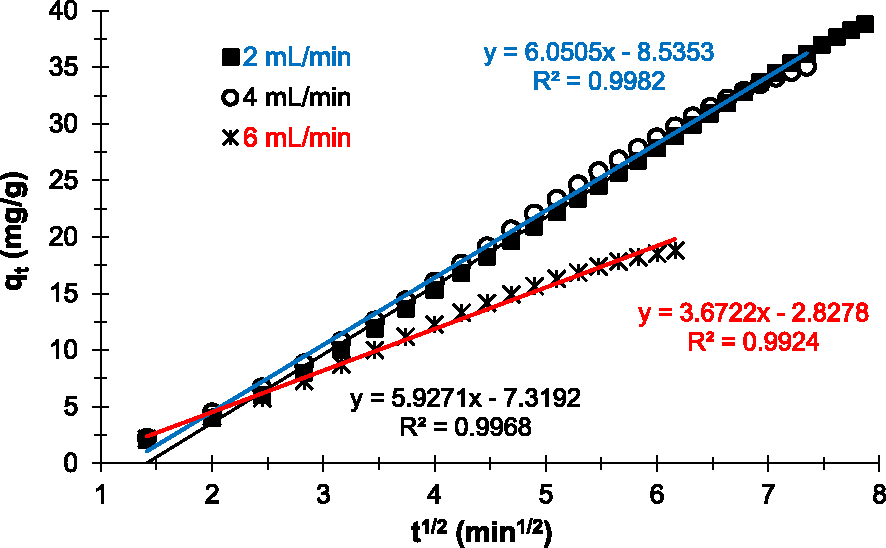
On the other hand, the linear regression coefficients R2 obtained for each plot are close to 1 (Table 2). Therefore, intraparticle diffusion plays an important role in the process (mechanism) of Cu2+ adsorption on the prepared AC in our experimental conditions [23]. Also, the intercept curve (Cd) informs on the boundary layer thickness. The higher the Cd values, the greater the contribution to surface grip in the speed-limiting step [45]. The results in Table 3 indicate that the lower the flow rate, the greater the adhesion of Cu2+ to the surface of the prepared adsorbent. However, regardless of the flow rate applied, the Cd values obtained are very high. This confirms that intraparticle diffusion is not the limiting step in Cu2+ adsorption on the prepared AC and that surface adsorption plays a predominant role in our experimental conditions.
4. Conclusion
This work aimed to prepare an activated carbon (AC) from coconut shells collected in Franceville in the Haut-Ogooué region (Gabon) with the activating agent ZnCl2. Then we carried out dynamic adsorption experiments of copper(II) ions (Cu2+) on fixed-bed columns in aqueous media at different experimental conditions, in order to determine optimal conditions for Cu2+ removal. Studies of Cu2+ adsorption kinetics were also performed.
Textural and chemical characterizations of the prepared AC revealed a predominantly microporous structure with a microporous volume of 0.082 cm3/g, an average pore size of 1.68 nm, a specific surface area (SBET) of 208.4 m2/g and a pH at the point of zero charge (pHpzc) of 6.3. Here, acid functional groups (carboxylic acid, phenol and lactone) are in majority on the surface of the prepared AC.
In dynamic adsorption experiments, it appears that the particle size (x) of the column bed, flow rate (D) and bed height (h) influence adsorption capacities at saturation (Qsat) and Cu2+ removal percentages on the prepared AC. The best Qsat and E (52.52 mg/g and 55.02% respectively) were obtained with 0.01 < x < 0.04 mm, D = 2 mL/min and h = 3 cm with Cu2+ concentration and pH constant (250 mg/L and 6.5, respectively).
Kinetic studies indicated that the Thomas and pseudo-first-order kinetics model best describe the mechanisms of Cu2+ adsorption in our experimental conditions. On the other hand, in addition to reversible interactions (physisorption), it appeared that irreversible reactions (chemisorption) also took place on the surface of the prepared adsorbent. Results from the intraparticle kinetic model indicate that intraparticle diffusion is not the limiting step in Cu2+ adsorption and that Cu2+ surface adsorption on the prepared AC plays a predominant role. Based on the results, the prepared AC could be used as adsorbent in depollution of aqueous media with low concentrations of copper(II) ions.
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that might benefit from this article, and have declared no affiliation other than their research organizations.
Acknowledgments
The authors are grateful to Professor Samuel Mignard and the CNRS Research Fellow Alexander Sachse of the Institute of Media and Materials Chemistry of Poitiers (IC2MP) for their help in the surface characterization of activated carbon.





 CC-BY 4.0
CC-BY 4.0