1 Introduction
The interest for photomagnetic molecular materials is growing. A compound is called photomagnetic when its magnetic properties are modified by light. The recent development of this research field is partly due to the potential applications of such systems to information storage: optical devices are expected to allow high density of information.
Recently, an increasing number of photomagnetic molecular materials have been synthesized, showing spectacular effects and involving various and complex mechanisms [1–9]. Among them are CoFe Prussian blue analogues. Hashimoto and co-workers discovered their photomagnetic properties in 1996 in the compound K0.2Co1.4[Fe(CN)6]1·6.9 H2O [10]. This was the first three-dimensional compound in which a metal-metal photo-induced electron transfer CoIII–FeII → CoII–FeIII*, leading to the formation of excited metastable magnetic pairs of long lifetime at low temperature [10, 11], is responsible for the photomagnetic properties. We showed in a previous work that a bond lengthening of the cobalt-ligand bonds accompanies the photo-induced electron transfer [12]. This system is one of the most studied [13–21] and we undertook a systematic study in order to identify the parameters responsible for the photomagnetism [12, 22–26].
The face-centred cubic Co4[Fe(CN)6]8/3□4/3·n H2O Prussian blue presents intrinsic [Fe(CN)6] vacancies □ due to the stoichiometry. The insertion of alkaline cations in the structure is accompanied by the filling of the vacancies by the anionic ferricyanide to ensure electroneutrality of the solid, according to:
The chemical formulae, above and below, are given for one conventional unit cell.
In the present paper, we study the photomagnetic properties of the CoFe Prussian blue analogues CxCo4[Fe(CN)6](8+x)/3□(4–x)/3 where C = Cs, Rb, K and Na.
2 Experimental section
2.1 Samples
Potassium hexacyanoferrate(III) (Acros, puriss. p.a.), cobalt(II) nitrate (Acros, p.a.) and cesium (Aldrich, puriss. p.a.), rubidium (Aldrich, p.a.), potassium (Acros, p.a.) and sodium (Acros, p.a.) nitrates were used as received.
Synthesis conditions were adapted to the nature of the alkali cation. We observed that the affinity of the alkali cation for the inorganic network increases with increasing size. For this reason, the rubidium derivatives were prepared with diluted aqueous solutions, while potassium and sodium ones were synthesized using concentrated aqueous solutions.
The cesium derivatives were synthesized as previously described [25]. The rubidium derivatives were prepared using diluted solutions, by addition of a solution made of cobalt(II) nitrate and various amount of rubidium nitrate to a potassium hexacyanoferrate(III) solution. To obtain the potassium and sodium derivatives, the cobalt(II) nitrate solution was added to a concentrated solution made of potassium hexacyanoferrate(III) and various amounts of alkali cations salt always used in large excess.
In all the syntheses, the initial pH of the solutions was adjusted to 5 using HNO3 diluted solutions. The addition rate was regulated to last 3 h. The powders were centrifuged, washed three times with distilled water and allowed to dry in air.
The X-ray powder diffraction patterns of all the compounds are consistent with a cubic system, face-centred network, schematised in Fig. 1.
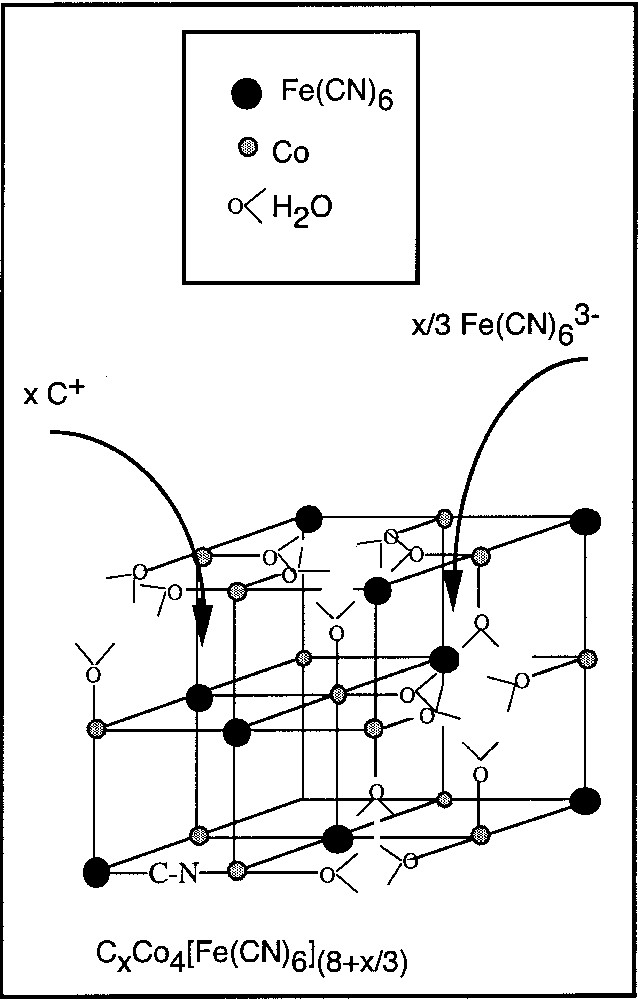
Schematic conventional face-centred cubic cell of a Prussian blue analogue.
The element analyses, related to the chemical formulae for an fcc conventional cell CxCo4[Fe(CN)6](8+x)/3□(4 –x)/3 are reported in Table 1. In the following, the compounds are named Cx, indicating the nature of the alkali cation C in the compound and its x amount per cell. The chemical formulae of compounds Cs0.3, Cs0.7, Cs1.2, and compounds C0 and Rb1.8 given in reference [25] and in reference [24] are also reported. Taking into account the uncertainty in the stoichiometric coefficients (±0.1), all the formulae correspond to neutral samples. The insertion of x alkali cations (C+) is accompanied by the insertion of x/3 additional [Fe(CN)6]3– anionic entities (Fig. 1).
Names, element analysis and proposed formulae for all compounds.
| Sample/Element | C | Co | Fe | C | N | H | O |
| C0 | K0.1Co4[Fe(CN)6]2.7□1.3·19 H2O | ||||||
| Cs0.3 | Cs0.3Co4[Fe(CN)6]2.8□1.2·18 H2O | ||||||
| Cs0.45 | Cs | proposed formula: Cs0.45Co4[Fe(CN)6]2.8□1.2·18 H2O | |||||
| % exp. | 5.10 | 20.40 | 13.65 | 16.97 | 19.21 | 3.11 | 21.51 |
| (% calc.) | (4.93) | (19.43) | (12.89) | (16.63) | (19.39) | (2.99) | (23.74) |
| Cs0.7 | Cs0.7Co4[Fe(CN)6]2.9□1.1·16 H2O | ||||||
| Cs0.95 | Cs | proposed formula: Cs0.95Co4[Fe(CN)6]3.0□1.0·16 H2O | |||||
| % exp. | 9.90 | 18.41 | 12.85 | 16.34 | 18.47 | 2.25 | 21.77 |
| (% calc.) | (9.82) | (18.33) | (13.03) | (16.81) | (19.60) | (2.51) | (19.90) |
| Cs1.2 | Cs1.2Co4[Fe(CN)6]3.2□0.8·16 H2O | ||||||
| Cs2 | Cs | proposed formula: Cs2.0Co4[Fe(CN)6]3.3□0.7·13 H2O | |||||
| % exp. | 17.35 | 15.17 | 12.09 | 16.87 | 18.91 | 1.13 | 18.48 |
| (% calc.) | (18.52) | (16.43) | (12.84) | (16.07) | (19.32) | (1.82) | (14.49) |
| Rb0.6 | Rb | proposed formula: Rb0.6Co4[Fe(CN)6]2.9□1.1·20 H2O | |||||
| % exp. | 3.81 | 16.78 | 11.86 | 17.94 | 19.13 | 2.40 | 28.08 |
| (% calc.) | (4.06) | (18.68) | (12.83) | (16.56) | (19.31) | (3.19) | (25.35) |
| Rb1.3 | Rb | proposed formula: Rb1.3Co4[Fe(CN)6]3.1□0.9·14 H2O | |||||
| % exp. | 8.56 | 17.81 | 13.34 | 16.77 | 19.35 | 2.05 | 22.12 |
| (% calc.) | (8.85) | (18.77) | (13.78) | (17.79) | (20.74) | (2.25) | (17.83) |
| Rb1.8 | Rb1.8Co4[Fe(CN)6]3.3□0.7·13 H2O | ||||||
| K0.85 | K | proposed formula: K0.85Co4[Fe(CN)6]2.95□1.05·18 H2O | |||||
| % exp. | 2.47 | 17.61 | 12.76 | 18.58 | 21.18 | 2.51 | 24.89 |
| (% calc.) | (2.55) | (19.35) | (13.52) | (17.45) | (20.35) | (2.98) | (23.63) |
| K1.8 | K | proposed formula: K1.8Co4[Fe(CN)6]3.3□0.7·14 H2O | |||||
| % exp. | 5.46 | 18.76 | 13.86 | 18.36 | 20.53 | 2.34 | 20.69 |
| (% calc.) | (5.59) | (18.74) | (14.65) | (16.84) | (22.05) | (2.24) | (17.81) |
| Na1.3 | Na | proposed formula: Na1.3Co4[Fe(CN)6]3.1□0.9·14 H2O | |||||
| % exp. | 2.47 | 19.54 | 13.82 | 18.94 | 21.62 | 2.35 | 21.26 |
| (% calc.) | (2.54) | (20.06) | (14.73) | (19.01) | (22.17) | (2.40) | (19.06) |
| Na1.8 | Na | proposed formula: Na1.8Co4[Fe(CN)6]3.3□0.7·14 H2O | |||||
| % exp. | 3.02 | 18.55 | 14.60 | 19.06 | 21.54 | 2.19 | 20.04 |
| (% calc.) | (3.37) | (19.18) | (14.98) | (19.35) | (22.56) | (2.29) | (18.23) |
The oxidation states of the metallic cations at 20 K were quantitatively determined by X-ray absorption near edge spectroscopy (XANES) at the cobalt and iron K edges as previously described [25]. The edge spectra of the compounds containing a mixture of CoIII and CoII ions were fairly well reproduced by linear combinations of spectra of two model samples Rb1.8 and C0, respectively composed of a majority of CoIII–FeII and CoII–FeIII pairs at 20 K [27]. Knowing the percentage of CoII and CoIII ions in the models [25, 27], the percentage of CoIII ions in each compound was obtained (Table 2).
Percentage of CoIIIat 20 K, from linear combination of the X-ray absorption spectra of the model compounds Rb1.8 and C0.
| Sample | % CoIII at 20 K |
| C0 | 0 |
| Cs0.3 | 7 |
| Cs0.45 | 14 |
| Cs0.7 | 40 |
| Cs0.95 | 63 |
| Cs1.2 | 66 |
| Cs2 | 82 |
| Rb0.6 | 37 |
| Rb1.3 | 58 |
| Rb1.8 | 82 |
| K0.85 | 62 |
| K1.8 | 66 |
| Na1.3 | 78 |
| Na1.8 | 78 |
2.2 Instrumentation
Photomagnetic experiments were carried out with a Quantum Design MPMS-5S magnetometer working in the dc mode, equipped with a multi-wire silica optical fibre. The fibre was connected to a broadband source of light (tungsten halogen lamp, 100 W), through interferential filters (100-nm bandwidth). A cut-off filter provided a high intensity in the 750 ± 50 nm range. The power received by the irradiated sample is estimated to P = 60 mW cm–2. The measurements were performed over the 10–300-K temperature range with an applied magnetic field of 500 G. In a first step, 3 mg of powder (pellet-shaped) was slowly cooled from 300 to 10 K to avoid quenching phenomena and then irradiated at 10 K during 4 h. The magnetic field was applied as soon as the irradiation began.
The temperature was raised above the Curie temperature and decreased again before measurement to get the Field Cooled Magnetisation (FCM) curve over the 10–300 K temperature range. The temperature was then raised above T = 200 K. At that temperature, all the samples relaxed and came back to their initial ground state, which allows us to measure then the magnetisation before irradiation (Minitial) over the 10– 300-K temperature range. To compare the samples, the amount of compound and the procedure were exactly the same. Excepted for the sodium derivatives, we checked that the wavelength range used for irradiation was the most efficient one.
Energy-dispersive X-ray diffraction patterns were recorded at 10 K over the 0.5–70 keV energy range on the DW11A energy-dispersive X-ray beam of the DCI ring of the LURE synchrotron facility at Orsay, France. The orientation of the detector was fixed at Θ = 5.8457° for compound Cs0.7 and Θ = 4.003° for compound Na1.8. The orientation was checked by measuring the X-ray pattern of a copper foil at room temperature. For the measurements, the powders were spread on between two tapes and slowly cooled from 300 to 10 K. At low temperature, the white X-ray beam induces the CoIII(LS)–FeII(LS) → CoII(HS)–FeIII(LS) photo-induced electron transfer. The X-ray source being the probe beam as well as the pumping beam makes sure that the whole diffracting sample is irradiated.
The study of the photo-excitation process was carried out at 10 K under continuous irradiation. X-ray powder diffraction patterns were recorded for increasing irradiation times (Figs. 2 and 3). For the first point, the acquisition time was 15 s. For subsequent points, the acquisition time was 30 s. During this time interval, the pattern change can be neglected. For clarity, the diffractograms in Figs. 2 and 3 are presented in the energy range containing the two most intense reflections.
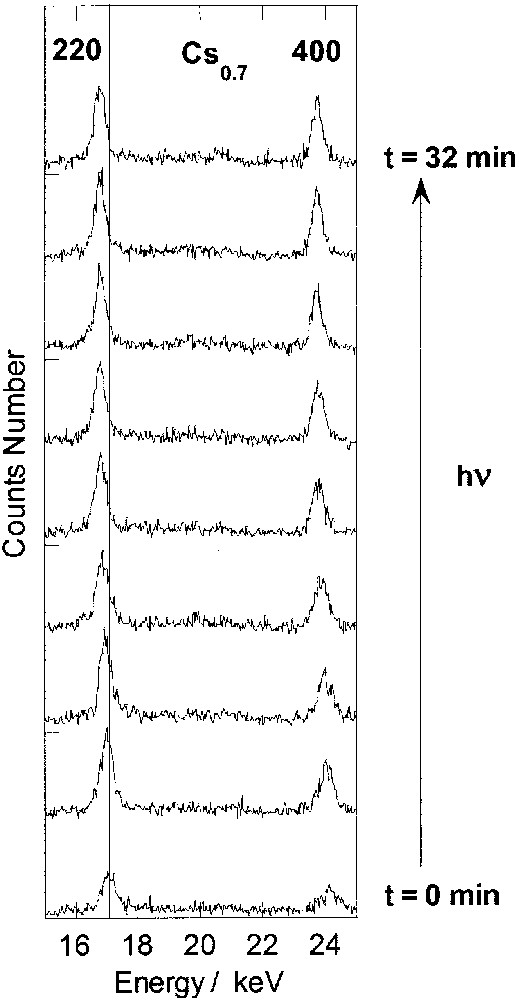
Energy-dispersive X-ray diffraction patterns recorded at 10 K for increasing irradiation time in compound Cs0.7 (220 and 400 reflections).
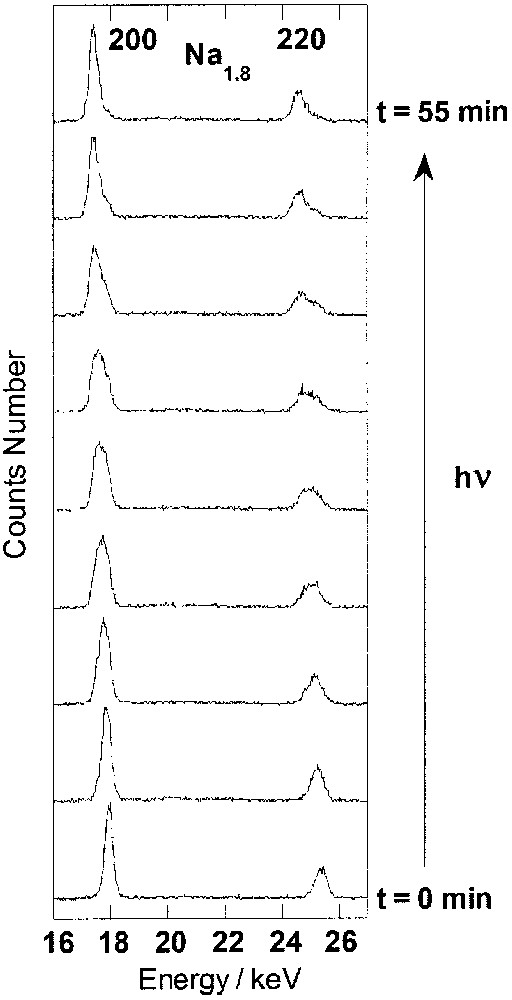
Energy-dispersive X-ray diffraction patterns recorded at 10 K for increasing irradiation time in compound Na1.8 (200 and 220 reflections).
3 Results and discussion
In order to identify the parameters of the system responsible for the photomagnetism, we first studied the photomagnetic properties of a series of CsxCo4[Fe(CN)6](8+x)/3□(4 –x)/3 compounds in which we varied the amount of cesium cations. In a second step, we studied the photomagnetic properties of other alkali derivatives, CxCo4[Fe(CN)6](8+x)/3□(4–x)/3, varying the nature of the alkali cation (C = Rb, K, Na), which were then compared to those of the first series.
3.1 Photomagnetism of the cesium derivatives
The photomagnetic properties of cesium derivatives were already discussed in a previous paper [25]. We showed that the photomagnetic effect depends on a compromise between the number of CoIII–FeII diamagnetic pairs and the network flexibility. Since then, the series has been completed and enables us to go further in the conclusions.
The magnetisation curves of compounds Cs0.3–Cs0.7 before and after irradiation over the 10–30-K temperature range are presented in Fig. 4. These compounds contain less than one alkali cation per cell. The corresponding magnetisation curves for compounds Cs0.95–Cs2, with one alkali cation per cell or more, are given in Fig. 5. The change in the photomagnetic properties along the series of caesium derivatives is discontinuous. The discontinuity appears around x = 1.
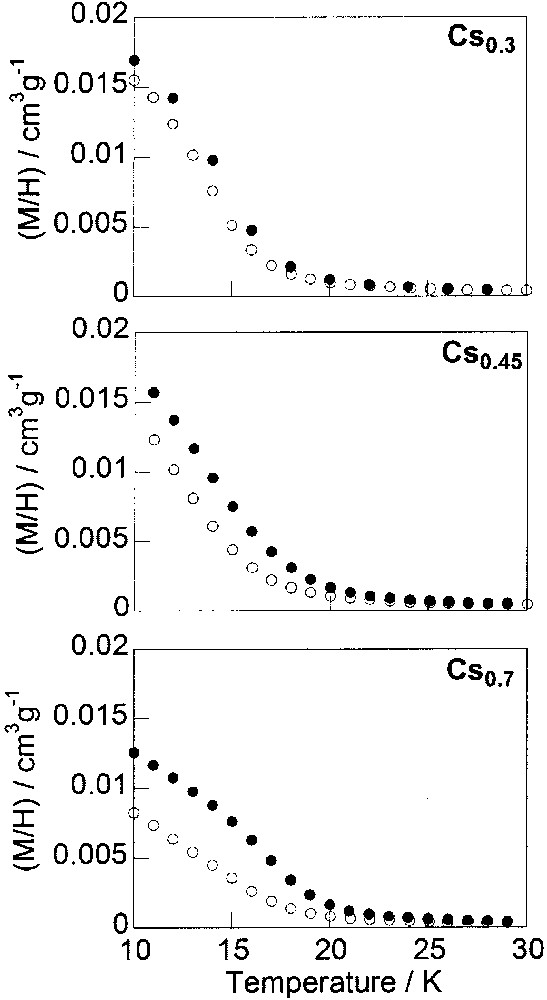
Thermal variation of the reduced magnetisation (M/H) per gram of compounds Cs0.3, Cs0.45 and Cs0.7 over the 10–30-K temperature range before (□) and after (•) irradiation.
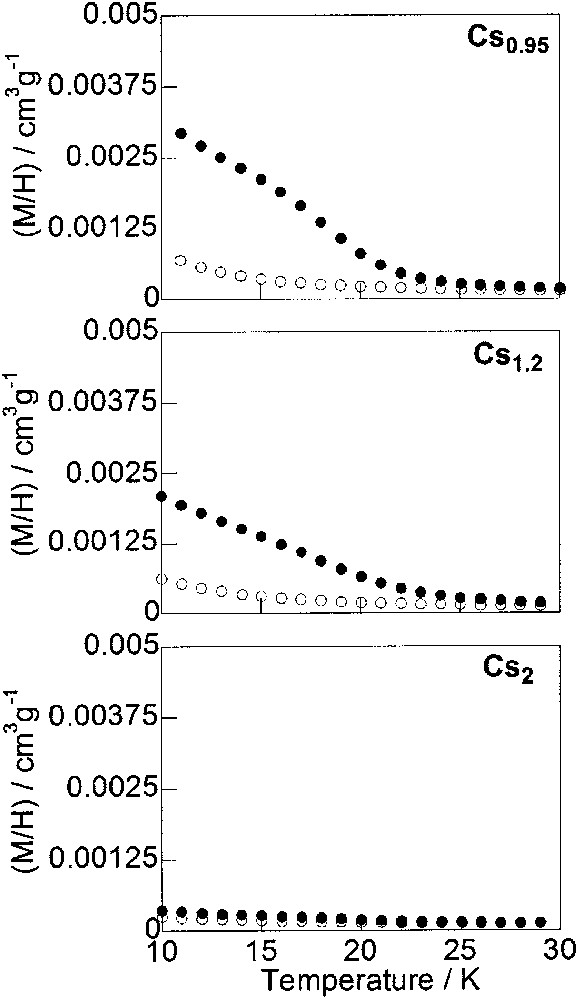
Thermal variation of the reduced magnetisation (M/H) per gram of compounds Cs0.95, Cs1.2 and Cs2 over the 10–30-K temperature range before (○) and after (•) irradiation.
Before irradiation, Cs0.3 is already ferrimagnetic, with a Curie temperature TC = 17 K [25] (Fig. 4), in agreement with the weak amount of diamagnetic pairs at 20 K (Table 2). After irradiation, the magnetisation at 10 K and TC slightly increase which means that the number of magnetic neighbours increases in the ferrimagnetic phase after irradiation. CoIII–FeII isolated diamagnetic pairs are photo-transformed into metastable (CoII–FeIII)* magnetic ones.
As the amount of cesium increases in the compounds [Cs0.45–Cs0.7], the initial magnetization at 10 K decreases. The Curie temperature also decreases, which means that the number of paramagnetic neighbours is decreasing in the sample. However, the magnetisation and the Curie temperature after irradiation at 10 K are approximately the same in the three compounds, close to the ones of the alkali cation free sample. CoIII–FeII isolated diamagnetic pairs are nearly all photo-transformed into metastable (CoII–FeIII)* magnetic ones. The determining factor of photomagnetism is the number of diamagnetic pairs present at low temperature before irradiation.
Cs0.95 is weakly paramagnetic before irradiation (Fig. 5) in agreement with the important amount of CoIII–FeII diamagnetic pairs at low temperature before irradiation (Table 2). After irradiation, the compound becomes ferrimagnetic below a Curie temperature slightly above the ones of the previous compounds (Cs0.3–Cs0.7), but the magnetisation at 10 K is far less than the magnetisation at 10 K in the three previous compounds. The Curie temperature being proportional to the amount of magnetic neighbours, its value in irradiated Cs0.95 shows that the photo-induced ferrimagnetic phase is mainly composed of CoII–FeIII* metastable pairs and not of CoII–FeIII* pairs diluted in CoIII–FeII diamagnetic ones, which would lead to a lower Curie temperature. The magnetisation at 10 K far less than in the previous compounds indicates that only limited domains of diamagnetic CoIII–FeII pairs are photo-transformed into limited domains of metastable (CoII–FeIII)* magnetic pairs. When the amount of alkali cations increases (Cs1.2–Cs2), the magnetisation curve before irradiation is approximately the same for these two compounds in agreement with a same amount of diamagnetic pairs at low temperature (Table 2). Only the magnetisation curves after irradiation varies. As the amount of alkali cation increases, the magnetisation at 10 K after irradiation progressively decreases accompanied by a progressive loss of the magnetic order. However, the Curie temperature of the ferrimagnetic contribution remains close to the one of all the other compounds which indicates again the formation of domains mainly composed of CoII–FeIII* pairs. The small magnetisation value at 10 K is due to the limited number and/or size of the photo-induced CoII–FeIII* domains. We ascribe the loss of photomagnetic properties to the rigidity of the inorganic network. The rigidity prevents the lengthening of the cobalt–ligand bonds (about 0.15 Å) accompanying the photo-induced electron transfer from Co(III)(low spin)–Fe(II)(low spin) to Co(II)(high spin)– Fe(III)(low spin) and the single occupancy of the two antibonding eg* orbitals of cobalt(II) [12, 25]. The increase of the rigidity of the network is related to the increasing number of [Fe(CN)6] filling the vacancies when the amount of alkali cations increases. It may also be related to the number and to the size of cesium cations since their interactions with the Co4[Fe(CN)6](8+x)/3 network may rigidify the structure. To summarize, for the compounds containing more than one alkali cation per cell, domains of diamagnetic CoIII–FeII pairs are photo-transformed into domains of metastable (CoII–FeIII)* magnetic entities. Photomagnetism is limited by the network flexibility.
The study evidences a discontinuity of the photomagnetic properties around x = 1. This discontinuity around x = 1 is not specific to the photomagnetic properties of the compounds. It also appears in the number of diamagnetic pairs per cell for example. When x < 1, the amount of diamagnetic pairs per cell is proportional to the number of alkali cation per cell. It is no more the case for x ≥ 1 (Table 2). The stoichiometry C1Co4[Fe(CN)6]3□1 (x = 1) is very particular. For this stoichiometry, the number of alkali cation and the number of [Fe(CN)6] vacancies per cell are exactly the same. For x < 1, the alkali cations are diluted, whereas the vacancies are concentrated in the compounds. The flexibility is important so that the determining factor is the number of diamagnetic pairs. For x > 1, on the contrary, the alkali cations are now concentrated, whereas the vacancies are diluted in the compounds and the determining factor becomes the network flexibility.
3.2 Photomagnetism of other alkali cations derivatives
To compare the photomagnetic properties of cesium and other alkali cations derivatives, it is necessary (i) to get CxCo4[Fe(CN)6](8+x)/3 compounds with exactly the same amount x of different alkali cations C and (ii) to quantitatively determine the amount of photo-transformed pairs. In order to compare the photomagnetic properties of the compounds, we define the photomagnetic efficiency E as (Mfinal – Minitial)/Minitial (Minitial and Mfinal are the magnetisations at 10 K before and after irradiation respectively). This so-defined E evidently involves a part related to the pure photo-excitation effect, i.e. the creation of magnetic pairs and a part related to the magnetic response of the sample to the external field. In magnetically ordered phase, the magnetic response depends on the applied magnetic field in a non-linear way. In the present study, we propose to use E to compare, in the same experimental conditions, the photomagnetic response of compounds CxCo4[Fe(CN)6](8+x)/3. For a given value of x, only the nature of C varies. If the photomagnetic properties do not depend on the nature of C, very close values of E are expected. On the contrary, if the photomagnetic properties depend on the nature of C, different value of E will arise. The photomagnetic efficiency E is reported in Fig. 6 versus the amount of alkali cations per cell for all the compounds.
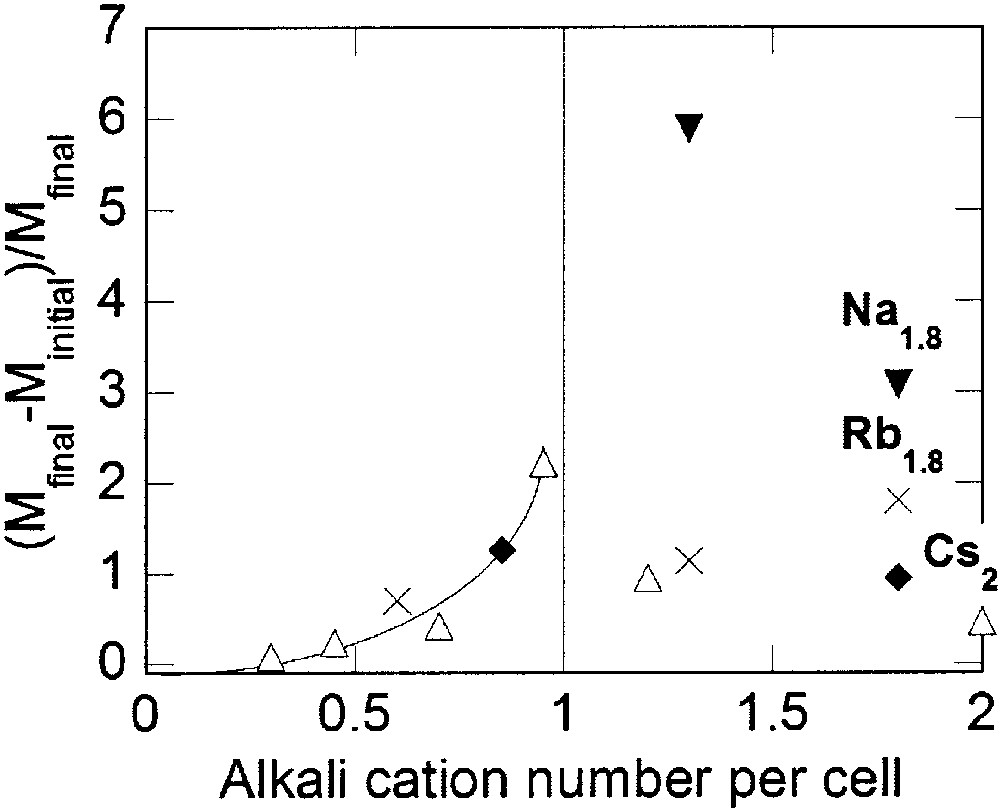
Photo-efficiency E = (Mfinal – Minitial)/Minitial, at 10 K of the Cs (Δ), Rb (×), K(♦) and Na (▾) derivatives vs alkali-cation content per unit cell.
When the amount of alkali cation per cell is less than one (x < 1), E increases with the amount of alkali cations, independently of the alkali cation nature. As along the caesium derivatives series, the amount of CoIII–FeII diamagnetic pairs increases with the amount of alkali cations per cell. For close values of x, the number of diamagnetic pairs at 20 K before irradiation is also close and independent on the nature of the alkali cation (Table 2). The CoIII–FeII isolated diamagnetic pairs are photo-transformed into metastable (CoII–FeIII)* magnetic ones. The inorganic network contains a large number of [Fe(CN)6] vacancies (> 1 per cell) and few alkali cations (< 1 per cell). It is flexible enough to allow the photo-transformation of nearly all the diamagnetic pairs. Like in the case of the caesium derivatives, the photomagnetism is a compromise between the number of diamagnetic pairs and the network flexibility. The determining factor is the number of diamagnetic pairs existing at low temperature before irradiation.
When the amount of alkali cations per cell is larger than one (x ≥ 1), E presents a much more complex variation, not only with the amount, but also with the nature of the alkali cation. This behaviour underlines that numerous parameters are involved in the photomagnetic properties. For a same alkali cation, E decreases with the cation insertion rate x, as in the caesium derivatives series. The decrease is due to the structural flexibility loss. It is noticeable that the ratios E of the compounds Na1.8, Rb1.8 and Cs2, which contain the same amount of diamagnetic pairs at low temperature before irradiation and have very close stoichiometries (i.e., the same amount of [Fe(CN)6] vacancies and the same average cobalt ion coordination sphere), are very different: E decreases when the size of the alkali cation increases. The result emphasizes the role of the alkali cation on the network flexibility for a constant number of the [Fe(CN)6] vacancies. To be brief, the bigger the cation is, the less flexible the structure is.
3.3 Structural transformation of the Cs0.7 and Na1.8 derivatives under irradiation
To go further in the understanding of the photo-excitation process, two compounds were selected for X-ray diffraction under continuous irradiation at 10 K: Cs0.7 with x < 1 contains a rather high amount of diamagnetic pairs at low temperature, whereas Na1.8 with x > 1 still presents enough network flexibility. The diffraction patterns are shown for increasing irradiation times in Fig. 2 for Cs0.7 and in Fig. 3 for Na1.8.
At 10 K, at the very beginning of irradiation, the patterns of both compounds are characteristic of a unique fcc phase.
For Cs0.7, during the excitation process, only one peak appears for each reflection. When the irradiation time increases, the peaks are shifted towards lower energy. After fitting the peaks to a Gaussian line shape, it is possible to conclude that there is no significant line width or intensity change. If two phases with different cell parameters were existing, the line would be broadened. The cell parameter increases. The behaviour is characteristic of a continuous second order transformation within the same phase. CoIII–FeII diamagnetic pairs with short Co– ligand bonds are locally photo-transformed into (CoII–FeIII)* pairs with long Co– ligand bonds within the same crystallographic phase. This structural observation is in agreement with the conclusions of the photomagnetic study. The initially ferrimagnetic phase remains ferrimagnetic, only a few randomly distributed CoIII–FeII diamagnetic pairs with short Co to ligand bonds are locally photo-transformed into (CoII–FeIII)* magnetic ones through a second-order transformation.
Instead, for Na1.8, after 10 min of irradiation, each reflection on the diffraction pattern splits into two peaks. A new peak appears at lower energy, the intensity of which increases with the irradiation time. The changes indicate the appearance and the growth of a new fcc phase with a longer cell parameter. Domains of CoIII–FeII pairs with short Co-ligand bonds are photo-transformed into domains of metastable CoII– FeIII* pairs with long cobalt-ligand bonds. This behaviour is characteristic of a first-order transition, in agreement with the conclusions of the photomagnetic study: limited diamagnetic domains mainly composed of CoIII–FeII pairs (with a short cell parameter) are photo-transformed into ferrimagnetic ones, mainly composed of CoII–FeIII* pairs (with a long cell parameter). Na1.8 contains a majority of CoIII– FeII diamagnetic pairs at low temperature before irradiation. Thus, the Co–ligand bond lengthening accompanying the photo-induced electron transfer leads to strong elastic interactions between the excitable species and cooperative effects and the structural effects are evidenced by our diffraction data (Fig. 3). The associated magnetic consequences appear in the abrupt spontaneous, first-order transition, with thermal hysteresis observed by Hashimoto et al. [28].
4 Conclusion
The study of the photomagnetic properties of CxCo4[Fe(CN)6](8+x)/3□(4–x)/3 Prussian blues reveals the complexity of the excitation process. Several parameters are implied: (a) the amount of diamagnetic pairs at low temperature before irradiation; (b) the flexibility of the inorganic network linked to the amount of [Fe(CN)6] vacancies; (c) the amount and the nature of the alkali cation.
In the present study we evidenced a discontinuity in the photomagnetic properties change with the insertion rate of alkali cations.
- 1. For compounds with x < 1, the photomagnetism is due to the presence at low temperature of isolated and diluted CoIII–FeII diamagnetic pairs, the number of which increases with the number of alkali cation in the structure. Those diamagneticpairs are locally and nearly totally transformed under irradiation into metastable CoII–FeIII* magnetic ones. The process occurs without crystallinity loss. The structure is flexible enough to allow the lengthening of the Co-ligand bond accompanying the photo-induced electron transfer. The process is a second-order transformation.
- 2. For all compounds with x ≥ 1, a majority of CoIII–FeII diamagnetic pairs is present, but the photomagnetic efficiency strongly depends on the amount and on the nature of the alkali cation. For those compounds, the determining factor of photomagnetism is the flexibility of the inorganic network, which decreases when the amount of alkali cation increases, the amount of [Fe(CN)6] vacancies decreases, and the size of the alkali cation increases.
- 3. Our study points out that sodium derivatives are more efficient than the others and that the most efficient compound among them should be Na1Co4[Fe(CN)6]3□1. It should contain one alkali cation and one vacancy per cell. Then it should be composed of a majority of diamagnetic pairs and should contain enough [Fe(CN)6] vacancies giving a maximum flexibility to the network. The compound has already been synthesized by Hashimoto and co-workers [28] and seems effectively to be the most efficient of the whole CoFe family.
Acknowledgements
We thank Françoise Villain for X-ray absorption spectroscopy at the Co and Fe K edges, François Varret for discussions and access to SQUID magnetometer and the European Community (Grant ERBFMRXCT980181), contract TMR/TOSS (FMRX-CT98-0199) and CNRS (‘Programme Matériaux’) for financial support.



